Theoretical minimal RNA rings mimick molecular evolution before tRNA-mediated translation: codon-amino acid affinities increase from early to late RNA rings

Jacques Demongeot; Hervé Seligmann

doi:10.5802/crbiol.1

Actualités

Theoretical minimal RNA rings mimick molecular evolution before tRNA-mediated translation: codon-amino acid affinities increase from early to late RNA rings
[Des ARNs circulaires possibles chaînons de l’évolution de la traduction médiée par les ARNts : les affinités codons-acides aminés augmentent en fonction de l’ancienneté des ARN circulaires]

Jacques Demongeot ¹ ; Hervé Seligmann ^1,²

¹ Université Grenoble Alpes, Faculty of Medicine, Laboratory AGEIS EA 7407, Team Tools for e-Gnosis Medical, F-38700 La Tronche, France
² The National Natural History Collections, The Hebrew University of Jerusalem, 9190401 Jerusalem, Israel

Comptes Rendus. Biologies, Volume 343 (2020) no. 1, pp. 111-122.

Résumés

Anglais
Français

Nucleotide affinities for noncovalent interactions with amino acids produce associations between mRNAs and cognate peptides, potentially regulating ribosomal translation. Correlations between nucleotide affinities and residue hydrophobicity are explored for 25 theoretical minimal RNA rings, 22 nucleotide-long RNAs designed in silico to code for each amino acid once after three translation rounds, and forming stem-loop hairpins. This design presumably mimicks life’s first RNAs. RNA rings resemble consensual tRNAs, suggesting proto-tRNA function, predicted anticodon and cognate amino acid. The 25 RNA rings and their presumed evolutionary order, deduced from the genetic code integration order of the amino acid cognate to their predicted anticodon, produces noteworthy associations with several ancient properties of the cell’s translational machinery. Here we use this system to explore the evolution of codon affinity-residue hydrophobicity correlations, assuming these reflect pre-tRNA and pre-ribosomal translations. This hypothesis expects that correlations decrease with genetic code inclusion orders of RNA ring cognates. RNA ring associations between nucleotide affinities and residue hydrophobicities resemble those from modern natural genes/proteins. Association strengths decrease with genetic code inclusion ranks of proto-tRNA cognate amino acids. In silico design of minimal RNA rings didn’t account for affinities between RNA and peptides coded by these RNAs. Yet, interactions between RNA rings and translated cognate peptides resemble modern natural genes. This property is strongest for ancient RNA rings, weakest for recent RNA rings, spanning a period during which modern tRNA- and ribosome-based translation presumably evolved. Results indicate that translation lacking tRNA-like adaptors based on codon-amino acid affinities and the genetic code pre-existed tRNA-mediated translation. Theoretical minimal RNA rings appear valid prebiotic peptide-RNA world models for the transition between pre-tRNA- and tRNA-mediated translations.

Les affinités nucléotidiques des interactions non covalentes avec les acides aminés produisent des associations entre les ARNm et les peptides apparentés, régulant potentiellement la traduction ribosomale. Les corrélations entre les affinités nucléotidiques et l’hydrophobicité des résidus sont explorées pour 25 ARNs circulaires théoriques d’une longueur minimale de 22 nucléotides, conçus in silico pour coder chaque acide aminé une fois et une seule après trois tours de traduction et former des structures « hairpin » (épingle à cheveux) maximales. Cette conception imite vraisemblablement les premiers ARNs de la vie. Les ARNs circulaires ressemblent à des ARNts consensuels, suggérant une fonction de proto-ARNt, mettant en jeu un anticodon prédit et un acide aminé apparenté. Les 25 ARNs circulaires et leur ordre d’évolution présumé, déduits de l’ordre d’intégration dans le code génétique de l’acide aminé apparenté à leur anticodon prédit, montrent des associations remarquables avec plusieurs propriétés anciennes du mécanisme de traduction de la cellule. Ici, nous les utilisons pour explorer l’évolution des corrélations entre hydrophobicité d’un résidu et affinité à son codon, en supposant qu’elles reflètent des propriétés de la traduction pré-ARNt et pré-ribosomique. Cette hypothèse suppose que les corrélations diminuent avec les ordres d’inclusion dans le code génétique du codon apparenté à un ARN circulaire. Les associations entre les affinités des nucléotides et les hydrophobicités des résidus ressemblent à celles existant actuellement entre gènes et protéines. Les forces d’association diminuent avec les rangs d’inclusion dans le code génétique des acides aminés apparentés au proto-ARNt. La conception des ARNs circulaires minimaux ne tient pas compte des affinités entre ceux-ci et les peptides qu’ils codent. Cependant, les interactions entre les ARNs circulaires et leurs peptides apparentés ressemblent à celles observées pour les gènes naturels actuels. Cette propriété est plus forte pour les ARNs circulaires anciens et plus faible pour les récents, couvrant une période au cours de laquelle la traduction moderne à base d’ARNts et de ribosomes a probablement évolué. Les résultats indiquent que la traduction usant d’adaptateurs fondés sur les affinités codon-acide aminé et sur le code génétique primitif a préexisté à une traduction médiée par l’ARNt. Les ARNs circulaires minimaux théoriques apparaissent ainsi comme des modèles prébiotiques pour la transition entre les traductions à médiation pré-ARNt et ARNt.

Métadonnées

Reçu le : 2019-06-15
Accepté le : 2020-02-21
Publié le : 2020-06-05

PMID

DOI : 10.5802/crbiol.1

Keywords: Secondary structure, Cyclic code, Circular RNAs, Circular code, Nonribosomal translation
Mot clés : Structure secondaire, Code cyclique, ARNs circulaires, Code circulaire, Traduction non ribosomale

Affiliations des auteurs :

Jacques Demongeot ¹ ; Hervé Seligmann ^{1, 2}

Licence :

CC-BY 4.0

Droits d'auteur : Les auteurs conservent leurs droits

@article{CRBIOL_2020__343_1_111_0,
     author = {Jacques Demongeot and Herv\'e Seligmann},
     title = {Theoretical minimal {RNA} rings mimick molecular evolution before {tRNA-mediated} translation: codon-amino acid affinities increase from early to late {RNA} rings},
     journal = {Comptes Rendus. Biologies},
     pages = {111--122},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {343},
     number = {1},
     year = {2020},
     doi = {10.5802/crbiol.1},
     language = {en},
}

TY  - JOUR
AU  - Jacques Demongeot
AU  - Hervé Seligmann
TI  - Theoretical minimal RNA rings mimick molecular evolution before tRNA-mediated translation: codon-amino acid affinities increase from early to late RNA rings
JO  - Comptes Rendus. Biologies
PY  - 2020
SP  - 111
EP  - 122
VL  - 343
IS  - 1
PB  - Académie des sciences, Paris
DO  - 10.5802/crbiol.1
LA  - en
ID  - CRBIOL_2020__343_1_111_0
ER  -

%0 Journal Article
%A Jacques Demongeot
%A Hervé Seligmann
%T Theoretical minimal RNA rings mimick molecular evolution before tRNA-mediated translation: codon-amino acid affinities increase from early to late RNA rings
%J Comptes Rendus. Biologies
%D 2020
%P 111-122
%V 343
%N 1
%I Académie des sciences, Paris
%R 10.5802/crbiol.1
%G en
%F CRBIOL_2020__343_1_111_0

Jacques Demongeot; Hervé Seligmann. Theoretical minimal RNA rings mimick molecular evolution before tRNA-mediated translation: codon-amino acid affinities increase from early to late RNA rings. Comptes Rendus. Biologies, Volume 343 (2020) no. 1, pp. 111-122. doi : 10.5802/crbiol.1. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.5802/crbiol.1/

Version originale du texte intégral (Proposez une traduction )

1. Introduction

Codon-amino acid assignments according to the genetic code are not random [1] because many codon and anticodon properties correlate with properties of cognate amino acids [2, 3, 4]. Numerous analyses indicate the genetic code minimizes error impacts for various processes and properties: mutations on protein structure [5, 6], how proteins fold [7, 8, 9], tRNA misloading by tRNA synthetases [10, 11, 12, 13], frameshifts during translation before and after these occur (before occurrence [14, 15, 16, 17], after occurrence [18, 19, 20, 21, 22, 23]). The genetic code maximizes the diversity of physicochemical properties of coded amino acids [24, 25] and optimizes error according to several properties at the same time [1].

1.1. Genetic code evolution

Numerous hypotheses on inclusion orders of amino acids in the genetic code have been deducted from different properties and experiments. These hypotheses predict orders by which amino acids were assigned to codon(s) [26, 27]. Most of these unrelated hypotheses predict congruent orders, justifying a consensual order of amino acid inclusion in the genetic code [26, 27]. Ulterior analyses produced genetic code inclusion orders that converge with these amino acid inclusion ranks. The average position of amino acid types in modern proteins correlates with these inclusion ranks. The mean position of ancient amino acids is closer to the protein C-terminus, recently included amino acids are on average closer to the protein N-terminus, which corresponds to the gene’s 5’ extremity with the initiation/start codon [28].

1.2. Stereochemical genetic code codon-amino acid assignments

This shows that structures of modern biomolecules embed fossilized information on the origins of life. Indeed, ribosome X-ray crystal structures show that contacts between ribosomal RNA nucleotide triplets and ribosomal protein residues favor amino acid-codon/anticodon assignments. Amino acids that integrated early the genetic code favor contacts with their codons, late amino acids favor contacts with their anticodons [29]. This shows two different steps during the formation of the genetic code: (1) an adaptor/tRNA-free translation where codons interacted directly with amino acids, and (2) tRNA-based translation. Both results confirm, at the level of ribosomal structure, the hypothesis that (at least some of) the genetic code’s assignments result from nucleotide-amino acid affinities due to stereochemical interactions.

The importance of stereochemical interactions is not surprising, as these also determined homochirality of life’s major molecules, right-handed RNA (R-RNA) and left-handed amino acids (L-amino acids), which interact better when these have opposite handedness [30, 31, 32, 33, 34]. The first step in genetic code evolution deduced from ribosomal crystal structures suggests direct codon-amino acid stereochemical interactions. This is in line with observations that in most mRNAs, nucleotide affinities for amino acids correlate with amino acid polar requirements [35, 36, 37]. These observations imply that frequencies of observed contacts between nucleotides and amino acids, from which nucleotide-amino acid affinities are deduced, are approximated by the amino acid hydrophobicity, as these interactions are broadly spoken hydrophobic interactions. This implies that genetic code assignments resulted from stereochemical interactions before proto-tRNAs switched from their function as initiators of RNA/DNA polymerizations [38, 39] to their main modern function in translation. Translations by direct codon-amino acid interactions are in line with a primordial peptide-RNA world, rather than a primordial RNA world [40].

1.3. Theoretical minimal RNA rings as models for the primitive RNA world

Here we study associations between codon affinities for their cognate amino acid and that amino acid’s hydrophobicity, specifically in the context of 25 theoretical minimal RNA rings [41, 42, 43, 44, 45]. These 22-nucleotide long RNAs were designed to code for a start and a stop codon and once for each of the genetic code’s 20 amino acids by three consecutive translation rounds (Figure 1). This ensures maximal coding capacity over the shortest possible length. Their design was also constrained to form a stem-loop hairpin. Independent secondary structure analyses confirmed most theoretical minimal RNA rings resemble proto-tRNAs [44, 45]. A cognate amino acid, in the sense of tRNA acylation, can be assigned to each RNA ring, based on their predicted anticodon sequence [46]. Theoretical RNA rings also fit predictions that circular RNAs had critical roles in the early formation of protogenomes [47]. Most importantly, their design assumes the genetic code’s pre-existence to tRNA-assisted translation. It is of note that some RNA ring secondary structures resemble more rRNAs than tRNAs [46], and that maturation of some modern tRNAs includes circularization [48].

Figure 1.
Translation in three rounds of theoretical minimal RNA ring. Numbers indicate codon order. * indicates stop codon.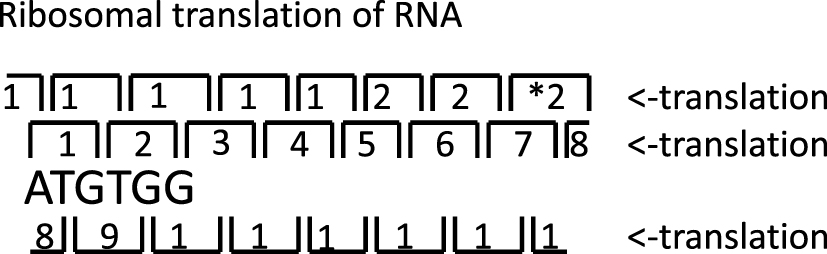

The design of theoretical minimal RNA rings minimizes sequence length and maximizes the diversity of coded amino acids. Circularized tRNAs are intermediates in post-transcriptional modifications of some tRNAs [40]. Circular RNAs regulate gene expression in modern cells [51, 52, 53, 54, 55, 56, 57] and are occasionally translated [58]. They code for proteins with different functions, frequently in muscles of mammals [59]. The assumption of overlap coding is also realistic: artificially designed genes coding over three overlapping frames for three predefined proteins from different protein domains are relatively easy to produce [60]. This fits with observations suggesting that overlap coding is a common property of genes [61, 62, 63, 64, 65, 66, 67, 68, 69]. Indeed, the genetic code is optimized for coding after frameshifts [1, 67, 68, 69].

We expect that associations between RNA ring codon affinities with cognate amino acid hydrophobicity in the peptides coded by the RNA rings resemble those observed in natural modern genes. Two evolutionary scenarios exist in this context. (1) This association appeared spontaneously and, in modern genes, is a carryover from an earlier translation mechanism lacking tRNA and ribosome. In this case its strength should decrease with the genetic code inclusion order of cognate amino acids of RNA rings. (2) This association results from an evolutionary process and reflects processes that still occur in modern cells. According to this scenario, the strength of this association should increase from early to late RNA rings.

2. Materials and methods

We translated the 25 peptides coded by the theoretical minimal RNA rings (Table 1) according to the standard genetic code and estimated the strength of associations between their codon-amino acid affinity and the hydrophobicity of their cognate amino acids forming the peptide. Codon-amino acid affinity is calculated by summing the affinity of single nucleotides forming the codon with the amino acid coded by the codon [35]. These single nucleotide affinities for amino acids are estimated from nucleotide-amino acid contact frequencies in crystal structures of interacting RNA-protein complexes [35].

Table 1.

Minimal RNA rings and corresponding peptide sequences according to regular translations. In column 1, r indicates secondary structures resembling more rRNAs, remaining are more tRNA-like, capitals indicate the presumed cognate amino acid of the RNA ring if considered as a proto-tRNA according to its predicted anticodon. * indicates stop codons. Columns 4 and 5 indicate Pearson correlation coefficients r ×100 between codon-amino acid affinity [35] and amino acid hydrophobicity estimated from distribution equilibria between vapor and aqueous solution (R1, log (RHvap/RHwater), R2, hydration potential, [73])

RNA	AA	CDs	Peptide	R1	R2
1	F	AATTCATGCCAGACTGGTATGA	NSCQTGMKFMPDWYEIHARLV*	−13.0	−13.7
2	M	CATGCCAGAAATTCTGGTATGA	HARNSGMTCQKFWYDMPEILV*	−10.7	−11.8
3	S	ATGGTGCCACTATTCAAGATGA	MVPLFKMNGATIQDEWCHYSR*	−20.9	−15.0
4	Pyl	ATGCTATTCACCAAGATGGTGA	MLFTKMVNAIHQDGECYSPRW*	−13.4	−8.3
5	V	ATGGTGCTACCATTCAAGATGA	MVLPFKMNGATIQDEWCYHSR*	−16.8	−9.7
6	N	ATGGCCTATTCACAAGATGTGA	MAYSQDVNGLFTRCEWPIHKM*	−19.1	−16.8
7	D	ATGCCACTGGTATTCAAGATGA	MPLVFKMNATGIQDECHWYSR*	−19.8	−14.1
8	R	ATGTGGCCTACATTCAAGATGA	MWPTFKMNVAYIQDECGLHSR*	−22.6	−18.6
9	Sec	ATGCCAAGATGGTATTCACTGA	MPRWYSLNAKMVFTECQDGIH*	−19.8	−14.1
10	L	GCAATGTTTATGGAGACCATAA	AMFMETISNVYGDHKQCLWRP*	−25.8	−19.8
11	P	TATGTTTGGAGACCAAGCATAA	YVWRPSMICLETKHNMFGDQA*	−24.4	−18.9
12	E	TTCATGCCAGAAACTGGTATGA	FMPETGMIHARNWYDSCQKLV*	−24.7	−19.7
13	G	ATGGTACTGCCATTCAAGATGA	MVLPFKMNGTAIQDEWYCHSR*	−23.6	−16.0
14	I	GCAGAATGTTTATGGACCATAA	AECLWTISRMFMDHKQNVYGP*	−29.0	−24.2
15	Q	AATATGTTTGGACCAAGCATAG	NMFGPSIEYVWTKHRICLDQA*	−35.7	−34.5
16	L	TATGTTTGGAAGCCAGACATAA	YVWKPDIICLEARHNMFGSQT*	−20.8	−22.7
17	K	TACATTTGGAAGCCAGATGTAA	YIWKPDVMHLEARCNTFGSQM*	−27.1	−27.0
18	S	ACAATGTTTATGGAAGCCATAG	TMFMEAIDNVYGSHRQCLWKP*	−32.9	−37.8
19	A	ATGGAAGCCATTTACAATGTAG	MEAIYNVDGSHLQCRWKPFTM*	−38.4	−38.3
20	W	TACAGATGGAAGCCATTTGTAA	YRWKPFVMQMEAICNTDGSHL*	−27.1	−27.0
21	C	AACATGCCAGATTCTGGTATGA	NMPDSGMKHARFWYETCQILV*	−24.8	−17.7
22	H	TGCCAGAAACATTCTGGTATGA	CQKHSGMMPETFWYDARNILV*	−21.8	−17.7
23	T	TATGGTTCTGCAAGAACCATGA	YGSARTMIWFCKNHDMVLQEP*	−28.2	−17.2
24	Y	TACCATTCTGCAAGAATGGTGA	YHSARMVMPFCKNGDTILQEW*	−21.7	−13.5
25	G	ATGGTGCCATTCAAGACTATGA	MVPFKTMNGAIQDYEWCHSRL*	−19.9	−14.5

These linear sums of affinities of single nucleotides with amino acids produce the same trinucleotide affinity for trinucleotides N1N2N3, N1N3N2, N2N1N3, N2N3N1, N3N1N2 and N3N2N1, though in most cases, these permutations do not code for the same amino acid. Hence this sum of single nucleotide affinities must be considered as an approximation of trinucleotide-amino acid affinities. Nevertheless, biases for codon-amino acid contacts observed in ribosomal crystal structures [29] correlate with these codon affinities calculated by summing single nucleotide affinities (Figure 2). This preliminary observation justifies the linear sum of single nucleotide affinities to approximate codon-amino acid affinities.

Position	Log	Pot
Round 1
1	0.100*	0.101*
2	−0.070*	−0.002*
3	−0.292*	−0.231*
4	−0.290*	−0.265*
5	−0.508*	−0.331*
6	−0.618*	−0.602*
7	−0.697*	−0.697*
Round 2
8	−0.535*	−0.612*
9	−0.333*	−0.321*
10	−0.074*	−0.043*
11	0.006*	−0.067*
12	−0.607*	−0.544*
13	−0.599*	−0.137*
14	−0.063*	−0.260*
Round 3
15	−0.775*	−0.459*
16	−0.116*	−0.116*
17	−0.055*	−0.047*
18	−0.375*	−0.333*
19	−0.380*	−0.433*
20	−0.028*	−0.019*
21	−0.210*	−0.199*
22-stop	n.d.	n.d.

Pearson correlation coefficients r were calculated between codon affinities and several estimates of amino acid polar requirements, experimental and calculated polar requirements [70, 71, 72], two estimates of proportions of accessible versus buried amino acid surfaces in proteins [71, 72], and several estimates of affinities of side chains of amino acids for solvent water [73, 74], other solvents [75, 76] and for water at different temperatures (at 25 ^°C versus 100 ^°C [78]).

3. Results and discussion

3.1. Codon affinity-amino acid hydrophobicity correlations at specific codons

Our first analysis considers each codon across the 25 theoretical minimal RNA rings and calculates the correlation between codon affinity and hydrophobicity for the amino acid coded by each codon. This produces 21 Pearson correlation coefficients r for each estimate of hydrophobicity, for all 21 codon positions coding for an amino acid, and aligned as shown in Table 2. These correlations are expected to reflect those observed for regular mRNAs and their cognate proteins. Affinities are estimated from nucleotide-residue contact frequencies and log-transformed to correspond to contact enthalpies. If affinities are proportional to amino acid hydrophobicities as observed in regular genes, correlations with log-transformed estimates of affinities should produce negative correlations with amino acid hydrophobicities.

Among seventeen different hydrophobicity scales tested, the highest number of positions for which negative associations between codon affinity and amino acid hydrophobicity is 20 among 21 positions, for the scales based on the distribution of equilibria between the dilute aqueous solution and the vapor phase at room temperature (log (RHvap/RHwater), hydration potential [74]). Note that Pro is absent from these scales. Hence the pattern observed in regular mRNAs and proteins (negative correlations) is also observed for most positions in theoretical RNA rings according to these hydrophobicity scales. This majority is statistically significant (P = 0.00001, two tailed sign test) and remains so also after considering test multiplicity, even according to Bonferroni’s overconservative correction (P = 0.05∕17 = 0.002941, which is still higher than P = 0.00001). The overall tendency is weaker when considering other hydrophobicity scales, notably those obtained according to similar equilibria between solvents, but other than water, the natural solvent of biological systems. These are not reported in the following as results were systematically strongest for the scales presented in [74].

This analysis also produces statistically significant correlations at specific codons in RNA rings. All six statistically significant correlations are negative as expected from modern mRNAs and proteins and are located at the transition between each translation round, for amino acids coded by the 6th, 7th, 8th, 12th, 15th, and 19th codons in RNA rings. This would suggest that peptides interact with their template RNA ring at each new translation round. This pattern emerging from theoretical RNA rings is not part of their design, and might reflect properties of RNA-templated, pre-tRNA translation.

Figure 2.
Observed bias for contacts between codon and cognate amino acid in the ribosome crystal structure (Johnson and Lee 2010) as a function of linear sum of single nucleotide affinities for cognate amino acid averaged across all synonymous codons (strong affinities correspond to low values on the x-axis). The correlation (r = −0.605, one tailed P = 0.003) justifies the use of the sums of single nucleotide affinities to approximate codon affinities.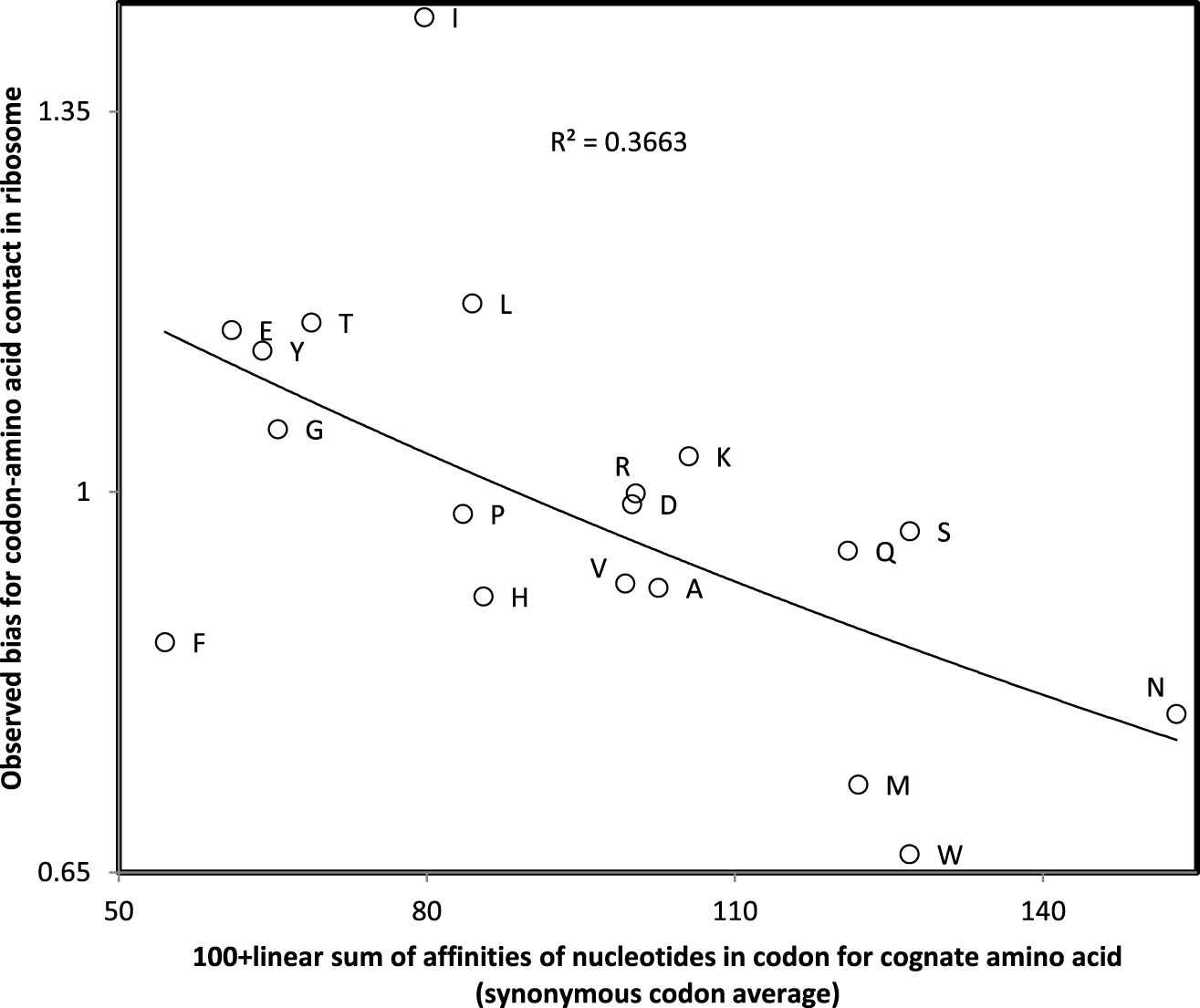

Correlations obtained for hydrophobicity scales estimated from distribution equilibria between neutral solution and cyclohexane at 25 ^°C and 100 ^°C [77] produce less clear patterns. Patterns are slightly stronger at 100 ^°C than 25 ^°C, putatively suggesting that the codon-amino acid associations we observe in modern organisms evolved originally at high temperatures, in line with some previous considerations on origins of life and the genetic code [78, 79, 80, 81, 82].

3.2. Codon affinity-amino acid hydrophobicity correlations for specific RNA rings

Our second analysis tests for correlations between codon affinity and amino acid hydrophobicity (distribution equilibria between the dilute aqueous solution and the vapor phase at room temperature [74]) across codons, for each specific RNA ring (Table 1). All 25 correlations are negative (P < 0.05 for RNA ring 19), a statistically significant majority of cases (P = 0.00000003, two tailed sign test). This means that the association between codon affinity and amino acid hydrophobicity for the 25 RNA rings resembles that observed in modern genes.

3.3. Evolution of associations between codon affinity and amino acid hydrophobicity

Each of the 25 theoretical minimal RNA rings, because of their similarity with consensus tRNA sequences, can be assigned to a cognate amino acid according to their predicted anticodon sequence, assuming a tRNA-like function. Each of these tRNA-cognate amino acids is assigned a rank of inclusion in the genetic code, according to various hypotheses on genetic code inclusion history. Interestingly, and despite that these numerous hypotheses have very different backgrounds, from mathematical (e.g. the natural circular code, [14], the algebraic model [84]), physicochemical (e.g. amino acid yields in experiments mimicking early earth condition [85], amino acid size-complexity [86]) to physiological (e.g. the metabolic coevolution hypothesis [87], the self-referential model [88]), they tend to predict overall congruent histories of genetic code assignments of amino acids (40 hypothetical inclusion orders reviewed in [26, 27]). Some hypotheses are derived from aminoacylating rules of small RNA helices [89, 90] and tRNAs [91], affecting protein folding [9, 92], enabling to define a primordial code in tRNA acceptor stems and an associated order of integration of amino acids in the genetic code.

The inclusion ranks of the RNA ring predicted cognate amino acids are assumed to reflect the history of the theoretical organic system based on these 25 theoretical RNA rings and their cognate peptides (cognate here is used in the sense of the peptide translated from the RNA ring as an ancient template for protein synthesis). We examined the associations of the Pearson correlation coefficients between codon affinity and amino acid hydrophobicity for the 25 RNA rings and the inclusion ranks of their cognate amino acid (cognate is used here in the sense of the amino acid presumably aminoacylated to the RNA ring in relation to its presumed tRNA-like function). The RNA rings with predicted anticodons matching cognate amino acids selenocysteine and pyrrolysine were assigned penultimate and last genetic code inclusion ranks.

Scenario 1 assumes that correlations between codon affinity and amino acid hydrophobicity reflect spontaneous associations that were the physicochemical basis for tRNA- and ribosome-free translation pre-existing modern translation. Along that scenario, codon affinity-amino acid hydrophobicity associations observed today would be remnants of this earlier translation mechanism. Hence Pearson correlation coefficients r between codon affinity and amino acid hydrophobicity of RNA rings are expected to increase (become more positive) with the inclusion rank of the amino acid assigned as proto-tRNA cognate for that RNA ring.

Figure 3.
Pearson correlation coefficient of association between amino acid polar requirement and codon affinity for that amino acid for 25 theoretical minimal RNA rings of 22 nucleotides coding after three translation rounds for a start and stop codon and one codon per amino acid, as a function of the genetic code inclusion order of the presumed cognate amino acid of that RNA ring if considered as a proto-tRNA. The tRNA cognate amino acid is determined by the nucleotide triplet at the predicted anticodon position. The genetic code inclusion order is according to Hartman’s primordial one nucleotide code, assuming G and C were first [93, 94, 95, 96, 97].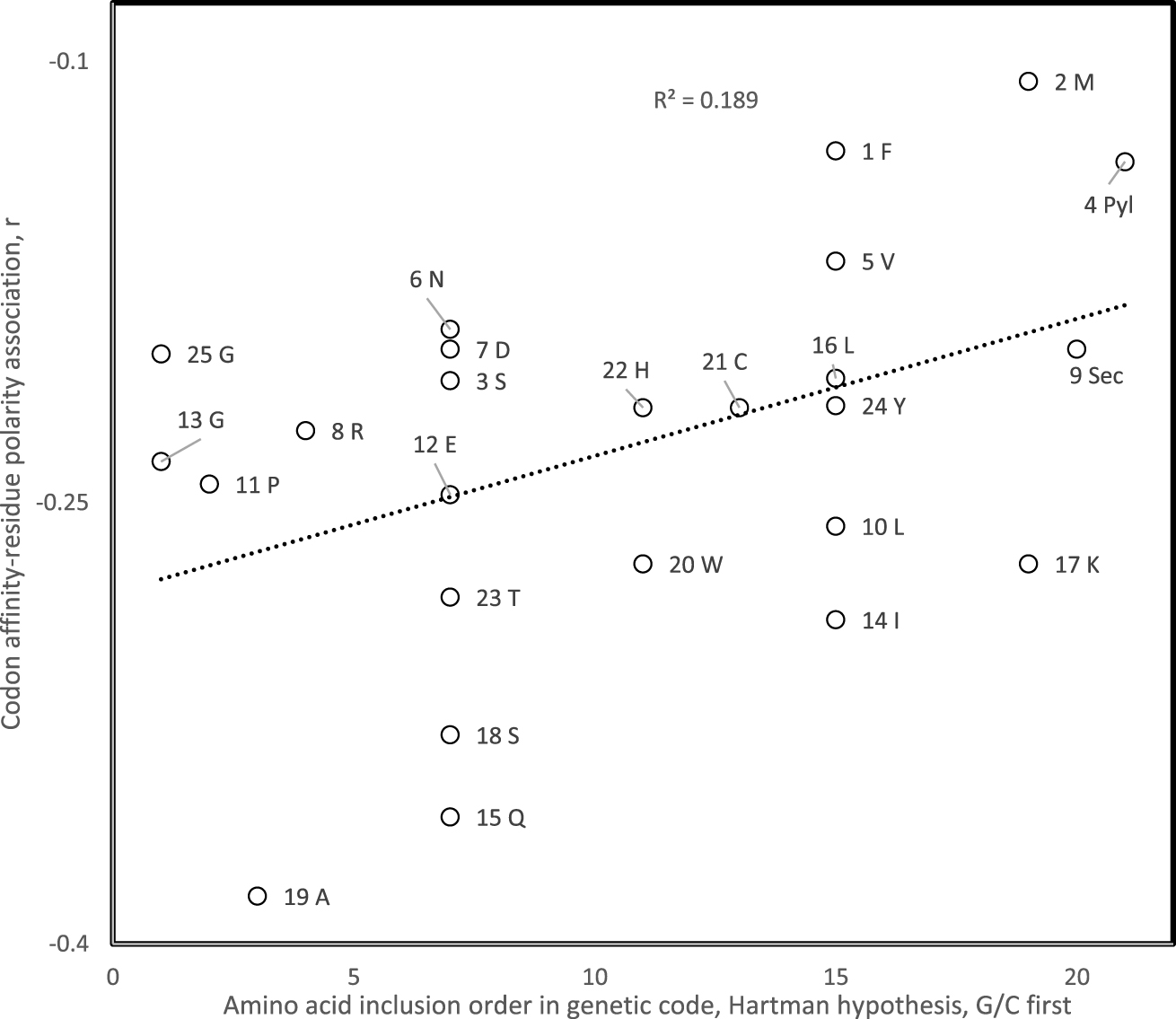

Scenario 2 expects that correlations evolved towards becoming more similar to what is known for extant genes and proteins, which is generally a negative correlation. Hence Pearson correlation coefficients r between codon affinity and amino acid hydrophobicity of RNA rings are expected to decrease (become more negative) with the inclusion rank of the amino acid assigned as proto-tRNA cognate for that RNA ring.

Correlation coefficients r obtained for associations between codon affinities and hydrophobicity estimated from distribution equilibria between vapor and aqueous solution fit scenario 1 for 38 among 40 hypotheses for genetic code evolution of amino acid inclusion orders, a significant majority (P = 8 × 10⁻⁸, two tailed sign test). The correlation with amino acid inclusion order is statistically significant at P < 0.05 for eight specific hypotheses for amino acid inclusion orders. The strongest positive association between the presumed inclusion order of the cognate amino acid of the RNA ring and the codon affinity-hydrophobicity correlation r is for Hartman’s hypothesis that assumes that the genetic code started as a one-letter code, then became a two- and then three-letter code, with G and C as primordial nucleotides (r = −0.43, one tailed P = 0.008, Figure 3) [93, 94, 95, 96]. Hence results are in line with scenario 1 that assumes that codon-amino acid hydrophobicity associations in modern gene-protein pairs are remnants of an ancient tRNA- and ribosome-free translation mechanism based on these physicochemical interactions [98], which de facto would have produced the genetic code codon-amino acid assignments [99].

4. Conclusions

Results of analyses of peptides coded by RNA rings and RNA ring codons indicate that codon-amino acid affinity-amino acid hydrophobicity associations were strongest/most negative for RNA rings assumed most ancient. Accordingly, such associations observed in modern genes and their proteins would be remnants of a more ancient translation mechanism lacking tRNAs and ribosome, based on direct physicochemical interactions between codon and amino acid. Codon-amino acid assignments in the genetic code would have resulted from these direct codon-amino acid interactions [99, 100], which would also explain biases for codon-amino acid contacts in the ribosome ([29], and herein Figure 2).

It is unclear how the design of theoretical minimal RNA rings implies complex evolutionary properties such as associations between codon affinity and cognate amino acid hydrophobicity. However, this system actually mimicks unexpectedly numerous and complex properties of the genetic code [99, 101], tRNAs [43], protein coding genes [102, 103], their proteins [104] and of replication origins [105]. This RNA ring system enables to recover probable evolutionary scenarios of tRNAs and rRNAs [104, 106, 107, 108, 109, 110, 111], and the assignment of AUG as universal initiation codon [112]. The design of RNA rings implies that the genetic code pre-existed the emergence of RNA rings. Hence because RNA rings resemble proto-tRNAs, the genetic code had to exist before tRNAs and proto-tRNAs. The association of codon affinity with hydrophobicity for RNA rings indicates that translation according to the genetic code pre-existed tRNA-mediated translation, potentially along a different codon structure where nucleotides at 1st and 2nd codon positions were switched [113, 114], but also evolved towards the situation observed in modern genes during the evolution of this RNA ring-based primordial RNA system [49, 50, 83]. Theoretical minimal RNA rings are realistic models for the RNA world during the transition from translation based on codon affinity for amino acids and lacking tRNA-like adaptors to tRNA-like mediated translation.

Acknowledgments

Thanks to Charles W. Jr Carter for his important advice on hydrophobicity estimates.

Bibliographie

[1] B. Kumar; S. Saini Analysis of the optimality of the standard genetic code, Mol. Biosys., Volume 12 (2016), pp. 2642-2651 | DOI

[2] C. R. Woese; D. H. Dugre; S. A. Dugre; M. Kondo; W. C. Saxinger On the fundamental nature and evolution of the genetic code, Cold Spring Harb. Symp. Quant. Biol., Volume 31 (1966), pp. 723-736 | DOI

[3] S. R. Pelc; M. G. E. Welton Stereochemical relationship between coding triplets and amino-acids, Nature, Volume 209 (1966), pp. 868-870 | DOI

[4] H. Seligmann; G. N. Amzallag Chemical interactions between amino acid and RNA: multiplicity of the levels of specificity explains origin of the genetic code, Die Naturwissenschaften, Volume 89 (2002), pp. 542-551 | DOI

[5] D. H. Ardell On error minimization in a sequential origin of the standard genetic code, J. Mol. Evol., Volume 47 (1998), pp. 1-13 | DOI

[6] S. J. Freeland; L. D. Hurst The genetic code is one in a million, J. Mol. Evol., Volume 47 (1998), pp. 238-248 | DOI

[7] A. Guilloux; J. L. Jestin The genetic code and its optimization for kinetic energy conservation in polypeptide chains, Biosystems, Volume 109 (2012), pp. 141-144 | arXiv | DOI

[8] B. Caudron; J. L. Jestin Sequence criteria for the anti-parallel character of protein beta-strands, J. Theor. Biol., Volume 315 (2012), pp. 146-149 | DOI

[9] H. Seligmann; G. Warthi Genetic code optimization for cotranslational protein folding: codon directional asymmetry correlates with antiparallel betasheets, tRNA synthetase classes, Comput. Struct. Biotechnol. J., Volume 15 (2017), pp. 414-424 | DOI

[10] H. Seligmann Do anticodons of misacylated tRNAs preferentially mismatch codons coding for the misloaded amino acid?, BMC Mol. Biol., Volume 11 (2010), 13473, 41 pages | DOI

[11] H. Seligmann Error compensation of tRNA misacylation by codon-anticodon mismatch prevents translational amino acid misinsertion, Comput. Biol. Chem., Volume 35 (2011), pp. 81-95 | DOI | Zbl

[12] H. Seligmann Coding constraints modulate chemically spontaneous mutational replication gradients in mitochondrial genomes, Curr. Genomics, Volume 13 (2012), pp. 37-54 | DOI

[13] R. M. Barthélémy; H. Seligmann Cryptic tRNAs in chaetognath mitochondrial genomes, Comput. Biol. Chem., Volume 95 (2016), pp. 119-132 | DOI

[14] D. G. Arquès; C. J. Michel A complementary circular code in the protein coding genes, J. Theor. Biol., Volume 182 (1996), pp. 45-58 | arXiv | DOI

[15] A. Ahmed; G. Frey; C. J. Michel Frameshift signals in genes associated with the circular code, Silico Biol., Volume 7 (2007), pp. 155-168

[16] N. El Houmami; H. Seligmann Evolution of nucleotide punctuation marks: from structural to linear signals, Front. Genet., Volume 8 (2017), 36 pages | DOI

[17] G. Warthi; H. Seligmann Transcripts with systematic nucleotide deletion of 1–12 nucleotide in human mitochondrion suggest potential non-canonical transcription, PLoS ONE, Volume 14 (2019) (e0217356) | DOI

[18] H. Seligmann; D. D. Pollock The ambush hypothesis: hidden stop codons prevent off-frame gene reading, DNA Cell. Biol., Volume 23 (2003), pp. 701-705 | DOI

[19] H. Seligmann Cost minimization of ribosomal frameshifts, J. Theor. Biol., Volume 249 (2007), 1007188, pp. 162-167 | DOI

[20] H. Seligmann The ambush hypothesis at the whole-organism level: off frame, ‘hidden’ stops in vertebrate mitochondrial genes increase developmental stability, Comput. Biol. Chem., Volume 34 (2010), 12818, pp. 80-85 | DOI | Zbl

[21] H. Seligmann Localized context-dependent effects of the “ambush” hypothesis: more off-frame stop codons downstream of shifty codons, DNA Cell. Biol., Volume 38 (2019), pp. 786-795 | DOI

[22] X. Wang; Q. Dong; G. Chen; J. Zhang; Y. Liu; J. Zhao; H. Peng; Y. Wang; Y. Cai; X. Wang; C. Yang; M. Lynch (2016 “The universal genetic code, protein coding genes and genomes of all species were optimized for frameshift tolerance”, bioRxiv, posted Aug 25, 2016, http://dx.doi.org/10.1101/067736)

[23] R. Geyer; M. A. Madany On the efficiency of the genetic code after frameshift mutations, PeerJ, Volume 6 (2018) (e4825) | DOI

[24] G. K. Philip; S. J. Freeland Did evolution select a nonrandom “alphabet” of amino acids?, Astrobiology, Volume 11 (2011), pp. 235-240 | DOI

[25] M. Ilardo; M. Meringer; S. Freeland; B. Rasulev; H. J. Cleaves II Extraordinarily adaptive properties of the genetically encoded amino acids, Sci. Rep., Volume 5 (2015), 9414 pages | DOI

[26] E. N. Trifonov Consensus temporal order of amino acids and evolution of the triplet code, Gene, Volume 261 (2000), pp. 139-151 | DOI

[27] E. N. Trifonov The triplet code from first principles, J. Biomol. Struct. Dyn., Volume 22 (2004), pp. 1-11 | DOI

[28] H. Seligmann Protein sequences recapitulate genetic code evolution, Comput. Struct. Biotech. J., Volume 16 (2018), pp. 177-199 | DOI

[29] D. B. F. Johnson; L. Wang Imprints of the genetic code in the ribosome, Proc. Natl. Acad. Sci. USA, Volume 107 (2010), pp. 8298-8303 | DOI

[30] R. Root-Bernstein Simultaneous origin of homochirality, the genetic code and its directionality, Bioessays, Volume 29 (2007), pp. 689-698 | DOI

[31] X. Han Da; H. Y. Wang; Z. L. Ji; A. F. Hu; Y. F. Zhao Amino acid homochirality may be linked to the origin of phosphate-based life, J. Mol. Evol., Volume 70 (2010), pp. 572-582 | DOI

[32] D. G. Blackmond The origin of biological homochirality, Phil. Trans. R. Soc. Lond. B, Volume 366 (2011), pp. 2878-2884 | DOI

[33] R. Breslow The origin of homochirality in amino acids and sugars on prebiotic earth, Tetrahedron Lett., Volume 52 (2011), pp. 4228-4232 | DOI

[34] C. J. Michel; H. Seligmann Bijective transformation circular codes and nucleotide exchanging RNA transcription, Biosystems, Volume 118 (2014), pp. 39-50 | DOI

[35] A. A. Polyansky; B. Zagrovic Evidence of direct complementarity interactions between messenger RNAs and their cognate proteins, Nucl. Acids Res., Volume 41 (2013), pp. 8434-8443 | DOI

[36] L. Bartonek; B. Zagrovic mRNA/protein sequence complementarity and its determinants: the impact of affinity scales, PLoS Comput. Biol., Volume 13 (2017) (e1005648) | DOI

[37] B. Zagrovic; L. Bartonek; A. A. Polyansky RNA-protein interactions in an unstructured context, FEBS Lett., Volume 592 (2018), pp. 2901-2916 | DOI

[38] N. Maizels; A. M. Weiner Phylogeny from function: evidence from the molecular fossil record that tRNA originated in replication, not translation, Proc. Natl. Acad. Sci. USA, Volume 91 (1994), pp. 6729-6734 | DOI

[39] H. Seligmann Swinger RNA self-hybridization and mitochondrial non-canonical swinger transcription, transcription systematically exchanging nucleotides, J. Theor. Biol., Volume 399 (2016), pp. 84-91 | DOI

[40] P. R. Wills; C. W. Carter Jr Insuperable problems of the genetic code initially emerging in an RNA world, Biosystems, Volume 165 (2018), pp. 155-166 | DOI

[41] J. Demongeot Sur la possibilité de considérer le code génétique comme un code à enchaînement, Rev. Biomaths, Volume 62 (1978), pp. 61-66

[42] J. Demongeot; J. Besson Genetic-code and cyclic codes, C. R. Acad. Sci. III, Volume 296 (1983), pp. 807-810 | arXiv

[43] J. Demongeot; J. Besson Genetic code and cyclic codes II, C. R. Acad. Sc. III, Volume 319 (1996), pp. 520-528

[44] J. Demongeot; A. Elena; G. Weil Potential-Hamiltonian decomposition of cellular automata. Application to degeneracy of genetic code and cyclic codes III, C. R. Biol., Volume 329 (2006), pp. 953-962 | DOI

[45] J. Demongeot; A. Moreira A possible circular RNA at the origin of life, J. Theor. Biol., Volume 249 (2007), pp. 314-324 | DOI

[46] H. Seligmann; D. Raoult Unifying view of stem-loop hairpin RNA as origin of current and ancient parasitic and non-parasitic RNAs, including in giant viruses, Curr. Opin. Microbiol., Volume 31 (2016), pp. 1-8 | DOI

[47] H. Seligmann; D. Raoult Stem-loop RNA hairpins in giant viruses: invading rRNA-like repeats and a template free RNA, Front. Microbiol., Volume 9 (2018), 101 pages | DOI

[48] G. Soslau Circular RNA (circRNA) was an important bridge in the switch from the RNA world to the DNA world, J. Theor. Biol., Volume 447 (2018), pp. 32-40 | DOI

[49] J. Salzman; C. Gawad; P. L. Wang; N. Lacayo; P. O. Brown Circular RNAs are the predominant transcript isoform from hundreds of human genes in diverse cell types, PLoS ONE, Volume 7 (2012) (e30733) | DOI

[50] E. Lasda; R. Parker Circular RNAs: diversity of form and function, RNA, Volume 20 (2014), pp. 1829-1842 | DOI

[51] S. P. Barrett; J. Salzman Circular RNAs: analysis, expression and potential functions, Development, Volume 143 (2016), pp. 1838-1847 | DOI

[52] Y. Zhang; W. Xue; X. Li; J. Zhang; S. Chen; J. L. Zhang; L. Yang; L. L. Chen The biogenesis of nascent circular RNAs, Cell Rep., Volume 15 (2016), pp. 611-624 | DOI

[53] S. Huang; B. Yang; B. J. Chen; N. Bliim; U. Ueberham; T. Arendt; M. Janitz The emerging role of circular RNAs in transcriptome regulation, Genomics, Volume 109 (2017), 104787, pp. 401-407 | DOI

[54] Y. Zhong; Y. Du; X. Yang; Y. Mo; C. Fan; F. Xiong; D. Ren; X. Ye; C. Li; Y. Wang; F. Wei; C. Guo; X. Wu; X. Li; Y. Li; G. Li; Z. Zeng; W. Xiong Circular RNAs function as ceRNAs to regulate and control human cancer progression, Mol. Cancer, Volume 17 (2018), 79 pages | DOI

[55] B. P. Nicolet; S. Engels; F. Aglialoro; E. van den Akker; M. von Lindern; M. C. Wolkers Circular RNA expression in human hematopoietic cells is widespread and cell-type specific, Nucl. Acids Res., Volume 46 (2018), pp. 8168-8180 | DOI

[56] N. R. Pamudurti; O. Bartok; M. Jens; R. Ashwal-Fluss; C. Stottmeister; L. Ruhe; M. Hanan; E. Wyler; D. Perez-Hernandez; E. Ramberger; S. Shenzis; M. Samson; G. Dittmar; M. Landthaler; M. Chekulaeva; N. Rajewsky; S. Kadener Translation of circRNA, Mol. Cell, Volume 66 (2017), pp. 9-21 | DOI

[57] I. Legnini; G. Di Timoteo; F. Rossi; M. Morlando; F. Briganti; O. Sthandler; T. Santini; A. Andronache; M. Wade; P. Laneve; N. Rajewsky; I. Bozzoni Circ-ZNF609 is a circular RNA that can be translated and functions in myogenesis, Mol. Cell, Volume 66 (2017), pp. 22-37 | DOI

[58] V. Opuu; M. Silvert; T. Simonson Computational design of fully overlapping coding schemes for protein pairs and triplets, Sci. Rep., Volume 7 (2017), 15873 pages | DOI

[59] E. Faure; L. Delaye; S. Tribolo; A. Levasseur; H. Seligmann; R. M. Barthélémy Probable presence of an ubiquitous cryptic mitochondrial gene on the antisense strand of the cytochrome oxidase I gene, Biol. Direct, Volume 6 (2011), 56 pages | DOI

[60] H. Seligmann Two genetic codes, one genome: frameshifted primate mitochondrial genes code for additional proteins in presence of antisense antitermination tRNAs, Biosystems, Volume 105 (2011), pp. 271-285 | DOI

[61] H. Seligmann An overlapping genetic code for frameshifted overlapping genes in Drosophila mitochondria: antisense antitermination tRNAs UAR insert serine, J. Theor. Biol., Volume 298 (2012), pp. 51-76 | DOI

[62] H. Seligmann Overlapping genetic code for overlapping frameshifted genes in Testudines, and Lepidochelys olivacea as special case, Comput. Biol. Chem., Volume 41 (2012), pp. 18-34 | DOI | Zbl

[63] H. Seligmann Directed mutations recode mitochondrial genes: from regular to stopless genetic codes, Mitochondrial DNA-New Insights (H. Seligmann; G. Warthi, eds.), IntechOpen, 2018 | DOI

[64] S. Itzkovitz; U. Alon The genetic code is nearly optimal for allowing information within protein-coding sequences, Genome Res., Volume 17 (2007), pp. 405-412 | DOI

[65] X. Wang; X. Wang; G. Chen; J. Zhang; Y. Liu; C. Yang The shiftability of protein coding genes: the genetic code was optimized for frameshift tolerating, PeerJ Preprints, Volume 3 (2015) (e806v1)

[66] R. Geyer; M. A. Madany On the efficiency of the genetic code after frameshift mutations, PeerJ, Volume 6 (2018) (e4825) | DOI

[67] C. R. Woese Evolution of the genetic code, Die Naturwissenschaften, Volume 60 (1973), pp. 447-459 | DOI

[68] R. Wolfenden; L. Andersson; P. M. Cullis; C. C. B. Southgate Affinities of amino acid side chains for solvent water, Biochemistry, Volume 20 (1981), pp. 849-855 | DOI

[69] D. C. Mathew; Z. Luthey-Schulten On the physical basis of the amino acid polar requirement, J. Mol. Evol., Volume 66 (2008), pp. 519-528 | DOI

[70] C. Chothia The nature of accessible and buried surfaces in proteins, J. Mol. Biol., Volume 105 (1976), pp. 1-12 | DOI

[71] J. Janin Surface and inside volumes in globular proteins, Nature, Volume 277 (1979), pp. 491-492 | DOI

[72] R. Wolfenden; P. M. Cullis; C. C. B. Southgate Water, protein folding, and the genetic code, Science, Volume 206 (1979), pp. 575-577 | DOI

[73] A. Radzicka; R. Wolfenden Comparing polarities of the amino acids: side-chain distribution coefficients between the vapor phase, cyclohexane, 1-octanol, and neutral aqueous solution, Biochemistry, Volume 27 (1988), pp. 1664-1670 | DOI

[74] R. Wolfenden Experimental measures of amino acid hydrophobicity and the topology of transmembrane and globular proteins, J. Gen. Physiol., Volume 129 (2007), pp. 357-362 | DOI

[75] M. Di Giulio The late stage of genetic code structuring took place at a high temperature, Gene, Volume 261 (2000), pp. 189-195 | DOI

[76] R. Wolfenden; C. A. Lewis; Y. Yuan; C. W. Carter Jr Temperature dependence of amino acid hydrophobicities, Proc. Natl. Acad. Sci. USA, Volume 112 (2015), pp. 7484-7488 | DOI

[77] M. Di Giulio The universal ancestor was a thermophile or a hyperthermophile: tests and further evidence, J. Theor. Biol., Volume 221 (2003), pp. 425-436 | DOI | Zbl

[78] M. Di Giulio The universal ancestor and the ancestor of bacteria were hyperthermophiles, J. Mol. Evol., Volume 57 (2003), pp. 721-730 | DOI

[79] S. Akanuma; Y. Nakajima; S. Yokobori; M. Kimura; N. Nemoto; T. Mase; K. Miyazono; M. Tanokura; A. Yamagishi Experimental evidence for the thermophilicity of ancestral life, Proc. Natl. Acad. Sci. USA, Volume 110 (2013), pp. 11067-11072 | DOI

[80] N. H. Sleep Geological and geochemical constraints on the origin and evolution of life, Astrobiology, Volume 18 (2018), pp. 1199-1219 | DOI

[81] J. E. M. Hornos; Y. M. M. Hornos Algebraic model for the evolution of the genetic code, Phys. Rev. Lett., Volume 71 (1993), pp. 4401-4404 | DOI

[82] S. L. Miller Production of amino acids under possible primitive earth conditions, Science, Volume 117 (1953), pp. 528-529 | DOI

[83] M. J. Dufton Genetic code synonym quotas and amino acid complexity: cutting the cost of proteins?, J. Theor. Biol., Volume 187 (1997), pp. 165-173 | DOI

[84] J. T. F. Wong A co-evolution theory of the genetic code, Proc. Natl. Acad. Sci. USA, Volume 72 (1975), pp. 1909-1912 | DOI

[85] R. C. Guimarães Self-referential encoding on modules of anticodon pairs - roots of the biological flow system, Life (Basel), Volume 7 (2017), 16 pages

[86] C. Francklyn; K. Musier-Forsyth; P. Schimmel Small RNA helices as substrates for aminoacylation and their relationship to charging of transfer RNAs, Euro. J. Biochem., Volume 206 (1992), pp. 315-321 | DOI

[87] C. W. Carter Jr; R. Wolfenden tRNA acceptor-stem and anticodon bases form independent codes related to protein folding, Proc. Natl. Acad. Sci. USA, Volume 112 (2015), pp. 7489-7494 | DOI

[88] C. W. Carter Jr; P. R. Wills Hierarchical groove discrimination by Class I and II aminoacyl-tRNA synthetases reveals a palimpsest of the operational RNA code in the tRNA acceptor-stem bases, Nucl. Acids Res., Volume 46 (2018), pp. 9667-9683 | DOI

[89] C. W. Carter Jr; R. Wolfenden Acceptor-stem and anticodon bases embed amino acid chemistry into tRNA, RNA Biol., Volume 13 (2016), pp. 145-151 | DOI

[90] H. Hartman Speculations on the evolution of the genetic code, Orig. Life Biosph., Volume 6 (1975), pp. 423-427 | DOI

[91] H. Hartman Speculations on the origin and evolution of metabolism, J. Mol. Evol., Volume 4 (1975), pp. 359-370 | DOI

[92] H Hartman Speculations on the evolution of the genetic code II, Orig. Life Biosph., Volume 9 (1978), pp. 133-136 | DOI

[93] H. Hartman Speculations on the origin of the genetic code, J. Mol. Evol., Volume 40 (1995), pp. 541-544 | DOI

[94] E. N. Trifonov Elucidating sequence codes: three codes for evolution, Ann. N.Y. Acad. Sci., Volume 870 (1999), pp. 330-338 | DOI

[95] M. Yarus The genetic code and RNA-amino acid affinities, Life (Basel), Volume 7 (2017), 13 pages

[96] J. Demongeot; H. Seligmann Spontaneous evolution of circular codes in theoretical minimal RNA rings, Gene, Volume 705 (2019), pp. 95-102 | DOI

[97] H. Seligmann First arrived, first served: competition between codons for codon-amino acid stereochemical interactions determined early genetic code assignments, Naturwissenschaften, Volume 107 (2020), 20 pages | DOI

[98] J. Demongeot; H. Seligmann Pentamers with non-redundant frames: bias for natural circular code codons, J. Mol. Evol., Volume 88 (2020), pp. 194-201 | DOI

[99] J. Demongeot; H. Seligmann More pieces of ancient than recent theoretical minimal proto-tRNA-like RNA rings in genes coding for tRNA synthetases, J. Mol. Evol., Volume 87 (2019), pp. 1-23 | DOI

[100] J. Demongeot; H. Seligmann Bias for 3’-dominant codon directional asymmetry in theoretical minimal RNA rings, J. Comput. Biol. (2019) (doi:10.1089/cmb.2018.0256) | DOI

[101] J. Demongeot; H. Seligmann Theoretical minimal RNA rings recapitulate the order of the genetic code’s codon-amino acid assignments, J. Theor. Biol., Volume 471 (2019), pp. 108-116 | DOI | Zbl

[102] J. Demongeot; H. Seligmann Theoretical minimal RNA rings designed according to coding constraints mimic deamination gradients, Naturwissenschaften, Volume 106 (2019), 44 pages | DOI

[103] J. Demongeot; H. Seligmann The uroboros theory of life’s origin: 22-nucleotide theoretical minimal RNA rings reflect evolution of genetic code and tRNA-rRNA translation machineries, Acta Biotheor., Volume 67 (2019), pp. 273-297 | DOI

[104] J. Demongeot; H. Seligmann Evolution of tRNA into rRNA secondary structures, Gene Rep. (2019) (100483) | DOI

[105] J. Demongeot; H. Seligmann Accretion history of large ribosomal subunits deduced from theoretical minimal RNA rings is congruent with histories derived from phylogenetic and structural methods, Gene, Volume 738 (2020) (144436) | DOI

[106] J. Demongeot; H. Seligmann Comparisons between small ribosomal RNA and theoretical minimal RNA ring secondary structures confirm phylogenetic and structural accretion histories, Sci. Rep., Volume 10 (2020), 7693 pages | DOI

[107] J. Demongeot; H. Seligmann RNA rings strengthen hairpin accretion hypotheses for tRNA evolution: a reply to commentaries by Z. F. Burton and M. Di Giulio, J. Mol. Evol., Volume 88 (2020), pp. 243-252 | DOI

[108] J. Demongeot; H. Seligmann The primordial tRNA acceptor stem code from theoretical minimal RNA ring clusters, BMC Genet., Volume 21 (2020), 7 pages | DOI

[109] J. Demongeot; H. Seligmann Why is AUG the start codon?: theoretical minimal RNA rings: maximizing coded information biases 1st codon for the universal initiation codon AUG, Bioessays (2020) (e1900201) | DOI

[110] H. Seligmann; J. Demongeot Codon directional asymmetry suggests swapped prebiotic 1st and 2nd codon positions, Int. J. Mol. Sci., Volume 21 (2020) (e347) | DOI

[111] J. Demongeot; H. Seligmann Deamination gradients within codons after 1 ↔ 2 position swap predict amino acid hydrophobicity and parallel β-sheet conformational preference, Biosystems, Volume 191–192 (2020) (104116)

[112] A. Soma; A. Onodera; J. Sugahara; A. Kanai; N. Yachie; M. Tomita; F. Kawamura; Y. Sekine Permuted tRNA genes expressed via a circular RNA intermediate in Cyanidioschyzon merolae, Science, Volume 318 (2007), pp. 450-453 | DOI

[113] T. Pan; R. R. Gutell; O. C. Uhlenbeck Folding of circularly permuted transfer RNAs, Science, Volume 254 (1991), pp. 1361-1364 | DOI

[114] A. Gutfraind; A. Kempf Error-reducing structure of the genetic code indicates code origin in non-thermophile organisms, Orig. Life Evol. Biosph., Volume 38 (2008), pp. 75-85 | DOI

Commentaires - Politique

Ces articles pourraient vous intéresser

Aminoglycosides and other factors promoting stop codon readthrough in human cells

Dialo Diop; Céline Chauvin; Olivier Jean-Jean

C. R. Biol (2007)

The genetic code of the fungal CTG clade

Manuel A.S. Santos; Ana C. Gomes; Maria C. Santos; ...

Comptes Rendus. Biologies (2011)

Translation initiation by factor-independent binding of eukaryotic ribosomes to internal ribosomal entry sites

Andrey V. Pisarev; Nikolay E. Shirokikh; Christopher U.T. Hellen

C. R. Biol (2005)