1. Introduction
In 1869, Mendeleev published his original version of the Periodic Table [1]. At that time, only 63 elements were known. They were ordered on the basis of their atomic weights and chemical properties. This fundamental concept, along with the principle of the filling of the electron shells, has become a guiding tool for the search of many new elements, including actinides and transactinides. At the time being, all the elements up to Z = 118 are known, so that the 7th row of the Periodic Table is complete (Figure 1).
Modern Periodic Table of the elements.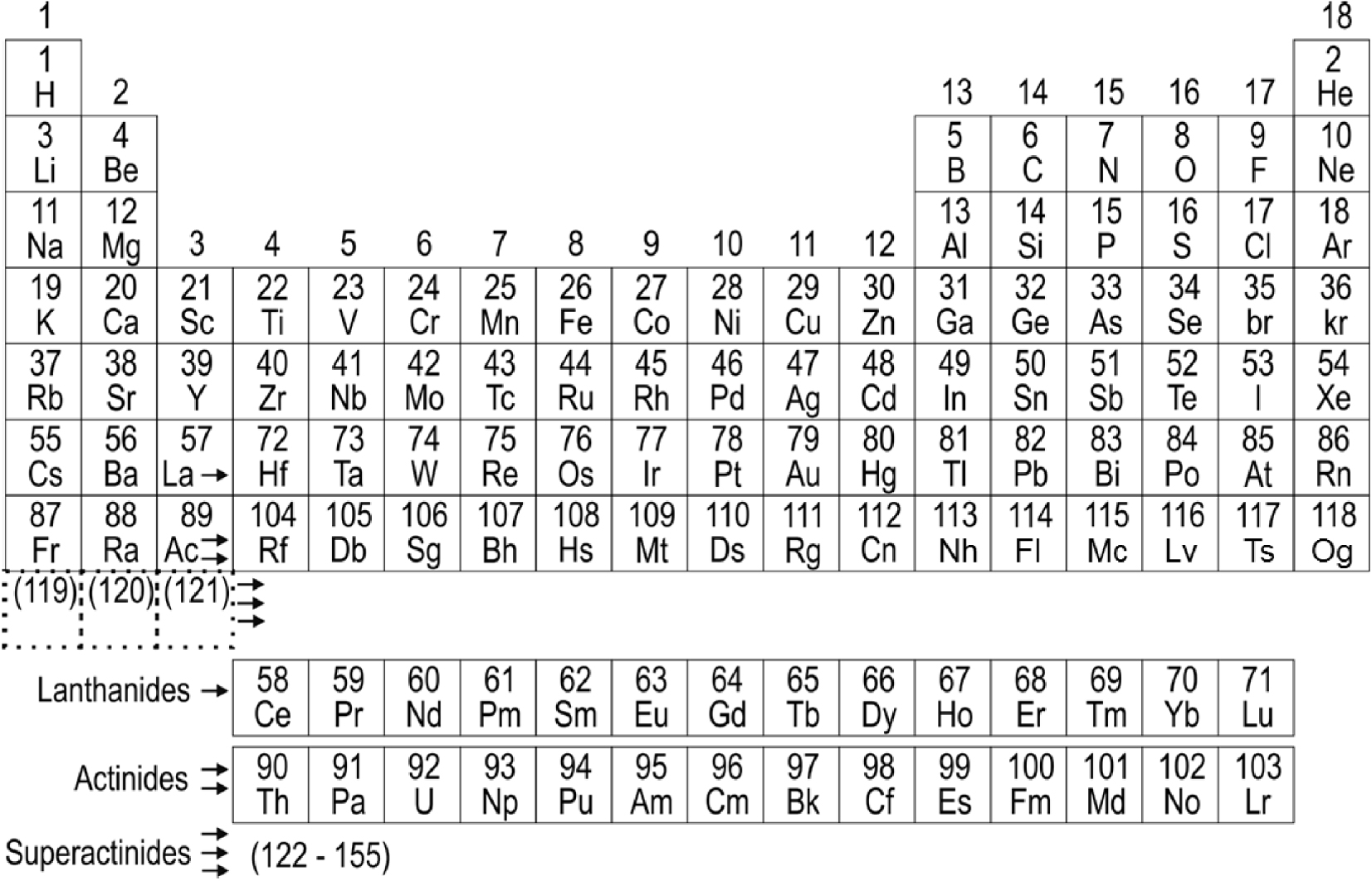
Elements beyond the actinide series, those from Z = 104 and heavier, are called “transactinides”, or superheavy elements (SHEs). They are artificially synthesized “one-atom-at-a-time” in heavy-ion induced nuclear fusion reactions at high-power accelerator facilities. Unique properties of these elements, instability and difficulties associated with their detection and identification make experimental research in this area extremely demanding and challenging. In their turn, nuclear and electronic structure theories are also confronted with problems in describing interactions between the large number of nucleons, as well as electron-nucleus and electron-electron interactions at such high Z numbers. Nevertheless, remarkable achievements have been observed in the area of nuclear physics, nuclear chemistry and relativistic electronic structure theory in the recent years accounting for successful production, identification and studies of physio-chemical properties of the superheavy elements. Recent comprehensive reviews on these topics can be found in Refs. [2, 3, 4, 5, 6, 7, 8].
2. Synthesis and discovery of superheavy elements
Search for superheavy elements started right after the 2nd World War. A fierce competition between the Lawrence Berkeley National Laboratory (LBNL), called at that time Lawrence Radiation Laboratory, USA, and the Joint Institute for Nuclear Research (JINR), Dubna, Russia, led to the discovery of elements 104, 105 and 106 (Figure 2) [9, 10]. After 1980, the priority went to the Gesellschaft für Schwerionenforschung (GSI), Darmstadt, Germany, where construction of the Universal Linear Accelerator (LINUX) was completed in 1975. Six heavier elements, 107 through 112, were synthesized there [11]. At the beginning of the next century, element 113 was created at RIKEN, Japan, using a similar experimental technique [12]. Further technical developments and availability of new ion beam and target materials, enabled Russian scientists at JINR in collaboration with the Lawrence Livermore National Laboratory (LLNL), USA, in the last two decades to successfully synthesize even heavier elements, 114 through 118 [2, 13]. Recently, GSI and RIKEN have attempted to create even heavier elements, 119 and 120, however, unsuccessfully until now [3]. The SHE factory, presently under construction at JINR in Dubna, will be a facility for the SHE production on a much larger scale opening further prospect for their synthesis and studies of physico-chemical properties [2].
The names of elements 104 through 118 have been approved by the IUPAC and IUPAP commissions, with the symbols shown in Figure 1. Two of the elements, 106, Seaborgium, and 118, Oganesson, were named after still living at the time scientists, Professors G. T. Seaborg (LBNL) and Yu. Ts. Oganessian (JINR), paying tribute to their great contribution to the field.
Timeline of discovery of superheavy elements.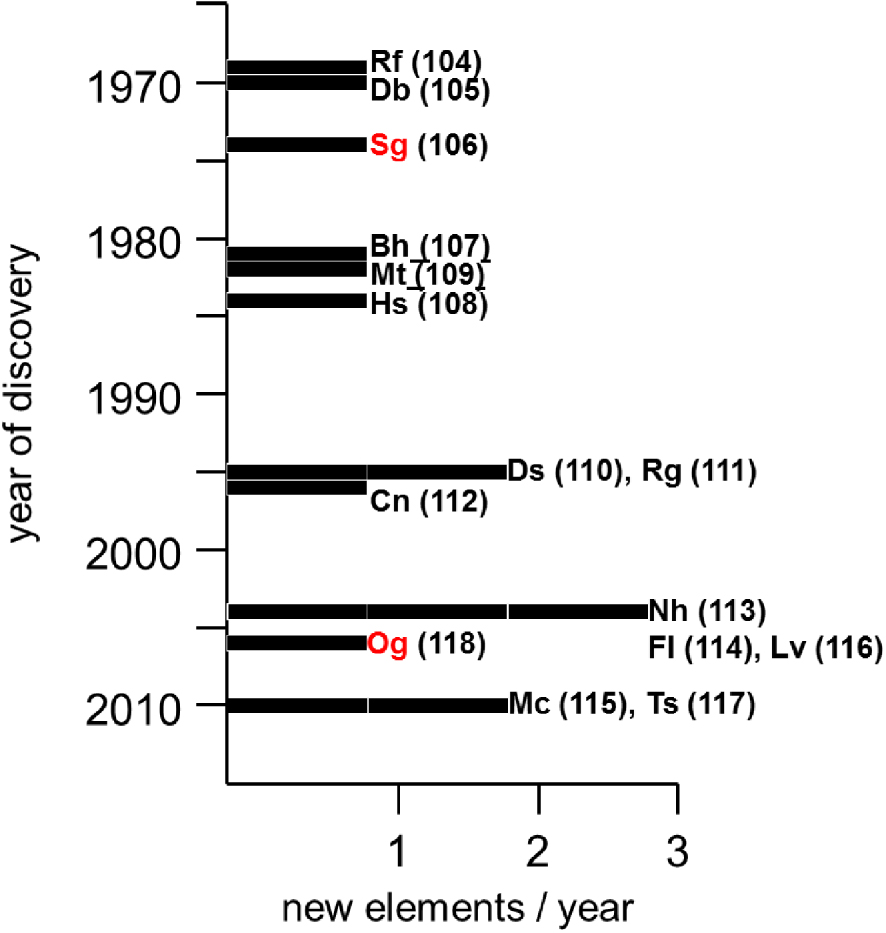
As was already mentioned, elements heavier than U are all man-made. They are produced either in high (neutron) flux nuclear reactors (up to Z = 100), or in accelerator-based nuclear fusion reactions (transfermium ones), or, unexpectedly, in a hydrogen-bomb explosion. There are two main types on the nuclear synthesis reactions that are used in the production of superheavy elements: “cold fusion” and “hot fusion” ones. They differ by a combination of target materials and projectiles (ion beams), as well as by the energy balance between them needed for the nuclear fusion.
The “cold fusion” reactions are characterized by low energy barriers between the two approaching positively charged nuclei, of the order of 10–15 MeV. There, medium-heavy projectiles like 54Cr, 58Fe, 63,64Ni, or 68,70Zn fuse with the 208Pb and 209Bi target nuclei. Elements Rf through Nh were created in such a way at GSI and RIKEN. The isotopes of the elements produced by this type of reactions are usually neutron-deficient and therefore very short-lived, so that they are not suitable for chemical studies. “Hot-fusion” reactions are characterized by high energy barriers between the nuclei, of the order of 40–50 MeV. They proceed with the use of the heavy (actinide) target materials (238U, 242,244Pu, 243Am, 248Cm, 249Cf) and light-ion beams (18O, 22Ne, or 26Mg). Isotopes of the elements produced via this type of reactions are longer-lived and therefore more suitable for chemical studies. Nuclear synthesis reactions utilizing the actinide targets (Pu through Cf) and the 48Ca beam, a magic stable nucleus (Z = 20 and N = 28), were found to significantly enhance production cross-sections of elements with Z > 112 leading to the successful synthesis of Fl through Og at JINR, Dubna [2, 13].
Synthesis of element 119 has been attempted via the 249Bk + 50Ti reaction at GSI and the 248Cm + 51V reaction at RIKEN, and of element 120 via the 244Pu + 58Fe reaction at JINR and the 238U + 64Ni, 248Cm + 54Cr and 249Cf + 50Ti reactions at GSI. These attempts were, however, unsuccessful. The search for these elements is going on [2, 3].
Beside the synthesis, the unambiguous identification is a big problem for SHEs, and only those (till Z = 113) decaying in known daughter products have been identified in a most rigorous way by measuring their α–α decay chains. For heavier elements, decaying in unknown isotopes, or undergoing spontaneous fission, chemistry may play a crucial role in their identification. Chemical experiments have to demonstrate a unique chemical character of the new elements, possibly with characteristic nuclear decay properties, to confirm their position in the right groups of the Periodic Table. In addition, studies of chemical properties of SHEs are of their own invaluable importance [4, 5, 6, 7, 8].
3. Electronic structure and relativistic effects
What do we want to know about the new superheavy elements?
- Are SHEs homologs of the lighter congeners and can be placed in respective chemical groups of the Periodic Table?
- Are periodicities in properties observed in the groups continued with the SHEs?
- How do increasingly important relativistic effects change those periodicities?
- Does the Periodic Table keep its predictive power beyond the 7th row?
- Where is the end of the Periodic Table?
With the development of the electronic structure theory, Schrödinger and Dirac equations, and the principle of Pauli, as well as with experimental determination of electronic configuration, it became clear that the latter, beside the nuclear charge, is lying in the basis of periodicity of the elements’ properties. An empirical rule, known as Madelung’s one, implies that the next electron should fill the (n + l) shell, where n is the principal and l is the azimuthal quantum numbers, respectively. Based on this rule, extension of the Periodic Table beyond the actinides was first suggested by Seaborg in 1968 [14]. He called elements heavier than Z = 121 “superactinides” (Figure 1), assuming also mixing of electronic configurations at the very high Z. However, with the further development of the theory it became clear that the simple Madelung’s rule does not work for the heaviest elements where relativistic effects are of paramount importance and where the “one-electron solution” is not anymore applicable.
As is known, relativistic effect is anything arising from the final speed of light [15]. With increasing nuclear charge, the velocity of the electron near the nucleus increases. As a consequence, its mass increases. Einstein’s equation gives it as
| (1) |
| (2) |
| (3) |
| (4) |
With increasing Z along the Periodic Table, the ratio becomes so large that from the 6th row onwards, the relativistic effects cannot be neglected anymore. For example, for Og, m∕m0 = 1.95. As a result of the relativistic mass increase, the spherically symmetric s and p1/2 atomic orbitals (AOs) are contracted and stabilized, which is called a direct relativistic effect. This effect was shown to originate from the inner K- and L-shell regions. AOs with higher l, i.e., d, f, g, etc., screened by the s and p1/2 AOs from the core, on the contrary, get destabilized and expanded, which is an indirect relativistic effect. The third relativistic effect is spin-orbit (SO) splitting of the AOs with l > 0. All the three effects are known to change approximately as Z2 for the valence shells down a column of the Periodic Table. The np1/2–np3/2 SO splitting reaches 12 eV at the end of the 7th row, and it is about 50 eV for element 164 [16].
As an example, Figures 3 and 4 show relativistic effects on AOs of group-12 elements: the 7s(Cn) AO contraction is 25% (Figure 3) and its stabilization is 5.8 eV (Figure 4), which is the maximum in the group and in the 7th row of the Periodic Table [17]. The 6d3/2–6d5/2 SO splitting in Cn is 3.3 eV, which is also large (Figure 4). For the heavier elements, relativistic effects on their valence orbitals are much more pronounced and could lead to properties very different from those of the lighter homologs.
Relativistic (rel) and non-relativistic (nr) radial charge densities of the 7s AO of Cn.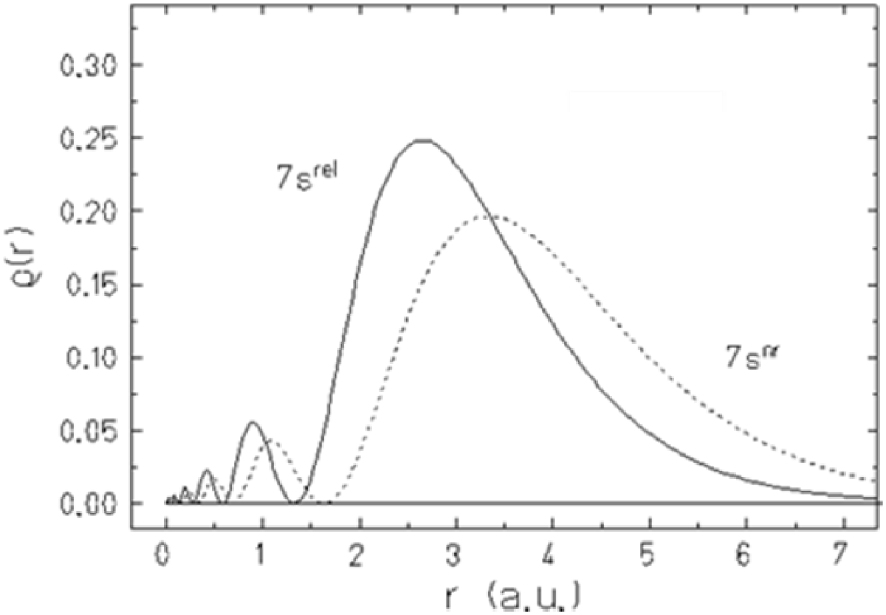
Relativistic Dirac–Fock (solid line) and nonrelativistic (dashed line) energies, E, and the maximum of the radial charge density, Rmax, of the valence AOs of group-12 elements.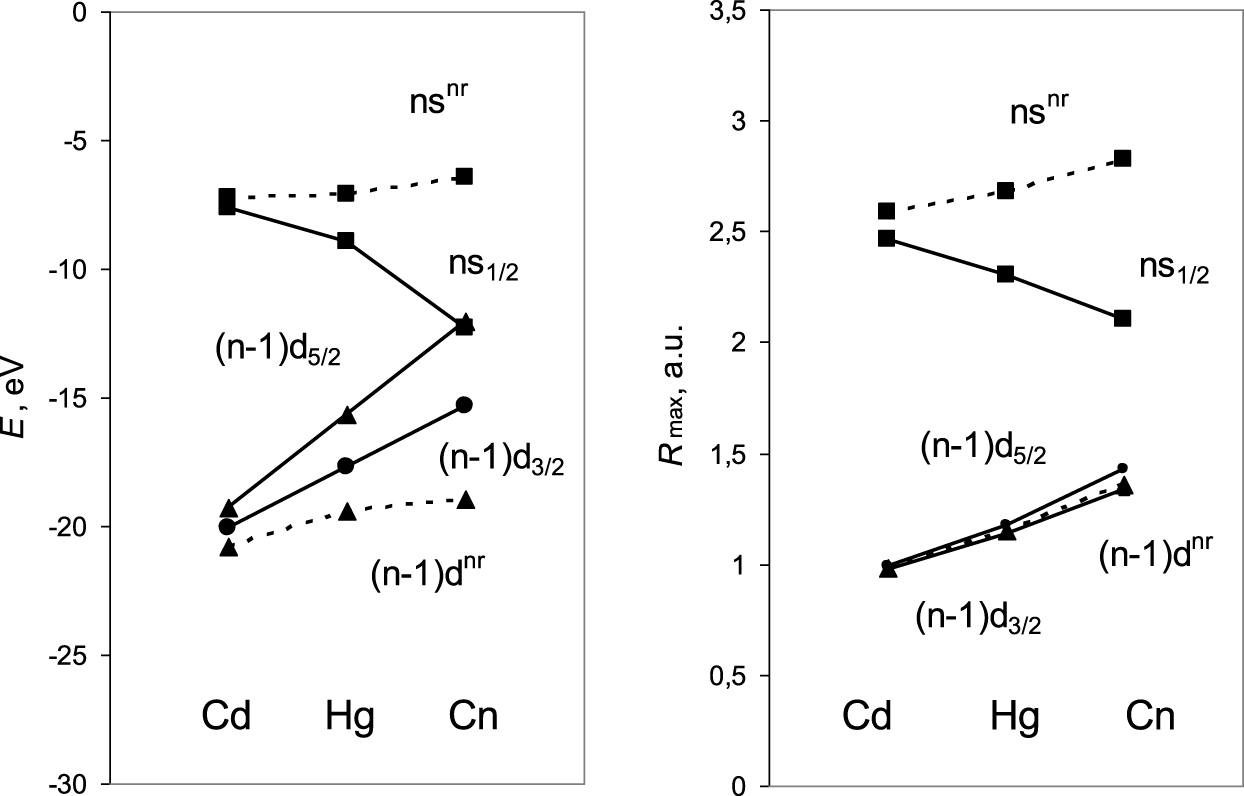
Due to the very high Z, Breit interaction and Quantum Electrodynamic (QED) effects start also to be important for SHEs [18]. They can reach a few % in ionization potentials, or electron affinities (EA) of SHEs and will be important in future high-resolution spectroscopy.
In the last two decades, relativistic quantum theory has remarkably advanced [19]. Modern methods and derived calculational algorithms account presently for relativistic and electron correlation effects in a most rigorous way: both effects were shown to contribute to more than 50% to binding energies and other properties of the heaviest elements. The methods are based on solution of the Dirac–Coulomb–Breit (DCB) equation. They take into account electron correlation and QED effects either self-consistently for atoms, or perturbatively for molecules.
Table 1 demonstrates accuracy of predictions of the ground state electron configurations of Lr and Rf depending on the level of theory: from single-configuration Dirac–Fock (DF) [16], to Multiconfiguration DF (MCDF) [20] and to DCB Coupled Cluster (CC), or Fock-Space CC (FSCC) [21], accounting for electron correlation at the (presently) highest level.
Ground state electron configurations of Lr and Rf obtained from Dirac–Fock, multiconfiguration Dirac–Fock and Dirac–Coulomb–Breit CC calculations
| Element | DF | MCDF | DCB + CC |
|---|---|---|---|
| Fricke, et al. [16] | Desclaux, et al. [20] | Eliav, et al. [21] | |
| (1970) | (1973) | (1996) | |
| Lr | 6d7s2 | 7s27p1/2 | 7s27p1/2 |
| Rf | 6d27s2 | 6d7s27p1/2 | 6d27s2 |
The electronic ground state of Lr(7s27p1/2) thus turned out to be different from that of Lu(6s25d). The relativistic stabilization of the 7p1/2 AO is responsible for such a change. For Rf, early DF predictions [16] were confirmed by the later DCB CC ones: a very high level of correlation was needed to obtain the true 6d27s2 ground state [21]. The 7s2 electron pair was shown then to be present in the ground state configurations of all the 7th row elements. For Og, belonging to the group of the noble gases, the DCB CC calculations have given EA of 0.058 eV [21]. This is also a relativistic effect due to the stabilization of the 8s AO, where an extra electron will fill in.
Element 122 is the heaviest element where accurate DCB CC calculations exist [21]. For heavier elements, the proximity of the valence SO bands makes the search for the ground state configuration very difficult. Table 2 shows that all the calculations generally agree on the ground state of the elements up to Z = 121, but they disagree at Z > 121 [16, 21, 22, 23]. An attempt to find the ground state electron configuration of element 140, as an example, using the MCDF method failed: There are so many configurations with similar energies that it was impossible to find the ground state due to computer limitations at that time [24]. Thus, for elements of the middle of the 8th row, with many closely-lying and mixed states, the usual classification on the basis of a simple electronic configuration, required for the placement of the element in a group of the Periodic Table, becomes problematic.
Ground states of elements 121–124 (Z = 120 core +) and 143 (Z = 120 core + 8p1∕22+)
| Method | 121 | 122 | 123 | 124 … | 143 | Ref. |
|---|---|---|---|---|---|---|
| DF | 8p | 7d8p | 6f7d8p | 6f38p | 5g176f27d2 | [16] |
| MCDF | 8p | 7d8p | 6f28p | 6f28p2 | 5f176f27d2 | [22] |
| DFT | 8p | 8p2 | 6f7d8p | 6f28p2 | - | [23] |
| DCB FSCC | 8p | 7d8p | - | - | - | [21] |
Several attempts have, however, been made in the past to predict the structure of the Periodic Table in this high Z region. As was mentioned, Seaborg designed a Periodic Table till Z = 168, with the 8th period containing 32 “superactinides”, where the filling of the 5g and 6f shells takes place [14]. (He also discussed the evolution of the Periodic Table later taking into account results of available at that time relativistic calculations [25].) Based on the DF calculations, Fricke, et al. have published a Table till Z = 172 [16]. They suggested, however, that the “superactinide” series will be longer, containing 34 elements from Z = 122 through 155, where the filling of the 8p1/2, 7d, 5g and 6f shells takes place. In a recent work based on MCDF calculations of highly charged ions of some elements of the 8th row, Pyykkö suggested that there should be 18 5g-elements from Z = 121 to Z = 138, followed by ten 7d elements from Z = 156 through 164, however, with elements 139 and 140 placed right after them in group 13 and 14, respectively [26]. There are also some other designs of the extended Periodic Table, so that discussions are still going on.
A question about the end of the Periodic Table has also been a subject of a long-standing debate. As is known, with increasing nuclear charge, the relativistic stabilization of the 1s level becomes so large that, within the one-electron Dirac picture, it will have energy less than − 2me c2 (Figure 5). This means that it will dive into the negative energy continuum. This should happen at a critical charge, Zcrit, equal to 173 ± 1 depending on the model (see [18, 24, 27] for details).
1s1/2 AO dependence on nuclear charge Z in the H-like atom. The 1s1/2 shell is diving into the negative energy continuum (−2me c2) at Zcrit.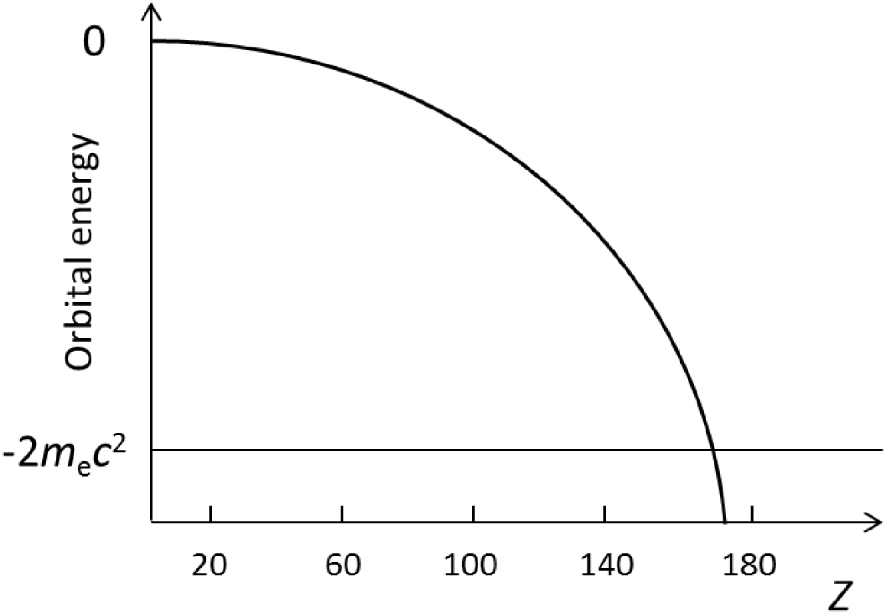
For Z = 172, the [120]5g188p1∕226f147d109s29p1∕22 8p3∕24 closed-shell ground state was obtained from DF calculations [27]. Recent considerations came, however, to the (preliminary) conclusion that beyond the one-electron Dirac picture, there should be no end of the Periodic Table at Z = 172, as there are no numerical or real physical indications that the atomic system become QED unstable. There should be a super-critical regime in atoms [28]. Investigations on this subject are still going on requiring considerations beyond standard relativistic mean-field theory.
The aspect of the nuclear stability will, however, be very probably the most decisive factor in answering the question “How far can we go?” A composite nuclear system that lives at least 10−14 s can be considered as chemical element [29]. With increasing Z, the elements will be very unstable and undergo α-decay or nuclear fission. The question, which element will be stable at very high Z, will depend on the balance between the repulsive Coulomb forces of many protons in a tiny nucleus and the attractive forces between the nucleons. Nuclear theory predictions for the stable magic nuclei depend on the model [30]. At the time being, almost all of them indicate that the most stable neutron shell should be at N = 184. The magic proton number is expected to be 120 and 126. The search for the island of stability is still going on and there are indications that some superheavy nuclei can live hundreds, or even millions of years [2, 3].
4. Studies of chemical properties
Even though for the transactinides, properties similar to those of the 5th and 6th row homologs are anticipated, it is not trivial to expect that they can be deduced from their position in the Periodic Table. Due to increasingly important relativistic effects deviations from the established trends in the groups can occur, so that simple extrapolations may lead to erroneous results. The validity of the ordering of the elements in this part of the Periodic Table is still to be proven by studies of their chemical properties.
Unfortunately, with increasing nuclear charge, cross sections and production rates of SHEs drop so rapidly that experimental chemical studies can only be performed, with reasonable efficiency, for isotopes having half-lives, t1∕2, of ∼ 1s and longer. This is achieved with the use of special fast chemistry separation techniques [4, 5, 6, 7]. In the gas phase, gas-phase chromatography exploits differences in volatility between the elements by measuring adsorption enthalpy, ΔHads, on the surface of the chromatography column, mostly quartz and gold. In the liquid phase, liquid chemistry chromatography exploits differences in complex formation between them by measuring distribution coefficient, Kd. Volatility of Rf through Hs compounds, complex formation of Rf, Db and Sg in acid solutions, as well as volatility of the Cn and Fl atoms have been studied so far [4, 5, 6, 7, 8].
Chemical information obtained from these experiments is, however, limited to the knowledge of only few properties. It mostly answers the question about whether a new element behaves similarly to its lighter congeners in the chemical group, or whether some deviations from observed trends occur due to increasingly important relativistic effects. Knowledge of many other properties can presently be gained only from theory. It is also theory that can establish relativistic effects influence on properties of elements by comparing results of relativistic with non-relativistic calculations [8, 17].
Gas-phase chemistry. One of the most illustrative examples of the strong influence of relativistic effects on properties of SHEs is high inertness and volatility of Cn. Due to the strongest stabilization of the 7s AO in group 12 (Figure 4) and in the 7th row of the Periodic Table [17], as well as its closed shell ground state 6d107s2 configuration, Cn was believed to behave like a noble-gas element. (Hg, as known, is liquid at room temperature). In 1975, Pitzer suggested that in Cn, a high excitation energy (6d107s2 → 6d107s7p1/2) of 8.6 eV into the atomic valence state, will not be compensated by the energy gain of the metallic bond formation [31]. The questions to the modern electronic structure theory were: is Cn metallic in the solid state, or is it more like a solid noble gas? How reactive is the Cn atom towards gold in comparison with Hg and Rn?
Recent relativistic calculations of solid-state properties (even though such a state is hypothetical, as there can be no two atoms of Cn produced simultaneously), have indicated that Cn should be a volatile liquid [32]. In this way, the trend towards the weakening of an atom-atom interaction in group 12 should continue towards Cn. For the interaction with gold, Density Functional Theory (DFT) cluster and periodic calculations [8, 33] predicted much smaller ΔHads of Cn on gold than that of Hg either. This means that in the gas-phase experiments with the chromatography column, having a negative temperature gradient (from room one to − 180 °C), Cn should adsorb on gold at the colder end of the column (more towards Rn), while Hg adsorbs right at the beginning of the column. Also, no adsorption of Cn on quartz was foreseen [8] (Figure 6).
Predicted adsorption positions (schematic) of Cn, Nh and Fl, with respect to their homologs and Rn, on the combined SiO2/gold surface detector system in gas-phase chromatography experiments [8, 33].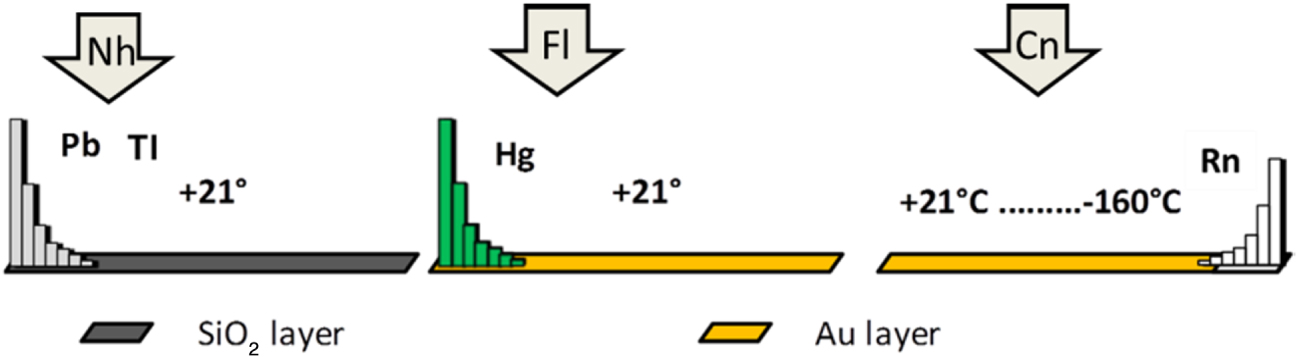
Fl, having a quasi-closed-shell ground state, 7s27p1∕22, should also be rather inert and volatile due to the relativistic stabilization of the 7s and 7p1/2 AOs. However, Fl should be more reactive than Cn towards gold [8, 33]. Nh(7s27p1/2) with one unpaired p1/2 electron should be more inert than Tl(6s26p), however, more reactive than Cn and Fl [33] (Figure 6). Experiments with Cn and Fl, having sufficiently long-lived isotopes (t1∕2 > 1s), have nicely confirmed these predictions: Cn was found to adsorb on gold detectors of the chromatography column at about 0 °C, while Hg to adsorb at the beginning of the column at room temperature [34]. Adsorption of Fl on gold was proven to be much weaker than that of Pb, but stronger than that of Cn, however, poor statistics of events did not allow for accurate measurements of ΔHads(Fl) [35]. Similar experiments on volatility of Nh are under way. Thus, the trends in the properties of group-12 and 14 elements, i.e., an increase in volatility and a decrease in reactivity with increasing Z, were shown to be continued with Cn and Fl. This is explained by the gradual relativistic stabilization of the ns and np1/2 AOs. In this way, position of Cn and Fl in groups 12 and 14, respectively, has been confirmed.
Elements at the beginning of the 6d series, Rf through Hs, where sufficiently long-lived isotopes exist, are not stable in the atomic state. They, however, form volatile halides, oxyhalides and oxides (of Hs) making them suitable for gas-phase chromatography studies [4, 5, 6, 7]. In turn, properties of these compounds were predicted on the basis of fully relativistic calculations [7, 8]. Both types of investigations have shown that behaviour of the volatile SHE species is in line with the trends in the respective groups, which is stipulated by smooth trends in properties of the valence (n − 1)d AOs, responsible for bonding.
Recently, a new class of compounds has been discovered for SHEs: it was shown that the 6d elements can form volatile carbonyls by analogy with their lighter homologs in the groups. Thus, Sg(CO)6 was synthesized on line in a reaction of the Sg atom with a mixture of He and CO gases [36]. Moreover, volatility of Sg(CO)6, as adsorption on a quartz chromatography column, was studied using gas-solid chromatography technique. Preceding fully relativistic DFT calculations on M(CO)6 (M = Mo, W, and Sg) have shown that all the group-6 species should have very similar properties, including interaction strength with quartz (see [8] for references). The experiments have indeed obtained very similar ΔHads values of the Mo, W and Sg carbonyls on quartz [36]. Thus, in good agreement with each other, experimental and theoretical studies have shown that Sg(CO)6 is as volatile as Mo(CO)6 and W(CO)6, and is therefore an ordinary group-6 member.
It has also presently become possible to measure the first M–CO bond dissociation energy (FBDE) of the gaseous carbonyls, including those of SHEs, using a gas-solid isothermal chromatography. This was done for Mo(CO)6 and W(CO)6 showing that the W–CO bond is stronger than the Mo–CO one [37]. To predict experimental outcome for Sg, calculations of FBDE of M(CO)6 (M = Mo, W, and Sg) (Figure 7) were performed using a variety of advanced relativistic methods [38].
Decomposition reaction of group-6 M(CO)6.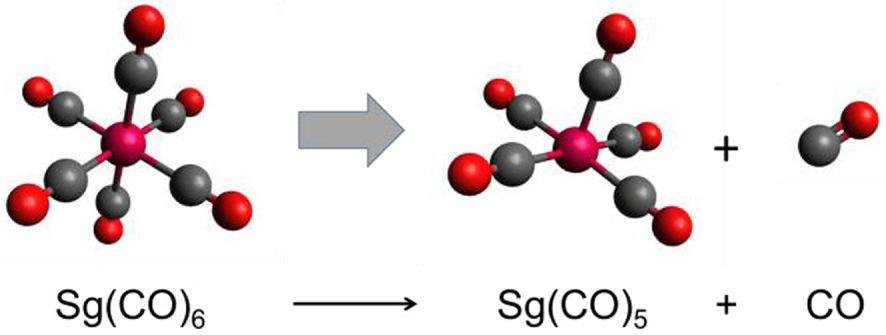
The results established a weaker Sg–CO bonding than the W–CO one. This was shown to be a relativistic effect: the non-relativistic M–CO FBDEs increase from W to Sg. Thus, for this type of compounds, relativistic effects on SHEs were shown to result in a deviation from the trend in the group, demonstrating once again that linear extrapolations may lead to erroneous predictions. (Results of the experiments on the FBDE for Sg(CO)6 are at the stage of evaluation.)
Energies of the ns AOs of group-1 elements (left panel); calculated dissociation energies of the MAu dimers, De (MAu), and adsorption enthalpies, − ΔHads(M), of the group-1 elements on transition metal surfaces (right panel) (see [8] for references therein).
For Mc through Og, longer-lived isotopes have still to be created suitable for experimental chemical studies. For these elements, only theoretical predictions exist. Og(7s27p1∕227p3∕24), standing in the group of noble gases, is another exciting case where strong relativistic effects are expected to significantly influence its properties. A large 7p1/2–7p3/2 SO separation of ∼12 eV and the relativistic destabilization of the 7p3/2 AO, should result in its higher chemical reactivity in comparison with the other noble gases. Calculations of the solid-state properties of Og have shown that, in contrast to the other homologs, it should be semiconductor at room temperature [39]. Og should also stronger adsorb on gold than Rn, with the energies in the range of chemisorption. Also, its chemical compounds should be more stable than those of Rn. Overall, trends in the properties of Og should be in line with those of the other noble gases (see [8] for a review and references therein).
Elements 119 and 120, prescribed to the first and second columns of the Periodic Table, respectively, are the next SHEs awaiting discovery. Their properties will be defined by the valence 8s AO whose relativistic contraction and stabilization (Figure 8, left panel) should lead to the reversal of the trends in groups 1 and 2 at Cs and Ba, respectively. This is predicted, e.g., for dissociation energies of their intermetallic dimers and ΔHads on transition metal surfaces (Figure 8, right panel) [8].
Provided these elements are synthesized, volatility (measurements of ΔHads) of the 119 and 120 species might be studied in the long term using an advanced (vacuum) chromatography designed for extremely short, presumably sub-milliseconds, t1/2 of their isotopes.
Aqueous chemistry. Beside the gas-phase studies, there has been quite a number of experimental and theoretical works on the complex formation and extraction behaviour of SHEs in aqueous solutions (see [5, 6, 7, 40] for reviews and references therein). Because the liquid chromatography experiments need much longer-lived isotopes than those used in the gas-phase studies, only Rf, Db and Sg were considered so far. The aim of the studies was to find out whether established trends in stability of oxidation states and complex formation in acid solutions (Kd values) were continued with the SHEs. As a result, behaviour of the SHEs in the liquid phase was found to be overall in line with the existing trends in the groups. However, some irregularities in the complex formation occurred depending on experimental conditions.
Future elements. Chemistry of elements heavier than Z = 120 rests on a purely theoretical basis. Due to very strong relativistic effects, as well as existence of open shells and their mixing, it will be much more different from anything known before. Without relativistic effects, it would, however, have also been different due to very large orbital effects. Very few molecular calculations exist in this domain [41]. Unusual oxidations states, coordination numbers and geometrical configurations should be observed for compounds of these elements.
5. Summary
Advances in the relativistic quantum theory and computational algorithms allowed for accurate predictions of electronic structures and properties of atoms, molecules, and complexes of SHEs and their homologs. With many of them carried out in a close link to the experimental research, those investigations have contributed to better understanding of the chemistry of these exotic elements and the role and magnitude of relativistic effects.
Relativistic effects were found to be of crucial importance for the elements beyond the 6th row of the Periodic Table and to be responsible for periodicities in properties. Relativity can, however, also cause deviations from the trends observed among the lighter elements. Thus, simple extrapolations from the lighter homologs may be unreliable in this high Z region.
The 7th row of the Periodic Table is now complete. For the 8th row, further developments in the electronic structure theory are required to accurately predict the ground state configurations, as well as elements heavier than Og have to be synthesized. The end of the Periodic Table is still to be determined from the nuclear and the electronic structure points of view. Together with investigations of properties of the future elements, this will enable one to answer the question whether the Periodic Table is still a useful tool for chemists, or whether its predictive power is lost.



 CC-BY 4.0
CC-BY 4.0