Abridged version
1 Introduction
Natural and artificial fracturing leads to rock medium fragmentation, which finally evolves to a three-dimensional puzzle of blocks. Fractures ending within the rock bulk are mechanically very unstable, and their growth make them meet other fractures, to finally produce a fully connected network. In both natural [14,17] and artificial fragmentation studies [3,6,7,10,14,18], the number N(r) of fragments of equivalent radius r (radius of the sphere having same the volume as the block) satisfies the condition (1)
| (1) |
This relation defines a fractal distribution of dimension D [19]. Trying to explain this law, several authors [1,4,17,19] created or used a model whose main principle is as follows. Considering an initial cubic volume, divided in eight identical cubic parts, each cube is given the same probability p to be divided in 8. This probability applies indefinitely to every resulting cube. By construction, this process leads to a distribution of N(r) that respects law (1). Moreover, D can be related to the fragmentation probability p by (2) [19]:
| (2) |
But even if such a process gives a correct model of experimental fragmentation (1), the simplified geometry (puzzle of cubes) does not account for a fragment's shape and arrangement in real cases (e.g., [2,12]).
2 The OBSIFRAC model
We developed a numerical model, named OBSIFRAC (OBject SImulator for rock FRACturing). From an initial, possibly pre-fragmented volume, plane fractures divide this volume into 2 or more son blocks. Fig. 1 illustrates, on a 2D section, the first steps of the cutting process, which can be continued as far as needed. Such a process finally produces a fully connected fracture network, in which every fracture abuts either on pre-existing fractures, or on the model boundaries. The fractured medium is therefore made up of a puzzle of polyhedral convex blocks, delimited by polygonal faces.
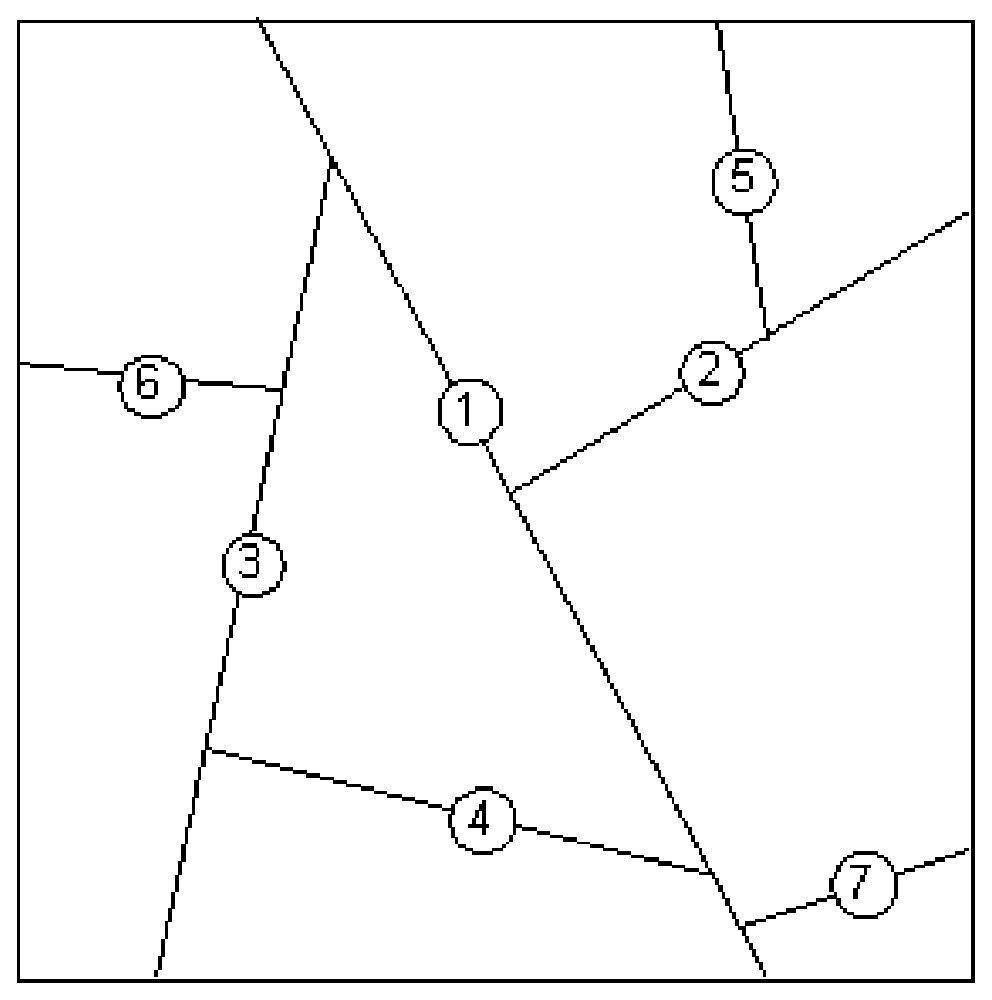
Processus de découpage des blocs par création successive des fractures (1 à 7). Dans cet exemple, les fractures ne recoupent pas les discontinuités existantes.
The block division process, involving successive fracture creation (1 to 7). In this example, fractures do not cross existing discontinuities.
The OBSIFRAC model is connected to a relational database management system (DBMS), which undertakes fully geometrical description of the system, for every step of the process.
The program successively creates a set of i fractures F1,F2,…,Fi. Starting from a (i−1) fracture network, the ith fracture is built after choosing its orientation (defined by its normal ), the seed point Gi from which it is extended, and the block Bi that it divides. The database is updated after each fracture creation, and keeps the memory of all successive states of the model. Gi, Ni, and Bi are chosen through different evolutionary motors.
3 Constant probability fragmentation
In this scenario, derived from the model of Allègre et al. [1], a proportion p of blocks, chosen at random among previously generated blocks, are simultaneously divided (salvoe). Point G and orientation are chosen at random in each block. Non-fragmented blocks are definitely excluded from the division process. The division probability p is the same for each block, and remains constant throughout the process. On 2D sections, fracture traces gather in extremely dense clusters, revealing very contrasted block sizes (Figs. 2 and 3). Block volumes have been studied at different stages of the process. Plotting number N(R) of elementary blocks of radius R (cubic root of volume) in log–log coordinates (Fig. 3) shows a linearity, revealing a power-law distribution of the form of (1) (Fig. 3, Table 1). The value for exponent D is about 0.7 for p=0.6. If p varies from 0.5 to 1, D values range from 0 to 3 (Table 1), and correspond to those given by relation (2). The main difference between the processes of Allègre et al. [1] and Turcotte [19] and our constant probability fragmentation process is that, in the latter, the volume of son blocks is not a constant fraction of the father block: the partition between the son blocks is not always the same, and depends on the position of the seed point Gi, and of the fracture orientation chosen in the father block. Our process is fractal, although point Gi is chosen random inside each block, and the volumes produced are random as well.
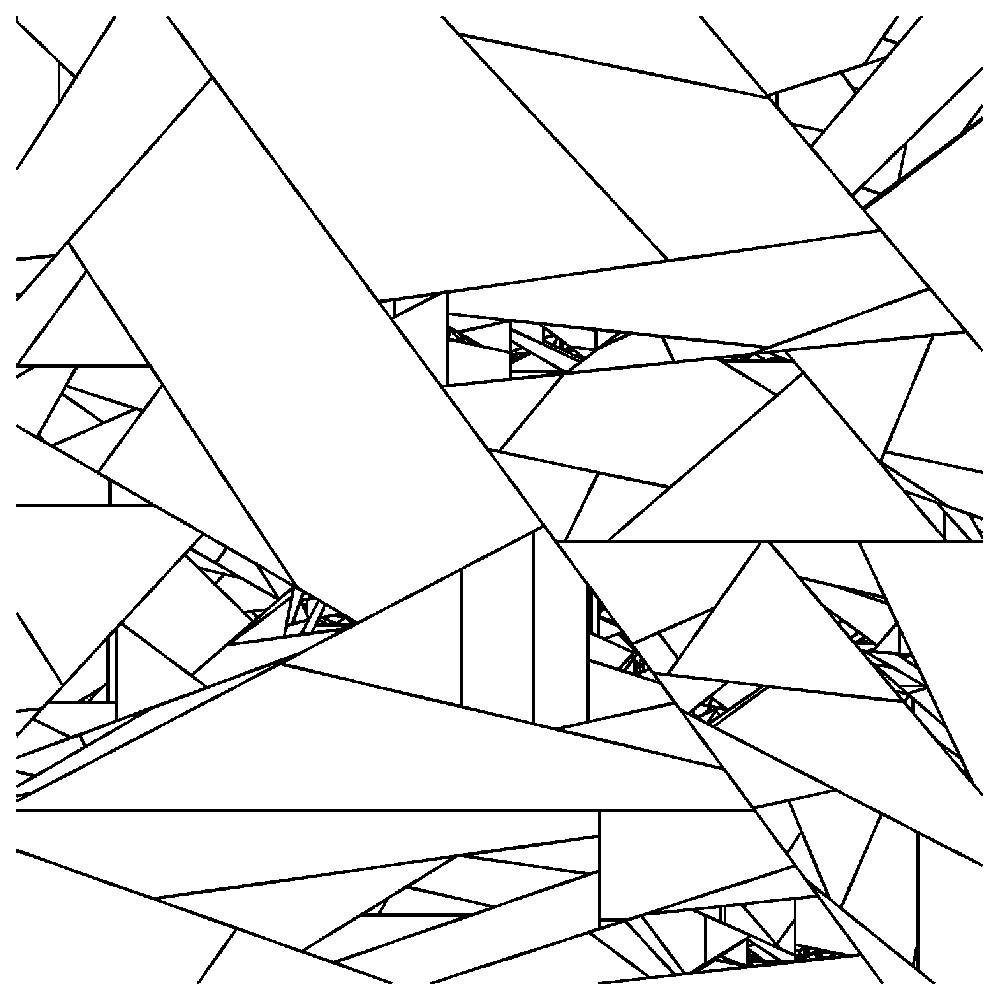
Fragmentation à probabilité constante p=0,6, à partir d'un état initial de N0=101 blocs. Section dans le modèle après 30 salves de fractures (71 841 blocs). La taille des blocs est extrêmement contrastée. De ce fait, seul un nombre limité de fractures apparaı̂t dans la coupe, les plus petits blocs étant concentrés dans des noyaux.
Constant-probability fragmentation with p=0.6. Initial state formed by N0=101 blocks. Section through the model after 30 fracture salvoes (71 841 blocks). Block size is extremely contrasted. Therefore, very few fractures are visible on this section. Smallest blocks gather in clusters.
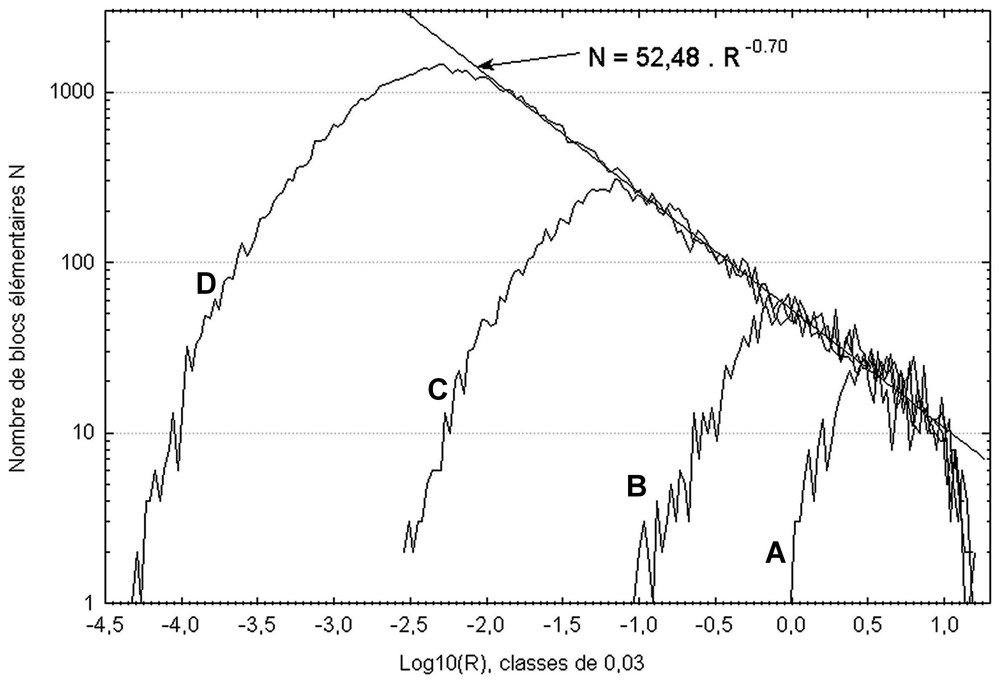
Fragmentation à probabilité constante p=0,6, à partir d'un état initial de N0=101 blocs. Distribution des volumes après cinq salves, 556 blocs (A), 10 salves, 1 718 blocs (B), 20 salves, 11 452 blocs (C), 30 salves, 71 918 blocs (D). La partie utile de chaque courbe montre une linéarité dont la pente est constante et dépend de p.
Constant-probability fragmentation with p=0.6. Initial state formed by N0=101 blocks. Volume distribution after five fracture salvoes, 556 blocks (A), 10 salvoes, 1 718 blocks (B), 20 salvoes, 11 452 blocks (C), 30 salvoes, 71 918 blocks (D). The useful portion of each curve shows a linearity, whose slope is constant and depends on the probability p.
Valeurs de la dimension fractale dans la fragmentation à probabilité constante, dans le modèle d'Allègre et al. [1] (D) et dans le modèle Obsifrac (D′). Les valeurs de D et D′ sont comparables pour les différentes valeurs de probabilité p.
Fractal dimension values, for constant-probability fragmentation, in Allègre et al. model [1] (D), and in OBSIFRAC model (D′). D and D′ are quite similar for the studied values of the probability p.
| p | 0,5 | 0,6 | 0,7 | 0,8 | 1,0 |
| D | 0 | 0,7 | 1,5 | 2,1 | 3,0 |
| D′ | 0 | 0,79 | 1,46 | 2,03 | 3,0 |
4 Random fragmentation
In this second scenario, one single block is chosen at random among the Ni blocks of step i, and will be cut. Each step produces one single fracture. The fragmentation probability (p=1/Ni at step i) obviously varies along the process and tends to 0. The 2D sections show a very heterogeneous fracture density, which is though less significant than in the constant probability case. Different distribution laws have been tested with Statistica® V 5.1 software for volume distribution adjustment. N(r) values do not fit log-normal, beta, gamma, power-law, Rayleigh, exponential, or extreme value laws. The maximum likelihood criterion method [13] reveals that the volume distribution closely matches a Weibull law (Fig. 3b, ΔF=0). The parameters of this law are then estimated by normal distribution transformation [9].
5 Random fragmentation with minimal distance between fractures
An existing discontinuity is likely to be preferentially reactivated, before any new fracture creation in its neighbourhood. The existence of a minimal distance ΔF between fractures can therefore be conceived: at a shorter distance than ΔF from each side of every fracture plane, fracture creation is mechanically very difficult. To take this feature into account in our random fragmentation model, we imposed that point Gi, which is chosen at random in the block, be situated at a greater distance than ΔF from any other fracture delimiting the block. In the case of Fig. 4, a minimal distance ΔF was fixed to 0.2 % of the total dimension of the model. Bigger values of ΔF cause the simulation to stop prematurely, because of the impossibility to find any block matching the condition. On 2D sections, the fractured network is similar to the one displayed in Fig. 5. However, volume simulated data cannot be adjusted by a Weibull law in this case. When ΔF is given a positive value, and after elimination of extreme values related to finite-size effect in the model, the significant part of the distribution reveals a power law in the form of (1). For ΔF=0.2 % of the size of the modelling volume, the exponent D is about 2.1. This value increases with ΔF, and reaches 2.7 for ΔF=0.1 %.
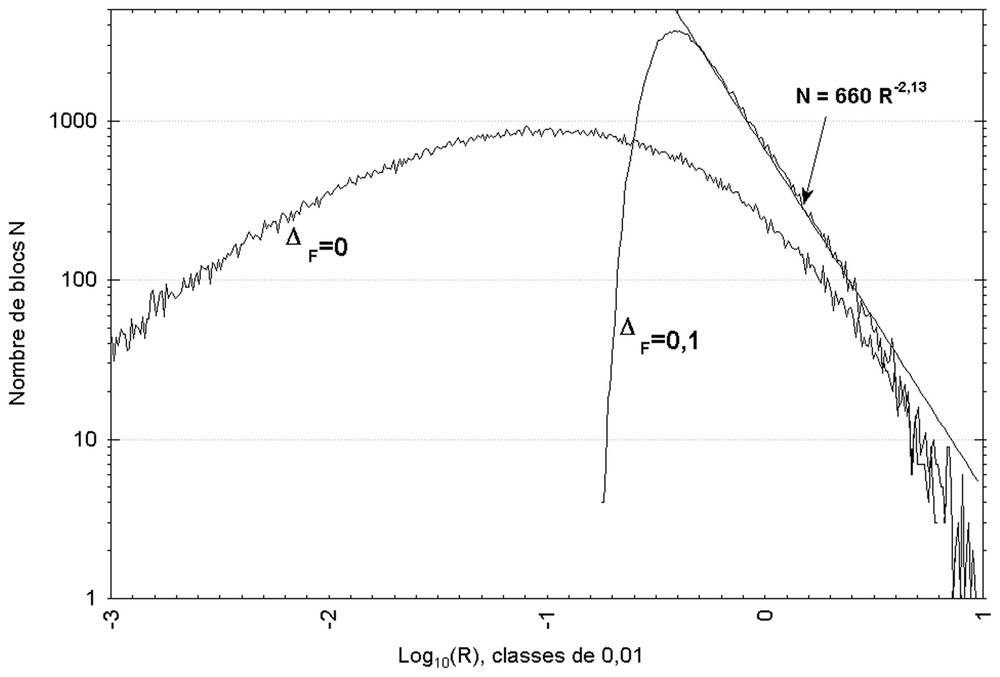
Fragmentation aléatoire, à partir d'un bloc initial cubique, 150 000 blocs. Distribution des volumes pour une distance interfracturale ΔF de 0 et 0,1.
Random fragmentation process, from one initial cubic block. 150 000 blocks. Volume distribution for a minimal distance between fractures ΔF=0 and 0.1.
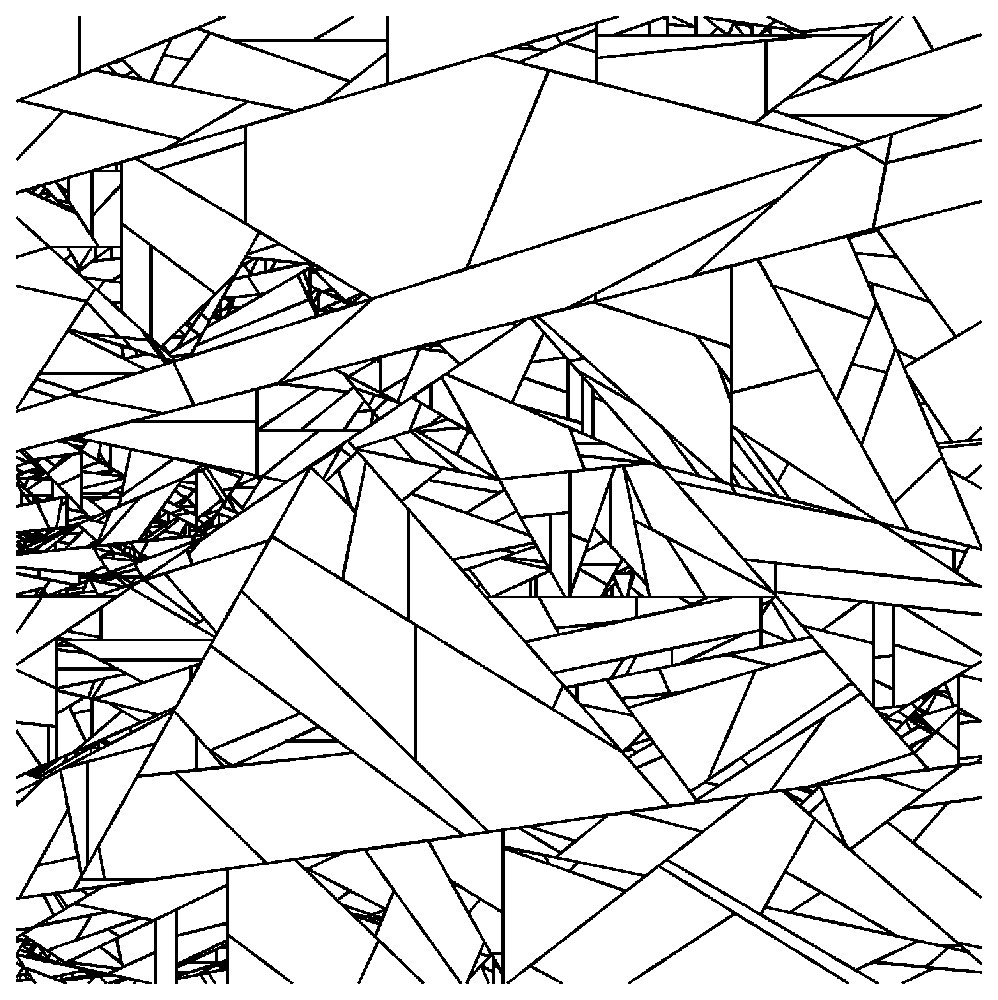
Fragmentation aléatoire, à partir d'un bloc initial cubique. Section dans le modèle après 150 000 fractures (150 001 blocs). Le contraste de taille des blocs est important, mais toutefois moindre que dans le cas d'une fragmentation à probabilité constante (Fig. 2). On observe des amas diffus de fractures, composés des plus petits blocs.
Random fragmentation process, from one initial cubic block. Section in the model after 150 000 fractures (150 001 blocks). Block size is slightly less contrasted than in constant-probability fragmentation (Fig. 2). Fractures clusters are made up of the smallest blocks.
6 Discussion and conclusions
For the three models presented above, where fractures orientations are random, similar results are obtained with more constrained orientations. Fracture orientation is therefore not an important factor for the N(r) law, and the case we presented is the most general one (random orientations).
Other protocols have been used to choose the values of (Bi,Ni,Gi). In particular, we demonstrated that the random choice of Gi in the whole modelling volume does not produce a distribution respecting relation (1). We restricted our presentation to processes involving power-law distributions.
On the basis of the simplified process imagined by Allègre et al. [1], and Turcotte [19], we tried to approach natural section appearance (traces complexity, density). The orthogonal network used by these authors, just as models involving disk-shaped [5,15] or rectangular fractures [11] cannot account for natural cases (e.g., [2,12]). We demonstrated that, even if several random factors were introduced into the process (fracture orientation, fracture position in the affected block), the resulting volume distribution remained a power law, with the same exponent D=ln(8p)/ln(2).
Although these two variation factors were added, the result does not give a realistic image of natural networks. Fractures gather in extremely dense clusters, distributed in the modelling volume. We imagined and tested a more realistic scenario, called random fragmentation, which clearly produces a Weibull law distribution for N(r). Even though such a law approaches a fractal distribution for very small values of r, our result does not match experimental or field studies.
When a minimal distance between fractures ΔF is imposed in our random fragmentation model, the N(r) distribution clearly approaches a power law, whose exponent increases with ΔF. In this way, we demonstrate that adding such a limitation to an initial purely stochastic process leads to fractal properties. These results encourage us to think that the mechanical phenomenon inhibiting new fractures creation in the close neighbourhood of an existing fracture could be responsible for the existence of fractal properties in rock mass fragmentation. As clusters of small fragments are likely to weaken the whole blocks puzzle, this feature should be taken into account in mechanical models.
1 Introduction
La fracturation des roches, naturelle [8] ou provoquée, aboutit à une fragmentation progressive. Cette évolution vers un milieu constitué par un assemblage de blocs est générale. L'instabilité mécanique aux extrémités libres des fractures favorise leur croissance, même sous de faibles sollicitations. Une analyse de la taille des fragments a été faite, aussi bien pour les cas naturels [14,17], que pour la fragmentation provoquée [3,6,7,10,14,18]. Le résultat fondamental et convergent de ces travaux est le suivant : en rapportant chaque fragment à son rayon équivalent r (rayon de la sphère de même volume), le nombre N(r) de fragments de rayon r est lié à r par la relation (1) :
| (1) |
Ce type de distribution est caractéristique d'une géométrie fractale de dimension D [16]. Pour expliquer cette relation, plusieurs auteurs [1,4,16,17] se sont basés sur un modèle dont nous rappelons ci-dessous l'idée principale : en partant d'un cube initial découpé en huit cubes identiques, le principe consiste à considérer que chaque cube possède une probabilité p d'être lui-même divisé en 8 et que cette probabilité s'applique indéfiniment à tous les cubes fils. Ce processus aboutit par construction à une distribution N(r) qui respecte la loi (1). De plus, D est lié à la probabilité de fragmentation p par la relation (2) [19] :
| (2) |
Cependant, même si ce modèle respecte la distribution expérimentale (1), la géométrie simplificatrice (assemblage de cubes) est peu apte à rendre compte des cas réels.
2 Le modèle Obsifrac
Nous avons réalisé un module numérique de fracturation baptisé Obsifrac (OBject SImulator for rock FRACturing) qui, à partir d'un volume initial éventuellement prédécoupé, divise ce volume en deux ou plusieurs blocs fils (Fig. 1). Ce principe peut être répété à volonté. Par souci de simplification, les fractures ont été considérées comme planes.
Dans l'enceinte du volume modélisé, on construit donc un réseau entièrement connecté, dans lequel toute fracture est limitée exclusivement, soit par des fractures préexistantes, soit par les bords externes du modèle. Le milieu fracturé est ainsi composé d'un assemblage de blocs polyédriques convexes, limités par des faces polygonales.
Le programme crée successivement une série de i fractures F1,F2,…,Fi. Partant d'un état composé de (i−1) fractures, la ie fracture est construite après avoir choisi un point Gi de cette fracture, son orientation étant définie par sa normale et le bloc Bi à diviser (qui peut être complexe dans le cas d'une fracture à propager à travers plusieurs blocs élémentaires). Obsifrac est connecté à un système de gestion de base de données (SGBD) qui permet de décrire entièrement l'état du système à chaque stade. Gi, Ni et Bi sont choisis par des moteurs dont le fonctionnement peut être configuré à la demande.
3 Fragmentation à probabilité constante
Ce premier scénario, inspiré de celui d'Allègre et al. [1] effectue la division simultanée (salve) d'une proportion p de blocs choisis parmi les blocs créés à l'étape précédente. Chaque bloc a donc la même probabilité p d'être divisé, constante au long du processus. À partir d'un état initial comprenant N0 blocs, au stade 1, blocs seront divisés en blocs fils. Dans chacun de ces blocs, un point G et une orientation seront choisis aléatoirement. Au stade i, blocs seront divisés pour produire blocs nouveaux. Les blocs restants non fracturés sont définitivement exclus du processus : ils ne pourront plus être fracturés.
Les images obtenues pour ce processus montrent un contraste extrême de tailles de blocs (Figs. 2 et 3) (cinq ordres de grandeur, pour un total de 105 blocs si p=0,6). Les plus petits d'entre eux s'organisent en noyaux répartis dans l'espace, si bien que les coupes ne montrent qu'un nombre limité de fractures.
Le nombre N(R) de blocs élémentaires de rayon R (racine cubique du volume) a été représenté en coordonnées bilogarithmiques (Fig. 3), pour différents stades i du processus. À un stade donné, la partie utile de cette distribution montre une linéarité, limitée de part et d'autre par un double effet de taille finie, qui révèle une loi puissance de la forme de (1) (Fig. 3 et Tableau 1). D est de l'ordre de 0,7 pour p=0,6. Pour p variant de 0,5 à 1, D évolue de 0 à 3 (Tableau 1). Les valeurs de D sont égales par ailleurs à celles données par la relation (2).
Notre modèle de fragmentation à probabilité constante permet donc de mettre en évidence un processus de nature fractale, alors même que, contrairement aux modèle d'Allègre et al. [1] et de Turcotte [19], dont il est dérivé, la position du point Gi et l'orientation de la fracture sont aléatoires au sein de chaque bloc et que les deux volumes produits par division sont, eux aussi, aléatoires.
4 Fragmentation aléatoire
Dans un second scénario, un bloc unique aléatoire est choisi parmi les Ni blocs constitutifs du modèle au stade i. Ce bloc sera partagé, chaque étape ne créant qu'une fracture unique. La probabilité de fragmentation d'un bloc n'est évidemment pas constante au cours du processus. Elle vaut 1/Ni au stade i et tend donc vers zéro. Les coupes dans ce modèle montrent une forte hétérogénéité de la densité de fracturation, comme dans le cas précédent, mais toutefois moins prononcée.
Un ajustement statistique de la distribution de N(r) a été tenté par diverses lois classiques (log-normale, bêta, gamma, Weibull, puissance, Rayleigh, exponentielle, valeur extrême), à l'aide du logiciel Statistica® V 5.1. En utilisant le critère du maximum de vraisemblance [13], il apparaı̂t que nos données simulées se rapprochent de façon très satisfaisante d'une loi de Weibull (Fig. 3b, ΔF=0), à l'exclusion de toutes les autres. L'estimation des paramètres de cette loi, ajustés sur les données simulées, est ensuite obtenue par transformation de la distribution normale [9].
5 Fragmentation aléatoire avec distance interfracturale minimale
Une discontinuité présente dans un milieu rocheux sera préférentiellement réactivée avant toute création de nouvelle fracture dans son voisinage. Il est donc légitime de concevoir l'existence d'une distance interfracturale minimale ΔF, représentant la zone, située de part et d'autre de chaque plan de fracture, et à l'intérieur de laquelle la création de nouvelles fractures est mécaniquement très difficile. Cette zone correspond au volume dans lequel toute fracture exerce un effet d'écrantage. Pour tenir compte de cette particularité physique dans le modèle à fracturation aléatoire, nous avons imposé que le point Gi, choisi aléatoirement à l'intérieur du bloc à découper, soit situé à une distance minimale ΔF de toutes les autres fractures limitant le bloc.
Dans le cas pratique présenté sur la Fig. 4, on a imposé une distance interfracturale minimale ΔF égale à 0,2 % de la dimension totale du modèle. Cette valeur, arbitraire, a cependant été conditionnée par la nécessité de ne pas « bloquer » la simulation par impossibilité de trouver un bloc suffisamment gros pour satisfaire la condition imposée. L'apparence du réseau obtenu en sections est similaire à celle de la Fig. 5. Cependant, l'ajustement de la distribution de N(r) produite par ce découpage ne peut plus se faire par la loi de Weibull. En imposant une valeur non nulle à ΔF, et après élimination des valeurs extrêmes dépendant de l'effet de taille finie du modèle, la partie significative de la distribution révèle une distribution en loi puissance du type de (1). Pour ΔF=0,2 %, D est de l'ordre de 2,1. Cette valeur augmente avec ΔF et atteint 2,7 pour ΔF=1 %.
6 Discussion et conclusions
Dans les trois modèles présentés dans ce travail, le choix des orientations est aléatoire. D'autres simulations, réalisées avec des orientations réglées (deux familles de fractures ou plus) aboutissent à des résultats parfaitement similaires. L'orientation des fractures n'étant donc pas un facteur déterminant sur la loi N(r), nous avons présenté ici le cas le plus général (fractures aléatoirement orientées).
D'autres protocoles pour choisir le triplet (Bi, Ni, Gi) ont été imaginés et éprouvés. Nous avons restreint notre présentation aux seuls processus aboutissant à une distribution en loi puissance. En particulier, nous avons montré que le choix aléatoire de Gi dans tout l'espace de modélisation n'aboutit pas à une distribution N(r) qui respecte (1).
Partant du processus simplifié imaginé par Allègre et al. [1] et Turcotte [19], nous avons recherché une meilleure ressemblance en coupe avec les réseaux naturels (complexité des traces, densité de fractures). Au même titre que les approches de modélisation 3D qui prévoient des fractures discales [5,15] ou rectangulaires [11], le modèle d'Allègre et al., limité à des fractures orthogonales, est en effet peu apte à rendre compte des cas réels (cf. [2,12]). Nous avons pu montrer que, même en ajoutant plusieurs nouveaux facteurs aléatoires dans ce processus (choix de l'orientation du plan de fracture, choix de la position de la fracture dans le bloc à découper), la nature du résultat n'était pas changée et que l'on conservait une distribution de N(r) en loi puissance avec le même exposant D=ln(8p)/ln(2).
Cependant, même en ajoutant ces deux causes de variabilité, le résultat obtenu reste encore très éloigné des réseaux naturels. En particulier, le découpage en blocs se concentre au niveau de noyaux de très petite taille, dispersés dans le volume total. Un scénario plus réaliste, appelé fragmentation aléatoire, a été testé. Ce scénario aboutit très clairement à une distribution N(r) de type Weibull. Même si une telle loi peut être rapprochée d'un processus fractal, notamment en considérant les petites valeur de r, le résultat obtenu dans notre modèle n'est pas en accord avec les données expérimentales ou de terrain.
En ajoutant une contrainte d'écrantage dans un modèle à fragmentation aléatoire, la distribution N(r) s'approche de façon satisfaisante d'une distribution en loi puissance. Nous montrons donc, par cette approche, que l'ajout d'une limitation à un processus de fragmentation purement stochastique à la base fait apparaı̂tre des propriétés fractales. Ce constat nous laisse penser qu'il existe un lien de cause à effet entre le phénomène mécanique responsable de l'inhibition de la création de fractures autour des fractures existantes et l'apparition des propriétés fractales dans la fragmentation des massifs. Ce résultat serait à prendre en compte dans les modèles servant de base aux calculs mécaniques. En effet, la multiplicité des échelles et notamment la présence dans les assemblages de blocs de groupes de petits éléments constitue un point faible, susceptible de déstabiliser l'ensemble sous une sollicitation mécanique.
Remerciements
Cet article constitue la contribution UMR LGCA n° 2789.



