Simplified vibratory characterization of alluvial basins

Jean-François Semblat; Roberto Paolucci; Anne-Marie Duval

doi:10.1016/S1631-0713(03)00058-0

Résumés

Anglais
Français

For the analysis of seismic wave amplification, modal methods are interesting tools to study the modal properties of geological structures. Modal approaches mainly lead to information on such parameters as fundamental frequencies and eigenmodes of alluvial basins. For a specific alluvial deposit in Nice (France), a simplified modal approach involving the Rayleigh method is considered. This approach assumes a set of admissible shape functions for the eigenmodes and allows a fast estimation of the fundamental frequency of the basin. The agreement with other numerical results (Boundary Element Method) and experimental ones is fully satisfactory. The simplified modal method then appears as an efficient mean for the global vibratory characterization of geological structures towards resonance.

L'analyse de l'amplification du mouvement sismique peut être réalisée en étudiant les propriétés vibratoires de structures géologiques. Les approches modales peuvent donner des informations telles que les fréquences propres et les modes propres de bassins sédimentaires. Pour étudier la résonance d'un bassin sédimentaire du centre de Nice, une approche modale simplifiée utilisant la méthode de Rayleigh est proposée. Cette approche suppose la connaissance d'une famille de fonctions modales admissibles et permet une détermination rapide de la fréquence fondamentale du bassin. La comparaison avec d'autres résultats numériques (obtenus par équations intégrales de frontière) et des mesures réalisées sur site est très probante. Cette méthode conduit donc aisément et rapidement à une caractérisation vibratoire globale de structures géologiques vis-à-vis de la résonance.

Version française abrégée

L'amplification locale du mouvement sismique dans les bassins sédimentaires est parfois très importante [1,2,7,10,11]. La propagation des ondes sismiques dans les structures géologiques de surface peut en effet conduire à une forte amplification du mouvement, due au contraste entre les propriétés mécaniques d'un bassin sédimentaire et celles d'un substratum rocheux. L'amplification du mouvement sismique peut également s'interpréter comme la résonance des couches de surface à certaines fréquences. Les effets de site peuvent alors être analysés en termes de résonance vibratoire des structures géologiques de surface [6,8,12]. Nous considérons dans cette note une approche modale simplifiée basée sur la méthode de Rayleigh [4,9], pour estimer directement la fréquence fondamentale d'une structure géologique.

La méthode modale considérée ici vise à estimer la fréquence « fondamentale » d'une structure géologique. Le processus de propagation d'ondes conduit généralement à une forte amplification du mouvement à des fréquences variées [11], mais, dans un but pratique, il est intéressant de déterminer une fréquence fondamentale unique par des approches simplifiées. La méthode de Rayleigh peut, en effet, permettre une estimation rapide et fiable de la fréquence de résonance d'une structure géologique [9].

Cette méthode considère que le déplacement d'un système élastique dans un de ses modes propres peut être approché par celui d'un système à un degré de liberté. Nous étudions ici le premier mode propre caractérisé par la fréquence : $ω_{0} = 2 π f_{0}$ . En notant V l'énergie élastique du système et T son énergie cinétique, la conservation de l'énergie totale d'un système élastique implique que V_max=T_max. On peut alors écrire le déplacement s_k(x,t) correspondant aux vibrations harmoniques à la fréquence ω₀. La valeur exacte de la fréquence fondamentale du système peut ainsi être obtenue lorsque la forme modale réelle ψ_k(x) est connue. Cependant, comme la solution exacte n'est généralement pas accessible, la valeur de ω₀ peut être estimée correctement en considérant une approximation réaliste de ψ_k(x). Cette approximation doit satisfaire à la fois les compatibilités géométriques et les conditions aux limites. Il a néanmoins été démontré [9] que la seconde condition peut ne pas être satisfaite complètement et que la forme modale peut être choisie dans une large gamme de fonctions, satisfaisant uniquement les compatibilités géométriques (cf. Éq. (7)). On peut alors déterminer la fréquence fondamentale à l'aide de la relation suivante :

ω_{0}^{2} ⩽ \min_{ψ_{k}} \frac{\int_{Ω} σ_{jl} (x) ϵ_{jl} (x) d Ω}{\int_{Ω} ρ (x) ψ_{x}^{2} (x) d Ω}

(6)

où σ_ij est le tenseur de contrainte, ε_ij le tenseur de déformation, ρ la masse volumique et ψ_k(x) la forme modale.

En vue de l'analyse vibratoire simplifiée, nous considérons un bassin sédimentaire situé dans le centre de Nice. Différents types de mesures [7] (bruit de fond, mouvements sismiques faibles) ainsi que des simulations numériques [11] ont permis d'analyser l'amplification des ondes sismiques dans le bassin principal. Pour évaluer la robustesse de la méthode, le bassin est supposé homogène et sa résonance vibratoire est analysée pour une sollicitation sismique antiplane en cisaillement, caractérisée par la célérité $V_{S} = \sqrt{μ / ρ}$ . Les caractéristiques mécaniques des deux milieux (bassin et substratum) sont les suivantes :

– bassin : ρ₁=2000 kg m⁻³, μ₁=180 MPa, ν=0,2, c'est-à-dire V_S=300 m s⁻¹ ;
– substratum : ρ₁=2300 kg m⁻³, μ₁=4500 MPa, ν=0,2, d'où V_S=1400 m s⁻¹ avec ρ la masse volumique, μ le module de cisaillement, ν le coefficient de Poisson et V_S la célérité des ondes de cisaillement.

Comme le montre la Fig. 1, l'interface entre le bassin et le substratum est décrite à l'aide de deux fonctions cosinus (parties ouest et est de la vallée). À partir de formes modales admissibles choisies judicieusement (cf. Éq. (7)), on estime les fréquences fondamentales de ces deux parties du bassin sédimentaire. Les résultats sont obtenus pour le premier mode en considérant différentes valeurs du module de cisaillement : μ₁=180 MPa (i.e. V_S=300 m s⁻¹), μ₂=120 MPa (i.e. V_S=245 m s⁻¹) et μ₃=90 MPa (i.e. V_S=212 m s⁻¹). Les résultats numériques obtenus par la méthode de Rayleigh sont comparés aux fréquences d'amplification maximale, obtenues expérimentalement et numériquement (méthode des éléments de frontière).

Fig. 1
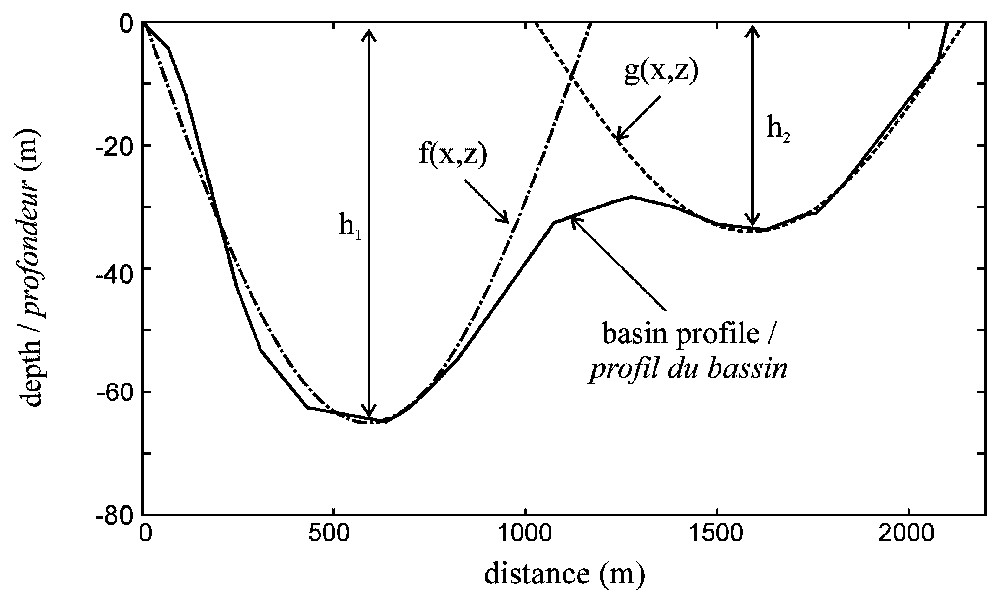
Homogeneous geological profile for the simplified modal analysis.
Description du profil géologique homogène pour l'approche modale simplifiée.

Les valeurs de fréquence obtenues (Tableau 1) sont comparées pour la résonance de la partie profonde du bassin (ouest) et la partie peu profonde (est), et ce, pour différentes valeurs du module de cisaillement. D'après ces résultats, les fréquences fondamentales issues de la méthode de Rayleigh sont en bon accord avec les fréquences de forte amplification, obtenues expérimentalement et par approche propagative. Pour un modèle de bassin homogène, la méthode de Rayleigh semble donc donner des résultats très intéressants, qui sont non seulement en accord avec les valeurs obtenues à l'aide d'autres modèles, mais également avec les résultats expérimentaux (Fig. 2).

	Western part	Eastern part
	Reference BEM	Fundamental	Reference BEM	Fundamental
	frequency	frequency	frequency	frequency
μ ₁	1.35 Hz	1.50 Hz	2.42 Hz	2.86 Hz
μ ₂	1.30 Hz	1.23 Hz	2.13 Hz	2.34 Hz
μ ₃	1.13 Hz	1.07 Hz	1.75 Hz	2.02 Hz

Fig. 2
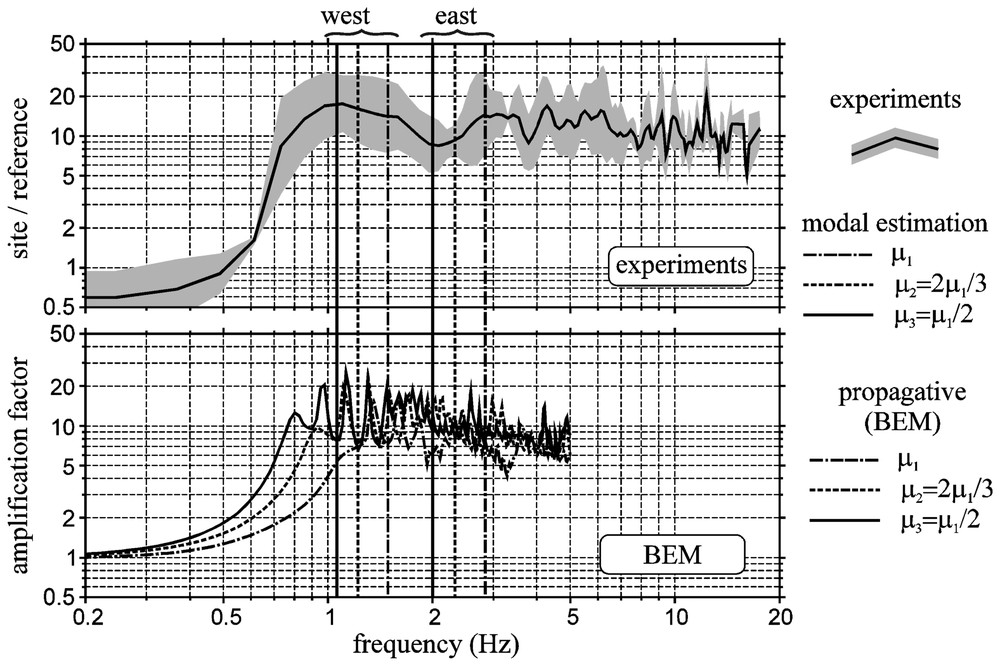
Fundamental frequencies from the simplified modal approach (vertical lines) compared with experimental (top) and propagative BEM results (bottom).
Fréquences fondamentales estimées par méthode modale simplifiée et comparaison avec les mesures (haut) et les simulations par la méthode des équations intégrales de frontière (bas).

1 Introduction

The local amplification of seismic motion in alluvial basins could sometimes be large [1,2,7,10,11,13]. Seismic wave propagation in surface geological structures can indeed lead to strong motion amplification due to the impedance contrast between the alluvial deposit and the bedrock. However, the amplification of seismic motion can also be considered as a result of the resonance of surface layers at peculiar frequencies. Site effects can then be analysed in terms of vibratory resonance of surface geological structures [6,8,12]. In this note, we consider a simplified modal approach based on the Rayleigh's method [4,9] for the direct estimation of the fundamental frequency of a geological structure.

The modal method considered herein aims at estimating the ‘fundamental’ frequency of an alluvial basin. The wave-propagation process generally leads to strong motion amplifications at various frequencies [11] but, from a practical point of view, it is interesting to estimate a unique fundamental frequency by a simplified efficient method. We will show herein that Rayleigh's method allows a fast and reliable estimation of the resonance frequency of a geological structure [9].

2 Simplified modal method

2.1 Basic principles of the method

The modal method considered herein aims at estimating the ‘fundamental’ frequency of a geological structure. It considers that the displacement of an elastic system in one of its eigenmodes can be approximated by the one of a single degree of freedom system. In this note, we study the first eigenmode characterized by the frequency $ω_{0} = 2 π f_{0}$ . Denoting V the elastic energy of the system and T its kinetic energy, the energy balance for an elastic system implies that V_max=T_max. The displacement s_k(x,t) corresponding to the harmonic vibrations at the frequency ω₀ can be written:

s_{k} (x, t) = ψ_{k} (x) e^{i ω_{0} t}

(1)

where x is the space coordinate, i the imaginary number, t time and ψ_k(x) the modal shape along direction k. Then we estimate the kinetic energy of the system as follows:

T (t) = \int_{Ω} \frac{1}{2} ρ (x) {(\frac{\partial s_{k}}{\partial t})}^{2} d Ω = - ω_{0}^{2} e^{2 i ω_{0} t} \int_{Ω} \frac{1}{2} ρ (x) ψ_{k}^{2} (x) d Ω

(2)

hence:

T_{\max} = \max_{t} T (t) = - ω_{0}^{2} \int_{Ω} \frac{1}{2} ρ (x) ψ_{k}^{2} (x) d Ω

(3)

The elastic energy V is then written:

V (t) = \int_{Ω} \frac{1}{2} σ_{jl} (x) ϵ_{jl} (x) d Ω

(4)

where

ϵ_{ij} = \frac{1}{2} (s_{i, j} + s_{j, i})

is the strain tensor and

σ_{ij} = λ ϵ_{ll} δ_{ij} + 2 μ ϵ_{ij}

the stress tensor given by the Hooke's law, with δ_ij the Kronecker's symbol, λ and μ the Lamé constants. As for T_max, V reaches its maximum value when |e^2iω₀t|=1. It then gives:

ω_{0}^{2} = \frac{\int_{Ω} σ_{jl} (x) ϵ_{jl} (x) d Ω}{\int_{Ω} ρ (x) ψ_{k}^{2} (x) d Ω}

(5)

Eq. (5) gives the exact value of the fundamental frequency of the system when the actual modal shape ψ_k(x) is known. However, since the exact solution is not generally known, the frequency value ω₀ can be correctly estimated by considering a realistic approximated mode shape ψ_k(x). This approximation must satisfy both the geometrical compatibilities and the limit conditions. Nevertheless, it has been shown [9] that the second condition can remain not completely fulfilled and that the modal shape can be chosen in a wide range of functions only satisfying the geometrical compatibilities. We can then determine the fundamental frequency thanks to the following approximation:

ω_{0}^{2} ⩽ \min_{ψ_{k}} \frac{\int_{Ω} σ_{jl} (x) ϵ_{jl} (x) d Ω}{\int_{Ω} ρ (x) ψ_{x}^{2} (x) d Ω}

(6)

2.2 Estimation of the fundamental frequency of a geological structure

To perform the simplified vibratory analysis, we consider an alluvial basin located in the centre of Nice (French Riviera). The properties of this site are well known, since numerous experiments were made as well as numerical simulations [7,11]. In this note, the basin is assumed homogeneous and its vibratory resonance is analysed for an antiplane seismic (shear) excitation characterized by the wave velocity $V_{S} = \sqrt{μ / ρ}$ . The mechanical features of both media (basin and bedrock) are the following:

– basin: ρ₁=2000 kg m⁻³, μ₁=180 MPa, ν=0.2, i.e. V_S=300 m s⁻¹;
– bedrock: ρ₁=2300 kg m⁻³, μ₁=4500 MPa, ν=0.2, i.e. V_S=1400 m s⁻¹,

where ρ is the mass density, μ the shear modulus, ν the Poisson's ratio and V_S the shear wave velocity.

As shown in Fig. 1, the interface between the basin and the bedrock is described by two cosine functions:

– western part of the basin: $f (x, z) = (h_{1} + 1) \cdot \cos (2.7 \times 10^{- 3} x + 1.55)$ ;
– eastern part of the basin: $g (x, z) = (h_{2} + 2) \cdot \cos (2.8 \times 10^{- 3} x - 1.3)$ .

Among the admissible mode shapes, we choose the following [9]:

ψ_{2} (x, z) = \cos^{r} (\frac{π}{2} (1 - f (x, z))) \sin^{2 s + 1} (\frac{(n + 1) π}{2} (1 + \frac{x}{a})) \cos^{t} (\frac{(2 m + 1) π}{2} \frac{z}{h})

(7)

where f(x,z) is defined previously. r⩾1 and t⩾1 are real parameters, s=0,1,… is an integer and m and n represent the orders of the modes along vertical and horizontal directions (respectively).

In that case, the inequality giving the fundamental frequency is then as follows:

ω_{0}^{2} ⩽ \min_{r, s, t} \frac{\int_{Ω} μ ({(\frac{\partial ψ_{2}}{\partial x})}^{2} + {(\frac{\partial ψ_{2}}{\partial z})}^{2}) d x d z}{\int_{Ω} ρ ψ_{2}^{2} (x, z) d x d z}

(8)

3 Modal estimation of the fundamental frequency

3.1 Fundamental frequencies for both parts of the basin

The fundamental frequencies (first eigenmode for each part of the basin) are estimated with Eq. (8), considering various shear modulus values: μ₁=180 MPa (i.e. V_S=300 m s⁻¹), μ₂=120 MPa (i.e. V_S=245 m s⁻¹) et μ₃=90 MPa (i.e. V_S=212 m s⁻¹). In Table 1, the numerical results given by Rayleigh's method are compared to the frequencies of maximum amplification given by the Boundary Element Method (with detailed analysis of the wave propagation process [3,5,11]).

From these results, it can be noticed that the fundamental frequencies given by Rayleigh's method are in good agreement when compared to the frequencies of large amplification known from the propagative approach. The agreement is satisfactory for the resonance of the deepest part of the basin (west) and for the thinnest part (east). Considering different values of the shear modulus, the fundamental frequencies logically decrease with decreasing modulus. For a homogeneous basin model, Rayleigh's method seems to give very interesting results that are in good agreement with numerical values given by a propagative approach [11].

3.2 Comparison between simplified modal method and amplification curves

The fundamental frequencies estimated by the simplified modal method are then compared with the whole amplification curves given by both experiments and propagative BEM simulations [7,11]. In Fig. 2, vertical lines represent the fundamental frequency values for western and eastern parts of the basin estimated for various shear moduli (μ₁; μ₂; μ₃). For the western part of the basin, the fundamental frequency f₃ estimated for μ₃ (solid line) is in very good agreement with both experimental (top) and BEM (bottom) amplification peak. For the eastern part of the basin, the agreement with the second amplification peak is very satisfactory for the shear modulus μ₁ (dotted-dashed line). It then gives an insight into the influence of the shear modulus (or wave velocity) of the basin on the resonance process. The influence on the amplification process itself is shown by the BEM propagative results (Fig. 2 and [11]).

4 Conclusion

The analysis of site effects by a simplified modal approach seems to give reliable results. The site considered herein is an alluvial basin located in the centre of Nice, from which experimental results give amplification factors ranging from 10 to 30 for frequencies around 1 Hz for the deepest part (west) and 2.8 Hz for the thinnest part (east).

Thanks to Rayleigh's method, the fundamental frequencies of both parts of the basin were rapidly estimated and are in good agreement with experimental and BEM numerical results. This simplified modal characterization of alluvial basins is of great interest for practical preliminary investigations on site effects, microzonation... To improve this modal approach, several issues should be addressed in the future, such as the velocity profile in the basin or the influence of damping [14].