1 Introduction
Active mountain piedmont is a suitable laboratory for understanding the processes of mountain building, because it concentrates most of seismotectonic and morphogenetic activity [1]. Its evolution is controlled by strong interactions between crustal deformation processes (faulting, folding), surface processes (erosion, transport, sedimentation) and climate (precipitation, glacial/interglacial cycles [4,11]). Such couplings occur at different space and timescales and trigger numerous feedback loops (Fig. 1). For instance, tectonic activity generates relief that controls surface processes in influencing erosion patterns, drainage network development, sedimentary basin growth, and local climate [17,19,21,31,35]. In return, erosion, transport and sedimentation induce large mass transfer across the range that modifies the dynamical equilibrium of orogenic wedges and trigger mechanical feedbacks (out-of-sequence thrust, duplex formation) [16,20,27,28,37].
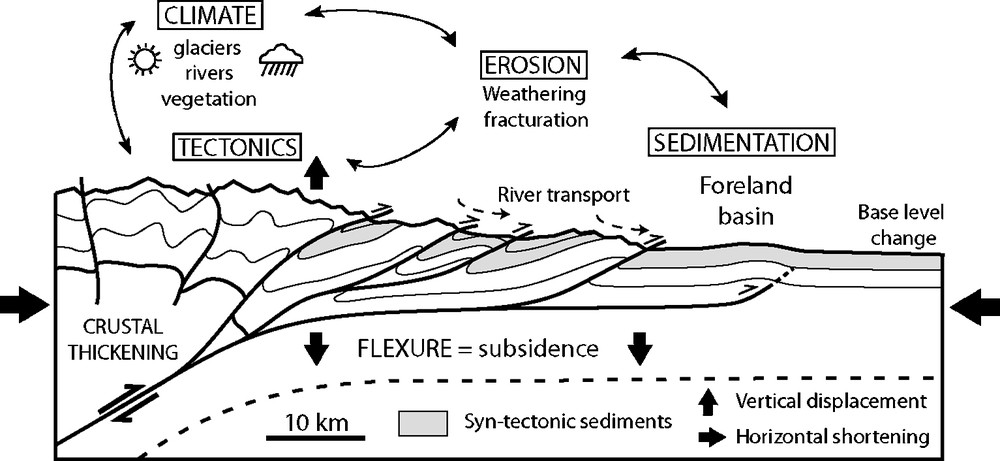
Section of a mountain piedmont illustrating couplings between tectonics, erosion, sedimentation and climate.
Fig. 1. Coupe illustrant les couplages tectonique–érosion–sédimentation–climat dans un piedmont de chaîne.
In the field, studying these couplings relies on the geometrical analysis and dating of morphological and structural markers (faults, folds, terraces, fans; [24,36]), on palaeoenvironmental studies [30] and on syntectonic sedimentation analysis [7,33]. These data document the major phases of mountain building and its climatic history, but are often too sparse for constraining the dynamics of processes that control its morphological evolution. To better constrain the relation between tectonics and erosion/sedimentation rates, it is therefore crucial to understand how the morphological markers form, evolve, and record deformation.
Several numerical and analogue models have studied interaction mechanisms that link tectonics and erosion to morphology. For instance, previous works show how orographic precipitation modifies the structural style of mountain ranges [21,37] and how tectonics processes control drainage network development [15,34,35]. Other models underline the impact of erosion and sedimentation on the structure and evolution of orogenic wedges [20,27] or the role of tectonics and climate on the maximal elevation of topography [3,23]. However, few works have developed experimental models dedicated to the morphostructural evolution of a whole mountain range piedmont, coupling both crustal deformation processes (thrusting, folding) and erosion–transport–sedimentation. To achieve this goal, we have developed a new approach that uses specific analogue materials and accurate measurement techniques. Here, we present the methodology, analyze and discuss the preliminary results to validate our experimental procedure and evaluate the potentialities of the approach. Further works about the physical properties of analogue materials, measurement techniques and comparisons between experiments and actual piedmonts will be described in more details in dedicated publications.
2 Methodology
2.1 Experimental set-up and protocol
The experimental set-up is an adaptation of a former apparatus used for studying deformation mechanisms in convergent settings (oceanic and continental subduction [12,25,27]) and for analyzing erosion–transport processes [8,14,15]. It is composed of:
- • a computerized deformation device;
- • a rainfall system for erosion;
- • an optical measurement bench (Fig. 2).
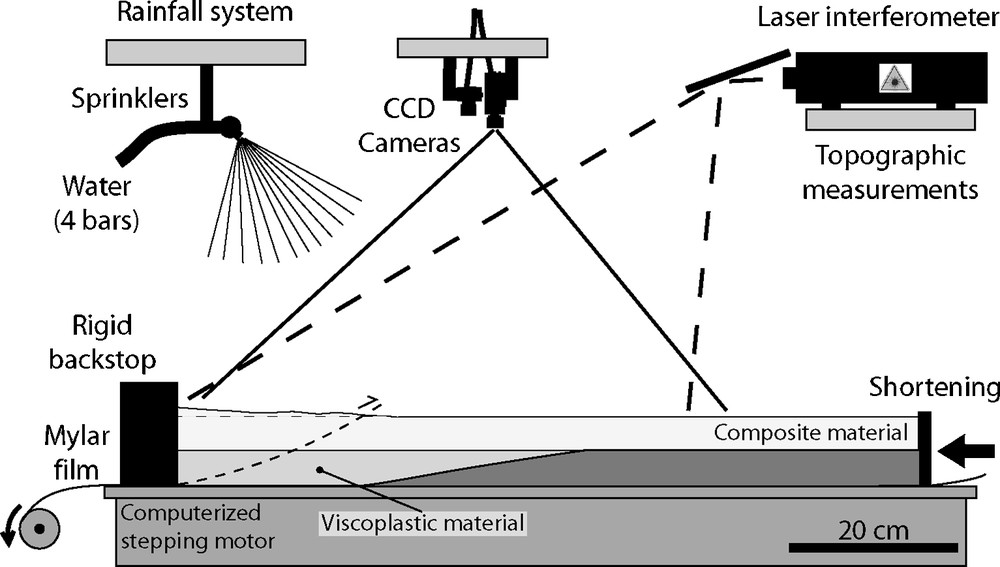
Experimental set-up. It is constituted by a deformation device, a rainfall system and CCD cameras coupled to a laser interferometer that measure deformation and topography.
Fig. 2. Dispositif expérimental composé d’un banc de déformation, d’un système de brumisation et de caméras CCD couplées à un interféromètre laser pour mesurer la déformation et la topographie.
2.2 Analogue material
Analogue materials in experimental models often consist in dry granular materials (sand [10,25,27]) or water-moisten powders (loess [23]; silica powder [3,8,34]; fly ash [14]). Our material has been selected after in-situ tests realized on a great variety of materials (glass microbeads and microspheres; silica, plastic, graphite, pumice powders; clay; talc). Its composition and characteristics have been determined to satisfy several physical criterions:
- • the material rheology must satisfy the Mohr–Coulomb failure criterion [6,9,10,22] so as to generate faults;
- • it should erode trough diffusive processes on hillslopes (landslide, solifluction) and advection in valleys (channels) so as to simulate the main erosion/transport processes that shape the morphology of natural relief and form drainage basin, crest, hillslope and riverbed features;
- • grain size distribution should be small enough and range over several orders of magnitude to ensure both varying transport distances of particles and grain sorting;
- • erosion rates should be high enough to limit experiment duration.
Thus, sedimentary deposits would be stratified and might record tectonic and stratigraphic structures (fault, fold, unconformity, cut-off, downlap…). Our tests on water-saturated materials show that deformation style, erosion/transport processes and therefore morphologies are strongly dependent on their physical properties. For instance, rounded and well-sorted materials, such as glass microbeads or PVC granules, erode rapidly by dominant landslide processes and have a limited mechanical strength. Some other angular compositions concentrated in silica powder erode slowly by incision and hardly deform due to their high cohesion. Accordingly, it appears that grain-size, grain-shape, and water-content control cohesion that is responsible for the observed erodabilities and deformation styles. The composition of our selected analogue material (median D50 at 105 μm) is made up with glass microbeads (40%), silica powder (40%) and plastic powder (20%). During experiments, it is progressively sifted and moistened with water (saturation rate around 25% in weight). Its physical characteristics are synthesized in Table 1.
Physical properties of the analogue material
Tableau 1 Propriétés physiques du matériau analogue
2.3 Boundary conditions and scaling
We used available geophysical data (DEM, seismic profiles, geodetic measurements) and field geological observations across active mountain ranges (Tian Shan, Taiwan; [5,7,29]) to determine initial boundary conditions of models (rheology, structure). We focused our study on the first 10–15 km of the continental crust and simplified the continental rheology by forming two main layers (Fig. 2). Typically, the brittle sedimentary cover is represented by 5–10 cm of composite material, whereas the deeper basement, whose mechanical behaviour is more ductile, is modelled with a viscoplastic material composed of a mixture of talc (65%) and mineral oil (35%). We used an initial model topography made of very low amplitude relief (less than 1 cm) because it fastens the development of drainage network by concentrating water flow, thus shortening the duration of experiments by several hours. This is justified because deformation at active mountain front propagates on pre-structured foreland topography where hydrographic network and inherited relief already exist.
Model scaling [18] has been defined with a semi-empirical approach. A rigorous scaling is difficult to achieve because some laws and physical properties in model and nature are not well constrained (cohesion, erosion threshold, erosion and transport laws; [23,34]). First, we performed several tests to compare the geometrical characteristics of experimental morphologies to their natural counterparts as observed from satellite pictures or field measurements. From analysis of valley, terrace and fan dimensions, a geometrical scaling ratio of 1–2 × 10−5 (1 cm ≈ 500–1000 m) has been defined (see for instance Figs. 3 and 4). This is similar to classical values used in analogue modelling [20,22]. Given the model dimensions (1.2 × 2.2 m), we reproduce a portion of piedmont that is about 100 km large. Second, writing the fundamental equation of dynamics for continuum medium in a non-dimension form [10] defines a dimensionless number that compares surface to body forces: σ/(ρ g L). The conservation of this number between model and nature leads to σ* = ρ* g* L*, with σ*, ρ*, g* and L* the model-to-nature ratios for cohesion, density, gravity, and length, respectively. Given that g* = 1 (experiment in the Earth's gravity field), ρ* ≈ 1.5 (sedimentary rocks to material mean density ratio; respectively 2400 and 1600 kg/m3) and L* = 1–2 × 10−5 (estimated geometrical scaling), σ* should be 1,5 × 10−5–3 × 10−5. If one considers that cohesion for consolidated sedimentary rocks is about 107–5 × 107 Pa (limestone, sandstone; [6]), analogue material cohesion should range between 150–1500 Pa. Cohesion of our moisten material has been estimated around 400–600 Pa with an apparatus similar to the Hubbert-type shear box [22]. This value is reasonable according to scaling. Further discussion of experiments and material physical properties are developed in a paper in preparation. Finally, the time ratio between model and nature has been estimated empirically with a specific set-up that calculates mean erosion rates of composite materials for various surface slopes. These measurements are performed with constant precipitation rates similar to typical experiments (around 30 mm/h). For topographic slopes ranging from 10 to 20°, mean erosion rates are respectively estimated at 2–5 mm/h. Compared to natural mean erosion rates (few mm/yr [4]), the time ratio in our model is roughly estimated between 5 × 10−10 and 1 × 10−09 (i.e. 1 s ≈ 35–70 yr and 1 h ≈ 125–250 kyr). By considering both temporal and geometrical scaling ratios, appropriate shortening velocities in the model should be around 20–40 mm/h to simulate natural convergence rates around 10–20 mm/yr. Typically, experiments span about 10 h, which is equivalent to 20 km shortening in 2 Myr. Note that such temporal and dynamical scaling calculations are empirical and somewhat speculative, as they have been performed with mean geologic and experimental values that present uncertainties. In addition, some distortions might arise with morphological modelling as some hydraulic and hillslope characteristic times are hardly downscaled in experiments [23,34]. However, our calculation is performed at a global scale with mean shortening and erosional velocities. Therefore, it would indicate smooth discrepancies between individual characteristic times of processes and provide a reasonable approximate time scale.
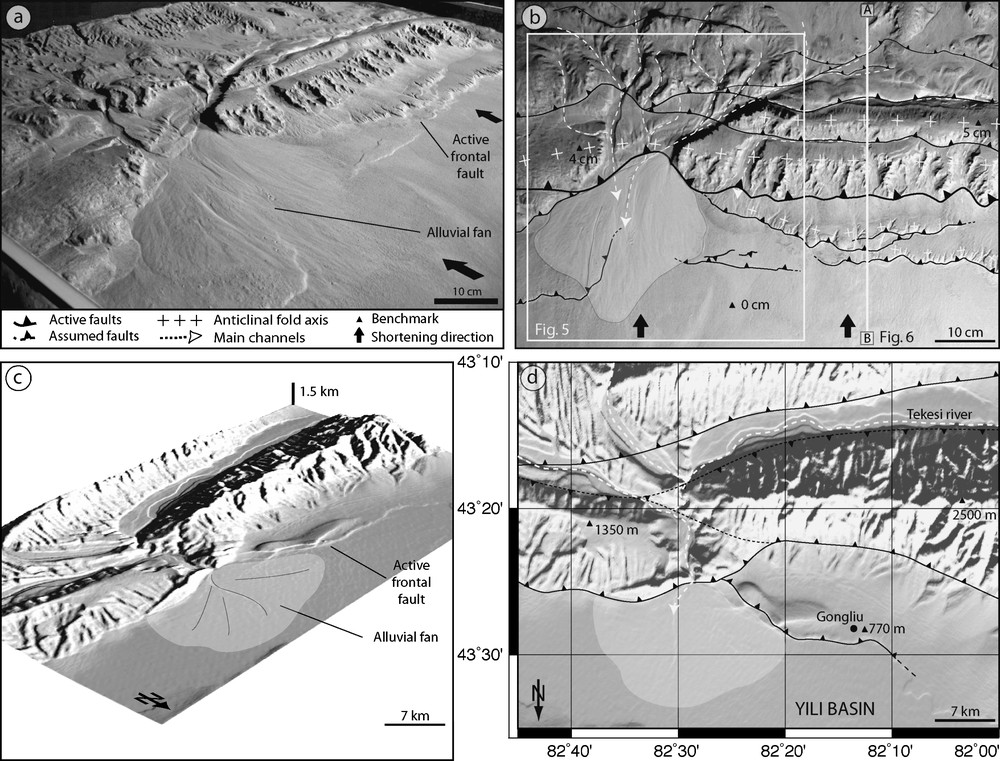
Experiment of piedmont formation in frontal convergence compared to the Tian-Shan mountain. (a) Oblique and (b) map views with structural sketch. White frame corresponds to Fig. 5. Cross-section A–B corresponds to Fig. 6. (c) Oblique and (d) map views with structural sketch of the Tekesi River flowing down to the intramontaneous Yili basin (SRTM data, NASA). Note that north is oriented downward.
Fig. 3. Expérience de formation de piedmont en convergence frontale comparée à un exemple dans le Tian-Shan. (a) Vue de trois quarts et (b) vue en plan interprétée. L’encadré blanc correspond à la Fig. 5. La coupe A–B correspond à la Fig. 6. (c) Vue oblique et (d) en plan de la rivière Tekesi s’écoulant vers le bassin intramontagneux de Yili (données SRTM, NASA). Noter que le nord est orienté vers le bas.
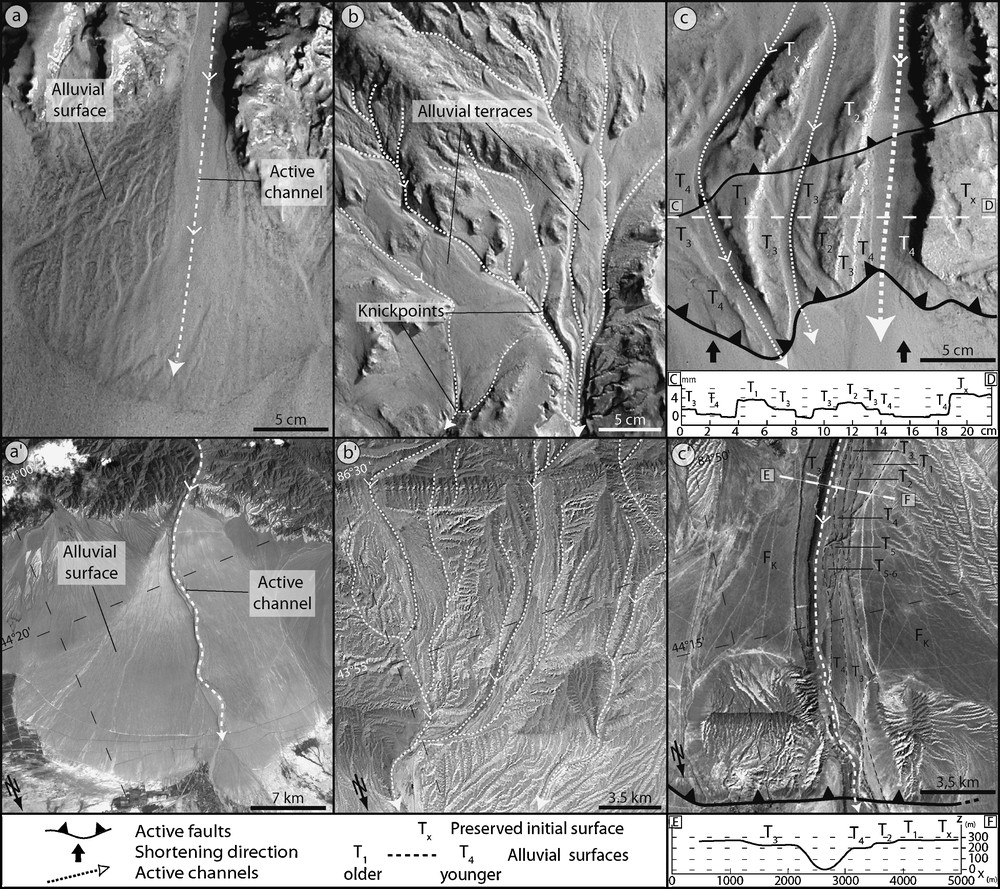
Pictures of morphological features in experiment and equivalents in nature from Tian Shan northern piedmont (Landsat 7 satellite images). (a,a′) Alluvial fans. Note active channels and old alluvial surfaces; (b,b′) channel network with sub-parallel channel patterns in piedmont drainage basins. Note alluvial surfaces and knickpoints in experiments; (c,c′) stair-step fluvial terraces. Several successive levels are preserved on both sides of active channels. Topographic profiles show the vertical height of each terrace. Note downward orientation of north for satellite pictures.
Fig. 4. Photographies de détail d’objets morphologiques expérimentaux et équivalents naturels extraits du piedmont nord du Tian Shan (Images satellites Landsat 7). (a,a′) Dépôts alluviaux en éventail. Remarquer les chenaux actifs et les surfaces alluviales anciennes ; (b,b′) réseau hydrographique subparallèle dans les bassins versants de piedmont. Noter la présence de surfaces alluviales entre les bras actifs et de ruptures dans le profil en long des rivières expérimentales (knickpoints) ; (c,c′) surfaces étagées. Plusieurs niveaux de terrasses s’échelonnent de part et d’autre des bras d’une rivière active. Des profils topographiques transversaux montrent leurs dénivelés verticaux respectifs. Noter l’orientation du nord vers le bas sur les images satellites.
3 First results
3.1 Validation of morphologies and deformation mechanisms
We performed several experiments to compare model surface morphologies and deformation mechanisms with natural cases. To illustrate our first results, we describe some examples of structural and morphological markers issued from a typical experiment and compare them with natural morphologies and structures from the Tian Shan mountain range (Figs. 3 and 4). In this experiment, rainfall and convergence rates were kept constant during 9 h, respectively at 30 mm/h and 40 mm/h. Rainfall was almost homogeneous over the model surface (less than 20% of lateral variations) and the imposed model shortening corresponds to a frontal convergence. Based on these parameters, we model a piedmont with a rapid convergence rate (about 20–30 mm/yr) and a relatively slow erosion rate (less than 1 mm/yr). Two digital pictures framed prior to final stage are presented in Figs. 3a and b. The overall morphology is dominated by two topographic ridges trending perpendicular to the direction of convergence. These structural reliefs are controlled by several reverse faults spaced by about 10 cm and dipping toward the buttress. This deformation pattern corresponds to a tectonic accretionary wedge similar to typical active piedmont structure [9,24]. The drainage network is characterized by upstream sub-parallel patterns and ‘en treillis’ network in the frontal deformation domain. Several fan-shape sedimentary bodies lie at the base of the deformation front. They are formed by the break in slope and drop of the transport capacity of channels that widen brutally when crossing the deformation front and reach the foreland basin. All these features can be considered as the equivalent of natural river networks (Fig. 3c and d).
We present three examples of morphotectonic features formed in this experiment (Fig. 4). The first example is an alluvial fan (Fig. 4a). Its fan shape (apex localized at the channel outlet and circular front) is linked to the sweeping and divagation motion of distributary channels on its surface. This dynamics leads to the coexistence of old, preserved alluvial surfaces and active channels. Its slope is 5–6° and its surface is around 250 cm2 (i.e. few hundreds of square kilometres in nature). On the field, slopes of most alluvial fans range below these experimental values (1.5 - 3̊ in Tian Shan piedmonts; Fig. 4a′). However, the morphology displays similar features as the one described above (Fig. 4a and a′). It suggests that transport processes in experiments may not be perfectly similar to natural ones [23] or that vertical and horizontal scaling may be different. Nevertheless, it does not prevent from having alluvial fans with a comparable morphological dynamics.
The second example illustrates the drainage network that forms in piedmont catchments (Fig. 4b). It has a general subparallel geometrical pattern with crests and preserved alluvial surfaces between channel branches. Several knickpoints, about 1 mm in amplitude (i.e. ±50–100 m in nature), are present along channel beds. These features form in response to channel incision and headward erosion that accompany internal catchment uplift. In nature (Fig. 4b′), drainage basins in piedmont display similar sub-parallel drainage patterns, channel characteristic dimensions (width, length) and landforms (crests). It suggests that erosion–transport processes in model respect the average proportion of land sculpting processes, i.e. diffusive processes on hillslopes and advective transport in channels.
Finally, the last example corresponds to a set of stair-step surfaces located above two active thrusts (Fig. 4c). They are linked to the drainage network dynamics (divagation, piracy, incision) that entails variations in hydraulic flows and a global migration of channels rightward (terracing T2, T3 and T4 on right edge; steep banks on left edge). A topographic profile perpendicular to the flowing direction indicates that the differential elevation between these surfaces is around 1 mm, i.e. more or less 50–100 m in nature. These relative heights can be correlated to the deformation front's uplift rate and to the dip of the frontal thrust. Such stair-step values and geometries compare well in amplitude and morphology to natural uplifted fluvial terraces deformed on active faults or propagation folds (see Fig. 4c′ framed on the Kuitun fold in the northern Tian-Shan piedmont [7,29]).
3.2 Example of morphostructural evolution analysis
To illustrate the morphostructural analysis that can be performed during experiments (Fig. 5), we present three steps of the deformation front evolution at the level of the major alluvial fan framed in Fig. 3b. These stages correspond respectively to 20, 22.5 and 25 cm of total shortening (that is, a picture every 1250–2500 m of shortening in reality). During the first 20 cm, three successive thrusts appear in sequence (Thrust 1, 2, 3). The branching of Thrust 2 on Thrust 1 has channelized the drainage network parallel to the trending direction of the range and left one single outlet that fed the large alluvial fan. The sedimentary history of this period is not differentiated and appears in blue in Fig. 5a. At the next stage (Fig. 5b), the river embanks in response to frontal thrust activity and three stair-step terraces form on the right riverbank. Different alluvial surfaces appear on the fan and can be time-correlated to the fluvial terraces. Their geometry corresponds to the sweeping motion of distributary channels: firstly clockwise (phase I) and secondly counterclockwise (phase II). This sweeping motion is partly due to the natural fan dynamics, but is also clearly influenced by the activity of thrust 3 that forces channel incision and fix outlet position. A fourth thrust forms about 10 cm in front of the previous one and forms a major virgation in front of the channel outlet. Such a curvature may be the result of a focused incision effect on deformation [26,32]. In unloading continuously the hanging wall, incision would decrease local vertical stress and favour fault dip increase. In 3D, along-strike variations in fault dip would be responsible for the observed arcuate fault scarp. Finally, at the last stage, shortening is mainly accommodated on the frontal thrust (Fig. 5c) and the older thrusts are only slightly active. The scarp associated with the new thrust localizes erosion that rises upward in reworking previously deposited sediments. A new generation of alluvial fan forms at the base of the growing relief. Future similar works will provide insights into the timing of alluvial fan growth and terrace nucleation in relation to thrust activity and deformation propagation.

Successive steps of the morphostructural analysis of the deformation front (location in Fig. 3b; 2.5 cm shortening between each step). (A) Pictures and superimposed displacement field. Note that vector lengths decrease across active thrusts. (B) Morphostructural interpretation of each step. Note river network evolution (regressive erosion, piracy) and alluvial dynamics (terraces, fans) associated with thrust activity.
Fig. 5. Stades successifs de l’évolution morphostructurale du front de déformation (localisation sur la Fig. 3b ; 2,5 cm de raccourcissement entre chaque étape). (A) Photographies et superposition du champ de déplacement. Noter les chutes de norme des vecteurs au franchissement des chevauchements actifs. (B) Interprétation morphostructurale de chaque étape. Remarquer l’évolution du réseau hydrographique (érosion régressive, captures) et la dynamique alluviale (terrasses, cônes) liée à l’activité des chevauchements.
3.3 Example of structural and stratigraphical analysis in cross-section
At the end of the experiment, serial sections are cut across the model to study its internal structure, determine the deformation style, and analyze syntectonic sedimentation. Fig. 6 shows one of these cross-sections located in Fig. 3b. The model displays a typical accretionary wedge structure with hinterlandward dipping thrusts that propagate in sequence toward the foreland. The most frontal thrusts display a flat and ramp geometry that generates low-amplitude box-shaped anticlines. Finely stratified syntectonic deposits fill piggyback and foreland basin. The laminations underline prograding (downlap) and tectonic structures (cut-off). A sharp change in the sedimentary composition occurs in the foreland sequence (Fig. 6). Based on the analysis of video movies taken during the experiment, this evolution is linked either to the progradation of proximal facies or to changes in alluvial fan hydraulics. Additional experiments are required to better characterize this diachronism and correlate its occurrence to foreland deformation history and hydraulics. This is a critical field issue, as natural equivalents are generally interpreted for identifying thrust reactivation or propagation.
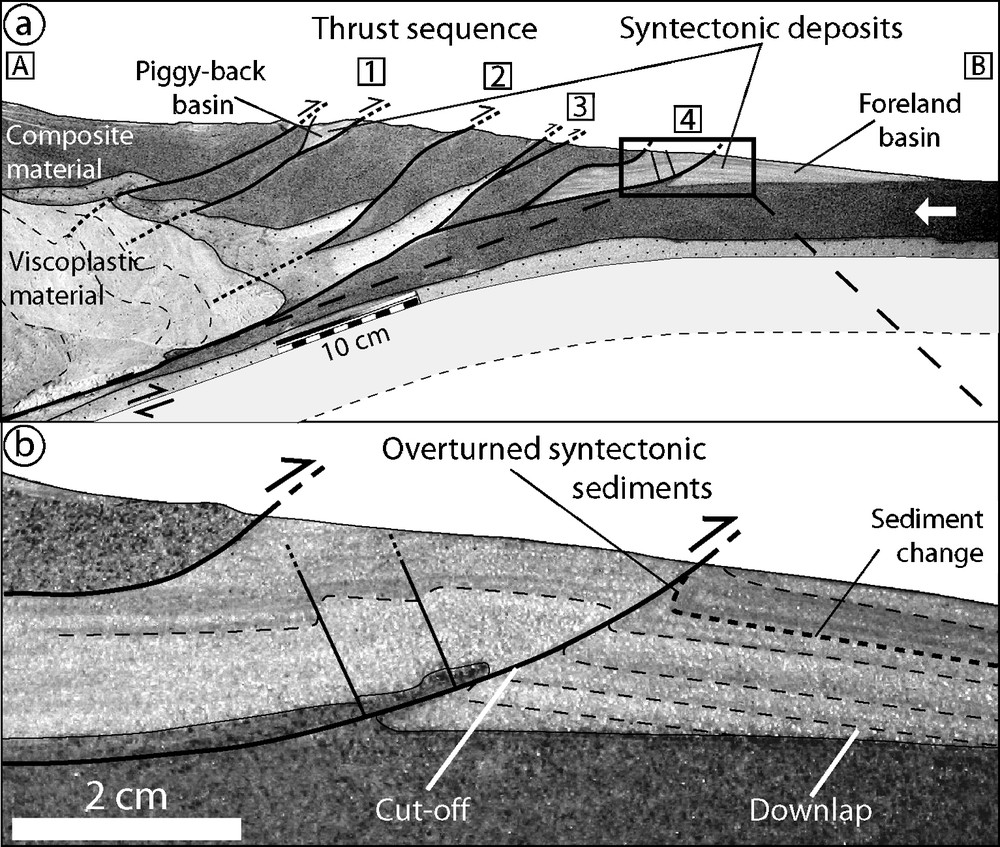
Cross-section performed at the end of experiment (see Fig. 3b for position). (a) Whole-model cross-section. (b) Close view of the deformation front. Note the details of syntectonic deposits that underline tectonic and stratigraphic structures (cut-off, downlap).
Fig. 6. Exemple de coupe réalisée au stade final de l’expérience (voir Fig. 3b pour la localisation). (a) Coupe de l’ensemble du modèle. (b) Vue rapprochée du front de déformation. Noter la finesse des dépôts syntectoniques préservés dans le bassin d’avant-pays et les structures tectoniques (cut-off) et stratigraphiques (downlap) qu’il contient.
4 Discussion and perspectives
The experiment described in this article demonstrates that, by using specific analogue materials and experimental set-up, the dynamic evolution of a mountain range piedmont can be modelled. Then, the formation of the morphological and structural markers that characterise its topography can be studied quantitatively. Even if several morphogenetic or tectonic processes are not accounted for in our models (differential or glacial erosion, flexural subsidence, etc.), the main morphogenetic processes are correctly simulated.
Concerning tectonic processes, the deformation pattern is characterized by folds and faults that root on a basal decollement and propagate in sequence toward the foreland. At depth, the use of a specific material that deforms by folding sustains active uplift in internal domains. This deformation simulates accretionary wedge building processes and trigger strain fields similar to active piedmonts (uplift, propagation, partitioning).
Modelling of erosion and transport processes by water runoff entails diffusive mechanisms on hillslopes (landslide, solifluction) and abrasion in channels (incision and lateral erosion). The combination of these morphogenetic processes generates topography with entrenched valleys and crests and morphological features similar to natural markers of piedmont, such as alluvial and fluvial terraces, wind gaps, lakes, and alluvial fans. Despite some local artefacts (overhangs, convex crests, flat-bed channels) that are linked to excessive capillary cohesion and hydraulic forces, the drainage network geometry displays sub-parallel geometry in internal zones and trellis at frontal structures that compare to natural hydrographic networks. Hydrodynamic phenomena such as antecedence, superimposition, piracy, headcut erosion, knickpoint migration, and terrace formation are also properly modelled.
The use of a specific analogue material composed of heterogeneous grains (granulometry, shape, and densities) favours particle sorting during transport and sedimentation. Sorting occurs both vertically (lamination) and horizontally (distal and proximal facies). This syntectonic sedimentation underlines structures (cut-off and downlap) that can be investigated to bring insights into the evolution of sedimentary rates, tectonic activity, and erosive phases of relief during experiments. Therefore, it would improve the understanding of relief dynamics record in sedimentary basins and its potential deciphering.
Finally, these experiments show numerous structural, morphological, and sedimentary features that can be directly compared to mountain range piedmonts. On the field, only the final stage of the dynamics is observed. Using this set-up, it is possible to study precisely and continuously how the markers form, evolve, and record relief history. It opens new and promising perspectives for experimental modelling, notably in geomorphology (relief dynamics), seismotectonics (active faults analysis), and sedimentology (sequential stratigraphy).
Acknowledgments
This study was funded by the ‘Reliefs’ and ‘Eclipse’ INSU–CNRS programs. We are thankful to J. Malavieille, J.-E. Hurtrez, Y. Lagabrielle, H. Philip, P.R. Cobbold and two anonymous reviewers for their constructive comments and suggestions that improved the manuscript. Many thanks to C. Romano and E. Berthebaud for technical assistance. Thanks to the GLADYS project (www.gladys-littoral.org) and University of Montpellier-2 for granulometric measurements and Scanning Electron Microscopy photography.


