1 Mineralogy of CO2 geological storage
Before thinking of manipulating carbon dioxide (CO2) at a large scale (which mankind has done already by burning large quantities of fossil fuels), it is useful to have a coherent view of the natural CO2 geochemical cycle. This will allow assessment of the extent of environmental anthropogenic perturbation and identification of the mineralogical mechanisms of interaction of carbon dioxide with its surrounding. A general scheme of the CO2 cycle without anthropogenic perturbation is given in Fig. 1 with emphasis on the main processes where mineralogical science will be most useful. More detailed representations of the carbon cycle can be found elsewhere (e.g., Gaillardet and Galy, 2008). In a simplified view, one considers generally that the flux of outgassing of CO2 from the solid Earth by magmatic and metamorphic processes is of the same order of magnitude as that of its export to the solid Earth in the form of carbonate minerals and of fossil organic matter. The feedback mechanisms within this cycle are still unclear and constitute the object of intense research (e.g., Berner, 1991; Gaillardet and Galy, 2008). Two major non-mutually exclusive hypotheses for these mechanisms are considered:
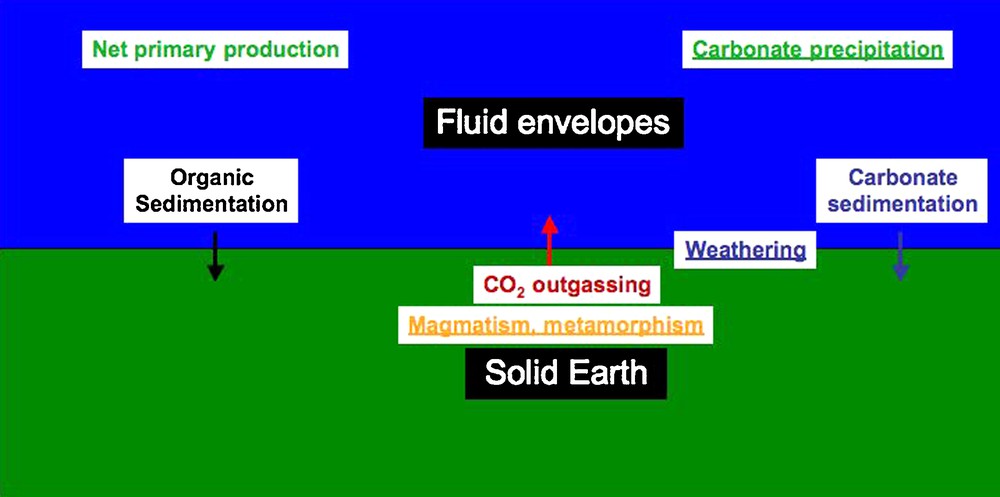
Schematic representation of the CO2 natural cycle in the mode of geochemical boxes. Arrows are indicative of fluxes of the order of 1013 moles of carbon per year. Weathering (alteration of minerals at the interface between solid Earth and fluid envelopes) and net primary production (essentially photosynthesis minus respiration on a global scale) are natural mechanisms of capture of CO2 outgassed from the solid Earth by magmatic and metamorphic processes. Processes in which mineralogical control is primordial are underlined.
Représentation schématique du cycle naturel de CO2 sous forme d’échanges entre réservoirs géochimiques. Les flèches représentent des flux de l’ordre de 1013 moles d’atomes de carbone par an. L’altération (réaction chimique des minéraux à l’interface entre la Terre solide et les enveloppes fluides) et la production primaire nette (essentiellement le bilan global photosynthèse-respiration) sont des mécanismes naturels qui permettent de capturer le CO2 dégazé depuis l’intérieur de la Terre par magmatisme et métamorphisme. Les processus dans lesquels la minéralogie joue un rôle primordial sont soulignés.
In the first, the alteration rate of minerals is indirectly correlated to CO2 contents of the atmosphere and hydrosphere (see a review in Kump et al., 2000) through temperature variations, erosion rates, role of vegetation, soil pressure of CO2, etc. The main chemical reactions involved in the alteration of minerals and subsequent precipitation of carbonates are summarized as dissolution of silicates (reaction (1)), precipitation of carbonates (reaction (2)), and capture of CO2 by chemical weathering (reaction (3), which represents the sum of reactions (1) and (2)):
| (1) |
| (2) |
| (3) |
In these chemical reactions, only silicates with divalent M cations such as Mg2+ and Ca2+ are represented, but dissolution reactions can also be written with monovalent cations (Na+, K+). However, for crystal chemical reasons, alkali cations are rarely involved in solid carbonate precipitation and thus in the global export of CO2 to the solid Earth (e.g., Oelkers et al., 2008). Conversely, such cations could be involved in reverse weathering on continental margins and are actually thought to potentially reduce the uptake of CO2 from mineral weathering (Mackenzie and Kump, 1995).
Positive feedback between the thermodynamic activity of CO2 and silicate dissolution is not easy to demonstrate, and the governing mechanisms are not well established. For example, positive temperature-silicate dissolution correlations have been demonstrated in the case of basalts (Dessert et al., 2003, Gaillardet et al., 1999) and suggested for granites (White and Blum, 1995). Of course, understanding in detail the mineralogical aspects of silicate dissolution and of carbonate precipitation is an essential component required for understanding that regulation.
The second hypothesis involves photosynthesis by bacteria, photosynthetic unicellular eukaryotes and green plants, as represented simplistically by reaction (4), which represents primary production via photosynthesis:
| (4) |
Oxygenic photosynthesis is enhanced as carbon dioxide increases, either through temperature increase or because of CO2 limitations of biomass in some ecosystems. The reverse reaction
| (5) |
| (6) |
Together, these two mechanisms–silicate dissolution/carbonate precipitation and transfer of organic matter to the solid Earth–are considered to be of the same order of magnitude. Perturbations due to glacial/interglacial alternations are not included in this framework because they mostly concern carbon dioxide redistribution between the atmosphere and the ocean. The burning of fossil fuel is very different because it modifies the transfer of CO2 from solid Earth to Earth's fluid envelopes. In that sense, it is almost useless to discuss the environmental consequences of fossil fuel burning in light of climate/CO2 correlations over the last 500,000 years. Although very different, it would be more appropriate to compare the CO2 contributed by fossil fuel burning with that resulting from major volcanic events that led to deposition of massive basaltic traps. Although to date, the levels of CO2 contributed by the latter process are poorly constrained, anthropogenic fossil fuel (extracted from the solid Earth) burning, which is estimated to involve about 6 × 1014 moles of carbon per year, might possibly be even larger. In response to that unusual perturbation, the Earth has initiated other “emergency” mechanisms to regulate CO2 levels.
First, because CO2 is a highly soluble gas, most of the carbon dioxide transferred from the solid Earth to Earth's fluid envelopes should indeed end up in the ocean. This is what will eventually happen, but it will require a characteristic absorption time of thousands of years. Quasi-immediate CO2 uptake by surface waters on the time scale of years accounts for about half of the 6 × 1014 moles of carbon per year. Although absorption of the rest will take much longer, this mechanism contributes to a decrease in the CO2 content of the atmosphere. As a means of enhancing this mechanism, several projects have proposed injection of some CO2 in the deep ocean, which would substantially shorten the thousands of years required for the uptake of the remaining carbon dioxide (e.g., Adams and Caldeira, 2008, and references therein). Whether an abrupt increase in dissolved CO2 in different compartments of the ocean will have an effect on pH and on marine ecosystems is, however, not well understood (e.g., Ricketts et al., 2009). In that respect, the highly publicized problems of the effect of ocean acidification on corals, although highly complex and due to multiple causes, are not very encouraging from the perspective of CO2 ocean storage.
Second, because the rate of photosynthesis is on the order of 1016 moles of carbon per year (e.g., Garrels et al., 1975), which is about 20 times faster than the anthropogenic perturbation, one might think that a small relative increase (∼ 1%) in the rate of reaction (4) would be enough to fully compensate for the additional emission of carbon dioxide from the burning of fossil fuels. The common belief that CO2, directly or indirectly (through temperature increase) favors the growth of green plants, adds credibility to this possibility. This would indeed be the case if CO2 were a limiting factor of reaction (4) on a global scale. This belief is not true, however, in most ecosystems. Other factors, such as available nitrogen and phosphorus, fix the global amount of biomass. The response of plants to increasing CO2 levels is highly complex (e.g., Dukes et al., 2005; Field et al., 1995) but, to roughly summarize, it appears that natural photosynthetic processes can thus only marginally absorb more CO2 than what they do now – an idea supported by recent experiments on the fumigation of forest plots with increased atmospheric CO2 by Schlesinger and Lichter (2001). The ideas of enhancing net primary production by planting trees and using more wood on a global scale are worth investigating, but they will have to deal with the natural and anthropogenic cycles of nitrogen and phosphorus, which will affect their actual CO2 impact in a complex manner. Other ideas such as ocean fertilization for enhancing sedimentation of organic matter (e.g., Buesseler et al., 2004; Coale et al., 2004) imply very complex ecological interactions in the ocean and will thus probably never be performed on a large scale. From an environmental perspective, the actual biomass enhancement, and thus CO2 capture due to human fertilization, is directly related to eutrophication, a major environmental problem that results in the capture of about 10–20% of the 6 × 1014 moles of carbon per year due to fossil fuel burning. However, such eutrophication will make the use of biomass enhancement for mitigating excess atmospheric carbon dioxide challenging on a large scale. The possible massive use of biomass fuels in the coming decades is related to these questions.
We are thus left with several 1014 moles of CO2 per year in excess of the non-anthropogenic, naturally regulated contribution that are presently and will continue for tens of years to be transferred from the solid Earth to Earth's fluid envelopes. One might decide not to try to regulate that new flux, noting that nobody knows what the effects of that increase will be; some even argue that this new flux might indeed be beneficial, as S. Ahrrenius proposed over 100 years ago: “By the influence of the increasing percentage of carbonic acid in the atmosphere, we may hope to enjoy ages with more equable and better climates, especially as regards the colder regions of the Earth, ages when the Earth will bring forth much more abundant crops than at present, for the benefit of rapidly propagating mankind” (Arrhenius, 1908). However, another possibility is that the consequences of increased CO2 levels in the atmosphere could be devastating, as suggested by relationships between stable isotopes of carbon in the geological record and major biosphere crises (e.g., Schidlowski, 1988); we thus should try to regulate the carbon dioxide levels in the atmosphere. Based on current understanding, Pacala and Socolow (2004) have proposed that atmospheric increases of CO2 concentration due to fossil fuel burning should not exceed 500 ppm by volume. However, there is no strong rationale for 500 ppm rather than other values, and thus this level should be taken as a symbolic threshold of about twice the pre-industrial level. Taking this into account, as well as economic and population growth considerations, Pacala and Socolow (2004) have proposed that 5 to 8 technologies should be used together for mitigating this increase, with each technology reducing the total release of CO2 by ∼ 1014 moles (∼ 4 Gigatons) per year in order to be significant.
Among those technologies, CO2 capture and geological storage is a possibility whose safety, feasibility, reliability, and costs need to be assessed. This technology is already used on a mid-sized scale, in particular as CO2 is injected underground to help oil and gas recoveries. Just to give a specific example (one not motivated by recovery considerations but rather by national environmental regulations), CO2 has been injected in a submarine aquifer by an hydrocarbon company offshore of Norway in the gas field of Sleipner at a rate of 3000 tons of CO2 per day for a total injection of 15 millions of tons of carbon dioxide (e.g., Akervoll et al., 2009; Lindeberg et al., 2009; Torp and Gale, 2004, and references therein). If the global target for CO2 geological storage is to avoid the release of about 200 Gtons of CO2 in the next 50 years (1014 moles of CO2 (≈ 4 Gigatons) per year during 50 years), we would need a few thousand sites of that type. This amount of storage is a lot, but this level is not out of reach if the technology is well understood. In order for that generalization to be acceptable, however, one needs to know in detail what will be the fate and reactivity of carbon dioxide underground, not only at the scale of years but also at a scale of thousands of years in order not to leave our descendants with unexpected adverse consequences. From the environmental mineralogy perspective, this level of CO2 capture and storage requires the following goals, among others: (1) that we understand the reactivity of the CO2 injected within rock porosity with the different minerals characteristic of each geological storage site; (2) that we are able to model the reaction rates of carbon dioxide with minerals for different thermodynamic activities of CO2 in presence of possible accessory co-injected fluids; (3) that we understand how different elements will be mobilized in the fluids as a result of these interactions. Achieving these goals requires both laboratory studies and detailed fieldwork at actual injection sites.
In this context, it is important to understand how the natural mechanisms by which our planet regulates CO2 by transfer of carbonates and refractory organic matter to the solid Earth, will be operating at different CO2 injection sites. Of course, the mechanisms at work in the global carbon cycle will never be identical to those operating in engineering projects in the subsurface. The purpose of this paper is rather to see how they may inspire better knowledge of the processes at work at injection sites. It is common knowledge that conversion of CO2 into solid carbonates or into organic matter, considered over the time scale of years, will involve a very small fraction (a few %) of the CO2 injected since, as discussed above, they can only regulate amounts of CO2 about 50 times less than the present day anthropogenic perturbation. This limitation immediately raises two questions that will be examined in the rest of that paper: (1) can silicate dissolution/carbonate precipitation reactions be accelerated in some special instances so that most of the injected CO2 would be stored not as supercritical fluid or as dissolved aqueous CO2 but rather as stable solid carbonates; (2) can significant conversion of CO2 into refractory organic matter or solid carbonates occur at carbon dioxide injection sites if specific conditions exist?
2 Mineralogical controls on carbonation kinetics
An important parameter for evaluating the amount of injected carbon dioxide that will be converted in a given time into solid carbonates is the rate of reaction (3) relative to the hydrodynamic parameters that characterize CO2 leakage to the surface or to other reservoirs. Because reaction (3) is a combination of reactions (1) and (2), it is important to determine which of the two steps is kinetically limiting. Data from Daval et al. (2009a) are shown in Fig. 2. Modeling of the extent of carbonation of wollastonite (CaSiO3) into calcite (CaCO3) is not significantly different with and without consideration of the measured kinetics of precipitation of calcite instead of its equilibrium formation (i.e. at infinite rate). This observation demonstrates that what limits the kinetics of carbonation in such laboratory experiments is silicate dissolution (reaction (1)) and not the rate of carbonate formation (reaction (2)). This result can confidently be extended to all situations of calcite formation as a result of alteration of silicates at temperatures close to 100 °C, because wollastonite is presumably the most reactive Ca-bearing silicate under these conditions (cf. Fig. 7 in Daval et al., 2009a). At a temperature typical of the Earth's surface, where Si is incorporated in clays rather than in amorphous silica, this statement could be more questionable because the slow precipitation rate of these phases maintain aqueous concentrations close to equilibrium with respect to silicate dissolution, such that the weathering of primary silicates could be ultimately controlled by the rate of clay formation (see e.g., Maher et al., 2009, Zhu, 2009 for further details).
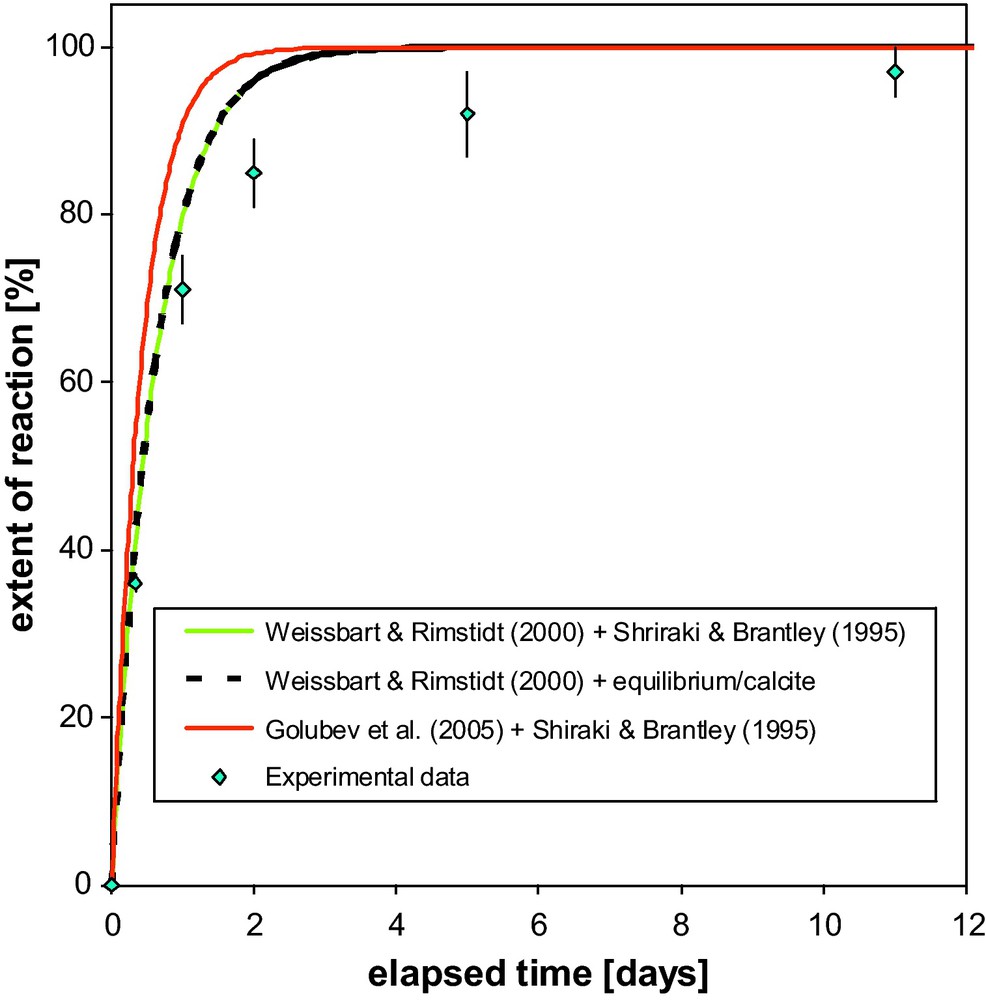
Normalised extent of CaSiO3 wollastonite carbonation as a function of time. The diamonds are the experimental data obtained by Daval et al. (2009a). The solid curves are the result of kinetic modeling of wollastonite carbonation using published rate laws for dissolution of wollastonite and precipitation of calcite, respectively by Weissbart and Rimstidt (2000); Golubev et al. (2005) and Shiraki and Brantley (1995); for details of the modelling strategy, see Daval et al. (2009a). The dashed line corresponds to the same modelling using infinitely rapid kinetics of calcite precipitation.
Taux normalisé de carbonatation de la wollastonite (CaSiO3) en fonction du temps. Les losanges représentent les données expérimentales obtenues par Daval et al. (2009a). Les courbes continues sont le résultat d’un modèle utilisant les données publiées de cinétiques de dissolution de la wollastonite par Weissbart et Rimstidt (2000) et Golubev et al. (2005), et de précipitation de calcite par Shiraki et Brantley (1995); les détails de la modélisation sont décrits dans Daval et al. (2009a). La courbe en pointillés correspond à la même modélisation, mais en utilisant une cinétique instantanée (infiniment rapide) de précipitation de la calcite.
In cases where the carbonate formed is magnesite (MgCO3), determination of the limiting step is not so clear and deserves more research. For instance, recent data on the precipitation kinetics of magnesite by Saldi (2009) suggest that at 100 °C, the rate constant of magnesite precipitation is 6 order of magnitude below that of calcite precipitation under similar conditions. However, the rate limiting step of the carbonation of Mg-rich silicates could still be the silicate dissolution reaction, at least below 120 °C. Moreover, at low temperatures, the carbonate formed would not be magnesite indeed, but rather hydrated magnesian carbonates such as hydromagnesite: Mg5(CO3)4(OH)2.4H2O (Hanchen et al., 2008; Saldi et al., 2009, and references therein), with more rapid, yet unknown, precipitation rates.
A key issue for controlling conversion of CO2 into solid carbonates is thus the rate of dissolution of silicate minerals. The reaction rate data in Fig. 2 for CaSiO3 (wollastonite) at a grain size of about 0.2 mm show that full transformation of the silicate into carbonate occurs rapidly. This rapid transformation is due to two factors: wollastonite dissolves rapidly and Ca2+ is a carbonate-forming cation. In that respect, geological sites containing large amounts of wollastonite would be interesting for converting injected CO2 into calcite, although wollastonite is not a common mineral. Other more common calcic minerals, e.g., anorthite, might also be favorable for carbonation, and more generally, minerals whose composition is dominated by magnesium and/or calcium would be interesting targets. This is the main idea behind projects involving CO2 injection in basic and ultrabasic geological contexts (e.g., Gislason et al., 2010; Kelemen and Matter, 2008; Matter and Kelemen, 2009; McGrail et al., 2006; Schaef and McGrail, 2009; Schaef et al., 2010). The main premise of these strategies is that reaction (1) is an acid-basic neutralization of the mineral (base) by dissolved carbon dioxide (acid). Anorthite, CaAl2Si2O8, an important component of basalts, could be an interesting subject in the perspective of geological storage of CO2 in basalts. In this regard, a few recent studies have focused on water-CO2-anorthite interactions (e.g., Berg and Banwart, 2000; Regnault et al., 2005; Sorai et al., 2007, Sorai and Sasaki, 2010). Indeed, basalts, although representing only ∼ 5% of the silicate rocks at Earth's surface contribute to more than 30% of reaction (1) (Dessert et al., 2003). In laboratory experiments, however, some promising minerals show unexpected slow carbonation rates at temperatures below 100 °C. Experimental studies of the dissolution of olivine (forsterite Mg2SiO4), even with small grains of 0.2 mm in characteristic sizes, have been highly disappointing because they yielded reaction rates being at least 4 orders of magnitude slower than that predicted by numerical simulation of the process (see Daval, 2009 and Daval et al., 2010b for details). Olivine, however, is one of the most thermodynamically favorable substrates for carbonation (Fig. 3), and is also one of the fastest dissolving minerals (Fig. 4). Therefore, this should make it an excellent substrate for conversion of CO2 into carbonates. Slow experimental carbonation rates below 100 °C emphasize complexities whose origins will be discussed below. Of course, it is possible to increase carbonation rate by increasing temperature (Fig. 5) or by decreasing grain size (e.g., Dufaud et al., 2009, Garcia et al., 2010). Although achieved in some cases, temperatures will seldom reach 90 °C at CO2 geological storage sites. Whereas temperature increase is an efficient but often impractical solution, increasing reactive surface area is an interesting option that deserves further research. Injection of CO2 under pressures higher than hydrostatic and lithostatic values at the injection point, sufficient to create microcracks in the rocks, might help to increase fluid/rock contact surface area by creation of microfractures, and thus presumably increase reactive surface area as well. This main issue of coupled mineralogy and geomechanics thus needs to be investigated in detail (see analogous studies in carbonation of concrete (e.g., Corvisier et al., 2010; Fabbri et al., 2009) and limestone (e.g., Le Guen et al., 2007)). It should be noted, however, that the issue of inducing fracturing underground has proven difficult on a societal basis, at least under populated areas (Giardini, 2009). On the other hand, ex situ carbonation (i.e. in a chemical plant at Earth's surface, see e.g., Gerdemann et al., 2007) of materials susceptible to carbonation, with continuous grinding to reduce grain sizes, might be a promising approach (a French project supported by ANR CO2 coordinated by Françoise Bodénan at BRGM in Orléans and by Florent Bourgeois at École de Chimie in Toulouse is an example of research efforts currently exploring this possibility). In this latter case, a condition of success is to dispose of materials favorable to carbonation, which are already present and occupying an important volume, and which cannot be disposed of in other manners. Mine waste materials would be interesting targets (see Wilson et al., 2006), especially if mining occurred in basic and ultrabasic rocks. Finally, even in the continental crust, ferromagnesian minerals such as biotite could be interesting targets.
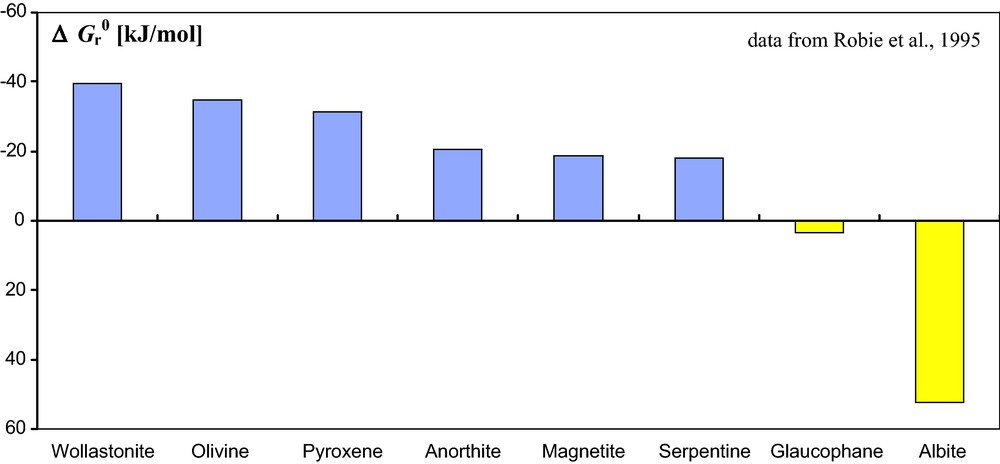
Standard Gibbs free energies for the carbonation reaction (3) of different silicate minerals. Obviously, minerals containing divalent carbonate forming cations are thermodynamically more prone to favor that reaction. Note that a favourable reaction is indicated by a negative standard Gibbs free energy.
Enthalpies libres standard de carbonatation (3) de différents silicates. Il apparaît logiquement que la carbonatation de minéraux qui contiennent des ions divalents formateurs de carbonates est thermodynamiquement favorisée. Note : une réaction thermodynamiquement favorisée correspond à des valeurs négatives de l’enthalpie libre.
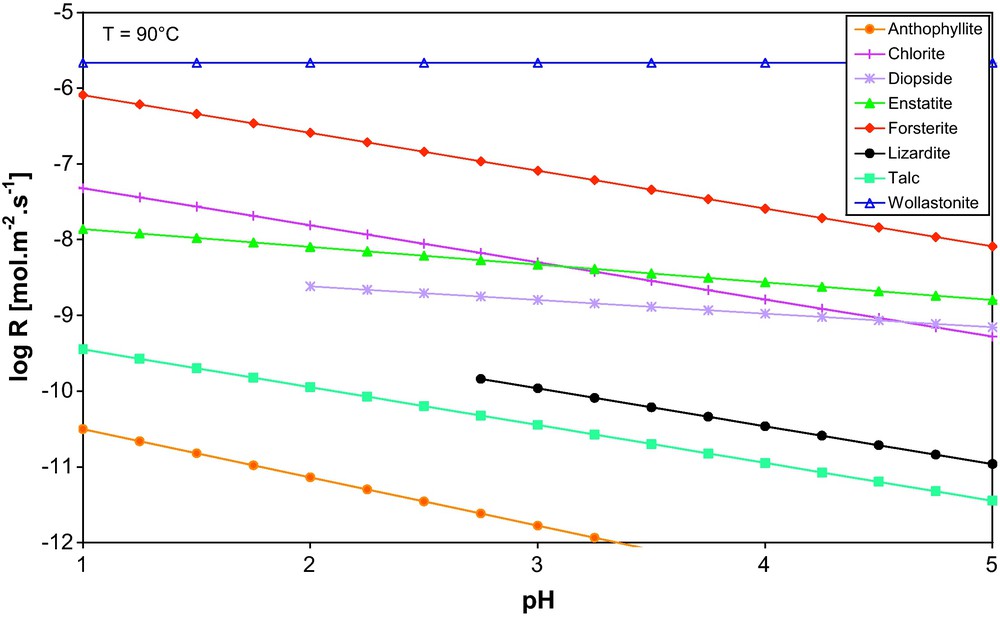
Dissolution rates of magnesian silicates as a function of pH extrapolated at 90 °C. For the sake of comparison, the dissolution rate of wollastonite was also mentioned in this graph. Data used for these calculations:
Vitesses de dissolution des silicates de magnésium en fonction du pH, extrapolées à 90 °C. À titre de comparaison, la vitesse de dissolution de la wollastonite a également été reportée. Données utilisées pour le calcul :
| Forsterite | Rosso and Rimstidt, 2000 |
| Enstatite | Oelkers and Schott, 2001 |
| Diopside | Knauss et al., 1993 |
| Lizardite | Hellmann et al., 2008 |
| Chlorite | Lowson et al., 2007 |
| Talc | Saldi et al., 2007 |
| Anthophyllite | Chen and Brantley, 1998 |
| Wollastonite | Weissbart and Rimstidt, 2000 |

Yield of the carbonation reaction (3) of forsterite Mg2SiO4 (modified after Gerdemann et al., 2007) after one hour of reaction with grain sizes of less than 75 μm. Notice the optimum of 50% at T = 185 °C and the very low yield at 90 °C. Conditions above 90 °C are generally considered as difficult for CO2 geological storage.
Taux de carbonatation (3) de la forstérite Mg2SiO4 (figure modifiée d’après Gerdemann et al., 2007), après une heure de réaction sur des grains de taille inférieure à 75 μm. Notez l’optimum de 50% à T = 185 °C et le très faible rendement à 90 °C. Des températures dépassant 90 °C sont souvent considérées comme compliquées pour le stockage géologique de CO2.
Even if the surface area problem could be solved, thanks to large porosities or to microfracturing, the effective dissolution rates of olivine and many other minerals will be in most cases still far too slow to make the rate of mineral carbonation competitive with the rate of hydrodynamic flow of CO2 out of the system. We thus have to understand why olivine, as a typical example, converts into carbonates so slowly in comparison to wollastonite, especially in light of the observation that the far-from-equilibrium dissolution rates of olivine reported in the literature are only one order of magnitude slower than that of wollastonite (Fig. 4). The answer is found in the detailed examination of the mineral surfaces that underwent dissolution in batch experiments at similar conditions (90 °C and pCO2 = 250 bar, duration: 2 days for wollastonite; 45 days for olivine) (Fig. 6). Whereas the silica layers shown in these pictures look different, they may originate from similar interfacial, nm-sized precursors. For both experiments, the bulk solution was found to be saturated with respect to SiO2(am), such that the interfacial Si-rich layers usually observed to form at far-from-equilibrium conditions in mixed-flow reactor experiments for these minerals (see e.g., Casey et al., 1993 for wollastonite; Pokrovsky and Schott, 2000a,b for olivine) were stabilized. For wollastonite, it is striking that the silica-rich amorphous layer kept growing during the carbonation process while its external interface stopped dissolving. Thus, the growth of the silica layer at the expense of wollastonite was possible because this coating did not prevent the fluid from reaching the pristine interface of wollastonite, which thus could keep on dissolving. Significant porosity of the silica layer in the case of wollastonite (Fig. 7, see also further images and details in Daval et al., 2009b) was found and actually allows the reaction to proceed by transport of solutes through the layer, whereas this transport was severely limited for forsterite. In this latter case, the thin silica layer was non-porous, blocking dissolution and thus carbonation of forsterite.

A. Transmission electron microscopy image of the surface of olivine during dissolution process in a batch experiment of olivine carbonation at 90 °C (after quench recovery and preparation by focused ion beam). A thin compact silica layer is observed at the surface of the mineral. B. Observation by scanning electron microscopy in a batch experiment of wollastonite carbonation at 90 °C as shown in Fig. 2. The silica layer is obviously much thicker than in the case of olivine but as seen in Fig. 2, it did not prevent reaction to proceed. Note the three order of magnitude difference in scale bar between A and B.
A. Image de microscopie électronique en transmission de la surface d’une olivine en cours de dissolution dans une expérience de carbonatation, en milieu fermé à 90 °C (après trempe, récupération et préparation par faisceau d’ions focalisés). Une fine couche compacte de silice amorphe est observée à la surface du minéral. B. Observation par microscopie électronique à balayage dans une expérience de carbonatation de wollastonite en milieu fermé à 90 °C, telle que montrée dans la Fig. 2. La couche de silice est bien plus épaisse que dans le cas de l’olivine, mais comme on le constate dans la Fig. 2, elle n’a pas empêché la carbonatation de se produire massivement et rapidement. Noter la différence de trois ordres de grandeur entre les barres d’échelle en A et en B.

Transmission electron microscopy image showing the high porosity at the nanometer scale of the silica rich amorphous phase that developed on the CaSiO3 wollastonite substrate. Note that irradiation damage under the electron beam produces significantly different microstructures in that gel phase. Calcite precipitates probably nucleating on or in the layer are also visible.
Image de microscopie électronique en transmission montrant l’importante porosité à nano-échelle de la silice amorphe développée sur le substrat de wollastonite CaSiO3. Note : on a testé que l’irradiation par le faisceau d’électrons produisait des défauts distincts de cette porosité dans le gel de silice. On observe également des précipités de calcite ayant nucléé sur ou dans la couche de silice.
The origin of such differences is so far unknown, and current research in our group is directed at ascertaining the origin of these surprising differences. Dissolution of nuclear waste glasses, where minor elements present in the initial material can strongly change the dissolution rate of the primary phase by modifying the structure of the secondary silica layer (see the case of Zr in Cailleteau et al., 2008), may be related to the dissolution process of silicate minerals. However, one major difference in the dissolution process of nuclear waste glasses and olivine is the much thinner silica layer on olivine, which makes its investigation highly challenging. Recent analytical developments in the surface analysis of minerals could help to resolve this problem (e.g., Daval et al., 2009b; Davis et al., 2009; Hellmann et al., 2003). Interesting studies could also be done on synthetic basaltic glasses with different minor elements in order to test the conjecture that alteration rates can be strongly modified by minor elements. In all cases, the issue will be to recognize, both in the laboratory and in the field, silica layers on different minerals and to determine how the chemistry of the surrounding fluid is manipulating their structure and properties, and in fine their alteration rates.
Finally, even if both grain size issues and the problem of passivating layers are solved, another fundamental difficulty might be encountered. Dissolution rate laws are usually measured under far from equilibrium conditions–in practice, under an active fluid flow which is constantly renewing the water/solid interface (the so-called mixed-flow reactor set-ups, see, e.g., Posey-Dowty et al. (1986) for a technical description). This experimental design might be very different from the hydrodynamic reality at CO2 injection sites where the flow will be on hydrological time scales rather than those typical of laboratory flow rates. Supporting this idea, a few field studies showed that fluid-rock interactions could occur over a broad range of degrees of undersaturation with respect to feldspars and other major rock forming minerals (e.g., Kampman et al., 2009; White et al., 2001; White et al., 2002). A consequence of having little renewal of the fluid in contact with minerals is that their dissolution rate might indeed be much slower than that measured under far from equilibrium conditions.
Overcoming this difference is one of the interests in performing batch experiments, which are obviously less precise than chemostats, but which allow integration of the real effect of different conditions of departures from equilibrium (see e.g., Daval et al., 2010c, for quantitative determination of kinetic parameters in batch reactors). In any case, accurate knowledge of the relations between mineral dissolution rate (R) and the Gibbs free energy of reaction (ΔGr) is necessary to foresee the long-term evolution of fluids and rocks after CO2 injection. The most widespread equation in geochemical codes that links R to ΔGr was established in the framework of transition-state theory (Eyring, 1935a,b; Lasaga, 1981), and states that R is roughly independent of ΔGr over a wide free energy range far-from-equilibrium (for instance, at 90 °C, the dissolution rate remains 95% of the far-from-equilibrium rate as long as ΔGr < −10 kJ mol−1), whereas it decreases linearly over a very narrow range of ΔGr values as equilibrium is approached. The simplest TST equation, that is used in most of the long-term simulation attempts of CO2 sequestration (e.g., Gherardi et al., 2007; Knauss et al., 2005; Xu et al., 2004, 2005) fails, however, to explain either sharp drops of dissolution rate close-to-equilibrium (see the comparison of the close-to-equilibrium data on feldspars weathering from Kampman et al. (2009) to the far-from-equilibrium dissolution rate of labradorite), or a decrease of mineral dissolution rate under conditions usually considered as to represent ‘far-from-equilibrium’ conditions (e.g., Beig and Luttge, 2006; Berger et al., 2002; Hellmann and Tisserand, 2006; Hellmann et al., 2010; or Taylor et al., 2000 for feldspars; Dixit and Carroll, 2007 or Daval et al., 2010a for pyroxenes; Cama et al., 2000 for clays). In that respect, the implementation in geochemical modeling of empirical kinetic rate laws that take into account the actual rate-affinity relations measured in recent studies was thus proposed to help bridge the gap between laboratory measurements and field estimations of weathering, at least partly (e.g., Daval et al., 2010a; Ganor et al., 2007; Maher et al., 2009; Zhu, 2009). Such results emphasize the need to increase our efforts to determine experimentally the effect of fluid composition on the dissolution rates of minerals, and eventually understand why the simplest TST expression fails to link far-from-equilibrium to close-to-equilibrium dissolution rates.
To date, the mechanistic reasons for these incorrect predictions of TST in the case of some minerals are not clear, and intensely debated. The existing explanations and/or alternative models can be divided into 4 main categories: (1) the actual interfacial phase which controls the dissolution of the primary silicates has an equilibrium constant different from that of the underlying phase (e.g., Bourcier et al., 1990; Grambow and Muller, 2001), such that the application of TST to the primary silicate may be meaningless; (2) dissolution is controlled by the spontaneous nucleation of etch pits at crystal defects (Lasaga and Luttge, 2003); (3) the silicate dissolution rate is controlled by the concentration of a precursor surface complex, and R – ΔGr relations more sophisticated than TST can be derived within the framework of TST (Oelkers et al., 1994; Oelkers, 2001); (4) the abovementioned discrepancies may not be ascribed to ΔGr directly, but to a combination of different processes such as the surface restructuring dynamics of primary silicates, diffusion of solutes across passivation barriers and others (Casey, 2008). Although reviewing in details all of the proposed mechanisms is beyond the scope of the present paper, the two first models will be briefly described because they heavily rely on mineralogical controls. Moreover, note that a thorough review of the 3rd category not discussed hereafter can be found in Schott et al. (2009).
The first idea is that the dissolution rate of primary phases would drop because the fluid would reach equilibrium not with the original mineral but with secondary phases coating the surface, potentially including silica layers that contain minor elements, which would determine the solid/fluid exchanges (see for e.g., Grambow and Muller (2001) for glasses and Oelkers (2001) for minerals; a theoretical review of some of these models is also available in Gin et al., 2008). Detailed knowledge of the structures and compositions of these secondary phases, as well as their observation in the field, will thus be another key for identifying appropriate field sites for efficient conversion of CO2 into solid carbonates. Although such a model may be consistent with our own observations on olivine, note that wollastonite carbonation cannot be explained in this framework because this mineral keeps on dissolving whereas saturation is reached with respect to SiO2(am) which coats its surface (Daval et al., 2010b). Thus, although interesting and as emphasized above, this model would need further development to be consistent for all silicates.
The second idea was proposed by Lasaga et al. in the early 1990s (e.g., Burch et al., 1993; Nagy et al., 1991; Taylor et al., 2000), and further explored and developed by Luttge et al. (e.g., Arvidson and Luttge, 2010; Beig and Luttge, 2006; Lasaga and Luttge, 2001; 2003; Lüttge, 2006). Basically, the observation of a dramatic drop in dissolution rate under conditions classically considered to be “far-from-equilibrium” (ΔGr << 0) led these authors to propose that the driving process of dissolution should be the spontaneous nucleation of etch pits at crystal defects (screw dislocations) when ΔGr < ΔGrcrit and where ΔGrcrit is the critical free energy required for opening an etch pit at a given crystal defect. Above ΔGrcrit, it is predicted that deep etch pits should not open up spontaneously, and this, in turn, would explain the slow dissolution rates observed in the range ΔGrcrit < ΔGr < 0. In spite of meaningful theoretical developments of this model by Lasaga and Luttge (2001, 2003) and convincing experimental evidence (e.g., Arvidson and Luttge, 2010; Beig and Luttge, 2006), it is worth noting that the parameters controlling the numerical value of ΔGrcrit are poorly constrained, and further research could aim at determining (1) the effective surface energies of silicate minerals and (2) the exact Burgers vectors of the dislocations from which etch pits actually originate.
To sum up this section about mineralogical controls on carbonation kinetics, it appears that the main obstacle to rapid carbonation of silicates at temperatures typical of the majority of envisaged CO2 storage sites is the relatively small reactive (i.e. pristine) surface area actually present in most geological settings. However, a detailed knowledge of the petrophysics of the site (actual reactive surface areas) and of involved mechanisms (passivating layers, role of other phases, e.g., Zuddas and Pachana, 2010, influence of crystal defects on R – ΔGr relations) might help to identify minerals and environments favorable to that process, especially in rocks containing significant basic and ultrabasic components. In cases where conversion of carbon dioxide into solid carbonates will be only marginal, a detailed knowledge of the fluid/mineral interface both in the laboratory and at the injection site, will still be the basis of our understanding of the environmental mineralogy of carbon dioxide geological storage.
3 Biomineralization in the context of CO2 geological storage
At the Earth's surface, life drives two important CO2 sinks, as described in the first section-the so-called biological pump and some CO2 conversion by biomineralization into solid carbonates which eventually are stored for million years in sedimentary rocks. Can processes similar to these two occur at CO2 injection sites?
Let us first examine the formation of carbonates, which on Earth is mostly biological, according to the following reaction:
| (7) |
In surface ocean waters, reaction (7) is usually thermodynamically favorable (unlike silica biomineralization by diatoms, which occurs in waters thermodynamically undersaturated with respect to solid silica), but it does not occur for kinetic reasons. Biology nevertheless allows CaCO3 precipitation to occur using highly complex mechanisms that are crudely summarized as a concentration of calcium and carbonate ions in order to overcome the kinetic barrier (similar to diatoms which concentrate silicon for overcoming both thermodynamic and kinetic barriers for silica precipitation). This concentration phenomenon occurs in intracellular vesicles such as the coccolithosomes of the coccolithophores (e.g., Young and Henriksen, 2003). It should be noted that, in principle, the formation of carbonates according to reaction (7) is adverse to CO2 storage because out of the two molecules of bicarbonate (which represents one form of carbon dioxide storage, the so-called ionic sequestration, which has the lifetime of the corresponding water mass), one carbon atom is liberated as carbon dioxide, dissolved in water and in equilibrium with atmospheric CO2. This is possibly why carbonate-forming organisms are in danger when atmospheric carbon dioxide increases by virtue of a Le Chatelier principle on reaction (7) or simply because their carbonate components might eventually dissolve. However, because one of the two carbon atoms present at the beginning of reaction (7) ends up in solid carbonates, which, if sedimentation conditions are favorable, constitute a very stable storage of CO2 in the solid Earth, the process subtracts carbon dioxide from the atmosphere/hydrosphere. This is somewhat of a paradox because the formation of carbonates by life liberates some CO2 but it is also the mechanism by which carbon dioxide is converted into a stable solid form that is separated from the hydrosphere/atmosphere system. The liberation of CO2 in reaction (7) is strongly decreased by coupling with the organic biological cycle as shown in reaction (6). The degree of coupling between reactions (7) and (4) on the large scale is one of the most difficult global geochemical mass balances to measure, but it is believed to be high. One might argue that organisms such as mussels, oysters, and snails obviously have no direct relationship with photosynthesis, which is true, but the amount of carbonate precipitation they represent is very small when compared to coccolithophores, foraminiferas, and corals, which either are photosynthetic (coccolithophores) or often coupled to photosynthetic symbionts (foramniferas and corals). It should be noted that even in case of perfect coupling of reactions (7) and (4), and if reaction (6) fully describes carbonate biomineralization, an increase of CO2 concentration (i.e. ocean acidification) will still be adverse to carbonate biomineralizing organisms if dissolution of CaCO3 occurs. Such a scenario would damage the carbonate shells and skeletons and favor an ecological transition (a major biological crisis and possible extinction event) toward non-carbonate producing organisms such as diatoms.
How can these concepts be transferred to the subterranean context of a CO2 injection site? Not easily, obviously. Of course, photosynthesis will not occur deep in the subsurface. But other mechanisms can lead deep biosphere microorganisms to induce carbonate precipitation. Although biomineralization of carbonates has not yet been documented in the subterranean biosphere, one microorganism, Sporosarcina pasteurii, also often called Bacillus pasteurii, isolated from wastewaters, has proven to be very efficient for carbonate biomineralization under underground conditions (Ferris et al., 2004; Mitchell and Ferris, 2005). This microorganism performs urea degradation, causing a pH increase which favors the precipitation of carbonates, according to the following urea hydrolysis (8) and carbonate precipitation (9) reactions:
| (8) |
| (9) |
Several laboratory experiments (Dupraz et al., 2009a,b) have shown that injection of urea and of B. pasteurii in a synthetic aquifer water (inspired by the Paris Basin Dogger aquifer) leads to an effective pH increase and to the formation of CaCO3 (Fig. 8). Of course, this has no operational value for CO2 injection and should only be considered as a useful model since urea degradation produces its own inorganic carbon, as shown by reaction (8). The next step in the context of possible application to carbon dioxide geological storage would be to find subterranean species with metabolisms related to that of B. pasteurii, able to degrade organic matter into ammonia and into partially or totally denitrogenized organic molecules according to a reaction of the type:
| (10) |

Examples of vaterite and aragonite CaCO3 carbonates (SEM images) formed as a result of the biological activity of B. pasteurii inoculated with urea in a synthetic Dogger aquifer water. Vaterite appears as spheres in which bacterial imprints are visible. Aragonite has a fibrous microstructure.
Exemples de carbonates CaCO3 (images de microscopie électronique à balayage) résultant de l’activité biologique de B. pasteurii inoculée, avec de l’urée, dans une eau synthétique de l’aquifère du Dogger. La vatérite se présente sous forme de sphères dans lesquelles des empreintes de cellules bactériennes sont visibles. L’aragonite a une microstructure fibreuse.
In that case, the hydrolysis of the amine would be associated with a pH increase, allowing conversion of injected CO2 into carbonate resulting in calcite precipitation. This process would imply that there is sufficient pre-existing organic matter in the injection reservoir or to co-inject wastewaters with the carbon dioxide, which can be envisaged since CO2 injection will never occur in potential water resource aquifers.
A second issue is the interaction of injected CO2 with the production of organic matter discussed in the first section of this paper. At the Earth's surface, some CO2 is converted into refractory organic matter, escaping the almost fully closed (to about 999 per mil) cycle of photosynthesis and respiration, thus constituting a second stable form of carbon dioxide storage (the so called kerogen reservoir, which has about one fifth of the mass of solid carbonates, a proportion that has been maintained over most of the Earth's history, e.g., Schidlowski, 1988). Can similar processes occur underground at CO2 injection sites? As already mentioned, no photosynthesis occurs in the absence of light; however, some other modes of primary production are adapted to underground conditions. Among those actually documented, methanogenesis is probably the most important (Fig. 9). Other metabolisms also exist (e.g., acetogenesis) that also mostly rely on H2 naturally present in the subsurface. Some CO2 might thus be pumped by thermodynamically favorable reactions with autochthonous or co-injected H2. The fate of the organic matter thus synthesized (in first instance methane and acetic acid) from CO2 and H2 in the deep subsurface is absolutely unknown because the knowledge of the biological cycle of organic molecules in the deep subsurface is only in its infancy. It is thus hard to speculate whether these processes could operate at CO2 injection sites for a durable conversion of carbon dioxide into stable organic matter in response to large CO2 overconcentrations. Also, the extent of biomass that could be stimulated by carbon dioxide injection and would thus constitute another form of CO2 storage is unknown. Geotechnical engineers contending with the development of massive biofilms in deep geothermal and oil fields installations know that biomass formation is not always negligible and that biocides need to be injected for avoiding these types of underground blooms (e.g., Fardeau et al., 2009, and references therein). The consequences of CO2 injection on autochthonous or co-injected microorganisms are thus largely unknown and need to be studied as a high priority. Indeed, methanogenesis, although considered by some as a way to backtransform CO2 into a useful CH4 resource in former gas reservoirs, could also be seen as a very adverse effect of the interaction of injected carbon dioxide with the deep biosphere. This is because methane has a stronger greenhouse gas potential than carbon dioxide, and even small leakages would be counterproductive with respect to greenhouse gas balance. Incubation experiments with cores drilled from the deep subsurface with special care to maintain the original (very small) biomass and to avoid contaminations are probably the most appropriate way to progress in this so far very poorly constrained research area. One point of knowledge we have in this ocean of unknowns is provided by the microbiology of oil fields (Ollivier and Magot, 2005) and by that of deep aquifers (e.g., Fardeau et al., 2009). We know from these studies that sulfate-reducing bacteria are prominent in these media (Fardeau et al., 2009; Ollivier and Magot, 2005). In ocean waters, methanogenesis and sulfate reduction are indeed sometimes intimately related; microbial consortia (or looser connections) of methanotrophic and sulfate-reducing organisms have been evidenced (e.g., Boetius et al., 2000), which transform methane according to the following reaction:
| (11) |
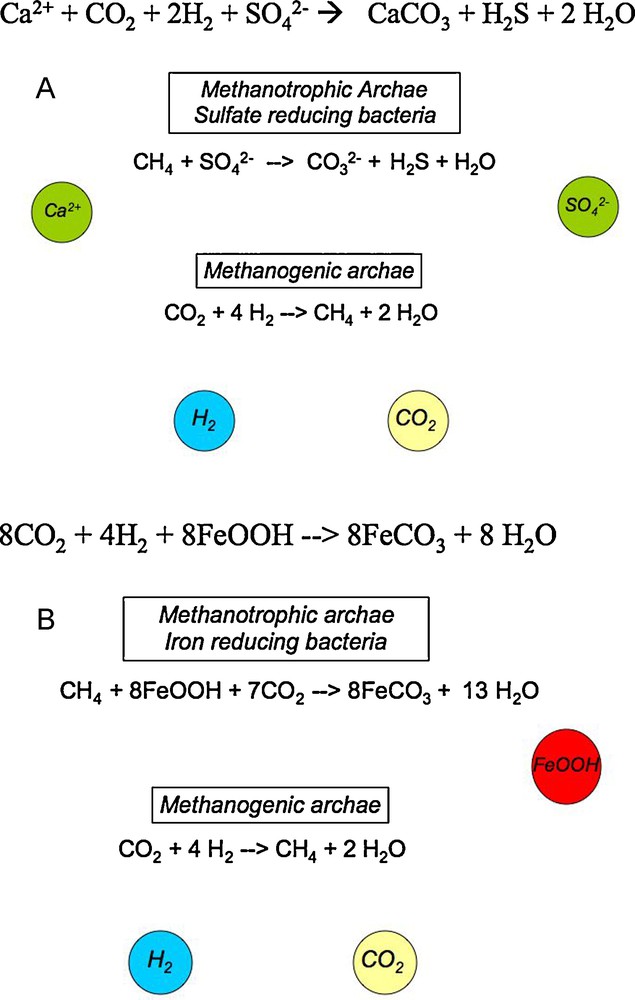
Hypothetical biological reactions that could be enhanced upon CO2 injection in the subsurface. Conversion of CO2 into methane is performed by methanogenic archae which have been well documented in the deep biosphere. A. The produced methane could be used by methanotrophic archae asociated to sulfate reducing bacteria. The result of this would be a basification of the environment and thus calcium carbonate precipitation by outgasing of H2S and use of Ca2+ present in poral water. Bacterial sulfate reduction is well documented in the subsurface whereas associations of methanotrophic archae with sulfate reducing bacteria have been reported from anoxic sea sediments (Boetius et al., 2000). B. In favorable environments, sulfate reduction could be hypothetically replaced by dissimilatory iron reduction (reduction of iron III oxides such as goethite FeOOH), thus eliminating the unfavorable outgassing of H2S and leading to the storage of carbon dioxide into a carbonate stable in the anoxic subsurface: FeCO3 siderite.
Réactions biologiques hypothétiques qui pourraient interagir avec une injection de CO2 en subsurface. La conversion de CO2 en méthane est faite par des archae méthanogènes, connues dans la biosphère profonde. A. Le méthane produit pourrait être utilisé par des archae méthanotrophes associées à des bactéries sulfato-réductrices. Il en résulterait une basification de l’environnement et donc une précipitation de carbonate couplée à un dégazage de H2S et à une utilisation de Ca2+ de l’eau porale. La réduction bactérienne des sulfates est bien documentée dans la biosphère profonde, tandis que des consortia archae méthanotrophes/bactéries sulfatoréductrices sont connus dans des sédiments marins anoxiques (Boetius et al., 2000). B. Dans des environnements favorables, la réduction des sulfates pourrait être hypothétiquement remplacée par de la réduction dissimilatrice de fer (réduction des oxydes de fer (III) tels que la goethite) éliminant alors le dégazage défavorable de H2S et résultant en un stockage de dioxyde de carbone en carbonate stable dans la subsurface anoxique sous forme de sidérite FeCO3.
In this process, carbonate ions are produced which eventually lead to the formation of calcium carbonates (e.g., Aloisi et al., 2000). The whole biological transformation of CO2 can thus be represented by the following reaction:
| (12) |
Whether such metabolic phenomena can occur underground, nobody knows. A potential subsurface biological process based on this reaction is shown in Fig. 9. It would store injected carbon dioxide as solid carbonates but would, however, be a potential problem because of the generation of H2S (a corrosive and strong greenhouse gas that could escape unless used by other microbes as it occurs on the ocean floor). Such a biological phenomenon is related to well-documented so-called souring in oil reservoirs (Ollivier and Magot, 2005). In some geological environments poor in sulfates or where iron-reducing metabolism would have been favored (e.g., in the presence of Geobacter or Shewanella species), the problem might be solved and could lead to durable conversion of the injected CO2 into solid carbonates, FeCO3 siderite in that case, according to the following reaction (see Fig. 9):
| (13) |
Such microbial processes and environments need to be actively searched for in the deep subsurface. Interestingly, it is worth noting that some siderite and ankerite precipitation are expected at some sites such as Frio (Xu et al., 2004)—far surpassing storage of injected CO2 in calcite. The role of ankerite has also been emphasized in McGrail et al., 2006. Identification of possible biomineralization processes requires field investigations of the mineralogy of the new carbonates formed from the injected carbon dioxide.
4 Conclusions
The purpose of this paper has been to show that by careful examination of the natural processes of carbon dioxide transfer from Earth's fluid envelopes to the solid Earth (i.e. precipitation of solid carbonates and formation of refractory organic matter), one might find innovative processes in the field of CO2 geological storage. We have emphasized two important environmental mineralogy aspects: (1) detailed understanding of the surface of silicates during their dissolution is a key to discovering and implementing rapid underground or ex situ carbonation of minerals; (2) understanding of carbonate biomineralization by deep biosphere microorganisms opens possibilities for subterranean biological conversion of carbon dioxide into stable carbonates. However, the deep biosphere also has the potential to complicate CO2 geological storage by generating some strong greenhouse gases such as CH4 and H2S. Subterranean microorganisms, therefore, need to be better mapped and understood. In any case, comparison of laboratory (bio)mineralogy studies with field observations (at CO2 injection pilot sites, in enhanced oil and gas recovery systems, and in natural CO2 fields) is a formidable opportunity (and challenge) for environmental mineralogy.
Acknowledgements
Parts of this research have been supported through funding by ADEME, Total, Schlumberger, and ANR (Agence nationale de le Recherche programmes CO2 carbonatation and CARMEX). The authors are grateful to Pr. Kate Maher for her insightful comments on this manuscript.


