1 Introduction
Along with Ca-, Al-rich inclusions (CAIs) and matrix, ferromagnesian chondrules are the building blocks of primitive meteorites (Scott and Krot, 2003). Although it is commonly accepted that chondrules were formed by partial melting of solid precursors, during brief, and possibly repetitive, high temperature events, there is still debate regarding the source of heating, the conditions of melting, the nature of their precursors, and the location and the timing of their formation (Jones et al., 2005; Kita et al., 2005; Zanda, 2004).
Since they are potentially some powerful isotopic chronometers for the first millions years history of the Solar System, the origin, the abundance and the distribution of short-lived radionuclides, such as 26Al, were abundantly studied (e.g. Chaussidon and Gounelle, 2007; Gounelle et al., 2007). Studies were tackled of various meteoritic components, such as CAIs, Al-rich chondrules and ferromagnesian chondrules, provide evidence for the widespread distribution of the short-lived radionuclide 26Al, which decays to 26Mg [half-life (T1/2) = 0.73 million years (Ma)], within the early Solar System (Jacobsen et al., 2008; Kita et al., 2005; Macpherson et al., 1995; Villeneuve et al., 2009 and refs therein). High precision Mg isotope data showed that 26Al and Mg isotopes have been homogenized at ± 10% in the inner Solar System at the time of formation of CAIs from the CV3 chondrite Allende (Villeneuve et al., 2009). The level of homogeneity of 26Al and Mg isotopes was recently challenged from very high-precision analyses of CAIs and of ameboid olivine aggregates (Larsen et al., 2011), but these latest data can also be interpreted with a homogeneous distribution when CV CAIs formed. A 26Al/27Al ratio of 5.26 (±0.12) × 10−5, as determined from the bulk 26Al isochron of Allende CAIs (Jacobsen et al., 2008) and also consistent with bulk CAI data from (Larsen et al., 2011), is considered in the following as the initial ratio of the Solar System and hereafter noted (26Al/27Al)0. With mineral isochrons showing (26Al/27Al)0 < 2 × 10−5, most chondrules from unequilibrated ordinary chondrites (UOCs) and carbonaceous chondrites (CCs) have recorded melting events which took place at least 1 Ma after CAIs (Kita et al., 2005; Villeneuve et al., 2009 and refs therein).
Mostefaoui et al. (2002) and Tachibana et al. (2003) found hints for correlations between 26Al relative ages of a set of ferromagnesian chondrules from Bishunpur (LL3.1) and Semarkona (LL3.0) UOCs (Hutcheon and Hutchison, 1989; Kita et al., 2000; Mostefaoui et al., 2002) and their pyroxene contents [px = pyroxene/(pyroxene + olivine)], their Si/Mg ratios, and to a lesser extent their volatile and moderately volatile elements concentrations (Mn/Mg, Cr/Mg, Na/Mg, K/Mg). However, no correlation with refractory elements (Ca, Al) and Fe was observed (Tachibana et al., 2003). These correlations were interpreted in the context of an open system model for the formation of chondrules, in which multiple heating events lead to repetitive evaporation and recondensation of the volatile and moderately volatile elements. Since Mg is relatively more refractory than Si and others elements (Mn, Cr…), it evaporates less rapidly from a chondrule melt during heating (Wang et al., 2001). Thus, a partial exchange of elements between chondrules precursors, enriched in Mg and refractory elements, and the gas, enriched in volatiles and Si, is expected. Accordingly, Tachibana et al., proposed that some Mg-rich precursors were extracted and preserved from the volatile-rich gas and cooled to form an earlier generation of Mg-rich chondrules, while others have interacted with the gas during cooling and formed a later generation of chondrules richer in volatiles and Si. By iterating this process over time, chondrules more and more volatile-rich and Si-rich would be formed resulting in a negative correlation between 26Al melting/crystallization ages and volatile content.
One problem is that the moderate precision on the measured chondrule initial 26Al/27Al ratios [hereafter noted (26Al/27Al)i, i.e. the ratio at the time of last melting/crystallization event] and thus on the relative 26Al ages means that the suggested correlations are not clear. The purpose of the current study is to test the reliability of these correlations by using the more precise set of 26Al relative ages for Semarkona chondrules, obtained by Villeneuve et al. (2009).
2 Methods
Fourteen ferromagnesian chondrules from Semarkona, previously studied for their 26Al relative ages (Table 1, Villeneuve et al., 2009), were examined for their mineralogy and chemistry by using the Hitachi S-4800 scanning electron microscope and the Cameca SX-100 electron microprobe at Université Henri-Poincaré in Nancy. Bulk chemical compositions were obtained from chemical mapping at regular steps of 5 to 10 μm depending on the size of the chondrule. A 15 kV and 100 nA beam of ∼2 to 5 μm diameter was used. Measured components were K2O, SiO2, FeO, Na2O, TiO2, CaO, Al2O3, MnO, MgO and Cr2O3. The counting time was 4 s per analysis and 22 500 (i.e. a square of 150 × 150) to 40 000 (i.e. a square of 200 × 200) analyses were performed per chondrule depending on their size. Thus, it took 25–45 h to map a single chondrule. It was assumed that backgrounds measured on standards were the same on chondrules. Moreover, alkali (Na and K) were measured at the beginning of each analysis in order to minimize losses from glass. After the sorting out of raw data (deletion of abnormal analyses – voids and cracks typically – with total abundances out of the range 95–105 wt% and analyses outside chondrule boundaries), from ∼10 000 to ∼25 000 analyses remained per chondrule. Since bulk analyses were done only for oxides, metal composition is not available. The visualisation of chemical maps was achieved with software for geological modelling named gOcad© (Fig. 1).
Données de (26Al/27Al)0 et d’âges relatifs 26Al des chondres ferromagnésiens de Semarkona (LL3.0) issus de Villeneuve et al., 2009.
| Chondrule | Type | (26Al/27Al)0 | 2σ | Relative age (Ma) | 2σ |
| Sem-Ch2 | I POP | 0.5043 × 10−5 | 0.1811 × 10−5 | 2.457 | + 0.465/−0.312 |
| Sem-Ch121 | I POP | 0.4765 × 10−5 | 0.1031 × 10−5 | 2.523 | + 0.257/−0.206 |
| Sem-Ch32 | I PP | 0.7245 × 10−5 | 0.1950 × 10−5 | 2.081 | + 0.330/−0.251 |
| Sem-Ch21 | II PO | 1.105 × 10−5 | 0.1393 × 10−5 | 1.637 | + 0.142/−0.125 |
| Sem-Ch83 | II PO | 0.3344 × 10−5 | 0.2229 × 10−5 | 3.002 | + 0.555/−0.362 |
| Sem-Ch136 | II PO | 0.7941 × 10−5 | 0.2926 × 10−5 | 1.985 | + 0.484/−0.330 |
| Sem-Ch62 | II POP | 0.4807 × 10−5 | 0.1101 × 10−5 | 2.513 | + 0.274/−0.217 |
| Sem-Ch76 | II POP | 0.3413 × 10−5 | 0.1198 × 10−5 | 2.874 | + 0.455/−0.317 |
| Sem-Ch113 | II POP | 0.7175 × 10−5 | 0.1254 × 10−5 | 2.092 | + 0.202/−0.170 |
| Sem-Ch114 | II POP | 0.8916 × 10−5 | 0.09056 × 10−5 | 1.863 | + 0.113/−0.102 |
| Sem-Ch137 | II POP | 0.5768 × 10−5 | 0.1031 × 10−5 | 2.322 | + 0.207/−0.173 |
| Sem-Ch64 | II PP | 0.6562 × 10−5 | 0.1184 × 10−5 | 2.186 | + 0.210/−0.174 |
| Sem-Ch81 | II PP | 0.7872 × 10−5 | 0.1115 × 10−5 | 1.994 | + 0.161/−0.139 |
| Sem-Ch138 | II PP | 1.619 × 10−5 | 0.1672 × 10−5 | 1.235 | + 0.115/−0.104 |
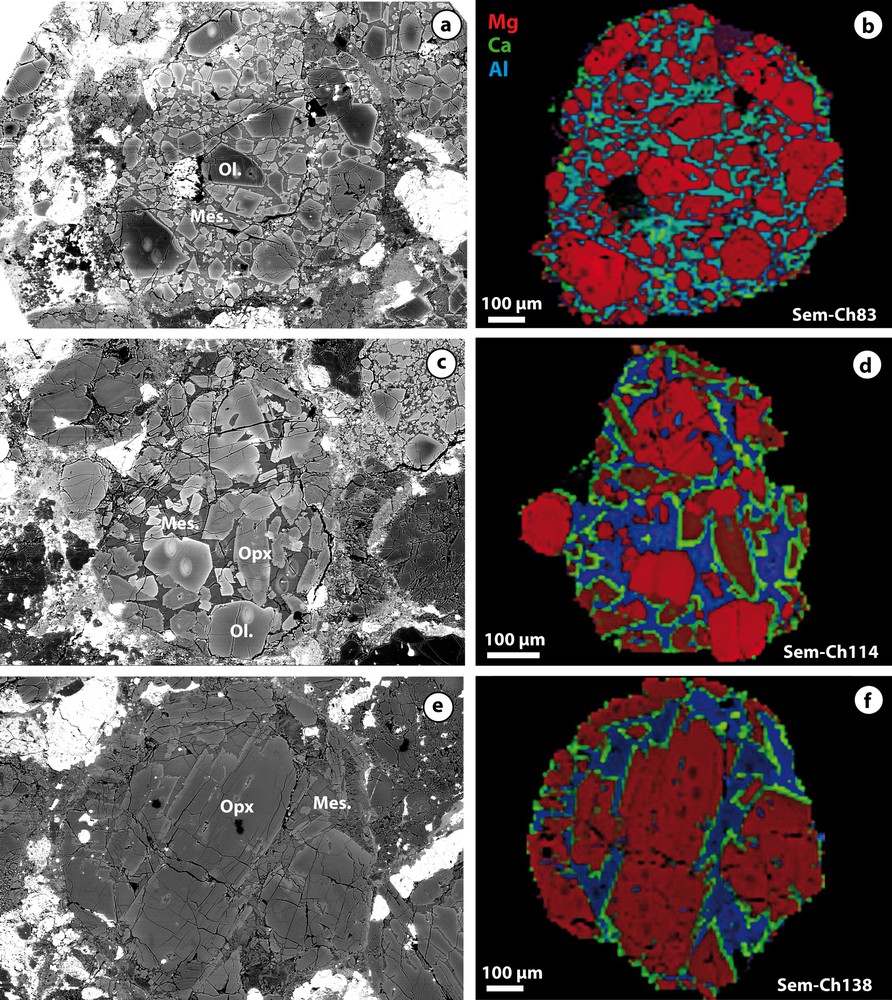
Backscattered electron images and corresponding chemical maps of three ferromagnesian chondrules from Semarkona. On chemical maps, Mg is in red, Ca in green and Al in blue. Ol.: olivine; Opx: low-Ca pyroxene; Mes.: mesostasis and Met.: Fe, Ni-metal. a and b: type II (FeO rich and oxydized) PO (porphyritic with olivine) chondrule; c and d: type II POP (porphyritic with olivine and pyroxene) chondrule; e and f: type II PP (porphyritic with pyroxene) chondrule.
Images en électrons rétrodiffusés et cartes chimiques associées de trois chondres ferromagnésiens provenant de la météorite Semarkona. Sur les cartes chimiques Mg est en rouge, Ca en vert et Al en bleu. Ol. : olivine; Opx : orthopyroxène; Mes. : mésostase et Met. : métal Fe, Ni ; a et b : chondre PO (porphyrique à olivine) de type II (riche en FeO et oxydé) ; c et d : chondre POP (porphyrique à olivine et pyroxène) de type II ; e et f : chondre PP (porphyrique à pyroxène) de type II.
It is not possible to calculate rigorously the error associated with each bulk composition because it depends on the standard deviation for each analysis, on the uncertainties in defining the boundaries of the chondrule or the different phases and on the differing densities of phases under the beam. Another source of uncertainty may arise from how representative a two dimensional cross-section is for a three dimensional object (Hezel, 2007). A reasonable estimation of the uncertainties can be done by dividing each chondrule into quarters and examining how the compositions of each quarter agree with one another (one standard deviation of the data subsets given in Table 2).
Compositions chimiques en roche totale des chondres ferromagnésiens de Semarkona (LL3.0).
| Chondrule | Type | Composition | Al2O3 | CaO | TiO2 | MgO | SiO2 | Cr2O3 | FeO | MnO | Na2O | K2O | Total |
| Sem-Ch2 | I POP | Bulk | 4.70 | 4.27 | 0.23 | 39.03 | 48.38 | 0.52 | 1.55 | 0.09 | 0.35 | 0.03 | 99.15 |
| 1sd | 0.45 | 0.33 | 0.01 | 0.90 | 0.73 | 0.01 | 0.11 | 0.00 | 0.03 | 0.00 | 1.28 | ||
| Sem-Ch121 | I POP | Bulk | 3.33 | 3.30 | 0.13 | 30.93 | 54.74 | 0.45 | 2.98 | 0.32 | 0.84 | 0.08 | 97.11 |
| 1sd | 1.08 | 0.85 | 0.03 | 2.02 | 2.76 | 0.02 | 0.19 | 0.03 | 0.08 | 0.01 | 1.15 | ||
| Sem-Ch32 | I PP | Bulk | 2.94 | 3.31 | 0.17 | 24.45 | 60.59 | 0.68 | 2.46 | 0.77 | 0.83 | 0.23 | 96.42 |
| 1sd | 0.75 | 0.67 | 0.03 | 2.60 | 2.14 | 0.06 | 0.26 | 0.07 | 0.06 | 0.01 | 2.34 | ||
| Sem-Ch21 | II PO | Bulk | 2.57 | 2.79 | 0.21 | 24.35 | 50.10 | 0.46 | 16.33 | 0.37 | 0.93 | 0.23 | 98.33 |
| 1sd | 0.35 | 0.29 | 0.02 | 0.42 | 2.59 | 0.02 | 0.05 | 0.01 | 0.06 | 0.03 | 2.15 | ||
| Sem-Ch83 | II PO | Bulk | 2.91 | 3.11 | 0.18 | 28.28 | 47.17 | 0.29 | 14.81 | 0.30 | 1.28 | 0.22 | 98.54 |
| 1sd | 0.19 | 0.15 | 0.01 | 1.18 | 1.25 | 0.04 | 0.52 | 0.01 | 0.09 | 0.01 | 0.79 | ||
| Sem-ch136 | II PO | Bulk | 3.45 | 4.07 | 0.17 | 24.86 | 49.39 | 0.51 | 13.61 | 0.26 | 1.22 | 0.25 | 97.78 |
| 1sd | 2.01 | 1.45 | 0.07 | 3.18 | 2.98 | 0.05 | 1.73 | 0.01 | 0.09 | 0.02 | 2.23 | ||
| Sem-Ch62 | II POP | Bulk | 2.32 | 1.75 | 0.11 | 23.70 | 52.24 | 0.53 | 15.61 | 0.54 | 1.10 | 0.14 | 98.04 |
| 1sd | 1.11 | 0.80 | 0.05 | 2.92 | 2.52 | 0.05 | 1.91 | 0.06 | 0.07 | 0.01 | 1.60 | ||
| Sem-Ch76 | II POP | Bulk | 2.62 | 2.57 | 0.11 | 26.95 | 52.28 | 0.57 | 11.27 | 0.56 | 1.03 | 0.13 | 98.09 |
| 1sd | 0.36 | 0.66 | 0.02 | 2.88 | 2.07 | 0.08 | 1.18 | 0.02 | 0.08 | 0.01 | 2.09 | ||
| Sem-Ch113 | II POP | Bulk | 2.52 | 2.19 | 0.10 | 25.51 | 52.71 | 0.63 | 13.33 | 0.54 | 0.73 | 0.09 | 98.36 |
| 1sd | 1.26 | 0.41 | 0.04 | 3.50 | 2.70 | 0.05 | 1.79 | 0.03 | 0.08 | 0.00 | 3.72 | ||
| Sem-ch114 | II POP | Bulk | 3.36 | 2.51 | 0.15 | 21.69 | 52.85 | 0.59 | 15.89 | 0.47 | 0.98 | 0.22 | 98.72 |
| 1sd | 0.91 | 0.19 | 0.03 | 2.43 | 3.70 | 0.03 | 1.75 | 0.01 | 0.05 | 0.03 | 1.56 | ||
| Sem-Ch137 | II POP | Bulk | 4.87 | 3.41 | 0.09 | 23.17 | 49.46 | 0.53 | 16.67 | 0.32 | 0.44 | 0.04 | 98.99 |
| 1sd | 1.04 | 0.70 | 0.02 | 2.17 | 1.75 | 0.03 | 1.52 | 0.04 | 0.03 | 0.00 | 1.79 | ||
| Sem-Ch64 | II PP | Bulk | 1.77 | 0.83 | 0.08 | 19.48 | 57.23 | 0.53 | 15.72 | 0.43 | 0.65 | 0.14 | 96.86 |
| 1sd | 0.23 | 0.20 | 0.01 | 1.61 | 1.30 | 0.03 | 1.25 | 0.03 | 0.05 | 0.02 | 3.95 | ||
| Sem-Ch81 | II PP | Bulk | 2.56 | 1.75 | 0.11 | 22.45 | 57.35 | 0.64 | 11.24 | 0.44 | 0.90 | 0.19 | 97.61 |
| 1sd | 1.16 | 0.65 | 0.04 | 3.42 | 5.97 | 0.07 | 1.69 | 0.07 | 0.01 | 0.02 | 0.05 | ||
| sem-Ch138 | II PP | Bulk | 2.00 | 0.67 | 0.10 | 21.48 | 57.62 | 0.34 | 14.57 | 0.42 | 0.81 | 0.06 | 98.05 |
| 1sd | 0.68 | 0.11 | 0.03 | 2.73 | 1.95 | 0.02 | 1.84 | 0.04 | 0.09 | 0.01 | 2.40 |
All the isotopic data and the analytical procedure for the measurement of Al/Mg ratios and Mg isotopes are given in Villeneuve et al. (2009, 2011).
3 Results
Examples of backscattered electron images and chemical images (Mg, Ca, Al) of the 14 studied chondrules are given in Fig. 1. The detailed description of the petrography and the mineralogy of these chondrules is given in the supplemental material of Villeneuve et al. (2009).
Bulk chemical compositions of the 14 chondrules from Semarkona are given in Table 2. Bulk compositions of the chondrules normalized to CI abundances (Lodders, 2003) are shown with the range of compositions of ferromagnesian chondrules from Semarkona (Jones and Scott, 1989; Jones, 1990, 1994, 1996) in Fig. 2. Compositions of the three type I and of the 11 type II chondrules are within the range of type I and type II chondrules reported in the literature (Fig. 2). Because the chondrules studied were initially chosen for their large surfaces of mesostasis available for ion probe analyses, they, broadly speaking, are more mesostasis-rich (from ∼17 to ∼50%) than the average of ferromagnesian chondrules from Semarkona (Jones, 1990; Jones and Scott, 1989). This explains why abundances in refractory elements (Ca, Al, and Ti), which are carried by the mesostasis, are in the upper part of the range of compositions for ferromagnesian chondrules (Fig. 2). Similarly, the relative deficiency in Mg is explained by the fact that this element is dominantly carried by silicates (especially olivine and pyroxene, Fig. 2).
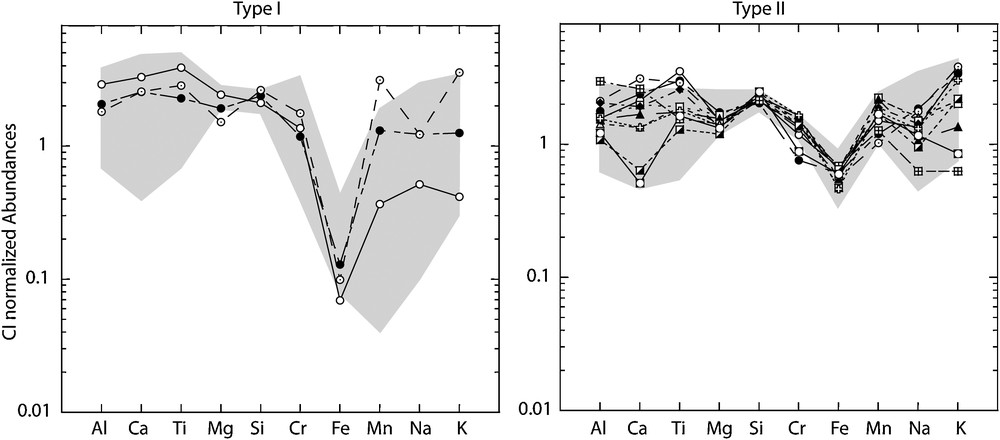
Bulk compositions normalized to CI (Lodders, 2003) for the 14 ferromagnesian chondrules from Semarkona studied. Grey fields are composition ranges measured for type I and type II chondrules from Semarkona by Jones (1990, 1994, 1996) and Jones and Scott (1989).
Composition chimique en roche totale, normalisée aux chondrites CI (Lodders, 2003), des 14 chondres ferromagnésiens de la météorite Semarkona étudiés. Les surfaces grisées correspondent aux gammes de compositions mesurées pour les chondres de Semarkona par Jones (1990, 1994, 1996) et Jones et Scott (1989).
Figure 3 shows relative 26Al ages versus chemical compositions of chondrules normalized to Mg and CI. In order to test the correlations observed by Tachibana et al. (2003), least squares linear regressions were calculated instead of weighted linear regressions. This procedure allows us:
- • to characterise the scattering of the data only, regardless of their associated errors;
- • to give the same weight to the two datasets although 26Al ages from Villeneuve et al. (2009) are more precise;
- • and to facilitate comparisons with Tachibana et al.
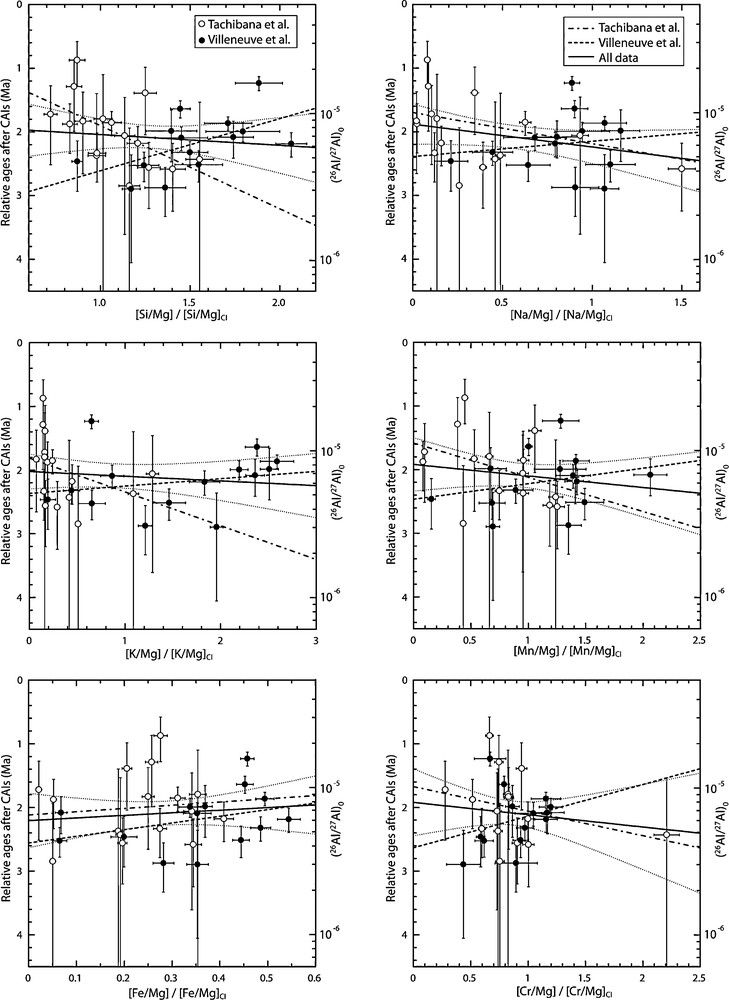
Relative 26Al ages versus bulk chemical compositions normalized on Mg and CI. Open circles are data from Tachibana et al. (2003) while filled circles are data from the current study. Thick dashed, thick dotted and dashed and thick solid lines are least squared linear regressions through our dataset, Tachibana et al., dataset and the two datasets respectively. Thin dotted curves are 95% confidence level intervals for least squares regressions through the two datasets. Errors on y axis are 2σ and errors on x axis are one standard deviation (1 sd).
Âges relatifs 26Al des chondres, comparés aux compositions chimiques en roche totale normalisées à Mg et aux CI. Les cercles vides et remplis correspondent respectivement aux données de Tachibana et al. (2003) et aux données de la présente étude. Les droites en tiretés, en tiretés et pointillés, et en trait plein correspondent respectivement aux régressions linéaires de moindres carrés déterminées au travers de nos données, des données de Tachibana et al. (2003) et des deux jeux de données. Les courbes en pointillés fins sont les intervalles de confiance à 95 % des droites de régression de moindres carrés au travers des deux jeux de données. Les erreurs en ordonnée sont à 2σ, tandis que celles en abscisse sont à 1 sd.
In any case, if linear regressions weighted by the errors on the data are slightly different from least squares linear regressions, both approaches lead to the same observations and conclusions. For each graph, linear regressions were calculated through Tachibana et al. dataset only, through the current dataset only, and through both datasets (Fig. 3). Associated linear correlation coefficients (r) that characterize the strength and the sign of a correlation are given in Table 3.
Coefficients de corrélation linéaire (r) calculés pour les régressions linéaires de moindres carrés. Il peut varier entre −1 et 1 et il caractérise la force d’une corrélation entre deux variables: la corrélation est d’autant plus forte que la valeur de r est proche de 1 ou −1. Habituellement, lorsque la valeur de r est comprise entre −0,5 et 0,5 on considère que la corrélation est faible. Le signe de r indique s’il s’agit d’une corrélation positive ou négative entre les deux variables.
| Dataset | Si/Mg | Al/Mg | Ca/Mg | Fe/Mg | Na/Mg | K/Mg | Cr/Mg | Mn/Mg |
| All | 0.117 | 0.208 | 0.267 | −0.117 | 0.296 | 0.127 | 0.131 | 0.172 |
| Tachibana et al. | 0.557 | 0.239 | 0.224 | −0.110 | 0.378 | 0.352 | 0.297 | 0.422 |
| Villeneuve et al. | −0.561 | −0.027 | 0.220 | −0.347 | −0.139 | −0.214 | −0.267 | −0.255 |
4 Discussion
4.1 Relationships between relative crystallization ages and bulk chemical compositions of chondrules
In agreement with observations of Tachibana et al. (2003), absolute values of the correlation coefficients are greatly inferior to 0.5 for regressions between 26Al relative crystallization ages and either refractory elements (Ca and Al) or Fe abundances: this is true for our data and for the combination of the two datasets (Fig. 3; Table 3). This means that these correlations, if any, are weak. For volatiles or moderately volatile elements (Cr, Mn, Na, K) and Si concentrations, the correlation coefficients are systematically negative for our dataset, i.e. negative correlations with 26Al relative crystallization ages, while they are positive for the Tachibana et al. dataset (Fig. 3; Table 3). Moreover, except for the correlation between Si and 26Al relative crystallization ages (r = –0.561 for our dataset and r = 0.557 for Tachibana et al. dataset), these coefficients are characteristic of weak correlations, i.e. less than 0.5 (Table 3). Finally, regressions calculated through the two datasets show low correlation coefficients (< 0.3, Table 3). In spite of the fact that the correlation for Si/Mg (those for Cr, Mn, Na and K are less convincing) shown by Tachibana et al. (2003) is statistically significant (r = 0.557, Table 3), all of the observations detailed here indicate that there is no clear evidence for correlations between the age of crystallization and the Si, Cr, Mn, Na and K composition of ferromagnesian chondrules. It is most likely that correlations noticed in earlier studies are due to biases that can be explained by the large uncertainties in (26Al/27Al)i and a non-statistically significant number of chondrules. Indeed, a detailed observation of the (26Al/27Al)i of the 17 chondrules used by Mostefaoui et al. (2002) and Tachibana et al. (2003) for their studies shows that, with the exception of three data which incidentally are out of the 95% confidence intervals, these ratios are all indistinguishable within their error bars. It means that in most cases, there is no significant difference of 26Al relative ages between these chondrules. Moreover, regressions between Si and 26Al relative ages show correlations that are statistically significant except that the correlation is positive for the Tachibana et al. dataset while it is negative for our dataset (Fig. 3).
4.2 Meaning of the lack of correlation
This lack of correlation between 26Al relative ages and bulk chemical compositions of chondrules can be interpreted in two different ways:
- • there is, indeed, no correlation between chemical compositions of chondrules and their age of formation. In that case, it means that the variability of chemical compositions observed in chondrules only derives from the variability of compositions of their precursors and does not depend on their evolution in the accretion disk. This interpretation is in line with the canonical view of chondrule formation in a closed system (Grossman, 1988). However, since numerous and strong arguments based on various approaches, i.e. petrography, experimentation, chemical and isotopic observations, clearly rule out the closed system view for the formation of chondrules, this possibility seems unlikely (Chaussidon et al., 2008; Clayton, 2004; Krot et al., 2004; Libourel and Chaussidon, 2011; Libourel et al., 2003, 2006; Matsunami et al., 1993; Nagahara et al., 1999; Pack et al., 2004; Ruzicka et al., 2007, 2008; Thiemens, 1996; Tissandier et al., 2002; Yu and Hewins, 1998; Yu et al., 2003);
- • correlations do exist between chemical compositions of chondrules and their age of formation, but on a timescale which is not resolvable with 26Al. Three possible reasons could exist for this. First, the half-life of 26Al could be too long and the analytic precision not good enough (∼100 000 years at best, Table 1) relative to the timescale for chondrule formation. Second, if analytically an internal 26Al isochron allows us to know the age of the last melting/crystallization event, nothing demonstrates that it was this event (and not an earlier one) which was associated with an eventual change in volatile and moderately volatile elements such as Si, Mn, Na or K. Third, contrary to the assumption made by Tachibana et al. (2003) in their model, there is no reason that chondrule precursors were heated and progressively enriched in volatiles and moderately volatile elements all at the same time and in the same way, i.e. with the same amount of added elements. Indeed, since in the case of ferromagnesian chondrules from Semarkona, for example, ages of formation extended for at least 2 Ma (Villeneuve et al., 2009), the probability that all chondrules have interacted in the same way with the same gas is highly unlikely. However, this does not preclude the existence of a chronological logic, maybe locally and at a small timescale, between chondrules’ chemical compositions and their age of formation.
5 Conclusions
This new set of bulk chemical compositions coupled with 26Al crystallization ages of ferromagnesian chondrules from Semarkona (Villeneuve et al., 2009) shows that, contrary to inferences made in previous studies (Mostefaoui et al., 2002; Tachibana et al., 2003), there is, in fact, no global correlation between 26Al ages of chondrules and their contents in volatile and moderately volatile elements (Fig. 3). If some kind of correlation between chemical compositions of chondrules and their age of formation exists, this must be at time scale that the 26Al-26Mg system is unable to resolve. Though interaction with the local nebular gas during the formation of ferromagnesian chondrules is likely, this process could have happened many times over at least 2 Myr, at different places and under different conditions, precluding the existence of a simple correlation between age and composition for all chondrules
Acknowledgements
This work was supported by grants from the European Research Council (ERC grant FP7/2007-2013 Grant agreement 226846, Cosmochemical Exploration of the first two Years of the Solar System [CEMYSS]) and ANR-08-BLAN-°260-CSD6. This is CRPG publication no 2124.