1 Introduction
In spite of the remarkable investigations of Pierre Pélerin de Maricourt in the 13th century and of William Gilbert (1544–1603) in the late 16th century, the magnetic force, i.e., the virtue by which a piece of the mineral magnetite, or lodestone (a variant spelling is loadstone), attracts iron, was still shrouded in mystery in the 17th and 18th centuries.
It seems that Robert Hooke (1635–1703), then curator of experiments of the Royal Society, was the first, in 1666, to try to determine a law of magnetic force by measuring how its intensity varied with distance (Palter, 1972). A piece of iron in one pan of a balance was attracted by a lodestone at distances between 6 inches and 1/8 of an inch, and the force of attraction was equilibrated by weights in the other pan. Hooke, who probably already had the idea of the inverse square law of gravitation, which he proposed later on to Newton, apparently wanted to see “whether gravitation be somewhat magnetical” (Palter, 1972). However, he gave his results as tables of weights versus distances (Birch, 1756), but did not use them to derive a mathematical law, let alone the inverse square law.
In the Philosophical Transactions of the Royal Society for 1710–1711, the physicist Francis Hauksbee (c. 1666–1713) published the results of his measurements of the deflection of a magnetised needle as a function of its distance to a lodestone (Hauksbee, 1710–1711).
In 1712, Newton, then President of the Royal Society, asked the mathematician Brook Taylor (1685–1731) and Hauksbee, who had succeeded Hooke as curator of experiments, to measure the magnetic force, using the “Great loadstone of the Society”. Again, no mathematical law was derived from the results (Hauksbee and Taylor, 1714–1716).
In the Netherlands, the physicist Pieter van Musschenbroek (1692–1761), using very sensitive scales, performed 146 experiments, measuring the attraction between lodestones shaped as spheres or parallelepipeds, or between spheres of lodestone and iron (van Musschenbroek, 1729). His results, published in 1729, were extensively quoted by the Swedish philosopher and physicist (and later mystic) Emanuel Swedenborg (1688–1772) (Swedenborg, 1734). As always, they were given as tables, and no simple law was derived.
The objective of the present paper is not to give a full account of the experiments conducted in the early 18th century, in the framework of “the quest of the magnetic law”, since it has been done by several authors (Palter, 1972). More modestly, we chose two experiments quite different in their principle, described accurately enough to be unambiguously interpreted, and we tried to infer what information, possibly hidden, they contain on the magnetic law (we found no satisfactory example of the so-called oscillation method). Specifically, we used the results obtained by Hauksbee (1710–1711) and by van Musschenbroek, in one of his experiments reported in his Elementes physicæ (1734), to show that their experimental results, despite the lack of direct evidence of an obvious law of dependence on the distance, were consistent with an inverse square law between magnetic charges.
2 Hauksbee's experiment
Hauksbee used a lodestone weighing about six pounds and performed experiments with one short needle, of half-length 1 inch, and with a longer one, of half-length 6 inches. He measured the angle by which the needle deviated from its rest position in the magnetic field of the Earth, as the lodestone was moved closer and closer to the needle (Fig. 1).
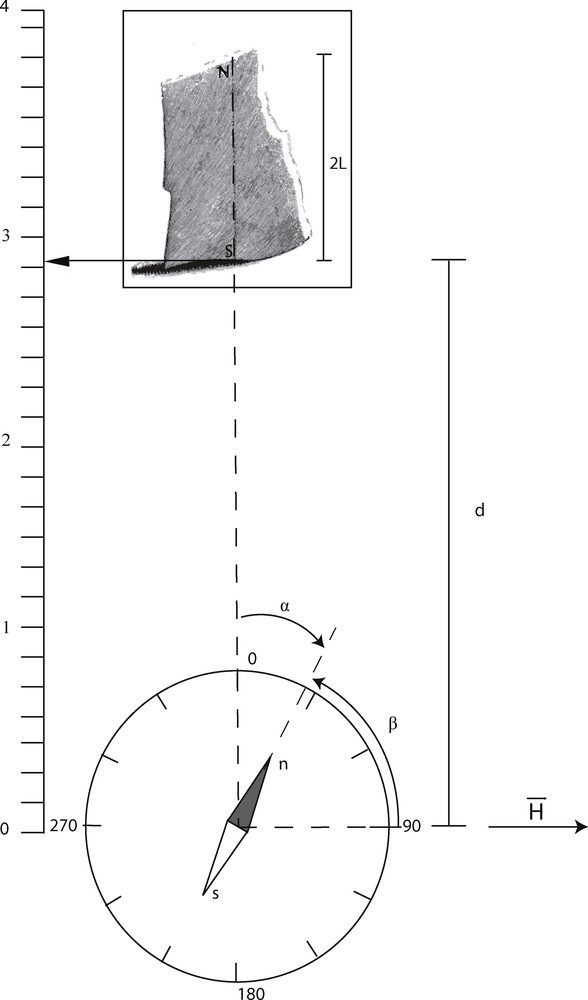
Hauksbee's measurement of the angle by which the needle deviated from its rest position in the magnetic field of the Earth, as the lodestone was moved closer and closer to the needle.
The angle of deviation β for distances d between 5 feet and 3 inches, for the short needle and 5 feet and 9 inches, for the long needle (1 inch = 2.54 cm and 1 foot = 12 inches), are given in the Tables 1 and 2 (angles in degrees and minutes).
Experiments by the short needle.
| Distances of the lodestone from the needle in inches | The several angles of the needle at the several distance |
| 3 | 87—00 |
| 6 | 84—00 |
| 9 | 78—30 |
| 12 | 69—00 |
| 15 | 56—45 |
| 18 | 43—30 |
| 21 | 33—00 |
| 24 | 24—00 |
| 27 | 18—00 |
| 30 | 13—30 |
| 33 | 11—00 |
| 36 | 8—45 |
| 39 | 7—00 |
| 42 | 5—30 |
| 45 | 4—30 |
| 48 | 3—50 |
| 51 | 3—20 |
| 54 | 3—00 |
| 57 | 2—45 |
| 60 | 2—30 |
Experiments by the long needle.
| Distances of the lodestone from the needle in inches | The several angles of the needle at the several distance |
| 09 | 87—30 |
| 12 | 81—45 |
| 15 | 72—15 |
| 18 | 53—20 |
| 21 | 35—00 |
| 24 | 24—10 |
| 27 | 17—50 |
| 30 | 13—10 |
| 33 | 10—10 |
| 36 | 8—00 |
| 39 | 6—30 |
| 42 | 5—15 |
| 45 | 4—10 |
| 48 | 3—30 |
| 51 | 3—00 |
| 54 | 3—35 |
| 57 | 2—15 |
| 60 | 2—00 |
Considering the angle α = 90°–β, we have compared a graph of the experimental values α vs. d to the graph of α vs. d, calculated assuming an inverse square law between magnetic masses at the poles of the stone and the needle. The length between the poles of the stone, assumed by Hauksbee to be on the shorter sides of the stone (Fig. 1), was 2L = 7 inches, and the length between the poles was 2l = 12 inches, for the long needle, and 2l = 2 inches, for the short needle. The distance d is the distance between the pole of the stone closer to the needle and the centre of the needle.
The potential created at the poles n and s of the needle by the masses m at the poles N and S of the stone, was calculated as a function of α and d. The force exerted at a pole n or s of the needle is equal to the gradient of the potential times the mass at the pole. The angle α was calculated, as a function of d, l, L, H, by writing that the couple exerted by the stone on the needle was equilibrated by the couple exerted by the horizontal component H of the magnetic field of the Earth whose value, in London about 1710, was H = 13 × 10−6 T (Gallet, 2013). The magnetic mass m at a pole of the stone is unknown. The stone weighed about 6 pounds (2.75 kg), so, if it had been pure magnetite, of magnetic moment per unit mass 96 A·m2 kg−1 (Hunt et al., 1995), its magnetic moment would have been M = 2Lm = 96 × 2.75 = 264 A·m2 (assuming that the magnetic moment of the stone is equal to the product of m by the distance beween poles 2L). However, it is very likely that the stone was inhomogeneous, undoubtedly weathered, and that its magnetisation was much inferior to that of pure magnetite. The best fit of the theoretical α vs. d curve with the experimental curve of Hauksbee was obtained by taking M = 9.78 A·m2, equal to 1/27th of the magnetic moment of pure magnetite. This value is in good agreement with the values found by Wasilewski and Kletetschka (1999) for various samples of lodestone. The calculations were made using the SI system of units. The sensitivity to the value adopted for the distance L between the poles of the magnet was explored and found to be quite small.
The theoretical curves α vs. d, compared to the experimental curves drawn from Hauksbee's data, for both the short and the long needle are given in Fig. 2. It can be seen that for distances greater than 50 cm for the short needle and 60 cm for the long needle, the experimental values of α agree very well with the values calculated by assuming an inverse square law for the action of each pole of the lodestone on each pole of the needle. The curves for the long and short needles become undistinguishable for distances greater than about two feet. For shorter distances, the values of the angle α measured with the short and the long needles, for the same value of d are somewhat different, due to the different configuration of the four poles. At the same time, the agreement between calculated and experimental values becomes less good.
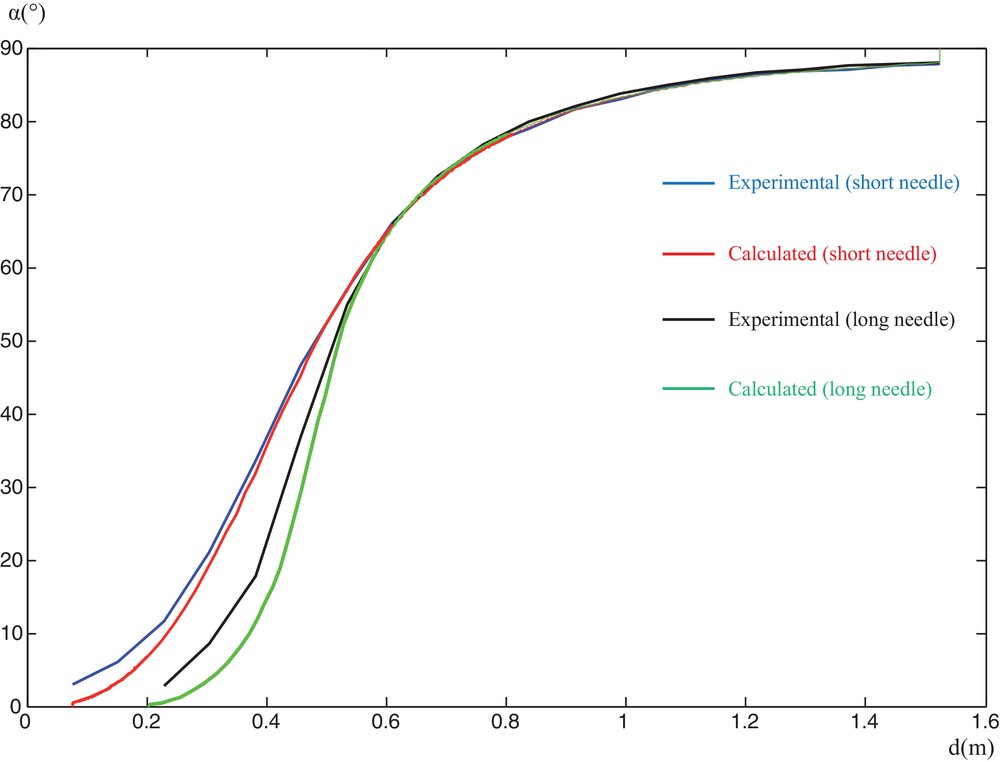
Theoretical curves α vs. d, compared to the experimental curves drawn from Hauksbee's data, for both the short and the long needle. Colour available on the net.
Hauksbee had remarked: “In these experiments I made use of two needles; one of radius of 6 inches, the other but of one inch: which last, after abundance of tryals, I found to be most accurate; besides the advantage it gave in beginning the experiment 6 inches nearer the stone than the other: and from two feet distance from the same, it became nearly agreeable to the angles made by the long needle to all the farther distances.” However, he did not otherwise comment on the results.
We represented the magnetic interactions between the magnet and the needle by interactions between magnetic masses located at the end of the needles and on the short sides of the lodestone. Had Hauksbee tried a quantitative interpretation of his observations, he would, no doubt, have adopted this representation. We tried a uniform distribution of magnetic poles, on the short sides of the stone, without improving the fit. More elaborate models would be useless, in the absence of better information on the stone, and they would have been out of reach for Hauksbee, a hundred years before Poisson's work. Of course, Hauksbee did not give any estimate of the uncertainties of his data; he just made the statement reported above about the short needle being more accurate.
3 van Musschenbroek's experiment
van Musschenbroek performed a great number of experiments to measure, in different conditions, the attraction between spherical pieces of lodestone or between a lodestone sphere and an iron sphere. We will consider the latter case (van Musschenbroek, 1734). It was well known in Musschenbroek's time that iron got magnetized in the presence of a magnet and lost its magnetization when the magnet was removed. But of course, the linear relation between density of magnetization and magnetic field was unknown.
The lodestone sphere was resting on a table, with its poles aligned vertically, and an iron sphere of identical diameter was hanging above it, at the end of a long piece of string attached to one pan of very sensitive scales; weights placed in the other pan equilibrated the weight of the iron sphere and the attractive force exerted by the lodestone. The distance was measured by inserting copper strips of known thickness between the spheres.
The results of Musschenbroek's experiments are given, for distances, in Rheinland lines and, for forces, in medicinal grains (i.e., used by apothecaries). A Rheinland inch (0.0262 m) contained 12 lines. A line was about equal to 2.18 mm (Niemann, 1823: 33). The value of the medicinal grain in the Netherlands was the weight of a mass of 55.6 mg (Niemann, 1823: 36).
The diameter of the spheres was equal to 0.95 inch = 0.025 m.
The values of the attractive force in grains were given for distances between 1 and 8 lines.
| Distance (lines) | Attractive virtue (grains) |
| 8 | 1 |
| 7 | 2 |
| 6 | 3¼ |
| 5 | 6 |
| 4 | 9 |
| 3 | 16 |
| 2 | 29 |
| 1 | 64 |
Plotting log F (attractive force) vs. log d (distance), it appears that the slope of the graph varies continuously with distance. In fact, Musschenbroek did not even tried to plot his results, but he used them to confirm his strange idea (on which he did not comment) that the attractive force was in “quadruple inverse ratio of the hollow spaces between the spheres”.
Using an inverse square law, we calculated the attractive force between a spherical magnet and an iron ball, in the conditions of Musschenbroek's experiments. We used the modern SI system, with forces expressed in newtons (1 grain = 5.56 × 10−3 N) and the distances in meters (1 line = 2.18 × 10−3 m). Necessary ingredients in the calculation are the magnetic susceptibility K of iron and the magnetic moment M of the magnet, which appear through their product MK (in A·m2), which is the only free parameter. As it is obviously unknown, we therefore resorted to reasonable assumptions. The value of the magnetic susceptibility of iron K varies between about 10,000 for extremely pure iron and about 50 for less pure iron where small carbide precipitates hinder the motion of the domain walls. As it was impossible, in Musschenbroek's time, to obtain very high purity iron, we chose a value K = 200, which together with M = 0.0312 A·m2 will give the best fit between the curves F(d) representing the experimental data and the calculated values (see Fig. 3 below).
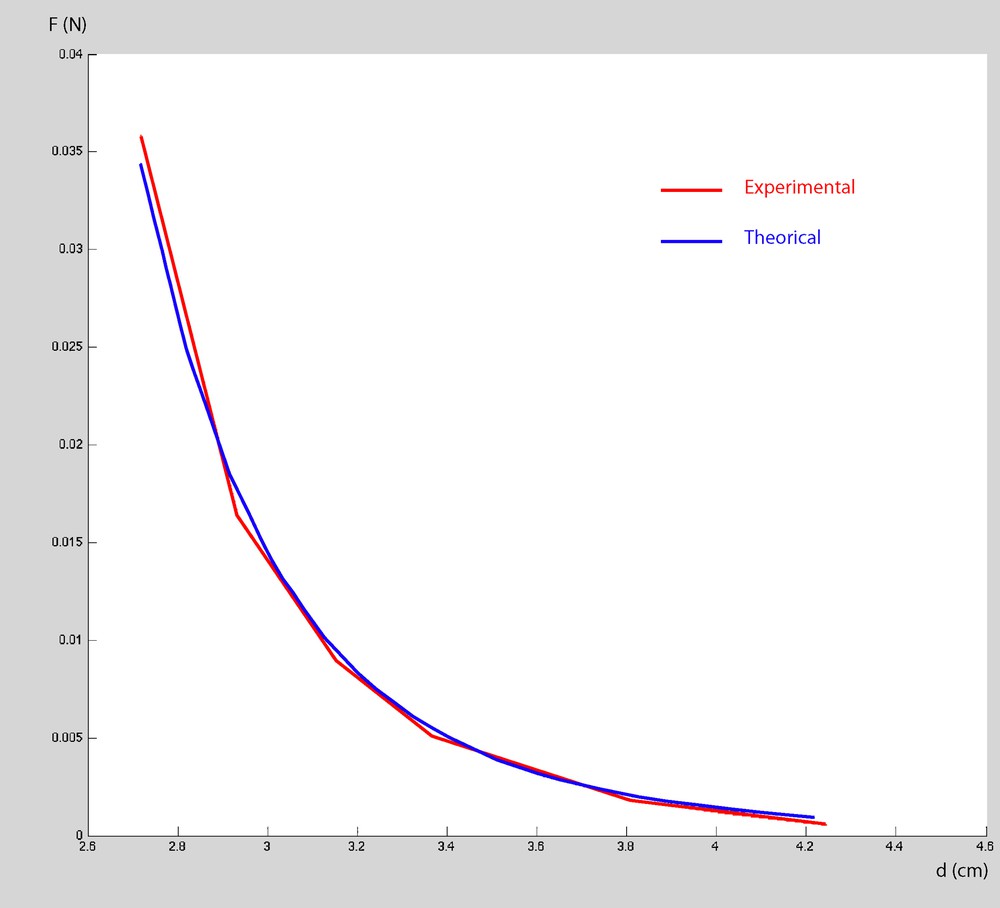
K = 200 and M = 0.0312 A·m2 give the best fit between the curves F(d) representing the experimental data and the calculated values. Colour available on the net.
Assuming, of necessity, that both spheres were homogeneous, it was possible to consider the magnet as equivalent to a dipole of moment M situated at its centre, magnetising the ball of soft iron, of magnetic susceptibility K. The attractive force exerted by M on a small element of volume of the iron ball is then calculated with the local value of the magnetic field of the magnet, and integrated over the whole volume of the sphere.
For large enough distances, the calculated F tends to vary as 1/d7, which is expected, given that the iron sphere, assumed to be uniformly magnetised, is equivalent to a dipole whose field varies like 1/d3, and that the attraction between two dipoles varies like 1/d4.
In principle, we should have added to F a corrective term due to the magnetisation of the iron ball by the Earth's magnetic field. However, the terrestrial field is weaker than that of the magnet, and over the range of distances covered by the data (d < 4.2 cm), the correction is negligible. However, it would become important for larger distances.
Musschenbroek, like many others, looked for a law in 1/dx, but found x varying with d, which puzzled him.
4 Conclusion
The purpose of the experiments of Hauksbee, Musschenbroek and others was to obtain a mathematical law for the variation of the magnetic force F with distance d, preferably as a power law of the form F = 1/dn, with n ≥ 2. These investigators had measured, as a function of distance, the resulting attractive force, or the torque, between magnets or between a magnet and iron.
Our calculation, using the results, both of Hauksbee and Musschenbroek, and an inverse square law between magnetic masses, gave an excellent fit (which would, no doubt, have satisfied the authors) between the experimental and calculated values of F(d). This proves, first that the approximations we made were acceptable, and second that Hauksbee and Musschenbroek were fine experimentalists. However, despite the care with which the experiments had been performed, the authors did not infer of them any consistent law.
Indeed, in a letter to John-Theophilus Desaguliers, a friend of Newton, van Musschenbroek (1724–1725) described some of his experiments and asserted: “But, from these [experiments], can we, in any way, assign a proportion between forces and distances? I for one, do not see it; you, surely, who are a very perceptive man, whose judgment on physical things, and especially experiments, I esteem as much as that of any mortal, examine carefully if there is some regularity and scrutinize all proportions; you will not find any”.
In 1762, Tobias Mayer (1723–1762), in an unpublished work (Forbes, 1972), before the fundamental work of Coulomb, proved the inverse square law by essentially the same method that we have used here: he calculated the attractive force between two straight magnets by assuming that there was a linear distribution of magnetism between the poles, and that every part of one magnet was attracted or repelled by every part of the other according to an inverse square law. He found an excellent agreement between the experimental and calculated values.
Could Hauksbee and van Musschenbroek have done it? van Musschenbroek, assuredly not, because, not knowing calculus nor the laws of induction, he lacked the necessary mathematical and physical background. However, Hauksbee did not need more than the knowledge of the positions of the poles of the magnet and of the needle, which he had defined, and the idea that there could be a force in 1/d2. He therefore could have done the calculation presented here. But he did not. It remains that his experiments, like those of van Musschenbroek, were unimpeachable.


