1. Introduction
Volcanic eruptions can propel large quantities of radiatively important and chemically reactive species into the atmosphere [e.g., Robock et al., 2009, Timmreck, 2012, Oppenheimer, 2002, Oppenheimer et al., 2014, Cadoux et al., 2015]. The atmospheric and climatic consequences have been widely studied drawing on evidence from direct observations [e.g., Guo et al., 2004], indirect and proxy records [e.g., Büntgen et al., 2020] and modelling efforts [e.g., Toohey et al., 2019]. While many factors come into play in influencing the climatic impact of a given eruption, the primary forcing agent is recognised as stratospheric sulphate aerosol and thus estimates of sulphur yields for past eruptions are a first order requirement for efforts to understand their climatic and societal consequences. Much attention has been given to determination of stratospheric sulphur yields but significant uncertainties remain in the estimates [Scaillet and Oppenheimer, 2024]. For example, estimates drawing on evidence from the rock record are sensitive to uncertainties in tephra mass (eruption magnitude), the abundance and composition of any vapour phase in the pre-eruptive reservoir, and the behaviour of volatile elements during storage and eruption [e.g., Marshall et al., 2022, Metcalfe et al., 2023, Venugopal et al., 2020, Schiavi et al., 2020, Schmidt and Black, 2022, Scaillet and Oppenheimer, 2023, 2024].
Sulphur yields can now be estimated with a range of spaceborne sensors [e.g., Pardini et al., 2017, Taylor et al., 2018]. Despite challenges in validation, this approach is regarded as the gold standard of eruptive sulphur yield quantification during an eruption, as it involves spectroscopic measurement of abundances of sulphur-bearing gases and aerosol. Sulphur yields of past events are also estimated from polar ice core records [e.g., Sigl et al., 2015] drawing on understanding of global atmospheric dispersion of point source tracer injections in the stratosphere. This approach also entails substantial uncertainties, for instance in the case of ice core signals that are not attributed to a particular volcano (the vast majority), the source location (and its proximity to the deposition site) is unknown. In effect, measurement of traces (ppb) of the emitted sulphur is used to extrapolate to global sulphur yields (Tg).
The third approach draws on petrological analyses of the erupted rocks [Devine et al., 1984] along with petrological arguments [Scaillet et al., 2003]. In this case, it is not the emitted sulphur that is measured but rather the non-emitted sulphur that is evaluated, based on analyses of sulphur contents in crystal-hosted glass inclusions and of matrix glass. The difference in these quantities is then used to estimate syn-eruptive sulphur yields by scaling to the estimated total eruptive rock mass [which itself typically has high uncertainty; Engwell et al., 2015, Bonadonna et al., 2015]. Realisation that this approach failed to yield estimates even close to the satellite-measured sulphur yields of eruptions, such as those of El Chichón in 1982 and Pinatubo in 1991, fuelled recognition that volatile-saturated pre-eruptive magmas may already contain an abundant sulphur-rich gas phase [e.g., Luhr et al., 1984, Westrich and Gerlach, 1992, Scaillet et al., 1998, Wallace and Edmonds, 2011]. This became known as the “excess sulphur” problem, and it is particularly acute for eruptions of evolved magmas, though less so for basaltic ones [e.g., Sharma et al., 2004]. The amount of this sulphur is not captured by the “petrologic method” [Devine et al., 1984]. Rather, it has been inferred from wider geochemical, petrological and geophysical knowledge of magma bodies [notably drawing on experimental petrology studies and thermodynamic calculations, e.g., Scaillet and Pichavant, 2003]. An alternative approach uses apatite as a proxy for volatile contents of magmas [e.g., Stock et al., 2016, Humphreys et al., 2021] but this also requires assumptions, in particular how to relate the volatile contents of apatite with those of the coexisting melt and gas, in addition to apatite occurrence. There remain few and sometimes inconclusive constraints on S partitioning between apatite and melt/fluid [e.g., Peng et al., 1997, Parat and Holtz, 2005]. While promising, this method requires further experimental work.
In general, very few eruptions before the satellite remote sensing era have been identified with any degree of confidence in ice core records (this requires geochemical fingerprinting of tephra grains in the ice cores). Thus, when all we have to go on are the proximal deposits of large eruptions, estimates of sulphur yield must rely on petrological and eruption magnitude assessments. While significant progress has been made in understanding the behaviour of sulphur in silicic magmas [e.g., Carroll and Webster, 1994, Scaillet et al., 1998, Clemente et al., 2004, Scaillet and Macdonald, 2006, Keppler, 2010, Zajacz et al., 2012, Masotta et al., 2016], permitting estimation of sulphur yields of quartz-oversaturated felsic arc magmas [e.g., Scaillet et al., 2003], for quartz-undersaturated, or alkali-rich magmas, the constraints are limited. This is despite recognition that the presence of alkalis increases sulphur solubility [e.g., Carroll and Rutherford, 1987, Ducea et al., 1994] and hence sulphur carrying capacity.
In addition to Tambora 1815 [Oppenheimer, 2003], renowned eruptions of alkali-rich phonolite to trachyte magmas include those of Campi Flegrei, Somma-Vesuvius (Italy) and Laacher See (Germany). In the case of the 13 kyr calBP [Reinig et al., 2021] eruption of Laacher See, estimates of sulphur yield range up to 150 Tg [Schmincke et al., 1999] influencing the parameterisation of climate models [e.g., Textor et al., 2003, Niemeier et al., 2020] as well as the search for potential sulphur signatures of the episode in polar ice core records [Baldini et al., 2018, Abbott et al., 2021]. Our aim here is to re-assess sulphur yields of Laacher See and other significant phonolite–trachyte eruptions drawing on improved understanding of volatile behaviour in alkalic magmas and focusing on eruptions for which pre-eruptive conditions—pressure (P), temperature (T), H2O content and, crucially, redox state—are experimentally constrained. We use relationships between the fugacities of key S-bearing species (H2S, SO2) and their concentrations in phonolite liquids to quantify the partial pressures of corresponding species in pre-eruptive magma reservoirs. We focus on the more evolved portions of erupted magmas since they are likely to accumulate volatiles during reservoir growth.
2. Methodology
We follow Anderson Jr et al. [1989] and Scaillet and Pichavant [2003] in calculating the partial pressures of dissolved volatile species using thermodynamic models and volatile concentrations measured in melt inclusions (MI). We consider primarily the role of H2O, CO2 and S-bearing species. For the latter, we use fugacity-concentration relationships established by Moncrieff [2000], as reported in Burgisser et al. [2012]. Since the melt compositions we are concerned with are broadly phonolitic, we use the water solubility model of Carroll and Blank [1997], established using a sodic phonolite. For CO2, the model used is that of Burgisser et al. [2012], which is also calibrated on Na-rich phonolite. As shown below, the majority of eruptions had dissolved CO2 contents below detection (<20 ppm), indicating partial pressures of CO2 below 10 MPa, the fluid being essentially a mixture of water and sulphur (+Cl). For any species i, the relationships between fugacity, fi, mole fraction, Xi, and partial pressure, Pi, is given by:
| (1) |
The total pressure is given by:
| (2) |
| (3) |
In the results presented below, the retrieved Ptot was checked against independent phase equilibrium constraints for pre-eruptive conditions. To accommodate uncertainties in fO2, we carried out calculations assuming that S is present either as H2S (reduced, or around the Quartz-Fayalite-Magnetite buffer, QFM) or SO2 (oxidized, i.e. 2 log units above QFM).
Evaluating the S yield related to the release of the gas phase present in the reservoir requires assessment of the quantity of this phase, a notoriously challenging task [Wallace et al., 1995]. Geochemical analyses based on trace element behaviour point to proportions ranging from 1 to 6 wt% of the gas phase (expressed as bubbles in the magmatic reservoir) which holds all volatiles, including H2O, CO2 and S-bearing species, the high end corresponding with the apical portion of evolved magma reservoirs [Wallace et al., 1995]. Gas amounts of 5–6 wt% are thought to correspond to a percolation threshold, beyond which bubbles interconnect, preventing accumulation of higher gas contents [Wallace, 2001]. Comparison of the sulphur yield of eruptions for which both petrological constraints and remote sensing, or ice core constraints on sulphur yield are available shows that, in most cases, both approaches agree if a gas content in the reservoir of about 5 wt% is assumed [Scaillet et al., 2003].
Estimation of gas content can also be achieved using the bulk vesicularity of pumice clasts, as recently shown for the rhyolite of the Changbaishan (Paektu) Millennium eruption in north Korea [Scaillet and Oppenheimer, 2023]. Here, the bulk gas content of magma at fragmentation (the sum of dissolved and exsolved volatiles) is restored assuming equilibrium conditions between gas and melt for both H2O and CO2 volatiles, which represent more than 95 wt% of the total volatile complement of evolved magmas. The calculation uses established solubility laws of H2O and CO2 in phonolitic liquids [Carroll and Blank, 1997, Burgisser et al., 2012] and a modified Redlich–Kwong equation of state for describing the fugacities of corresponding species in the gas phase [Holloway, 1987]. Once that bulk H2O and CO2 contents are known, the amount of excess gas, if present, at reservoir conditions can be calculated if the pre-eruptive pressure is adequately constrained. The calculation assumes also that the magma retains volatiles during ascent, which has been shown to hold for felsic eruptions along a significant part of their ascent path [e.g., Newman et al., 1988]. The lower melt viscosity of phonolitic magmas [Andújar and Scaillet, 2012] may permit loss of gas during early stages of magma ascent, however.
An example of such calculation is shown in Figure 1, using a bulk vesicularity of 0.75, and pre-eruption P–T of 200 MPa and 800 °C. These P–T values are typical for evolved reservoirs, including for those feeding phonolitic–trachytic eruptions [Scaillet et al., 2008, Fabbrizio and Carroll, 2008, Andújar et al., 2010]. We show the effect of remaining CO2 in the matrix glass at fragmentation, for two H2O contents in matrix glass (0.5 wt% and 1 wt%), on the restored amount of gas in a reservoir holding a phonolitic melt at 200 MPa and 800 °C. In Figure 1, a magma reaching 10 ppm CO2 and 0.5 wt% H2O in the residual (matrix) glass at fragmentation yields a gas content of 4 wt%. Such a magma would have a silicate melt with 1.05 wt% dissolved H2O and 434 ppm dissolved CO2. Increasing the residual H2O content of the matrix glass at fragmentation to 1 wt% (orange curve) would increase the gas amount to slightly over 5 wt% with the dissolved H2O content increasing to 2.46 wt% and the dissolved CO2 decreasing to 319 ppm.
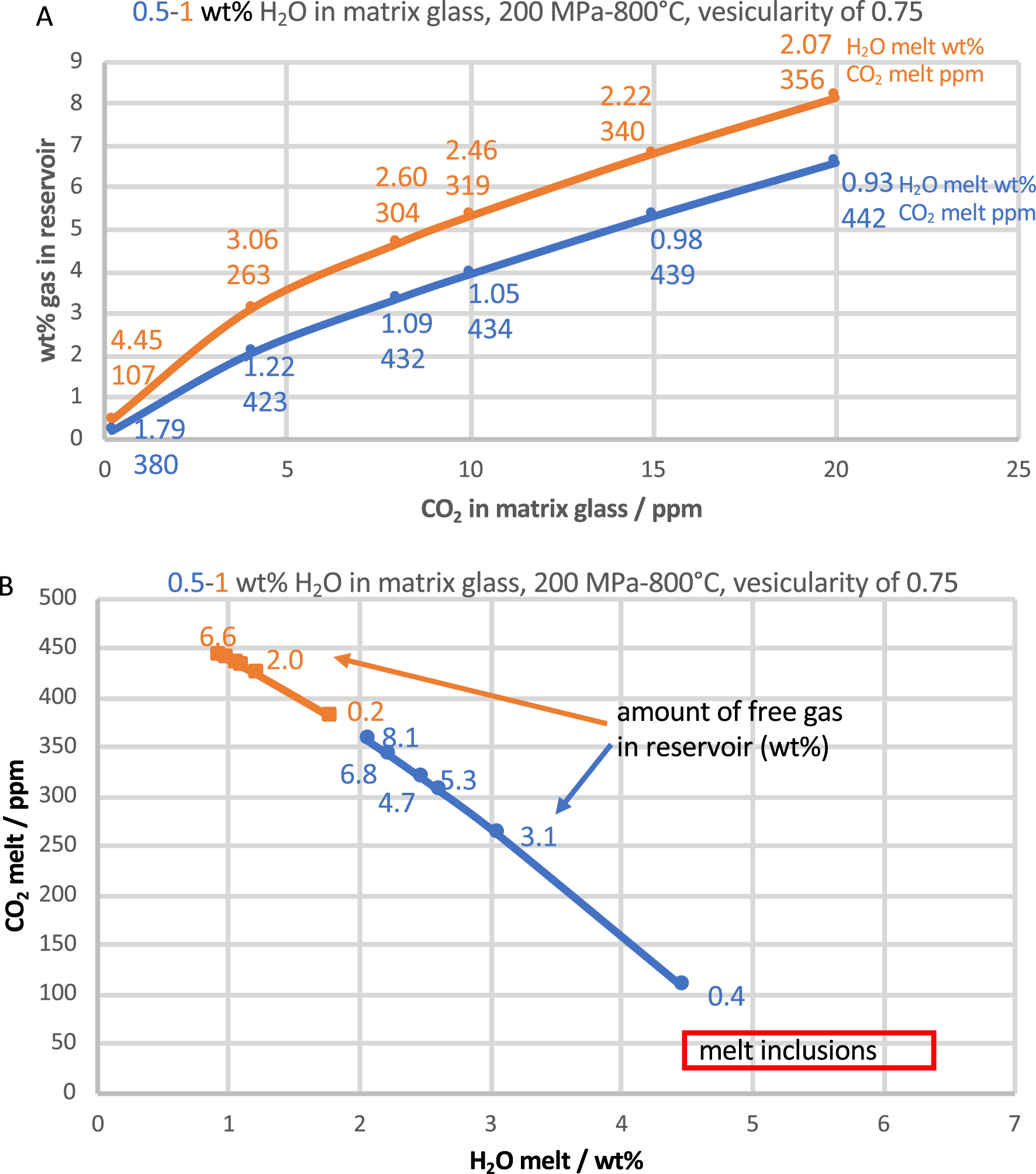
(a) evolution of gas mass fraction in the reservoir with the residual CO2 content in the matrix glass for two H2O content in the matrix glass: blue 1 wt% H2O and orange 0.5 wt% H2O. Both sets of calculations are performed for a terminal bulk vesicularity of 0.75. The dissolved H2O (wt%) and CO2 (ppm) contents of the melt phase in the reservoir are shown along each curve. (b) Same data as in (a) but showing how the dissolved H2O and CO2 contents in the melt vary. The red box shows typical pre-eruptive conditions for phonolitic–trachytic magmas, inferred from the analyses of dissolved volatiles in crystal-hosted glass inclusions. Masquer
(a) evolution of gas mass fraction in the reservoir with the residual CO2 content in the matrix glass for two H2O content in the matrix glass: blue 1 wt% H2O and orange 0.5 wt% H2O. Both sets of calculations are performed for ... Lire la suite
The residual volatiles in the matrix glass at fragmentation are poorly constrained for phonolitic eruptions, in particular the CO2. For silicic magmas (rhyolites) available data typically show H2O in the range 0–2 wt% and up to 20–30 ppm CO2 [e.g., Newman et al., 1988, Wadsworth et al., 2020] and it is likely that phonolitic magmas display comparable values. In Figure 1b, the same calculations are shown but using a conventional diagram of dissolved H2O–CO2 contents in the silicate melt. The data define a single isobaric trend, showing how the amount of excess gas varies with residual CO2 for two different residual H2O contents. As in Figure 1a, increasing CO2 content leads to an increase in the amount of excess gas but also to an increase in dissolved CO2 content at pre-eruptive conditions. These calculations can be compared with typical pre-eruptive H2O–CO2 contents of phonolitic magmas as inferred from H2O–CO2 analyses in melt inclusions, which typically reveal elevated water contents (up to 6–7 wt%) and CO2 contents below detection limit [e.g. Cioni, 2000]. Inspection of Figure 1b suggests that phonolitic magmas have excess gas contents corresponding with the low end of the range inferred for silicic magmas [Scaillet et al., 2003, Wallace, 2005].
Since we lack precise knowledge of residual volatiles in phonolitic to trachytic matrix glass at fragmentation, in the following we assume a gas content in the reservoir of 5 wt%, bearing in mind that it likely represents a maximum in most cases.
A critical aspect in performing calculations of S yields is the accuracy of melt sulphur contents, which are widely determined by electron microprobe analyses of glass inclusions in phenocrysts. This instrument affords relatively low detection limits, of order of 50–200 ppm depending on analytical conditions. Figure 2 illustrates how the calculated mass of emitted sulphur varies with melt sulphur contents, based on a notional eruption of 4 km3 of DRE magma, initially stored at 200 MPa, with 5–6 wt% H2O and 20 ppm CO2 in melt along with sulphur, and coexisting with 5 wt% of excess gas. The calculations are shown for both reduced and oxidized conditions. For the reduced case, taking the case of a magma whose pre-eruptive S content is at 200 ppm (and 5 wt% H2O in melt), produces a yield of about 9.3 Tg S. Varying the S abundance by ±50 ppm corresponds to a range in the S yield from 5.3 Tg (150 ppm S) to 14.3 Tg (250 ppm). In other words a typical 50 ppm analytical uncertainty, equivalent to the standard deviation of that element in a group of melt inclusions of a single event, propagates into 50% uncertainty in the calculated S yield from the gas phase.
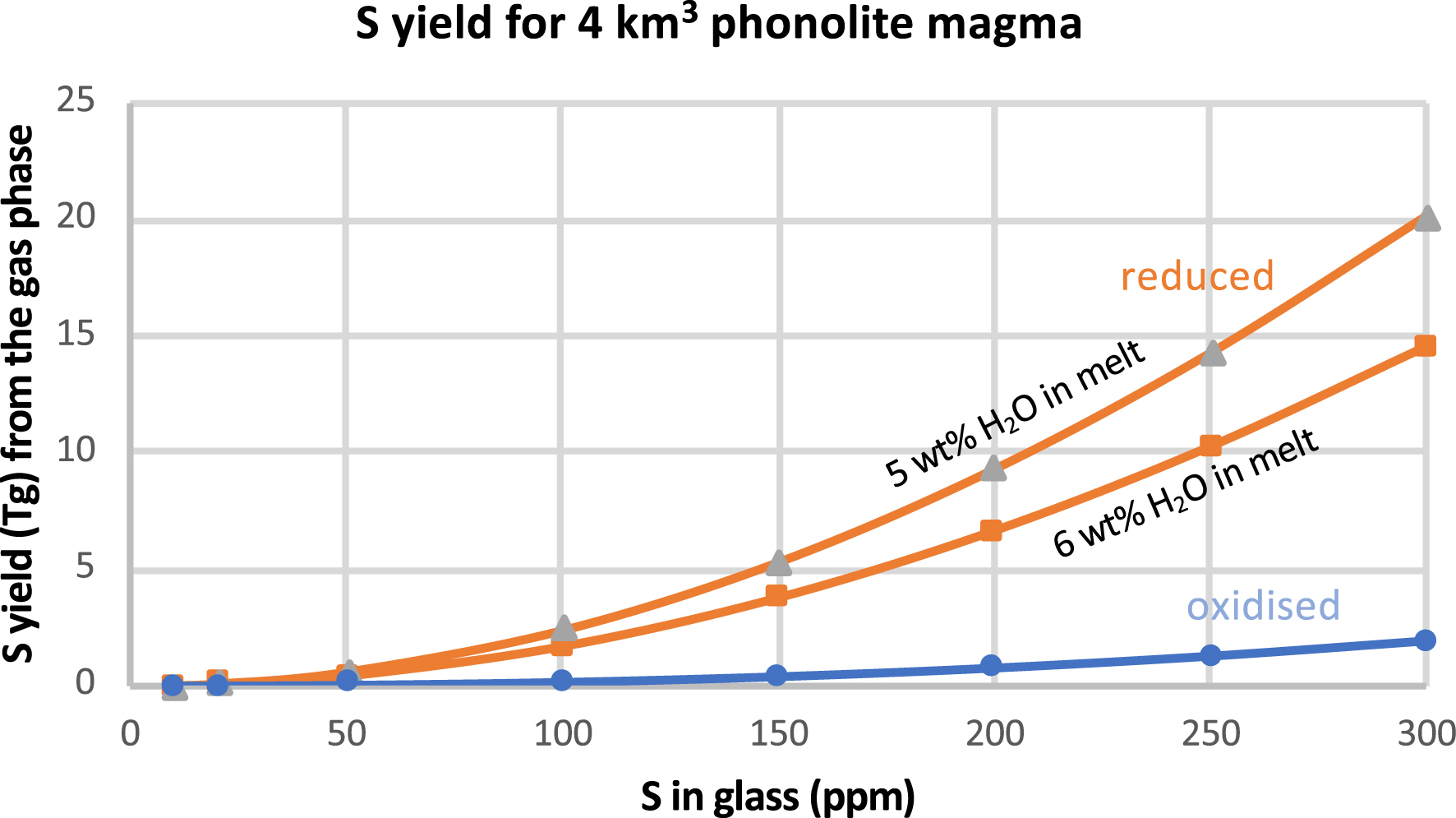
Variation of the sulphur yield with pre-eruptive melt sulphur content (S in glass) for a phonolitic magma stored at 200 MPa, 760 °C and with 5 wt% excess gas, calculated for either reduced (pyrrhotite-bearing) or oxidized conditions. For reduced conditions, results are shown for two pre-eruptive melt water contents. A variation in ±50 ppm of sulphur in matrix glass corresponds to a variation of the calculated sulphur yield of ±50%.
While the situation for oxidized conditions seems less critical, an uncertainty of order 50% in S yield still emerges. The two curves shown for reduced conditions illustrate also that the melt water content is a critical parameter. An increase of H2O content of 1 wt% (from 5 to 6 wt%) for the same magma reduces S yield by around 30% to 6.3 Tg. It is thus essential to quantify as precisely as possible pre-eruptive conditions in order to calculate volatile yields associated with volcanic eruptions.
2.1. Caveats
Our method is primarily aimed at estimating the S content of bubbles, whether in the residual melt or trapped along with a melt inclusion inside a phenocryst. If at equilibrium, the bubble composition is independent of its location (inside a melt inclusion within the crystal or outside the crystal). Methods have been developed to determine the composition of gas bubbles coexisting with melt inclusions in phenocrysts [e.g., Wallace et al., 2015, 2021, Aster et al., 2016], including their solid compounds or precipitates [e.g. Venugopal et al., 2020, Schiavi et al., 2020]. These reveal that a significant part of CO2 and S of the MI and coexisting bubble in basaltic rocks resides in the bubble. What could affect our calculations is if the bubbles in the melt inclusions are shrinkage bubbles arising from cooling, or in other words, if exsolution of volatiles has occurred after entrapment as inferred for mafic compositions [e.g. Wallace et al., 2015, Venugopal et al., 2020, Schiavi et al., 2020], thereby changing the amount of S (and CO2) dissolved in the melt inclusion pre-eruptively, which would change the corresponding fugacities. However, while exsolution during cooling is conceivable for low viscous mafic melts, the colder and viscous felsic melts we consider here are much less susceptible. The fact that S contents of matrix glass are comparable to those of melt inclusions in explosively erupted felsic magmas [e.g., Westrich and Gerlach, 1992] is direct evidence for limited exsolution of S before the glass transition temperature is crossed.
Conversely, some of the S present in the excess fluid in the reservoir could condense as a solid phase during eruption (i.e. upon cooling) [Rose Jr, 1977, Schmauss and Keppler, 2014], such as shown for the Pinatubo 1991 eruption [Jakubowski et al., 2002]. This process would reduce the amount of S released to the atmosphere. An additional process excluded in our calculations is breakdown of S-bearing minerals, such as pyrrhotite or anhydrite, during magma ascent. For “cold” magmas, however, this process is kinetically inhibited, as shown by Gerlach et al. [1996] for the 1991 Pinatubo eruption.
The preceding discussion illustrates some key sources of uncertainty in the petrologic method, in addition to uncertainties in eruption magnitude and proportion of exsolved fluid, which both scale linearly with S yield. In most cases, eruption magnitude is uncertain at least to a factor of two [Scaillet and Oppenheimer, 2024]. While these sources of uncertainty may seem very large, even spaceborne observations of eruption yields are subject to comparable uncertainty, as are extrapolations of ice core S abundances to total S yields to the stratosphere.
3. Application
The essential figures calculated for each event are listed in Table 1, while Figure 3 compares the S content of the corresponding fluid phase with that estimated for other arc-related magmas.
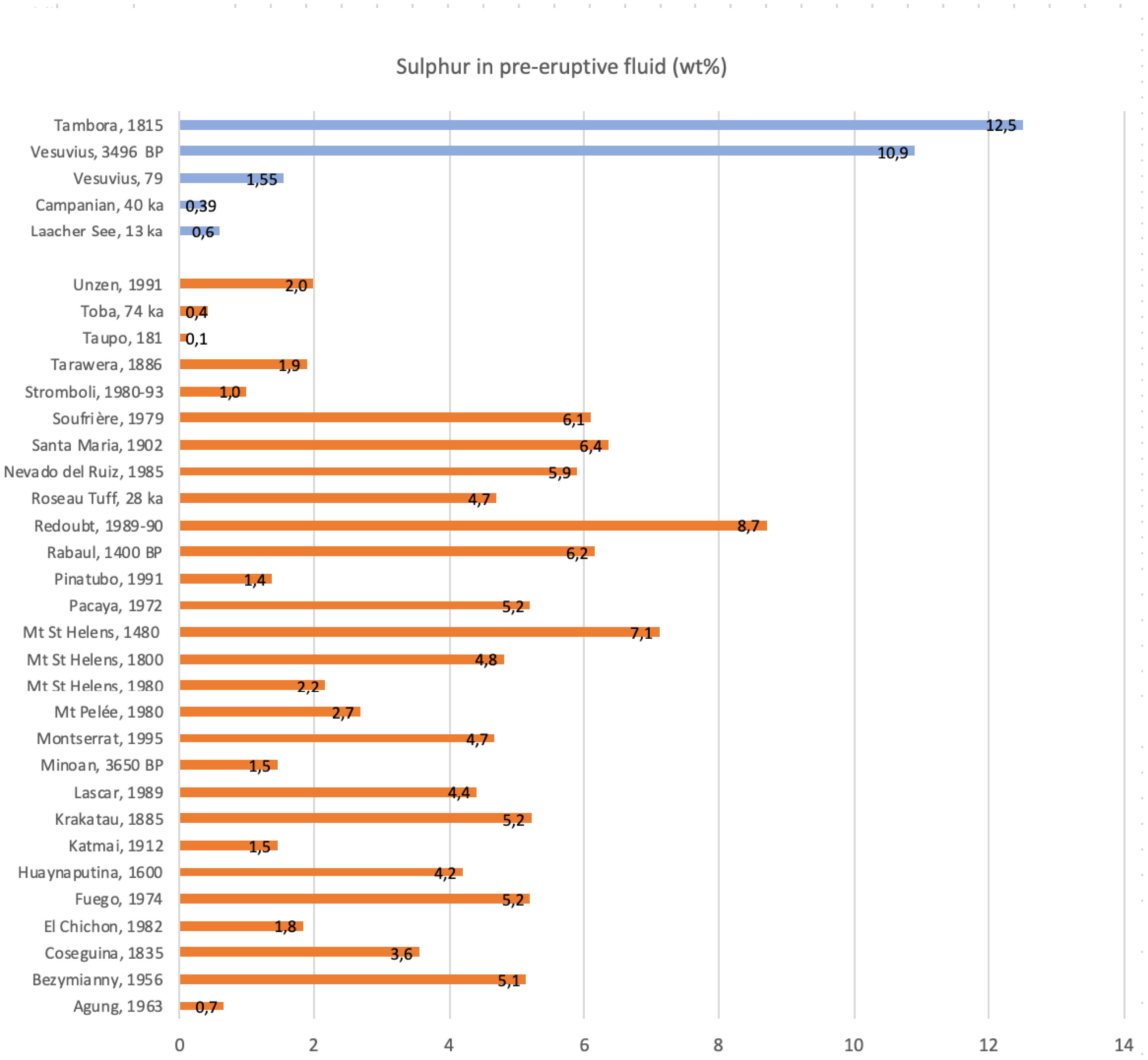
The sulphur content of the excess gas phase (in wt%) in the reservoir of several volcanic eruptions, calculated using petrologic and thermodynamic constraints on pre-eruptive P–T–H2O-fO2 conditions. Data for calco-alkaline magmas are from Scaillet et al. [2003]. See text for details of calculations.
Volatile contents, fluid phase compositions and calculated sulphur yields of famous phonolite–trachyte eruptions
| Tambora | Laacher See | Campanian Ignimbrite (Plinian) | Vesuvius Pompei | Vesuvius Avellino | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Reduced | Oxidised | Reduced | Oxidised | Reduced | Oxidised | Reduced | Oxidised | Reduced | Oxidised | |
| P, bar | 1010 | 800 | 1796 | 1760 | 1950 | 1950 | 1940 | 1920 | 2020 | 1900 |
| T, °Ca | 935 | 935 | 760 | 760 | 760 | 760 | 815 | 815 | 785 | 785 |
| H2O, wt%a | 0.030 | 0.030 | 0.056 | 0.056 | 0.060 | 0.060 | 0.063 | 0.063 | 0.060 | 0.060 |
| CO2, ppma | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| S, ppma | 732 | 732 | 270 | 270 | 100 | 100 | 200 | 200 | 560 | 560 |
| fH2O, barb | 510 | 510 | 1209 | 1209 | 1330 | 1330 | 1422 | 1422 | 1330 | 1330 |
| fCO2, barc | 197 | 197 | 197 | 197 | 197 | 197 | 197 | 197 | 197 | 197 |
| fH2S, bard | 331 | 45 | 6 | 25 | 194 | |||||
| fSO2, bare | 95 | 10 | 1 | 5 | 52 | |||||
| PH20, bar | 555 | 548 | 1639 | 1633 | 1830 | 1830 | 1799 | 1797 | 1763 | 1748 |
| PCO2, bar | 154 | 162 | 122 | 123 | 116 | 116 | 117 | 118 | 114 | 118 |
| PH2S, bar | 296 | 0 | 35 | 0 | 5 | 0 | 19 | 0 | 143 | 0 |
| PSO2, bar | 0 | 88 | 0 | 7 | 0 | 1 | 0 | 3 | 0 | 37 |
| Fluid composition, molar | ||||||||||
| XH2O | 0.550 | 0.685 | 0.912 | 0.928 | 0.938 | 0.938 | 0.927 | 0.936 | 0.873 | 0.920 |
| XCO2 | 0.152 | 0.203 | 0.068 | 0.070 | 0.060 | 0.060 | 0.060 | 0.061 | 0.056 | 0.062 |
| XH2S | 0.293 | 0.020 | 0.002 | 0.010 | 0.071 | |||||
| XSO2 | 0.110 | 0.004 | 0.000 | 0.002 | 0.019 | |||||
| Fluid composition, wt% | ||||||||||
| H2O | 0.3725 | 0.4355 | 0.8179 | 0.8330 | 0.8621 | 0.8647 | 0.8485 | 0.8569 | 0.7631 | 0.8067 |
| CO2 | 0.2525 | 0.3151 | 0.1488 | 0.1538 | 0.1337 | 0.1341 | 0.1349 | 0.1373 | 0.1202 | 0.1334 |
| H2S | 0.3750 | 0.0333 | 0.0042 | 0.0166 | 0.1167 | |||||
| SO2 | 0.2494 | 0.0131 | 0.0012 | 0.0058 | 0.0599 | |||||
| S fluid, wt% | 0.3516 | 0.1247 | 0.0312 | 0.0066 | 0.0039 | 0.0006 | 0.0155 | 0.0029 | 0.1094 | 0.0299 |
| Bulk S content, wt% | 0.352 | 0.125 | 0.156 | 0.033 | 0.020 | 0.003 | 0.078 | 0.015 | 0.547 | 0.150 |
| Fluid, wt% | 0.01 | 0.01 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| vol magma, km3 | 35 | 35 | 4.04 | 4.04 | 23 | 23 | 0.50 | 0.5 | 0.1 | 0.1 |
| mass S, Tg | 283 | 100 | 14.5 | 3.1 | 10.3 | 1.6 | 0.89 | 0.17 | 1.26 | 0.34 |
a The pre-eruptive temperature. dissolved H2O, S and CO2 contents come from: Tambora: Self et al. [2004], Pouget et al. [2023], Andújar and Scaillet [2012]; Laacher See: Harms et al. [2004], Berndt et al. [2001], HarmsSchmincke [2000]; Campanian Ignimbrite: Signorelli et al. [2001], Marianelli et al. [2006]; Vesuvius: Scaillet et al. [2008], Cioni [2000], Signorelli et al. [1999].
b fH2O = 10((Log(wt% H2O)−Log(0.0329))/0.7238), from Carroll and Blank [1997].
c fCO2 = 10((Log(wt% CO2)−Log(0.000005611))/1.112), from Burgisser et al. [2012].
d fH2S = 10((Log(wt% S)−Log(0.004))/0.501), from Burgisser et al. [2012].
e fSO2 = 10((Log(wt% S)−Log(0.01))/0.437), from Burgisser et al. [2012].
3.1. Tambora
We first consider the 1815 eruption of Tambora, for which independent estimates of sulphur yield are available based on recorded deposition of sulphur in bipolar ice cores. These indicate a stratospheric injection of 28 Tg of S [Toohey and Sigl, 2017], approximately three times the amount measured for the Pinatubo emission. A recent re-evaluation of volatile yields (based on melt inclusions) has concluded that about 74 Tg S were emitted from melt degassing [Pouget et al., 2023]. The eruption, with an estimated output of 30–40 km3 DRE of magma [Self et al., 2004, Kandlbauer and Sparks, 2014] is around 4–8 times greater in magnitude than that of Pinatubo. From Self et al. [2004] and Andújar and Scaillet [2012], the magma was stored at a pressure of around 100 MPa, a temperature of 935 °C, with a melt water content of about 3 wt% at an fO2 around QFM+2. The average sulphur content of melt inclusions ranges from 689 to 775 ppm [Self et al., 2004, Pouget et al., 2023] and in the following we take a value midway between these two studies (732 ppm).
For reduced conditions, the fluid phase would have more than 30 wt% sulphur, while for oxidised conditions the sulphur content would be around 11 wt% (Table 1, Figure 3). For a 5 wt% gas phase in the reservoir and 35 km3 DRE of magma, the upper bounds for the sulphur released from the excess gas are 1415 Tg (reduced) and 502 Tg (oxidised), the lower value being already more than 10 times the stratospheric S injection estimated based on ice core records. For 1 wt% excess gas, the corresponding amounts are 283 and 100 Tg S, respectively. Considering the inferred high fO2 [Self et al., 2004], the lower bounds of these ranges seem more appropriate. This suggests that had the reservoir been gas-saturated, the amount of such a free gas phase was <1 wt%, or <0.5 wt% considering that a significant part of S yield comes from melt degassing alone [Self et al., 2004, Pouget et al., 2023]. The low vesicularity of Tambora pumices [<60%, Suhendro et al., 2021] compared with other plinian eruptions of felsic magmas [70–80%, Thomas et al., 1994], is consistent with a low pre-eruptive excess gas content. This first example already illustrates that the assumption of abundant gas in the reservoir may not be universal, calling for a case by case approach when calculating past S emissions. Gas loss prior to eruption during magma storage has been inferred for the so-called Millenium Eruption of Paektu [Scaillet and Oppenheimer, 2023] and the 1815 Tambora event may be an additional example.
3.2. Laacher See
Pre-eruptive conditions have been experimentally determined by Harms et al. [2004] and Berndt et al. [2001]. These works concluded that the uppermost part of the magma reservoir, which yielded most (4 km3 DRE) of the erupted material was comparatively cool (about 760 °C), water-rich (5–6 wt% dissolved H2O) and possibly gas-saturated, and in the pressure range of 150 to 200 MPa. This magma appears to have been relatively oxidised, based on S6+/S2- ratios in melt inclusions [HarmsSchmincke, 2000] and the presence of hauyne in the mineral assemblage [Wörner and Schmincke, 1984, Berndt et al., 2001]. The sulphur coming from melt degassing of that part has been estimated at 0.45 Tg [HarmsSchmincke, 2000]. The lowermost, more mafic part of the erupted magma (2.3 km3 DRE), is thought to have been gas-free, reflecting its lower water content (4 wt% H2O). Accordingly, its contribution to the sulphur yield corresponds to the sulphur exsolved from melt during decompression, estimated as 1.45 Tg [HarmsSchmincke, 2000].
Analyses of melt inclusions from the upper part of the Laacher See reservoir indicate a pre-eruptive S content average of 270 ppm [HarmsSchmincke, 2000]. Calculations of S-species fugacities and partial pressures, and the corresponding fluid phase compositions are reported in Table 1. The sulphur content of the fluid varies between 3.1 wt% (reduced) and 0.7 wt% (oxidised), falling within the range estimated for typical arc magmas [Scaillet et al., 2003] (Figure 3). Assuming an upper value of gas content in reservoirs of 5 wt% (which includes the contribution of all gas species) and taking a magma DRE volume of 4 km3, then, depending on redox state, the Laacher See eruption may have released up to 1.5 Tg (oxidised) or 13.6 Tg (reduced) sulphur in addition to that released by the melt [0.45 + 1.45 = 1.9 Tg, HarmsSchmincke, 2000]. This amounts to a total release of sulphur in the range 3–15 Tg.
3.3. Campanian ignimbrite
The 39.85 ka BP [Giaccio et al., 2017] Campanian Ignimbrite erupted an estimated 155–265 km3 DRE (or 4.1–6.9 × 1014 kg) of magma [Marti et al., 2016, Silleni et al., 2020]. Phase equilibrium constraints show that the upper part of the magma body was stored at pressures of 140 to 200 MPa, at a temperature of 740–780 °C, and at or close to H2O saturation, i.e. with dissolved H2O in the melt of about 6 wt% [Fabbrizio and Carroll, 2008], the latter consistent with melt inclusion constraints [Marianelli et al., 2006]. These temperature estimates are significantly lower than those based on clinopyroxene-melt thermometry [900–950 °C; Forni et al., 2016], suggesting that clinopyroxene may record early stages of magma evolution and not later pre-eruptive conditions.
The pre-eruptive sulphur content of the melt has been studied in some detail by Signorelli et al. [2001] by analysing melt inclusions in phenocrysts belonging to the early plinian phase of the event, which ejected an estimated 23 km3 DRE of magma [Marti et al., 2016]. Melt inclusions in phenocrysts inferred to record pre-eruptive conditions (salitic pyroxenes) have sulphur contents below the detection limit of electron microprobe (EMPA) (approximately 200 ppm for the given analytical conditions). Whole rock analyses (which are representative of matrix glass analyses owing to the low crystal content of the rock of about 5%) indicate values of 110–140 ppm of undegassed sulphur [Signorelli et al., 2001]. Sulphur measurements made by Marianelli et al. [2006] of various MI from both the fallout or ignimbrite deposits range from below 100 ppm for the H2O-rich MI to over 500 ppm for H2O-poor MI. For our calculations, we take a pre-eruptive sulphur content of 100 ppm, assuming that the H2O-rich portion represents the top part of the reservoir which fueled the plinian column. The prevalence of pyrrhotite inclusions in pyroxene suggests reduced conditions [Signorelli et al., 2001]. MELTs simulation of liquid lines of descent has also suggested that the redox state during crystallization was around QFM [Fowler et al., 2007]. Some petrological information on volatiles is available for both H2O and CO2 but not for sulphur for the voluminous ignimbrite component of the deposit [Moretti et al., 2019], precluding evaluation of its pre-eruptive sulphur budget.
The results (Table 1) indicate a sulphur content of the gas phase of 0.4 wt% under reduced conditions (Figure 3). For the 23 km3 (DRE) magma erupted in the plinian phase, the sulphur yield arising from exsolved gas (5 wt%) in the reservoir under reduced conditions amounts to 9.7 Tg. This is similar to the 10 Tg S erupted by the 1991 Pinatubo eruption which ejected 5 km3 DRE of magma [Guo et al., 2004], underscoring the fact that alkaline magmas do not necessarily eject more S than calc-alkaline magmas. Similar calculations performed for oxidised conditions (all SO2) yield a sulphur fluid content of 0.15 wt% (Figure 3) and a bulk sulphur yield of 0.8 Tg, which is a tenth of the reduced scenario. Taking the higher estimate inferred for the plinian phase as representative of the entire erupted magma would imply a total S yield of order 100 Tg S. Note, however, that this scaling implies a constant gas content in the reservoir, which is unlikely considering the propensity of gas bubbles to migrate upwards, as demonstrated for the Bishop Tuff [Wallace et al., 1995]. It also assumes that all eruptive components (plinian, ignimbrite) are equally able to release their volatiles into the atmosphere, which is also unlikely [e.g., Peccia et al., 2023].
3.4. Vesuvius
The erupted volume of phonolite to tephriphonolite magmas for the renowned 79 CE eruption is estimated as 1.5 km3 DRE [Cioni et al., 2008], around a third that of Pinatubo’s 1991 eruption. Pre-eruptive conditions of the phonolite magma have been defined via phase equilibrium and melt inclusion studies [Cioni, 2000, Scaillet et al., 2008] indicating a reservoir pressure of 200 ± 20 MPa, temperature of 815 ± 10 °C and water-rich conditions (6–6.5 wt%). The sulphur content of phonolitic melt inclusions was found to be below the EMPA detection limit [200 ppm, Cioni, 2000], therefore we take this figure as the maximum sulphur concentration at the top of the reservoir. Similarly, the CO2 content was found to be below the FTIR analysis detection limit [Cioni, 2000], and therefore we use a pre-eruptive value of 20 ppm. Redox conditions have been estimated to lie around the NNO solid buffer, consistent with presence of sulphide globules.
For these conditions, our calculations indicate that the fluid phase in the apical portion of the magma body had a sulphur content of 1.6 wt% (Table 1, Figure 3), if reduced, corresponding to a sulphur yield for the phonolitic part of the deposit [about 0.5 km3 DRE, Cioni et al., 2008] of around 0.8 Tg, comparable to that released by the 1980 El Chichón eruption [Mexico, Krueger et al., 2008]. Alternatively, for oxidising conditions, with SO2 prevalent over H2S in the fluid, then we calculate a sulphur content of the fluid of 0.3 wt% yielding 0.1 Tg of sulphur to the atmosphere.
Pre-eruptive conditions for the Bronze Age Avellino plinian eruption, dated 1890 calBCE [Sevink et al., 2021], are similar to those for the 79 CE “Pompeii” eruption in terms of P–T–H2O [Scaillet et al., 2008, Balcone-Boissard et al., 2012]. The sulphur content appears to have been higher than for the 79 CE eruption, averaging 560 ppm [Signorelli et al., 1999]. This gives a sulphur content in the fluid of 11 wt% for reduced, or 3 wt% for oxidised, conditions. The modest magnitude, estimated as 0.9 km3 DRE, of which 0.1 km3 were phonolite [Cioni et al., 2008, Sulpizio et al., 2010], translates into a sulphur yield of less than 1.5 Tg in both cases (1.2–0.17 Tg, respectively).
4. Discussion
Our estimated upper limits for the sulphur yields of these renowned eruptions are comparatively modest, with the possible exception of the Campanian Ignimbrite. The restored gas+melt S contents (i.e. S content of the magma before eruption, excluding that locked in sulphide/sulphate minerals, which is not available for degassing) range from 37 ppm up to 5130 ppm (Table 1). In detail, considering the likely redox state (with regard to S) of erupted magmas (oxidized for Laacher See and sulphide-bearing for the others), the bulk content of S is in general of order several 102 ppm and not several 103 ppm, except for Avellino. This parameter is compared with the values calculated for calc-alkaline magmas by Scaillet et al. [2003] using the same general methodology (Figure 4).
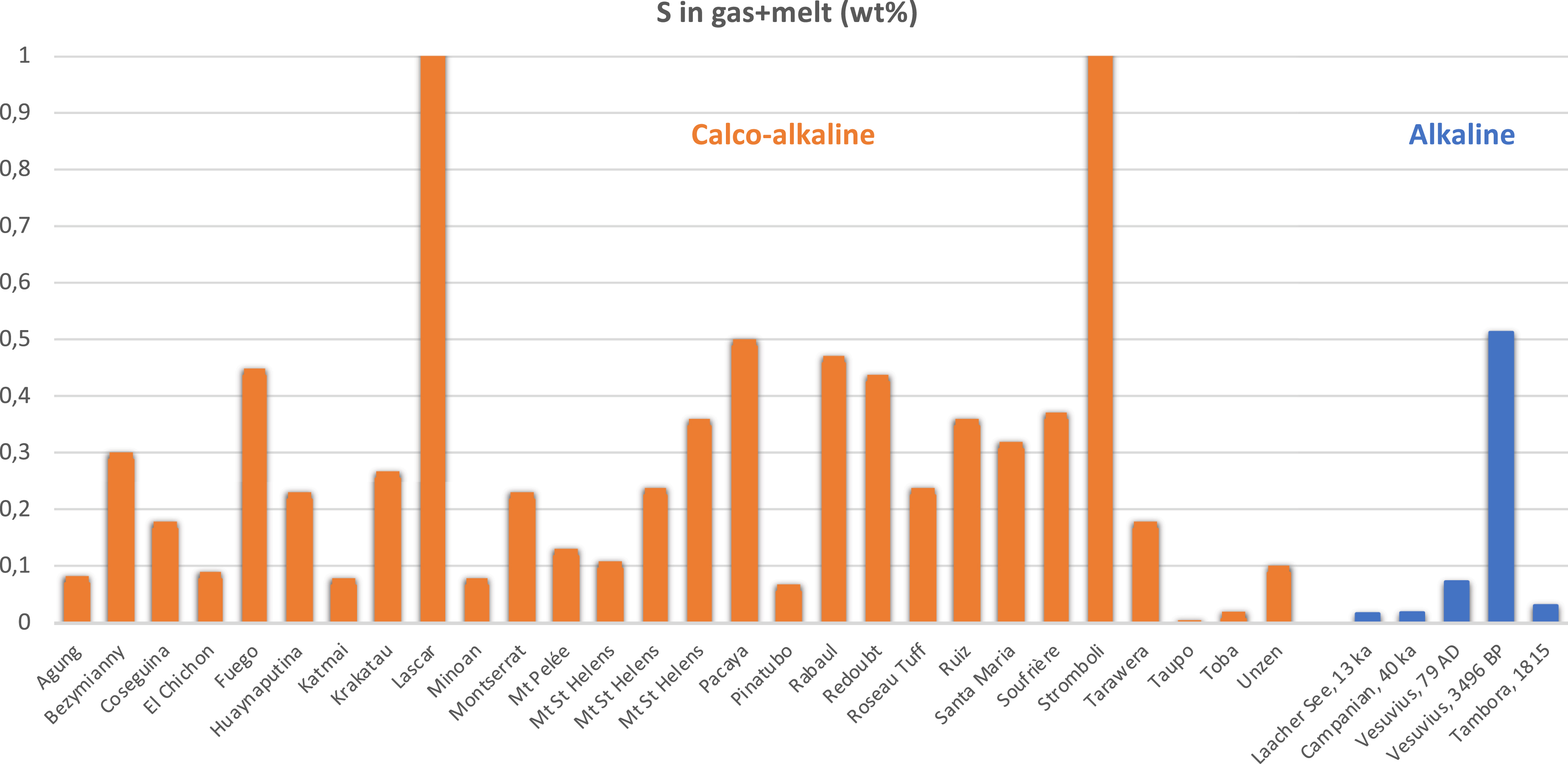
The calculated bulk sulphur content stored in both melt and pre-existing gas phases. Data from calco-alkaline magmas are from Scaillet et al. [2003]. The values corresponding to Láscar and Stromboli volcanoes are beyond the range shown (7 and 36 wt% sulphur respectively).
Excluding the case of Avellino eruption, the bulk S contents of alkaline magmas appear to be slightly lower than those of arc magmas. This could reflect the oxidized nature of calc-alkaline magmas which allows efficient mafic-to-felsic S transfer during fractionation, by inhibiting extensive sulphide fractionation [e.g. Scaillet and Macdonald, 2006]. However, the case of Laacher See, an oxidized yet S-poor magma, does not fit with such a scenario. The apparent low S content of alkaline felsic magmas may primarily reflect the source rather than a process but additional data are clearly needed to furnish a more robust statistical lens on this question.
The sulphur yield of alkaline magmas is positively correlated with the volume (DRE) of magma emitted, falling along the same trend defined by arc magmas (Figure 5). At a given volume a dispersion of 1–2 orders of magnitude in sulphur yield is apparent, in particular for large eruptions, stressing that eruption size alone is not a good guide to S yield (and potential climate impact).
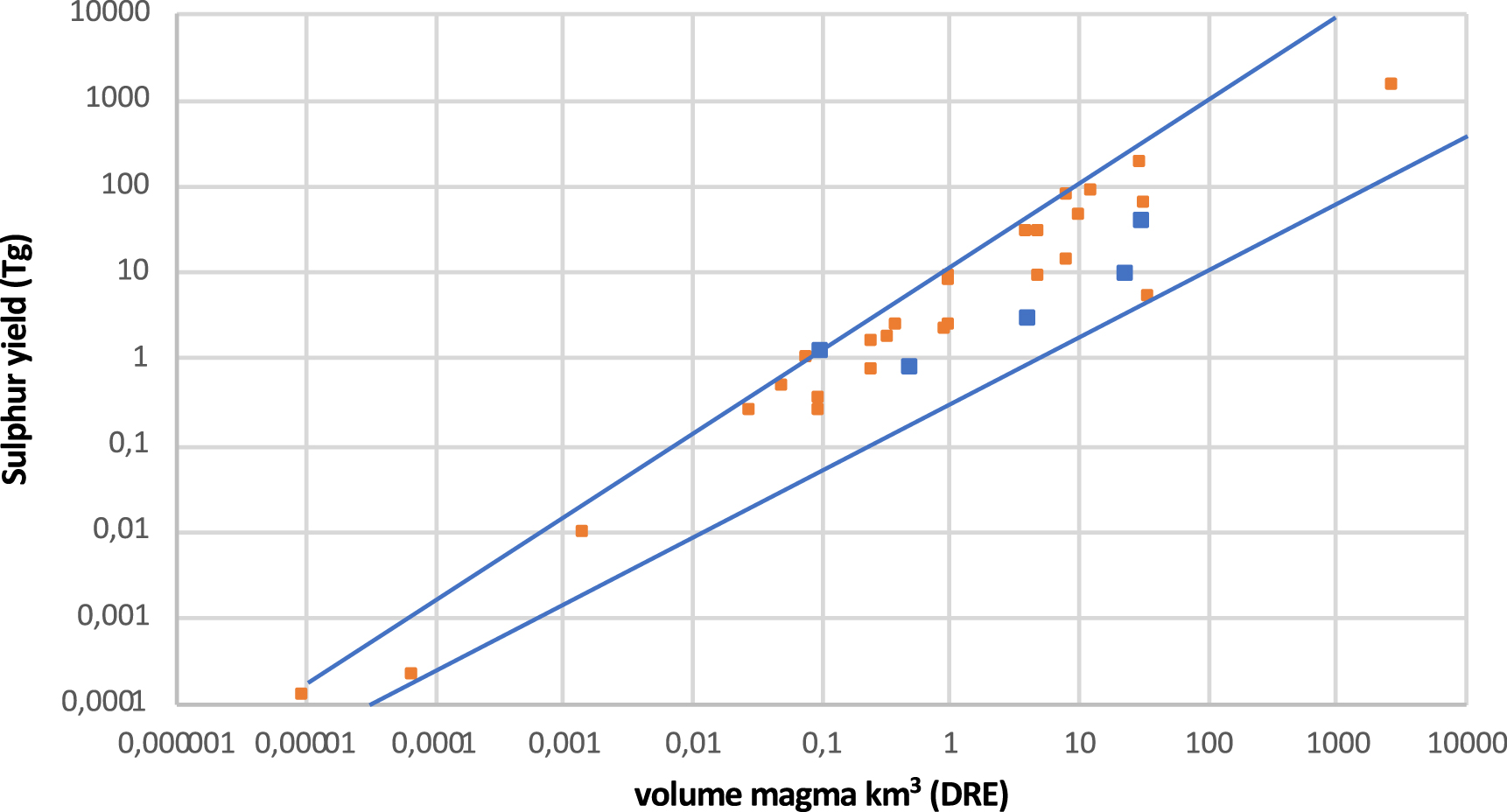
Relationship between volume of magma erupted and corresponding sulphur yield for calco-alkaline (orange) and alkaline (blue) magmas. The data for calco-alkaline magmas are from Scaillet et al. [2003].
Below we consider our S estimates for alkaline magmas in the light of previous estimates, and discuss their relevance in the context of climate proxies and modelling efforts.
4.1. Laacher See
Schmincke et al. [1999] and HarmsSchmincke [2000] estimated syn-eruptive exsolution and degassing of order 2 Tg S for the Laacher See eruption. Drawing an analogy with Pinatubo 1991, Schmincke et al. [1999] suggested the total yield could have been as much as 150 Tg S. Based on more specific consideration of the mineralogy and petrology of Laacher See’s products, HarmsSchmincke [2000] suggested a total yield of at least 10 Tg S, speculating that it may have been “appreciably more”. A subsequent work acknowledging the implications of redox state suggested a range of 1.7–49 Tg S [Textor et al., 2003]. More recently, Baldini et al. [2018] argued for a release of order 42 Tg S drawing on scaling arguments and sulphur emissions data for other non-basaltic eruptions. This high emission led them to suggest a prominent sulphur anomaly in the Greenland Ice Sheet Project 2 (GISP2) core might represent the Laacher See eruption, though this match has been discounted by subsequent high-precision dating of the eruption [Reinig et al., 2021]. They also suggested that with such a high sulphur yield, the eruption may have played a role in triggering the Younger Dryas.
A study by Graf and Timmreck [2001] presented a simulation of the climate response to the Laacher See eruption, based on a 7.5 Tg S injection. Though not intended as palaeoclimate simulations, work by Niemeier et al. [2020] nevertheless has some bearing on understanding dispersal of the Laacher See ash and gas emissions and their radiative effects. They modelled sulphur chemistry and ash dispersion for a range of scenarios predicated on a “Laacher See-type” eruption with 0.75, 7.5 and 50 Tg S emissions. Based on our upper limit of 3–15 Tg of S, the lower emission scenarios would be more representative for understanding the potential climatic impacts of the Laacher See eruption, and for targeting any search of polar ice core records for its signature (which will ultimately rest on geochemical fingerprinting of ash grains). We stress that the oxidised nature of erupted rocks points to an S yield for the Laacher See event lying at the lower end of our calculated range, i.e. 3 Tg S.
The 3 Tg S estimate corresponding to oxidised conditions, as suggested by petrological arguments, may seem counterintuitive but the lower sulphur content of the gas phase at high fO2 is an unavoidable consequence of the higher solubility of sulphur in silicate melt at high fO2 [Carroll and Rutherford, 1987]: in other words higher sulphur contents are achieved with lower PSO 2 relative to PH 2S: As readily apparent from Equation (1), a lower PSO 2 translates into a lower mole fraction of SO2 in the coexisting fluid phase, and thus a lower sulphur content.
4.2. Campanian ignimbrite
Our calculations for the Campanian Ignimbrite allow for a sizeable sulphur release (up to an order of magnitude greater than that of the 1991 Pinatubo eruption). However, they are not consistent with far higher estimates, exceeding 1 Pg S [Scaillet et al., 2003, and reported in Fedele et al., 2007]. Meanwhile, Marti et al. [2016] estimated a yield of 84–89 Tg S. Clearly, it is the mass of erupted magma that makes this event potentially important from the viewpoint of S yield, not intrinsically high S content of the magma (Figure 2).
Curiously, very few data are presently available for S content in MI in minerals from the different CI deposits. This is probably because most of the MI have S concentrations below typical EMPA detection limits, although some data [Webster et al., 2003] suggest SO2 contents up to 2800 ppm. The genesis of the CI magma is debated, and reflects complex open-system processes of crystallization, assimilation and recharge [Fowler et al., 2007]. Based on MI data, Marianelli et al. [2006] suggested that the plinian phase (corresponding to >20 km3 of magma) was fed by magma which had ascended from the main magma body to a depth of 2–3 km depth. If this is the case, the presence of a large amount of fluid phase in the deeper (6–8 km) reservoir could be questioned. Recent work has also suggested that a large part of the magma erupted derived from thermal reactivation of a large body of crystal mush in the deeper reservoir [Forni et al., 2016, Di Salvo et al., 2020]. In this scenario, the process by which a free, S-bearing, fluid phase accumulates in the reservoir is unclear [see Parmigiani et al., 2016]. Further progress in estimating the S release to the atmosphere for CI eruption requires deeper understanding of the petrogenesis of the magma combined with more comprehensive MI studies. The behaviour of volatiles associated with ignimbrite formation (i.e., processes accompanying and following column collapse) also requires further study [e.g., Peccia et al., 2023].
4.3. Vesuvius
We note that our low estimated yield of sulphur for the 79 CE eruption is consistent with the lack of a prominent sulphur anomaly in Greenland ice cores at depths consistent with the age of the 79 CE eruption [Plunkett et al., 2022].
5. Concluding remarks
Our calculations highlight the important role of redox conditions, with estimates of sulphur yields for the considered eruptions differing by an order of magnitude depending on whether reduced or oxidised conditions apply. Clearly oxidising conditions, which enhance the solubility of sulphur in silicate melts, limit sulphur partition into the fluid phase. Other factors being equal, higher temperature should have the same effect because increasing temperature increases sulphur solubility in silicate melts [e.g., Clemente et al., 2004].
The role of chlorine needs to be addressed as well. Experiments have shown that addition of chlorine increases the solubility of sulphur by a factor of up to two in rhyodacite melt [Botcharnikov et al., 2004]. Phonolite and trachyte magmas are generally Cl-rich [e.g., Signorelli and Carroll, 2000], hence an abundance of chlorine may affect sulphur behaviour as well. The results of Botcharnikov et al. [2004] suggest that our calculated sulphur contents for the gas phase could be overestimated by 50% or more. We note however that in the case of Vesuvius, whose mafic melt inclusions hold up to 2000 ppm S [Cioni et al., 1995], the Cl-rich character of felsic MI (up to 1 wt% Cl) did not act to sustain high S contents during magma evolution, possibly because sulphur was continuously scavenged into the fluid during fractionation.
Our results clearly discount any suggestion that alkaline magmas, i.e., trachytes and phonolites, are special in respect of sulphur emissions during explosive eruptions. Excluding perhaps the case of Campanian Ignimbrite, the other eruptions we have considered yield sulphur emissions comparable with, or even lower than, those associated with the 1991 Pinatubo eruption. It appears also that there is considerable variability between alkaline magmas. Without robust petrological control, simple extrapolation from one case to another (even for similar chemistries such as with Vesuvius 79 CE and Avellino) is inadvisable.
While we restrict our work to only four centres for which volcanological and petrological knowledge is extensive, we note that many other alkalic provinces deserve similar attention: oceanic island volcanoes can erupt voluminous quantities of trachyte or phonolite, such as manifested in the Canary islands [Andújar et al., 2008]. Further prominent examples include the Kenyan flood phonolites, which comprise more than 50,000 km3 of Miocene lavas and tephra deposits [Macdonald, 2002], and alkaline volcanic centres of the West Antarctic Rift System. More experimental work is needed to quantify the S behaviour in alkaline undersaturated magmas, in particular in the presence of a multicomponent fluid phase, in addition to the requirements for detailed petrological understanding of erupted products.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Funding
This work was partly funded by labex VOLTAIRE project (ANR-10-LABX-100-01) and equipex PLANEX (ANR-11-EQPX-0036). CO acknowledges support from NERC grant NE/N009312/1.
Acknowledgements
The manuscript greatly benefited from the constructive comments of two anonymous reviewers and from the efficient editorial handling of Francois Chabaux.





 CC-BY 4.0
CC-BY 4.0
Vous devez vous connecter pour continuer.
S'authentifier