1. Introduction
The external surface of the continents, extending from the outer limits of the vegetation down to and including the zone of groundwater, has been called “the Critical Zone” to highlight its crucial role for the “availability of life-sustaining resources” [Gaillardet et al., 2018]. While surface freshwater storage components (streams, lakes, snow, glaciers) are easily observable components of our landscapes, a major part of continental water resources resides below ground in groundwater systems and is broadly inaccessible to direct observations. Groundwater systems are hosted in thick and complex heterogeneous aquifers [Gleeson et al., 2014]. Water flows slowly in geological layers over depths up to kilometers, locally intercepting the surface where it interacts with rivers or wetlands, and therefore atmosphere and ocean [Alley et al., 2002].
Geophysical methods are key for characterizing and monitoring the subsurface part of hydrological systems, at spatial and temporal scales ranging from the pore scale to kilometers, and from seconds to years [Hermans et al., 2023]. These are indirect methods that infer different physical properties of the subsurface, such as electrical resistivity [McGarr et al., 2021], seismic velocity [Blazevic et al., 2020], density [Crossley et al., 2013], spontaneous potential [Grobbe et al., 2021], and hydrogen content of pore fluid [Schmidt and Rempe, 2020], which are related to volumetric water content. Satellite-based methods such as Interferometry of Synthetic Aperture Radar (InSAR), and the Gravity Recovery and Climate Experiment (GRACE) are crucial tools that can be used to quantify groundwater storage changes across large geographical areas. InSAR provides precise surface deformation measurements with a precision on the order of a few mm/year across areas ranging from 100 km2 to 5000 km2 [Castellazzi et al., 2016], but its application is limited to aquifers that undergo measurable deformation due to poroelastic responses to changes in the water table. GRACE measures the Earth’s gravity field with high sensitivity [Schmidt et al., 2008], allowing it to detect mass changes equivalent to a water disk about 1 centimeter thick at the land surface, spanning a few hundred kilometers or more [Longuevergne et al., 2010]. These techniques are effective for monitoring groundwater fluctuations at regional and basin scales [Leblanc et al., 2009, Syed et al., 2008], though their spatial resolution is limited and not suitable for detailed local studies, typically on the order of hundreds of meters.
Cosmic-ray geophysical methods offer promising alternatives for soil moisture estimation and groundwater assessment at intermediate spatial scales. Cosmic-ray neutron sensing has proven effective in estimating soil moisture content over areas spanning several hundred meters, providing near-surface volumetric soil moisture measurements [Evans et al., 2016, Köhli et al., 2015]. Similarly, the attenuation of underground cosmic-ray electron flux has been proven to be sensitive to variations in soil water content following rainfall events [Taketa et al., 2022]. However, these methods are limited to shallow depths, typically at the centimeter scale, offering insights primarily into the uppermost layers of soil. At this scale, there is a gap of geophysical methods that can accurately quantify groundwater variations, that is, that can directly relate the physical property measured to the volumetric water content in a specific area.
Muography is a rather recent geophysical method that is directly sensitive to the density of geological bodies. It makes use of cosmic-ray muons, which are sub-atomic particles generated from the interaction of cosmic rays with the Earth’s atmosphere. Due to their penetrating nature, muons can reach deep underground, making them suitable for non-invasive imaging of geological bodies [Bonechi et al., 2020]. Muography consists of measuring the attenuation of the natural muon flux arriving to the surface of the Earth after it traverses matter. By detecting the flux of muons from different directions, it is possible to reconstruct images of density contrasts in geological bodies. A key consideration of muography is that the detector must be positioned downhill or beneath the region of interest, as muons arrive from above. This positioning requirement makes tunnels and natural cavities suitable locations for deploying muon detectors, providing opportunities to apply the method. This imaging technique has been successfully applied to various geophysical applications [Bonomi et al., 2020], including imaging of the density distribution of volcanic edifices [Bajou et al., 2023, Rosas-Carbajal et al., 2017], detecting hidden cavities [Morishima et al., 2017, Cimmino et al., 2019], reconstructing the bedrock morphology underneath an active glacier [Nishiyama et al., 2019], mapping underground structures [Borselli et al., 2022], mining exploration of ore bodies [Beni et al., 2023], and detecting the presence of discontinuities produced by karstic networks [Lesparre et al., 2016], among other applications [Cohu et al., 2023].
The continuous acquisition of muon data has shown promising potential to monitor hydrothermal activity in volcanoes, such as La Soufrière de Guadeloupe in the Lesser Antilles, France [Jourde et al., 2016a, Le Gonidec et al., 2019]. Muography has also been utilized for a time-lapse study of mass density changes over time [Oláh et al., 2023], and for monitoring gravity-driven debris flows in the Sakurajima volcano, Japan [Oláh et al., 2021]. The mentioned time-lapse and monitoring applications suggest that Muography could be key to bridge the current gap in groundwater storage estimations between the regional satellite and the punctual borehole measurements previously mentioned. Variations in groundwater content directly translate into fluctuations in the amount of matter encountered by muons as they reach underground detectors. This direct interplay between subsurface mass changes and muon rate measured could result in significant variations due to evolving water storage changes.
Previous work has established a correlation between middle-atmosphere temperature variations and the muon rate registered underground [Osprey et al., 2009]. This finding highlighted the sensitivity of muography to atmospheric conditions and emphasized the importance of considering such external factors in the interpretation of underground muon measurements [Tramontini et al., 2019], since this effect becomes increasingly significant as the overburden opacity of the site increases [Grashorn et al., 2010].
In this work, we use Muography to study groundwater variations in the surroundings of the Mont Terri Underground Rock Laboratory (URL, Switzerland). After correcting for the atmospheric temperature effect, we analyze the muon rate variations from a series of continuous muon measurements, and we compare the corrected muon rates with different datasets associated to groundwater content. We propose a model to explain the differences in muon rate sensitivity to groundwater variations observed in the different regions scanned. We end with discussions about the implications for future experiments and potential uses of Muography in hydrogeophysics in general.
2. Experimental setup
The Mont Terri Underground Rock Laboratory (URL) is a research facility located in the Jura Mountains in Switzerland (Figure 1). The facility has been operational since 1996 and has been used for various research projects related to hydrogeological, geochemical, and geotechnical characterisation of a clay formation focused on radioactive waste and CO2 storage, including more recently heat storage [Bossart et al., 2018]. The geological profile and hydrogeological classification at the Mont Terri URL is presented in Figure 2a. The study region contains two distinct karstified aquifers, separated by a shaly aquitard. The local aquifer, located to the north of the valley, presents higher inflow rates compared to the regional aquifer located in the southern part. Based on the hydrogeological classification by Marschall et al. [2004], the local aquifer is primarily composed of sandy limestones that exhibit fissures and karstic features, with inflow rates ranging from 12 l⋅s−1 to 200 l⋅s−1 due to localised water-conducting features. Conversely, the regional aquifer comprises fissured and karstic limestones, with inflow rates exceeding 1 l⋅s−1. Acting as a barrier between these aquifers, the aquitard is composed of shaly marls, limestones and marly clay. Due to this distinct setup, the Mont Terri URL stands as an exceptional site for conducting muography experiments within the context of hydrogeological studies.
(a) Mont Terri’s placemarks. (b) Aerial view of Mont Terri, with motorway tunnel and rock laboratory. Image taken from the Mont-Terri URL website https://www.mont-terri.ch.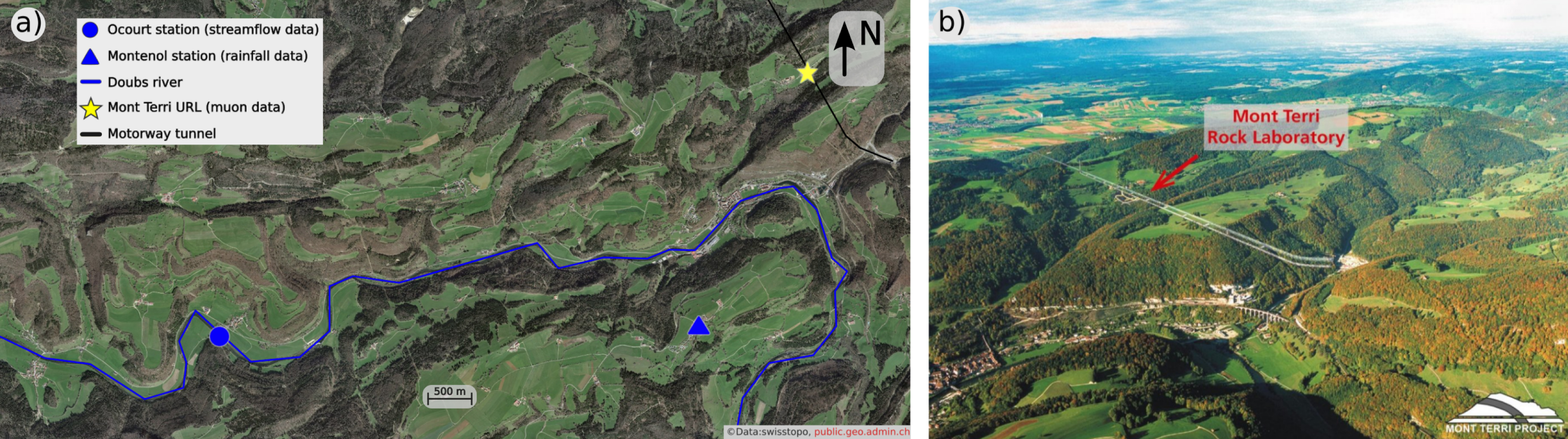
(a) Geological profile adapted from Nussbaum et al. [2017]. Hydrogeological classification from Marschall et al. [2004]. Geological map based on the Geological Atlas of Switzerland 1:25,000, map No. 40 “St-Ursanne”, available through https://map.geo.admin.ch. (b) The muon detector deployed in the Mont Terri Underground Rock Laboratory (URL).
The muon detector used in this study was developed by the DIAPHANE project [e.g., Marteau et al., 2012, 2017]. It consists of three detection matrices composed by Nx = 16 and Ny = 16 plastic scintillators bars, in the horizontal and vertical directions, which define 16 × 16 pixels of 5 × 5 cm2 each (Figure 2b). The distance between the front and rear matrices is set to 100 cm. When a muon passes through the three matrices of the detector in time coincidence, an event is registered and the corresponding trajectory is reconstructed from the sets of pixels fired in each matrix. Muon detection is accomplished through the use of wavelength-shifting (WLS) optical fibers that transport the photons generated by the scintillators to the photomultipliers (PMTs) for detection. More details on the optoelectronic chain can be found in Marteau et al. [2014]. Due to the large rock volume under study in relation to the size of the detector, we admit a point-like approximation of the detector where events with pixels in the same relative direction are considered to correspond to the same trajectory [Lesparre et al., 2010]. This approximation yields a total of (2Nx − 1) × (2Ny − 1) = 961 axes of observation , where (i,j) = (x,y)front − (x,y)rear and (x,y)front and (x,y)rear represent the (x,y) pixels in the front and the rear matrices, respectively. Thus, each correspond to an unique angular direction.
In this work, we use a muon dataset acquired by the muon detector deployed in the Mont Terri URL from October 2016 to February 2018. The dataset encompasses 365 days of observations, accounting for data acquisition interruptions for work at the site. The detector was installed in the Niche IS, 220 m below the surface, with an inclination of 65° and oriented 152°N. Due to the employed setting, the range of length of rock traversed by the muons is of 200–500 m. Preceding the underground measurements, a calibration experiment was conducted by measuring the open-sky muon flux at the zenith [Lesparre et al., 2010].
3. Methodology
3.1. Computing the muon image
The physical quantity estimated by muography is the opacity, 𝜚 (mwe), which represents the amount of matter traversed by the muons along their trajectories and is given by:
| (1) |
A muon image consists of presenting the estimated values of average density for each axis of observation of the muon detector . To obtain it, we first need to estimate the integrated muon flux, I (cm−2⋅sr−1⋅s−1), which quantifies the flux of muons that have energies above a certain threshold. The dependency of this integrated flux with the opacity is expressed by
| (2) |
We estimate the integrated muon flux along each axis of observation as , where is the number of muons detected along each axis of observation, ΔT(s) is the acquisition duration, and is the direction-dependent acceptance function, which quantifies the detector’s efficiency for detecting muons. is obtained from a calibration experiment at open-sky conditions, where the measured muon rate is compared to the theoretically expected integrated muon flux :
| (3) |
Once the integrated muon flux is estimated, we use tabulated values of the (I,𝜚,𝜃) dependence to determine the opacity . For each value of integrated flux and its corresponding zenith angle () we do a 3-D interpolation in the (I,𝜚,𝜃) space. Finally, we use a 2-meters horizontal resolution Digital Elevation Model to compute the rock thickness traversed by the muons across the axes of observation, . Then, the average density muon image is given by .
3.2. Time series of muon rate
To study the influence of groundwater storage changes between the Mont Terri URL and the surface on our muon measurements, we create time series of the measured muon rate, that is, the number of muons measured per unit of time. Our muon detector can discriminate 961 different axes of observation. In order to improve the temporal resolution of the time series, we merge the signals from adjacent directions together when studying time variations [Jourde et al., 2016b]. We compute the average cosmic muon rate time series, R, using a 30-day width Hamming moving average window [Hamming, 1998]. The associated confidence interval is determined as the standard deviation of the mean [Bevington and Robinson, 2003]. We assume that the time intervals between consecutive muon detections follow an exponential distribution [Leo, 1994], which is consistent with the assumption that R follows a Poisson process [Gaisser et al., 2016].
Due to the significant amount of rock between the surface and the tunnel, only relatively high-energy muons arrive to our detector. Tramontini et al. [2019] showed that in this case the muon rate might be sensitive to temperature variations in the middle atmosphere and we therefore need to account for this effect before interpreting the time series in terms of groundwater variations. For this, we use the effective temperature Teff (K) [Grashorn et al., 2010], which is a weighted average of the atmospheric temperature profile, and the effective temperature coefficient 𝛼T [Barrett et al., 1952], which gives the relative change in the muon rate R given a relative change in Teff. 𝛼T depends on the zenith angle and the opacity and we follow Tramontini et al. [2019] to calculate its value. To account for the muon rate variations caused by temperature changes in the atmosphere we use the following equation:
| (4) |
where ΔR = R −⟨R⟩, ΔTeff = Teff −⟨Teff⟩, ⟨R⟩ is the mean muon rate and ⟨Teff⟩ is the mean effective temperature. We compute Teff using the same 30-day width Hamming moving average window as R, and we compute ⟨Teff⟩ and ⟨R⟩ for each uninterrupted acquisition period separately.
3.3. Time series of opacity
From the measured integrated muon flux, and the calibration experiment that provides the experimental acceptance, we estimate the corresponding opacity 𝜚 (mwe), using the same tabulated values of the (I,𝜚,𝜃) dependence that we use for computing the muon image. As with R, we merge the signals from adjacent directions together when studying time variations to improve the temporal resolution of the time series. We compute the opacity variations time series as Δ𝜚 =𝜚 −⟨𝜚⟩, where ⟨𝜚⟩ is the mean opacity. We compute Δ𝜚 using the same 30-day width Hamming moving average window as R, and we compute ⟨𝜚⟩ for each uninterrupted acquisition period separately.
3.4. Time series of groundwater content
In this work, we use two parameters from the ERA5 and ERA5-Land climate reanalysis datasets, which are produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). These datasets assimilate global observations into atmospheric models to create a comprehensive and consistent dataset using the laws of physics [Hersbach et al., 2020]. ERA5 provides hourly data on atmospheric, land-surface, and sea-state parameters. The data are available on regular latitude-longitude grids with a resolution of 0.25° × 0.25° (∼31 km). The data covers atmospheric parameters at 37 pressure levels ranging from 1000 hPa to 1 hPa. For various land applications, ERA5-Land offers an improved accuracy by replaying the land component of ERA5 climate reanalysis [Muñoz-Sabater et al., 2021]. ERA5-Land also provides an enhanced resolution of 0.1° × 0.1° (∼11 km) and offers parameters on the four levels of the ECMWF surface model. We use these data to compute the time series of effective temperature in the atmosphere and correct for this effect in our muon time series, as presented previously.
From ERA5, we use the atmospheric temperature, spanning all 37 atmospheric pressure levels. From ERA5-LAND, we take the volumetric soil water content estimated across the four layers of the ECMWF surface model, vi (m3⋅m−3) (i = 1, 2, 3, 4), which together encompasses the first 289 cm of soil. The corresponding thickness of each layer are Δh1 = 7 cm, Δh2 = 21 cm, Δh3 = 72 cm and Δh4 = 189 cm for the layer 1, 2, 3 and 4, respectively. This parameter is associated with soil texture or classification, soil depth, and the underlying groundwater level. Both parameters are listed four times a day (00:00, 06:00, 12:00, and 18:00 hr).
In addition, we analyse the stream flow of the Doubs River, measured at the Ocourt station, and the rainfall registered at the Montenol station for estimating the amount of groundwater within the study region (Figure 1a). The distance between these two stations is approximately 5 km. These datasets play an important role in hydrological processes and can serve as indicators of groundwater storage changes. Stream flow and rainfall data provide information about groundwater discharge and recharge, respectively. In order to compare the observed muon rate fluctuations to variations in groundwater content, we define the weighted volumetric soil water in the first 289 cm of soil, v (m3⋅m−3), as . We compute v using a 30-day width Hamming moving average window. We define Δv = v −⟨v⟩, where ⟨v⟩ is the mean weighted volumetric soil and is computed for each uninterrupted acquisition period separately.
4. Results
From the calibration experiment, we measured a total acceptance of (1385 ± 67) cm2⋅sr, which we then used to calculate the muon image of average density for the whole measured period. In Figure 3 we present it, projected over the surface given by the intersection of the topography and each axis of observation, and superposed to the geological map (Figure 2a). We observe two distinct regions at each side of the valley: a high-density region to the north of the valley (HD) and a low-density region to its south (LD). Additionally, we observe a smaller region characterized by high densities located behind the southern ridge. Table 1 summarizes the volume of rock, average rock thickness, average muon rate, average opacity, average density and the estimated acceptance for the HD, LD, and combined (HD and LD) regions. Even if the LD region is characterized by a lower density, it has a higher opacity because of the larger amount of rock traversed by the muons.
Muon image of average density between the muon detector, located inside the Mont-Terri tunnel, and the surface. The detector’s axes of observation are represented with gray lines. The average density values are plotted over the topography, together with the geological map. The black, green and blue dashed lines indicate the motorway tunnel, the HD region, and the LD region, respectively. A nearest-neighbour interpolation is used to account for the angular resolution of the axes of observation. The geological map is based on the Geological Atlas of Switzerland 1:25,000, map No. 40 “St-Ursanne”, and is available through https://map.geo.admin.ch.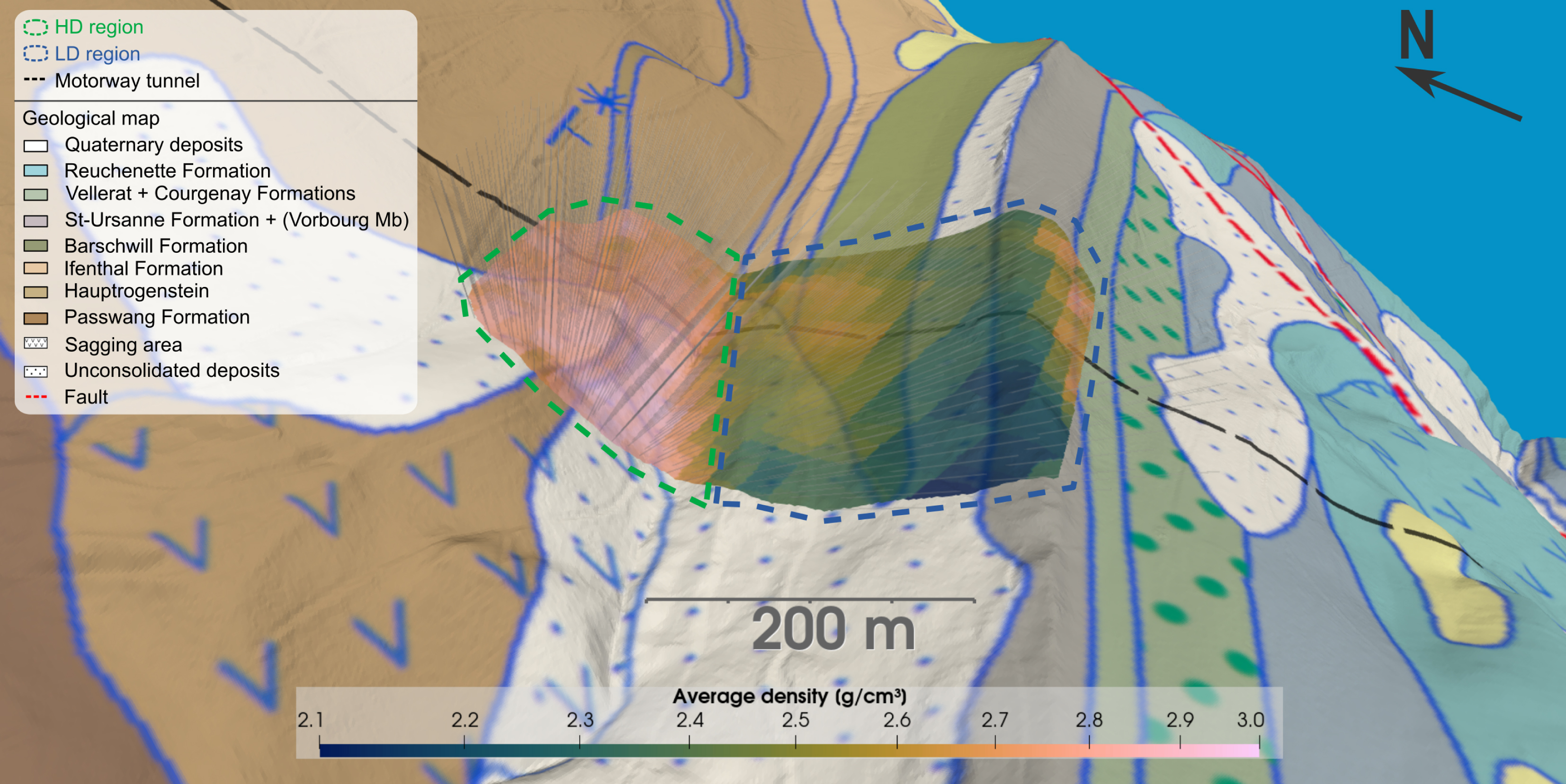
The scanned volume of rock V , the average opacity ⟨𝜚⟩, the average muon rate ⟨R⟩, the average rock thickness ⟨L⟩, the average density ⟨𝜌⟩ and the estimated acceptance in each region
| Region | V (m3) | ⟨𝜚⟩ (mwe) | ⟨R⟩ (d−1) | ⟨L⟩ (m) | ⟨𝜌⟩ (g⋅cm−3) | (cm2⋅sr) |
|---|---|---|---|---|---|---|
| High-density (HD) | 4.0 × 106 | 600 ± 50 | 605 ± 7 | 230 ± 14 | 2.82 ± 0.2 | 984 ± 45 |
| Low-density (LD) | 7.7 × 106 | 800 ± 200 | 194 ± 5 | 339 ± 81 | 2.5 ± 0.1 | 401 ± 22 |
| HD and LD | 11.0 × 106 | 670 ± 160 | 800 ± 10 | 270 ± 72 | 2.7 ± 0.2 | 1385 ± 67 |
For ⟨𝜚⟩, ⟨R⟩, ⟨L⟩ and ⟨𝜌⟩, the dispersion across the axes of observation within each region is also provided.
Similar patterns can be observed between the average density values and the geological formations (cf. Figure 3). The HD region corresponds to sandy limestone formations that constitute the local aquifer (the Ifenthal, Hauptrogenstein and Passwang formations). The LD region corresponds to the local aquifer as well as the fissured and karstic limestones that compose the regional aquifer (mainly the Saint-Ursanne formation in the study region), along with the aquitard (the Barschwill formation). Mean density is spatially variable. Mid-density values are found on the crest of the mountain, which might also be linked to the larger thickness of the weathered rock. The high-density values located behind the southern ridge are partly correlated to the presence of the Saint-Ursanne formation. Note that as the density values obtained are averages through the muon paths, these values not only reflect the density of the outcrop formations, but also of the geological formations traversed in the subsurface. For instance, the LD region also intersects the Ifenthal, Hauptrogenstein and Passwang formations (Figure 2a).
We compute the muon rate time series for the three selected regions (cf. Methodology). As an example, the ⟨R⟩ and ⟨Teff⟩ time series of the LD region are shown in Figure 4. We can observe a clear seasonal variation in the two time series, with lower muon rates and effective temperatures during winter. To correct the time series for the atmospheric temperature effect, we computed a specific effective temperature coefficient 𝛼T (cf. Table 2). 𝛼T remains constant within the defined uncertainty range. This arises from the dependence of 𝛼T on the mean value of Emin ×cos(𝜃), which is associated with the production and propagation of muon parent particles through the atmosphere [Grashorn et al., 2010, Gaisser et al., 2016]. While Emin is higher in the LD region, the corresponding cos(𝜃) is lower. Conversely, in the HD region, Emin is lower, but cos(𝜃) is higher. As a result, these opposing effects on Emin × cos(𝜃) balance each other. The corrected muon rate time series for each region are shown in Figure 5, now in terms of their relative changes (ΔR/⟨R⟩)corrected computed using Equation (4). The time series of the HD and (HD and LD) regions seem stable after the temperature correction. But the LD region presents significant muon rate variations throughout the acquisition period, with amplitude variations from −4% to 4% relative to the time series average value of 194 muons per day, and well above the 95% confidence interval.
Muon rate R in the Low-Density (LD) region and effective temperature Teff time series represented as blue and orange lines, respectively. The colored surface delimits the 95% confidence interval. To illustrate the effect of the correction derived from Equation (4), the corrected muon rate in the LD region is shown as a gray line, with the corresponding 95% confidence interval outlined by dashed lines. The gray surface indicate a period where the muon data acquisition was interrupted for work at the Mont Terri URL.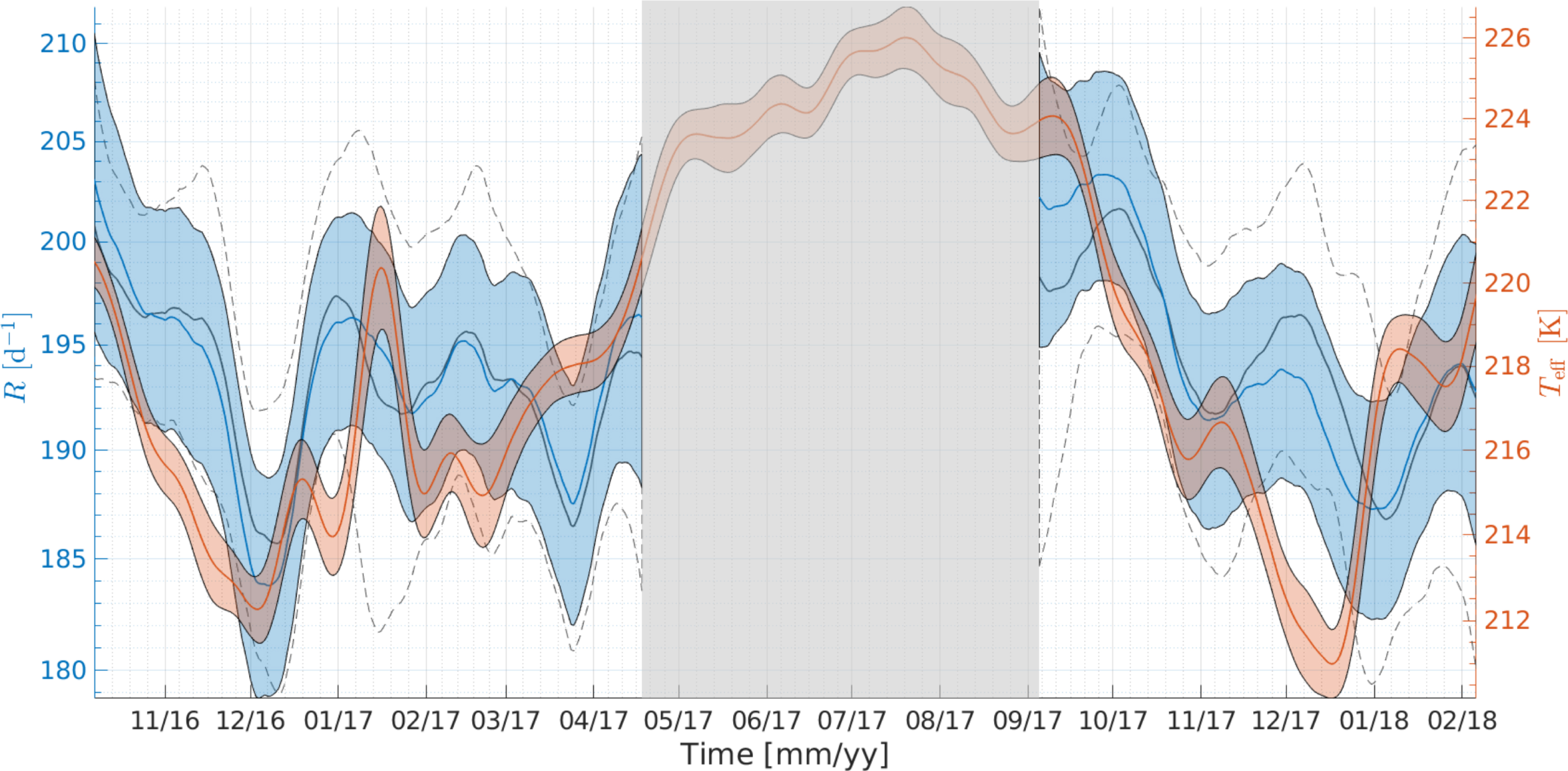
(a) Rock volume and axes of observation involved in each region studied. (b) Deviation from the mean of the filtered muon rate (ΔR/⟨R⟩)corrected time series. The colored surface delimits the 95% confidence interval. The gray surface indicate a period where the muon data acquisition was interrupted for work at the Mont Terri URL.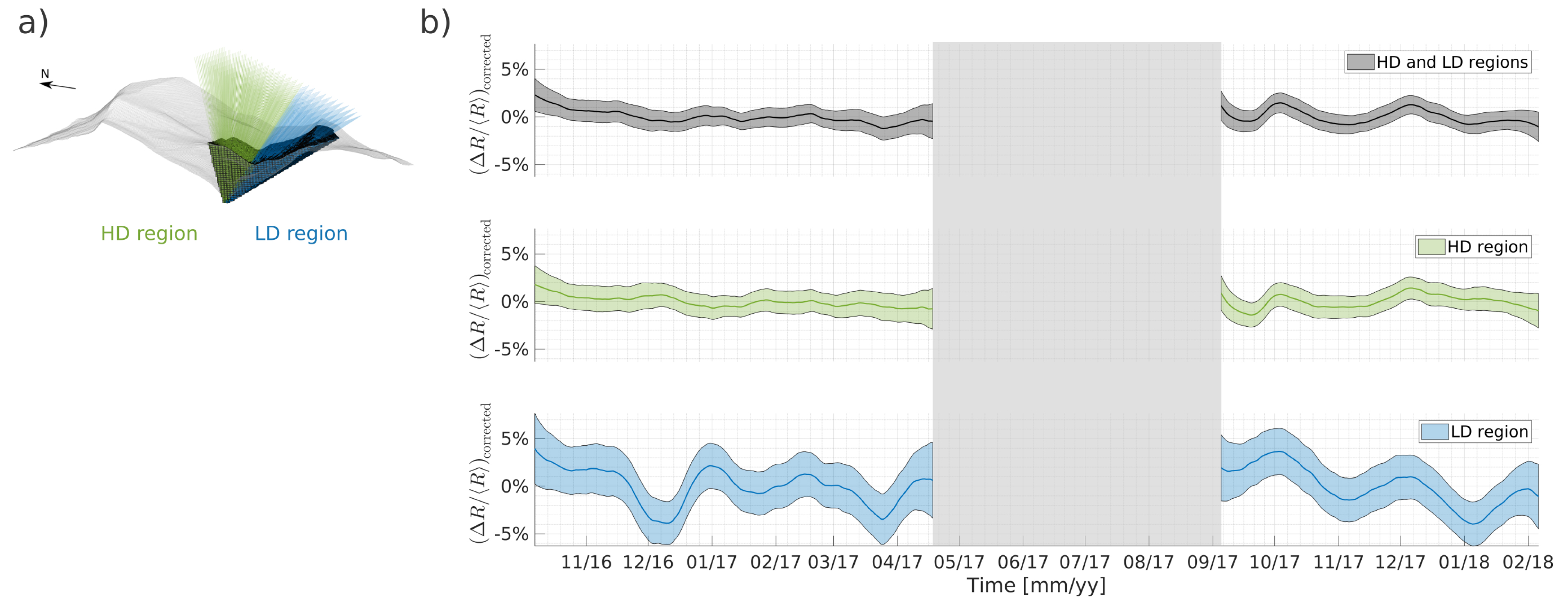
Computed values of 𝛼T for each region
| Region | 𝛼T |
|---|---|
| HD | 0.65 ± 0.02stat ± 0.03syst |
| LD | 0.63 ± 0.02stat ± 0.03syst |
| HD and LD | 0.65 ± 0.02stat ± 0.03syst |
To analyze the muon rate changes in the LD region, we present estimated time series of the relative soil water content, the Doubs river stream flow, and the rainfall precipitation (Figure 6, cf. Methodology). Note that the axis of the muon rate variations has been inverted in order to make the comparison with the relative soil water content straightforward. We also present the absolute opacity variations estimated from the corrected muon rate variations, together with the absolute volumetric soil water content (see Methodology). While the river streamflow and rainfall variations are not simple to analyze, the soil water content variations show similarities between groundwater content and the muon rate, and absolute opacity changes. Higher values of opacity (or, conversely, lower muon rates) seem to follow the increase in soil water content. However, we notice that in terms of groundwater storage, the scales are very different. If we consider for example the first increase in volumetric soil water content (Figure 6b), a variation of approximately 0.06 m3⋅m−3 can be observed. Since the total length of the considered layer is of 289 cm, this soil water content variation corresponds to a change of 0.17 mwe of opacity. However, the corresponding absolute opacity change is of 12 mwe, that is, almost an order of magnitude larger. We discuss the possible explanations for this misfit in the following Section.
(a) Deviation from the mean of the filtered muon rate (ΔR/⟨R⟩)corrected in the LD region and deviation from the mean of the weighted volumetric soil water Δv/⟨v⟩ represented as blue and purple lines, respectively. (b) Opacity deviations from the mean value in the LD region, and weighted volumetric soil water represented as green and purple lines, respectively. (c) Doubs river stream flow and rainfall datasets are represented as purple and gray bars, respectively. The colored surfaces delimits the 95% confidence interval. The gray surface indicate a period where the muon data acquisition was interrupted for work at the Mont Terri URL.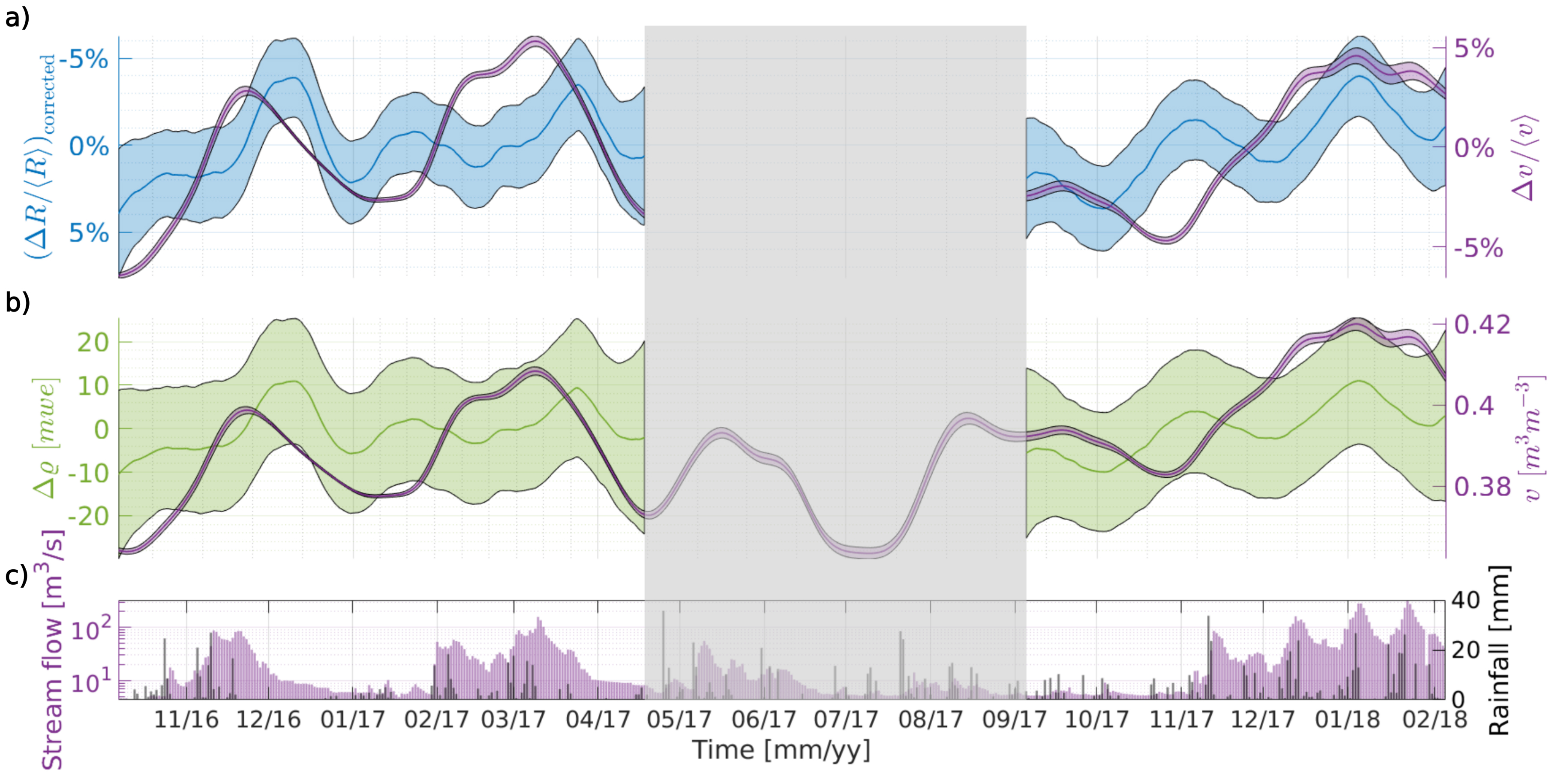
5. Discussion
Our analyses suggest that the muon method is sensitive to the different rock formations above the Mont Terri URL (Figure 3), and that the corrected muon rate variations are linked to groundwater variations in these formations. But these variations are not observed in all the regions scanned by the detector, and it is not clear whether the difference in the variations observed are due to the presence of aquifers and aquitards, or to a systematic sensitivity effect due to the experiment design. To analyse the relation between the muon rate and groundwater variations, we first bring into consideration possible external sources of muon rate variations other than the effective atmospheric temperature effect. We then propose a method to quantify the influence of the water table variation in our particular experiment, and then propose an interpretation for the results obtained.
5.1. External sources of muon rate variations
The natural flux of muons arriving to the Earth’s surface can vary according to other effects than the atmospheric temperature change [Spurio, 2014]. We need to consider these effects before concluding that the registered variations are due to density changes in the scanned rock volume.
Due to the rather high opacity conditions under which we conducted this experiment (Table 1), the impact of barometric variations on the muon rate is negligible. Only low-energy muons of around 10 GeV are influenced by atmospheric pressure fluctuations [Lesparre et al., 2010], and these are filtered out within the first meters of rock in our experimental setup. In our configuration, the minimum energy of detected muons ranges from ∼140 GeV to ∼410 GeV, when considering a medium of standard rock with a density of 2.65 g/cm3. This correspond to a barometric coefficient 𝛽p below 10−2% hPa [Sagisaka, 1986]. As a result, the effect on ΔR/⟨R⟩ is of the order of 0.15%, calculated as the product of 𝛽p and the difference between atmospheric pressure and its mean value.
The Earth’s magnetic field deflects low-energy cosmic rays, stopping them from entering the atmosphere through the magnetosphere and generating muons. This geomagnetic influence is significant for muons arriving at sea level with energies up to ∼5 GeV [Spurio, 2014]. Considering that muons with energies between 1 GeV and 100 GeV loose energy as they traverse matter at a rate of ∼0.25 GeV/mwe [Groom et al., 2001], the muons affected by the geomagnetic field variations would only be able to traverse ∼20 mwe. Similarly to the case of pressure variations, because of the overburden opacity of the Mont Terri URL the geomagnetic effect is negligible. In addition, temporal variations originating from fluctuations in primary cosmic rays or in the geomagnetic field due to solar wind typically manifest on significantly shorter (e.g., seconds to hours) or longer (e.g., an ∼11-year solar cycle) time scales.
5.2. Muon rate changes due to groundwater variations
The temporal variations shown in Figure 5 reveal a fundamental difference between the LD and HD regions. This suggests a distinct cause affecting the muon rate in each region, as opposed to a global effect such as the formerly mentioned, or a malfunctioning of the muon detector. The differences in the muon rate behavior could be related to the particular geological formations present in each region, and the difference in inflow rates and groundwater storage associated to these formations. According to Marschall et al. [2004], the LD region has inflow rates higher than 1 l/s, and in the HD region the inflow rates are in the range between 12 l/s and 200 l/s, which represents a difference up to two orders of magnitude. A lower inflow rate can result in groundwater accumulating and discharging over longer time periods, within the LD region, rendering the density changes due to groundwater variations visible through muon observations. This stands in contrast to the HD region, where the higher inflow rates would allow the infiltrated water to flow rapidly without generating a density contrast for a significant amount of time. However, it should be noted that the inflow rate measurements were done locally within the Mont Terri URL. In karstic formations, inflow rates can exhibit large spatial variability due to their inherent heterogeneity [Goldscheider and Drew, 2007]. Therefore, the difference in muon rate variations may not be solely attributed to the difference in groundwater variations in the two regions, but could also be influenced by local-scale karstic heterogeneity.
Unfortunately, there are no instrumented boreholes in the region to compare the muon rate changes in the LD zone with water table variations. This is why we resorted to 3 parameters of hydrological interest depicted in Figure 6: precipitation, stream flow of a nearby river (cf. Figure 1 for locations), and a model-based estimation of soil water content in the near subsurface (cf. Methodology). The latter is the parameter of most interest because it provides a volumetric mass change, which is what directly affects the muons traversing the rock. Its drawback is that it only contemplates the first 289 cm of soil, and it is a regional estimate from satellite observations. It is important to note that soil hydraulic properties can exhibit significant variability at local scales, ranging from meters to hundreds of meters [Vereecken et al., 2016]. Therefore, satellite-derived models should be interpreted with caution, particularly when comparing them to measurements conducted at the spatial resolution of muography analysis. Nonetheless, we found that this estimate correlates well with the local Doubs stream flow variations, and therefore we use it as a proxy for the groundwater variations. We present it as a time series of relative changes (Δv/⟨v⟩) in the same way as the muon rate variations, and of absolute values to compare to the absolute opacity estimates (Figure 6b).
In Figures 6a and 6b, we observe similar variation patterns between the muon rate and inferred opacity, and the groundwater variations. Despite not being coincident throughout the whole acquisition period, the anticorrelation between these curves is clearer in the first uninterrupted period of muon acquisition, and presents the same trend during the second one. Three distinct peaks in volumetric soil water content (November 2016, March 2017 and January 2018) correspond to muon rate minima, which appear with a slight time shift. This behaviour is consistent with our expectations from muon observations, where an increase in groundwater content augments the opacity along muon trajectories, conversely resulting in a reduction in the associated muon rate. The relative soil water decrease around November 2017, however, does not have a corresponding muon increase. This discrepancy may be due to local-scale karstic heterogeneity, where variations in groundwater storage or preferential flow paths at smaller scales could affect the muon rate response, regardless of the overall soil water content trends. Besides the correlation trends that follow the expected behaviour, the absolute opacity estimates shown in Figure 6b allow us to estimate the groundwater storage changes directly from the muon measurements. As stated in the Results section, although the trends are similar, the amplitude of these variations are very different from the groundwater storage changes assessed by the satellite observations.
To understand this discrepancy, we consider a simple theoretical model to compute the impact of a groundwater content change in the muon measurements, along the different axes of observation (Figure 7). We consider a layer of water-saturated rock of height Δz (m), located at a depth d (m) following the topography. The saturated layer height is given by Δz = w/p, where w (m) and p correspond to the amount of infiltrated water, and the layer porosity, respectively. We then compute ΔL (m); the length of the muon trajectory L that lies inside the considered layer. ΔL thus corresponds to the distance traveled by muons, in a certain axis of observation, inside the water-saturated layer. Figure 7 illustrates the model with an example, where an axis of observation intersects a water-saturated layer of height Δz = 2 m in two segments, resulting in muons traversing a total distance of ΔL =Δ L1 +Δ L2 ≃ 30 m within the water-saturated layer, where ΔL1 and ΔL2 represent the distance travelled by muons in each segment. We define the Amplification Factor (mwe⋅m−1) as the ratio between the opacity change, due to groundwater change along the axis of observation, to the actual amount of infiltrated water, which is the same for every viewpoint: . Δ𝜚 is given by Δ𝜚 = p ×Δ L ×𝜌water, where 𝜌water = 1 g⋅cm−3 is the density of water.
Illustration of the water-saturated layer model used to calculate the impact of groundwater variations in muon measurements. A single axis of observation of the muon detector is represented as an orange straight line, the topography is represented as a green curve, and the water-saturated layer of height Δz at a depth d is represented as a blue surface. ΔL =Δ L1 +Δ L2 corresponds to the distance traveled by muons in the water-saturated layer.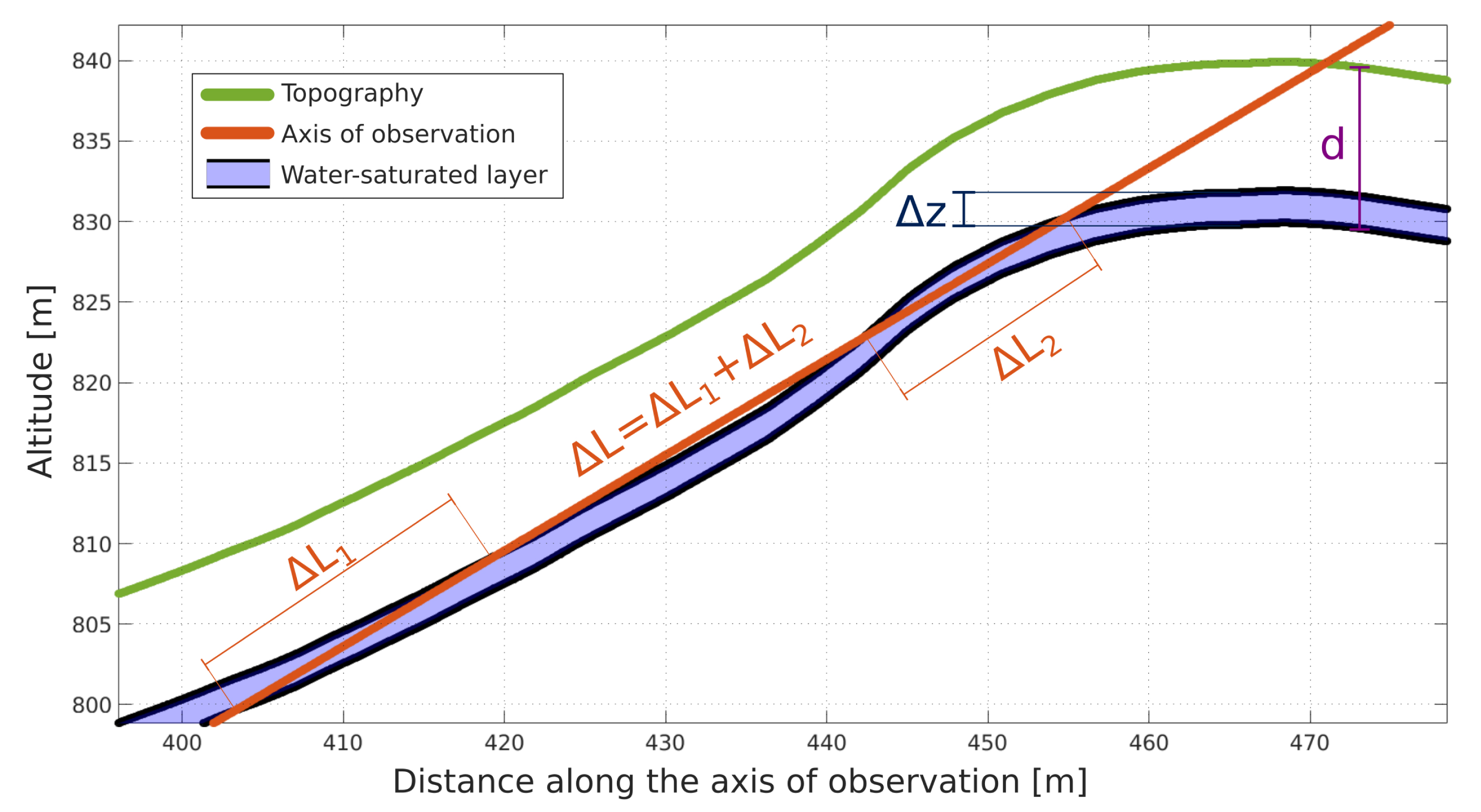
In Figure 8 we present the computed Amplification Factor in each axis of observation for w = 0.3 m, d = 10 m and p = 0.3. These values were arbitrarily chosen in order to obtain an initial approximation of the amplification effect. To better account for the topography of the site, we synthetically increased the number of axes of observation from 31 × 31 to 61 × 61 to have a more precise mapping, but the surface of investigation remains the same as in our real muon experiment. We find that while in the HD region, indicating a negligible amplification effect, in the LD region, that is, in the region where significant muon rate variations are observed (Figure 8). We assess the influence of each parameter on the computation of by modifying the values of porosity (Np = 4 linearly spaced values from 0.2 to 0.5), infiltrated water (Nw = 10 linearly spaced values from 0.1 m to 3 m), and the layer depth (Nd = 33 linearly spaced values from 6 m to 102 m). From these Np × Nw × Nd = 1320 computations, we determine that primarily depends on the depth at which water starts to accumulate, d. This is shown in Figure 9a, where we present the mean value of , , of the study region by considering all the axes of observation for each parameter combination. Figure 9b shows the corresponding standard deviation of , .
Amplification factor expressing the ratio of opacity change in each axis of observation to an increase in groundwater storage of 0.3 m (cf. Figure 7). The amplification factor values are plotted over the topography. The green and blue dashed lines indicate the HD and LD regions, respectively. A nearest-neighbour interpolation is used to account for the angular resolution of the axes of observation.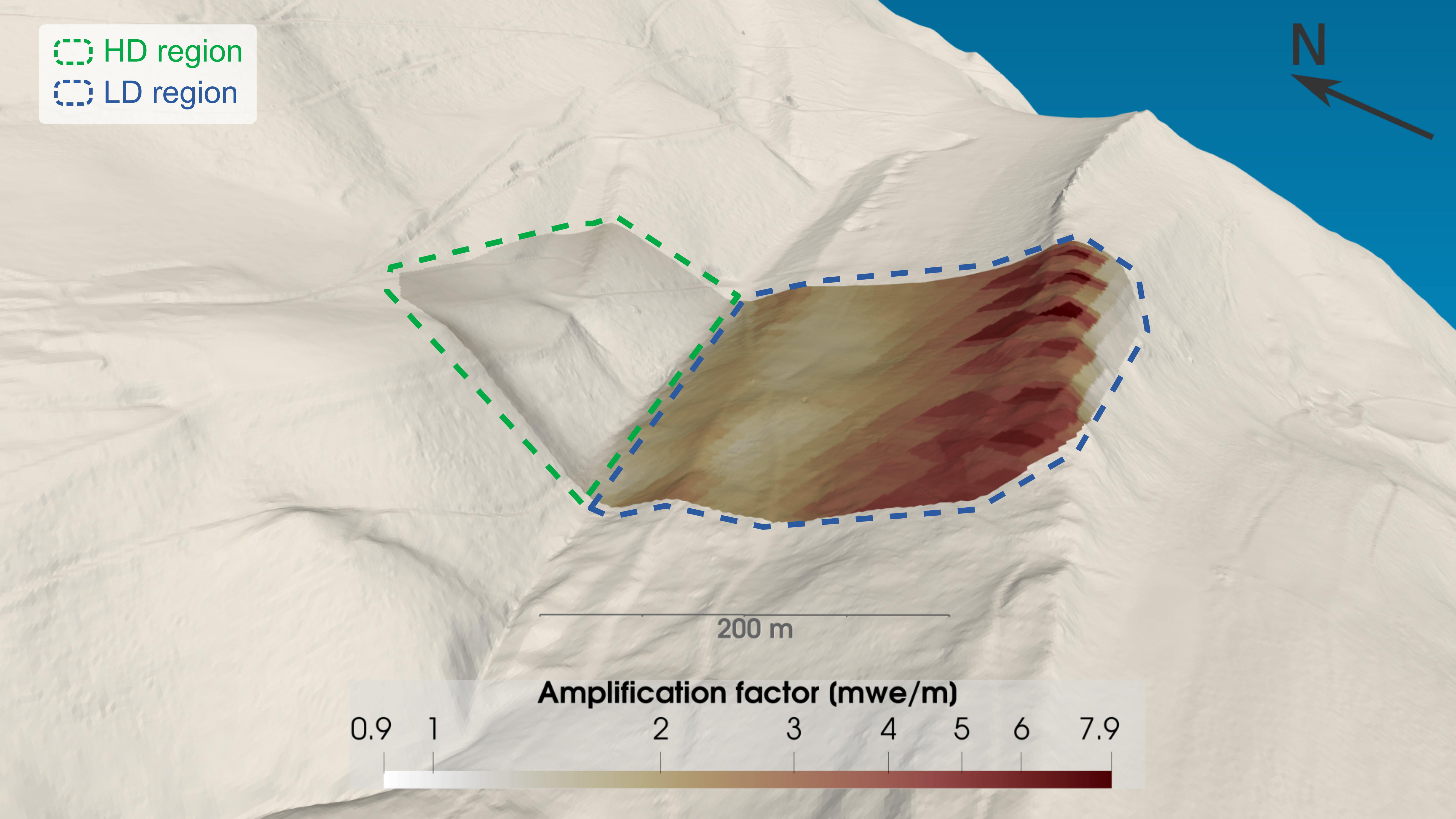
(a) Mean value of , , for the combined HD and LD regions in function of depth of the water-saturated layer d and the infiltrated water w, and for different porosity values p. (b) Standard deviation of , , for the combined HD and LD regions in function of d and w, and for different porosity values p.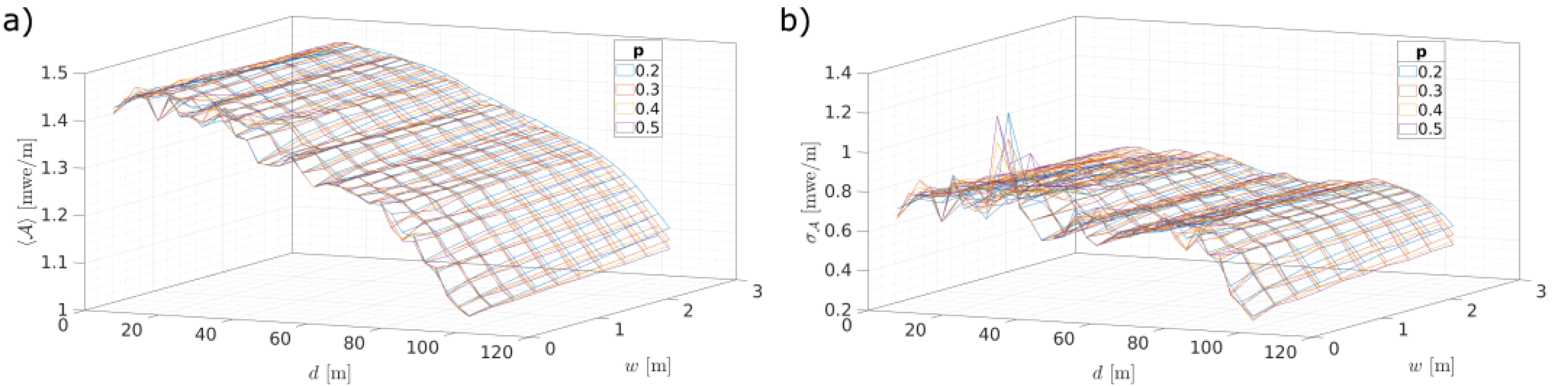
Based on this result, we compute the mean Amplification Factor as a function of d, , for the LD region, the HD region, and the combined HD and LD regions. is computed as the weighted mean value of for each region separately, when modifying the amount of infiltrated water and the porosity of the rock as described. The weighted mean is computed using inverse-variance weights and is defined by:
| (5) |
| (6) |
Mean Amplification Factor for the LD region (blue), the HD region (green) and the combined HD and LD regions (black) as a function of the depth of the water table. Each data point is calculated considering all the axes of observation belonging to the considered region. The error bars represent the standard error of the weighted mean using variance-defined weights, and account for the dispersion due to different porosities and water infiltrations.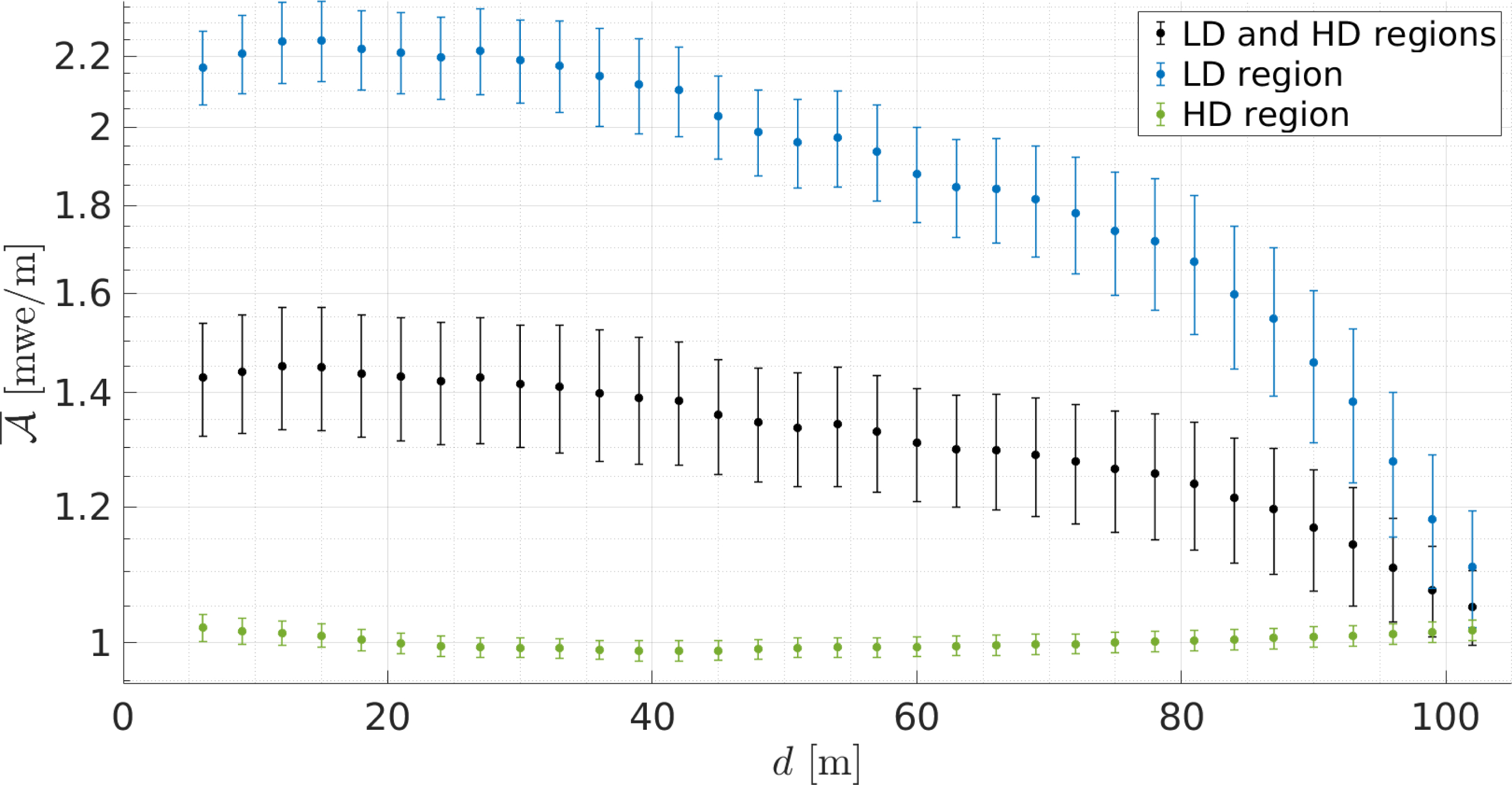
Our geometrical considerations thus suggest that the sensitivity or not to groundwater variations seem to depend largely on the geometry of acquisition of the muon experiment. This is an exciting result for the future applications of muography in hydrology, since it means that the sensitivity could be increased by considering a good setup, where ideally the detectors axes of observation should be oriented almost parallel to the varying groundwater table. In our case, this model allows to explain why we only observe muon rate changes in the LD region. The model also suggests that the amplitude discrepancies between the satellite and muon estimates of groundwater variation may arise from the geometrical amplification factor. However, we note that the misfit between the soil water content variations and the absolute observed opacity values is not fully explained by the amplification factor alone. Several other factors likely contribute to this discrepancy. One is the uncertainty in the absolute observed opacity (Figure 6b). Another is that the amplification factor only accounts for the effect of a water-saturated layer parallel to the surface, while water content variations may also occur in more complex geometries. Moreover, local-scale features, such as preferential flow paths and karst heterogeneity, may influence water distribution in ways not captured by regional-scale satellite data.
6. Conclusions
We used, for the first time, a continuous acquisition of Muography data to estimate groundwater storage variations in the subsurface. After correcting for the only significant external effect on the variation of the incoming muon flux, the temperature changes in the middle atmosphere, we found two distinct regions (LD and HD) where the muon rate evolution over time is different: in the LD region we observe muon rate changes that are correlated to estimates of volumetric soil water content from satellite measurements, whereas the HD region does not present significant variations over the period of measurements. We attribute this difference to (1) the difference in the geometry in which the muon trajectory intersects the saturation-varying layer, illustrated by the Amplification Factor in the Discussion section, and (2) to a less extent, the LD region’s lower inflow rates potentially facilitating more observable groundwater phenomena.
The sensitivity analyses on the Amplification Factor reveal the large impact of the geometry given by the trajectories of detected muons and the topography. We thus point to the possibility of enhancing the sensitivity of the method in groundwater storage estimations by adequately setting the experiment geometry. From the study of the Mont Terri URL, we find that the amplification factor primarily depends on the depth of water accumulation, rather than the rock porosity or the amount of infiltrated water. This underscores the added value of muography in hydrogeophysics, potentially shedding light not only on the groundwater storage variations, but also on assessing the depth of the water table.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Funding
This study of the MD experiment of the Mont Terri project (https://www.mont-terri.ch) is funded by Swisstopo.
Acknowledgments
We extend our gratitude to Thierry Theurillat and Senecio Schefer for their technical and logistical assistance at Mont Terri URL, and to Pauline Baland for providing the geological map, as well as David Jaeggi and Vincent Regard for providing the rainfall dataset. The ECMWF data is available from https://www.ecmwf.int/. The Doubs river stream flow is available from https://www.hydrodaten.admin.ch/. Muon data used for all calculations are displayed in figures and are available in the supplementary material. This study uses perceptually uniform color maps to avoid visual distortion of the data and exclusion of readers with colour-vision deficiencies [Crameri et al., 2020].




 CC-BY 4.0
CC-BY 4.0