Reception at very large distances of monochromatic Rayleigh wave of the 2018–2019 Mayotte crisis: attenuation factor of <i>Ms</i> magnitude

Jacques Talandier

doi:10.5802/crgeos.270

Article de recherche

Reception at very large distances of monochromatic Rayleigh wave of the 2018–2019 Mayotte crisis: attenuation factor of Ms magnitude
[Réception à très grande distance des trains d’ondes de Rayleigh monochromatiques de la crise de Mayotte 2018–2019 : facteur d’atténuation de l’échelle de magnitude Ms]

Jacques Talandier ¹

¹ 55 rue des 2 villages, 33220 Saint Avit Saint Nazaire, France

Comptes Rendus. Géoscience, Volume 356 (2024), pp. 117-122.

Résumés

Anglais
Français

During the strong 2018 and 2019 submarine volcano-seismic events on the Fani Maoré volcano on the eastern flank of the island of Mayotte (Indian Ocean), numerous unusual long-period monochromatic Rayleigh wave trains (VLPs) were recorded. Similar perfectly monochromatic signals but with much lower intensities were previously observed in 2011, 2013 and 2017 from the Rocard submarine volcano (Society hot spot, French Polynesia). The VLPs of Mayotte and Rocard are the only signals of this type observed so far. Perfectly monochromatic and recorded up to the antipodes, the Rayleigh wave trains of Mayotte allow verifying experimentally the attenuation factor of the Ms magnitude scale, thus justifying the reception of these signals from sources of modest energy at very large distances.

Lors des forts événements volcanosismiques sous-marins de 2018 et 2019 du volcan Fani Maoré, sur le flanc Est de l’île de Mayotte (Océan Indien), de nombreux trains d’ondes de Rayleigh monochromatiques inhabituels à longue période (VLP) ont été enregistrés. Issus du volcan sous-marin Rocard (point chaud de la Société, Polynésie française), des signaux similaires parfaitement monochromatiques mais d’intensités beaucoup plus faibles ont été précédemment observés en 2011, 2013 et 2017. Les VLP de Mayotte et du Rocard sont les seuls signaux de ce type observés à ce jour. Parfaitement monochromatiques et enregistrés jusqu’aux antipodes, les trains d’ondes de Rayleigh de Mayotte permettent de vérifier expérimentalement le facteur d’atténuation de l’échelle de magnitude Ms, justifiant ainsi la réception à très grande distance de ces signaux issus de sources d’énergie modeste.

Métadonnées

Reçu le : 2024-03-05
Révisé le : 2024-06-12
Accepté le : 2024-06-25
Publié le : 2024-08-01

DOI : 10.5802/crgeos.270

Keywords: Mayotte crisis, Monochromatic Rayleigh wave trains (VLPs), Magnitude Ms
Mot clés : Crise de Mayotte, Trains d’ondes de Rayleigh monochromatiques (VLP), Magnitude Ms

Affiliations des auteurs :

Jacques Talandier ¹

¹ 55 rue des 2 villages, 33220 Saint Avit Saint Nazaire, France

Licence :

CC-BY 4.0

Droits d'auteur : Les auteurs conservent leurs droits

@article{CRGEOS_2024__356_G1_117_0,
     author = {Jacques Talandier},
     title = {Reception at very large distances of monochromatic {Rayleigh} wave of the 2018{\textendash}2019 {Mayotte} crisis: attenuation factor of {\protect\emph{Ms}} magnitude},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {117--122},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {356},
     year = {2024},
     doi = {10.5802/crgeos.270},
     language = {en},
}

TY  - JOUR
AU  - Jacques Talandier
TI  - Reception at very large distances of monochromatic Rayleigh wave of the 2018–2019 Mayotte crisis: attenuation factor of Ms magnitude
JO  - Comptes Rendus. Géoscience
PY  - 2024
SP  - 117
EP  - 122
VL  - 356
PB  - Académie des sciences, Paris
DO  - 10.5802/crgeos.270
LA  - en
ID  - CRGEOS_2024__356_G1_117_0
ER  -

%0 Journal Article
%A Jacques Talandier
%T Reception at very large distances of monochromatic Rayleigh wave of the 2018–2019 Mayotte crisis: attenuation factor of Ms magnitude
%J Comptes Rendus. Géoscience
%D 2024
%P 117-122
%V 356
%I Académie des sciences, Paris
%R 10.5802/crgeos.270
%G en
%F CRGEOS_2024__356_G1_117_0

Jacques Talandier. Reception at very large distances of monochromatic Rayleigh wave of the 2018–2019 Mayotte crisis: attenuation factor of Ms magnitude. Comptes Rendus. Géoscience, Volume 356 (2024), pp. 117-122. doi : 10.5802/crgeos.270. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.5802/crgeos.270/

Version originale du texte intégral (Proposez une traduction )

1. Introduction

The rapid measurement, if possible in real time and at a single seismic observatory, of the “size” of an earthquake remains an important aspect of observational Seismology. Among the various magnitude scales previously developed, the surface-wave magnitude Ms, obtained at a period close to 20 s has become the most widely used measure of teleseismic events.

Ms = {log}_{10} (A / T) + 1.66 {log}_{10} (Δ) + 3.3

(1)

where Δ is the epicentral distance, A is the amplitude of the zero-to-peak vertical displacement in μm, and T is the signal period.

In a comprehensive study of this magnitude scale Ms, Okal [1989] concludes that despite several problems at shorter distances, the use of the correction 1.66 Log₁₀(Δ) in the 20–160° range can be justified. The purpose of the present approach is to experimentally study this attenuation factor.

It has long been known, however that any magnitude scale measured at a constant period T saturates when the duration of rupture along the fault becomes comparable to T. This phenomenon was explained in detail by Aki [1967, 1972] and later by Geller [1976], Geller and Kanamori [1977], as being due to destructive interference occurring when the source breakup time exceeds the period used for measurement, in this case 20 s. To avoid this saturation effect, Okal and Talandier [1989] and Okal [1989] developed the Mm (Mantle Magnitude) magnitude scale using the longest period of the frequency spectrum, defined by the source time and therefore the fault rupture length. Mm is directly related to the seismic moment by the relation:

Mm = {Log}_{10} (Mo) + 13

(2)

where Mo is in N-m.

In a similar approach, to avoid this Ms saturation effect, Hanks and Kanamori [1979] developed the Mw mantle magnitude scale:

Mw = 2 / 3 {Log}_{10} (Mo) - 6.07 .

(3)

But we will note that here Mw is obtained from Mo while on the contrary Mo is deduced from Mm which makes it possible to use this last scale of magnitude for the rapid measurement of earthquakes and to elaborate alerts in particular to Tsunamis [Talandier et al., 1987, Talandier and Okal, 1989].

2. Monochromatic Rayleigh wavetrains (VLPs) of the 2018–2019 Fani Maoré (Mayotte) and 2011, 2013, and 2017 Rocard volcano/seismic crises

Figure 1 shows the 11/11/2018 Rayleigh wave trains from Mayotte and 29/04/2013 from Rocard with perfectly monochromatic signals of 15.6 and 17.1 s and duration of ca. 2000 and 3000 s. respectively. Figure 2 illustrates the time series and frequency spectra of the Rayleigh waves of the VLP of 11/11/2018 from Mayotte in 5 stations located from 2800 to 16,000 km away from the source. Consistency of the times and spectra confirms the total absence of frequency dispersion characterizing the propagation of this type of phase: a textbook case, never encountered in practice, these wave trains are perfectly monochromatic. Figure 3 shows that the monochromatic Rayleigh wave train corresponds to the resonance of a chamber excited by an earthquake.

Figure 1.
Long period Rayleigh wave trains generated during the Mayotte (right panel) and Rocard (left panel) volcano seismic events. Perfectly monochromatic long duration signals of 15.6 and 17.1 sec period.

Figure 2.
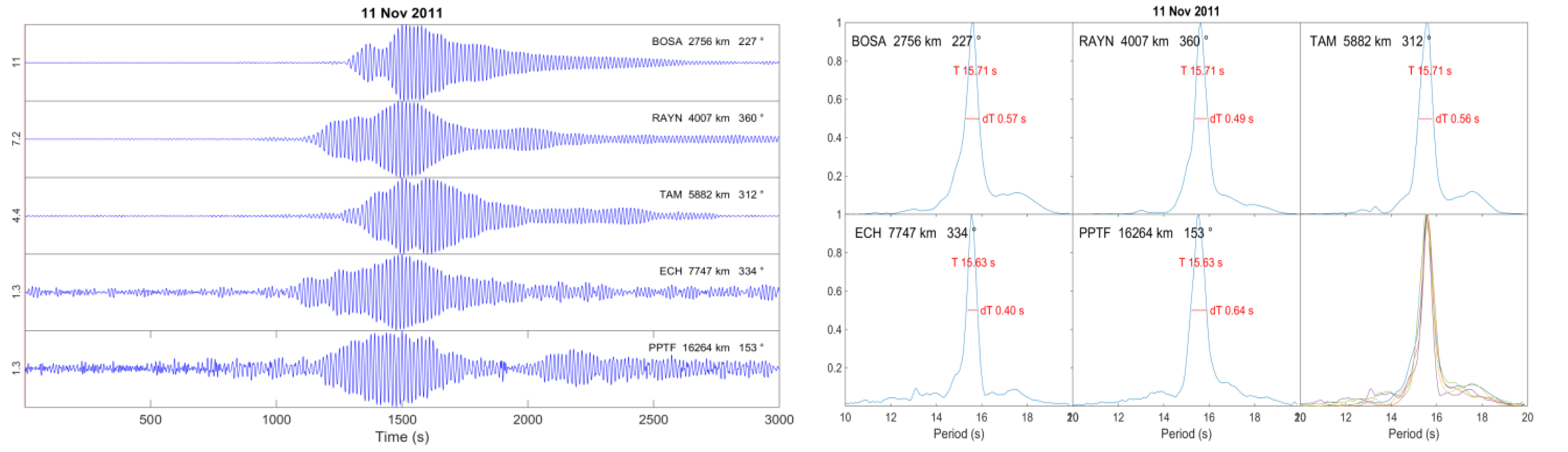
Time series and frequency spectra of monochromatic Rayleigh wave trains from Mayotte on 11/11/2018 in 5 stations located from 2800 to 16,000 km away from the source. Peak-to-peak amplitudes in μm. Consistency of times and spectra confirms the total absence of frequency dispersion characterizing the propagation of this type of phase.

Figure 3.
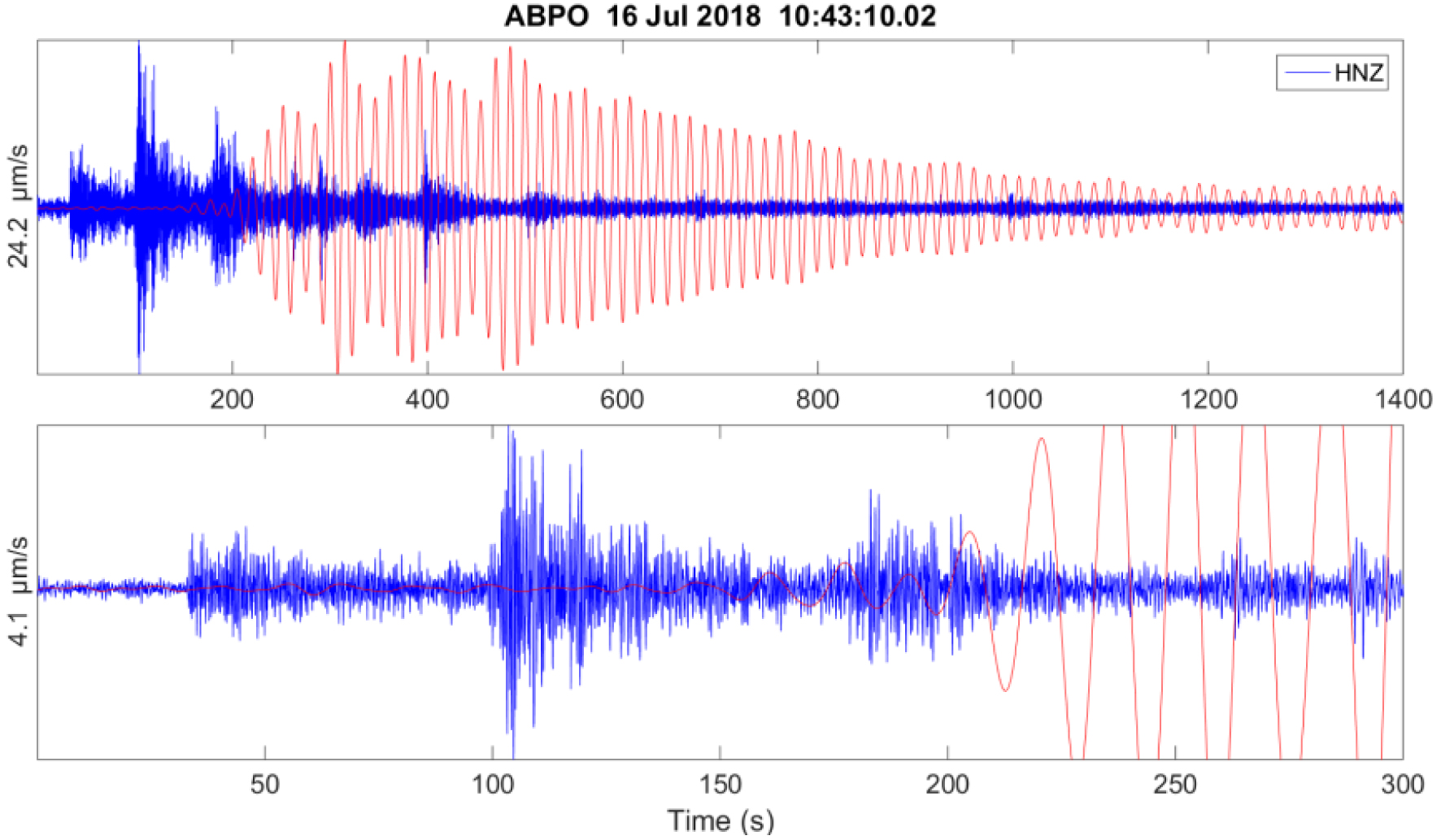
(a) VLP and its peak to peak amplitude. The amplitude of the Short Periods signal is normalized. (b) CP signal with evidence of the increasing amplitude of the VLP. We see that the resonance is excited by an earthquake.

3. Experimental verification of the attenuation factor 1.66 log (Δ) of the Ms magnitude relation

Figure 4 shows the amplitude versus distance of the Mayotte Rayleigh wave trains of 11/11/2018. Close of 1 the slope of the regression line, defined with 41 records for a wide range of distances Δ (700 to 17,000 km), corresponds to the geometric expansion in 1/Δ.

Figure 4.
Amplitude versus distance of the Mayotte Rayleigh wave trains of 11/11/2018. In green the slope line −1.66 of the attenuation coefficient of Ms. In red the regression line with the slope obtained of −1.06. In blue the regression line by imposing a slope of −1.0. In dashed the high and low limits encompassing 90% of the data. Despite a rather high dispersion due to the impact of the structure of the earth’s crust on the amplitude of these Rayleigh waves of relatively short wavelengths, close of 1 the regression line defined with 41 records implies a geometric expansion in 1/Δ.

The Ms magnitude measured over a period obviously cannot characterize the source of these Rayleigh wave trains comprising some 160 oscillations. However, it is interesting to document the evolution of Ms over a wide range of distances since the most intense of these signals (31/07/2018 and 11/11/2018) were recorded as far as Tahiti and Hawaii located 16,300 km and 17,300 km away from the source respectively.

Figure 5 shows Ms as a function of distance. The slope of 0.60 of the regression line is close to the attenuation factor of Richter’s formula [1.66 log(Δ)], minus the geometric expansion in 1/Δ. Defined for the measurement of earthquakes with dispersed Rayleigh waves of broad frequency spectrum, this relation does not apply to the perfectly monochromatic ones of Rocard and Mayotte. This means that the factor 0.66 characterizes the frequency dispersion of Rayleigh waves of earthquakes. Validating the attenuation factor 1.66 log(Δ) of Richter’s Ms formula we also justify the reception of Rayleigh wave trains from Mayotte at very large distances.

Figure 5.
Magnitude Ms as a function of distance. Same data set as Figure 4. In green materialization of the concept of magnitude independent of the distance at which the measurement is made. From 0.60, the slope of the regression line (red) is close to the 0.66 slope (blue) corresponding to the attenuation factor of Richter’s formula [1.66 log(Δ)] minus the geometric expansion in 1/Δ. Defined for the measurement of earthquakes with dispersed Rayleigh waves of broad frequency spectrum, this relationship does not apply to the perfectly monochromatic VLPs of Rocard and Mayotte. This means that the factor 0.66 characterizes the frequency dispersion of earthquake Rayleigh waves.

The maximum amplitude of the Rayleigh wave train, shown in these figures, is used to calculate the magnitude. In addition to the fact that the source cannot be characterized by a measurement on a single period, it is clear that the Ms magnitude cannot be applied to monochromatic signals. The values obtained by Cesca et al. [2020], Sadeghi and Suzuki [2021] and Bhattacharya [2022] cannot therefore be significant.

4. Comments on the articles concerning the application of the Ms magnitude to Rayleigh waves in Mayotte

It has been shown that for monochromatic waves, therefore not dispersed, the application of the magnitude scale Ms leads to values dependent on the distance at the measuring point, the negation of the notion of magnitude. Cesca et al. [2020] use the magnitude Ms to characterize the November 11, 2018 VLP. Referring to Figure 5 showing the evolution of Ms as a function of distance, it is therefore surprising that these authors obtain a coherent value of Ms (M s = 5.1). Indeed, they use data from 4 stations at unspecified distances after eliminating those for which a deviation from a magnitude ratio of ∼1, which they attribute to the radiation pattern of the source, and LSZ and FURI stations due to changes in instrumental responses. And this whereas Figure 6 indicates that the radiation of these Rayleigh waves does not present a directional effect. Finally, it was verified that in 2018 the instrumental responses of FURI and LSZ from the USGS IU network were correct.

Figure 6.
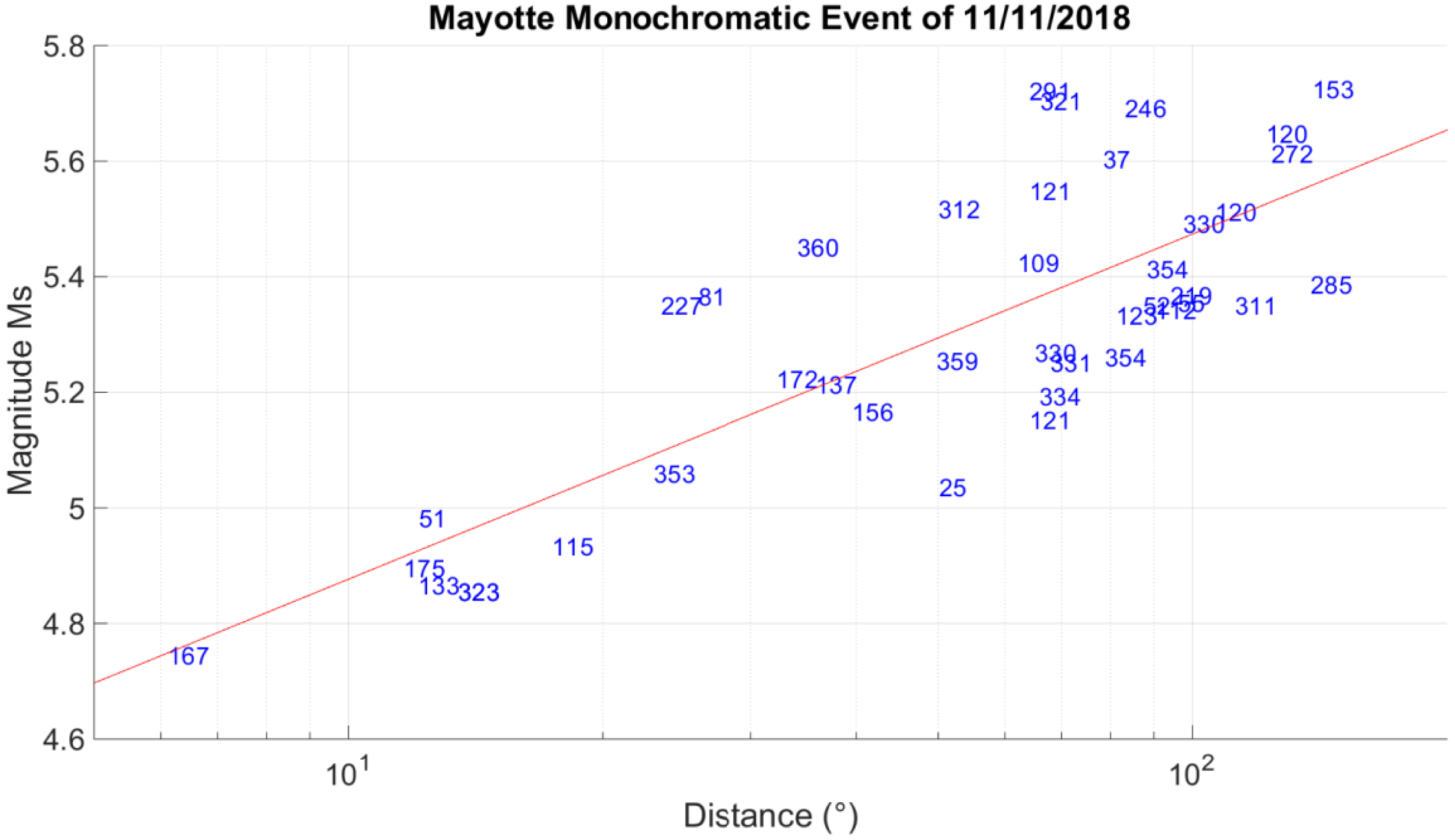
This extension of Figure 5 shows the azimuths station seen from the source, in blue. We can see that the radiation from these source of these Rayleigh waves has no directional effect.

In a similar way Sadeghi and Suzuki [2021] use seismic data from the 26 Iranian seismic stations, estimate the Ms of 5.07 to characterize this VLP of 11 November 2018. Likewise, Bhattacharya [2022] obtained Ms magnitudes between 3.15 and 4.94 for 251 VLPs of the Mayotte crisis using the following formula:

\begin{matrix} Ms & = & Ms_BB (Broad Band) \\ Ms & = & {log}_{10} (V_{max} / 2 π) + 1.66 {log}_{10} (Δ) + 0.3 \end{matrix}

where V_max is maximum ground velocity (nm/s), zero to peak, of surface waves in vertical component and Δ is epicentral distance 2°⩽Δ⩽160° [Bormann and Dewey, 2012].

The Mo is deduced from Mw, which in turn is deduced from Ms. This amounts to estimating the Mo on the basis of the amplitude of one of the signal periods, which comprise 150 to 190 of them!

Not taking into account the resonant nature of the sources and their durations, from 30 to 60 min, Cesca et al. [2020], Sadeghi and Suzuki [2021] and Bhattacharya [2022] treat these monochromatic VLPs as dispersed Rayleigh waves of earthquakes.

5. Conclusions

We have shown that:

The Rayleigh wave trains (VLPs) generated during the Rocard and Mayotte volcano seismic events are perfectly monochromatic.
These Rayleigh wave trains allow us to demonstrate that the attenuation factor, 1.66, of the Ms magnitude scale takes into account the geometric attenuation in 1/Δ and the frequency dispersion effect corresponding to the coefficient 0.66.
Originating from moderate energy events, the largest of these signals (31/07/2018, 11/11/2018) were correctly recorded up to very large distances (PPT-Tahiti: 16,300 km; HAW-Hawaii: 17,300 km). The cause is propagation damping limited to geometric attenuation in 1/Δ.
The radiation from the source of these monochromatic Rayleigh wave trains has no directional effect.

Declaration of interests

The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.

Acknowledgment

Thank you to the anonymous reviewer for these pertinent and constructive comments.

Bibliographie

[Aki, 1967] K. Aki Scaling law of earthquakes pectrum, J. Geophys. Res., Volume 72 (1967), pp. 1217-1231 | DOI

[Aki, 1972] K. Aki Scaling law of earthquake source-time function, Geophys. J. R. Astron. Soc., Volume 31 (1972), pp. 3-25 | DOI

[Bhattacharya, 2022] S. N. Bhattacharya Monochromatic Rayleigh waves of a period around 15 s recorded from long-period earthquakes at the east of Mayotte, North Mozambique Channel, and characteristics of oscillations at the source, Pure Appl. Geophys., Volume 179 (2022), pp. 2067-2082 | DOI

[Bormann and Dewey, 2012] P. Bormann; J. W. Dewey The new IASPEI standards for determining magnitudes from digital data and their relation to classical magnitudes. Data Sheet 3.1., New Manual of Seismological Observatory Practice (NMSOP-2) (P. Bormann, ed.), IASPEI, GFZ, German Research Centre of Geosciences, Potsdam, 2012 | DOI

[Cesca et al., 2020] S. Cesca; J. Letort; H. N. T. Razafindrakoto; S. Heimann; E. Rivalta; M. P. Isken; M. Nikkhoo; L. Passarelli; G. M. Petersen Drainage of a deep magma reservoir near Mayotte inferred from seismicity and deformation, Nat. Geosci., Volume 13 (2020), pp. 87-93 | DOI

[Geller and Kanamori, 1977] R. J. Geller; H. Kanamori Magnitudes of great shallow earthquakes from 1904 to 1952, Bull. Seismol. Soc. Am., Volume 67 (1977), pp. 587-598 | DOI

[Geller, 1976] R. J. Geller Scaling relations for earthquake source parameters and magnitudes, Bull. Seismol. Soc. Am., Volume 66 (1976), pp. 1501-1523 | DOI

[Hanks and Kanamori, 1979] T. C. Hanks; H. Kanamori A moment magnitude scale, J. Geophys. Res., Volume 84 (1979), pp. 2348-2350 | DOI

[Okal and Talandier, 1989] E. A. Okal; J. Talandier Mm: a variable-period mantle magnitude, J. Geophys. Res., Volume 94 (1989) no. B4, pp. 4169-4193 | DOI

[Okal, 1989] E. A. Okal A theoretical discussion of time domain magnitudes: the Prague formula for M $_{s}$ and the mantle magnitude Mm, J. Geophys. Res.: Solid Earth, Volume 94 (1989) no. B4, pp. 4194-4204 | DOI

[Sadeghi and Suzuki, 2021] H. Sadeghi; S. Suzuki Observation of the long-period monotonic seismic waves of the November 11, 2018, Mayotte event by Iranian broadband seismic stations, Earth Planets Space, Volume 73 (2021), 97 | DOI

[Talandier and Okal, 1989] J. Talandier; E. A. Okal An algorithm for automated tsunami warning in French Polynesia based on mantle magnitudes, Bull. Seismol. Soc. Am., Volume 79 (1989) no. 4, pp. 1177-1193 | DOI

[Talandier et al., 1987] J. Talandier; D. Reymond; E. A. Okal Mm: use of a variable-period mantle magnitude for the rapid one-station estimation of teleseismic moments, Geophys. Res. Lett., Volume 14 (1987) no. 8, pp. 840-843 | DOI

Commentaires - Politique