Abridged English version
1 Introduction
The DORIS system (Doppler Orbit determination and Radiopositioning by Satellite), developed by the French ‘Centre national d’études spatiales' (CNES) has been currently used for the past 14 years for precise orbit determination as well as precise geodetic positioning of ground tracking stations. From the very beginning, the ‘Institut géographique national’ (IGN) has been in charge of the installation and the maintenance of the permanent geodetic tracking network. It has also been involved in the realization of DORIS coordinates datasets obtained from combination of different sources. More recently, in close cooperation with the Jet Propulsion Laboratory (JPL), it has gradually become an active analysis center of the newly-created International DORIS Service (IDS) [20]. In this paper, we present these three closely related key components, focusing on new estimation strategies for DORIS data processing and emphasizing derived new geodetic results.
2 The DORIS tracking network
The DORIS observing network (56 stations), operationally installed and maintained by IGN [7], possesses an extremely good geographical distribution (Fig. 1), leading to a truly homogenous worldwide coverage (almost 50% in the southern hemisphere, number to be compared with 10 or 20% for other techniques in ITRF2000). Only two types of antennas are used (10 Alcatel and 46 Starec), leading to long-term continuous time series of observations for more than 10 years for most stations. Since 1999, an important renovation task has been undertaken to improve antenna support stability and to meet present-day geodetic requirements for local-tie accuracy.
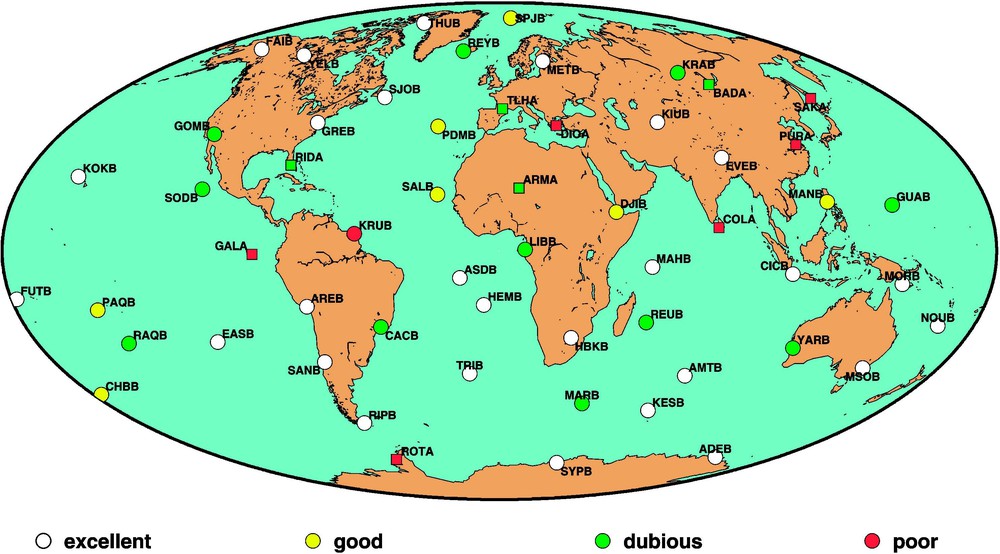
Carte des stations permanentes DORIS (septembre 2003). Les antennes Alcatel sont représentées par des cercles, les antennes Starec par des carrés. La couleur indique la qualité de la monumentation géodésique (blanc = excellent, jaune = bon, vert = douteux, rouge = mauvais).
Map of permanent DORIS tracking stations (September 2003). Circles represent the Alcatel antennas, squares represent the Starec antennas. Colors indicate the quality of the geodetic monumentation (white = excellent, yellow = good, green = dubious, red = poor).
3 DORIS terrestrial reference frame
Since 1993, IGN has been regularly providing successive realizations of the DORIS terrestrial reference frame, starting with positions-only solutions at a specific reference epoch, such as JCOD4 to JCOD7, and more recently recent realizations of the International Terrestrial Reference Frame (ITRF), including positions and velocities as well as full covariance information, such as ITRF96, ITRF97 and ITRF2000 [1].
Fig. 2 shows how these estimations have gradually improved with time, by comparing to a more recent DORIS estimation (IGN03D02) that we have specially derived by reprocessing more than 10 years of DORIS data from 1993.0 to 2003.5 using a GRACE-derived gravity field (GGM01C) [19,24]. In these comparisons, the precision of the JCOD datasets continuously improved from 3.0 to 4.0 cm with the JCOD solutions to now reaching a 1.5- to 2.0-cm level with ITRF2000. In these plots, the best agreement is obtained at the epoch of minimum variance for which errors in velocity estimation do not map into errors in position residuals at an arbitrary reference epoch.
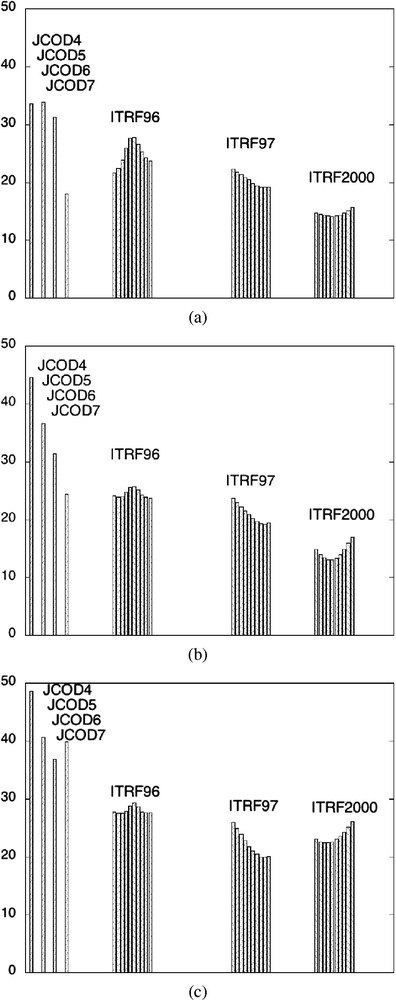
Comparaisons à plusieurs époques de référence des jeux de coordonnées historiques JCOD4, JCOD5, JCOD6, JCOD7, ITRF96, ITRF97 et ITRF2000 par rapport à une référence DORIS plus récente (IGN03D02). Résidus moyens quadratiques pondérés en latitude (a), longitude (b) et vertical (c) (en mm).
Comparisons at different reference epochs between historical coordinate datasets (JCOD4, JCOD5, JCOD6, JCOD7, ITRF96, ITRF97, ITRF2000) and a recent DORIS realization (IGN03D02). Weighted Root Mean Squares (WRMS) in latitude (a), longitude (b) and height (c) (in mm).
Fig. 3 shows a similar comparison, using a GPS-derived solution, using only GPS position and velocity information combined with the associated DORIS-GPS local ties using appropriate weighting. This provides a more external reference for comparison, but unfortunately limited to the DORIS stations in collocation with the permanent GPS receivers of the International GPS Service (IGS) [2], which represent about half of the total DORIS network. On those plots, typically a 5- to 10-mm agreement can be obtained for the most recent realization such as ITRF2000. However, we think that such a number could be rather optimistic, as the ITRF2000 positions are mainly driven by previous GPS solutions, due to the current formal errors in GPS positions and velocities used in the ITRF computations.
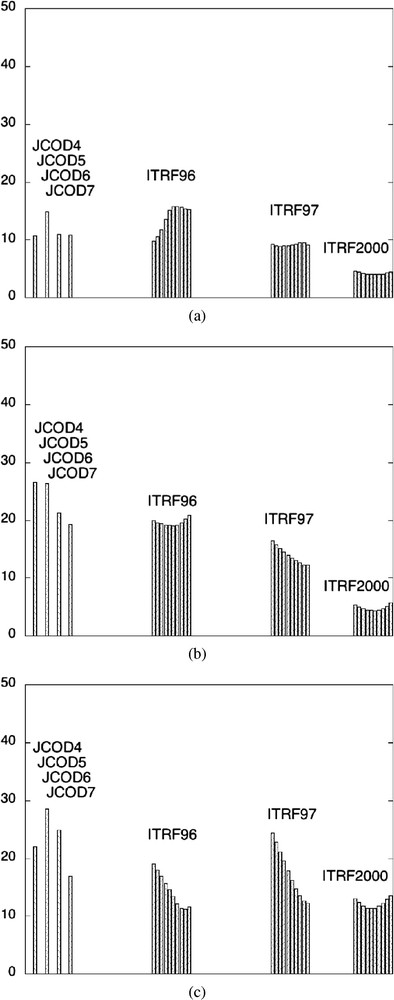
Évolution temporelle de l'exactitude en position des jeux de coordonnées DORIS JCOD et ITRF. Résidus moyens quadratiques pondérés en latitude (a), longitude (b) et vertical (c) (en mm).
Time evolution of DORIS station coordinate accuracy for JCOD and ITRF datasets. Weighted Root Mean Squares (WRMS) in latitude (a), longitude (b) and height (c) (in mm).
4 Processing DORIS data in a multi-satellite mode
For precise DORIS geodetic positioning, we process the DORIS data from all available satellites using the Gipsy/Oasis II software from JPL. We have in fact developed a new filtering method, making full profit of all available information for clocks and atmospheric parameters.
In particular, for any satellite S and and any ground beacon G and , the estimated frequency offsets Δf must verify the following equation:
| (1) |
If we express the slant tropospheric correction from the zenith tropospheric correction and the mapping function M, we have:
| (7) |
We estimate the tropospheric parameter to be satellite independent, as it only depends on the local ground station atmosphere evolution (mostly due to humidity variation). We have also chosen to estimate the zenith tropospheric delay rather frequently (every 30 min when DORIS data are available), but adding temporal constraints (5 cm for 1 day). Other software adopts a more classical approach and estimates this parameter per pass, making it also satellite-dependent and losing then some valuable information about the timing evolution of this physical parameter.
To demonstrate the interest of this improved filtering technique (clocks condition equations and tropospheric time constraints), we have reprocessed one entire year of the most recent DORIS data with a six-satellite constellation (2002.5 to 2003.5) using three different estimation strategies: the classical method using least squares combinations of single-satellites results (without all Jason/DORIS data or with Jason/DORIS data only outside the South Atlantic Anomaly region) and our newly developed multi-satellites approach without the Jason/DORIS data [25]. As a matter of fact, problems concerning the DORIS/Jason data were found when the satellite clock crosses the South Atlantic Anomaly region and previously reported [27].
Fig. 4 shows that a significant improvement (about 20%) can be found when using our improved filtering approach for geodetic positioning applications.
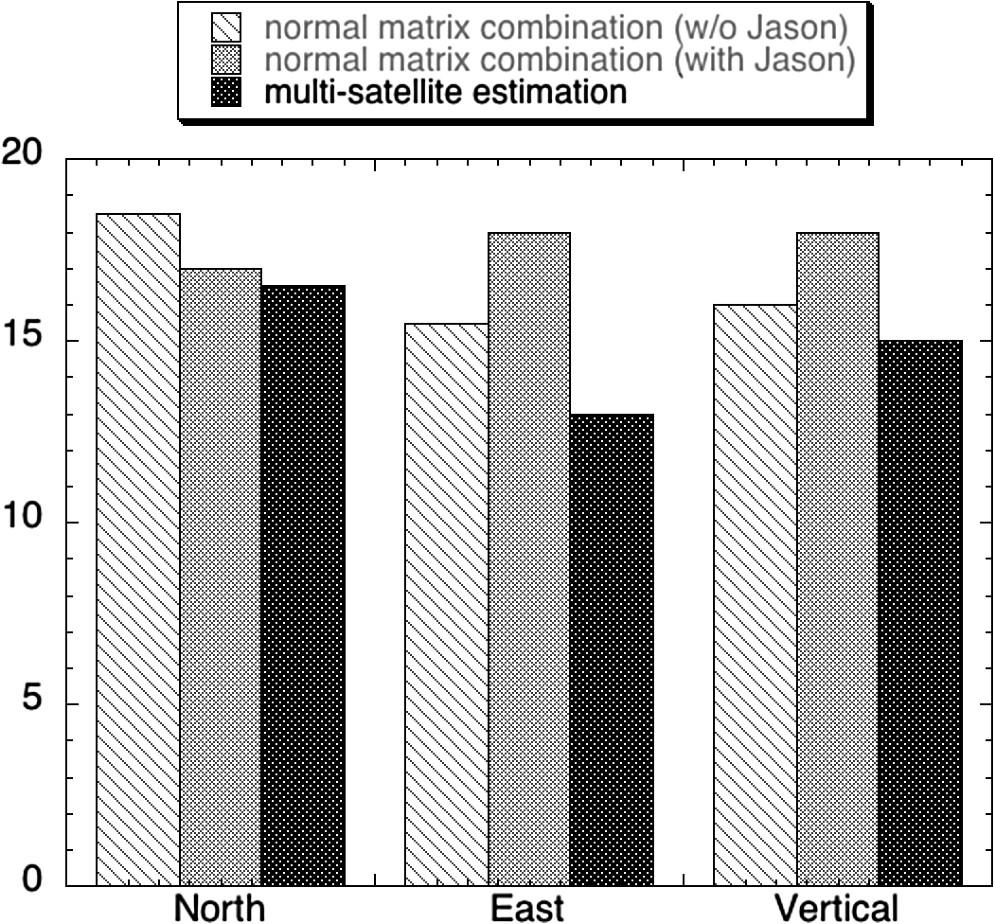
Précision géodésique de solutions annuelles DORIS suivant différentes stratégies de calcul.
Geodetic precision of annual DORIS solutions based on different estimation strategies.
5 Conclusions
Since 1986, the IGN has played a key role in the deployment and maintenance of the permanent DORIS tracking network, which is presently been improved to meet the more severe geodetic requirements for participation in the Global Geodetic Observing System (GGOS) project [16] of the International Association of Geodesy (IAG). Since the beginning, IGN has also delivered frequent and continuously improved solutions of the DORIS Terrestrial Reference Frame, whose best realization is available in the ITRF2000, leading to a sub-centimeter reference. More recently, in close cooperation with JPL, IGN has become an active Analysis Centre of the newly-created IDS. A new filtering strategy has been developed for processing all DORIS satellites Doppler data but Jason. This strategy is presented here in full details and compared to the classical approach used in other software. Comparisons show that this method provides significantly improved geodetic results (20%) when comparing with the classical and sub-optimal single-satellite data processing. Recent results using a GRACE-derived gravity field model (GGM01C) show that centimeter-level accuracy can now be obtained with DORIS.
Acknowledgement
The realization of the DORIS time series was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
1 Introduction
Le système DORIS (Détermination d'orbite et radiopositionnement intégré sur satellite) a été développé par le Centre national d'études spatiales (Cnes) pour des besoins d'orbitographie précise, liés initialement à la mission franco-américaine Topex/Poséidon [8]. Les performances orbitographiques obtenues en temps réel à bord du satellite avec le logiciel DIODE [12] montrent des résultats de l'ordre de 3 à 5 m (3-D) en routine et des simulations montrent que des précisions sub-métriques sont envisageables pour Jason. En temps différé, en combinaison avec des mesures GPS, des résultats de l'ordre du centimètre ont été obtenus récemment pour le satellite Jason [9,13] pour la composante radiale. De tels résultats permettent aussi d'obtenir, depuis plus de 14 ans, d'excellentes précisions géodésiques pour les stations du réseau d'orbitographie DORIS pour des applications géodésiques ou géophysiques [5,6,22]. Dès le début de ce système, l'IGN a été un partenaire du Cnes, apportant son expertise géodésique et, plus particulièrement, assurant la responsabilité de l'installation et de la maintenance du réseau permanent d'orbitographie et réalisant, de manière successive dans le temps, un repère de référence lié à DORIS de plus en plus performant. Cette dernière activité a évolué progressivement par l'adaptation du logiciel Gipsy/Oasis II du Jet Propulsion Laboratory [21] et son utilisation scientifique pour réaliser des calculs DORIS de localisation géodésique. Le système DORIS connaît actuellement une mutation importante, liée à son internationalisation progressive dans le contexte du nouveau service scientifique International DORIS Service (IDS) [20] de l'Association internationale de géodésie (AIG). Dans ce nouveau contexte, il nous a paru important de rappeler ici les différentes contributions de l'IGN au projet DORIS et de présenter à cette occasion la nouvelle méthode de traitement des mesures DORIS pour la localisation géodésique, en comparant les résultats obtenus à ceux issus d'une méthode classique, mais sub-optimale.
2 Le réseau d'orbitographie DORIS
Depuis le début du système DORIS, l'IGN est responsable de l'installation et de la maintenance des stations du réseau permanent d'orbitographie. La Fig. 1 montre l'excellente répartition géographique des 56 stations actuelles. Ce réseau, établi dans 33 pays différents, dans le cadre de coopérations scientifiques bilatérales, se répartit harmonieusement entre l'hémisphère nord et l'hémisphère sud. Ceci n'est malheureusement pas le cas des autres réseaux de géodésie spatiale. Par exemple, les réseaux laser et VLBI souffrent d'une répartition privilégiant trop l'Europe et les États-Unis, pour des raisons économiques et politiques [2,14,17]. Dans l'ITRF2000, 49 % des stations DORIS se trouvent dans l'hémisphère nord, alors que ce même pourcentage est de 84 % pour GPS, 85 % pour le laser et 92 % pour le VLBI, soit 79 % en moyenne pour l'ensemble de l'ITRF2000. On comprend ainsi la contribution importante du système DORIS en termes de répartition géographique du réseau de poursuite.
Actuellement, uniquement deux types d'antennes DORIS sont utilisés : Alcatel (10) et Starec (46), comme indiqués sur la Fig. 1. Les antennes Alcatel de première génération sont toutes progressivement remplacées au fur et à mesure des disponibilités de matériel par des antennes Starec plus compactes. Cet aspect est important pour des considérations géodésiques et géophysiques. En effet, le GPS qui a un réseau beaucoup plus dense souffre depuis toujours de la multiplicité des types d'équipements et de leurs changements fréquents. Plusieurs auteurs ont décrit des mouvements erronés déduits de résultats de positions GPS, provenant en fait de changement d'antennes ou simplement de radômes de protection [15]. Enfin, il faut noter que le réseau DORIS est demeuré très stable dans le temps, puisque 25 stations observent de manière continue depuis plus de 13 ans [26].
En 1999, compte tenu des nouvelles performances de localisation obtenues par plusieurs groupes dans le monde, une étude critique du réseau a été entreprise par le Service d'installation et de maintenance des balises (SIMB), qui dépend de l'IGN. Depuis cette date, une amélioration progressive des sites est en cours [7]. Actuellement, la stabilité de l'antenne est estimée comme bonne ou excellente pour 34 stations, acceptable pour 15 et insuffisante pour 7 (Fig. 1). Cette estimation est basée sur plusieurs critères objectifs : stabilité de l'assise du support d'antenne (bloc de béton ancré en profondeur, dalle béton, mur de bâtiment, etc.), stabilité et rigidité du support d'antenne (pylône – haubané ou autoporteur – de section et de hauteur variables, pilier béton), type d'antenne, ancienneté de l'installation.
Installé par des géodésiens, ce réseau a été implanté, à chaque fois que cela était possible, en colocation (installation proche dans un rayon de quelques kilomètres) avec d'autres techniques géodésiques fondamentales de l'International Earth Rotation and Reference Systems Service (IERS). Il faut noter que presque toutes ces stations laser et VLBI se trouvaient déjà en colocation avec des récepteurs GPS et que deux stations (Greenbelt, sur la cote est des États-Unis et Hartebeesthoek en Afrique du Sud) possèdent les quatre techniques simultanément. Les rattachements géodésiques de l'antenne DORIS à un ou plusieurs points de ces sites ont été effectués, soit par le SIMB, soit par des organismes géodésiques partenaires. La qualité de ces rattachements est actuellement excellente : 26 ont une précision inférieure à 2 mm, sept ont une précision comprise entre 2 mm et 1 cm et seulement deux ont une précision supérieure à 1 cm. Il faut noter que certains sites DORIS sont d'accès particulièrement difficiles (un à cinq bateaux par an pour atteindre certaines stations situées en Antarctique ou sur des îles de l'Atlantique sud ou de l'océan Indien). Cela demande donc une organisation logistique importante en liaison avec les organismes hôtes, ainsi que d'autres organismes géodésiques intéressés.
Dès le début de l'installation du réseau permanent DORIS, les colocations avec d'autres types d'instruments d'observation ont été privilégiées : observatoires laser (7), radio-télescopes VLBI (6), puis GPS (33) et enfin marégraphes (20, dont 16 effectivement rattachés par le SIMB), gravimètres, stations temps–fréquence. Ceci a été réalisé dans une perspective à long terme d'observations géophysiques, qui s'insère donc désormais dans la logique du Projet Global Geodetic Observing System (GGOS) [16].
3 Maintenance du système de référence terrestre lié à DORIS
Dans le cadre du projet DORIS, l'IGN a régulièrement fourni, pour les besoins d'orbitographie du Cnes, des coordonnées précises des stations DORIS. Les premières réalisations du repère de référence DORIS datent de 1993 (JCOD4) et 1995 (JCOD5, JCOD6 à JCOD7) et ne comportaient que des estimations de position à une époque de référence [3]. Cette activité de calcul a ensuite été rapidement intégrée dans la réalisation de l'International Terrestrial Reference Frame (ITRF) [4]. Ces nouvelles réalisations incluaient alors des estimations de position, mais aussi des estimations de vitesse, pour tenir compte des effets de mouvements tectoniques et de subsidences éventuelles.
Pour valider a posteriori la qualité de ces réalisations historiques, nous avons comparé individuellement chacune de ces réalisations successives à une référence plus récente (IGN03D02), que nous avons estimée en utilisant toutes les mesures DORIS de 1993,0 à 2003,5 ainsi que les rattachements entre antennes DORIS d'un même site avec une pondération appropriée [26]. En effet, pour un même site, plusieurs antennes DORIS ont pu être installées au cours du temps, pour diverses raisons :
- – remplacement d'une antenne détruite par des événements climatiques exceptionnels ;
- – amélioration de la stabilité de l'antenne par changement de support impliquant un déplacement du point de référence de l'antenne ;
- – amélioration de la qualité du rattachement par l'utilisation d'un type d'antenne plus facile à rattacher de manière précise.
La Fig. 2 montre les résultats de cette comparaison.
Pour les jeux de coordonnées les plus anciens (JCOD4 à JCOD5), ne comportant aucune estimation de vitesse, nous n'avons effectué la comparaison qu'à l'époque de référence du jeu, afin de ne pas perturber notre étude par des incertitudes sur la vitesse des stations. Pour les jeux plus récents de type ITRF, nous les avons comparé à plusieurs époques de référence, justement afin de mettre en évidence ces erreurs de vitesse. On voit clairement sur la Fig. 2 que les réalisations de type ITRF apportent une amélioration significative à la précision des coordonnées de stations DORIS, typiquement de 3–4 à 1,5–2 cm. De plus, l'ITRF2000 est nettement supérieur aux réalisations antérieures. Pour l'ITRF97 et l'ITRF2000, on peut aussi observer que les résidus possèdent un minimum. Ceci était prévisible, car les imprécisions en vitesse se traduisent dans ce type de test par une augmentation quadratique des résidus dans le passé et dans le futur. Une autre manière, mathématiquement plus correcte, d'exprimer ces résidus aurait été de le faire à l'époque de variance minimum, ce que certains logiciels, comme CATREF [1,18] permettent de faire.
Cette comparaison inclut aussi des erreurs dans la référence IGN03D02 elle-même, qui, issue d'un processus d'estimation, souffre aussi d'erreurs inhérentes. Pour mettre en évidence de telles erreurs, nous avons refait la même étude en modifiant la référence. Dans cette deuxième étude, nous avons construit une référence DORIS à partir d'une solution positions/vitesses de stations GPS [11] que nous avons cumulée, au sens des moindres carrés, avec les observations de rattachements GPS/DORIS issues du SIMB, convenablement pondérées. Les résultats GPS ayant actuellement une précision de 2–3 mm en planimétrie et de 5 mm en altimétrie [2], cette nouvelle référence est potentiellement plus exacte que la première, issue des seules mesures DORIS. Elle a aussi l'avantage d'être entièrement externe au système DORIS. Son inconvénient est de ne fournir des informations que pour les stations DORIS en colocation avec des stations GPS, soit environ la moitié du réseau complet.
La Fig. 3 montre les comparaisons des mêmes jeux historiques à cette nouvelle référence.
Ces nouvelles comparaisons confirment aussi les améliorations successives qui ont été faites entre les premiers jeux JCOD et les premiers ITRF pour aboutir récemment à l'ITRF2000, au moins pour les sites en colocation GPS/DORIS. On voit aussi que l'accord avec cette nouvelle référence est aussi bien meilleur : 5 mm en planimétrie et 1 cm en altimétrie pour l'ITRF2000. Cela provient d'une meilleure exactitude de la référence [1], mais aussi du fait que la pondération entre les solutions GPS et DORIS utilisées dans les calculs des différents ITRF privilégie naturellement le GPS, du fait de sa très haute précision formelle et aussi à cause du nombre plus important de solutions GPS obtenues en utilisant des modèles physiques de correction et des modèles d'estimation plus proches, fournissant ainsi un meilleur accord avec cette nouvelle référence elle-même issue de résultats GPS.
4 Traitements géodésiques DORIS en mode multi-satellite
Généralement, les calculs géodésiques DORIS sont réalisés par les différents centres d'analyse de l'IDS [20], en plusieurs étapes successives. Tout d'abord, un premier calcul est réalisé par satellite. Ensuite, une solution globale (positions et vitesses de toutes les stations) est obtenue en cumulant les matrices normales élémentaires obtenues par satellites. Nous allons décrire ici brièvement la nouvelle méthode développée à l'IGN à partir du logiciel Gipsy/Oasis II du Jet Propulsion Laboratory (JPL) [10] et montrer que l'approche classique, si elle est efficace d'un point de vue calculatoire, n'est que sub-optimale d'un point de vue mathématique.
La mesure DORIS (notée D) correspond à une différence de phase de porteuse entre un instant de début de comptage et un instant de fin de comptage par le récepteur à bord du satellite S.
Pour un instant t ( ou ), la phase DORIS peut s'écrire sous la forme suivante [21] :
| (1) |
Pendant une durée limitée, équivalente à celle d'un passage de satellite, soit environ 10 à 30 min pour les altitudes des satellites considérés, chaque horloge peut être modélisée simplement par un polynôme du premier degré :
| (2) |
| (3) |
| (4) |
Si on note le temps de début du comptage Doppler DORIS et le temps de fin de comptage, et si on note la mesure DORIS, on a donc :
| (5) |
L'approche classique consiste à estimer un paramètre de fréquence par passage , sans distinguer la fréquence sol de la fréquence bord. Toutefois, lorsque plusieurs satellites observent plusieurs balises DORIS simultanément ou de manière suffisamment proches dans le temps, ces paramètres ne sont pas indépendants, car ils vérifient par construction l'équation aux conditions suivantes, pour deux satellites S et et deux balises au sol G et :
| (6) |
Le logiciel Gipsy/Oasis permet lui d'estimer directement les paramètres de fréquence et de manière indépendante, en imposant que l'un des satellites soit la référence de fréquence . On peut aussi noter que l'équation (6) doit toujours être vérifiée, même si les observations DORIS ne sont pas exactement simultanées (condition qui deviendrait indispensable si on voulait adopter une technique différentielle de type GPS). Il suffit simplement que les quatre mesures DORIS (deux satellites, deux balises au sol) soient effectuées durant une période de temps suffisamment courte, pour que la modélisation linéaire des horloges définie par les équations (2) et (3) reste vérifiée. Dans un tel cas, l'approche classique estimerait quatre paramètres indépendants, alors que notre approche n'en estime que trois, fournissant ainsi des informations supplémentaires [25].
Enfin, il faut noter que la correction troposphérique n'est pas quelconque et qu'elle peut s'écrire sous la forme classique suivante :
| (7) |
Dans une approche classique, est estimé de manière indépendante par passage sous la forme d'un nouveau biais de type , dépendant alors du satellite.
Pour tenir compte de la variabilité du milieu atmosphérique, nous proposons d'estimer ce paramètre de manière indépendante du satellite et par intervalle de temps, typiquement 30 min à 1 h, en ajoutant des contraintes d'évolution temporelles [23], de l'ordre de 2 à 10 cm par jour, ce qui est cohérent avec la variabilité constatée pour des résultats équivalents issus de mesures GPS [2]. Une valeur plus précise pourrait d'ailleurs être estimée à partir de la base de données d'allongement troposphériques de l'International GPS Service (IGS). En fait, pour diminuer le temps de calcul, ce paramètre n'est estimé qu'à chaque début de passage, mais uniquement si le paramètre précédent est distant de plus de 30 min. Cette méthode assure une corrélation entre les observations multi-satellites, tout en assurant un certain lissage du paramètre troposphérique au cours du temps.
Afin de montrer l'intérêt de cette méthode multi-satellites, nous avons traité un an de données DORIS de 2002,5 à 2003,5, en utilisant le nouveau modèle de champ GGM01C issu de la mission GRACE [19,24], de trois manières différentes : en cumulant les matrices normales obtenues par des calculs mono-satellite en utilisant tous les satellites DORIS (méthode classique), en ne cumulant pas les matrices normales de tous les satellites DORIS sans tenir compte de Jason, puis en estimant directement les paramètres en mode multi-satellites sans utiliser les mesures Jason (notre méthode). Chacune de ces trois solutions a été comparée de manière indépendante à la solution IGN03D02, plus précise, car utilisant toutes les mesures DORIS de 1993 à 2004 (Fig. 4).
La période choisie est particulièrement intéressante, car six satellites DORIS sont disponibles, fournissant ainsi des résultats de localisation améliorés [26]. Dans chaque cas, nous avons traité les données par arc d'un jour, puis nous les avons combinées pour obtenir des solutions hebdomadaires de localisation DORIS [26].
Compte tenu du problème mis en évidence récemment sur les données DORIS du satellite Jason [27], nous avons considéré deux types de solutions cumulés : avec ou sans les résultats Jason, en retirant éventuellement les données DORIS/Jason des stations situées à l'intérieur ou à proximité de l'anomalie de l'Atlantique sud. Dans le cas de la méthode multi-satellites, un calcul global avec les données DORIS/Jason est actuellement impossible sans correction, car le comportement de l'oscillateur à bord de Jason ne peut plus être considéré comme un paramètre constant pendant des périodes de plusieurs minutes lors des passages au-dessus de l'anomalie Sud-Atlantique [27].
La Fig. 4 montre que solution multi-satellites permet d'obtenir une amélioration significative (environ 20 %) de la localisation géodésique DORIS par rapport à une approche plus classique (cumul de matrices normales). Ceci confirme que l'ajout des équations aux conditions pour les horloges bord et sol et des équations de contraintes pour les paramètres de correction troposphérique permet de rajouter des informations utiles dans le filtrage des données DORIS.
Enfin, l'apport des données Jason dans la solution cumulée n'apporte pas actuellement d'amélioration significative des résultats, montrant ainsi que certains problèmes subsistent encore dans la localisation issue des mesures DORIS/Jason.
5 Conclusions
Depuis 1986, l'IGN a joué un rôle majeur dans le déploiement, puis la maintenance du réseau de poursuite DORIS. En particulier, une politique volontaire de colocation des installations avec d'autres techniques fondamentales de géodésie spatiale ou d'autres stations d'intérêt géodésique (gravimètre) ou géophysique (marégraphe) porte maintenant ses fruits dans le contexte du projet international GGOS de l'AIG. Une rénovation complète des implantations DORIS est en cours pour préparer les futures applications. Après avoir fourni des coordonnées géodésiques précises de ces stations, puis avoir utilisé de tels résultats pour réaliser le système de référence terrestre ITRF, l'IGN réalise depuis plusieurs années des calculs de localisation DORIS. La nouvelle approche proposée, utilisant de manière optimale le mode multi-satellites, permet d'obtenir une amélioration dans la précision et l'exactitude de ces résultats de localisation géodésique, typiquement de l'ordre du centimètre.
Acknowledgments
La réalisation des séries temporelles DORIS a été faite au Jet Propulsion Laboratory, California Institute of Technology, dans le cadre d'un contrat de recherche avec la National Aeronautics and Space Administration (NASA).


