Le gnomon est le plus ancien instrument d’astronomie, ce qui ne signifie pas qu’il n’est plus utilisé aujourd’hui, comme on le verra par la suite. Le mot γνωμων signifie en grec indicateur – sous entendu tige qui porte ombre–, ce qui est équivoque, car il convient de distinguer l’indicateur seul (simple bâton planté verticalement en terre qui est l’instrument astronomique) du porte-ombre dont étaient munis les cadrans solaires antiques.
Selon la doxographie classique (Dumont, 1988), le gnomon aurait été inventé par Anaximandre (d’après Diogène Laërce), ce que confirme la Souda. Mais on sait par Hérodote que les Grecs tiennent le gnomon des Babyloniens1. Il ne fait donc aucun doute que l’utilisation de cet instrument à des fins astronomiques a dû être découverte assez tôt par différentes cultures (cf. infra) et qu’en Grèce son usage est attesté2 dès le Ve siècle av. J.-C. Chez les Babyloniens, l’analyse des tablettes MUL.APIN laisse à penser que l’usage du gnomon est attesté (Steel, 2013) dès le second millénaire av. J.-C. et que les solstices et les équinoxes sont définis, par exemple, en utilisant le rapport de l’ombre d’un gnomon.
L’étude de cette dernière a permis, dès les premiers temps de l’astronomie, de déterminer les constantes fondamentales comme la latitude ϕ du lieu, l’obliquité ɛ de l’écliptique, mais également les dates des équinoxes et des solstices (donc la durée de l’année), les points cardinaux, les directions des levers et couchers du Soleil, sans oublier l’indication du midi solaire (Evans, 1998 ; Neugebauer, 1975). Comme instrument, le gnomon est réduit à une tige parfaitement verticale dont on observe surtout l’ombre méridienne, ce qui suppose que cette dernière est matérialisée sur un sol parfaitement de niveau.
Lorsque le Soleil culmine au méridien sud (Fig. 1), on peut extraire de sa hauteur deux paramètres qu’il convient d’isoler3, à savoir la latitude du lieu et l’obliquité. Il faut pour cela mesurer la longueur R de l’ombre du gnomon de longueur a. On a alors :
- • aux équinoxes R = a tan ϕ ;
- • au solstice d’été R = a tan (ϕ–ɛ) ;
- • au solstice d’hiver R = a tan (ϕ + ɛ).
Or, comme l’avait déjà remarqué Ptolémée4, l’usage du gnomon pour déterminer les équinoxes et les solstices n’est pas recommandé, et ceci pour plusieurs raisons que l’on va détailler.
Aux équinoxes, la variation de déclinaison du Soleil est de 0° 1′ par heure. Il en résulte qu’au lieu de suivre une droite parfaite comme en sont munis de nombreux cadrans solaires, l’extrémité de l’ombre décrit une courbe complexe que l’on peut assimiler à une droite oblique. Prenons par exemple un gnomon de 100 cm installé à 30° de latitude ; supposons que la déclinaison soit nulle à 7 h du matin et voyons comment se comporte l’ombre jusqu’à 17 h. La déclinaison aura donc varié de 0° 10′ en 10 heures d’éclairement ; l’ordonnée de l’ombre dans un repère centré sur le gnomon sera passée de 57,7 cm le matin à 56,3 cm l’après-midi, soit 1,4 cm de variation, ou, si l’on mesure la longueur de l’ombre, celle-ci sera passée de 434,8 cm à 431,8 cm. Si l’observateur considère qu’à midi vrai, la déclinaison du Soleil est nulle, il mesure une ombre méridienne de 57,5 cm et finalement en conclut une latitude de 29° 54′.
Déterminer l’instant précis de l’équinoxe est difficile et nécessite des approximations successives quant à la position de l’ombre de part et d’autre du jour de l’équinoxe. L’arc hyperbolique (très proche d’une droite) décrit par l’ombre étant très semblable d’un jour à l’autre, cela ne facilite pas la détermination précise de l’instant équinoxial. C’est la raison pour laquelle Ptolémée (et avant lui Hipparque) détermine le jour et l’instant à l’aide d’une armille équatoriale5. En fait, une seule mesure ne suffit pas pour obtenir la latitude avec précision ; le fait que l’instant où la déclinaison du Soleil est nulle ne coïncide généralement pas avec le midi vrai local (sauf hasard) constitue une véritable difficulté, que même plus tard les méridiennes à œilleton ne résoudront pas directement.
L’autre conséquence de la variation très importante de la déclinaison à ces périodes fait que la culmination du Soleil s’établit en dehors du méridien local. En d’autres termes, ce n’est pas lorsque le Soleil est dans la direction du Sud géographique qu’il culmine.
Sur la Fig. 2, on a représenté en pointillés la trajectoire diurne d’un astre de déclinaison invariable : la culmination a bien lieu au méridien local. Avec le Soleil, ceci n’est vrai qu’aux solstices ; aux équinoxes, la variation de déclinaison vient contrebalancer le mouvement diurne, de sorte que la culmination se fait en dehors du méridien, le Soleil ayant alors un angle horaire H donné par
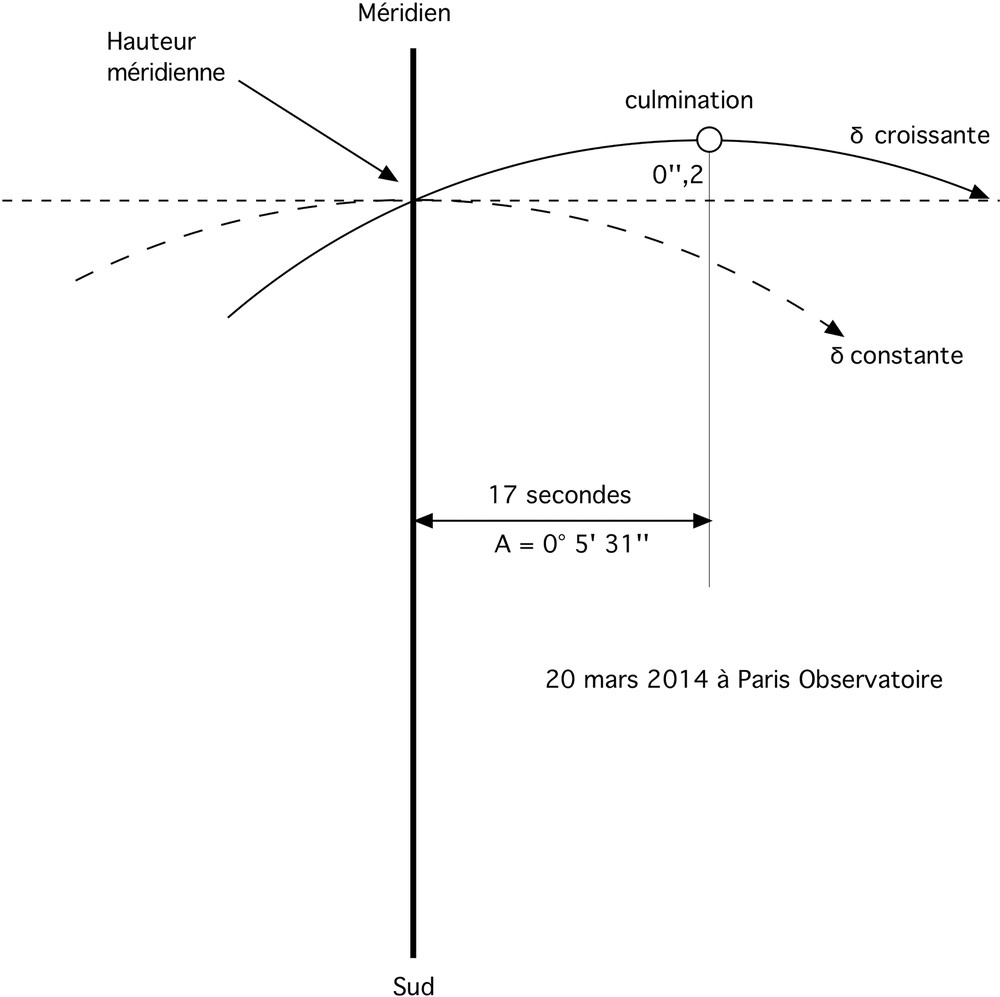
Décalage entre passage au méridien et culmination du Soleil aux équinoxes.
Shift of the Sun between its crossing at the meridian and its culmination at the equinoxes.
Il est donc préférable de ne pas utiliser le Soleil au voisinage des équinoxes pour déterminer le méridien du lieu avec un gnomon, mais de réaliser cette mesure aux alentours des solstices.
Ces périodes pourtant ne sont pas non plus exemptes d’inconvénients ; le plus spectaculaire est sans aucun doute la très grande variation de l’azimut du Soleil à midi solaire au solstice d’été. En d’autres termes, l’ombre d’un gnomon tourne très vite en été à midi. On donne dans le Tableau 1, cette variation en une minute de temps pour deux latitudes et pour les deux solstices6.
On vérifie bien que la variation d’azimut est très importante au solstice d’été et qu’elle s’accentue lorsque la latitude se rapproche de celle du tropique du Cancer. L’enseignement que l’on peut tirer de ces exemples est qu’il est préférable de tracer une méridienne avec un gnomon en hiver7 : relever la direction de l’ombre au voisinage du solstice d’été s’avère particulièrement difficile en raison de sa vitesse. Sans compter que la déclinaison de l’astre du jour ne variant pratiquement pas d’un jour à l’autre, la mesure précise du jour du solstice ne peut se faire que par encadrement.
Mais le corollaire de cette importante vitesse de rotation de l’ombre est que la hauteur du Soleil ne varie pratiquement pas au voisinage du méridien8, de sorte que même si l’on se trompe un peu sur l’instant où l’ombre est la plus courte, cela n’a pas de conséquence sur le résultat, comme le montre le Tableau 2.
Variation within 1 minute of the Sun height at solar noon for two latitudes and the two solstices.
| Variation hauteur en 1 min | Latitude 30° | Latitude 48° |
| Solstice d’été | ≈ 0′14″ | ≈ 0′3″ |
| Solstice d’hiver | ≈ 0′2″ | ≈ 0′1″ |
Il est tout à fait impossible, avec un simple gnomon, de mettre en évidence de si faibles variations de la hauteur du Soleil, ce qui supposerait des mesures de la longueur de l’ombre faites au centième de millimètre, par exemple avec un gnomon de 100 cm9. Ce qui explique que les mesures effectuées dès la très haute Antiquité pour déterminer l’obliquité de l’écliptique aux solstices sont assez fiables (cf. infra).
Si un observateur a mesuré les hauteurs méridiennes au solstice d’été hété et au solstice d’hiver hhiver, il peut alors déduire directement les deux paramètres recherchés (latitude et obliquité) selon :
Malgré toute la rigueur apportée aux mesures de longueur d’ombre, un autre phénomène bien connu et bien plus considérable vient altérer la précision des mesures : l’effet de pénombre. Lié au diamètre apparent du Soleil (0° 32′ en moyenne), la pénombre provoque une zone de flou à l’extrémité de l’ombre d’un gnomon, pénombre d’autant plus importante que la hauteur du Soleil est faible. Il en résulte une incertitude dans la mesure de la longueur de l’ombre, particulièrement sensible au solstice d’hiver. Sur la Fig. 3, on a remplacé le gnomon par une plaque sans épaisseur de 100 cm de haut placée à 48° de latitude. Dans le Tableau 3, on donne les valeurs en centimètres de l’ombre pure (PA′) qui correspond au bord supérieur du Soleil, de l’ombre du photocentre (PO′) et enfin de l’ombre partielle du bord inférieur du Soleil (PB′).
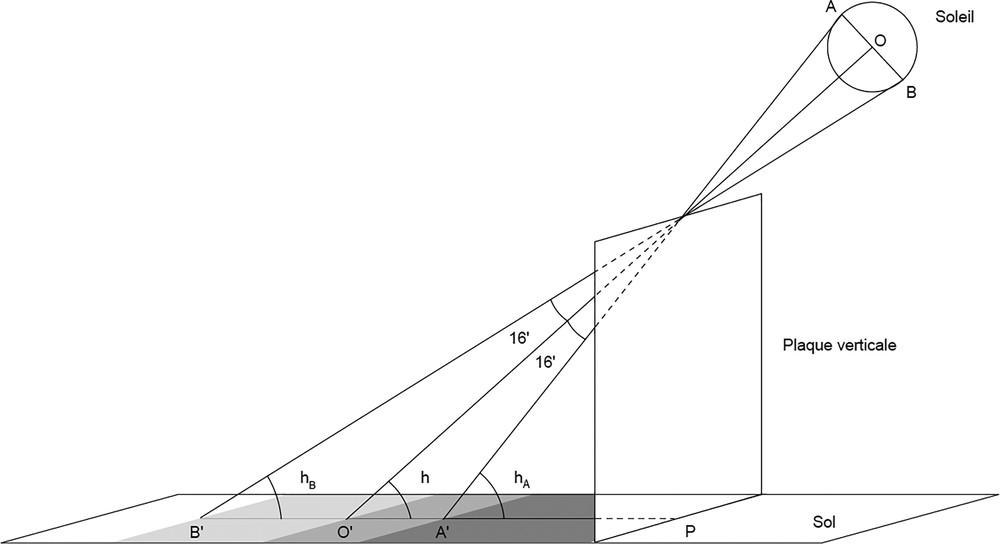
Effet de pénombre dû au diamètre solaire.
Effect of the penumbra due to the Sun diameter.
Variation in centimeters of the pure umbra (PA′), which corresponds to the higher edge, of the umbra of the photocenter (PO′) and last of the partial umbra of the Sun lower border (PB′).
| Hauteur | PA′ | PO′ | PB′ |
| 60° | 57,1 | 57,7 | 58,4 |
| 40° | 118,1 | 119,2 | 120,3 |
| 20° | 270,8 | 274,7 | 278,8 |
En théorie, on doit mesurer PO′ ; la zone A′O′ est une zone de transition variable, floue, entre l’ombre pure et l’ombre diluée O′B′. On remarque que cette zone de flou est d’autant plus large que le Soleil est bas. On établit facilement que PA′ = a cotan(h + 16′), où a est la longueur du gnomon et h la hauteur vraie du Soleil. L’observateur10 va avoir tendance à mesurer PA′ au lieu de PO′ et donc à commettre une erreur voisine de 16′ dans la détermination de la hauteur du Soleil. En latitude, cela représente une erreur de presque 30 km en direction du sud11.
Il faut mentionner pour finir que la hauteur du Soleil est affectée par la réfraction12 ; celle-ci n’est sensible (pour un gnomon) que pour des hauteurs inférieures à 45° où elle vaut 0° 1′. La réfraction relève la hauteur du Soleil et cela devient non négligeable pour des hauteurs voisines de 20° où la réfraction se rapproche de 0° 3′ ; mais les hauteurs méridiennes basses ne s’observent qu’en Europe, de sorte qu’à l’époque de Ptolémée à Alexandrie, la réfraction méridienne altérait la hauteur au maximum d’environ 0° 1′.
Malgré tous ces inconvénients, le gnomon permet d’obtenir, en multipliant les observations, des paramètres très acceptables, qui peuvent être exploités ultérieurement, en particulier pour vérifier la diminution de l’obliquité de l’écliptique (cf. infra). Ce qui signifie concrètement que l’on détermine la date d’un équinoxe ou d’un solstice par encadrements, en faisant des mesures, autant que faire se peut, un mois avant et un mois après le phénomène supposé. Cela suppose, – et il n’est pas inutile de le rappeler –, que le gnomon doit être parfaitement vertical et le sol nivelé. Un gnomon a s’écartant de la verticale d’un angle z entraîne à midi une erreur dans la longueur de l’ombre mesurée, qui, au lieu de valoir R = a tan(ϕ–δ), vaut R = a [tan(ϕ–δ) cos z + sin z], où δ est la déclinaison du Soleil, qui est égale à 0° aux équinoxes et à ± ɛ aux solstices13.
Terminons cette liste des bienfaits et des méfaits du gnomon en soulignant que la qualité de l’ombre, ce qu’on appelait jadis son épaisseur, entre également en ligne de compte. Un ciel nébuleux ou légèrement voilé n’engendre pas une ombre contrastée et nette en raison du moindre éclairement de la périphérie, de sorte que l’appréciation de l’ombre pure s’en trouve altérée.
Rappelons également qu’Érastosthène, au IIIe siècle av. J.-C., comme le rapporte Cléomède dans sa Théorie élémentaire14, a déterminé la valeur de la circonférence terrestre en utilisant très probablement un gnomon amélioré15 ; il a ainsi déterminé la différence de latitude entre Syène (située sur le tropique du Cancer) et Alexandrie par les ombres solsticiales.
Dans l’Antiquité, astronomes et géographes expriment la latitude d’un lieu en fonction du rapport de l’ombre équinoxiale à un gnomon, sans doute en utilisant des tables usuelles16. Par exemple, Vitruve, dans le livre IX du De architectura17, exprime la latitude de toute une série de villes et de lieux (Rome, Athènes, Rhodes, Alexandrie, Tarente) de la façon suivante : « Au moment de l’équinoxe, le Soleil, situé dans le Bélier ou la Balance, engendre une ombre égale aux 8/9 de la longueur du gnomon à la latitude de Rome ». Ce qui correspond à une latitude18 de 41° 38′. Cette façon d’exprimer la latitude, très ancienne puisqu’elle remonte aux Babyloniens, ne cessa apparemment jamais d’être utilisée, puisqu’on la retrouve bien ancrée en Inde au XVIIIe siècle (cf. infra).
Comme on l’a vu, l’effet de pénombre est donc de loin ce qui engendre la plus grande erreur dans l’utilisation à des fins astronomiques du gnomon. Conscients de cet inconvénient, les astronomes de l’Antiquité ont tenté de minimiser cet effet, en munissant le sommet du gnomon d’une sphère ou d’un œilleton. L’exemple le plus connu est l’obélisque ramené à Rome par Auguste et installé sur le Champs de Mars vers 10 av. J.-C. comme gnomon d’une très grande méridienne19. Pline20 nous dit que son concepteur plaça au sommet une boule dorée pour atténuer la dilution de l’extrémité de l’ombre. Si une telle sphère diminue effectivement l’effet de pénombre, la forme elliptique de son ombre au sol, très étalée en hiver, ne résout pas complètement le problème, qui ici consiste à lire l’heure et la date. Une autre solution a été de munir le sommet du gnomon d’un œilleton ; selon Karl Manitius (1912)21, ce sont les astronomes byzantins du Ve siècle de notre ère qui auraient eu cette idée, mais il est probable que cet artifice était connu bien avant (Fig. 4).

L’obélisque de la place de la Concorde à Paris a été utilisé en l’an 2000 comme gnomon pour tracer au sol un gigantesque cadran solaire.
The Obélisque of the Palace de la Concorde, Paris, was used as gnomon in 2000 to draw a gigantic sundial on the square ground.
En dehors du monde méditerranéen, le gnomon fut utilisé, entre autres, en Inde et en Chine. Ce sont en fait les Chinois qui ont érigé le plus précocement, semble-t-il, le gnomon comme instrument d’astronomie (Cullen, 1996; Needham, 1970) dans cette partie du monde. On sait qu’il faisait généralement 8 pieds (soit 1,96 m), mais pouvait atteindre 10 pieds (Gaubil, 1847; Maspero, 1939)22. Il se terminait par une pointe, l’introduction de l’œilleton étant tardive23. Le fait est que l’on possède des annales qui remontent jusqu’au XIe siècle av. J.-C. et qui rapportent des observations solsticiales. Elles n’ont été connues en Europe qu’au XVIIIe siècle, principalement par l’intermédiaire du père Gaubil. Laplace, dans un mémoire célèbre (Laplace, 1809)24, a fait le premier une synthèse des observations les plus anciennes de l’obliquité afin de mettre en évidence sa variation séculaire. Il a justement utilisé les observations rapportées par le père Gaubil en les discutant méticuleusement et en les corrigeant afin de les rapporter au photocentre géocentrique du Soleil. Laplace a sélectionné en tout onze observations (quatre av. J.-C.), dont six sont chinoises, ces dernières étant choisies pour leur précision et également pour leur haute antiquité (Chen, 2002). Il a ensuite comparé l’obliquité déduite des observations à celle donnée par sa formule établie par la mécanique céleste, pour en conclure que « l’ensemble de ces observations établit d’une manière incontestable la diminution successive de l’obliquité de l’écliptique ». L’ancienneté des mesures faites avec un gnomon a donc été un élément déterminant pour valider un résultat important des travaux de mécanique céleste.
Dans le plus important texte de l’astronomie indienne qui date des IVe–Ve siècles, le Surya Siddhanta (« solution du Soleil ») (Chen, 2002)25, un chapitre contient de nombreuses applications liées au gnomon : il s’agit de la résolution de toute une série de problèmes d’astronomie classique à l’aide du gnomon, comme la détermination de la latitude, de la déclinaison du Soleil, etc. Par la suite, le gnomon ne cessa jamais d’être utilisé, notamment en architecture pour déterminer l’orientation d’un site ou d’un temple26.
Le gnomon connu en Inde ses lettres de noblesse au XVIIIe siècle, lorsque le maharaja Sawai Jai Singh II (1688–1744) fonda l’observatoire de Jaipur27 vers 1718 au Rajasthan, le plus remarquable des cinq observatoires indiens érigés par le maharaja. Il est composé d’une vingtaine de cadrans solaires géants, ce qui en fait le plus important observatoire « gnomonique » connu. Il est en effet assez extraordinaire qu’en ce début du XVIIIe siècle, on crée des observatoires sans lunette astronomique, mais uniquement avec des instruments que l’on s’attendrait à trouver dans un observatoire antique ou de la Renaissance (Blanpied, 1975). L’objectif initial du maharaja était, à l’instar de Tycho Brahe, d’améliorer les tables astronomiques existantes. S’il est difficile d’estimer quel a été l’apport de tous ces cadrans et instruments solaires dans l’établissement des tables, il n’en demeure pas moins que cet astronome éclairé a doté l’Inde de plusieurs observatoires magnifiques esthétiquement et imaginé des instruments gnomoniques uniques au monde, de par leur beauté et leur originalité28.
La construction de ces cadrans solaires en maçonnerie et en marbre s’est étalée sur une vingtaine d’années. Leur état de décrépitude était tel qu’au début du XXe siècle ils ont fait l’objet d’une importante restauration, effectuée sous la direction d’un militaire de l’armée britannique et astronome amateur29.
Parmi les instruments astronomiques de Jaipur, les Rama Yantra constituent une version très élaborée du gnomon, une sorte d’avatar esthétique (Fig. 5). Les deux instruments forment des cylindres complémentaires ouverts à l’intérieur pour faciliter les mesures (l’observateur peut ainsi aller faire ses mesures dans le cylindre qui est aussi haut que large). La base est constituée de 12 secteurs de 12° gradués finement (horizontaux et verticaux), séparés par 12 secteurs vides de 18°, formant un cercle de 3,5 m de rayon au centre duquel est installé un gnomon de 8 cm d’épaisseur et de 3,5 m de haut30. L’ombre du gnomon permet de lire à la fois l’azimut et la hauteur du Soleil. Mais l’effet de pénombre est assez considérable et permet au mieux d’obtenir la hauteur du Soleil avec une précision31 de ± 6′.
À côté de cet usage « prestigieux » du gnomon dans un observatoire, l’instrument a continué d’être largement utilisé au XVIIIe siècle en Inde, comme on peut le constater en lisant le Voyage dans les mers de l’Inde de l’astronome Guillaume le Gentil de la Galaisière (Le Gentil, 1779). Bloqué en Inde de 1761 à 1769 pour observer le passage de Vénus devant le Soleil, Le Gentil apprit beaucoup sur l’astronomie tamoule32 ; il rapporte que le gnomon servait aux Brahmanes à orienter les temples, les pyramides et les pagodes par la méthode du « piquet indien », qui consiste à tracer la méridienne par l’ombre la plus courte à l’aide de cercles. Le gnomon servait surtout à déterminer la latitude des villes par l’observation de l’ombre équinoxiale et entrait dans le calcul des éclipses du Soleil et de la Lune.
Le remède aux problèmes liés à la pénombre était déjà connu dans l’Antiquité, comme on l’a vu, puisqu’on munissait le sommet du gnomon d’un œilleton. Ce qui a naturellement débouché sur les méridiennes, c’est-à-dire des instruments où l’on observe une tache de lumière dans de l’ombre. Le sextant astronomique préfigure en quelque sorte les méridiennes occidentales ; construit dans une enceinte close, c’est un instrument géant comportant un arc gradué de grande dimension et orienté exactement sur la direction nord–sud. Un oculus (un œilleton en quelque sorte, que l’on peut considérer comme le sommet d’un gnomon fictif) laisse entrer les rayons du Soleil, qui forment une tache de lumière que l’on peut observer très finement et en déduire la hauteur du Soleil.
Le sextant astronomique de l’observatoire d’Ulug Beg est à cet égard le plus célèbre, avec un rayon d’un peu de plus de 40 m, bien que celui de Rayy soit bien plus ancien (Oudet, 1994). Ces grands instruments perses de l’Islam médiéval servaient notamment à déterminer l’obliquité de l’écliptique, la latitude du lieu, ainsi que, bien sûr, les dates de début des saisons. Leur précision est nettement supérieure à celle des gnomons.
En Occident, il faut attendre le XVIe siècle et surtout le XVIIe siècle pour les méridiennes prennent un essor important (Heilbron, 2003)33. Une des plus célèbre reste sans aucun doute celle que fit construite J.-D. Cassini à Bologne dans la cathédrale San Petronio. Longue de 68 m avec un œilleton placé à 27 m de haut, cette méridienne fut un instrument astronomique remarquable (Paltrinieri, 2001) ; les plus grands astronomes y travaillèrent (Cassini, Riccioli, Grimaldi, Manfredi…). Pendant près de 80 ans, de 1655 à 1736, environ 4500 observations méridiennes y furent effectuées34, ce qui permit de mettre en évidence que l’obliquité avait diminué de 69″ en 77 ans (valeur deux fois trop grande). Car le but principal de ces méridiennes était bien de vérifier que la valeur de l’obliquité diminuait avec le temps. Cette variation séculaire, de l’ordre de 47″ par siècle (valeur moderne), nécessitait des instruments sensibles. Cassini, on le sait, débuta la construction d’une autre méridienne à l’Observatoire de Paris qui fut achevée par son fils Jacques Cassini en 1732. Longue de 32 m avec un œilleton placé à 10 m de haut, cette méridienne très précise fut exploitée pleinement de 1730 à 1755. Il ressort de l’analyse des résultats (Descamp, 2014)35 que l’on obtenait une précision de 10″ dans la hauteur du Soleil, ce qui est remarquable et qui met sur le même pied d’égalité la ligne avec un instrument sophistiqué de l’époque comme le quart de cercle.
On ne peut passer sous silence une autre méridienne, plus tardive, mais aux ambitions encore plus grandes : celle que fit construire l’astronome Lemonier en 1743 dans l’église Saint-Sulpice à Paris (Lemonier, 1746 ; Fig. 6). Celui-ci y fit des observations jusqu’en 1799, en compagnie d’illustres astronomes comme Lalande, Grandjean de Fouchy, La Condamine, Le Gentil. Constituée d’une bande de laiton de 4 mm et longue de près de 40 m au sol et de 10 m au mur, avec deux œilletons placés à 24 m et 26 m, la méridienne de Saint-Sulpice devait, selon son constructeur, permettre de mettre en évidence la nutation qui est voisine de 18″, en observant la tache solaire pendant un cycle complet du nœud lunaire (environ 18,6 ans), ce qui, avec une telle hauteur de gnomon, devait se traduire au sol par presque 3 mm d’écart.

Vue de la méridienne de l’église Saint-Sulpice à Paris. Construite pour mettre en évidence la nutation, cette méridienne se prolonge verticalement sur un obélisque où l’on observait la tache solaire au solstice d’hiver.
The meridian of the St-Sulpice church, Paris. It was designed to characterize the mutation. The vertical prolongation of this meridian is materialized by an obelisk meridian where the solar spot was observed at the twinter solstice.
Malheureusement, aucune de ces méridiennes ne réussit véritablement à réaliser les ambitions que leurs constructeurs leur avaient fixées, essentiellement pour un seul et même problème : l’édifice qui supporte l’œilleton n’est pas stable, de sorte que la mise en évidence de variations très faibles de l’obliquité est anéantie par le lent mouvement de la structure. Ce fut le cas à l’Observatoire de Paris, avec le basculement de la façade vers le sud, et à l’église Saint-Sulpice, avec l’enfoncement du mur, comme Lalande (1764) le supputa assez tôt36.
La fin du XVIIIe siècle sonna le glas des méridiennes, ces « gnomons de lumière » comme on pourrait les qualifier, les astronomes leur préférant à juste titre les quarts de cercle munis de lunettes, dont la précision était bien supérieure.
Au XXe siècle, le gnomon a connu une brève heure de gloire pendant la seconde guerre mondiale : plusieurs constructeurs d’instruments d’aviation ont développé pour l’armée américaine des boussoles solaires, utilisées notamment dans le désert de l’Afrique du Nord, car elles étaient indépendantes des anomalies magnétiques locales. Ces boussoles étaient la reprise d’un cadran solaire analemmatique particulier, développé par le mathématicien français Antoine Parent37 en 1701. Celui-ci cherchait à généraliser un cadran analemmatique horizontal (qui utilise l’azimut du Soleil pour connaître l’heure) sous toutes les latitudes (sauf les latitudes trop boréales). Il a ainsi conçu une boussole qui est une sorte d’abaque composé de courbes elliptiques fermées, couplées à des courbes hyperboliques (Fig. 7). Fonctionnant à l’aide d’un gnomon mobile, cette boussole permet de déterminer l’azimut (et donc le nord géographique) du Soleil en fonction de la date et de la latitude38 avec une précision de 0,3°.
Enfin, au printemps 2018, la NASA prévoit d’envoyer sur Mars l’atterrisseur InSight (Interior Exploration using Seismic Investigations Geodesy and Heat Transport), dont une des expériences majeures repose sur le sismomètre SEIS (expérience française), son but étant d’étudier l’activité sismique de la planète rouge (Fig. 8). Pour des raisons d’exploitation des données, l’orientation du sismomètre doit être connue avec une précision inférieure au degré sur le sol de la planète Mars. Le champ magnétique martien étant trop faible, la seule solution est d’utiliser le système d’accroche du sismomètre comme gnomon afin de déduire de la position de son ombre où est situé le nord géographique martien. Cela suppose de connaître les coordonnées géographiques de l’atterrisseur (latitude et longitude martiennes) et de disposer d’une théorie du mouvement du Soleil pour un observateur martien39. Il s’agit là de l’exploitation d’une particularité classique du gnomon, à savoir qu’à un instant donné, la mesure de l’azimut de l’ombre permet de déterminer le Nord ; autrement dit, on va utiliser le gnomon comme une boussole martienne. Une mire a été placée au pied du « gnomon » afin de mesurer l’azimut de l’ombre. En vérité, c’est un gnomon un peu spécial, car sa forme est loin d’être idéale pour relever la position de l’ombre !
Il est assez amusant et plutôt inattendu que, dans une expérience scientifique faisant appel à une très haute technologie – qui plus est se déroulant sur une autre planète du système solaire –, un instrument aussi simple et rudimentaire qu’un gnomon soit utilisé.
Remerciements
Cet article a été invité dans le cadre des prix 2017 de l’Académie des sciences (prix Paul Doistau – Émile Blutet). Il a été expertisé et approuvé par Françoise Combes et Vincent Courtillot.
This paper has been invited in the frame of the 2017 prizes of the French Academy of Sciences (prix Paul Doistau – Émile Blutet). It has been reviewed/approved by Françoise Combes and Vincent Courtillot.
1 Hérodote, Histoire, Livre II, chap. 109. Sur le gnomon au fil des siècles et dans différentes cultures, voir Gandz (1930–1931).
2 Ptolémée, Almageste, Livre III, chap. 1, traduction en anglais de G. J. Toomer, Londres, 1984, p. 139.
3 En dehors du méridien, la hauteur h du Soleil s’obtient par : sinh = sinϕ sinδ + cosϕ cosδ cosH, où δ est la déclinaison du Soleil et H son angle horaire. Si H = 0°, on a bien h = 90° – ϕ + δ. Principe de fonctionnement du gnomon pour la hauteur méridienne du Soleil. Principle of the gnomon workings for calculating the Sun meridian height.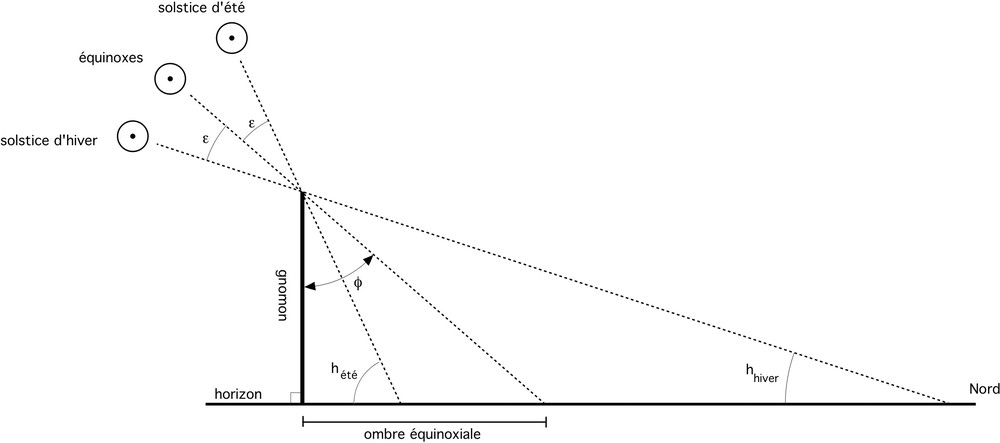
4 Almageste, livre II, fin du chapitre V. Ptolémée écrit que l’instant de l’équinoxe n’est pas bien déterminé, mais sans donner la raison de cette mauvaise détermination, alors que pour le solstice d’été il précise que les extrémités de l’ombre ne sont pas bien distinctes. Dans l’Almageste, et déjà du temps d’Hipparque, les équinoxes sont observés à l’aide d’une armille équatoriale (Livre III, chap. 1) (Pedersen, 2011).
5 Almageste, livre III, chap. 1. Notons que l’usage de la fonction tangente n’étant pas connu dans l’Antiquité, Ptolémée décrit une méthode utilisant une table des cordes pour obtenir la hauteur (ou son complément la distance zénithale) à partir de la longueur de l’ombre : voir Brummelen (2009) pour l’introduction de la fonction tangente chez les Arabo-Perses en utilisant l’ombre du gnomon.oir Rome (1943). Il est à noter que, pour placer correctement l’armille, il faut, d’une part, l’orienter selon le méridien du lieu, mais également la placer dans le plan de l’équateur céleste, ce qui suppose de connaître la latitude du lieu. L’inclinaison de l’équateur céleste était obtenue, d’après Théon d’Alexandrie, en prenant le point situé à mi-chemin entre les deux hauteurs du Soleil aux deux solstices. Une fois bien mis en place, on observe à quel instant (si le phénomène a lieu le jour) la face nord de l’armille commence à être éclairée, ce qui signifie que le Soleil franchit l’équateur.
6 On trouvera une étude approfondie du problème de la variation d’azimut au cours de l’année dans Savoie (2007).
| Variation azimut en 1 min | Latitude 30° | Latitude 48° |
| Solstice d’été | ≈ 2° | ≈ 0° 33′ |
| Solstice d’hiver | ≈ 0°17′ | ≈ 0° 15′ |
7 Néanmoins, on peut contourner le problème de la variation rapide de l’azimut en été en utilisant la méthode du « piquet indien ». C’est sans doute ce qui a été mis à profit le 21 juin 1667 lorsque les astronomes-académiciens ont tracé la méridienne sur laquelle allait être bâti l’Observatoire de Paris. La méthode du « piquet indien » (appellation d’origine arabe selon Sédillot, cf. infra) devait être bien connue dans l’Antiquité ; sa description détaillée pour l’orientation d’une armille est donnée clairement pour la première fois dans le chapitre III des Hypotyposes de Proclus au Ve siècle (traduction due à Alain Segonds†, correspondance personnelle) : « Pour ce qui est de la méridienne, on la détermine ainsi : on dresse perpendiculairement à la plaque en question un gnomon et l’on trace autour du pied du gnomon pris comme centre un cercle ; puis nous observons à quel moment dans le matin l’extrémité de l’ombre du gnomon tombe sur le cercle, et nous marquerons exactement ce point ; derechef, [nous observons] quand cela se produit dans l’après-midi et, de la même façon, nous marquerons ce nouveau point. Puis, en utilisant une règle parfaitement exacte, nous tracerons une droite qui part du point déterminé le matin et va jusqu’à celui qui a été déterminé l’après-midi ; ensuite, nous partagerons en deux parties égales cette droite et, en utilisant la même règle, nous mènerons à partir de l’intersection une droite jusqu’au centre du cercle et nous la prolongerons jusqu’à la circonférence du cercle. Et ainsi l’on aura obtenu une ligne méridienne, qui mérite absolument son nom, parce que tous les jours, à midi, l’ombre produite par les gnomons tombe sur cette ligne ».
8 Voir Savoie (2007). On démontre qu’au voisinage du premier vertical en été, l’azimut du Soleil varie très peu au contraire de sa hauteur qui file rapidement.
9 Sans compter que pour les latitudes basses, la longueur de l’ombre est très courte (environ 11,5 cm pour une latitude 30° avec un gnomon de 100 cm), ce qui ne facilite guère les mesures.
10 Sur les nombreux essais effectués par des observateurs sur la distinction de l’ombre pure et de la pénombre, voir Ferrari (2010).
11 J.-B. Delambre (1817) attribue à cet effet de pénombre la sous-estimation par Ptolémée de la latitude d’Alexandrie qu’il prend égale à 30° 58′ (valeur moderne = 31° 12′). C’est aussi ce que pensait Laplace (cf. infra dans son mémoire sur la diminution de l’obliquité).
12 Il faudrait tenir compte en toute rigueur de la parallaxe du Soleil (qui atteint au maximum 9″ à l’horizon), qui dépend de la hauteur de cet astre au-dessus de l’horizon. Avec les méridiennes, beaucoup plus précises que les simples gnomons, les astronomes prenaient en compte cette quantité dans la réduction de la hauteur apparente du Soleil. On obtient la hauteur vraie hv de celui-ci (donc le photocentre solaire géocentrique) à partir de la hauteur apparente mesurée hap par : hv = hap – réfraction + parallaxe – demi-diamètre solaire. Voir par exemple La Hire (1735), à propos de qui il est à noter qu’il insère en pp. 183–186 un chapitre sur la construction et l’usage du gnomon. En fait, le gnomon est encore en usage dans l’astronomie française du début du XVIIIe siècle, même s’il est réduit à un instrument de seconde zone pour la mesure de la latitude ; voir par exemple La Connaissance des temps (1702), qui préconise l’usage d’un gnomon à œilleton sur un sol parfaitement nivelé.
13 On vérifie ainsi qu’à 40° de latitude, un gnomon de 100 cm s’écartant de 5 mm de la verticale (z = 0° 17′) entraîne une erreur d’environ 6′ dans l’obliquité et de 9′ dans la latitude en opérant avec des hauteurs solsticiales. Aux équinoxes, on commet une erreur voisine dans la latitude.
14 Cléomède, Théorie élémentaire, trad. et notes R. Goulet, Vrin, Paris, 1980, pp. 124–125.
15 Par « gnomon amélioré », il faut entendre un cadran solaire sphérique dont le sommet du gnomon occupe le centre : on lit directement l’angle dans la concavité. Cléomède précise bien qu’Ératosthène fait ses mesures aux deux solstices.
16 Ces rapports ne sont pas tous corrects; le meilleur exemple est celui donné par Strabon dans sa Géographie, I, 1, 4, qui s’interroge sur le fait que Marseille est à la même latitude que Byzance. Voir également (Szabo et Maula, 1986).
17 Vitruve, De l’architecture, Livre IX, texte établi, traduit et commenté par J. Soubiran, Les Belles Lettres, Paris, 1969, p. 26 (chap. VII, 1). On retrouve certaines valeurs dans l’Histoire naturelle de Pline.
18 Si y est la longueur de l’ombre et a la hauteur du gnomon, on a y/a = tanϕ. Si a = 1 et y = 8/9, on a directement, de façon moderne, tanϕ = 8/9.
19 Sur les controverses liées à cette méridienne, voir Bonnin (2015). Rappelons que jamais les obélisques n’ont été utilisés par les Égyptiens à des fins astronomiques ou horaires.
20 Pline, Histoire naturelle, Livre 36, chap. 15.
21 Manitius ne donne hélas pas sa source. L.-A. Sédillot (1841) attribue l’invention de l’œilleton surmontant un gnomon aux Arabes, sans être convaincant. La traduction donnée par J.-J. Sédillot (1834) contient quantité de problèmes relatifs à l’usage du gnomon au XIIIe siècle par al-Marrakuchi.
22 H. Maspero (1939) écrit : « Il semble que l’on ait commencé par employer des gnomons de 10 pieds de hauteur ; mais ce nombre, qui ne rentrait pas facilement dans le calcul du triangle rectangle, fondé sur les rapports des nombres 3, 4 et 5 et de leurs carrés, fut bientôt abandonné pour 8, nombre double de la hauteur du triangle rectangle dans le triangle étalon : le gnomon de 8 pieds devint le gnomon classique des astronomes chinois et sauf quelques changements éphémères, il le resta jusqu’à la dynastie mandchoue, époque où les jésuites firent adopter le gnomon de 10 pieds pour entrer dans le système décimal. Au temps des Han et pendant près de 20 siècles, on n’employa normalement que le gnomon de 8 pieds ».
23 Voir Maspero (1939), p. 273. Maspero précise que l’attribution aux Chinois du gnomon à trou dans l’Antiquité est une erreur qui remonte à E. Biot, qui a pris un tube de visée destiné à mesurer le diamètre du Soleil pour un gnomon à trou.
24 Laplace a donné un résumé de ses calculs dans son Exposition du Système du Monde. La liste publiée deux siècles avant par Riccioli dans son Almagestum novum paru à Bologne en 1651, chap. XXVII, p. 162, ne commence qu’à Aristarque.
25 Translation of the Surya-Siddhanta, with notes and an appendix by Rev. Ebenezer Burgess, New Haven, 1860, chap III.
26 C’est le cas par exemple du Mayamata, traité d’architecture écrit aux alentours de l’an 1000 au Sud de l’Inde : voir Dagens (1970) ; Filliozat (1951).
27 Le texte le plus important sur Jaipur est dû à Virenda Nath Sharma (1995). Il faut également lire l’ouvrage de celui qui a restauré l’observatoire de Jaipur au début du XXe siècle, à savoir Garret (1902)A. ff. Garrett (1902). Ce lieutenant anglais fut assisté par l’érudit indien Chandradhar Guleri.
28 On trouvera une étude approfondie de certains des cadrans solaires de Jaipur dans Savoie (2014).
29 L’observatoire de Jaipur a été restauré en 1870, puis à nouveau en 1901–1902 par A. ff. Garrett. Sur cette restauration et les problèmes qu’elle pose, voir Virenda Nath Sharma (1995), pp. 149–151. On ne perdra jamais de vue que les instruments visibles aujourd’hui dont des reconstitutions. Voir aussi Kaye (1918).
30 Dans le deuxième Rama Yantra c’est le contraire : on a 12 secteurs de 18̊ séparés par 12 secteurs « vides » de 12°. Le même instrument a été construit par Jai Singh à l’observatoire de Dehli. Un des deux Rama Yantra de l’observatoire de Jaipur en Inde. On voit ici l’ombre du sommet du gnomon se projeter sur la partie cylindrique verticale. L’effet de pénombre est considérable et affecte la précision lors de la mesure de la hauteur du Soleil. One of the two Rama Yantra of Jaipur Observatory, India. One can see projection of the gnomon apex on the vertical cylindric part. But the effect of the penumbra is important and affects the precision of the Sun height measurement.
31 Ordre de grandeur d’après Virenda Nath Sharma (1995), pp. 81–82. En fait, la précision tombe en dessous du degré pour certaines hauteurs du Soleil. On prétend que pour limiter l’effet de pénombre, il suffit de placer un cheveu perpendiculairement à l’ombre, de telle sorte qu’on puisse lire, à l’intersection de la pénombre du gnomon et de l’ombre du cheveu ou d’une tige mince, la bonne valeur. Pour avoir expérimenté in situ cette technique sur plusieurs instruments de Jaipur, je peux témoigner que la marge d’incertitude demeure malgré tout assez élevée et que l’utilisation d’un cheveu en guise de réticule accentuant l’ombre diluée n’est pas toujours probante. L’instrument le plus précis de Jaipur reste la méridienne-sextant, peu connue du public, située dans la structure latérale du grand cadran équatorial, et qui fonctionne avec un œilleton.
32 Le Gentil décrit longuement les méthodes des Brahmanes et commente les inconvénients bien connus du gnomon dans la détermination de la latitude.
33 Il s’agit d’un ouvrage magistral, le plus complet qui existe sur les méridiennes. Au XVIe siècle, le gnomon est encore considéré comme le symbole d’une astronomie « fondamentale », comme on peut le voir sur des frontispices. Ceux de G. J. Rheticus par exemple comportent presque tous des obélisques ou des gnomons : ses très brèves Tabulae Astronomicae parues à Wittenberg en 1542 sont illustrées par un gnomon avec ses trois ombres équinoxiales et solsticiales. Ses Ephémérides de 1550 parues à Leipzig (premières éphémérides coperniciennes) sont illustrées par un obélisque qui est strictement le même que celui de son Canon Doctrinae triangulorum paru un an plus tard dans la même ville. Quant à son ouvrage posthume, Opus palatinum de triangulis paru en 1596, il est magnifiquement orné de deux obélisques surmontés d’une sphère.
34 On trouvera l’ensemble des observations effectuées avec cette méridienne dans Manfredio (1736). Chaque jour où cela était possible, l’observateur notait l’aspect du ciel ; il notait également le diamètre apparent du Soleil et sa distance zénithale à midi vrai.
35 Cet article fait un point très complet sur la précision des méridiennes en général.
36 Lalande part du fait que l’obliquité mesurée en 1763 avait la même valeur qu’en 1745. Dans le même volume, voir le résumé de Grandjean de Fouchy pp. 130–131. Sur la comparaison des hauteurs solsticiales d’hiver, observées en 1762 et 1764, avec celles qui ont été vues à l’obélisque du gnomon de Saint-Sulpice en 1743 et 1744, voir également Histoire de l’Académie royale des Sciences (année 1765), Paris, pp. 75–77 (imprimé en 1768). On y décrit notamment la méthode de mesure : « M. le Monnier employa pour ces observations la même méthode qu’il avait mise en pratique pour celle du solstice d’été, il marqua sur le marbre avec du crayon, pendant quelques jours, devant et après le solstice, la trace des deux bords supérieur et inférieur de l’image, et calculant ensuite la déclinaison par la distance du Soleil au solstice, il en tira la position du point solsticial. »
37 La note technique proprement dite de A. Parent (1666–1716) est manuscrite et se trouve dans les Procès-verbaux de l’Académie royale des Sciences, 1701, folios 194–207 et folios 415 à 421 (disponible sur Gallica, http://www.gallica.bnf.fr). Il s’agit d’une description géométrique d’un analemmatique rectilinéaire. Sur l’analemmatique de Parent, voir Janin (1975).
38 Voir par exemple (War Department, 1943). Compas solaire de type Abrams utilisé pendant la Seconde Guerre mondiale. L’ombre du gnomon permet de déterminer la direction du nord géographique en fonction de la date et de la latitude. Abrams-type solar compass used during the Second World War. The gnonom penumbra allows determining the geographic North according to date and latitude.
39 L’atterrisseur devrait être situé un peu au-dessus de l’équateur martien, donc dans une zone « intertropicale ». En décembre 2018, le Soleil sera sous l’équateur martien, l’ombre du gnomon sera donc dirigée vers le nord à midi vrai. Vue artistique de l’atterrisseur Insight sur la planète Mars. On voit au premier plan le sismomètre (recouvert d’une protection). Artistic picture of the Insight undercarriage on the planet Mars. One can see, in the foreground, the seismometer covered with its protective lid.


