1 Introduction and key concepts
Thermodynamically favored reactions of small organic molecules, such as combustion, are generally quite slow at room temperature. They must proceed over large activation barriers during bond-breaking and -making. Protein folding is generally much less favored thermodynamically (protein function often requires proteins to be flexible and at the brink of stability), yet folding is fast at room temperature. In the test tube, denatured states of natural proteins last only for milliseconds to hours under conditions favorable for folding, in contrast to the long shelf life of organic compounds.
So-called ‘water-soluble’ globular proteins really fold in a crowded cellular environment in vivo; the largest ones are aided out of misfolded states by chaperones. Yet these proteins unfold and refold spontaneously many times during their lifecycle, and simple mass-action considerations show that cells do not contain enough chaperones to take care of all folding [1]: hence Christian Anfinsen's seminal discovery that the amino acid sequence generally suffices to guide folding of small proteins or protein domains [2], after ribosomal synthesis is complete and without helper-molecules.
The high speed of protein folding, compared to most barrier-controlled chemical reactions, is due to the near-cancellation of enthalpic and entropic contributions to the free energy during the folding process. Proteins can make energy-lowering contacts and become compact in small steps, so no large mismatch appears en route to the folded product. Small barriers in the free energy of folding are distributed along several reaction coordinates, rather than being lumped into one local high-energy barrier. Energy-landscape theory, a statistical-mechanical treatment of protein folding, predicts that this cancellation could be nearly perfect [3]. Such proteins would fold downhill in free energy, on timescales as short as about 0.5 μs for a bundle of three helices.
Natural proteins are not quite that fast, but could proteins be engineered to verify that downhill folding is possible? Fig. 1 shows that the smallest and fastest known folders indeed accomplish the job in about a microsecond. There is kinetic experimental evidence that the folding rate of these fastest folders is limited only by a slight roughness of the free energy surface, with a root-mean-square value kJ mol−1 [4].

Correlation of the folding rate with fold complexity (quantified by absolute contact order [50] and illustrated by three folds of increasing complexity). The red line shows the average logarithm of the rate for natural proteins and constructs not specifically engineered for speed from [50]. The black line estimates the folding speed limited only by fold complexity; it decreases exponentially with increasing fold complexity [7]. An alternative model based on homopolymer theory posits a ‘softer’ linear decrease of the speed limit with sequence length [36]. The molecular rate leading to the native state has been observed directly for (3) [14] and for an engineered WW domain [24]. Other speed limit candidates include a single helix (1) [51], the three helix bundle α-3D (2) [26], and the 20 residue trp-cage, observed at 4 μs, with a speed limit probably near 0.5 μs based on our plot [52]. Speed limits estimated from fast-forming intermediates include apomyoglobin (4) [46] and phosphoglycerate kinase (5) [28].
Since downhill-folding proteins can be engineered, a transition state barrier is not a physicochemical requirement for the folding process. What then about the majority of proteins in Fig. 1, whose folding rates lie below the speed limit? Such proteins are said to be ‘energetically frustrated’ [3]. In addition to the speed limit set by the purely topological requirements of matching up multiple elements of secondary structure in key tertiary contacts, their speed is hampered by non-native contacts and changes in protein–solvent interactions, such as squeezing water molecules out of the hydrophobic core. Such undesirable interactions (from the vantage point of efficient folding) create roughness on the energy landscape.
If barriers are not inherently required by the physics of folding, perhaps their roots are to be found in constraints imposed by evolution [5]. Four such constraints, resulting from the interplay of physics with evolution of the amino acid code, of the protein synthesis machinery, for protein function, and against protein aggregation, are considered here.
1. The genetic code evolved early from RNA-peptide interactions, but it is now nearly ‘frozen’. Natural proteins are made of 20 natural amino acids, with additional residues and post-translational modifications occurring in different organelles and organisms. A finite amino acid alphabet prevents perfect packing of protein cores. Proteins are not like three-dimensional jigsaw puzzles whose pieces fit together perfectly. An analysis of the mass-dimension1 of proteins has shown that it is only about 2.5, not 3 [6]. Proteins are filled with gaps, niches and crevasses of varying size. An imperfect fit means that alternative non-native fits cannot be completely eliminated, and manifest themselves as roughness on the energy landscape. This causes the small roughness of ca. observed in downhill folding experiments of peptides and small proteins [4,7]. Such ‘residual energetic frustration’ is of great interest in protein structure prediction: fitting the core together requires more than just two-body interactions among side chains (each sidechain typically contacts 2–4 others in the core); otherwise current ab initio structure-prediction algorithms, based largely on site-specific and two-body energy terms, would already be successful at predicting accurate native structures, whereas they predict approximate folds [8]. One might say that for small proteins with small cores, folding is nearly a solved problem, but for slow folders, the devil is in the details of multi-body contributions to the free energy surface.
2. Another example of an evolved but now frozen boundary condition is the way proteins are synthesized on the ribosome in vivo: protein synthesis requires much longer than microseconds, so proteins cannot initially fold very rapidly. One could therefore argue that there is no evolutionary pressure for fast folding. By itself, this argument fails: a typical protein, folding in 1 s with an equilibrium constant of 1000 and functioning hours to days before degradation, is wholly or partially unfolded thousands of times, for a total of about 1–100 s during its existence, so post-translational folding is only the first of many folding events. Cells do not contain enough chaperonins to take care of all cellular proteins, so many proteins have to refold without specific assistance before they aggregate or are ubiquitinated/degraded. Paradoxically, the situation may be worse for highly stable very fast folders because they go through the unfolding-refolding transitions far more frequently [9]. The cytoplasm is a densely packed environment and may ‘jam’ such events, but it may also trap proteins once they unfold, favoring proteins that do not fold – and therefore unfold – too easily.
3. The most important currently evolving source of energetic frustration is probably protein function. Proteins evolve for function, not just for thermodynamic and kinetic ‘foldability’, and the sequence requirements for function can be incompatible with efficient folding [5]. Function affects folding in many ways. Long loops required for binding will have a large entropy deficit and can slow down folding [10]. Charged or polar residues and water pockets in the protein core may be required for the binding of substrates or prosthetic groups, reducing the core's hydrophobicity, a major driving force for folding [11]. Glycines are incorporated into structures to increase flexibility, such as in DNA-binding proteins that must flex upon binding; the increased flexibility of glycine-containing protein backbones favors the unfolded state entropically [12,13]. This suggests that shortening of loops and replacement of functional sidechains by more secondary/tertiary structure-friendly sidechains could speed up the folding process, at the expense of function.
4. To function, many proteins must first of all remain folded. Paradoxically, very fast-folding proteins are particularly prone to aggregation despite their increased stability because they lack a large barrier that provides a penalty for partial unfolding [14]. This is a problem because the propensity for forming extended structure locally upon partial unfolding is innate to polypeptides even in their monomeric form [15]. Thus barriers may have evolved to prevent proteins from making excursions into ‘forbidden territory’ [16]. Crowding could enhance such barriers to unfolding further. Although an example remains to be demonstrated, this concept predicts that some proteins unfolded in the test tube under ‘physiological conditions’ may in fact be folded in vivo. An analogous idea from physics is that spheres will freeze into a lattice (like stacked oranges) if confined to a sufficiently small volume, even if the energy between them is purely repulsive [17].
Of course, evolution against aggregation or for function must operate within the constraints imposed by the physical properties of the polypeptide chain and cell environment. The observed distribution of folding barriers is thus a trade-off between full optimization for folding (which yields downhill folders without barriers at the top of Fig. 1), and optimization for function, yielding proteins that fold slowly for their size.
2 Downhill folding
During the last 10 years, the energy-landscape theory has moved from outsider status to central paradigm of protein folding. For many proteins, the theory predicts the same kind of kinetics as activation barrier models [18], namely:
| (2.1) |
Landscape theory makes a key prediction that can be tested by very fast folding of engineered proteins: that the entropy and enthalpy contributions can cancel under ideal folding conditions (Fig. 2) [3]. In this picture, when all stresses against folding (denaturants, ‘bad’ sidechains, high temperature, etc.) are removed, the protein folds ‘downhill’ without any barriers greater than 1–2RT (‘type-0’ folding scenario). When stresses are applied, the cancellation is less perfect and the protein must cross a barrier (‘type-1’ folding scenario). Without a barrier, the activation energy disappears from Eq. (2.1), and the prefactor can be observed directly, without resorting to extrapolated Arrhenius plots [14].
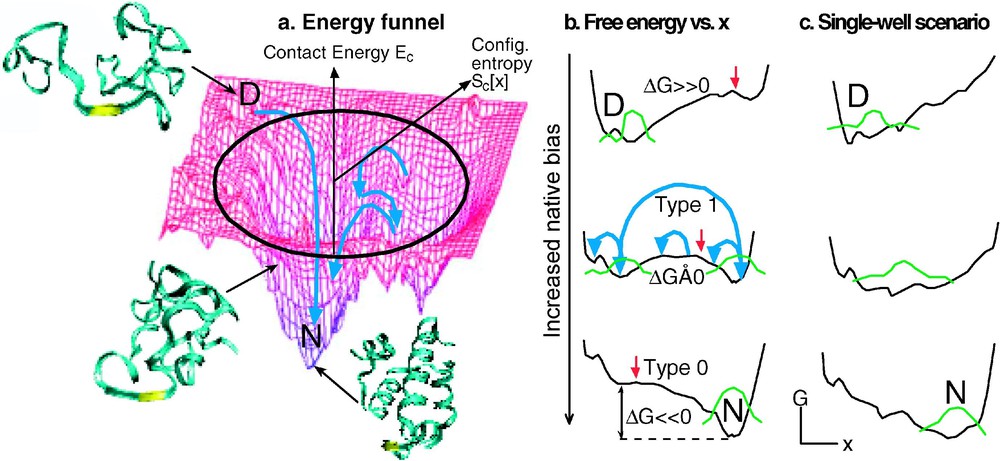
(a) Energy or enthalpy funnel, with unfolded conformation at high energy, compact globule at moderate energy, and native state at low energy. The radial coordinate is proportional to the logarithm of the number of protein conformations at a given energy (the configurational entropy, which is higher at higher energy). The angular coordinate symbolizes the many other folding coordinates. (b) Free energy plots reduced to 1 reaction coordinate (2–5 are probably needed for a realistic description of folding). The bias towards the native state increases from the top to the bottom. The middle plot corresponds to most natural proteins (type-1 or barrier-limited folding, the green protein population is split into two states). The bottom plot corresponds to the extreme native bias possible with engineered proteins under highly stabilizing solvent conditions (type-0 or downhill folding). The large blue arrow corresponds to slow, exponential type-1 folding; the small blue arrows correspond to fast diffusive motions that lead to type-0 folding. Note that the free energy surface retains roughness even in the downhill case, caused by unavoidable frustration of folding by the finite amino acid alphabet and physical constraints. (c) Single-well downhill folding scenario at all biases towards the native state, as discussed by Muñoz and coworkers [40]. Unlike (b), in this case strong deviations from cooperative thermodynamics are expected.
Let us consider how downhill folding arises from the energy-landscape picture of folding. Fig. 2a shows a 3-D projection of a ‘folding funnel’. A folding funnel is a plot of the enthalpy against configurational entropy. Both decrease as more native contacts are made during folding: the enthalpy because favorable contacts are made during folding, the configurational entropy because the protein becomes more compact and less flexible. From the funnel picture, the free energy of reaction
| (2.2) |
1. Landscape theory, combined with linear response theory, predicts that downhill folding shows up gradually when a protein is engineered to fold increasingly fast [14]. This is illustrated in Fig. 2b. The natural protein ensemble explores the free energy surface on the time scale of the prefactor (short blue arrows), but it must be activated to cross over the barrier, which occurs with much slower rate coefficient k (long blue arrow) [7]. The slower process washes out the faster process; only the rate k can be measured, yielding reaction kinetics with a single exponential decay . In terms of classical transition-state theory, we would say that the activated protein is in equilibrium with the native and denatured states because is so much faster than k. As the native bias increases and the barrier decreases, k approaches , and the equilibrium assumption of transition state theory breaks down. In that case, protein population diffusing with rates on the order of can be observed directly. This has been observed experimentally for α-helical and β-sheet proteins especially engineered for a strong native bias (e.g., Fig. 3a). The time scale was found to be ∼1 μs for a five-helix bundle [14], and ∼3.5 μs for a triple stranded β-sheet [24]. The latter is in good agreement with the folding rate for isolated β-hairpins [4,25]. Experiments by Gai and coworkers show that a 3-helix bundle can fold even faster, setting an upper limit of 0.5 μs on for that case (Fig. 1) [26]. The merger of the activated and prefactor time scales, when full downhill folding is achieved, has recently been observed for lambda repressor [7], as has the transition from type-0 to type-1 folding when denaturant is added or the temperature is raised (Fig. 2b) [21].
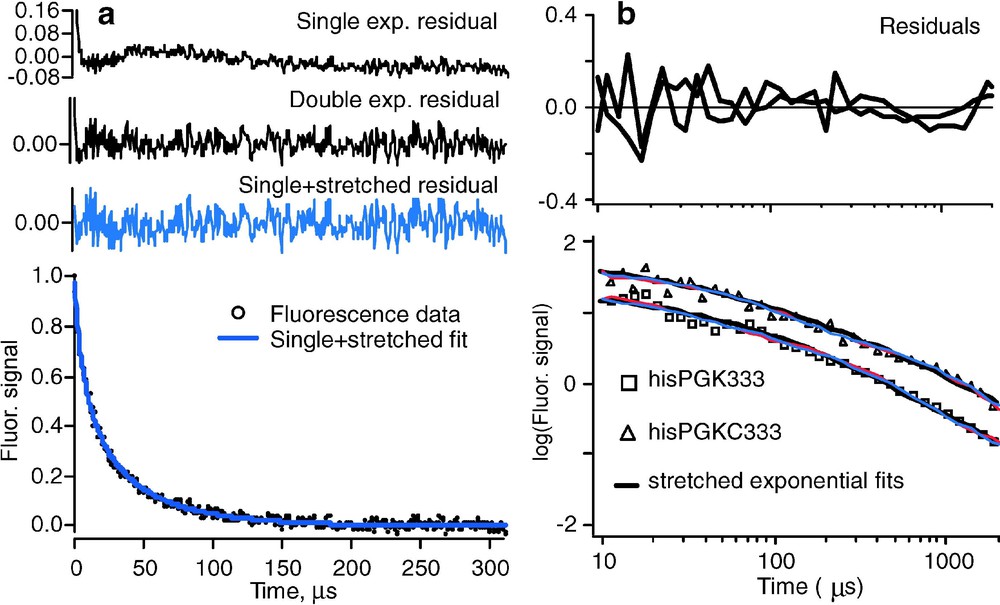
(a) Folding kinetics of , showing strong deviations from single exponential kinetics [21]. At higher temperature, or for less stable mutants of the same protein, activated barrier single exponential kinetics are observed [14]. (b) Nonexponential refolding kinetics of phosphoglycerate kinase and its C-terminal domain from the cold denatured state, showing nonexponential kinetics independent of the presence of the N-terminal domain [28]. In both experiments, fluorescence-detected temperature jumps were analyzed.
2. According to Eq. (2.1), folding is an orderly process with a single rate coefficient k. Downhill folding on a multidimensional rough free-energy landscape need not be so orderly: different proteins can take different paths and the protein population is not herded through a single ‘mountain pass’ (transition state). Although the prefactor roughly describes the time scale for downhill folding ‘at the speed limit’, such fast folding is no longer necessarily described by a single exponential function . Nonexponential decays indicative of such a heterogeneous folding process were observed by Sabelko et al. and later Osváth et al. for downhill formation of a compact globular state during refolding of phosphoglycerate kinase from a cold denatured state (Fig. 3b) [27,28]. In that work, use was made of the principle, illustrated by the red arrows in Fig. 2, that the folding barrier moves towards the native state when the native state is stabilized. This shift can be used to map cold denatured populations of proteins into the barrier region from where they fold downhill. The kinetics can be fitted to a stretched exponential function with (Fig. 3b). Maximum stretching occurs at the temperature of maximal stability, and single exponential activated kinetics occur under more denaturing conditions, in agreement with a transition from downhill (type-0) to barrier-limited (type-1) folding when the native state is destabilized [3]. More recently, the downhill phase of a mutant folding to the native state has also been found to fit a stretched exponential, with (Fig. 3a) [21]. The experimental observations could be roughly reproduced with a 1-dimensional free energy surface, but a surface with at least two reaction coordinates provided better agreement. It should not come as a surprise that one coordinate is not sufficient to describe folding: protein folding is neither as simple as organic molecule bond breaking/making (where a single reaction coordinate often suffices), nor is it as cooperative as water freezing (where one reaction coordinate, called ‘order parameter’, also suffices, despite the very many molecular coordinates involved).
3. Other types of experiments also have set limits on . Single molecule FRET experiments have been able to set an upper limit on of ca. 200 μs, compatible with the direct measurement in 1 [29,30]. The original experimental estimate of the folding speed limit (1 μs, close to the direct observation discussed above) was made by Eaton and coworkers based on 40 μs contact formation rates in denatured cytochrome c, extrapolated to denaturant-free solution [31]. Several groups have carried out extensive measurements of loop formation, an elementary process which sets a lower limit on folding times of 10–100 ns, depending on loop length [32–34]. Good models for the loop length dependence exists; the one by Szabo, Schulten and Luthey-Schulten seems to fit the size-dependence best [35]. Measurements of secondary structure formation by several groups have pushed the lower limit of helix formation to 50 ns, and for β-hairpins to 700 ns, as absolute limits on the folding rate [4,36]. Muñoz and coworkers observed collapse, another limiting factor for folding on the 100-ns timescale [37]. Real proteins of course have to do all those things (form secondary structure, form loops, collapse, etc.) to fold, and even in the best designed protein small barriers (∼1RT, too low for activated rate theory to work) remain as discussed earlier. This is why the measurements on downhill-folding proteins yield minimal folding times longer than 0.5 μs.
4. Another prediction of the energy-landscape model is that different rates are obtained by different spectroscopic probes during downhill folding. This is illustrated in Fig. 4. When there is a barrier, protein populations are small in the region along x where probes such as infrared, circular dichroism, fluorescence, or NMR spectroscopy switch from their denatured to their native signatures. Thus the observed signals are a linear combination of only the folded and unfolded state signals, and they are probe-independent. When landscape roughness is the only barrier left, kinetics are no longer homogeneous, and different results are observed with different probes. This has been confirmed for peptides whose free energy surface computed by MD is rough and flat [38], as well as for designed downhill folders [21]. When there is no substantial barrier in the energy landscape, the residual ‘roughness’ can be quantified directly. Direct measurements on a small peptide yield values of , which agrees with the roughness computed from replica-exchange molecular dynamics simulations [4,38]. Fitting a Langevin model to experimental data for a five-helix bundle also yields [7].
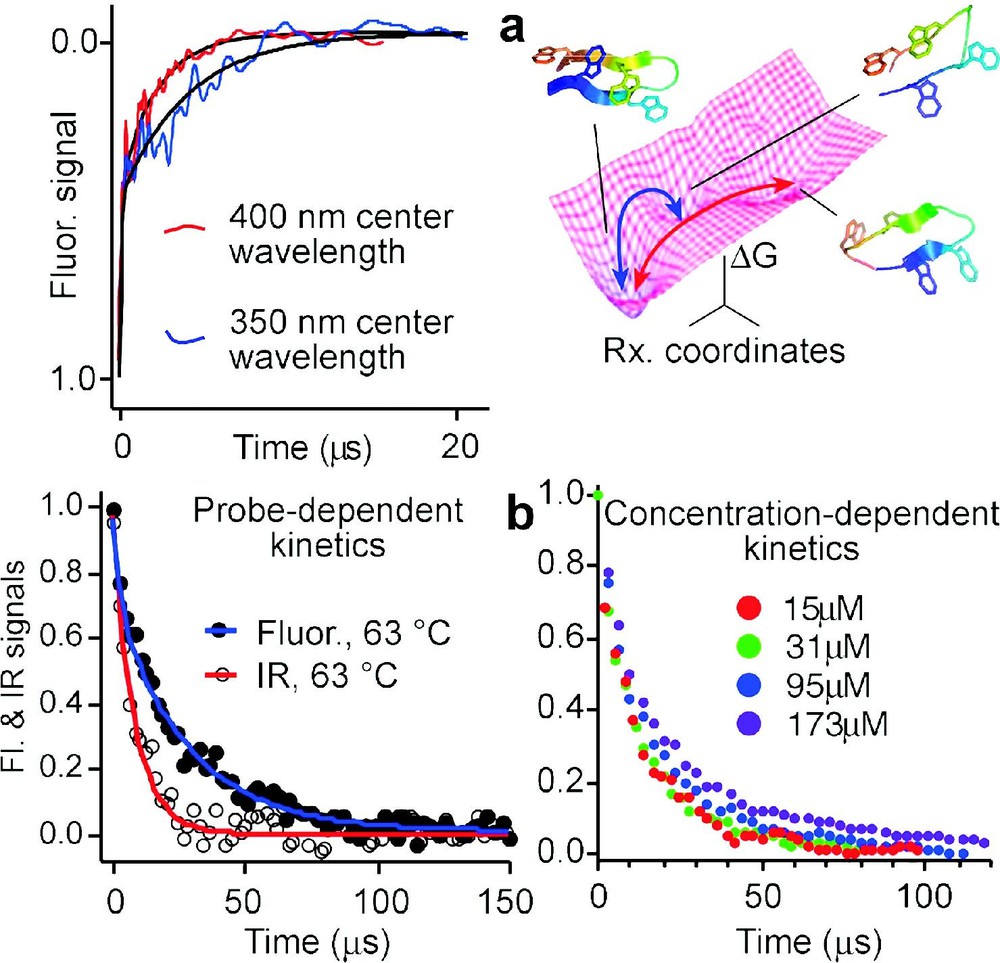
Proteins or peptides folding on a rough downhill free energy surface do not have a single well-defined rate: (a) Difference in relaxation rates observed for the beta hairpin peptide trpzip2 at two different fluorescence wavelengths [4], and two possible paths on the free energy surface with structures computed by molecular dynamics [38]; (b) Infrared and fluorescence spectroscopy yield different folding/unfolding kinetics for the helix bundle Q33Y mutant at 63 °C, and kinetics of the D14A mutant are aggregation-dependent above 30-μmol concentration (see Fig. 5 for a comparison of the two). Slower folding mutants, which fold over an activation barrier, show neither a wavelength dependence nor transient aggregation below 200 μmol.
5. A thermodynamic criterion for a more extreme type of downhill folding than the ‘type-1 under stress/type-0 without stress’ scenario of energy-landscape theory has been proposed by Muñoz and coworkers [39]. In the original energy-landscape picture, proteins in presence of a stress (e.g., high temperature, or an unfavorable mutation) will fold over a small barrier, and type-0 folding can occur only when the stress is reduced (e.g., by lowering the temperature towards the point of minimum free energy). If instead the protein retains a single well that simply shifts along x towards the denatured state when a stress is applied, two separate thermodynamic states never occur (Fig. 2c) [40]. As a result, different spectroscopic probes will not match during denaturation even at high stress, the denaturation transition will be much less steep, and ‘baselines’ before and after the unfolding transition will be substantial. Data on the small protein BBL fit this kind of picture [39]. It may turn out that very small proteins and peptides with only a few hydrophobically buried residues can follow such a single well scenario, while larger downhill-folding proteins such as engineered make a type-0–type-1 transition when stress is applied.
6. A final kinetic consequence of downhill folding is the unusual folding Arrhenius plot ( vs. ) observed in very fast folding proteins (Fig. 5). As mentioned earlier, proteins folding over a barrier usually exhibit a maximum in the folding rate, giving the Arrhenius plot a ‘parabolic’ appearance, in contrast to the straight line of negative slope expected for most small molecule reactions. This is attributed to the hydrophobic effect, which acts as a major driving force during folding. When hydrophobic amino acid side chains are in contact with water, the water molecules become more ordered; polar/charged side chains induce less order, as seen in neutron scattering experiments. Burial of hydrophobic sidechains thus lowers the free energy of the protein–solvent system, inducing a rapid collapse of the polypeptide chain under conditions favoring the native state. In very fast folders, the formation of secondary structure and diffusion processes establishing the correct fold compete with collapse, leading to a loss of this ‘parabolic’ signature [7]. Fig. 5 shows that both very negative and very positive slopes show up, and that these slopes are extremely sensitive to single-point mutations.
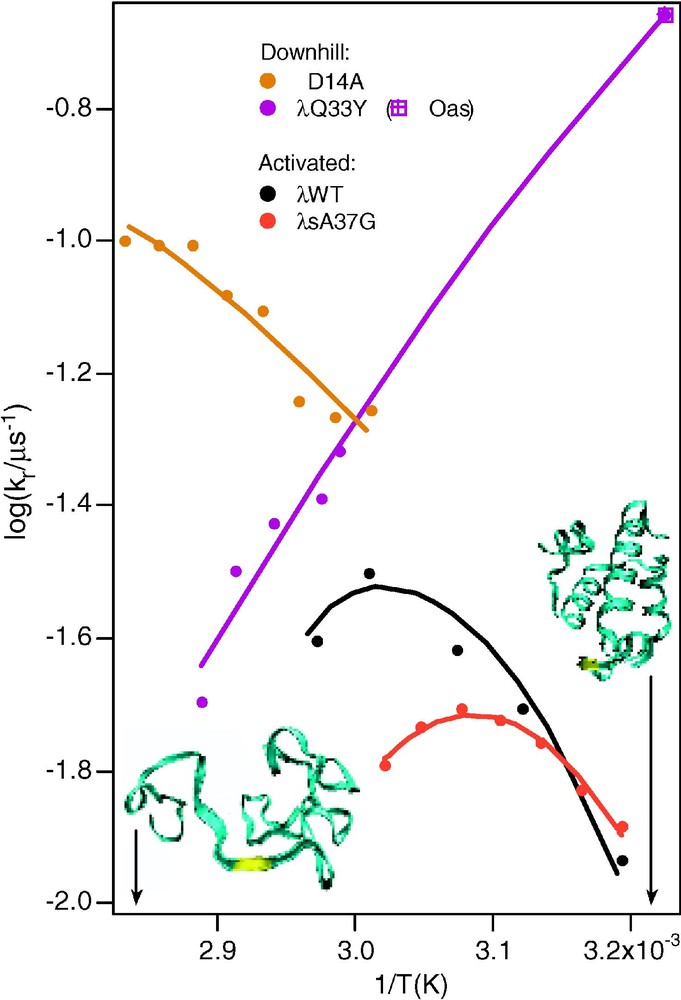
Arrhenius plots for the wild-type and for a slow-folding mutant, and for two very fast folding mutants of [13]. The curved plots of the wild-type and slow folding mutant are normal for activated folding, because the activation barrier of proteins is sensitive to temperature. The two arrows and structures indicate temperatures where the protein is either mostly folded or mostly unfolded.
3 Functional evolutionary constraints on folding
It used to be thought that proteins must fold over a linear sequence of many barriers before reaching the native state [41]. Then it was recognized that some proteins could fold in a single step over just one barrier [42]. Then the possibility of parallel processes was recognized [43]. Now it appears that engineered proteins can relax downhill to the native state without even a single barrier much greater than kJ mol−1 [14].
Yet natural proteins do have folding barriers greater than 3 kJ mol−1. If the folding barrier is not required by the physics of folding, why is it usually there? The real paradox is not why proteins fold so rapidly, but why they fold so slowly. Why do not all small proteins fold in a few microseconds? The answer may tell us something about protein function, which, unlike the fundamental physical interactions of hydrogen bonding, hydrophobicity, etc., is subject to continuing evolutionary pressure. Here are some possible reasons why natural proteins fold so slowly.
1. In order to function, most proteins must avoid aggregation. It has been proposed that folding barriers help prevent aggregation [16]. Aggregation occurs when proteins misfold into non-native structures and associate into clusters and eventually fibers consisting of stacked β-sheets. Recent work has shown that proteins acquire local extended structure (the type found in beta sheets) upon heat denaturation, even in the monomeric state [15]. Thus the propensity for forming β-sheet aggregates is already built into the sequence, and not even a property that emerges only at higher protein concentration.
Fast folders would be particularly prone to such aggregation because rapid folding also implies rapid unfolding, even with improved protein stability. For example, a protein that folds in 1 μs and has an equilibrium constant of 5000 unfolds on average every 5 ms. In the absence of a barrier at intermediate reaction coordinate x, partial unfolding will occur even more often. Such fast folders would be vulnerable to the protein degradation machinery. In contrast, a free barrier at intermediate x would exclude large populations of partially unfolded proteins.
The prediction is therefore that downhill folders should be more prone to aggregation, despite the fact that they are thermodynamically more stable than native states. This apparently paradoxical prediction has been observed experimentally [14]. Slow-folding mutants of the 5-helix bundle that destabilize the native state show no propensity for aggregation up to nearly millimolar concentrations. Mutants that stabilize the native state and speed up folding near the speed limit show a strong propensity for aggregation, as illustrated in Fig. 4b.
2. In order to function, proteins must also have sequences that support the function: binding sites, flexible backbones to accommodate substrate diffusion into the protein or conformational changes upon binding, and loops that mediate protein–protein interactions are just a few examples of function-specific features of the sequence. Amino acid side chains necessary for function may decrease hydrophobicity, destabilize secondary structure, require a larger decrease in conformational entropy upon folding, or introduce non-native interactions into the folding process. In general terms, these factors increase the ‘energetic frustration’ of proteins, producing proteins in Fig. 1 that fold at sub-optimal rates for a given complexity of the fold. Two examples of such effects are discussed next, although much work remains to be done to see how widespread the evolutionary competition between folding and function really is.
The WW domain binding module provides a good example of how a long binding loop can affect folding kinetics [10]. The wild-type Pin WW domain has a large loop connecting β-strands 1 and 2. The loop binds to proline-rich PPXP motifs, enabling signal transduction. A mutation analysis of the loop has shown that it forms in the rate-limiting step of folding [44]. Wild-type Pin WW domain is not a particularly fast folder for its small size, requiring about 75 μs to fold. When the large Pin loop is replaced by the smaller FBP WW domain loop, the relaxation rate speeds up to 3.5 μs. At the same time, a functional assay shows that the binding function of the module has been drastically decreased by altering its amino acid composition [10]. The simplest explanation of these observations is that the large loop is needed to recognize the PPXP motif, but slows down folding because a more difficult conformational search is required to form the proper loop geometry. The smaller replacement loop less capable of binding, but forms more efficiently.
An example of how a binding pocket affects the folding rate is provided by the 8-helix bundle myoglobin (Fig. 6), the first protein to have its X-ray crystal structure determined. The protein contains two sub-domains. The ‘functional’ one consists of the CDEF helices; in the folded apo-protein, there is a large cavity with two histidine and other polar residues, which bind the iron and haem group that fits into the cavity. The ‘structural’ sub-domain consists of the ABGH helices, which are tightly packed together by hydrophobic residues. Topologically, the two sub domains are very similar 4-helix bundles, and there is no reason why their folding rates should differ from one another. Stopped-flow circular dichroism and hydrogen exchange NMR experiments have shown that the CDCEF helices form native-like structure in ∼1 s [45]. Fluorescence-detected temperature-jump experiments have shown that the ABGH core forms from the cold denatured state in ∼7 μs, much closer to the expected downhill speed limit of ∼1 μs [46]. The simplest explanation of these observations is that the ABGH core is optimized for fast folding and provides a scaffold for the CDEF to loosely fold, so it can bind the haem group that finally stabilizes the pocket in the CDEF sub-domain. This explanation makes a straight-forward prediction: it should be possible to redesign the CDEF core with larger and more hydrophobic sidechains, trading off folding speed for reduced haem binding ability. Indeed, it has been shown by Wright and coworkers that substitution of one of the two iron-binding histidines by a phenylalanine speeds up folding of the CDEF sub-domain by a factor of 2.5, while reducing haem binding affinity [11]. It remains to be seen whether more extensive redesign can bring the folding time into the μs regime, while resulting in total loss of haem binding.
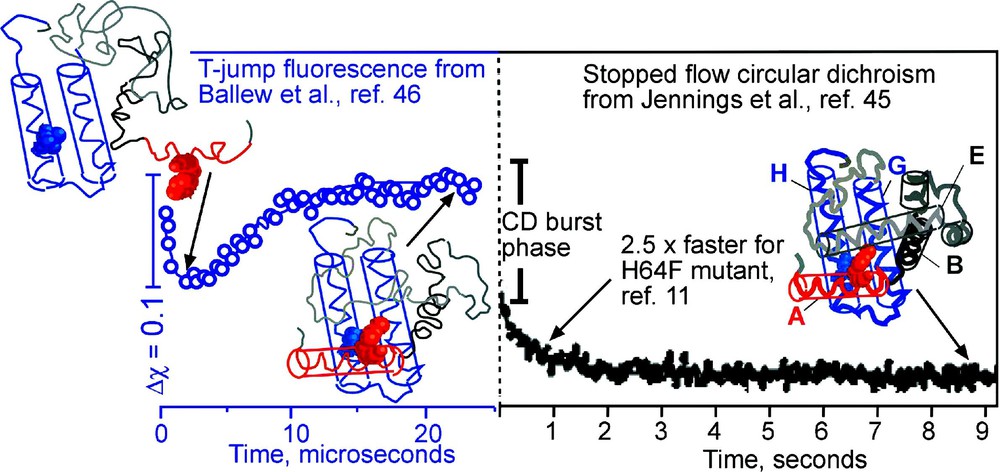
Anti-correlation between function and folding of apomyoglobin. The topologically similar ABGH domain (folding observed by T-jump on the left) and CDEF domain (folding observed by stopped-flow on right) differ by five orders of magnitude in their folding rates. The functional CDEF domain must accommodate the haem group. A His64Phe mutation speeds up the folding of the domain by 2.5 while reducing binding affinity. Representative cartoon structures of the protein deduced from the experiments at various stages of folding are shown.
3. A significant fraction of proteins is not even folded in vitro under ‘physiological’ conditions (usually meaning something like 25 °C, 50 millimolar phosphate, pH 7). Some of these proteins are extreme cases where folding occurs only as part of the protein's binding function. The ‘fly fishing’ mechanism has been proposed to explain how folding concurrent with binding can enhance specific binding interactions, therefore enabling protein function [47].
For many ‘unfolded’ proteins, there may be yet another explanation: The cellular matrix, via a multitude of nonspecific interactions, can have a stabilizing effect on the folding thermodynamics of proteins at the verge of stability. For example, it is well known that cosmotropes such as glycerol or sugars can stabilize the native state [48], inducing folding in vitro. Similarly, the cellular matrix is full of carbohydrates, glycosylated proteins and other molecules that could shift the folding equilibrium.
The cellular matrix could also act by crowding (still allowing the unfolded chain to explore interstitial spaces, but excluding expanded conformations of the protein), or even by confining the protein [49], thereby disfavoring the higher entropy unfolded state. For proteins that already fold in vitro, such as lysozyme, crowding may also hinder slow folding processes such as the formation of disulfide bridges [23]; however, disulfide bridge formation, proline isomerization, and other slow processes are not obligatory for folding, in the sense that the sidechains which cause them can generally be engineered out of proteins.
4 Summary: evolution, physics, and the free-energy landscape
The free-energy landscapes of proteins are sculpted by evolution subject to physics, which dictates the nature of the interactions between parts of the protein and between the protein and its local environment:
| (4.1) |
As we learned from Anfinsen [2], the amino acid sequence is the principal determinant of protein structure for small proteins, laying the foundation for the native local minimum via hydrophobicity, hydrogen bonding, and many other weak backbone/sidechain interactions. The solvent environment in vivo or in vitro modulates the stabilities of local minima, and of interconversion barriers connecting local minima on the free-energy landscape. Usually this environmental modulation relative to simple aqueous solvent is small (a few RT), but the resulting effects can be dramatic: a seemingly small modification of sequence or environment may cause proteins to unfold, aggregate, fold to a new state, or accelerate folding dramatically, as in the engineered downhill folders.
This sensitivity is both biological and physical in origin. On the biological side, proteins have generally evolved for function and against aggregation, leaving the minima sub-optimally shallow and barriers sub-optimally high as far as folding of the isolated protein is concerned: natural proteins tend to be energetically frustrated, not topologically limited. Physics dictates that protein populations and rates depend exponentially on the free energy ( is the thermodynamic equivalent of Eq. (2.1)). Therefore, small changes in free energy can have a large effect on protein populations and their dynamics. In fact, when we talk about a pathway ‘opening up’ and another ‘closing’, what we really mean is that the free energy of these pathways has been shifted a little bit. The free-energy landscape of natural proteins is full of such pathways, hence the bewildering array of folding behaviors; hence also our ability to landscape the landscape and engineer downhill folders.
Several ways in which evolution and physics affect sequence and environment have been discussed here. Physics dictates fundamental interactions such as the need for hydrophobic contacts or location of backbone hydrogen bonds, which in turn set limits on the foldable sequences, and how the solvent environment interacts with the protein. Evolution dictates the need for function (including suppression of aggregation when required for function), which is possible only with certain combinations of sidechains that facilitate binding, catalysis, or protein flexibility. The physical requirements of foldability and the evolutionary requirement of function can clash.
Proteins engineered to fold downhill are a prime example. From them, we have learned that activation barriers are not an obligatory physicochemical feature of protein folding. The weak interactions that guide folding can cooperate sufficiently in engineered proteins to abolish significant free-energy barriers. Ironically, what is usually referred to as “cooperative folding” among two states connected by an activation barrier, results from insufficient cooperation between the guiding forces for folding in natural proteins. We generally found that replacement of functional loops, removal of residues that may create flexibility for binding function, or replacement of residues by more hydrophobic residues at the expense of function, provides a successful route for designing highly stabilized downhill folders. This can be accompanied by an increased tendency to aggregate.
Highly stable downhill folders can do more than just prove that the origin of folding barriers must not be sought in physical chemistry alone, but also in protein evolution. They could serve as optimal starting points for the design of new protein functions because the compromises of their former natural function have been largely removed.
Acknowledgement
This work was supported by National Science Foundation grant MCB 0316925.
1 If an imaginary sphere within the core of a protein, containing mass m of sidechain and backbone atoms, were increased in diameter, one might expect m to increase as if the sphere were uniformly filled. It increases as . In that sense, proteins are only 2.5-dimensional objects.


