1 Introduction
Many papers and books on the dynamics of ecological systems have appeared. Many of them start from the Lotka–Volterra model [1,2], which describes populations in competition. They may exhibit many interesting features, such as chaos (e.g., the recent papers on the topic [3–6]) and phase transitions (e.g., [3,7,8]). The possible existence of chaos became evident since the work of May [9,10]. However, the studies concerning chaos in biological populations usually do not contain the discussion of the role of the inherited genetic information in it. The discussion of a predator–prey model with genetics has been started by Ray et al. [11], who showed that the system passes from the oscillatory solution of the Lotka–Volterra equations into a steady-state regime, which exhibits some features of self-organized criticality (SOC). Our study [8] on the topic was the Lotka–Volterra dynamics of two interacting populations, prey and predator, with the genetic information inherited according to the Penna model [12] of genetic evolution; we showed that during time evolution, the populations can experience a series of dynamical phase transitions that are connected with the different types of the dominant phenotypes present in the populations. Evolution is understoood as the interplay of the two processes: mutation, in which the DNA of the organisms experiences small chemical changes, and selection, through which the better adapted organisms have more offsprings than the others. The problem of speciation from evolution has been studied recently by McManus et al. [13] in terms of a microscopic model. They confirmed that the mutation and selection are sufficient for the appearance of the speciation. We followed their result and we consider in this study a closed ecosystem with a variable number of species competing for the same energy resources. The total energy of the ecosystem cannot exceed the value
Our model belongs to the class of Lotka–Volterra systems describing a variable number of the species competing for the same limited energy resources. The energy resources are self-regenerating and the regeneration depends on the number of the living organisms.
2 Evolution of energy resources
All species in the ecosystem under consideration use the same energy resources. In the model, the number NE(t) of the energy units available for the species satisfies the differential equation
| (1) |
| (2) |
In the case when N(t)=0, i.e. if there are no living organisms in the ecosystem, Eq. (1) reduces to the well known logistic differential equation:
| (3) |
| (4) |
We adapt the above solution into our model (Eq. (1)). To this end we assume that the individuals from all species in the ecosystem under consideration may reproduce only at discrete time t=0,1,2,3,… (otherwise N(t)=const), whereas NE(t) remains a continuous function of t between these discrete time values. Say, if there is N(t0) individuals at the discrete time value t=t0, then the value N(t) remains constant (N(t)=N(t0)) in the whole time interval [t0,t0+1). The analytical solution of Eq. (1) in this time interval is the following
| (5) |
3 Species evolution
We restrict ourselves to diploid organisms and we follow the biological species concept that the individuals belonging to different species cannot reproduce themselves, i.e., they represent genetically isolated groups. The populations of each species are characterized by genotype, phenotype and sex. Once the individuals are diploid organisms, there are two copies of each gene (alleles) in their genome – one member of each pair is contributed by each parent. In our case, the genotype is determined by 2L alleles (we have chosen L=16 locii in computer simulations) located in two chromosomes. We agreed that the first L′ sites in the chromosomes represent the housekeeping genes [15], i.e. the genes that are necessary during the whole life of every organism. We assumed that there also exist L−L′ additional ‘death genes’, which are switched on at a specific age a=1,2,…,L−L′ of living individual. The idea of the chronological genes has been borrowed from the Penna model [12,16] of biological ageing. The term ‘death gene’ has been introduced by Cebrat [17], who discussed the biological meaning of the genes that are chronologically switched on in the Penna model. The maximum age of individuals is set to a=L−L′. It is the same for all species. All species have also the same number L′ of housekeeping genes and the same number L−L′ of chronological genes. However, they differ in the reproduction age aR, i.e., the age at which the individual can produce the offsprings. Individuals can die earlier due to inherited defective genes. We assume that it is always the case, when an individual reaches the age a=L−L′ or in its history until the age a there have appeared three inactive genes in the genotype (inactive gene means two inactive alleles).
We make a simplified assumption, that each function of an organism (does not matter what species) has been coded with a bit-string consisting of 16 bits generated with the help of a computer random number generator. These bit-strings represent the patterns (classes) for the genes. We assume that there are L possible patterns and the genes of all species have to be represented by bit-strings that differ from the respective pattern by a Hamming distance H⩽2. Otherwise the bit-strings do not represent the genes. In order to distinguish the species, we have introduced the concept of an ideal predecessor, called Eve, who uniquely determines all individuals belonging to the particular species. Namely, the individuals have genes which may differ from the genes of Eve only by a Hamming distance H⩽1. Genes, which differ from the genes of Eve by a Hamming distance H>1 and, simultaneously, which differ from the pattern by a Hamming distance H⩽2 represent mutated genes. They are potential candidates to contribute to a new species, but they are considered as inactive genes for the species under consideration. If there happens to be another individual with the mutant gene in the same locus then these two mutants can mate (different sex is necessary as well as the age a⩾aR) and they can produce offsprings. In the latter case, the new species is created with Eve, who represents Eve of the old species, except for the mutant genes. In our computer simulations, the new species ususally are extinct due to the mechanism of genetic drift. However, after long periods of ‘stasis’, there happen bursts of the new species, which are able to live for a few thousands of generations or even more. They also can adapt better to the surrounding and they can dominate other species. The small changes of the inherited genetic information are realized through the point mutations.
A point mutation changes a single bit within the 16-bit-string representation of a gene and according to the above assumptions the gene affected by a mutation may pass to one of three states: S=1 (gene specific for the species), S=2 (mutant gene, potential candidate of a new species), S=0 (defective gene). In the model, the bit-string representing a defected gene (S=0) can be mutated, with probability p=0.1. Hence, there is still a possibility for back mutations. Genes are mutated only at the stage of the zygote creation – one mutation per individual.
The life cycle of diploids needs an intermediate stage when one of the two copies of each gene is passed from the parent to a haploid gamete. Next, the two gametes produced by parents of different sex unite to form a zygote.
In the model, phenotype is defined as a fractional representation of the 16-bit-string genes, where each gene is translated uniquely into a fractional number x from the interval [−1,1], e.g.,
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |

Phenotype-surrounding interaction function
We decided to determine the amount of possible offsprings by projecting the fitness of the parents, QF (female) and QM (male),onto the number of produced zygotes
| (11) |
We assume that the sex of a diploid individual is determined with the help of a random number generator at the moment when it is born and it is unchanged during its life.
4 Computer algorithm
We investigate the species with respect to speciation. In most computer simulations, we observed evolving single species and analysed the offsprings of the new mutant species originating from the old one. The secondary order speciation, i.e., the speciation taken place from the mutant species, has not been considered. However, we investigated the case when initially there are a few species in the ecosystem and the results qualitatively were the same as for single initial species.
In the simulation, it is very important to prepare the genetic information in a proper way. It is obvious that in the evolution process some genes are not necessary during the whole life, e.g., they may become important only near the end of the life, and it is possible that they could be defective since the individual under consideration was born. Therefore, first we prepare the initial species in the time-independent surrounding for a few thousands generations until the inherited genetic information is represented by a steady-state flow between suceeding generations. Then the distribution of inactive genes becomes time independent. Only after that, we switch on the fluctuations of the surrounding, which in our case are represented by the coefficient
4.1 Initial species preparation
- (1) Generate L bit-strings (16 bits) representing life functions of the organism and which are the patterns for genes.
- (2)
Generate Ns predecessors (Eve) of the initial species (Hamming distance of each gene from the respective pattern, H<=2, and then
- (3) For each Eve, representing the species 1,2,…,Ns construct NM males and NF females (NM=NF) who have each gene at distance H⩽1 from the corresponding gene of Eve.
- (4)
Evolve separately each species 1,2,…,Ns as follows:
- (i) increase the age of all individuals by 1;
- (ii) remove from the population all individuals who should die because they have exceeded the maximum age (L−L′) or during their life until now they have collected three inactive ‘chronological’ genes;
- (iii) [optionally] the Verhulst factor is applied, i.e. every individual survives with the same probability (1−(NM+NF)/Nmax), where Nmax is the maximum allowed number of individuals in the population under consideration;
- (iv) select at random a female and a male for whom a⩾aR and let them produce Nzygote according to Eq. (11);
- (v) each zygote is mutated; we assume that the housekeeping genes cannot be inactive; therefore, at least one defected housekeeping gene kills zygote; the total number of zygotes in the population that survive cannot exceed the number
- (vi) decrease the total number of energy units by the number N(t) of all individuals (parents and their new-born offsprings), i.e., NE(t)=NE(t−1)−N(t);
- (vii) regenerate the ecosystem energy according to Eq. (5);
- (viii) goto (i) unless the stop criterion is fulfilled.
4.2 Species in variable surrounding
- (5) All Ns species are put together in the ecosystem.
- (6) t=t+1.
- (7) Calculate b(t) representing surrounding fluctuation.
- (8) Check all individuals from the old species with respect to mutants (who have, at least at one locus, k=1,…,L, two bit-strings representing the pair of the alleles at state S(1)=2 and S(2)=2). If there is in the population an individual representing a mutant, then create Eve, the pattern of new species, and look for other mutants in the same species consistent with the created Eve. Determine a new value of the reproduction age aR∈[1,L−L′] for the species with the help of the computer random number generator. Remove new species from the old species.
- (9) Step (i) from above.
- (10) Step (ii) from above.
- (11) Step (iii) from above.
- (12) Step (iv) from above.
- (13) Step (v), but now NR concerns all species.
- (14) Step (vi), where N(t) concerns all species.
- (15) Step (vii).
- (16) Goto (6) unless the end of the simulation.
5 Results and discussion
Limiting the amount of energy resources in the ecosystem introduces strong selection between the species competing for the resources. In our case, the selection takes place through limiting the number of the new-born offsprings in the ecosystem. Namely, in the model, their number cannot exceed the value
In Fig. 2, we show the effect of the changing environment on the old population (aR=5, L=16, L′=5), which was aging in a time-independent surrounding through 40 000 generations. The changing enviroment is modelled with the help of the coefficient b(t) in the function V(x,t) (Eq. (7)). We have chosen:
| (12) |
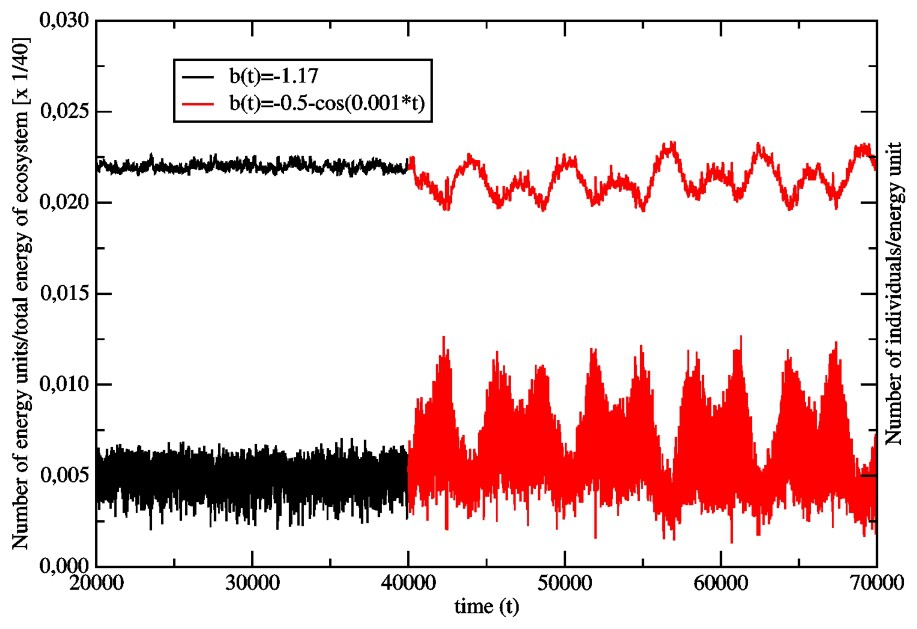
Effect of the transition from the time-independent surrounding (b(t)=−1.17,
Effect of the transition from the time-independent surrounding (b(t)=−1.17,
In Fig. 3 we have presented the age profiles of the fraction of the inactive ‘chronological’ genes in the population from Fig. 2. The profiles concerning the generations at
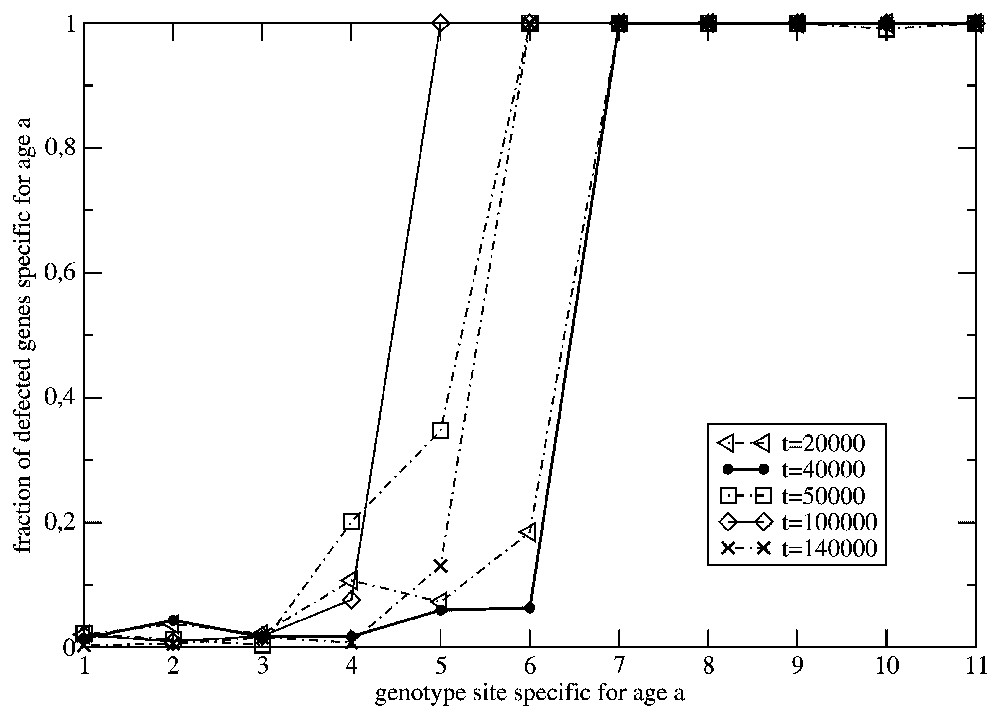
The effect of the change of the time-independent surrounding to the one varying in time, at
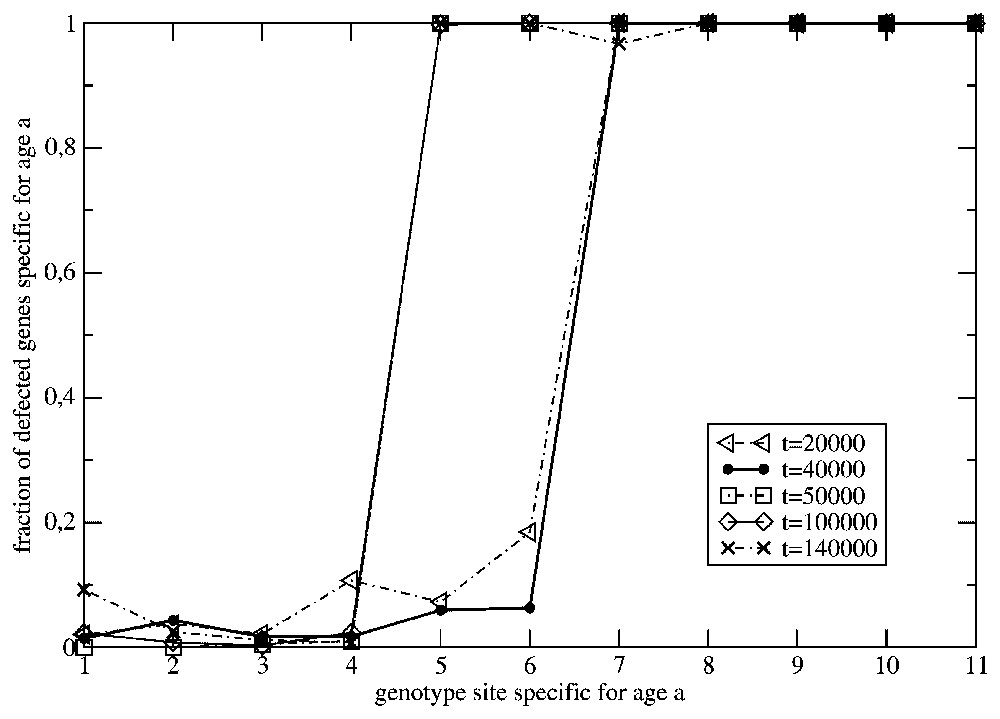
The same as in in Fig. 2, but ω=0.01.
The evolution of the average phenotype of the species from the example in Fig. 2 has been shown in Fig. 5. The same data, but presented with the help of a histogram, have been shown in Fig. 6.
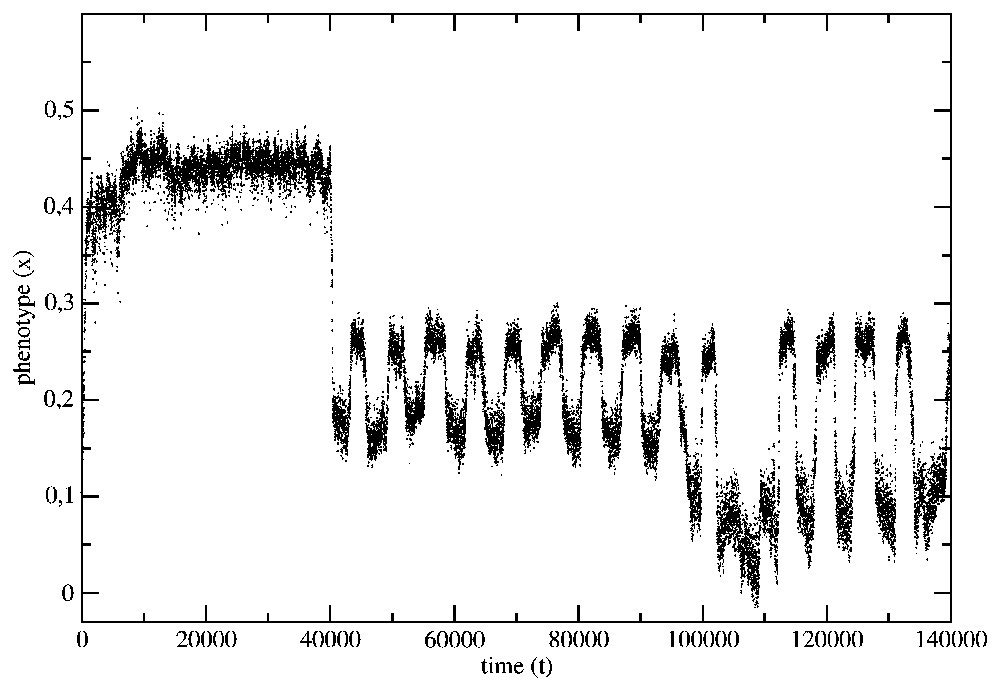
The phenotype evolution for the situation presented in Fig. 2.

The histogram of the average usage of the phenotype x in the evolving species (from Fig. 2) when there is a time-independent surrounding (r.h.m. histogram), and when there is a fluctuating environment.
Notice that there is a trend to minimize the environment fluctuations and that the genes, which were well adapted in the time-independent environment, do not have the ability to follow the environment fluctuations. They can be even eliminated from the genetic bank of the species if the fluctuations become more frequent.
The environmental changes influence the size of all species in the ecosystem and this is the reason why some of them may be eliminated. The regeneration of the energy resources in the ecosystem takes some time and too rapid a growth of some species, e.g., mutant species, acts as a sudden cataclysm for the other species. The Lotka–Volterra systems have a self-regulatory character and there exist threshold values for the fraction of destroyed population above which the system returns to its previous state [8,18]. However, in the case of genetic populations, if the catastrophe is applied for many generations, one can observe that the age profile of the fraction of defective genes in the population may loose its stability and next the species becomes extincted [8]. Thus the appearance of the new species, even for a relatively short period, can eliminate the old species.
In our computer simulations, we associate a new value, aR, of the reproduction age with every new species appearing in the course of evolution. The value is determined with the help of a computer random-number generator. Thus, we have also the possibility to investigate the effect of the reproduction age on the adaptation of the species to the fluctuating surrounding. We have observed that the events representing the appearance of the new species with the small value aR (aR∼1), are usually represented by short-duration ‘bursts’ of the population size and they vanish as rapidly as they have appeared. In the example in Fig. 7, the are represented by the highest blobs painted in black, at the bottom of the figure. This phenomenon is easy to explain as in this case the life span of individuals is practically shrinking to the activity of single genes and the individuals die after they reproduce themselves. The active genes cannot effectively adapt to the changing environment. How important the range of life span for species stability is, can be also concluded from the histograms in Fig. 8.

The effect of the speciation from the old species (earlier aging for 40 000 generations in a time-independent environment) in a fluctuating environment (
The effect of the speciation from the old species (earlier aging for 40 000 generations in a time-independent environment) in a fluctuating environment (

Histograms of the phenotype usage in the environment changing with the frequency ω=0.02 in the case of three species: the predecessor population (aR=5), and two descendant populations (aR=7, aR=2). The frequency of the environment changes is ω=0.02.
Histograms of the average usage of the phenotype x of the species representing the predecessor (aR=5) and two descendant species (aR=2,7) are presented in Fig. 8. It is evident that the average value x representing the species with aR=2 oscillates far away from the optimum values (variable minima of V(x,t)), because there is an insufficient number of genes adapted to the variable surrounding. The situation is a little bit better with the predecessor (old species). However, it is evident that it cannot be stable over a long time in a variable surrounding. The most stable species is the one for which aR=7, because in its population there are inherited genes which have adapted to the variable surrounding (the range of x is almost symmetric with respect to x=0).
In this study, we did not discuss the mechanism of speciation in the new species. We have restricted our analysis to the ‘first-order’ speciation originating from old species and we discussed in detail its effect on the inherited genetic information. We could expect a chain of events representing speciation with the species being better and better adapted to the environment. The younger the species, the more probable speciation, and one should observe peaks in the number of speciation events in a short period.
6 Conclusions
We have discussed a model of species evolution in an ecosystem where the energy resources regenerate themselves according to a logistic differential equation. The number of species present in the ecosystem under consideration results from evolution, which is understoood as the interplay of the two processes only, mutation and selection. We observed that after long periods of ‘stasis’ there are bursts of the new species that are able to live for thousands of generations. We have observed that in a variable surrounding, the species for which the reproduction age aR is too small are very unstable, even if their size substantially exceeds the specific size for other species. In our model, they usually cause the elimination of other species. Simultaneously, the resulting increase in the energy resources makes the next speciations possible.
There are two approaches to the description of species evolution: the one with continuous evolutionary changes and the theory of punctated equilibrium [19,20], according to which the evolutionary activity occurs in bursts. It is often the case that the mathematical models concerning the species evolution are restricted to pure species dynamics consideration or pure genetics evolution. We have shown that the small changes of the inherited genetic information could be the mechanisms of the abrupt evolutionary changes.


