1 Introduction
Une évolution majeure dans le domaine de la chirurgie abdominale a été le développement de la chirurgie laparoscopique. Dans ce type de chirurgie, des opérations comme la résection hépatique sont effectuées au travers de petites incisions. Une caméra vidéo et des instruments spéciaux sont introduits dans l'abdomen du patient et permettent au chirurgien d'effectuer des opérations beaucoup moins traumatisantes pour l'organisme. Le principal inconvénient de cette technique est de rendre les gestes du chirurgien plus compliqués et de le priver d'informations tactiles et visuelles directes. Le chirurgien doit donc apprendre de nouvelles procédures et s'adapter à un nouveau type de coordination œil–main. Dans ce contexte, un système de simulation chirurgicale apparaît comme un outil important pour la formation et l'entraînement des chirurgiens.
Parmi les différents points clés nécessaires à l'élaboration d'un simulateur de chirurgie 〚1, 2〛, la représentation géométrique et physique des organes du corps humain demeure un des plus importants. Le modèle déformable qui représente un organe doit être à la fois très réaliste (visuellement et physiquement) et très efficace, afin de permettre de simuler des déformations en temps réel. Plusieurs méthodes ont été proposées : les modèles masse–ressort 〚3, 4〛, les déformations libres 〚5〛, l'élasticité linéaire, utilisée avec la méthode des volumes finis 〚6〛 ou avec la méthode des éléments finis 〚7〛.
Depuis le début du projet de simulation de chirurgie dans notre laboratoire, nous fondons nos modèles déformables sur la théorie de l'élasticité linéaire et la méthode des éléments finis 〚8, 9〛. Cependant, même si ces modèles nous permettent de simuler les déformations de structures anatomiques comme le foie, ils constituent une bonne approximation de la réalité. En effet, l'utilisation d'une relation linéaire entre la déformation et le déplacement ne permet pas aux modèles d'être invariants par rotation. Il en résulte des distorsions très peu réalistes dès que l'hypothèse des petits déplacements n'est plus vérifiée. C'est pourquoi nous nous sommes intéressés à l'équivalent en grands déplacements du modèle d'élasticité linéaire, à savoir le modèle de St Venant–Kirchhoff.
L'élasticité non linéaire est en général utilisée lorsque les principaux objectifs sont la précision et le réalisme biomécanique de la déformation, et non pas l'efficacité et le fonctionnement en temps réel. Par exemple Vidrascu utilise un modèle de Mooney–Rivlin incompressible pour simuler les déformations du foie 〚10〛. Malgré l'utilisation d'une méthode de décomposition de domaine, les calculs prennent plusieurs minutes. Vuskovic et Kauer utilisent eux aussi des modèles non linéaires (loi néo-Hookéenne et modèle de Veronda–Westmann) pour calculer les propriétés biomécaniques du foie à partir de mesures effectuées in vivo 〚11〛. Cette fois encore, le temps réel n'est pas nécessaire. Des modèles d'élasticité non linéaire sont utilisés pour simuler les déformations d'autres organes, comme par exemple le cerveau, afin de prédire les déformations engendrées par des gestes chirurgicaux (ouverture de la dure-mère, ablation d'une tumeur) ou par le développement ou la régression de lésions cérébrales 〚12〛, ou encore la peau, dans le but d'en étudier l'élasticité 〚13〛. On trouve aussi des applications de l'élasticité de St Venant–Kirchhoff en animation 〚14〛.
Les exemples d'utilisation de modèles non linéaires dans des applications temps réel sont rares. Pour la simulation de chirurgie gynécologique, Szekely et al. utilisent un modèle de Mooney–Rivlin 〚15, 16〛, qui fonctionne en temps réel par le biais d'une parallélisation massive 〚17〛. Par ailleurs, Zhuang utilise un modèle d'élasticité en grands déplacements pour simuler la manipulation d'objets dans un environnement virtuel 〚18〛. À notre connaissance, aucun de ces modèles ne se prête aux changements de topologie.
Dans cette article, nous proposons un nouveau modèle déformable dynamique temps réel, qui s'appuie sur l'expérience acquise dans notre équipe avec les modèles élastiques linéaires 〚9〛, mais qui reste valable pour les grands déplacements. Ce modèle autorise les changements de topologie, et donc la simulation de la découpe ou de la suture des tissus mous. Nous allons tout d'abord introduire la théorie de l'élasticité linéaire et sa mise en œuvre au travers de la méthode des éléments finis, pour ensuite mettre en évidence les limitations de ce modèle lorsque l'hypothèse des petits déplacements n'est plus vérifiée. Nous nous concentrerons ensuite sur notre mise en œuvre de l'élasticité de St Venant–Kirchhoff et des contraintes d'incompressibilité 〚19, 20, 27〛.
2 Les limites de l'élasticité linéaire
L'élasticité linéaire est souvent utilisée pour la modélisation de matériaux déformables, principalement en raison de la simplicité des équations qui la gouvernent et de la possibilité d'optimiser les temps de calcul. Le comportement physique d'un tissu élastique peut être considéré comme linéaire dès lors que ses déformations et ses déplacements sont suffisamment petits 〚21, 22〛 (typiquement inférieurs à 10% de la taille de l'objet). Nous représentons la déformation d'un modèle volumique à partir de sa forme au repos par un champ de déplacement pour et nous écrivons
L'énergie élastique linéaire Wl, pour un matériau homogène isotrope, s'écrit en fonction du tenseur de déformation de Green–St Venant linéarisé El sous la forme suivante 〚23〛 (éq. (5)) :
| 5 |
L'équation (5), connue sous le nom de loi de Hooke, montre que l'énergie élastique linéaire d'un objet déformable est une fonction quadratique du champ de déplacement.
2.1 La méthode des éléments finis
La méthode des éléments finis est un moyen classique de résoudre les équations de la mécanique des milieux continus. C'est un outil mathématique permettant de discrétiser un problème variationnel continu 〚24〛. Cette méthode est basée sur une subdivision du domaine d'intérêt en volumes élémentaires. Nous avons choisi d'utiliser des éléments finis de type P1 pour lesquels l'élément de volume est un tétraèdre (Fig. 1). En chaque point du tétraèdre le vecteur déplacement est interpolé à partir des valeurs des déplacements Uk des sommets Pk. Pour les éléments P1, les fonctions d'interpolation Λk sont linéaires ( sont les coordonnées barycentriques de M dans le tétraèdre) (éqs. (6) et (7)) :

Élément fini P1.
| 6 |
| 7 |
En utilisant cette équation pour U, on obtient la formulation de l'énergie de déformation élastique linéaire dans le tétraèdre (éq. (8)) :
| 8 |
Finalement, on obtient la force appliquée par le tétraèdre sur le sommet Pp en dérivant l'énergie élastique par rapport à la position de ce sommet (éq. (9)) :
| 9 |
Nous utilisons cette formulation de l'élasticité linéaire depuis plusieurs années au travers de deux modèles déformables, le modèle pré-calculé 〚25〛 et le modèle masse–tenseur 〚8〛. De plus, nous les avons étendus à l'élasticité linéaire anisotrope 〚9〛, ce qui permet de modéliser des matériaux renforcés par des fibres, qui sont très répandus parmi les tissus biologiques (muscles, tendons...), ou d'autres structures anatomiques, comme les vaisseaux sanguins.
2.2 Le problème de l'invariance par rotation
La principale limitation du modèle linéaire est qu'il n'est pas invariant par rotation. Lorsqu'un élément de volume subit une rotation, il l'interprète comme une augmentation de l'énergie élastique, qui se traduit par une distorsion. La Fig. 2 montre la déformation que subit un modèle élastique linéaire lorsqu'il est soumis à une rotation.
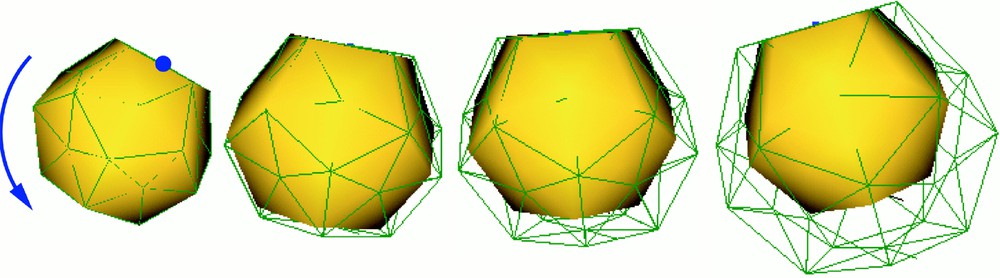
Dilatation d'un matériau élastique linéaire (en représentation filaire) sous l'effet d'une rotation globale (la représentation surfacique est celle d'un objet rigide subissant la même rotation).
Lorsqu'il s'agit d'une rotation globale, on pourrait imaginer résoudre le problème par un changement de repère approprié. Mais, dans la plupart des cas, il n'y a qu'une partie de l'objet simulé qui subit une rotation par rapport au reste du domaine. C'est en particulier le cas dès lors qu'une partie de l'objet est fixée et que le reste est soumis à un ensemble de contraintes entraînant une rotation locale. La Fig. 3 montre un cylindre dont la face inférieure a été fixée. La face supérieure est soumise à une force dirigée vers la droite. Nous avons représenté sur la Fig. 3a les déformations entraînées pour plusieurs valeurs successives de l'intensité de la force. On observe, comme sur la Fig. 2, une dilatation du modèle aux endroits où il subit une rotation. Sur la Fig. 3b, nous avons représenté à l'aide de flèches les trajectoires de certains points sur la face supérieure du cylindre. Nous constatons que ces points suivent, au cours de la déformation, une trajectoire linéaire, qui est responsable de la dilatation observée. Cette dilatation est d'autant plus irréaliste qu'elle n'est pas isotrope, puisqu'elle ne se produit que dans le plan de rotation. On le constate en observant la déformation subie par la face supérieure du cylindre (Fig. 3c).

Plusieurs déformations successives d'un cylindre élastique linéaire, entraînant des rotations de plus en plus importantes de la partie supérieure du modèle. (a) Vue de coté. (b) Vue de coté en rendu filaire, avec une représentation des trajectoires suivies par certains points. (c) Vues du dessus.
Le comportement irréaliste du modèle d'élasticité linéaire, lorsqu'il subit des grands déplacements, nous a conduit à considérer un modèle d'élasticité très proche du modèle linéaire, mais qui reste valable pour les grandes déformations, le modèle d'élasticité de St Venant–Kirchhoff.
3 Le modèle d'élasticité de St Venant–Kirchhoff
Le modèle d'élasticité de St Venant Kirchhoff est la généralisation du modèle linéaire pour les grands déplacements. L'équation de base de l'énergie est la même (éq. (10)) :
| 10 |
| 11 |
L'énergie de déformation, qui est une fonction quadratique du gradient du champ de déplacements dans le cas linéaire, est maintenant un polynôme de degré quatre par rapport à ∇U (éq. (12)) :
| 12 |
3.1 Le modèle masse–tenseur non linéaire
En conservant les conventions de notations utilisées pour l'élasticité linéaire, nous exprimons l'énergie de déformation d'un tétraèdre pour le modèle d'élasticité de St Venant–Kirchhoff sous la forme (éq. (13)) :
| 13 |
Comme on pouvait s'y attendre, cette énergie comporte maintenant, en plus du terme quadratique de l'élasticité linéaire, des termes d'ordre trois et quatre mettant en œuvre respectivement les déplacements de trois et quatre sommets du tétraèdre. Ces termes font apparaître les nouvelles grandeurs et qui sont respectivement des vecteurs et des scalaires de rigidité. Ils viennent compléter les tenseurs de rigidité (éq. (8)) et dépendent des fonctions de forme du tétraèdre (éq. (6)) et des coefficients de Lamé du matériau (éq. (14)) :
| 14 |
La force exercée par le tétraèdre sur chacun de ses sommets Pp est alors dérivée de l'énergie élastique pour donner une équation polynomiale de degré trois (éq. (15)) :
On remarque que le premier terme de la force élastique, correspond exactement à la force rencontrée dans le cas de l'élasticité linéaire.
L'idée principale du modèle masse–tenseur est de séparer, pour chaque tétraèdre, la force appliquée sur un sommet en deux parties : une force créée par le déplacement du sommet et une somme de forces dues aux déplacements de ses voisins (éq. (16)) :
| 16 |
De cette façon, nous pouvons définir, pour chaque tétraèdre, un ensemble de tenseurs de rigidité locaux pour les sommets () et pour les arêtes (). Après avoir effectué la même opération pour tous les tétraèdres, on peut accumuler, sur les sommets et les arêtes du maillage, les contributions correspondantes pour former les tenseurs de rigidité globaux :
Ces tenseurs de rigidité sont calculés au moment de la construction du modèle et sont stockés sur chaque sommet et arête du maillage.
Le même principe peut être appliqué au terme quadratique et au terme cubique de l'éq. (15). Le premier apporte des vecteurs de rigidité pour les sommets, les arêtes et les triangles, alors que le second définit des scalaires de rigidité pour les sommets, les arêtes, les triangles et les tétraèdres. Le Tableau 1 résume la répartition de toutes ces informations de rigidité sur chaque primitive géométrique du maillage.
Stockage des informations de rigidité sur les composantes géométrique du maillage.
| Répartition des informations de rigidité | Tenseurs | Vecteurs | Scalaires |
| Sommet Vp | Bpp | Cppp | Dpppp |
| Arête Epj | Bpj | Cppj Cjpp | Djppp Djjjp Djpjp |
| Cjpp Cpjj | Dpjjp Djjpp | ||
| Face Fpjk | Cjkp | Djkpp Djpkp Dpjkp | |
| Ckjp | Djjkp Djkjp Dkjjp | ||
| Cpjk | Dkkjp Dkjkp Djkkp | ||
| Tétraèdre Tpjkl | Djklp Djlkp Dkjlp | ||
| Dkljp Dljkp Dlkjp |
Étant donné un maillage tétraédrique d'un solide – dans notre cas une structure anatomique –, nous construisons une structure de données comprenant les notions de sommet, d'arête, de triangle et de tétraèdre, avec toutes les relations de voisinage nécessaires. Pour chaque sommet, nous stockons sa position actuelle Pp, sa position au repos P0p et ses informations de rigidité. Pour chaque arête et chaque triangle nous stockons les informations de rigidité. Enfin, pour chaque tétraèdre, nous stockons les coefficients de Lamé λ et μ, les quatre vecteurs de forme αk et les informations de rigidité.
Durant la simulation, nous calculons les forces pour chaque sommet, arête, triangle et tétraèdre, puis nous mettons à jour la position des sommets en considérant que l'équation qui gouverne le mouvement de notre modèle élastique est une équation différentielle newtonienne, de la forme (éq. (17)) :
| 17 |
Cette équation est reliée aux équations différentielles rencontrées en mécanique des milieux continus 〚26〛 (éq. (18)) :
| 18 |
D'après la théorie des éléments finis, la matrice de masse M et la matrice d'amortissement C sont creuses et dépendent des propriétés de chaque tétraèdre. Dans notre cas, nous considérons que M et C sont des matrices diagonales, c'est-à-dire que la masse et les effets d'amortissement sont concentrés sur les sommets du maillage. Cette simplification, appelée mass-lumping, découple les mouvements de chacun des nœuds et permet donc d'écrire l'éq. (18) comme un ensemble d'équations différentielles indépendantes du type (17), une pour chaque sommet.
De plus, nous avons choisi un schéma d'intégration explicite, dans lequel les forces élastiques sont estimées à l'instant t pour calculer la nouvelle position du sommet à l'instant t+1 (éq. (19)) :
| 19 |
Cette intégration explicite permet une remise à jour du modèle avec une fréquence compatible avec les besoins de la simulation. Une approche fondée sur un schéma semi-implicite permettrait un comportement plus rigide, mais demanderait la résolution d'un système linéaire à chaque itération, ce qui est trop coûteux en temps de calcul, compte tenu de la taille des maillages.
Un des gestes de base de la simulation de chirurgie consiste à découper des tissus mous. Avec notre modèle déformable, ce geste peut être effectué de manière très efficace. Nous simulons l'action d'un bistouri électrique sur un tissu mou en supprimant successivement tous les tétraèdres qui sont en contact avec l'extrémité de l'instrument. Lorsque l'on supprime un tétraèdre, environ 280 soustractions de réels sont effectuées pour retrancher la contribution du tétraèdre aux informations de rigidité des sommets, arêtes et triangles voisins. En mettant à jour localement les informations de rigidité, le tissu garde exactement les mêmes propriétés que si nous avions retiré le tétraèdre correspondant sur le maillage au repos. Grâce à la continuité volumique de la modélisation par les éléments finis, la déformation du tissu reste réaliste durant la découpe.
3.2 Contraintes d'incompressibilité
Les tissus vivants, qui sont composés essentiellement d'eau, peuvent être considérés comme quasiment incompressibles. Cette propriété est particulièrement difficile à modéliser et conduit la plupart du temps à des problèmes d'instabilité. C'est le cas avec le modèle de St Venant–Kirchhoff, car le matériau simulé atteint un comportement incompressible lorsque la constante de Lamé λ tend vers l'infini. Mais prendre une valeur trop grande pour λ nous forcerait à diminuer le pas de temps et donc à augmenter le temps de convergence. Une autre raison qui nous a poussé à ajouter une contrainte d'incompressibilité externe au modèle élastique est liée au modèle lui-même : le principal avantage du modèle de St Venant-Kirchhoff est d'utiliser le tenseur de déformation E, qui est invariant par rotation. Mais il est aussi invariant par symétrie, ce qui peut conduire au retournement de certains tétraèdres lorsqu'ils sont soumis à de fortes contraintes. Ce retournement sera rendu impossible par une contrainte géométrique de conservation du volume.
Nous avons donc choisi de pénaliser la variation de volume de chaque tétraèdre en appliquant, sur chacun de ses sommets, une force dirigée selon la normale à la face opposée. La norme de cette force étant proportionnelle au carré de la variation relative de volume et le sens étant donné par le signe de cette variation (Fig. 4) :

Pénalisation de la variation de volume. La position au repos est représenté en pointillés.
Ces forces agissent comme une augmentation de la pression à l'intérieur du tétraèdre. Cette méthode est relativement proche des multiplicateurs de Lagrange, qui sont souvent utilisés pour résoudre les problèmes de minimisation d'énergie sous contrainte.
3.3 Résultats
Afin de mettre en évidence l'apport du modèle masse–tenseur «grands déplacements», nous avons renouvelé l'expérience proposée au § 2 sur le cylindre (Fig. 3). On peut ainsi apprécier l'avantage du modèle non linéaire, qui se déforme de manière beaucoup plus réaliste. En effet, on constate sur la Fig. 5a que les points peuvent maintenant suivre des trajectoires non rectilignes, permettant au cylindre de se courber naturellement. Si on compare ce résultat avec le modèle linéaire (Fig. 5b et c), on se rend compte de l'erreur commise par ce dernier dès que l'on sort de l'hypothèse des petits déplacements. Le modèle non linéaire permet au cylindre de se plier sans que sa longueur augmente ni que sa section se déforme. On peut aussi apprécier l'avantage qu'il présente en termes de conservation du volume.

Application d'une force sur la face supérieure du cylindre (la face inférieure étant fixée). Comparaison entre le modèle linéaire (rendu en filaire) et le modèle « grands déplacements » (en rendu surfacique). (a) Déformations successives du cylindre utilisant le modèle masse–tenseur « grands déplacements ». Les flèches indiquent les trajectoires de certains points. (b) Comparaison des déformations du modèle linéaire (rendu filaire) et du modèle « grands déplacements » (en rendu surfacique). (c) Même expérience que (b), mais vue de dessus.
La Fig. 6 présente la comparaison du modèle masse–tenseur non linéaire avec son homologue linéaire. Les modèles déformables ont été fixés au centre de leur face antérieure : cette zone correspond au hile hépatique, c'est-à-dire à l'endroit où les différents arbres vasculaires (artériel, veineux et biliaire) pénètrent dans le parenchyme hépatique. Nous utilisons un coefficient μ de l'ordre de alors que les valeurs de λ sont issues du compromis entre un comportement le plus incompressible possible (λ très grand) et un temps de calcul correct. En général, cela nous mène à des valeurs de λ comprises entre et Nous avons alors appliqué des forces sur le lobe droit du foie. Si on utilise le modèle linéaire, la partie droite du foie subit une importante (et irréaliste) augmentation de volume, alors qu'avec le modèle non linéaire, le lobe droit est capable de subir une rotation partielle, ce qui donne une impression de déformation beaucoup plus proche de la réalité.
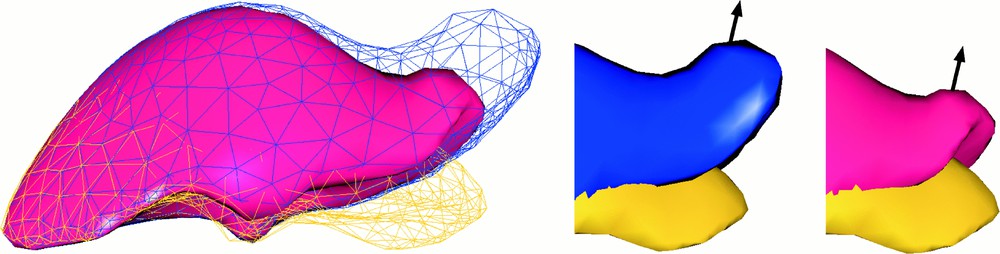
Comparaison entre le modèle linéaire et le modèle non linéaire pour simuler les déformation d'un foie. (a) Comparaison des déformations du modèle linéaire (en rendu filaire) et du modèle non linéaire (en rendu surfacique). La position au repos est représentée par maillage en représentation filaire du bas (jaune). (b) Gros plan sur la zone de plus forte déformation. La forme au repos est représentée par le modèle du bas (jaune). On constate une forte différence vis-à-vis de la conservation du volume entre le modèle linéaire (à gauche) et le modèle « grands déplacements » (à droite).
Lorsque l'on ajoute la contrainte d'incompressibilité décrite au paragraphe précédent, on obtient des variations de volume encore plus faibles (voir Tableau 2). L'ajout de cette contrainte a aussi pour effet de stabiliser le comportement dans les zones de plus forte déformation.
Résultats de variations de volume. Pour le cylindre, les appellations gauche, milieu et droit font référence aux différents stades de déformation des Figs. 3 et 5a.
| Variation de volume (%) | Linéaire | Non linéaire | Non linéaire incompressible | ||||||||
| Cylindre gauche | milieu | droit | 7 | 28 | 63 | 0.3 | 1 | 2 | 0.2 | 0.5 | 1 |
| Foie | 9 | 1.5 | 0.7 |
Enfin, nous présentons un exemple de simulation d'un geste classique de chirurgie laparoscopique sur le foie. Le chirurgien opère à l'aide de deux instruments. Celui de droite est une pince avec laquelle il va saisir une zone du lobe droit du foie afin de le mettre sous tension, pendant qu'il va découper le parenchyme hépatique avec l'instrument de gauche. Au fur et à mesure de la découpe, le chirurgien écarte la partie du foie qu'il veut supprimer afin de faciliter la suite de la découpe. Cette partie peut alors subir un important mouvement de rotation qui sera fidèlement simulé par notre modèle non linéaire (Fig. 7).

Simulation de chirurgie laparoscopique du foie en utilisant le modèle masse–tenseur « grands déplacements ». Sur les deux dernières images, la forme au repos est représentée en rendu filaire.
Évidemment, le temps de calcul des forces pour ce modèle non linéaire est nettement plus long que dans le cas linéaire. D'abord, parce qu'il nous faut parcourir, en plus des sommets et des arêtes, tous les triangles et tous les tétraèdres du maillage. Ensuite, parce que les expressions des forces sont nettement plus compliquées. Après avoir factorisé au maximum les calculs, nous avons obtenu une fréquence de simulation cinq fois inférieure à celle du modèle linéaire, soit environ 9 Hz sur un pentium PIII 600 MHz pour un modèle de foie comportant 6 342 tétraèdres (ce qui correspond à 1 394 sommets), alors qu'avec le modèle linéaire nous atteignons la fréquence de 45 Hz. Ce temps de calcul permet néanmoins d'obtenir une fréquence de 30 Hz avec un maillage comportant environ 2 000 tétraèdres, ce qui est suffisant pour atteindre le temps réel visuel avec des objets relativement complexes et pour fournir un retour d'effort réaliste en utilisant la méthode d'extrapolation des forces décrite dans 〚9〛. Une architecture multiprocesseurs, disponible aujourd'hui à un prix raisonnable, permettrait déjà de traiter des maillages plus complexes ou d'atteindre une fréquence de simulation supérieure. En effet, en raison de l'utilisation d'un schéma d'intégration explicite, le calcul des forces internes et l'intégration du mouvement se font sommet par sommet, ce qui permet de paralléliser ces calcul en décomposant le maillage en sous-domaines.
4 Conclusion
Nous avons proposé, dans cet article, un nouveau modèle déformable fondé sur l'élasticité en grands déplacements, la méthode des éléments finis et un schéma d'intégration explicite dynamique. Il résout les problèmes d'invariance par rotation posés par l'élasticité linéaire et tient compte des propriétés d'incompressibilité des tissus biologiques. Le fait d'inclure ce modèle dans notre prototype de simulateur de chirurgie améliore son réalisme biomécanique et donc accroît son intérêt pour la formation et l'entraînement des chirurgiens.
La validation d'un simulateur de chirurgie est un problème délicat. La comparaison avec des données réelles pose de nombreuses difficultés techniques et éthiques. Nous évaluons principalement nos développements en nous basant sur le retour des chirurgiens à qui nous faisons essayer le simulateur. Un protocole de comparaison de différents modèles et d'évaluation en milieu hospitalier est aujourd'hui en cours de mise en place en collaboration avec l'Institut de recherche sur le cancer de l'appareil digestif (Ircad) à Strasbourg.
Nos futurs travaux porteront sur l'amélioration de l'efficacité grâce à une nouvelle formulation de l'élasticité en grands déplacements. Nous envisageons aussi d'introduire les réseaux vasculaires à l'intérieur du parenchyme hépatique et de compléter nos modèles géométriques et physiques avec des composantes physiologiques (prise en compte de l'écoulement sanguin, de la respiration, etc.).
Abridged version
A major and recent evolution in abdominal surgery has been the development of laparoscopic surgery. In this type of surgery, abdominal operations such as hepatic resection are performed through small incisions. A video camera and special surgical tools are introduced into the abdomen, allowing the surgeon to perform a less invasive procedure. A drawback of this technique lies essentially in the need for more complex gestures and in the loss of direct visual and tactile information. Therefore, the surgeon needs to learn and adapt himself to this new type of surgery and in particular to a new type of hand–eye coordination. In this context, surgical simulation systems could be of great help in the training process of surgeons.
Among the several key problems in the development of a surgical simulator, the geometrical and physical representation of human organs remains among the most important. The deformable model must be at the same time very realistic (both visually and physically) and very efficient to allow real-time deformations.
Linear elasticity is often used for the modelling of deformable materials, mainly because the equations remain quite simple and the computation time can be optimised. The physical behaviour of soft tissue may be considered as linear elastic if its displacement and deformation remain small (typically less than 10% of the mesh size).
The linear elastic energy for homogeneous isotropic materials, is defined by the following formula (Hooke's law, eq. (1)):
| 1 |
Finite element method is a classical way to solve continuum mechanics equations. It is a mathematical framework allowing to discretise a continuous variational problem. We chose to use P1 finite elements where the elementary volume is a tetrahedron. By interpolating the displacement vector in the tetrahedron as a function of the displacements of its vertices, we can obtain the force applied by the tetrahedron on the vertex Pp (eq. (2)):
| 2 |
The main limitation of the linear model is that it is not invariant with respect to rotations. When the object undergoes a rotation, the elastic energy increases, leading to strong distorsions. In the case of a global rotation of the object, we could solve the problem with a specific change of the reference frame. But this solution proves itself to be ineffective when only one part of the object undergoes a rotation (which is the case in general). This unrealistic behaviour of the linear elastic model for large displacements led us to consider different models of elasticity.
The St Venant–Kirchhoff model is a generalisation of the linear model for large displacements, and is a particular case of hyper-elastic materials. The basic energy equation is the same (eq. 3), but now E stands for the complete Green-St Venant strain tensor:
| 3 |
Elastic energy, which was a quadratic function of in the linear case, is now a polynomial of order four with respect to The finite element method leads to the new formulation of the elastic force applied on the vertices of the mesh (eq. (4)):
| 4 |
Living tissue, which is essentially made of water, is nearly incompressible. This property is difficult to model and leads in most cases to instability problems. We choose to penalise volume variation by applying to each vertex of the tetrahedron a force directed along the normal of the opposite face, the norm of the force being the square of the relative volume variation.
We obtain a new deformable model, which is invariant with respect to rotation. This property improves the biomechanical realism of the simulated deformations. Obviously, the computation time of this model is larger than for the linear model because the force equation is much more complex. Nevertheless, with this non-linear model, we can reach a frequency update of 30 Hz on meshes made of about 2 000 tetrahedra, which is sufficient to reach visual real-time with quite complex objects.



