Abridged version
1 Introduction
It is in theory established that erosion of steep slope lining a passive margin promotes a consequent uplift of this margin, if the lithosphere responds flexurally to denudational unloading [5]. The uplift continues at the rate of erosion much later after the tectonics has acted. The models attach a particular importance to the influence of the drainage network, which controls erosion [7,12,13]. In this paper, we suggest confronting theory of [5] with the case of the erosion of a steep slope, lining the Atlantic margin, which presents a strong contrast of erodibility connected to a lateral variation of lithology. The example is that of the ‘Seuil du Poitou’ (Fig. 1), where a major unconformity separates a carbonate domain and a siliceous domain (with granitic dominant).
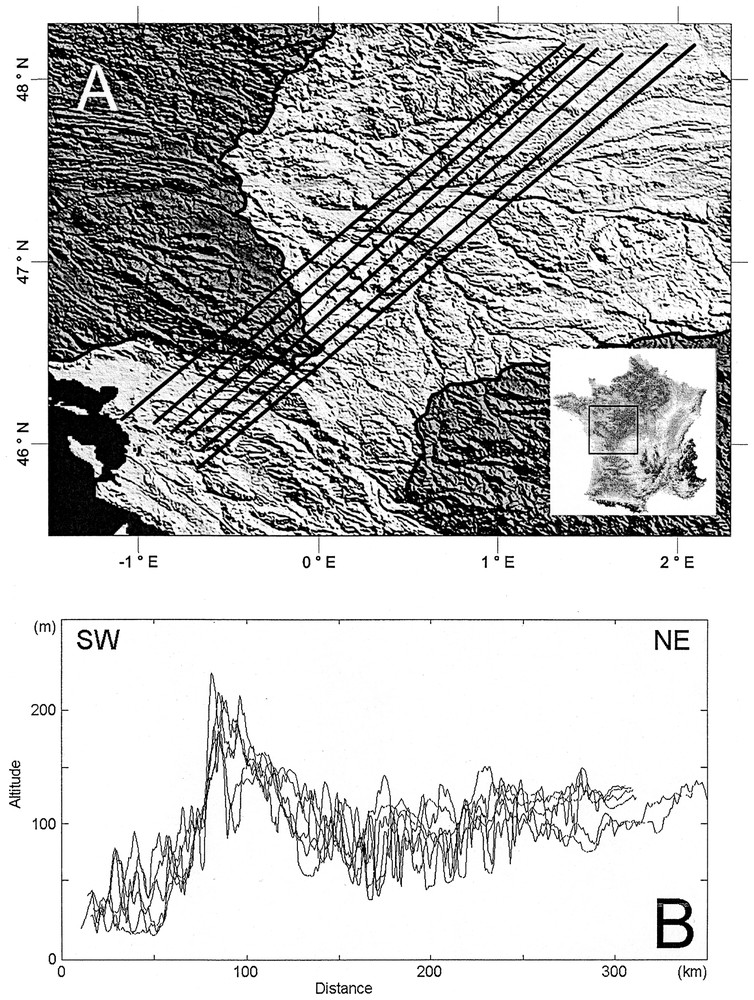
A. Localisation du seuil du Poitou dans l'Ouest de la France. Les lignes noires représentent les profils topographiques échantillonnés. La couverture calcaire du Jurassique est en gris pâle, le socle cristallin varisque en gris foncé et l'océan en noir. Le MNT est issu de la base de données GTOPO30. B. Ensemble des profils topographiques échantillonnés depuis les marais littoraux flandriens au sud-ouest et au-delà du bassin versant de la Loire au nord-est. Noter l'escarpement prononcé du seuil du Poitou et la flexure de la topographie vers le bassin versant de la Loire.
A. Location of the ‘Seuil du Poitou’ in western France. Topographic profiles used are the black straight line. Jurassic limestones substrate is in pale grey; crystalline substratum is in dark grey and ocean in black. The DEM used was obtained from GTOPO30 database. B. The whole topographic profiles sampled since the Flandrian salt marsh to the southwest and beyond the watershed of the Loire River to the northeast. Note the steep slope pronounced by the ‘Seuil du Poitou’ and the flexure of the topography towards the Loire watershed.
2 The ‘Seuil du Poitou’ (SP)
The SP is a 120 km-long steep slope that trends WNW–ESE, parallel to the Variscan South Armorican Shear Zone [3]. This orientation is also that of the faults that have controlled the development of the eastern passive margin of the Atlantic Ocean [1]. The SP limits a low elevation continental plateau (mean elevation 120 m), which presents an evident flexure (Fig. 1B). The plateau is drained in the large catchment basin of the Loire River. The SP is a scarp that cuts (Fig. 1) the ancient boundary of the Jurassic transgressive limestones on the Variscan basement [4]. This break promoted a vertical offset of about 120 m of Eocene limestones [14,15]. Some authors propose also successive fault slip in the Miocene and in the Pliocene from observations of offset river systems [8] and erosion surfaces [16].
3 The model
Flexure responding to denudational unloading is modelled (Figs. 2 and 3) assuming a thin elastic plate overlying an inviscid fluid according to:
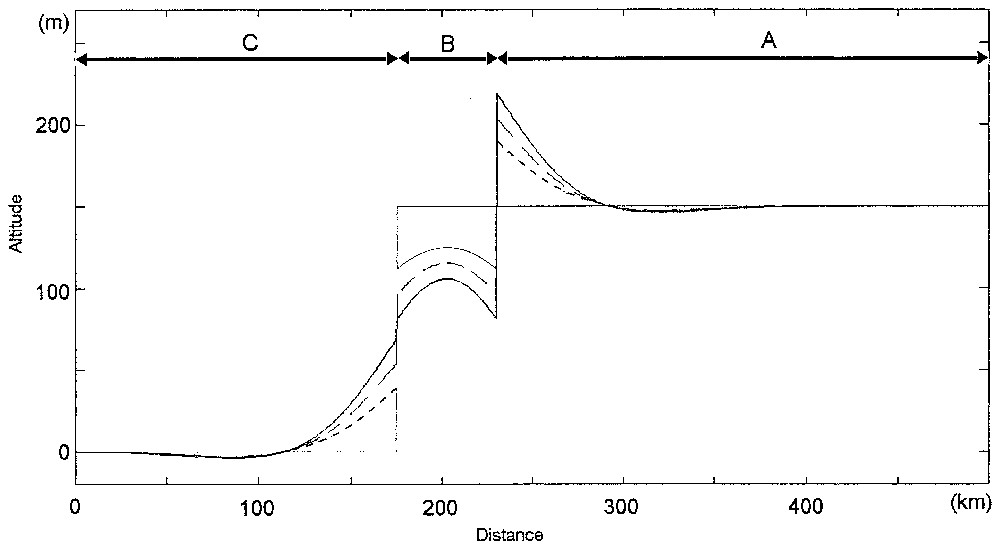
Illustration du modèle de réponse isostatique flexurale à l'érosion différentielle d'un plateau continental limité par un escarpement. La dénudation massique est réalisée depuis un partage des eaux fixe sur le plateau. Le pas de temps du modèle est de 0,1 Ma et l'épaisseur équivalente élastique égale à 11 km. Les taux d'érosion sont respectivement de 15, 30 et 15 m Ma−1 pour les domaines A, B et C. Profil topographique respectivement après 1 Ma (pointillés), 3 Ma (tirets espacés) et 5 Ma (trait plein) d'érosion.
Illustration of the model of flexural isostasy in response to the differential erosion of a continental plateau bounded by a steep escarpment. The denudational unloading is realised since a fixed point of water sharing on the plateau. Time step of the model is 0.1 Ma and the elastic equivalent thickness is 11 km. The rates of erosion are respectively 15, 30, and 15 m Ma−1 for domains A, B and C. Resulting topographic profiles after 1 Ma (dotted line), 3 Ma (spaced dotted line) and 5 Ma (full line) of erosion, respectively.
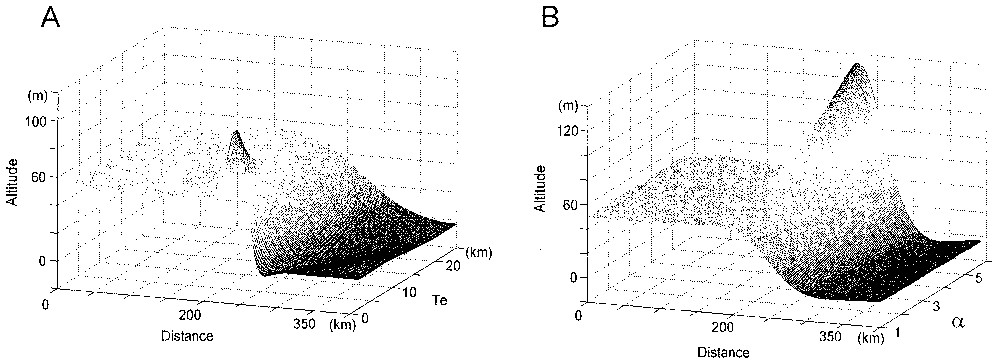
A. Modélisation de la flexure théorique pour différentes épaisseurs équivalentes élastiques (Te), avec taux d'érosion fixes. B. Modélisation de la flexure théorique pour différents rapports d'érosion (α) entre le plateau et le niveau de base (exemple: α=3, l'érosion vers le niveau de base est trois fois plus forte que sur le plateau).
A. Theoretical flexure for different effective elastic thickness (Te) with fixed erosion rates. B. Theoretical flexure for different ratio of erosion (α) between the plateau and the base level (example: α=3, the erosion towards the base level is three times as strong as on the plateau).
Vertical flexure was calculated in the wavenumber domain from:
4 Results
Adopting the configuration of [5], we considered that the SP was responsible for a vertical slope. We fixed the height of the plateau limited by the SP to 150 m above the current sea level. The limit between the wide watershed of the Loire River and the small catchment of the coastal rivers is situated at an average distance of 50 km from the Flandrian shoreline. The rate of erosion towards the Loire basin is deduced from the recent measurements of cosmogenic 10Be produced in sands taken in the bed of the river and some of its tributaries [11]. The elastic equivalent thickness is fixed to 11 km in reference to flexure models of the north Pyrenean domain and of the Aquitaine Basin [9]. Parameters determining the flexural rigidity of the model are those usually given in the literature [9].
The model is applied with a time step of 100 ka. After 5 Myr, it corresponds to an erosion of 75 m towards the Loire. Between the Loire watershed and the border of the steep slope, the relief amplitudes require applying erosion naturally more important, but which differs depending on the nature of the substratum, 150 m for the limestones and 200 m for the crystalline basement, respectively (Fig. 4). On a smaller scale, this difference is attested by deeper valley incision in the crystalline basement than in the limestones.


Résultats de la modélisation sur un temps d'érosion cumulé de 5 Ma: en trait plein grisé, la topographie réelle, en trait plein noir, la topographie synthétique, en tirets serrés l'érosion totale par secteur, en tirets espacés la flexure totale. A. Profils et modèle sur substratum cristallin. B. Profils et modèle sur substratum calcaire. Noter l'amplitude plus forte des reliefs et de la flexure dans le cristallin par rapport aux calcaires et la nécessité d'imposer une érosion plus forte dans le cristallin.
Modelling results after 5 Ma of erosion: grey line = real topography, black line = synthetic topography, tight dotted line = total erosion by sector, spaced out dotted line = total flexure. A. Profiles and model calculated across the crystalline basement. B. Profiles and model calculated across the limestones substrate. Note the stronger amplitude of reliefs and flexure and necessity to impose stronger erosion in the crystalline basement than in limestones.
5 Conclusions
A simple physical model simulating the isostatic rebound of the border of a passive margin in response to erosional unloading allows us to represent the flexure of the topography of the Loire catchment basin observed in the north of the SP (Fig. 1B). Erosion time necessary for the growth of the observed flexure is 5 Myr. Erosion was stronger in the crystalline basement than in the limestones. The limestone plateau presents an inherited, very dense karstic network, developed since the end of the Cretaceous [10]. One may suppose that on the last five millions years, the surface runoff and of this fact mechanical erosion were more intense on the crystalline basement than on the limestones where the inherited karst favoured the infiltration.
1 Introduction
Il est théoriquement établi que l'érosion de l'escarpement bordant une marge passive entraı̂ne un soulèvement conséquent de cette marge, pourvu que la plaque se flexure en réponse au rebond isostatique compensant la dénudation [5]. D'autres travaux développent ce concept, avec des simulations numériques plus approfondies de l'évolution à long terme des marges escarpées du Sud de l'Afrique [7,12] et de l'Australie [13]. Les modèles attachent une importance particulière à l'influence de la répartition des réseaux de drainage qui contrôlent l'érosion. Ainsi, la dénudation de l'escarpement est d'autant plus importante que le partage des eaux est, dès l'origine, éloigné de la ligne de crête. Le contrôle lithologique est également examiné, dans la mesure où la plus ou moins forte résistance du substrat à l'incision fluviale détermine le recul de l'escarpement et la dénudation de la marge. Les conséquences de ces variations lithologiques en terme de réponse isostatique demeurent malgré tout assez théoriques. Nous proposons de confronter cette théorie au cas de l'érosion d'un escarpement bordant la marge atlantique, qui présente un fort contraste d'érodibilité lié à une variation latérale de lithologie. La modélisation unidimensionnelle est classique, elle est directe et consiste à simuler la forme de la topographie au premier ordre. L'exemple est celui du Seuil du Poitou (Fig. 1), où existe une discordance majeure qui sépare un domaine carbonaté (les calcaires de la transgression jurassique) et un domaine siliceux à dominante granitique (le socle hercynien).
2 Le seuil du Poitou (SP)
Le seuil du Poitou est un escarpement de 120 km de long, orienté selon un axe WNW–ESE, qui se superpose à l'orientation du cisaillement varisque sud-armoricain [3]. Cette direction est également celle des failles qui ont contrôlé la formation de la marge passive de l'Atlantique au Mésozoı̈que [1]. Morphologiquement, le SP représente une rupture topographique nette (Fig. 1) et escarpée sur son versant littoral (Fig. 1B). Il culmine à 250 m d'altitude au-dessus des marais de l'Ouest (Marais poitevin et Marais charentais), comblés depuis le Flandrien. Sur le versant opposé, le SP limite un plateau continental peu élevé (120 m d'altitude moyenne), qui présente une nette flexure à grand rayon de courbure (Fig. 1B). Le plateau est drainé dans le large bassin versant de la Loire (Fig. 1A). La singularité du SP est qu'il recoupe (Fig. 1A) l'ancienne limite des dépôts calcaires de la transgression jurassique [4] sur le substratum hercynien. La topographie est rapportée au jeu d'un segment de faille qui affaisse, vers le sud-ouest, des calcaires lacustres du Sannoisien sur une hauteur d'environ 120 m entre le plateau et la dépression de Saint-Maixent [14,15]. La période de la rupture n'est pas identifiée de manière précise. Pour les uns, l'essentiel du décalage s'est produit à l'Oligocène [14]. D'autres auteurs proposent des jeux successifs au Miocène, puis au Pliocène, à partir d'observations de décalages du réseau hydrographique [8] ou de surfaces d'érosion [16].
3 Principe du modèle
La simulation consiste à calculer la réponse flexurale à la dénudation d'une plaque élastique d'épaisseur constante reposant sur un fluide non visqueux [5]. Elle est donnée par la relation suivante dans un repère orthonormé unitaire selon un profil d'axe x :
La rigidité flexurale D est donnée par , où E est le module d'Young, Te l'épaisseur équivalente élastique de la plaque et ν le coefficient de Poisson. La dénudation l(x) vaut , où ρ est la densité moyenne des matériaux érodés et z(x) la hauteur enlevée. L'équation de la réponse flexurale est calculée dans le domaine fréquentiel et vaut :
La flexure w de la plaque mince élastique est de fait amplifiée par une décharge non uniforme de sa surface (Fig. 2). Le contraste est introduit avant allégement par un décalage en escalier de la surface, figurant l'escarpement bordier d'une marge passive. Du fait du contraste topographique, la dénudation est plus importante vers le littoral que sur le plateau. Les masses soustraites sont évacuées à l'extérieur du système et ne provoquent aucune surcharge sur le modèle (Fig. 2). Cela revient à admettre, en première approximation, que les produits érodés transitent dans le réseau hydrographique continental jusqu'à l'océan, où ils sont dissous, ou bien qu'ils sont déposés à l'infini, bien au-delà des limites du modèle. Outre l'influence de la position initiale de la ligne de partage des eaux déjà évoquée en introduction, deux paramètres déterminent également le résultat du modèle. D'une part, l'épaisseur équivalente élastique de la plaque qui, pour un différentiel d'érosion donné, provoque une flexure d'autant plus ample que cette épaisseur est réduite (Fig. 3A). D'autre part, le différentiel d'érosion qui, pour une épaisseur équivalente élastique donnée, génère une flexure d'autant plus ample que l'érosion vers le littoral est importante (Fig. 3B).
4 Résultats
Adoptant la configuration décrite ci-dessus, nous considérons que le SP est à l'origine un escarpement vertical. L'hypothèse est raisonnable si l'on admet que cette rupture se superpose à des accidents très raides affectant la croûte varisque. Nous fixons l'altitude du plateau limité par le SP à 150 m au-dessus du niveau actuel de la mer. C'est en effet l'altitude maximum des buttes témoins vers le bassin de Paris (Fig. 1A et B). Ce dénivelé est également de l'ordre de grandeur du décalage tectonique vertical évalué le long du SP. La ligne de partage des eaux entre le large bassin versant de la Loire et les petits bassins versants côtiers (Charente, Sèvres, Vendée) se situe à une distance moyenne de 50 km par rapport aux rivages des marais flandriens. Le réseau hydrographique étant décalé par le SP [8], nous admettons que cette position du partage des eaux est héritée. Elle est donc considérée comme un paramètre fixe du modèle. Le taux d'érosion vers la Loire est déduit des résultats récents des mesures de 10Be cosmogénique produit dans les sables prélevés dans le lit du fleuve et de certains de ses affluents [11]. Utilisant la régression linéaire établie entre les taux d'érosion et les altitudes moyennes des bassins versants [11], on déduit un taux de dénudation de 15 m Ma−1 dans le cas du plateau drainé à une altitude moyenne de 120 m. L'épaisseur équivalente élastique est fixée à 11 km, par référence à celle utilisée dans le modèle de flexure du domaine nord-pyrénéen et du Bassin aquitain [9]. Les paramètres déterminant la rigidité flexurale de la plaque sont également ceux couramment utilisés dans la littérature et valables pour le Nord des Pyrénées [9], à savoir : un module d'Young de 106 N m−2 et un coefficient de Poisson de 0,25. Enfin, la densité des matériaux érodés correspond à une valeur moyenne de régolite calcaire ou granitique, soit 2700 kg m−3.
Le modèle est appliqué avec un pas de temps i de 100 ka. Après sommation et simplification des termes semblables, la topographie finale T(x,n) selon un profil d'axe x et un délai de temps n est la somme de la topographie initiale T(x,0), de l'érosion E(x,i) et de la réponse flexurale F(x,i), avec :
La topographie finale est ainsi ajustée aux points d'altitude maximale, échantillonnés selon différents profils sur le modèle numérique de terrain. Les résultats sont représentés sur la Fig. 4. Ainsi, les meilleurs ajustements de la topographie sur le plateau sont obtenus pour des durées de temps cumulé de 5 Ma. Sur cette période, cela correspond à une érosion de 75 m vers la Loire en appliquant le taux d'érosion de 15 mm ka−1 choisi plus haut. Entre la ligne de partage des eaux et la bordure de l'escarpement, l'amplitude des reliefs nécessite d'appliquer une érosion bien entendu plus importante, mais qui diffère selon la nature du substratum. Pour des profils échantillonnés à travers le substratum calcaire et qui ont la particularité de culminer aux environs de 200 m (Fig. 4B), l'érosion est de 30 m Ma−1. En revanche, pour des profils échantillonnés à travers le substratum cristallin et qui, pour leur part, culminent aux environs de 250 m, l'érosion est de 40 m Ma−1 (Fig. 4A). Enfin, nous remarquons que, dès les premiers incréments du modèle, la flexure de la topographie a pour conséquence un soulèvement du domaine littoral en forme « de cloche topographique ». L'ajustement de cette nouvelle topographie aux points les plus hauts de ce domaine impose un taux d'érosion différent selon le substratum. Il est, en effet, moins fort dans les calcaires (15 m Ma−1) que dans le cristallin (25 m Ma−1). Un examen attentif des profils réels, sous le tracé de « la cloche topographique théorique » (Fig. 4), indique d'ailleurs que le creusement des vallées est nettement plus marqué dans le substrat cristallin que dans les calcaires.
Un des résultats essentiels du modèle est donc la part supplémentaire de dénudation que l'on doit imposer dans le cristallin, par rapport aux calcaires, pour justifier la croissance plus importante du relief. Cette différence se traduit, au premier ordre, par une flexure plus prononcée et une amplitude plus forte du SP au niveau des profils traversant le substratum cristallin par rapport à ceux traversant les calcaires (Fig. 4). Sur le terrain, nous observons que la différence d'érosion se traduit effectivement par une incision plus profonde des vallées fluviales dans le socle cristallin que dans le substrat calcaire. En effet, selon le principe établi par Bonnet et al. [2], le report des demi-largeurs en fonction des profondeurs des vallées qui entaillent le SP (Fig. 5) indique bien que l'encaissement est plus profond dans le cristallin que dans les calcaires.
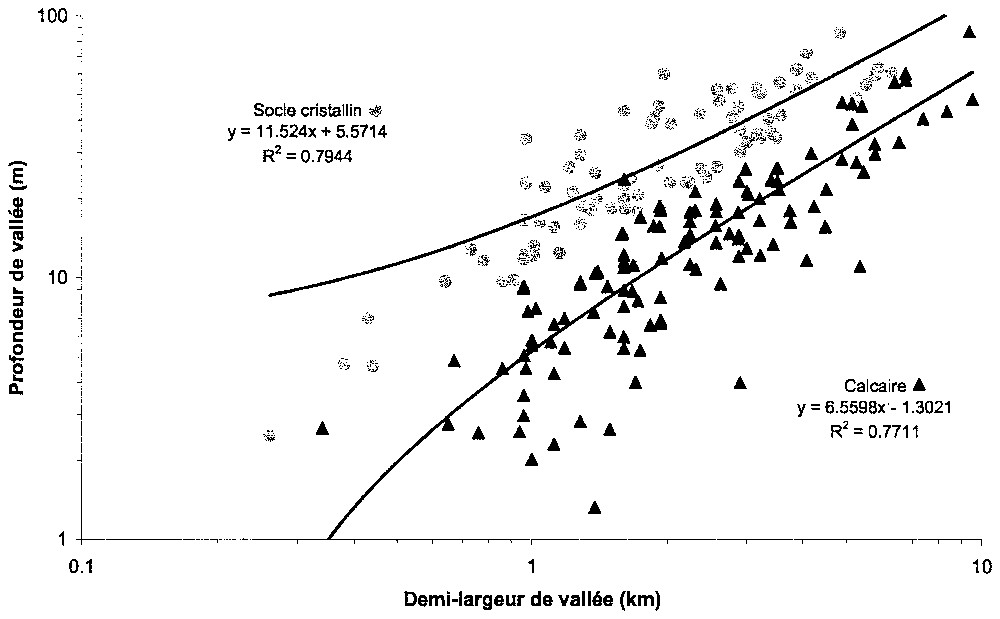
Répartition log–log des demi-largeurs des vallées en fonction de leur profondeur.
Log–log plot of half-valley width versus valley depth.
5 Conclusions
L'application d'un modèle physique simple, unidirectionnel, simulant le rebond isostatique de la bordure d'une marge passive sous l'effet de l'érosion permet de figurer la flexure de la topographie du bassin versant de la Loire, observée au nord du SP (Fig. 1). La période d'érosion nécessaire à la croissance de la flexure, telle qu'on l'observe aujourd'hui, est de 5 Ma. On doit, dans ce cas, admettre que la rupture tectonique et l'essentiel du mouvement vertical qui ont généré l'escarpement du SP sont antérieurs à cette période et se sont donc accomplis au plus tard au début du Pliocène.
Au-delà de ces aspects régionaux, une conclusion sans doute plus originale de notre modélisation, confrontée à l'observation (Fig. 5), est la mise en évidence, au niveau du SP, d'un taux d'érosion pratiquement deux fois plus élevé sur le substrat cristallin que sur le substrat calcaire. Les conséquences sont une élévation topographique et une incision fluviale plus importantes des reliefs cristallins par comparaison aux reliefs calcaires. Cela mérite discussion. En effet, on considère habituellement que les paysages carbonatés « solubles » doivent subir une dénudation totale, associant à l'érosion mécanique une forte érosion chimique, plus importante que les paysages cristallins peu ou pas « solubles » [6]. Cela est vérifié si l'érosion mécanique et l'érosion chimiques sont en équilibre [6]. Or, le plateau calcaire jurassique du Poitou présente un réseau karstique hérité, très dense, développé depuis le Crétacé [10]. On peut donc supposer que, sur les cinq derniers millions d'années, le ruissellement et de ce fait, l'érosion mécanique de l'escarpement du SP, furent plus intenses sur le socle cristallin que sur les calcaires, où le karst hérité a favorisé l'infiltration.
Remerciements
Cette étude a bénéficié des soutiens financiers du Programme national de recherche en hydrologie de l'INSU–CNRS (projet 01 PNRH 14) et du conseil général de Charente-Maritime. Les auteurs remercient Jean-Pierre Burg et un expert anonyme, qui ont contribué à améliorer la version initiale du projet de note.



