Abridged English version
Even if kriging has solved the estimation of grades in natural media since 1965 [7], several methodological issues occur in the case of heterogeneous media. We will not detail here the important question of the inference of a spatial structure. Furthermore, costs allotted to site investigation and remediation, although increasing, still limit the sampling effort. When the spatial structure is weak or masked by a few high grades, soft data may then be of value to improve the precision of the estimates. Cheap and potentially abundant, is such information useful in practice for the grade estimation?
The best empirical correlation between a numeric variable and a qualitative one is obtained with the mean grade for each category of the soft variable. In this model, Z(x) is a ‘scattered variable’ of its mean M(x) by category, which can be written E[Z(x)∣M(x)]=M(x). The cokriging estimate of Z with M allows the block estimation of Z, which corresponds to the actual selection, whereas a selection based on the soft variable would correspond to a selection on a punctual support.
The relationship between the soft variable and the grade is explored through several statistics: mean and median of the grades by category of the soft variable, rank means, grade histograms.
This method is easily generalized in the case of several soft variables. However, a correspondence analysis summarizes in a few non-correlated factors most of the information contained in the soft variables. If they are correlated with the grades, the resulting factors may then be introduced in the grade estimation process.
To illustrate the above methodology, we discuss the relationship between several qualitative soil characteristics and benzo(a)pyren grades (BaP), a carcinogenic Polycyclic Aromatic Hydrocarbon, on a former coke plant.
Qualitative characteristics of samples have been observed on the sampled points: presence/absence of coal, coal tar, smell, limestone grains, stonework pieces, greenish colour of the sample, dross, etc. Among several statistics, the grade histogram is of interest. Fig. 2 illustrates the relationship between two qualitative variables and the BaP grades. While the presence of stonework pieces is not preferentially associated to small of large BaP grades, the presence of coal tar systematically corresponds to large BaP grades. Consequently, with a reduced cost, this auxiliary variable brings some information about the pollution.
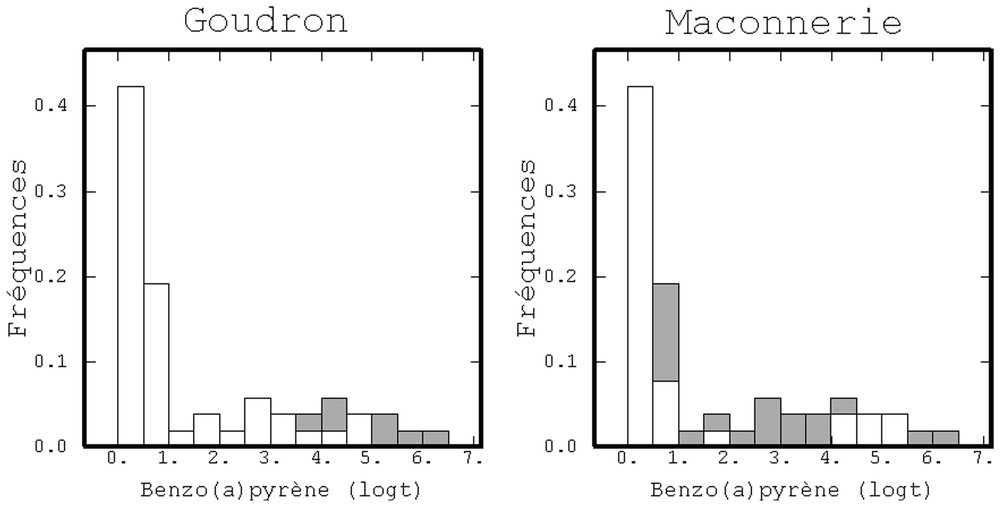
Histogrammes par classe du logarithme translaté de BaP. Blanc : absence de l'indice ; gris : présence.
Histograms of BaP translated logarithms. White : absence of the soft variable ; grey : presence.
A correspondence analysis is performed on all the soft variables. The first factors represent 33.6% and 23.5% of the total variance of the data (Fig. 3). The greenish colour, limestone grains and presence of coal in soil mainly indicate that we are dealing with a soil in place, whereas the other variables are more indicators of backfill; consequently, the first factor (called ‘auxiliary factor’ hereafter) distinguishes backfilled materials (high values) and soil in place.

AFC sur les indices qualitatifs : projection des indices sur les deux premiers facteurs.
Correspondence analysis on soft variables : projection of variables on the first factors.
The experimental variogram of BaP is fitted by the model and used for the ordinary kriging of the grades (OK). All the estimations are performed punctually with a unique neighbourhood over a grid.
Working in the framework of a linear model of coregionalization, bivariate variogram models are then fitted on the BaP grade Z and (a) its mean for each category of coal tar (absence/presence) and (b) the auxiliary factor (see Fig. 6 for the coal tar).
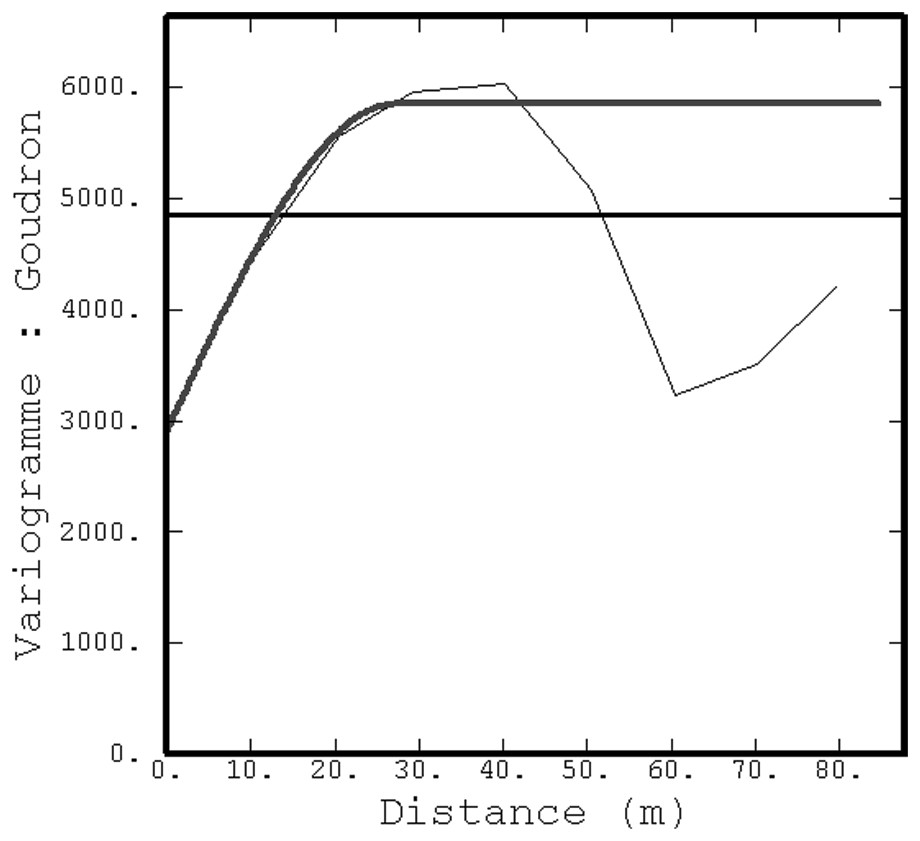

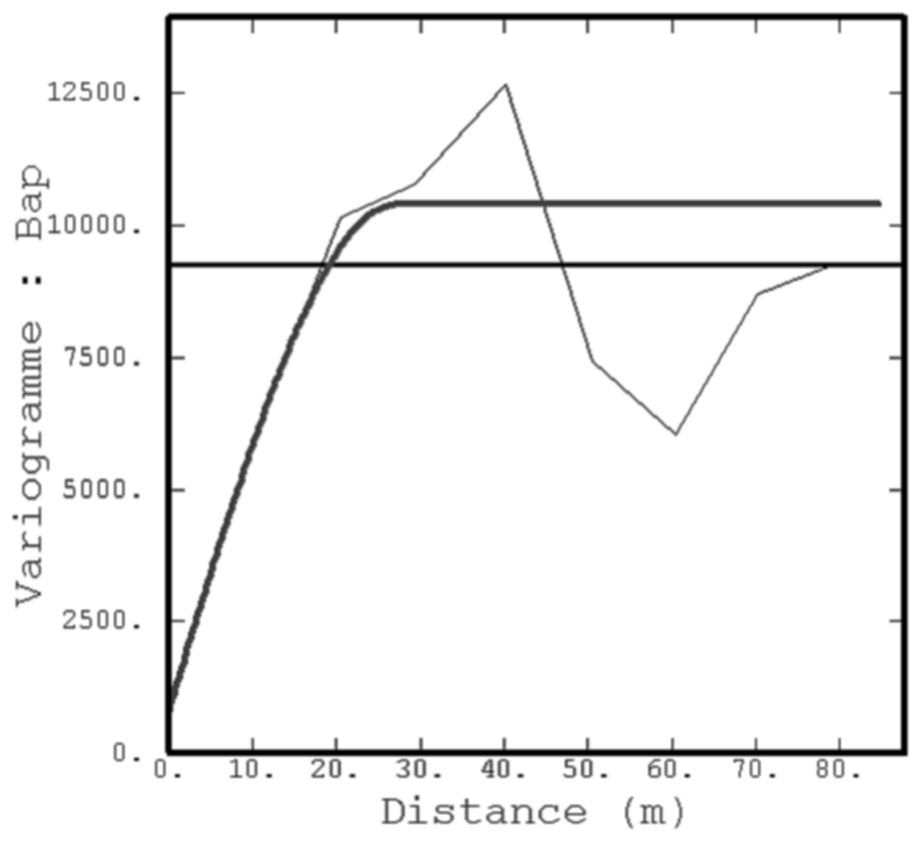
Modèle ajusté entre la teneur en BaP et sa moyenne par classe de goudron.
Variogram model between BaP grades and their mean by class of coal tar.
Cokriging BaP grades with isotopic (all variables known at the same locations) soft data does not improve sensibly the results. To assess the gain in precision obtained by using more densely sampled soft data, 50% of randomly selected BaP grades are used as a validation set. OK of the other 50% BaP grades is performed at the location of the validation samples. This result is compared with those obtained by ordinary cokriging (OCK) with the presence of coal tar, assumed known on all samples, and OCK with the auxiliary factor. Fig. 7 shows the improvement brought by the cokriging, particularly for the highest real value and the small grades. Mean error and mean square error between the OK estimates and the real BaP grades are computed on this validation set (Table 2). Both cokriging results lead to improved mean errors and mean square errors compared to the OK, in particular for the OCK with coal tar.
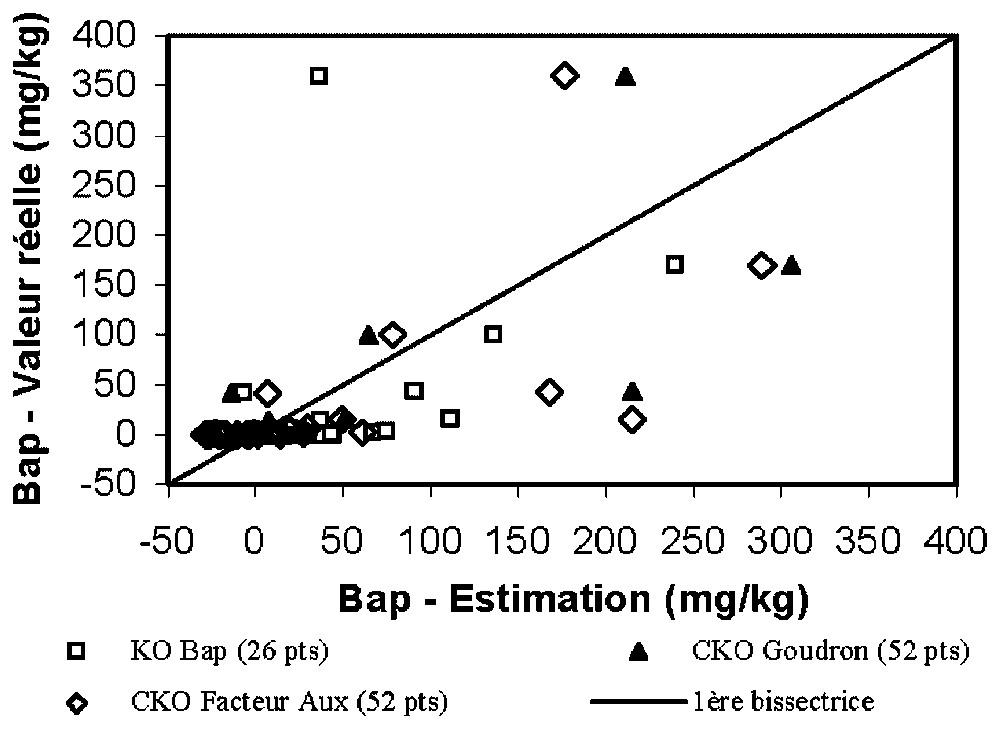
Nuages de corrélation entre les teneurs de BaP de validation et leur estimation par krigeage ordinaire, cokrigeage avec le goudron et cokrigeage avec le facteur auxiliaire.
Scatter diagrams between validation BaP grades and their estimate by ordinary kriging (KO) and cokriging with the coal tar or the auxiliary factor.
Erreurs moyennes et quadratiques moyennes sur les teneurs en BaP aux 26 points de validation, obtenues par krigeage des teneurs seules ou par leur cokrigeage avec l'une ou l'autre des variables auxiliaires
Mean errors and quadratic mean errors for the 26 validation BaP grades, obtained by ordinary kriging (KO) and cokriging with either the coal tar or the auxiliary factor
| Type d'estimation | Erreur moyenne | Erreur quadratique |
| (ppm) | moyenne | |
| KO BaP | 15,28 | 6253 |
| CK avec goudron | 5,93 | 3309 |
| CK avec facteur | 8,66 | 4980 |
In conclusion, the use of multivariate geostatistics, by improving the grade estimation using auxiliary soft information, is of real importance. From this point of view, this technical note discusses how to choose in practice a relevant auxiliary variable and presents the added value of this soft information for the grade estimation. If this is confirmed on other sites, this will give useful hints for the choice of more efficient sampling strategies of polluted sites.
1 Introduction
Si l'estimation des teneurs dans les milieux naturels est résolue depuis 1965 [7] grâce au krigeage, sa mise en œuvre pour des milieux fortement hétérogènes pose plusieurs questions méthodologiques. D'une part, le fort contraste des teneurs dans ces milieux rend délicate la mise en évidence d'une éventuelle structure spatiale ; cette question de l'inférence du variogramme, approfondie dans [6], n'est pas abordée ici. D'autre part, des informations qualitatives complètent fréquemment les données d'échantillonnage. Lorsqu'elles sont corrélées aux teneurs, des informations faciles à acquérir, peu coûteuses et, par suite, potentiellement abondantes, permettraient d'améliorer la précision des estimations, notamment lorsque la structure spatiale inférée sur les teneurs est médiocre. Plusieurs statistiques permettent de caractériser les liaisons entre des variables qualitatives et des variables numériques, comme les teneurs. Cette note a pour objectif de montrer comment extraire de ces informations qualitatives des variables auxiliaires utilisables pour le cokrigeage des teneurs.
Pour une friche industrielle polluée par des hydrocarbures aromatiques polycycliques (HAP), nous examinons les liaisons entre différents indices qualitatifs ainsi que les teneurs dans les sols, et nous évaluons l'amélioration de la précision obtenue dans l'estimation des teneurs, en incorporant ces indices dans le cokrigeage de la teneur.
2 Méthodologie
Dans de nombreux domaines, des observations qualitatives apportent une information sur la variable d'intérêt, par exemple les teneurs en place. Usuellement, ces observations sont codées numériquement, par exemple 0 pour « absence », 1 pour « faible » et 2 pour « fort ». Un tel codage, arbitraire, pose problème pour incorporer ces observations comme variables auxiliaires dans un cokrigeage des teneurs [2].
Plusieurs statistiques sont utilisées classiquement pour examiner les relations entre une variable qualitative ou indice, supposée désormais codée en N classes ou catégories, et une variable continue, désignée par « teneur » dans la suite (voir par exemple [9]) : moyenne, médiane et histogramme des teneurs par classe de l'indice, moyenne des rangs. Les teneurs sont ordonnées par ordre croissant, puis numérotées suivant leur « rang », compris entre 1 et le nombre de mesures. La moyenne de ces rangs par classe de l'indice présente l'avantage d'être robuste vis-à-vis de teneurs très fortes. Les histogrammes des teneurs par classe d'indice correspondent à la loi conditionnelle des teneurs ; sur les mesures disponibles, ils décrivent exhaustivement la relation teneurs–catégories, point à point.
On sait que la meilleure corrélation point à point entre une variable numérique Z et toute fonction de l'indice P est la régression de Z sur P : la moyenne de Z par classe de P permet ainsi de convertir l'indice P en une grandeur de même « dimension » que Z, et maximisant leur corrélation, sans nécessiter aucun codage arbitraire. Dans le cas de fonctions aléatoires, on commencera par vérifier la stationnarité spatiale de la loi conditionnelle de Z(x) relativement à P(x). Dans la suite, le couple de fonctions aléatoires (Z(x), P(x)) est supposé stationnaire.
Posons M(x)=E[Z(x)|P(x)]. Alors, dans la décomposition de Z en moyenne par classe et résidu Z(x)=M(x)+R(x), la moyenne de R(x) par classe est nulle. Par suite, E[Z(x)|M(x)]=M(x) et Z(x) est une « dispersée » de M(x). Par conséquent, à même tonnage de sol remué (le tonnage de « minerai »), une sélection sur M(x) entraı̂ne une moindre récupération de la pollution (le « métal » en termes miniers, voir [8]) qu'une sélection sur la teneur Z(x), si celle-ci était connue. Si les moyennes par classe sont différentes (ou si les classes de même teneur moyenne sont regroupées), il y a bijection entre M et P. La sélection sur l'indice ne doit pas faire illusion : même avec une couverture très dense, les erreurs de sélection sont inévitables, et d'autant plus marquées que la variance des teneurs par classe est importante. De plus, la sélection sur l'indice ne permet pas de tenir compte de la différence de support entre l'échantillon, quasi « ponctuel », et l'unité minimale de sélection, par exemple le godet d'une pelleteuse, qui lui est supérieure de plusieurs ordres de grandeur.
Considérons un indice à deux catégories, et soit I l'indicatrice de l'une des catégories. M(x) s'écrit : .
Soit M1=E[Z(x)|I(x)=1] et M0=E[Z(x)|I(x)=0] ; un calcul simple montre que le variogramme de la moyenne par classe M(x) est proportionnel à celui de l'indicatrice :
Lorsque plusieurs indices sont relevés, la méthode se généralise en définissant une variable moyenne par classe pour chaque indice, ou en croisant les catégories des différents indices (cas de la stratification exhaustive), avec regroupement éventuel des classes de même moyenne conditionnelle de la teneur.
Un exemple de cokrigeage de Z pour plusieurs indices, dans un modèle légèrement différent, est présenté dans la référence [4].
Dans le cas de plusieurs indices, l'analyse factorielle des correspondances synthétise l'information des différentes variables qualitatives. Les indicatrices de l'ensemble des catégories sont décomposées en facteurs point à point non corrélés, dont on conserve ceux qui restituent une part importante de l'information. Si ces facteurs sont corrélés aux teneurs, ils sont utilisables comme variables auxiliaires pour le cokrigeage des teneurs.
3 Exemple d'une pollution par des HAP
Lors d'audits de sites industriels potentiellement pollués, il est parfois encore admis qu'une bonne connaissance de l'historique du site, complétée par quelques prélèvements « de contrôle », suffirait pour délimiter les zones à dépolluer. Mais les risques résultant d'une connaissance approximative de cet historique rendent indispensable un échantillonnage systématique [6], souvent limité pour des raisons de coût. Pour palier le nombre trop restreint de mesures, des approches macro-exploratoires cherchent à tirer de l'information de sites similaires (voir [3] pour une approche par réseaux de neurones artificiels). Ces méthodes sont cependant inopérantes pour l'estimation locale pour un site donné. Les observations qualitatives peuvent alors fournir une information supplémentaire peu coûteuse et potentiellement abondante.
Le site étudié, situé dans le département du Nord (59), est une partie de la zone d'épandage d'une ancienne cokerie, fermée en 1973, remblayé et nivelé depuis, et présentant une importante pollution par des hydrocarbures aromatiques polycycliques. Une zone de 1 ha a été reconnue par 52 sondages, implantés suivant une grille carrée de 10 m de côté, localement resserrée à 5 m (Fig. 1). Les échantillons sont des carottes de 1 m de long et 45 mm de diamètre forées au fond de fosses à 1,5 m de profondeur.
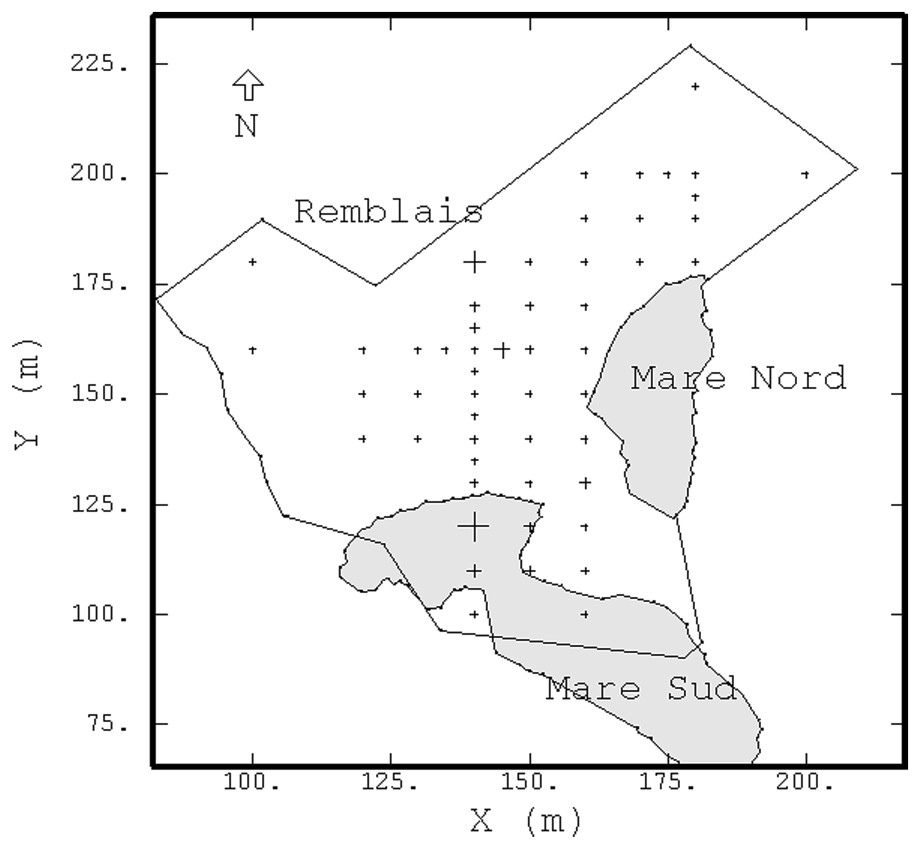
Implantation proportionnelle des teneurs en BaP, informations issues de l'étude historique et limites du site.
Proportional location of BaP grades, historical information and site contour.
Les 16 HAP de la liste US EPA ont été analysés par chromatographie liquide haute pression (HPLC) après séchage des échantillons à l'air libre et tamisage à 2 mm, suivant les normes Afnor. Le benzo(a)pyrène (BaP), HAP à cinq cycles, présente des effets cancérigènes avérés [1]. Souvent considéré comme représentatif du comportement des autres HAP, il est retenu pour l'examen des relations entre concentration et information qualitative. La moyenne expérimentale des concentrations en BaP est égale à 37,83 ppm. L'écart type, de 96,25 ppm, correspond à un coefficient de variation important, d'environ 2,5, valeur usuelle pour ces produits.
4 Des indices organoleptiques aux variables auxiliaires
Durant l'échantillonnage, huit indices pédologiques et organoleptiques ont été relevés sur les sondages : présence/absence d'odeur, de goudron, de charbon (dans les remblais ou dans le sol), débris de maçonnerie, laitier, couleur verdâtre des limons, présence de craie dans le sol. Informations peu coûteuses, ces indices constituent-ils des indicateurs de la pollution, ou lui sont-ils liés ?
Un indice utilisé pour guider l'échantillonnage doit nécessairement détecter toutes les teneurs « fortes » parmi les échantillons prélevés, au risque sans cela de manquer des zones contaminées. Mais un indice significativement corrélé à la concentration est également utilisable pour améliorer l'estimation. Nous examinons donc les relations entre différentes variables auxiliaires et les teneurs.
4.1 Statistiques élémentaires
La moyenne et la médiane des concentrations en BaP par classe des variables qualitatives, ainsi que les moyennes des rangs, sont reprises dans le Tableau 1 pour deux indices.
Statistiques de la concentration en BaP par classe (absence (a) et présence (p)) d'indices qualitatifs : effectifs, moyennes, médianes et moyennes des rangs
Statistics of BaP grades by category of soft variable (absence (a), presence (p)) : number of samples, means, medians and mean ranks
| Indice | p/a | Effectif | Moyenne | Médiane | Moyenne des rangs |
| Goudron | a | 45 | 10,36 | 0,59 | 21,38 |
| p | 7 | 214,43 | 89,00 | 41,43 | |
| Maçonnerie | a | 33 | 23,35 | 0,24 | 18,33 |
| p | 19 | 62,99 | 6,90 | 33,68 |
Pour le goudron, l'absence ou la présence se révèle bien discriminante, à la fois pour la moyenne et la médiane des teneurs. Quant aux débris de maçonnerie, observés plus fréquemment que les traces de goudron, les écarts sur la moyenne ou la médiane par classe sont notables, mais plus réduits que pour le goudron. Les trois statistiques vont ici dans le même sens, et semblent informatives.
4.2 Histogrammes par classe
L'histogramme du logarithme translaté des teneurs logt[Z(x)]=ln[1+Z(x)] montre qu'aucun des indices ne détecte l'ensemble des mesures supérieures à 10 ppm, valeur guide usuellement considérée pour le BaP (soit 2,4 en logarithme translaté) (Fig. 2).
- • Goudron : tous les sondages présentant du goudron ont une teneur supérieure à 30 ppm. Certaines teneurs fortes ne sont pas détectées, et ce seul indice est donc inutilisable pour guider l'échantillonnage.
- • Débris de maçonnerie : leur présence s'observe pour des teneurs supérieures à 0,5 ppm ; comme, là encore, toutes les fortes teneurs ne sont pas détectées, cet indice est peu intéressant en vue d'un cokrigeage (ce qui a été vérifié).
Les histogrammes sont un outil commode pour visualiser les relations entre indices et teneurs. La liaison non systématique entre indices et teneurs fortes nous oriente vers un cokrigeage de ces variables.
4.3 Analyse factorielle des correspondances
Les deux premiers facteurs de l'analyse factorielle des correspondances pour les huit indices relevés, expriment respectivement 33,6 % et 23,5 % de la variance totale (Fig. 3).
Les indices liés au sol en place, craie, couleur verdâtre et charbon (sol), sont regroupés, les autres indices étant associés aux matériaux rapportés. Le premier facteur, désigné dans la suite comme facteur auxiliaire, peut donc s'interpréter comme une variable distinguant les remblais et matériaux rapportés (valeurs élevées) du sol en place (valeurs plutôt négatives), information qui n'avait pas été relevée lors de la campagne d'investigation. La proximité des indices odeur et goudron est cohérente, sur le terrain le goudron étant souvent source d'odeur.
D'après le nuage de corrélation entre BaP et le facteur auxiliaire (Fig. 4), les concentrations faibles correspondent essentiellement à un sol en place, et les concentrations fortes et intermédiaires aux remblais. La majorité des fortes teneurs correspondent à une valeur élevée du facteur auxiliaire, d'où la possibilité d'inclure ce dernier dans un cokrigeage de la teneur.

Nuage de corrélation entre le premier facteur auxiliaire et la concentration en BaP.
Scatter diagram between the auxiliary factor and BaP grades.
5 Estimation des teneurs en place
Le variogramme expérimental de BaP est ajusté par le modèle isotrope en tenant compte des resserrements d'échantillonnage à petite distance. Le modèle ajusté comprend une structure sphérique de portée 30 m. Son expression générale, pour une portée a, est :
Les estimations ponctuelles des teneurs sont effectuées d'abord par krigeage ordinaire (KO) en voisinage unique, aux nœuds d'une grille, superposée aux contours du site. Les calculs sont effectués avec le logiciel Isatis, version 4.1 [5].
L'effet de pépite relatif étant important, l'estimation est peu précise, même à proximité immédiate des points expérimentaux.
Deux zones de valeurs fortes, au sud et au nord, ressortent sur la carte d'estimation (Fig. 5). Elles s'expliquent par l'historique du site, mais seule celle au sud, recoupant une mare à goudron, correspond aux anciennes infrastructures. A posteriori, les teneurs fortes au nord ont été justifiées par le dépôt provisoire de matériaux extraits du site.

Krigeage ordinaire des teneurs en BaP.
Ordinary kriging of BaP grades.
6 Apport des variables auxiliaires pour l'estimation des concentrations en BaP
Le cokrigeage nécessite l'ajustement d'un modèle variographique bivariable. Dans les deux cas, le modèle bivariable retenu est le modèle linéaire de corégionalisation, dans lequel les structures croisées s'expriment comme une combinaison linéaire des composantes élémentaires des variogrammes simples (cf. Fig. 6, pour la concentration en BaP et sa moyenne par classe pour le goudron) [2].
Pour le modèle entre BaP et la moyenne par classe de goudron, comme pour celui entre BaP et le facteur auxiliaire, l'effet de pépite est absent des variogrammes croisés. La corrélation spatiale croisée entre la teneur en BaP et ces variables auxiliaires gagne donc à être exploitée. Les cokrigeages entre la concentration en BaP et les deux variables auxiliaires améliorent les résultats du krigeage ; cette amélioration est néanmoins limitée, les variables étant connues aux mêmes points (configuration isotopique).
Afin d'évaluer le gain effectif dû à la prise en compte d'une telle information, nous avons retiré aléatoirement la moitié des échantillons pour la teneur, soit 26 valeurs de validation, les variables auxiliaires restant disponibles en tous les points. L'estimation de la teneur aux points de validation utilise les mêmes modèles variographiques que précédemment. L'erreur d'estimation est ensuite calculée en ces points de validation, d'abord pour le krigeage, puis pour le cokrigeage avec l'une ou l'autre des deux variables auxiliaires précédentes, goudron et facteur auxiliaire obtenu par ACP (voir Tableau 2).
Pour le goudron, comme pour le facteur auxiliaire, l'apport du cokrigeage est décisif par rapport au krigeage ordinaire de la teneur : l'utilisation du goudron conduit notamment à une diminution de l'erreur moyenne de l'ordre de 60 %. Le nuage de corrélation entre les teneurs mesurées aux 26 points de validation et les différentes estimations montre que le gain obtenu par cokrigeage provient en majeure partie de la concentration la plus élevée de BaP (Fig. 7). Après retrait de ce point, les erreurs et les erreurs quadratiques moyennes restent cependant plus faibles par cokrigeage.
Laquelle des variables auxiliaires, moyenne par classe ou facteur d'une analyse factorielle des indices, améliore-t-elle le mieux, par cokrigeage, l'estimation de la teneur en BaP ?
Certaines teneurs sont estimées avec des valeurs faiblement négatives. Dans le cokrigeage par le facteur auxiliaire, ces valeurs coı̈ncident avec des teneurs très faibles, tandis que pour le krigeage de BaP ou le cokrigeage par le goudron, une teneur de 40 ppm en BaP est estimée négative. Par rapport au cokrigeage par le facteur auxiliaire, le cokrigeage par le goudron évite une surestimation des teneurs faibles.
Huit points de validation ont une teneur mesurée supérieure à 10 ppm. Les trois estimations « ratent » un de ces points. À cette coupure, le KO et le CKO avec le goudron sélectionnent à tort respectivement 15 et 14 points de validation, contre six par le CKO avec le facteur auxiliaire. Sur cet exemple, le facteur auxiliaire serait donc préférable.
Une étude détaillée permettrait de préciser l'apport des différents indices. Un échantillonnage complémentaire du site par de nombreux sondages, sur lesquels les indices utiles seraient relevés, améliorerait à un coût réaliste la précision de l'estimation.
7 Conclusion
L'incertitude associée à l'estimation des teneurs dans des milieux hétérogènes reste souvent élevée, à cause de la forte variabilité spatiale, notamment à très petite distance, qui se traduit par un important effet de pépite ; cette incertitude est accrue par le nombre souvent faible d'échantillons prélevés.
Le relevé d'indices organoleptiques, combiné à l'analyse des correspondances, peut améliorer sensiblement l'estimation des teneurs en place. Si ces résultats se confirment pour d'autres sites, une stratégie d'échantillonnage pour une meilleure évaluation des sites pollués pourra être proposée.
Remerciements
Les auteurs tiennent à remercier Ghislain de Marsily pour sa relecture et ses remarques.


