Dérive à la surface de l'océan sous l'effet des vagues

Fabrice Ardhuin; François-Régis Martin-Lauzer; Bertrand Chapron; Philippe Craneguy; Fanny Girard-Ardhuin; Tanos Elfouhaily

doi:10.1016/j.crte.2004.04.007

Océanographie

Dérive à la surface de l'océan sous l'effet des vagues
[Wave-induced drift at the ocean surface]

Presented by: Jean Aubouin

Fabrice Ardhuin ¹ ; François-Régis Martin-Lauzer ¹; Bertrand Chapron ²; Philippe Craneguy ³; Fanny Girard-Ardhuin ⁴; Tanos Elfouhaily ⁵

¹ Centre militaire d'océanographie, Service hydrographique et océanographique de la Marine, 29609 Brest, France
² Laboratoire d'océanographie spatiale, Ifremer, Centre de Brest, BP 70, 29280 Plouzané, France
³ Avelmor, 29280 Plouzané, France
⁴ ENSTB–TAMCIC, 29238 Plouzané, France
⁵ Institut de recherche sur les phénomènes hors équilibre (IRPHE/CNRS), 13288 Marseille, France

Comptes Rendus. Géoscience, Volume 336 (2004) no. 12, pp. 1121-1130.

Abstracts

French
English

Pour déterminer le mouvement de dérive à la surface de l'océan, nous utilisons une séparation du déplacement en un mouvement induit par le courant local, influencé par le vent et les vagues, et un mouvement induit par les vagues, générées par les vents (locaux et lointains). Elle est appliquée ici pour estimer la dérive des boulettes d'hydrocarbures issues du naufrage du pétrolier Prestige-Nassau en novembre 2002. Les vagues contribuent pour au moins un tiers de la dérive à 1 m sous la surface, avec une direction moyenne orientée de 30° à droite de la direction de propagation de la mer du vent. Ce résultat n'est pas nouveau, mais il était jusqu'alors obtenu avec des modèles spécifiques. La méthode de calcul présentée ici est générale et utilise les résultats de modèles numériques classiques.

We model the drift velocity near the ocean surface separating the motion induced by the local current, itself influenced by winds and waves, and the motion induced by the waves, which are generated by local and remote winds. Application to the drift of ‘tar balls’, following the sinking of the oil tanker Prestige-Nassau in November 2002, shows that waves contribute at least one third of the drift for pollutants floating 1 m below the surface, with a mean direction about 30° to the right of the wind-sea direction. Although not new, this result was previously obtained with specific models, whereas the formalism used here combines classical wave and circulation forecasting models.

Metadata

Received: 2003-08-18
Accepted: 2004-04-26
Published online: 2004-06-10

DOI: 10.1016/j.crte.2004.04.007

Mots-clés : dérive, vagues, pollution
Keywords: drift, waves, pollution

Author's affiliations:

Fabrice Ardhuin ¹; François-Régis Martin-Lauzer ¹; Bertrand Chapron ²; Philippe Craneguy ³; Fanny Girard-Ardhuin ⁴; Tanos Elfouhaily ⁵

¹ Centre militaire d'océanographie, Service hydrographique et océanographique de la Marine, 29609 Brest, France
² Laboratoire d'océanographie spatiale, Ifremer, Centre de Brest, BP 70, 29280 Plouzané, France
³ Avelmor, 29280 Plouzané, France
⁴ ENSTB–TAMCIC, 29238 Plouzané, France
⁵ Institut de recherche sur les phénomènes hors équilibre (IRPHE/CNRS), 13288 Marseille, France

@article{CRGEOS_2004__336_12_1121_0,
     author = {Fabrice Ardhuin and Fran\c{c}ois-R\'egis Martin-Lauzer and Bertrand Chapron and Philippe Craneguy and Fanny Girard-Ardhuin and Tanos Elfouhaily},
     title = {D\'erive \`a la surface de l'oc\'ean sous l'effet des vagues},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {1121--1130},
     publisher = {Elsevier},
     volume = {336},
     number = {12},
     year = {2004},
     doi = {10.1016/j.crte.2004.04.007},
     language = {fr},
}

TY  - JOUR
AU  - Fabrice Ardhuin
AU  - François-Régis Martin-Lauzer
AU  - Bertrand Chapron
AU  - Philippe Craneguy
AU  - Fanny Girard-Ardhuin
AU  - Tanos Elfouhaily
TI  - Dérive à la surface de l'océan sous l'effet des vagues
JO  - Comptes Rendus. Géoscience
PY  - 2004
SP  - 1121
EP  - 1130
VL  - 336
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crte.2004.04.007
LA  - fr
ID  - CRGEOS_2004__336_12_1121_0
ER  -

%0 Journal Article
%A Fabrice Ardhuin
%A François-Régis Martin-Lauzer
%A Bertrand Chapron
%A Philippe Craneguy
%A Fanny Girard-Ardhuin
%A Tanos Elfouhaily
%T Dérive à la surface de l'océan sous l'effet des vagues
%J Comptes Rendus. Géoscience
%D 2004
%P 1121-1130
%V 336
%N 12
%I Elsevier
%R 10.1016/j.crte.2004.04.007
%G fr
%F CRGEOS_2004__336_12_1121_0

Fabrice Ardhuin; François-Régis Martin-Lauzer; Bertrand Chapron; Philippe Craneguy; Fanny Girard-Ardhuin; Tanos Elfouhaily. Dérive à la surface de l'océan sous l'effet des vagues. Comptes Rendus. Géoscience, Volume 336 (2004) no. 12, pp. 1121-1130. doi : 10.1016/j.crte.2004.04.007. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2004.04.007/

Version originale du texte intégral

Abridged English version

Near-surface drift in the ocean is the result of the action of the wind, the current, and the waves. Here we generalize a recent result [22] that gives wave effects on the three-dimensional mean flow, as a result of the Stokes drift $u^{st}$ , radiation stresses, and wave generation by the wind, a logical extension of the depth-integrated momentum and mass conservation equations [18,24]. The equation for the mean flow momentum involves three important wave-induced terms. One is the wave-induced Coriolis force acting on the mean flow that ensures a zero net mass transport for stationary and uniform wave conditions [11], by driving a Hasselmann current ${\hat{u}}^{e, H}$ opposed to the Stokes drift ${\hat{u}}^{st}$ . ${\hat{u}}^{e, H}$ is an Eulerian mean current, as measured at a fixed position, while ${\hat{u}}^{st}$ is a Lagrangian drift velocity, as measured following the wave-only motion of water particles around their orbits. Another term is the well-known radiation stress due to gradients in the wave field [24] that drives the surf zone dynamics [27], and the last one is the rate of change of the wave momentum minus the wind to wave momentum flux [22]. This last term can be interpreted as the local wave to mean flow momentum transfer, essentially due to wave breaking. The practical advantage of the present method is the simple combination of information from a spectral wave model with a Reynolds-averaged primitive equation model of the ocean circulation, each giving the best possible description of the wave field and the circulation, respectively, in general conditions.

We apply this theory to the computation of the near-surface drift of tar balls that we assume to follow (Lagrangian) water particle velocities for a given depth. Looking at horizontally uniform conditions, the equations reduce to a one-dimensional evolution equation for the velocity profile. We first solve stationary conditions (Fig. 1) with a constant vertical eddy viscosity. This viscosity introduces a difference between the Eulerian wave-induced current profile and that of the Stokes drift, giving a net wave-induced drift at the surface in a direction to the right (left in the southern hemisphere) of the wave propagation direction.

Fig. 1
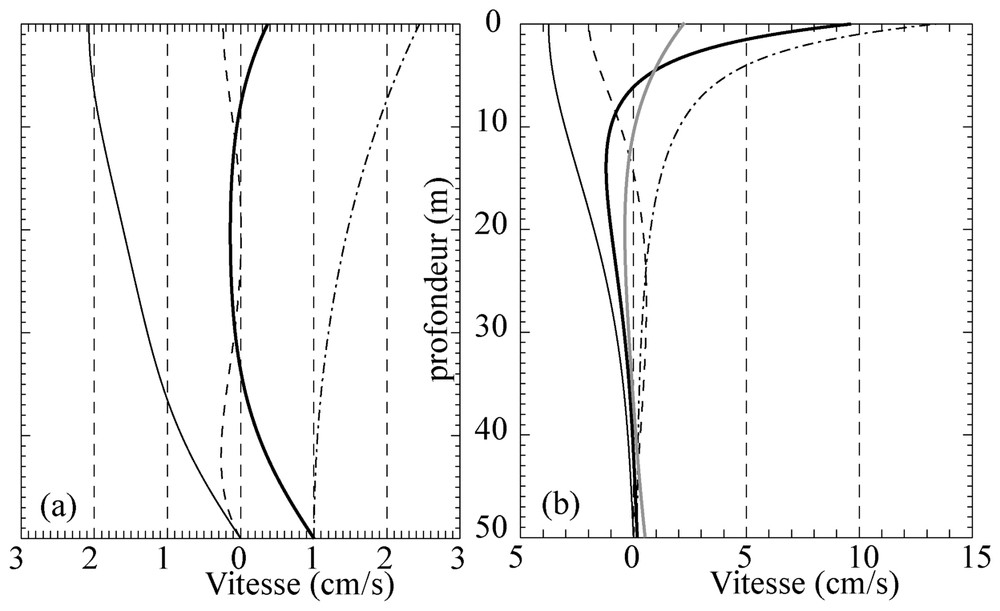
Profils de vitesse induite par les vagues calculés (a) pour des vagues monochromatiques, avec h=50 m, δ_e/h=0,23, δ_st/h=0,65 et H_s=4 m, paramètres utilisés par Xu et Bowen, (b) pour δ_e/h=0,3, valeur qui sous-estime encore l'intensité du mélange, et des vagues aléatoires unidirectionnelles avec le spectre en fréquence calculé pour le 3 mars 2003 dans le golfe de Gascogne, avec H_s=4,9 m et T_p=12 s. Trait plein fin: composante ${\hat{u}}_{1}^{e, H}$ de la vitesse eulérienne générée par les vagues sur l'axe de propagation des vagues, tirets: composante perpendiculaire ${\hat{u}}_{2}^{e, H}$ de cette même vitesse, trait mixte: dérive de Stokes u₁^st. Trait épais: dérive induite par les vagues dans la direction de propagation: ${\hat{u}}_{1}^{e, H} + u_{1}^{st}$ . En gris épais, ${\hat{u}}_{1}^{e, H} + u_{1}^{st}$ pour des vagues monochromatiques de même hauteur et de période T=T_p=12 s.
Wave-induced drift profiles as computed (a) for monochromatic waves, with h=50 m, δ_e/h=0.23, δ_st/h=0.65, and H_s=4 m, (b) for δ_e/h=0.3 and random unidirectional waves with a frequency spectrum computed for 3 March 2003 in the Bay of Biscay with H_s=4.9 m and T_p=12 s. Thin solid: Eulerian wave-induced velocity component to the east ${\hat{u}}_{1}^{e, H}$ , dashed: component to the north ${\hat{u}}_{2}^{e, H}$ of the same velocity, dash-dotted: Stokes drift u₁^st, thick solid: mean wave-induced Lagrangian drift ${\hat{u}}_{1}^{e, H} + u_{1}^{st}$ in the direction of wave propagation. In light grey, ${\hat{u}}_{1}^{e, H} + u_{1}^{st}$ is shown for monochromatic waves with the same height and period T=T_p=12 s.

Including these wave effects in a realistic mixed layer model, using computed wave spectra and fluxes at the buoy ‘Brittany’ (station number 62 163 in the northern Bay of Biscay), we compute synthetic trajectories by integrating the velocity at that point for a fixed depth z=−1.25 m. Consistent with previous studies, we find that the wave-induced drift is 20–30% of the Ekman drift in the top meter of the ocean, about 30° to the right of the downwind direction.

Wave effects on surface drift are thus significant and are readily introduced with our method in a generic ocean mixed layer or circulation model by using information from a wave model. That information could also include, in particular for the coastal ocean, a sea-state-dependent wind stress [21]. Improvements are expected with the development of parameterizations for near surface mixing in the presence of waves, but more measurements will be needed.

1 Introduction

Les vagues exercent un effet sur la circulation moyenne de l'océan parce qu'elles ne sont pas linéaires, même si cette non-linéarité est généralement faible. La moyenne des équations du mouvement comporte donc un terme résiduel, moyenne du mouvement rapide des vagues [24]. Par ailleurs, les vagues sont la source principale de la rugosité au-dessus de la surface de l'océan et supportent donc l'essentiel de la tension de vent [5]. Enfin, au-dessous de la surface, la redistribution de cette tension sous forme de flux turbulent dans la couche mélangée est déterminée par le champ de vagues, les caractéristiques de son déferlement et les circulations de Langmuir, qui résultent de la présence des vagues [9,25,29].

La surface de l'océan est le lieu d'une forte variation verticale des vitesses horizontales, passant rapidement de la vitesse du vent à 10 m au-dessus de la surface, U₁₀=O(10) m s⁻¹, à la vitesse du courant, U=O(0,1) m s⁻¹, à quelques mètres sous la surface. Cette transition se fait par l'intermédiaire de vagues auxquelles sont associées des fluctuations de vitesse de l'ordre de 1 m s⁻¹.

Toutefois, la position verticale d'une particule d'air ou d'eau fluctue sous l'effet des vagues. Or, une particule d'eau sur la crête d'une vague se déplace un peu plus rapidement et en sens opposé que lorsqu'elle se retrouve dans un creux quelques secondes plus tard. En suivant les particules au cours ce déplacement oscillant, on observe donc un déplacement moyen dans le sens de propagation. Il s'agit de la dérive de Stokes $u^{st}$ . Par ailleurs, dans un référentiel en rotation, la force de Coriolis correspondant au mouvement rapide d'oscillation des vagues modifie ce mouvement de telle sorte que les oscillations de vitesse verticale w̃ et horizontale ũ ont une corrélation ũ w̃ non nulle, dont la divergence, comme pour un tenseur de Reynolds classique, agit comme une force additionnelle pour le mouvement moyen. Cette force, mise en évidence par Hasselmann [11], est $T^{H} = f \times u^{st}$ , où f est le paramètre de Coriolis.

En l'absence de turbulence, gradient de pression ou autre force extérieure, et pour un état stationnaire, la force de Hasselmann T^H est équilibrée par la force de Coriolis $f \times u^{e}$ , correspondant au courant eulérien moyen. On trouve donc que ${\hat{u}}^{e} = {\hat{u}}^{e, H} = - u^{st}$ , les vagues induisant un courant eulérien moyen ${\hat{u}}^{e, H}$ . La vitesse moyenne de dérive induite par les vagues, en suivant une particule d'eau, est la somme ${\hat{u}}^{e, H} + u^{st}$ du courant eulérien et du mouvement de dérive de Stokes. Elle est donc nulle dans ce cas.

Cependant, il suffit d'introduire un mélange visqueux ou turbulent pour que le profil vertical de ${\hat{u}}^{e, H}$ soit modifié, devenant beaucoup moins cisaillé que la dérive de Stokes, alors que le transport eulérien (intégrale verticale du courant horizontal ${\hat{u}}^{e, H}$ ) reste exactement opposé au transport de Stokes [28]. Ainsi, la dérive induite par les vagues $({\hat{u}}^{e, H} + u^{st})$ est non nulle en surface. Ces effets sont encore mal pris en compte dans les modèles de prévision de dérive appliqués aux polluants, objets ou microorganismes. L'objectif de la présente communication est donc de démontrer l'importance de ces phénomènes et à partir d'applications pratiques des connaissances actuelles qui n'ont jamais été utilisées, et de faire ressortir ainsi les insuffisances théoriques auxquelles il convient de s'attaquer.

Le formalisme utilisé pour séparer le mouvement des vagues du mouvement moyen est décrit au § 2. Ces équations sont utilisées au § 3 pour estimer la vitesse de dérive de la pollution issue du pétrolier Prestige-Nassau. Les conclusions et plusieurs perspectives d'amélioration sont présentées au § 4.

2 Équations du mouvement moyen

Notre objectif est la prise en compte précise des vagues dans le calcul des propriétés de l'océan à des échelles horizontales supérieures au kilomètre. Cela impose de calculer les effets des vagues avec un modèle spectral de prévision de l'état de la mer, solution la plus performante actuellement, et de les incorporer dans un modèle de circulation aux équations primitives (moyenne de Reynolds des équations de Navier–Stokes).

La représentation des effets moyens des fluctuations de la surface avec les vagues nécessite un changement de coordonnées, avec une coordonnée verticale qui épouse la surface libre. Le formalisme le plus usité est la moyenne lagrangienne généralisée (GLM [1]), dont les coordonnées transformées suivent le mouvement moyen des particules. Il aboutit à une équation en trois dimensions (3D) d'évolution de la quantité de mouvement moyenne hors quantité de mouvement des vagues. Une modélisation numérique spécifique a donné d'excellents résultats [10], mais l'application pratique de la GLM au sens indiqué ci-dessus (modèle spectral de vagues et équations primitives) nécessite quelques vérifications, qui sont en cours, et sortent du cadre de la présente étude. On peut noter que, sous certaines conditions [7,19], la GLM donne les équations de Craik–Leibovich, utilisées dans l'étude du mélange en surface.

Nous utilisons ici les résultats de Mellor [22], qui a transformé la coordonnée verticale seulement, obtenant une équation 3D pour la quantité de mouvement totale (comprenant les vagues) et une équation en deux dimensions (2D sur l'horizontale) pour l'énergie des vagues. Passer de deux équations à une équation 3D pour la quantité de mouvement sans les vagues est apparemment anodin. Toutefois, cela nécessite une représentation des effets de guide d'onde, qui apparaissent en présence de déferlement : une variation locale (sur la verticale) des propriétés des vagues doit être compensée au cours de la propagation, car les profils verticaux observés pour les différents paramètres (vitesse, énergie…) ont toujours la forme spécifique aux ondes libres [26], dictée par les propriétés du guide d'onde (profondeur et profil de courant). Les équations 3D données ci-dessous ne sont donc pas formellement justifiées en présence de déferlement. Les applications faites ici négligeront donc les modifications probables des profils verticaux des termes de couplage vagues–courant pour des vagues réelles, qui déferlent.

Les équations 2D sont nécessairement égales aux équations 3D intégrées sur la verticale, et décrivent les échanges de quantité de mouvement entre océan, vagues et circulation. Les équations 2D sont donc données pour faciliter la compréhension du couplage vagues–courant, tandis que les applications seront réalisées à partir des équations 3D, dont la forme générale est donnée ci-dessous, mais dans des conditions simples (stationnarité et/ou uniformité). Par ailleurs, la modélisation numérique de l'océan utilisant souvent une séparation en modes barotropes (2D) et baroclines (3D), les deux jeux d'équations seront nécessaires dans ce cas.

2.1 Équations 2D pour le transport : mouvement intégré sur la verticale

Les équations du mouvement moyen comprenant l'effet des vagues [24] sont données ici sous une forme générale, en incluant la force de Coriolis [2,18].

On note par des indices muets α ou β les composantes de vecteurs horizontaux dans un repère cartésien. La direction verticale locale est particularisée par la pesanteur, et on note par l'indice z les composantes verticales, le vecteur $e_{z}$ désignant le vecteur unitaire pointant vers le haut. La sommation est implicite sur les indices apparaissant deux fois. Enfin, on note ρ^w et ρ^a les masses volumiques de l'eau de mer et de l'air, supposées uniformes, g l'accélération de la gravité, μ^w la viscosité dynamique de l'eau, f le paramètre de Coriolis, projection sur la verticale du double du vecteur de rotation angulaire de la Terre, et h la profondeur locale. On néglige ici la composante horizontale de la rotation terrestre [11]. L'opérateur de moyenne est une double moyenne temporelle, d'abord sur des échelles de temps, courtes par rapport à la période des vagues et longues par rapport aux fluctuations turbulentes plus rapides, puis sur une échelle de temps de l'ordre d'un groupe de vagues (une dizaine de périodes). Enfin, p^m est la pression corrigée de la pression due aux vagues et de la pression hydrostatique d'équilibre $- g z$ [12].

En séparant le vecteur de quantité de mouvement horizontale moyenne $M$ en la somme des contributions du mouvement moyen et des vagues, $M^{m} + M^{w}$ [12], on obtient [2],

\frac{\partial M^{m}}{\partial t} = [\nabla \cdot τ^{m} - f e_{z} \times M^{m} + {\hat{p}}^{a} \nabla \hat{η} + {(p^{m} + ρ^{w} gh)}_{- h} \nabla h + τ^{a} - τ^{b}] - f e_{z} \times M^{w} + \nabla \cdot τ^{rad} - \frac{\partial M^{w}}{\partial t}

(1)

avec t le temps, η l'élévation de la surface libre, p^a la pression atmosphérique à la surface de l'océan, τ^m un tenseur horizontal qui contient les termes d'advection de quantité de mouvement, le gradient de pression et les tensions visqueuses,

τ_{α β}^{m} = - \underset{- h}{\int^{\hat{η}}} ρ^{w} ({\hat{u}}_{α} {\hat{u}}_{β}) + δ_{α β} (p^{m} - ρ^{w} g z) + μ^{w} \frac{\partial^{2} {\hat{u}}_{1}}{\partial x_{β} \partial x_{β}} d z

(2)

τ^a et τ^b sont respctivement les tensions totales (visqueuse et turbulente), en surface (due au vent) et au fond (frottement sur le fond). Les moyennes

\hat{η}

et

{\hat{p}}^{a}

sont sur des échelles de temps bien supérieures à la période des vagues. Les trois derniers termes de (1) représentent l'effet des vagues sur la circulation moyenne.

- f e_{z} \times M^{w}

est la force de Coriolis induite par la quantité de mouvement des vagues. On comprend bien alors que, si elle n'est équilibrée que par la force de Coriolis

f e_{z} \times M^{m}

induite par le mouvement moyen, alors le transport du courant eulérien

M^{m}

est exactement opposé au transport de Stokes

M^{w}

. Dans ces conditions, le transport de masse induit par les vagues, somme de ces deux contributions, est exactement égal à zéro. En revanche, on comprend aussi que, pour des variations temporelles du champ de vagues plus rapides que la période d'inertie,

M^{w}

, qui est un résultat instantané de la présence des vagues, ne sera pas compensée tout de suite par

M^{m}

, dont le temps d'ajustement est la période d'inertie

T_{I} = 2 π / f

[11].

On note $k = |k|$ le nombre d'onde des vagues se propageant dans la direction du vecteur $k$ . Le tenseur de radiation τ^rad correspond à l'excès de flux de quantité de mouvement, du fait de la présence des vagues [24]. Sa divergence est donc une force pour le mouvement moyen. Cette force est bien connue pour être le moteur principal de la circulation littorale [27]. Ce terme se calcule en utilisant la théorie linéaire des vagues pour des vagues aléatoires, représentées par le spectre en vecteur d'onde $F (k)$ . En notant C(k) et C_g(k) les vitesses de phase et de groupe, on obtient :

τ_{α β}^{rad} = U_{α} M_{β}^{w} + U_{β} M_{α}^{w} + ρ^{w} g \int F (k) [(\frac{1}{2} - \frac{C_{g}}{C}) δ_{α β} - \frac{C_{g}}{C} k_{α} k_{β} / k^{2}] d k

(3)

Les deux premiers termes de (3) sont souvent séparés, afin de garder la même expression avec ou sans le courant moyen

U

[24].

Le dernier terme de (1), $- \partial M^{w} / \partial t$ , est la fraction de la tension de vent qui est gagnée ou perdue par l'écoulement moyen lors de sa dissipation ou de son stockage par le champ de vagues, qui agit comme un « tampon » à quantité de mouvement. Ce terme est facilement calculable par un modèle de vagues spectral en phase moyennée comme WAM [17], à partir du spectre des vagues $F (k)$ , distribution de la variance de l'élévation de la surface sur les nombres d'onde $k$ :

M^{w} = ρ^{w} g \int F (k) k / C d k

(4)

Enfin, la conservation de la masse est exprimée par :

ρ^{w} \frac{\partial \hat{η}}{\partial t} + \frac{\partial M_{α}^{m}}{\partial x_{α}} = - \frac{\partial M_{α}^{w}}{\partial x_{α}}

(5)

Les deux équations (1) et (5), pour les inconnues

M^{m}

et

\hat{η}

, sont donc des équations de Saint-Venant, modifiées par la prise en compte du forçage par les vagues, considéré comme extérieur à la circulation moyenne et connu.

2.2 Équations 3D : structure verticale

Puisque nous nous intéressons à la vitesse de dérive au voisinage de la surface, il convient de distribuer la quantité de mouvement sur la verticale pour obtenir le profil de vitesse. Cela est aisé pour les vagues dont la quantité de mouvement moyenne est la dérive de Stokes, $M^{w} = \int_{- h}^{\hat{η}} u^{st} (z) d z$ . Au second ordre en cambrure des vagues, on a [16] :

u^{st} (z) = \int σ k F (k) \frac{\cosh [2 k (z + h)]}{\sinh^{2} (k h)} d k

(6)

où σ est la pulsation intrinsèque des vagues, telle que

σ^{2} = g k \tanh (k h)

.

Il est beaucoup plus délicat d'obtenir la vitesse eulèrienne moyenne ${\hat{u}}^{e}$ , qui est telle que $M^{m} = \int_{- h}^{\hat{η}} {\hat{u}}^{e} (z) d z$ . En effet, ${\hat{u}}^{e}$ ne peut être obtenue que par résolution numérique d'équations 3D, dont l'intégrale sur la verticale doit donner (1). On utilise ici les équations établies par Mellor [22]. La coordonnée verticale ς est définie comme :

z = s (x, y, ς, t) = \hat{η} + ς D + \tilde{s}

(7)

avec s̃ lié au déplacement vertical sous l'effet des vagues, tel que

\hat{\tilde{s}} = 0

[22]. On généralise cette coordonnée pour des vagues aléatoires. Connaissant les amplitudes

Z_{1, k}^{s_{1}}

des vagues libres (de premier ordre), on a en première approximation :

\tilde{s} = \sum_{k, s_{1}} \frac{\sinh [k D (1 + ς)]}{\sinh (k D)} Z_{1, k}^{s_{1}} e^{i ψ_{1, k}^{s_{1}}}

(8)

avec la hauteur d'eau moyenne

D = h + \hat{η}

, s₁ un indice de signe égal à 1 ou −1, et

ψ_{1, k}^{s_{1}}

la phase des vagues de nombre d'onde

k

se propageant dans la direction du vecteur

s_{1} k

.

Mellor a montré que les fluctuations s̃ du changement de coordonnée verticale permettent d'obtenir des équations pour le mouvement moyen, avec une claire séparation de l'air et de l'eau : la moyenne suit l'interface. L'intérêt de ces équations est que s̃ n'y apparaît pas dans sa forme finale (Mellor, Éqs. (50) et (51)) que l'on peut combiner pour obtenir, pour $- h ⩽ z ⩽ \hat{η}$ ou −1⩽ς⩽0 :

\frac{\partial {\hat{u}}^{e}}{\partial t} = - ({\hat{u}}^{e} + u^{st}) \nabla \cdot ({\hat{u}}^{e} + u^{st}) - f e_{z} \times ({\hat{u}}^{e} + u^{st}) + Ω \frac{\partial {\hat{u}}^{e}}{\partial ς} + \frac{1}{ρ^{w}} \nabla (g \hat{η} + {\hat{p}}^{a}) + D \int (\nabla b - ς \frac{\partial b}{\partial ς} \nabla D) + \nabla \cdot (T^{rad} + R_{h}) + \frac{\partial}{\partial ς} ({\tilde{s}}_{α} \tilde{s}) + \frac{1}{D} \frac{\partial}{\partial ς} [\frac{K_{z}}{D} \frac{\partial {\hat{u}}^{e}}{\partial ς}] + T^{in} (z) - \frac{\partial u^{st}}{\partial t}

(9)

avec b la flottabilité,

Ω

une vitesse verticale moyenne [22], T_αβ^rad le tenseur de radiation noté par Mellor, et

T^{in}

l'accélération due au transfert de quantité de mouvement du vent vers le champ de vagues, et notée

\bar{{\tilde{s}}_{α} {\tilde{p}}^{w}}

par Mellor). Il faut souligner que ces équations négligent les couplages vagues–ondes internes [18].

Par ailleurs, la conservation de la masse (Éq. (50) de Mellor) s'écrit :

\nabla \cdot [D ({\hat{u}}^{e} + u^{st})] + \frac{\partial Ω}{\partial ς} + \frac{\partial \hat{η}}{\partial t} = 0

(10)

et l'équation d'advection de tout traceur passif de concentration

c = \hat{c} + c'

est (Mellor, Éq. (54)) :

\frac{\partial (D \hat{c})}{\partial t} + \nabla \cdot [D \hat{c} ({\hat{u}}^{e} + u^{st})] + \frac{\partial (Ω \hat{c})}{\partial ς} + \frac{\partial \bar{c' w'}}{\partial ς} = 0

(11)

La condition de continuité des contraintes en surface impose un flux de quantité de mouvement turbulent en surface

(K_{z} / D) (\partial {\hat{u}}^{e} / \partial ς)

égal à τ^a−τⁱⁿ, où

τ^{in} = \int T^{in} (z) d z

est la quantité de mouvement communiquée au champ de vagues.

Nous considérons désormais un champ de vagues uniforme. On recherche alors une solution uniforme sur l'horizontale, ce qui supprime les gradients horizontaux dans (11), et la vitesse verticale $Ω$ , pour donner :

\frac{\partial {\hat{u}}^{e}}{\partial t} = - f e_{z} \times ({\hat{u}}^{e} + u^{st}) + \frac{\partial}{\partial z} [K_{z} \frac{\partial {\hat{u}}^{e}}{\partial z}] + T^{in} (z) - \frac{\partial u^{st}}{\partial t}

(12)

Tout le problème se reporte alors sur la paramétrisation du coefficient de mélange vertical K_z. Le courant eulérien moyen

{\hat{u}}^{e}

est calculé en résolvant (12), avec une clôture turbulente adéquate permettant de déterminer K_z.

3 Applications au calcul de dérive

Pour calculer la dérive effective d'un petit objet ou d'un polluant, il suffit de connaître le champ de vitesse eulérien de l'eau $u^{e}$ , mesuré en un point fixe, et le champ Lagrangien moyen $u^{e} + u^{st}$ , déterminé en suivant la trajectoire d'une particule d'eau, ainsi que la traînée de l'objet. Une petite particule ayant la densité de l'eau dérivera suivant la vitesse lagrangienne. Un objet plus important aura un mouvement intermédiaire entre le mouvement eulérien et le mouvement lagrangien, et on peut penser qu'un corps immergé suivra le mouvement lagrangien, filtré de la dérive de Stokes des vagues de longueur d'onde plus courte ou comparable à la taille de l'objet. Enfin, un gros objet, par exemple un navire, peut modifier le champ de vagues et alors récupérer la quantité de mouvement perdue par ce dernier par déferlement ou par réflexion.

Pour le cas de la pollution qui nous intéresse, une fois la nappe de pétrole fragmentée en « boulettes », on supposera que la dérive suit la trajectoire lagrangienne des particules d'eau avec une immersion fixe, à la vitesse ${\hat{u}}^{e} + u^{st}$ , avec $u^{st}$ calculé à partir de toutes les vagues jusqu'à de petites longueurs d'onde de l'ordre de 1 m.

Nous considérons d'abord le cas stationnaire et supposons que le flux de quantité de mouvement τⁱⁿ est injecté en surface à z=0, de telle sorte que $T^{in} (z) - \partial u^{st} / \partial t = 0$ dans (12). La solution la plus simple est alors obtenue pour une viscosité turbulente K_z uniforme (dans l'espace) et stationnaire (dans le temps). Ainsi, parmi les trois termes dont l'effet est calculé par Xu et Bowen [31], nous nous intéressons ici à la force de Hasselmann, $T^{H} (z) = f e_{z} \times u^{st}$ , qui engendre le courant de Hasselmann ${\hat{u}}^{e, H}$ . On peut appliquer directement les résultats analytiques de Xu et Bowen [31], qui donnent ${\hat{u}}^{e, H}$ (qu'ils notent q₃), ce qui permet de calculer la vitesse de dérive totale induite par les vagues, ${\hat{u}}^{e, H} + {\hat{u}}^{st}$ , à laquelle ils convient de rajouter la vitesse d'Ekman classique ${\hat{u}}^{e, E}$ [6] pour obtenir la dérive effective.

La forme du profil de ${\hat{u}}^{e, H}$ est exprimée en fonction de la profondeur de Stokes $δ_{st} = 1 / 2 k$ avec k le nombre d'onde des vagues, et de la profondeur d'Ekman $δ_{e} = {(2 K_{z} / f)}^{1 / 2}$ . L'amplitude de la dérive est donnée par la hauteur significative des vagues H_s. Pour des vagues aléatoires, la vitesse eulérienne se calcule par superposition linéaire des solutions de Xu et Bowen pour les composantes monochromatiques : à chaque composante correspond un δ_st différent.

Pour faciliter la comparaison, nous avons repris les valeurs de δ_e et δ_st utilisées par Xu et Bowen (Fig. 1a). Elles donnent une faible dérive en surface, qui est dans le sens de propagation des vagues. En effet, la turbulence « mélange » le profil du courant eulérien de retour, qui ne peut alors compenser complètement la dérive lagrangienne.

Il est probable que cette dérive soit généralement plus marquée dans le sens de propagation des vagues que ce que montre la Fig. 1a. En effet, pour une période de vagues T=12 s et une profondeur h=50 m, on a δ_st/h=0,32. Cet effet est amplifié par la distribution spectrale des vagues. Alors que toutes les composantes du spectre contribuent à la dérive en surface, la contribution des vagues courtes diminue fortement avec la profondeur, ce qui accentue le cisaillement vertical de la dérive de Stokes. Quand on ajoute la vitesse eulérienne, faiblement cisaillée, on trouve donc une plus forte dérive lagrangienne en surface, qui décroît rapidement avec la profondeur. En même temps, dans le golfe de Gascogne, en hiver, on peut trouver une couche d'Ekman plus profonde. Dans ce cas, δ_e est plus grand et le profil de ${\hat{u}}^{e, H}$ est plus uniforme.

Nous avons donc augmenté δ_e/h jusqu'à 0,3, soit K_z=1,2×10⁻² m² s⁻¹ pour h=50 m et 48° de latitude nord. Cette valeur correspond à une viscosité turbulente dans une couche logarithmique K_z,log=κ|z|w_★², pour z=−1 m et w_★²=3 cm s⁻¹, soit un fort vent à 10 m, U₁₀≃20 m s⁻¹. κ=0,4 est la constante de von Kármán et w_★=(τ_a/ρ^w)^1/2 est la vitesse de frottement sous l'eau.

Pour un spectre de vagues réaliste, avec H_s=4,9 m and T_p=12 s, on obtient bien une forte dérive dans le sens de propagation des vagues (Fig. 1b), compensée par un sous-courant entre 10 et 20 m de profondeur. Il n'existe pas, à notre connaissance, d'observations d'un tel sous-courant. On remarque que ce courant est relativement faible, car distribué sur une profondeur bien supérieure à la profondeur de Stokes. Par ailleurs, il faut ajouter à ces vitesses la dérive d'Ekman, qui contribue aussi à masquer ce courant de retour.

On note aussi que la dérive totale due aux vagues est déviée à droite de la direction de propagation des vagues d'environ 20° (à gauche dans l'hémisphère sud). Ce résultat est qualitativement en accord avec des mesures de vitesse et de cisaillement par flotteurs dérivants, réalisées en mer Adriatique, à environ un mètre sous la surface (Pierre-Marie Poulain, université de Trieste, communication personnelle, 2003). De plus, les vagues sont rarement unidirectionnelles, et la mer du vent a souvent un angle différent de la houle. On peut ainsi trouver une dérive à droite du vent si la houle se propage dans une direction à droite de celle de la mer du vent. On comprend aussi que le cisaillement vertical du profil de vitesse, avec une rotation éventuelle sur la verticale, peut être la simple conséquence d'un « cisaillement » du spectre directionnel des vagues, avec différentes directions moyennes des vagues pour différentes fréquences.

Les résultats présentés sur la Fig. 1 sont indicatifs, la limitation essentielle étant l'hypothèse de viscosité K_z uniforme. En effet, pour une surface plane (sans vagues), K_z augmente à peu près comme $κ | z | w_{★}^{2}$ . C'est en utilisant ce profil linéaire de K_z que Madsen [20] a montré que les angles de déviation dans une spirale d'Ekman réelle (hodographe des vitesses d'un profil vertical) sont fortement réduits par rapport aux calculs classiques d'Ekman, avec K_z uniforme et constant [6].

Pour ce qui est de l'effet sur la dérive induite par les vagues, on peut citer les calculs de Jenkins [15] qui a montré que l'effet net des vagues est une dérive d'environ 3 % de la vitesse du vent à 23–30° à droite du vent, en utilisant un profil linéaire de K_z réaliste, avec les équations lagrangiennes du mouvement.

Plutôt que d'utiliser le modèle de Jenkins, coûteux et spécifique à une situation homogène horizontalement, nous montrons ici une application qui peut être faite dans les modèles numériques visant à représenter la circulation océanique, utilisant classiquement une paramétrisation de la turbulence avec un ou deux équations d'évolution pour des paramètres de la turbulence, par exemple l'énergie cinétique turbulente et une longueur de mélange. C'est le cas des paramétrisations décrites par Mellor et Yamada [23] et de celle que nous utiliserons ici, décrite par Gaspar et al. [8].

En analysant les conditions de vent et vagues prévues à la bouée Brittany par le centre NCEP de la NOAA et pour des échéances de 0 à 21 h chaque jour, le calcul de la dérive de Stokes en surface montre qu'elle varie entre 1 et 2 % du vent à 10 m U₁₀. Les profils de vitesse de Stokes ont été intégrés dans un modèle 1-D (vertical) de couche de mélange, résolvant l'Éq. (12) avec une paramétrisation de K_z décrite par Gaspar et al. [8]. Le problème est par ailleurs généralisé pour prendre en compte la stratification thermohaline de la couche de surface, intégrée à partir d'un profil climatologique (données du SHOM) avec les forçages atmosphériques analysés (flux de chaleur en surface), fournis par le modèle ARPEGE (Météo France).

Les différentes contributions à la dérive sont indiquées sur la Fig. 2, en surface et à 1,25 m d'immersion. La dérive due aux vagues est calculée comme étant la dérive de Stokes plus la différence entre une simulation prenant en compte les vagues et une simulation sans l'effet des vagues. La dérive totale à cette immersion est donc la somme de cette contribution des vagues (courbe épaisse noire continue) et de la dérive d'Ekman (tirets noirs). On remarque que le courant d'Ekman est du même ordre que la dérive de Stokes en surface, ce qui avait déjà été établi [14,15,28]. La dérive totale due aux vagues est légèrement inférieure à la dérive de Stokes, à cause du courant eulérien de retour.

Fig. 2
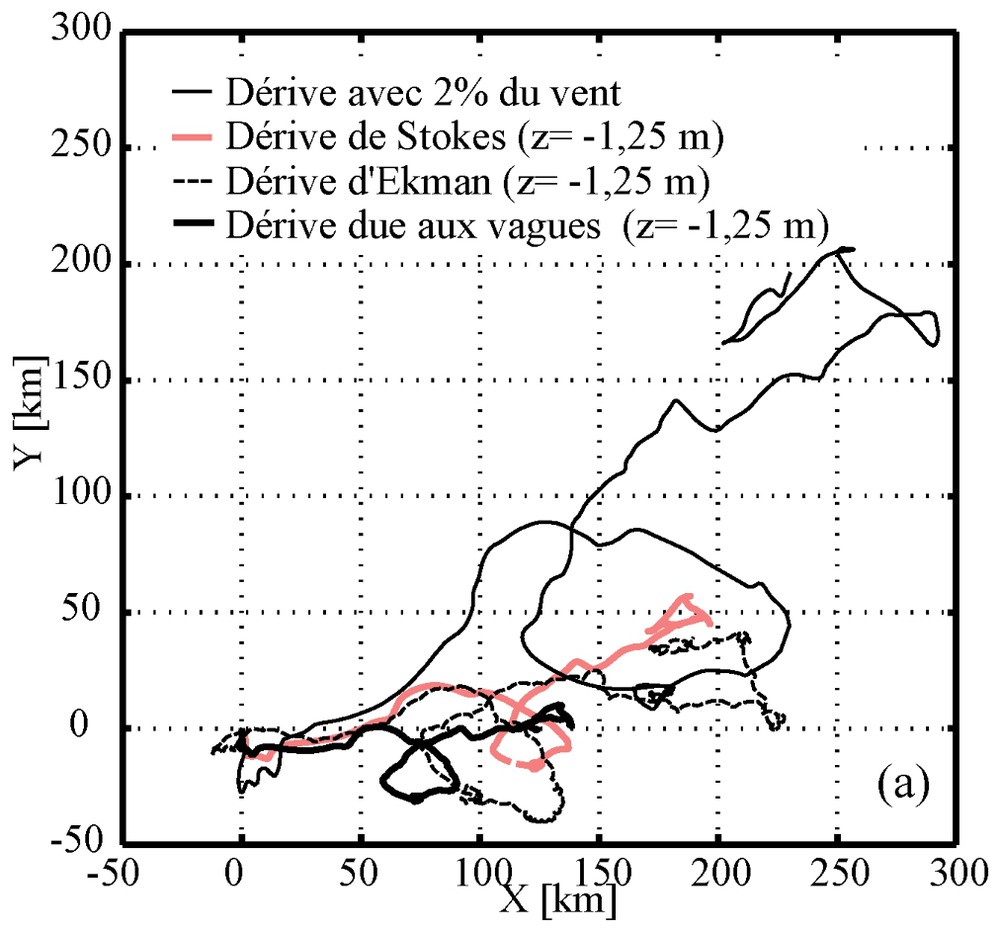
Trajectoires de dérive du 15 novembre 2002 au 15 janvier 2003, en supposant uniformes les conditions prévues à la bouée Brittany (bouée 62 163, au nord du golfe de Gascogne) par la NOAA/NCEP. La courbe continue épaisse est la dérive à 1,25 m d'immersion, induite par les vagues seulement; c'est donc la somme de la dérive de Stokes et de la contribution des vagues au courant eulérien. La dérive effective est la somme de cette dérive due aux vagues et de la dérive d'Ekman (pointillés noirs épais). Les tirets fins représentent une dérive hypothétique avec une vitesse de 2% de la vitesse du vent, indiquant donc la force et la vitesse du vent.
Drift trajectories from 15 November 2002 to 15 January 2003, assuming uniform conditions as predicted at buoy Brittany (ID number 62 163, northern Bay of Biscay) by NOAA/NCEP. The thick black solid line is the total wave-induced drift at 1.25 m below the sea surface, sum of the Stokes drift and of the contribution of waves to the Eulerian drift. The actual drift is thus sum of this drift and the Ekman drift (black dashed). The thin dashed line is a hypothetical trajectory with a velocity equal to 2% of the wind speed, thus indicating wind strength and direction.

On remarque enfin que la dérive est très sensible à la profondeur d'immersion, à cause du fort cisaillement en surface de la dérive de Stokes. Or, pour les boulettes de pétrole issues de la cargaison du Prestige, ce paramètre n'a pas été vérifié. Pour ce qui est de la modélisation, la distribution des immersions des boulettes peut être calculée en prenant en compte l'équilibre entre la diffusion verticale due à la turbulence et la flottabilité des hydrocarbures. Ici, nous n'avons calculé qu'une trajectoire à immersion constante. Outre ces questions de comportement physico-chimique de la matière suivie, les résultats sont représentatifs d'une situation d'hiver en milieu océanique, avec une couche de mélange assez profonde et des états de mer bien développés.

La variété des états de mer réels empêche une paramétrisation simple de la dérive sous l'effet des vagues en fonction du vent local. Ainsi, les déplacements fictifs d'une particule donnés par l'intégration de la vitesse de Stokes ${\hat{u}}^{st}$ et l'intégration de 2 % de la vitesse du vent U₁₀ donnent une distance de déplacement similaire, mais une direction et un historique des positions sensiblement différents (Fig. 2). Un calcul complet à partir de spectres d'état de mer est donc souhaitable. Ce calcul est facile, pourvu que l'on dispose de cette information, qui est, de fait, calculée dans tout modèle de prévision de l'état de mer. Les résultats présentés sur la Fig. 2, bien que schématiques (conditions uniformes sur l'horizontale) et sans validation par des observations de dérive, sont indicatifs des processus contribuant à la dérive dans des conditions hivernales.

4 Conclusions et perspectives d'amélioration

La prise en compte directe des vagues dans le calcul de dérive est assez simple et donne une correction importante qui ne peut pas être négligée. Pour le cas du Prestige, l'introduction de l'effet des vagues, tel qu'il est décrit ici, dans un modèle tridimensionnel réaliste de l'océan Atlantique nord-est est en cours, ce qui permet de représenter l'ensemble des phénomènes, en particulier la vitesse géostrophique, qui est importante le long de la côte Cantabrique. Des résultats préliminaires reproduisent assez bien le temps de déplacement de la pollution entre le naufrage au large de la Galice et l'arrivée de boulettes d'hydrocarbures sur les côtes des Landes.

Toutefois, l'essentiel de la difficulté réside dans la paramétrisation du mélange vertical, d'autant que ce mélange dépend aussi des vagues, par le déferlement et les phénomènes de couplage vagues–courant, tels que les circulations de Langmuir [4,25], intimement liées à une variabilité horizontale conjointe des vagues et des courants [7]. Ces circulations de Langmuir nécessitent des paramétrisations spécifiques des variations horizontales des vagues et du courant et du mélange vertical qu'elles induisent [30]. De plus, le couplage vagues–ondes internes, susceptible d'avoir une effet sur le mélange à la base de la couche de mélange, est souvent oublié.

L'effet du déferlement est un peu plus étudié. Craig et Banner [3] ont indiqué comment représenter l'énergie cinétique turbulente (ECT) qu'il apporte, en introduisant un flux d'ECT en surface de l'ordre de $100 ρ^{a} u_{★}^{3}$ , avec u_★=(τ_a/ρ^a)^1/2 la vitesse de frottement dans l'air. Or, ce facteur 100 est fortement variable quand on le calcule à partir du terme de dissipation d'énergie dans le modèle de prévision des vagues [13]. L'ECT pénètre peu dans l'océan, car elle est dissipée en chaleur près de la surface, cela peut avoir une incidence importante sur le mélange des premiers mètres sous la surface, et donc aussi sur le profil de vitesse de dérive dans cette région.

Il reste à voir si ces idées sont applicables au voisinage immédiat de la surface, y compris pour |z|<z₀, où z₀ est la rugosité de la surface, car la différence des profils de ${\hat{u}}^{e, H}$ et ${\hat{u}}^{st}$ , et donc la dérive nette induite par les vagues, est sensible à l'intensité du mélange en surface, comme l'indique la Fig. 1. Beaucoup de travail sur le mélange reste donc à accomplir pour arriver à une modélisation cohérente de la dérive. Le manque d'observation des vitesses et de la turbulence près de la surface est probablement le frein le plus important à l'amélioration des prévisions de dérive à la surface de l'océan.

References

[1] D.G. Andrews; M.E. McIntyre An exact theory of nonlinear waves on a Lagrangian-mean flow, J. Fluid Mech., Volume 89 (1978), pp. 609-646

[2] F. Ardhuin, B. Chapron, T. Elfouhaily, Waves and the air–sea momentum budget, implications for ocean circulation modelling, J. Phys. Oceanogr. (in press)

[3] P.D. Craig; M.L. Banner Modeling wave-enhanced turbulence in the ocean surface layer, J. Phys. Oceanogr., Volume 24 (1994), pp. 2546-2559

[4] A.D.D. Craik; S. Leibovich A rational model for Langmuir circulations, J. Fluid Mech., Volume 73 (1976), pp. 401-426

[5] M.A. Donelan On the fraction of wave momentum retained by waves (J.C. Nihoul, ed.), Marine Forecasting, Predictability and Modelling in Ocean Hydrodynamics, Elsevier, Amsterdam, 1979, pp. 141-159

[6] V.W. Ekman On the influence of the earth's rotation on ocean currents, Ark. Mat. Astron. Fys., Volume 2 (1905), pp. 1-53

[7] C. Garrett Generation of Langmuir circulations by surface waves – a feedback mechanism, J. Mar. Res., Volume 34 (1976), pp. 117-130

[8] J.-P. Gaspar; Y. Grégoris; J.-M. Lefevre A simple eddy kinetic energy model for simulations of oceanic vertical mixing: tests at station Papa and long-term upper ocean study site, J. Geophys. Res., Volume 95 (1990) no. C9, pp. 16179-16193

[9] A. Gnanadesikan; R.A. Weller Structure and instability of the Ekman spiral in the presence of surface gravity waves, J. Phys. Oceanogr., Volume 25 (1995), pp. 3148-3171

[10] J. Groeneweg; J.A. Battjes Three-dimensional wave effects on a steady current, J. Fluid Mech., Volume 478 (2003), pp. 325-343

[11] K. Hasselmann Wave-driven inertial oscillations, Geophys. Fluid Dyn., Volume 1 (1970), pp. 463-502

[12] K. Hasselmann On the mass and momentum transfer between short gravity waves and larger-scale motions, J. Fluid Mech., Volume 4 (1971), pp. 189-205

[13] P.A.E.M. Janssen; O. Saetra; C. Wettre; H. Hersbach Impact of the sea state on the atmosphere and ocean (F. Ardhuin, ed.), Proc. CD of the 2003 Waves and Operational Oceanography Workshop, Service hydrographique et océanographique de la Marine, Brest, France, 2004

[14] A.D. Jenkins A theory for steady and variable wind- and wave-induced currents, J. Phys. Oceanogr., Volume 16 (1986), pp. 1370-1377

[15] A.D. Jenkins Wind and wave induced currents in a rotating sea with depth-varying eddy viscosity, J. Phys. Oceanogr., Volume 17 (1987), pp. 938-951

[16] K.E. Kenyon Stokes drift for random gravity waves, J. Geophys. Res., Volume 74 (1969), pp. 6991-6994

[17] G.J. Komen; L. Cavaleri; M. Donelan; K. Hasselmann; S. Hasselmann; P.A.E.M. Janssen Dynamics and Modelling of Ocean Waves, Cambridge University Press, Cambridge, 1994

[18] V.N. Kudryavtsev The coupling of wind and internal waves, J. Fluid Mech., Volume 278 (1994), pp. 33-62

[19] S. Leibovich The form and dynamics of Langmuir circulations, Annu. Rev. Fluid Mech., Volume 15 (1983), pp. 391-427

[20] O.S. Madsen A realistic model of the wind-induced Ekman boundary layer, J. Phys. Oceanogr., Volume 7 (1977), pp. 248-255

[21] C. Mastenbroek; G. Burgers; P.A.E.M. Janssen The dynamical coupling of a wave model and a storm surge model through the atmospheric boundary layer, J. Phys. Oceanogr., Volume 23 (1993), pp. 1856-1867

[22] G.L. Mellor The three-dimensional current and surface wave equations fluid problems, J. Phys. Oceanogr., Volume 33 (2003), pp. 1978-1989

[23] G.L. Mellor; T. Yamada Development of a turbulence closure model for geophysical, Rev. Geophys. Space Phys., Volume 20 (1982) no. C2, pp. 851-875

[24] O.M. Phillips The Dynamics of the Upper Ocean, Cambridge University Press, London, 1977 (336 p)

[25] E.A. Terray; M.A. Donelan; Y.C. Agrawal; W.M. Drennan; K.K. Kahma; A.J. Williams; P.A. Hwang; S.A. Kitaigorodskii Estimates of kinetic energy dissipation under breaking waves, J. Phys. Oceanogr., Volume 26 (1996), pp. 792-807

[26] E.B. Thornton; R.F. Kraphol Wave particle velocity measured under ocean waves, J. Geophys. Res., Volume 79 (1974) no. 6, pp. 847-852

[27] E.B. Thornton; R.T. Guza Surf zone longshore currents and random waves: field data and models, J. Phys. Oceanogr., Volume 16 (1986) no. 7, pp. 1165-1178

[28] J.E. Weber Ekman currents and mixing due to surface gravity waves, J. Phys. Oceanogr., Volume 11 (1981), pp. 1431-1435

[29] J.C. McWilliams; P.P. Sullivan; C.-H. Moeng Langmuir turbulence in the ocean, J. Fluid Mech., Volume 334 (1997), pp. 1-30

[30] J.C. McWilliams; P.P. Sullivan Vertical mixing by Langmuir circulations, Spill Sci. Technol. Bull., Volume 6 (2001) no. 3–4, pp. 225-237

[31] Z. Xu; A.J. Bowen Wave- and wind-driven flow in water of finite depth, J. Phys. Oceanogr., Volume 24 (1994), pp. 1850-1866

Comments - Policy