Abridged English version
Flow and transport in the upper soil layers represent an important problem for agriculture and subsurface hydrology. The transport of particles through a saturated porous medium is of interest in a number of other fields like transport in petroleum reservoirs or analysis of filtration systems. Mobile suspended particles in groundwater can serve as carriers for sorbing contaminants and thereby enhance pollutant mobility [4,10]. The transport mechanisms of colloids in saturated porous media have been studied in great detail. Particle transport in the subsurface has only recently attracted significant attention [9,11,15]. Understanding the fate and transport of suspended particles in porous media has a great implication on the reduction of the risk of drinking-water-supply contamination. In this study, the short-pulse method is used to inject suspended particles during flow through a porous medium. Two types of particles are used: artificial ones (Rilsan) ranging between 2 and 50 μm with a mode of 25 μm and natural ones (silt) ranging between 2 and 40 μm with a mode of 15 μm. Rilsan particles are used because of their density approaching that of water. The column is packed with crushed gravel beads 1.15 to 3.15 mm in size. The total porosity of this highly permeable medium is 0.47 and the hydraulic conductivity is .
The experimental set-up (Fig. 1) consists of a water reservoir, a pump controlling the steady-state flow rate, a numerical flowmeter, a pulse injection loop, and a Plexiglas column of 35.5-cm length and 8.9-cm inner diameter. The detection system consists of a turbidimeter and a fluorimeter. The injected pulse is chosen very small (2% of the pore volume) in order not to disturb the water flow in the column. The concentration of suspended particles is 0.1 g l−1. Many experiments were conducted using two types of particles with different Darcy velocities from 0.013 to 0.437 cm s−1. The on-line detection system allows observing the transport behaviour of the conservative tracer and of each type of suspended particles. A mathematical model is used to determine the hydrodispersive parameters and particle deposition rates. The transport of particles through a saturated porous medium is described by the convective–dispersive equation (Eq. (1)) with a first-order particle deposition kinetic [7]. The analytical solution of Eq. (1) with initial and boundary conditions (2) is given by Eq. (3) [14]. Using similar transformations as in the linear graphical method [14], this solution is developed [16] as a non-dimensional equation (Eq. (4)), where some non-dimensional parameters are expressed by Eqs. (5) and (6). This method is applied to determine the dispersivity α, the recovery rate R and the particle deposition rate . The 22 particle experiments have been interpreted by the above theory. The breakthrough curves are fitted with the analytical solutions (Fig. 2) and the transport parameters are determined. The results obtained are summarized in Table 1. The parameters calculated by the model for both particles and dissolved tracer depend on the flow rate. Fig. 3 shows the variation of different parameters obtained as a function of the Darcy velocity. The fractions of recovered particles decrease with decreasing flow rate. The recovery rate is more important for silt particles than for Rilsan particles, in spite of their higher density. This effect can be explained by the size of the silt particles, which are in proportion finer than the Rilsan particles. The particle deposition rates are also presented as a function of the Darcy velocity: they increase with increasing the latter. This increase of the particle deposition rate with flow velocity, confirmed by experimental data with colloids, occurs for low velocities; a decrease is recorded after a ‘critical velocity’ is reached. We demonstrate the existence of this critical flow rate, determined experimentally, beyond which the particle deposition rate decreases with flow velocity. The breakthrough curves also show that beyond this critical flow velocity, particles arrive earlier in the effluent than a nonsorbing solute (Fig. 4). This suggests that particles have an average migration velocity higher than that of a tracer. The studies conducted at the pore scale using physical micromodels [3,13] provide direct observation of the size exclusion phenomenon for colloids travelling through porous media.
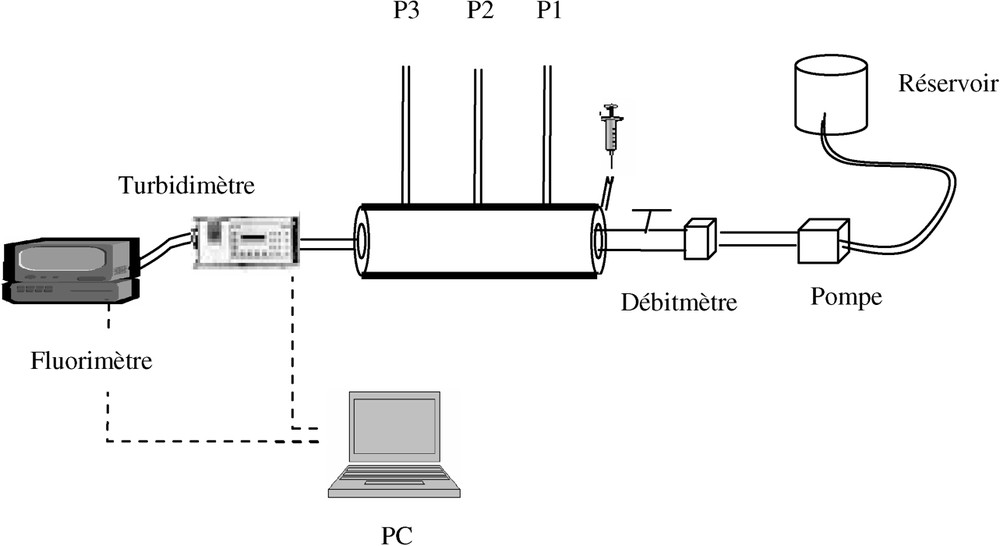
Schéma du dispositif expérimental de traçage.
Schematic drawing of the tracing experimental set-up.
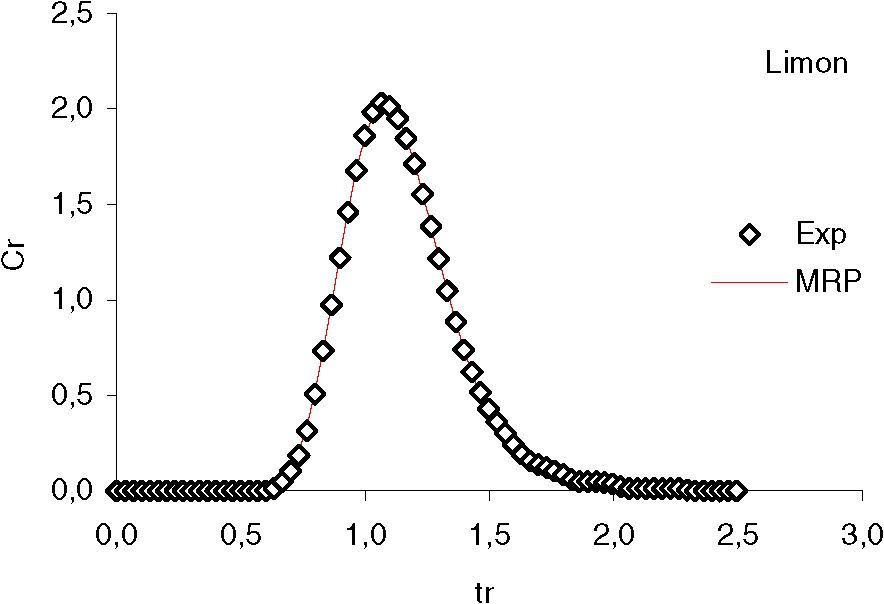
Calage de la solution analytique sur une courbe expérimentale de restitution.
Adjustment of a breakthrough curve of the tracer experiments.
Paramètres de transport calculés par la méthode analytique pour les limons
Particle transport parameters computed by analytical method for silts
| Débit Q (ml min−1) | Vitesse de Darcy U (cm s−1) | Temps de convection (s) | Dispersivité longitudinale (cm) | Taux de restitution | Cinétique de dépôt (h−1) | ||
| Traceur | MES | Traceur | MES | MES | MES | ||
| 1630 | 0,437 | 52,9 | 51,6 | 0,50 | 0,75 | 73,5 | 24,87 |
| 1400 | 0,375 | 59,9 | 55,6 | 0,49 | 0,73 | 68,6 | 27,59 |
| 1300 | 0,349 | 63,6 | 59,4 | 0,48 | 0,17 | 62,8 | 32,88 |
| 903 | 0,242 | 86,8 | 82,1 | 0,57 | 0,68 | 48,3 | 34,67 |
| 708 | 0,189 | 107,8 | 101,4 | 0,57 | 0,70 | 37,3 | 37,45 |
| 500 | 0,135 | 147,1 | 156,2 | 0,58 | 0,70 | 28,4 | 31,16 |
| 355 | 0,095 | 200,9 | 215,7 | 0,68 | 0,75 | 25,6 | 25,50 |
| 199 | 0,053 | 356,7 | 438,4 | 0,6 | 0,46 | 16,3 | 16,33 |
| 100 | 0,027 | 665,9 | 706,8 | 0,77 | 0,75 | 12,0 | 12,54 |
| 50 | 0,013 | 1289,8 | 1362,4 | 0,68 | 0,73 | 6,8 | 7,27 |
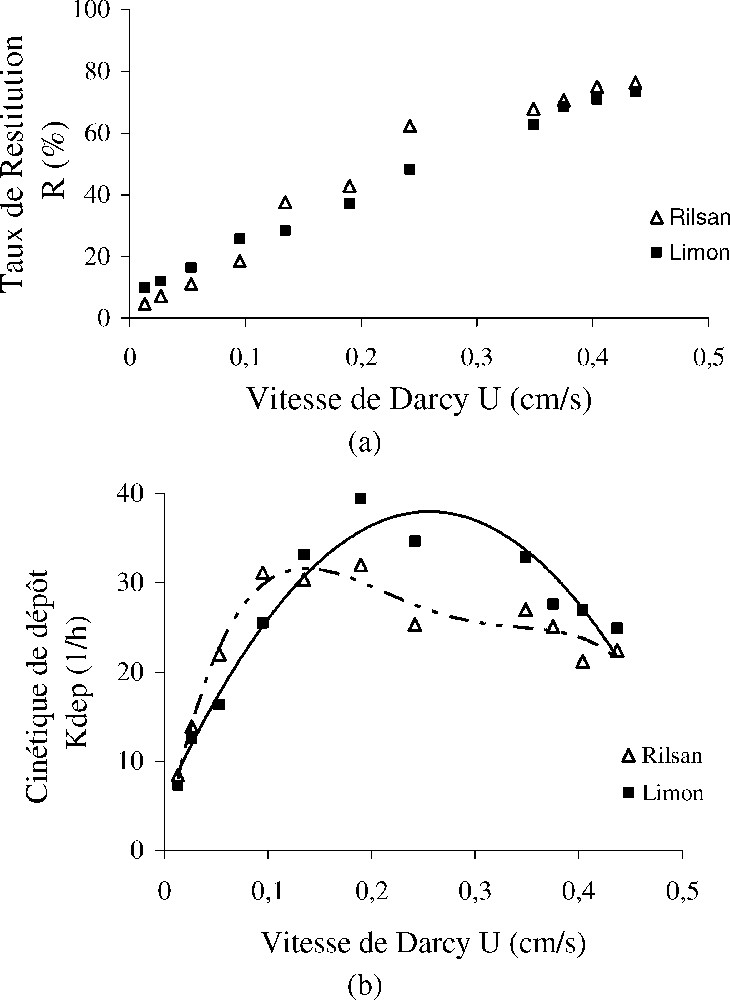
(a) Influence de la vitesse de Darcy sur le taux de restitution R. (b) Influence de la vitesse de Darcy sur la cinétique de dépôt .
(a) Influence of the Darcy velocity on the recovery rate R. (b) Influence of the Darcy velocity on the deposition rate .
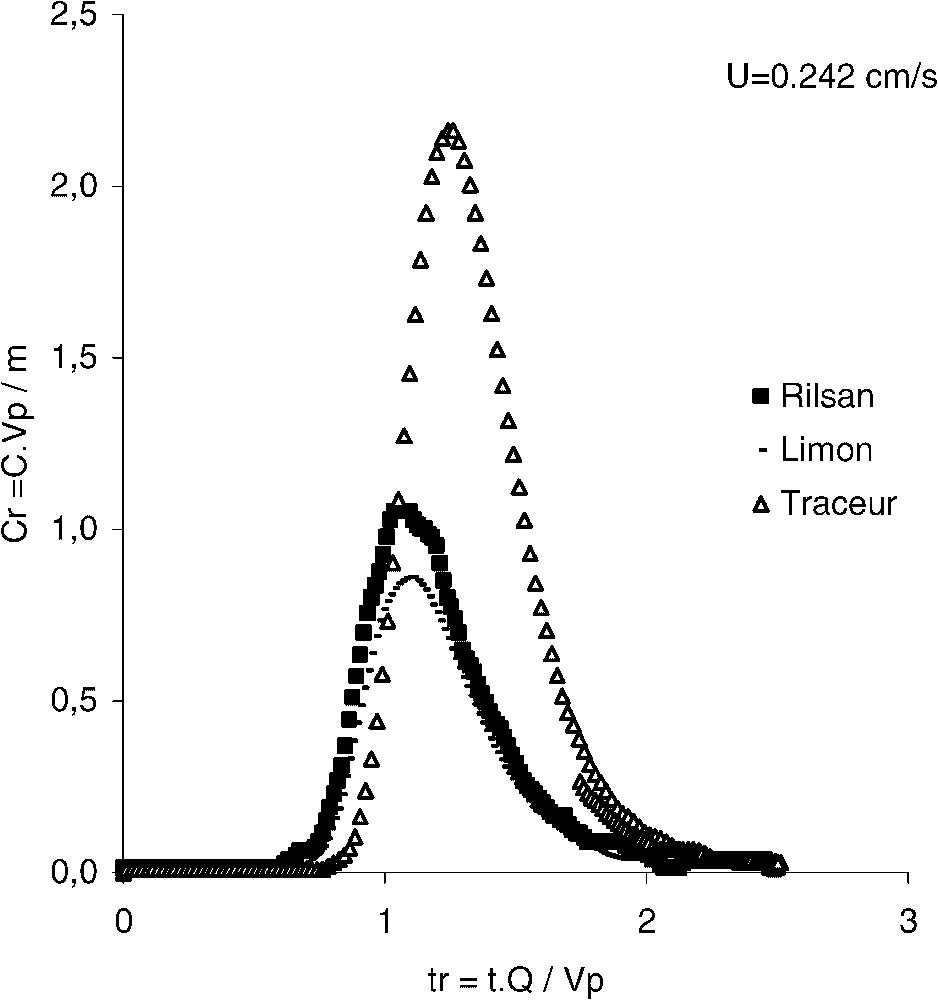
Courbes de restitution des particules et du traceur dissous.
Breakthrough curves of the tracer and particles experiments.
The slope of the log–log relationship obtained in this study between particle deposition rate and flow velocity is 0.6 and is larger than those obtained for colloids [7]. In this study, the flow rates are very high and suspended particles are coarser. Fig. 5 illustrates a comparison of the recovery rate between silt and Rilsan particles. The recovery curves (see also Fig. 4) show that Rilsan particles are better recovered than silt particles because of inertial effects. It is also observed that both types of particles migrate through the porous medium at the same velocity. The grain-size analysis of the suspended particles at the outlet is performed using a Coulter Multisizer particle counter. According to the micro-granulometric spectrum (Fig. 6), we observe that there is no size selection for Rilsan particles transport. Particles of various diameters migrate through the porous medium. But for silt particles, most sizes are transported only at a higher flow rate. This phenomenon is related to the Rilsan density, which is close to that of water.

Comparaison des courbes de restitution des deux types de particules.
Comparison between the breakthrough curves of the two particle types.
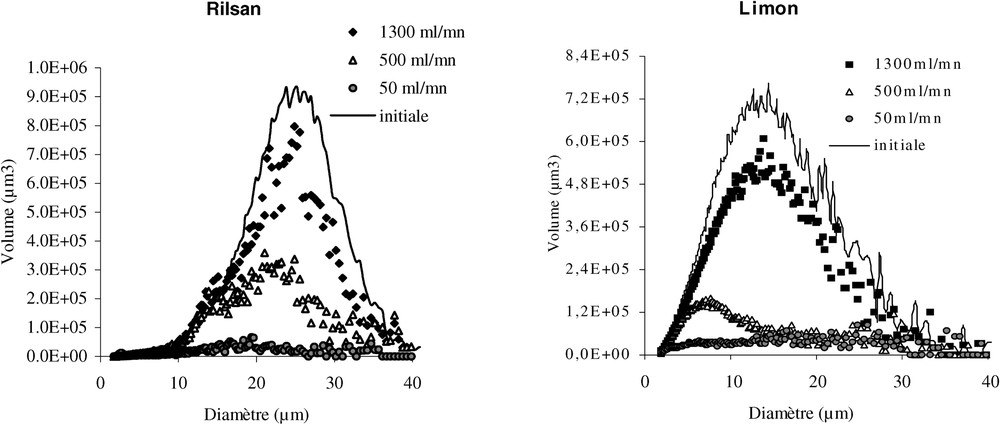
Spectre micro-granulométrique des MES restituées.
Micro-granulometric spectrum of suspended particles at the outlet.
In conclusion, all transport parameters depend on the flow velocity. We have shown the existence of a critical flow beyond which particles arrive earlier in the effluent than a conservative solute. This behaviour is explained by the size-exclusion effect: preferential pathways through the pore space for different particle sizes [5]. The studies conducted on a two-dimensional model [12] demonstrate the role played by high-permeability zones in particle transport and deposition. Below the critical flow rate, the deposition kinetic coefficient increases with the Darcian velocity with a power law. The control of grain size at the outlet allows determining that Rilsan particles are better recovered than silt particles. Thanks to the dispersivity of the injected suspension, it can also be concluded that Rilsan particles' size distribution is better preserved than that of silt particles.
1 Introduction
Le transport des contaminants à travers les couches de sol et les aquifères peut être facilité par la présence de matières en suspension [4,10]. Ces dernières vont exercer un effet sur la perméabilité de l'interface et ensuite, une fois introduites dans le sol, elles pourront, soit se comporter comme des vecteurs de pollution, soit comme des freins par leur dépôt. Dans ce domaine de transport de masse en milieu poreux, beaucoup d'études sont consacrées aux éléments dissous et aux colloïdes, mais peu de travaux concernent le transport de particules, notamment en suspension [9,11,15]. La migration des matières organiques et dissoutes est régie par la convection, la dispersion et les échanges physico-chimiques avec le milieu. Deux phénomènes, autres que la convection et la dispersion, sont importants dans l'étude du transport des particules : dépôt et détachement des particules au cours du transport. Le transport et le dépôt des MES dans un milieu poreux dépendent de mécanismes liés à l'environnement physicochimique [4], mais aussi à la taille et la nature des particules [12]. Nous présentons une étude du comportement de transport et de la cinétique de dépôt de particules synthétiques et de limons, par des essais de traçages réalisés dans une colonne de laboratoire. Ces travaux, centrés sur l'expérimentation et la modélisation mathématique, visent à déterminer les effets de la vitesse d'écoulement sur les paramètres hydrodispersifs, ainsi que sur la cinétique de dépôt des matières en suspension.
2 Dispositif expérimental
Les MES utilisées sont de deux types : des particules naturelles de limons, dont la taille moyenne est de 15 μm et des particules de polyamide (Rilsan), dont la taille moyenne est de 25 μm. Ces dernières ont été choisies pour leur densité (1,04), proche de celle de l'eau. Les spectres micro-granulométriques montrent que les dimensions des particules de Rilsan sont comprises entre 2 et 50 μm, et que celles des particules de limons varient entre 2 et 40 μm. La collision entre les particules et les grains du milieu joue un rôle important dans le transport ou la rétention de ces particules. Le milieu poreux est constitué d'un gravier concassé dont la dimension des grains est comprise entre 1,15 et 3,15 mm. La colonne en Plexiglas a un diamètre intérieur de 89 mm et une longueur de 355 mm. Après le remplissage de la colonne par le gravier, le milieu est saturé par de l'eau à pH 6,8. La porosité totale du milieu est alors voisine de 47 % et sa perméabilité mesurée est proche de .
Le dispositif expérimental (Fig. 1) est composé d'un réservoir d'eau, d'une pompe à débit constant, d'un débitmètre et d'une seringue servant à injecter la suspension. La colonne est équipée de trois piézomètres, qui permettent de contrôler la charge hydraulique le long du milieu poreux. L'injection en continu favorise les blocages et la filtration dans le milieu, réduisant sa perméabilité [7]. L'injection instantanée permet alors de s'affranchir de cette évolution du milieu durant les essais. Les essais sont effectués sous un écoulement continu d'eau et une injection brève de la suspension de particules, mélangée à un traceur conservatif de référence (fluorescéine à 0,5 mg l−1). Le volume injecté de 20 ml (2 % du volume des pores) est choisi de façon à ne pas perturber l'écoulement dans la colonne. La concentration des particules a été fixée à 100 mg l−1 dans la seringue. Les expériences sur le transport/dépôt des MES sont effectuées en faisant varier le débit pour obtenir une vitesse de Darcy allant de 0,013 à 0,437 cm s−1. La procédure d'essai consiste à commencer par le plus fort débit, de façon à éviter de détacher, au cours des essais suivants, les particules piégées au préalable dans l'espace poral. L'effluent est suivi à la sortie de la colonne par un fluorimètre et un turbidimètre, qui permettent de comparer le comportement des MES et du traceur dissous.
3 Résultats et discussion
3.1 Théorie et interprétation des traçages
Le transport/dépôt des MES dans un milieu poreux est régi par l'équation de convection–dispersion (Éq. (1)) avec la cinétique de dépôt de premier ordre (relargage des particules négligé) [7]. Cette hypothèse est vérifiée pour cette étude, car la quantité des MES injectée est faible et le débit d'écoulement est maintenu constant durant l'essai.
| (1) |
Les conditions initiales et aux limites adoptées pour obtenir la solution analytique sont les suivantes :
| (2) |
La solution analytique de l'Éq. (1) avec les conditions (2) est donnée par [15] :
| (3) |
La dernière condition aux limites n'étant pas réaliste, on admet cependant que la solution analytique obtenue est acceptable, même pour une colonne finie. En s'inspirant de la méthode graphique linéaire [14], cette solution a été développée sous forme adimensionnelle pour obtenir une nouvelle méthode dite méthode de régression parabolique (MRP), qui permet de déterminer les paramètres de transport [16]. Cette équation adimensionnelle s'écrit :
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Si on admet que ( est la dispersivité longitudinale), le nombre de Péclet est défini par :
| (10) |
La concentration de l'effluent en particules et en traceur est suivie dans le temps pour les 22 essais de traçage effectués. Le calage des courbes de restitution expérimentales avec la solution analytique (Fig. 2) a permis d'estimer les paramètres hydrodispersifs. Le Tableau 1 donne, pour les essais avec la suspension limon/fluorescéine, les valeurs des paramètres de transport tels que le temps de convection pure , la dispersivité longitudinale , le taux de restitution R et le coefficient cinétique de dépôt .
3.2 Influence de la vitesse d'écoulement
La vitesse d'écoulement est un paramètre hydrodynamique important dans le transport et le dépôt de particules dans un milieu poreux. Les Figs. 3a et b montrent l'influence de la vitesse sur le taux de restitution des particules (Rilsan et limon) et le coefficient cinétique de dépôt. On peut constater que les deux types de particules ont un comportement globalement similaire (Fig. 3a). Cependant, à faible vitesse, la restitution des particules de limon est plus importante que celle du Rilsan. Ce comportement peut être expliqué par la granulométrie du limon comportant plus de fines, mais aussi par la nature minéralogique des particules de Rilsan (polyamide) dont les charges de surface peuvent contribuer à créer des mécanismes de rétention avec les grains du milieu poreux. En effet, dans le transport de particules en milieu poreux, les charges de surface des particules et des grains du milieu jouent un rôle important. Ait Akbour et al. [1] ont mis en évidence la nature répulsive des forces entre la surface de sable et celle d'argile pour empêcher le dépôt des particules. Le taux de restitution augmente avec la vitesse d'écoulement dans le milieu. En effet, à faible débit, les forces hydrodynamiques exercées par l'écoulement sont insuffisantes pour entraîner les particules les plus grosses qui restent alors piégées dans le milieu. Pour ce qui est de la rétention des particules dans le milieu poreux, le coefficient cinétique de dépôt augmente avec la vitesse jusqu'à une valeur critique, au-delà de laquelle la tendance s'inverse (Fig. 3b). Cette vitesse critique est plus faible pour les particules de Rilsan. Herzig et al. [6] ont décrit les différents mécanismes de la « filtration profonde » et ont proposé une équation linéaire pour la cinétique de dépôt. D'autres auteurs [7,15] ont montré que cette variation obéit à une loi puissance. Dans notre cas, pour les faibles vitesses, augmente avec la vitesse de Darcy selon une puissance de 0,6 . Masséi et al. [9] ont trouvé une puissance de 0,7 pour des particules en suspension de même nature (limon). Kretzschmar et al. [7], qui ont étudié le transport de colloïdes dans un milieu poreux, ont trouvé des valeurs de la loi puissance bien inférieures. Ceci est expliqué par le fait que les colloïdes ne se déposent pas aussi facilement que les particules de limon à des vitesses d'écoulement faibles. La diminution de la cinétique de dépôt à partir d'une vitesse critique peut être expliquée par l'importance que prennent les forces hydrodynamiques par rapport aux forces de gravité à cette vitesse.
3.3 Comportement général de transport des particules
Pour mettre en évidence le comportement de transport/dépôt des MES, les essais de traçage permettent de comparer les paramètres de transport entre un traceur dissous conservatif et la suspension de particules. Les courbes de restitution des particules et du traceur dissous (Fig. 4) montrent deux comportements : la restitution des particules se produit avant celle du traceur ; seule une fraction des particules est restituée. Les MES sont donc transportées plus rapidement que le traceur dissous. Le rapport entre la vitesse des particules et celle du traceur dissous est voisin de 1,1. Ce comportement de transport peut être attribué au phénomène d'exclusion de taille [5,7] ou de chromatographie hydrodynamique [2]. Selon De Marsily [8], les grosses particules « échantillonnent » les vitesses les plus élevées dans la colonne, car elles ne peuvent s'approcher des parois du fait de leur dimension. Les études menées sur des micro-modèles fournissent une observation directe de ce phénomène pour les colloïdes [3,13]. L'analyse du transport de particules de latex dans un milieu poreux bidimensionnel [12] montre le rôle joué par les zones de grande perméabilité sur le transfert et le dépôt des particules.
3.4 Effets de la vitesse d'écoulement sur le transport des particules
Les courbes de restitution des particules de Rilsan et de limons (Fig. 5) pour une même vitesse de Darcy montrent que le temps de transfert des particules solides est identique et que la restitution des particules de Rilsan est plus importante pour une grande vitesse d'écoulement. Ce comportement est conforme à la nature des particules de limons, qui sont beaucoup plus denses que celles de Rilsan et donc plus sujettes aux effets de sédimentation et d'inertie. Mais à faible vitesse, le taux de restitution des particules de limons est légèrement supérieur à celui du Rilsan (Fig. 3). Ce résultat est expliqué par la distribution des tailles des particules de Rilsan, qui sont plus grosses et donc moins bien transportées à des vitesses faibles, mais aussi par leur nature minéralogique, qui leur confère des forces de surface attractives. Hormis l'analyse quantitative du transport, une analyse qualitative sur les particules restituées à la sortie de la colonne est effectuée par micro-granulométrie pour différents débits. La Fig. 6 présente les distributions volumiques des particules en fonction de leur dimension. L'analyse des échantillons montre que, pour les particules de Rilsan, il n'y a pas de sélection de taille des particules restituées quelle que soit la vitesse d'écoulement. Ceci est lié à la densité des particules utilisées , qui est très proche de celle de l'eau et qui ne favorise pas la décantation. En revanche, pour les limons, la taille des particules restituées diminue lorsque la vitesse (donc la force hydrodynamique appliquée sur les particules) diminue. Les effets de gravité favorisent la sédimentation des grosses particules de limons à de faibles vitesses d'écoulement.
4 Conclusions
Nous avons mis en évidence l'influence de la vitesse d'écoulement sur les divers paramètres hydrodispersifs en présence de matières en suspension. Dans le gravier, lorsque le débit augmente, le taux de restitution et le coefficient cinétique de dépôt augmentent. Les injections instantanées effectuées séparément avec les MES et le traceur dissous pour les différents débits testés ont montré un déphasage entre la restitution de la fluorescéine et des particules en suspension. Les matières en suspension sont transportées considérablement plus vite que la fluorescéine pour les forts débits (supérieurs à 200 ml min−1). Ce comportement est confirmé en injectant le mélange Rilsan–fluorescéine et s'explique par le phénomène d'exclusion de taille. Ceci montre que, sous certaines conditions, les particules en suspension peuvent être des vecteurs de pollution d'une célérité plus grande que les éléments dissous. Ce comportement peut jouer un rôle important dans le transfert de polluants par les particules vers les aquifères. Le dépôt de particules ne semble pas affecter la perméabilité du milieu, eu égard à la faible concentration de la suspension injectée et au caractère instantané de l'injection. D'autre part, la porosité importante du milieu poreux ne permet pas une rétention significative de particules fines utilisées dans l'écoulement. Les effets de minéralogie et de granulométrie des particules injectées se manifestent aussi bien sur le taux de restitution que sur la sélection de taille des MES à la sortie de la colonne. Les particules les plus denses ne sont pas transportées par l'écoulement à de faibles vitesses et se déposent dans le milieu.


