Paramètres statistiques de la houle au large de la côte sud-aquitaine

Stéphane Abadie; Rémi Butel; Hélène Dupuis; Christophe Brière

doi:10.1016/j.crte.2005.03.012

Océanographie

Paramètres statistiques de la houle au large de la côte sud-aquitaine

Présenté par : Jean-François Minster

Stéphane Abadie ¹ ; Rémi Butel ² ; Hélène Dupuis ² ; Christophe Brière ¹

¹ Laboratoire de sciences appliquées au génie civil et côtier, université de Pau et des pays de l'Adour, allée du parc Montaury, 64600 Anglet, France
² DGO, université Bordeaux-1–UMR 5805, av. des facultés, 33405 Talence cedex, France

Comptes Rendus. Géoscience, Volume 337 (2005) no. 8, pp. 769-776.

Résumés

Français
Anglais

Une analyse des paramètres statistiques de la houle pour la zone côtière sud-aquitaine a été réalisée par comparaison de deux jeux de données : une mesure locale sur une période courte et des résultats de simulation du modèle Wavewatch III sur 6 ans et 9 mois. On montre qu'il existe une très bonne corrélation entre les hauteurs significatives $(H_{s})$ issues respectivement de la mesure et des simulations. La corrélation pour les périodes pic $(T_{p})$ et les directions de pic $(D_{p})$ est moins bonne, du fait respectivement du caractère intrinsèquement instable du paramètre $T_{p}$ et de la distribution particulièrement étroite de $D_{p}$ . Le traitement statistique des sorties du modèle ajusté sur la mesure permet de donner une évaluation des paramètres statistiques de la houle dans cette zone. Le lien entre les trois paramètres $(H_{s}, T_{p}, D_{p})$ est enfin analysé sous la forme d'une classification des états de mer. Cette dernière classification montre la prédominance des houles, en grande majorité d'une direction avoisinant les 300°, sur les mers du vent.

Statistical parameters of waves on the south Aquitaine coast have been determined by comparison of two datasets: in situ local measurements on a short duration and numerical simulation outputs from the WAVEWATCH III model over a period of 6 years and 9 months. Data and simulation results are well correlated in the case of the significant wave height, whereas in the case of the peak periods $(T_{p})$ and directions $(D_{p})$ , this correlation is lower. This is due respectively to the intrinsic unstable nature of $T_{p}$ and the narrow distribution of $D_{p}$ . An adjustment of simulation data on measurement is then used to give an evaluation of the wave statistics for the southern fraction of the French Atlantic coast. Eventually, the relationships between the three statistical variables $(H_{s}, T_{p}, D_{p})$ are analysed in order to determine representative sea states. The classification obtained shows the predominance of swell regimes, distributed on a very narrow angular sector over wind sea regimes.

Métadonnées

Reçu le : 2004-07-20
Accepté le : 2005-03-15
Publié le : 2005-04-20

DOI : 10.1016/j.crte.2005.03.012

Mot clés : Vagues, Houle, Mer du vent, Direction, Statistiques, États de mer, Aquitaine, France
Keywords: Waves, Swell, Wind sea, Direction, Statistics, Sea states, Aquitaine, France

Affiliations des auteurs :

Stéphane Abadie ¹ ; Rémi Butel ² ; Hélène Dupuis ² ; Christophe Brière ¹

@article{CRGEOS_2005__337_8_769_0,
     author = {St\'ephane Abadie and R\'emi Butel and H\'el\`ene Dupuis and Christophe Bri\`ere},
     title = {Param\`etres statistiques de la houle au large de la c\^ote sud-aquitaine},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {769--776},
     publisher = {Elsevier},
     volume = {337},
     number = {8},
     year = {2005},
     doi = {10.1016/j.crte.2005.03.012},
     language = {fr},
}

TY  - JOUR
AU  - Stéphane Abadie
AU  - Rémi Butel
AU  - Hélène Dupuis
AU  - Christophe Brière
TI  - Paramètres statistiques de la houle au large de la côte sud-aquitaine
JO  - Comptes Rendus. Géoscience
PY  - 2005
SP  - 769
EP  - 776
VL  - 337
IS  - 8
PB  - Elsevier
DO  - 10.1016/j.crte.2005.03.012
LA  - fr
ID  - CRGEOS_2005__337_8_769_0
ER  -

%0 Journal Article
%A Stéphane Abadie
%A Rémi Butel
%A Hélène Dupuis
%A Christophe Brière
%T Paramètres statistiques de la houle au large de la côte sud-aquitaine
%J Comptes Rendus. Géoscience
%D 2005
%P 769-776
%V 337
%N 8
%I Elsevier
%R 10.1016/j.crte.2005.03.012
%G fr
%F CRGEOS_2005__337_8_769_0

Stéphane Abadie; Rémi Butel; Hélène Dupuis; Christophe Brière. Paramètres statistiques de la houle au large de la côte sud-aquitaine. Comptes Rendus. Géoscience, Volume 337 (2005) no. 8, pp. 769-776. doi : 10.1016/j.crte.2005.03.012. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2005.03.012/

Version originale du texte intégral

Abridged English version

The Aquitaine coast, southern part of the French Atlantic coast, is exposed to very energetic waves that are responsible for large sand transport rates and quick shoreline changes [8]. However, local wave characteristics are not really accurately defined because of the lack of in-situ measurements. In this paper, we focused our attention on the Aquitaine south coast (Fig. 1). There, although wave measurements have been carried out offshore of the Adour rivermouth [9] (Fig. 1, Datawell2), directional properties of the waves have never been investigated up to now.

Fig. 1
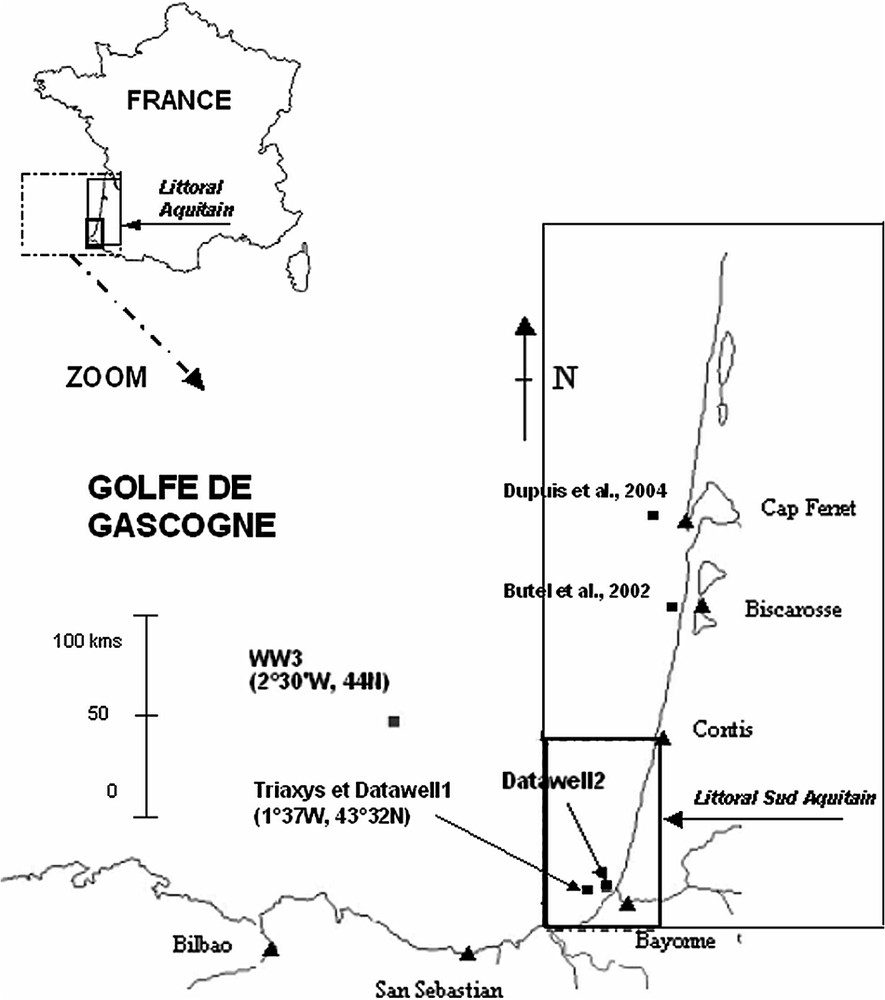
En haut à gauche : positionnement du littoral aquitain. Figure agrandie : zone géographique d'étude et localisation des points de mesure et de simulation.
Top left: location of the Aquitaine nearshore zone in France; zoomed area: south Aquitaine coast, location of the measurement points and WW3 model output.

In this study, two datasets have been analysed in order to fill this gap: in-situ data covering nine months during spring and summer, measured by a directional waverider and an about seven-year numerical simulation outputs from the Wavewatch III model [10,11] at the point $2 ° 30^{'} W$ , $44 ° N$ (see Fig. 1, resp. Triaxys and WW3). The correlation between three statistical parameters (significant wave height $H_{s}$ , peak period $T_{p}$ and peak direction $D_{p}$ ) of both datasets has been analysed first. Measurements and simulations of the first parameter $H_{s}$ are in a very good agreement, as shown by the high correlation coefficient value $(R^{2} = 0.86)$ (Fig. 2). An adjustment Eq. (1) fits simulation outputs on in-situ data and allows us to take into account the wave height negative gradient between offshore and coastal zone. Peak periods appear in a less good agreement ( $R^{2} = 0.48$ and $R^{2} = 0.57$ if $H_{s} > 1.5 m$ ) mainly due to the unstable nature of this parameter [5]. The comparison of peak directions shows relatively weak correlation coefficients (0.47 and 0.51 if $H_{s} > 1.5 m$ ). This is mainly due to the very narrow distribution of wave incidences. However, despite of these seemingly weak correlations, time series exhibit roughly the same trends for both parameters of the two datasets.

Fig. 2
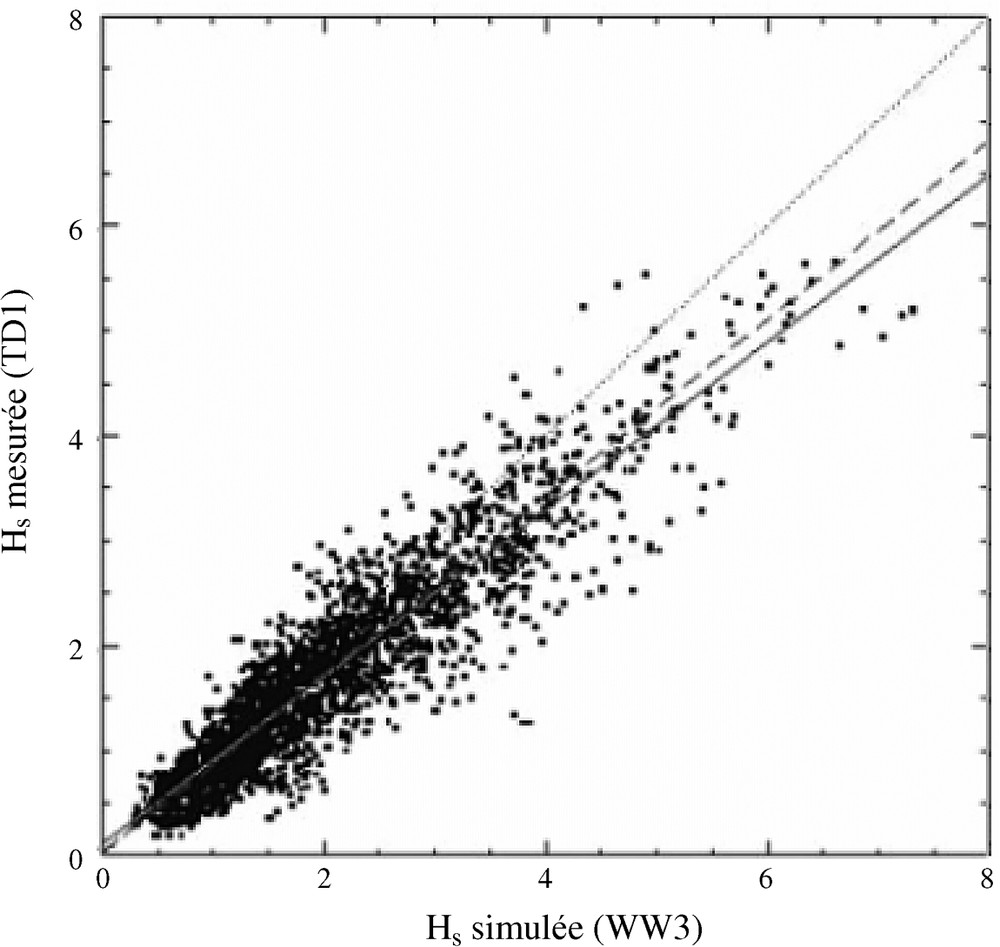
Corrélation mesures (TD1)/modèle numérique (WW3) pour la variable $H_{s}$ sur la période commune. Régression linéaire (1) : droite trait plein ; droite y=x : droite en pointillé ; ACP : droite en traits tirés.
Significant wave height: measurements (TD1) versus simulation (WW3). Continuous line: linear fitting (1), dotted line: y=x, dashed line: ACP.

The statistics of the three studied parameters are presented in Table 2. WW3CO are the statistics of $H_{s}$ based on WW3 data but adjusted on in-situ dataset using Eq. (1). It is the most representative statistics for the parameter $H_{s}$ because the TD1 (i.e. Triaxys + Datawell1) dataset is too short and the WW3 simulation point is too offshore. A comparison of $H_{s}$ distribution is also made with statistics from an older measurement dataset (Datawell2 [4]). Obvious differences are due to the weakness of the depth around waverider D2 implying shoaling as well as refraction non negligible influences. Statistical parameters of $T_{p}$ and $D_{p}$ have been calculated using WW3 data. Statistical results on peak directions are, to our knowledge, the first evaluation of the directional wave climate in this region. Its main property is the narrowness of the angular distribution since about 80% of $D_{p}$ values are restricted within a 40° sector. $D_{p}$ mean value is slightly superior to 300°, which is approximately the normal direction to the shore between the towns of Biarritz and Capbreton.

Tableau 2

Paramètres statistiques pour $H_{s}, T_{p}$ et $D_{p}$ (voir Tableau 1 pour les caractéristiques des sources de données). WW3CO fait référence aux données de WW3 corrigées par l'équation (1). Les statistiques WW3 et WW3CO sont calculées sur 6 ans et 9 mois

Statistics of $H_{s}, T_{p}$ and $D_{p}$ (see Table 1 to see the characteristics of the different datasets). WW3CO means WW3 data corrected using Eq. (1). Statistics WW3 and WW3CO have been calculated considering the period of 6 years and 9 months

Variable	Source	min.	max.	moy. (mean)	med.	écart. (st. dev.)	asym. (skew.)	< 2 m	$2 < \dots < 4$	> 4 m	Durée (duration)
$H_{s} (m)$	TD1	0,17	7,83	1,46	1,21	0,93	1,49	77,78%	20,24%	1,98%	527 J
$H_{s}$	WW3	0,17	9,59	1,83	1,51	1,12	1,42	66,47%	27,96%	5,56%	2511 J
$H_{s}$	WW3CO	0,25	7,75	1,57	1,32	0,89	1,42	75,26%	22,60%	2,14%	2511 J
$H_{s}$	D2							66,5%	22,5%	11%
variable	source	min.	max.	moy.	med.	écart.	asym.	< 9 s	$9 < \dots < 13$	> 13 s	durée
$T_{p} (s)$	TD1	2,63	25	8,99	9,09	2,63	0,08	46,51%	49,09%	4,40%	527 J
$T_{p}$	WW3	2,61	21,06	9,59	9,9	3,08	−0,23	38,29%	48,07%	13,65%	2511 J
variable	source	min.	max.	moy.	med.	écart.	asym.	$275 < \dots < 315$	$315 < \dots < 360$	autre	durée
$D_{p} (°)$	T	0	357	307,6	306	19,2	0,4	84%	13%	3%	∼218 J
$D_{p}$	WW3	0	359,9	301,9	295,5	36,7	0,4	80%	6%	14%	2511 J

The last part of the paper is an attempt to define sea states from WW3 simulations. These sea states have been obtained with a simulated annealing method [7], already used in this research field [2]. The objective is to determine the centres of a fixed number of classes (sea states) in the 3D space $(H_{s}, T_{p}, D_{p})$ that minimize a ‘total distance’ between them and the points of the class. Table 3 presents the results of the class computation. $H_{s}^{*}$ is the significant wave height of gravity centres modified by Eq. (1). This classification points out the predominance (66%) of mean to high energy swell regimes (classes 1, 2, 3, 4 and 5), normal to the shore (between Biarritz and Capbreton). Then, wind sea states (classes 6, 7, 8, 10 and 12) are found with an occurrence probability of about 27%. Their incoming directions are most of the time 300° or the north direction. Storm swells appear at last with a probability of 7.5% and a peak direction about 300°. These weak probability events must however have a strong action on coastal dynamics.

Tableau 3

Classifications des états de mer à partir des simulations WW3 au point $2 ° 30^{'} W$ , 44°N. 2511 jours, soit 19481 simulations. $H_{s}^{*}$ est la hauteur significative des barycentres corrigée par (1). La dernière colonne précise le type de vague (houle océanique ou mer du vent), la saison d'occurrence et le secteur angulaire approximatif de provenance

Sea states calculated from WW3 simulation results at point $2 ° 30^{'} W$ , 44°N. 2511 days (19481 data). $H_{s}^{*}$ is the significant wave height of the gravity centres corrected by (1). In the last column wave kind (swell or wind sea), seasonal occurrence and incoming angular sector have been indicated

N° classe	Probabilité (%)	$H_{s} (m)$	$H_{s}^{*} (m)$	$T_{p} (s)$	$D_{p}$ (°)	Caractéristiques
1	17,85	1,29	1,14	10,15	299,7	houle, printemps et automne, W–NW
2	15,46	0,85	0,79	8,48	297,2	houle, été, W–NW
3	12,74	2,10	1,79	11,04	299	houle, automne, hiver, printemps, W–NW
4	9,96	2,85	2,38	13,02	296,6	houle, hiver, W–NW
5	9,60	1,43	1,25	12,88	289,3	houle, hiver W–NW
6	8,11	1,37	1,20	5,42	297,8	mer du vent, été, W–NW
7	6,90	1,18	1,05	5,16	2,7	mer du vent, été, nord
8	6,64	3,14	2,61	8,41	301,3	mer du vent, annuel, W–NW
9	5,11	4,06	3,35	13,87	295,9	houle, hiver, fortes tempêtes, W–NW
10	3,16	0,81	0,76	4,19	57,2	mer du vent, été, nord-est
11	2,38	5,54	4,53	12,45	297	houle, hiver, très fortes tempêtes, W–NW
12	2,10	1,08	0,97	4,24	182,8	mer du vent, automne, hiver, printemps, sud

1 Introduction

Les paramètres de la houle sont un élément fondamental, tant pour le dimensionnement et la construction d'ouvrages côtiers que pour l'évaluation du transport sédimentaire littoral. Ce constat est d'autant plus vrai pour la côte Aquitaine, exposée à des houles particulièrement énergétiques. En termes de moyens de mesure, cette portion du littoral atlantique français a été longtemps sous-équipée. En effet, les mesures non directionnelles sont peu nombreuses et les mesures directionnelles rares et très récentes [1,3,5]. Sur la côte sud-aquitaine (Sud des Landes et côte basque) (Fig. 1), qui fait l'objet de cette étude, des mesures non directionnelles ont déjà été réalisées [4,9]. Ces données sont difficilement exploitables du fait du manque d'informations sur la provenance de la houle, qui peut engendrer des erreurs importantes dans les calculs de propagation, indispensables au dimensionnement des ouvrages. La direction incidente de la houle est également un paramètre fondamental dans le calcul de la dérive littorale, susceptible de déplacer une quantité importante de sédiment parallèlement à la côte [8].

Ce travail vise à combler le manque d'information sur la direction des houles et à fournir des statistiques représentatives de la zone proche de la côte, où la houle n'est pas encore soumise à l'action des fonds. On espère ainsi couvrir une frange littorale assez importante en évitant les distorsions locales qui peuvent être causées par cette action du fond. L'étude s'appuie sur deux jeux de données principaux. Des mesures locales au point ( $1 ° 36, 8^{'} W$ et $43 ° 31, 8^{'} N$ ) par des fonds de 50 m et les sorties du modèle numérique Wavewatch III [10,11] au point $2 ° 30^{'} O$ , $44 ° N$ (voir Fig. 1). Les caractéristiques de ces données sont présentées dans le Tableau 1. Le jeu de données n° 1 a été fourni par une bouée directionnelle Triaxys (Axys Technologies) gérée par l'université de Pau et des pays de l'Adour. Les paramètres mesurés concernés par cette étude sont : la hauteur significative $H_{s}$ $(= H_{1 / 3})$ , la période de pic $T_{p}$ et la direction de pic $D_{p}$ . Durant l'automne 2002 et l'hiver 2003, le houlographe Triaxys, tombé en panne, a été remplacé par une bouée Datawell non directionnelle. Le paramètre directionnel $D_{p}$ n'a donc été mesuré que durant deux saisons successives, printemps et été (jeu de données T), alors que les paramètres $H_{s}$ et $T_{p}$ couvrent également l'automne et l'hiver en recoupant les jeux n° 1 et n° 2 (jeu de données TD1).

Jeux de données	N° 1	N° 2	N° 3 = N° 1 + N° 2	N° 4	N° 5
Type de données	Mesures Triaxys	Mesures Datawell	Mesures	Modèle	Mesures Datawell
Dénomination	T	D1	TD1	WW3	D2
Lieu	$1 ° {36.8}^{'} W$	$1 ° {36.8}^{'} W$	$1 ° {36.8}^{'} W$	$2 ° 30^{'} W$	$1 ° {32.6}^{'} W$
	$43 ° {31.8}^{'} N$	$43 ° {31.8}^{'} N$	$43 ° {31.8}^{'} N$	44°N	$43 ° {32.80}^{'} N$
Période concernée	2002:16/04 à 09/08	22/10/2002	∼13 mois	01/01/1997	1989 à 1994
	et 2003:01/03 à 09/09	à 03/02/2003		à 30/09/2003
Durée d'enregistrement	1/2 H	20 min			20 min
Données par jour	24	48		8	∼8
Paramètres fournis	$H_{s}, T_{p}, D_{p}$	$H_{s}, T_{p}$	$H_{s}, T_{p}$	$H_{s}, T_{p}, D_{p}$	$H_{s}, T_{p}$
Nombre de données	5238	4653	10846	19451	7951
Saisons	Printemps/été	Automne/hiver	Toutes	Toutes	Toutes
Profondeur (m)	50	50	50	>1000	20

Les simulations du modèle numérique WW3 donnent les trois paramètres $H_{s}$ , $T_{p}$ et $D_{p}$ . Elles ont été archivées à partir de 1997 (http://www.fnmoc.navy.mil) et couvrent donc une période plus longue de 6 ans et 9 mois. Enfin, certains résultats provenant de la mesure non directionnelle (D2) effectuée entre 1989 et 1994 sont également présentés, car ils constituent l'état de l'art actuel sur les statistiques de houle dans cette zone.

L'article est construit en deux parties. Dans la première partie, les deux sources principales de données sont comparées et une analyse des corrélations est effectuée. Dans la seconde, les paramètres statistiques issus principalement de la simulation numérique sont présentés.

2 Comparaison mesures/simulations

La comparaison mesure (TD1)/modélisation (WW3) de $H_{s}$ , la variable hauteur significative de vague (Fig. 2), montre une compacité du nuage de points attestant une très bonne corrélation $(R^{2} = 0, 86)$ . En revanche, cette comparaison indique des hauteurs de vagues simulées plus importantes en moyenne que celles mesurées (biais moyen de 0,26 m). Cette différence provient vraisemblablement de la localisation plus au large du point de simulation WW3. Il semble, en effet, que la hauteur significative des vagues soit plus importante en moyenne au large que vers la côte dans cette zone [2]. La bonne corrélation des données et des simulations (Fig. 2) permet d'envisager un ajustement des données simulées autorisant la prise en compte de cette différence. La correction linéaire suivante a été adoptée :

H_{s_{ww 3 co}} = 0, 797 H_{s_{ww 3}} + 0, 113

(1)

Nous utiliserons par la suite le sigle WW3CO pour faire référence aux données du modèle ajustées sur les mesures.

La comparaison, non présentée ici, des mesures (TD1) et des simulations (WW3) pour le paramètre période de pic $(T_{p})$ montre une corrélation inférieure $(R^{2} = 0, 48)$ à celle relative à la hauteur significative. Si les tendances entre les séries temporelles concordent, il apparaît cependant fréquemment des décrochages brusques non corrélés, dans la mesure ou la modélisation, qui témoignent du caractère instable de ce paramètre et expliquent la faiblesse du coefficient de corrélation. Au même point géographique ( $44 ° 39, 085^{'} N$ , $01 ° 26, 800^{'} W$ ), Dupuis et al. [5] obtiennent des corrélations également faibles ( $R^{2} = 0, 27$ et $R^{2} = 0, 56$ ) pour la période pic en comparant deux à deux, trois jeux de mesures in situ à partir de capteurs de houle différents. Pour ce même jeu de données, ils montrent une corrélation de la période moyenne respectivement de 0,97 et 0,84. Notons enfin que le coefficient de corrélation entre période de pic mesurée et simulée devient égal à 0,57 si l'on réduit les données aux événements les plus énergétiques ( $H_{s} > 1, 5 m$ ).

La comparaison mesure $(T)$ /simulation (WW3) pour le paramètre direction de pic (également non représentée) indique une corrélation également moyenne (0,47 et 0,51 si on considère les évènements énergétiques $H_{s} > 1, 5 m$ ), mais qui provient cette fois des caractéristiques de la distribution des directions de pic dans les deux jeux de données. Ces directions varient très peu autour de 300° (direction de provenance), ce qui, dans l'étude de la corrélation, donne un nuage de points assez compact, mais très limité, dans l'axe de la droite de régression. La valeur du coefficient de corrélation est due à cette distribution particulière, mais l'accord des tendances entre les séries temporelles apparaît correct. Un biais faible de 3,83° est observé entre les deux jeux de données ; les angles de provenance mesurés sont ainsi légèrement plus importants (plus au nord) que ceux simulés.

3 Paramètres statistiques et climat de houle

Les trois paramètres statistiques $(H_{s}, T_{p}, D_{p})$ issus de la mesure et de la simulation numérique sont présentés dans le Tableau 2. Les statistiques TD1 et T (cf. Tableau 1), qui ne couvrent que des périodes courtes (respectivement 13 mois et 10 mois), ne sont a priori pas représentatives du climat annuel et ne sont présentées ici qu'à titre indicatif. Les résultats statistiques réellement exploitables provenant de simulations sur une période plus longue (WW3 pour $T_{p}$ et $D_{p}$ et WW3CO pour $H_{s}$ ) sont indiqués en italique dans le tableau. TD1 donne des statistiques proches de WW3CO, ce qui indique que la période de mesure de 13 mois en 2002/2003 a été statistiquement conforme au climat moyen de la zone, obtenu sur 6 ans et 9 mois. La distribution de $H_{s}$ calculée à partir des statistiques de la bouée D2 (voir Tableau 1) [4] est assez différente de celle obtenue par WW3CO. On observe notamment un pourcentage plus important d'événements impliquant des hauteurs significatives supérieures à 4 m pour la bouée D2. Cette différence notable peut s'expliquer par des phénomènes de levée et de réfraction, qui sont une conséquence directe de la faible profondeur au voisinage du point de mesure D2. Cette comparaison montre l'intérêt d'effectuer les mesures en profondeur suffisamment élevée, de manière à s'affranchir de ces effets locaux.

Les statistiques WW3CO peuvent être comparées aux paramètres de la bouée de Biscarosse donnés par Butel et al. [2]. Les moyennes sont légèrement plus importantes au sud de l'Aquitaine (WW3CO, $H_{s_{moy}} = 1, 57 m$ , $H_{s_{med}} = 1, 32 m$ ) qu'au nord (Biscarosse, $H_{s_{moy}} = 1, 36 m$ , $H_{s_{med}} = 1, 1 m$ ) et les écarts types comparables (respectivement, 0,89 et 0,87). La distribution des $H_{s}$ pour Biscarosse (respectivement, 82,23 %, 16,47 % et 1,29 %, à comparer aux colonnes 9,10 et 11 du Tableau 2 pour WW3CO) indique également une proportion de houles inférieures à 2 m, légèrement plus importante au nord qu'au sud.

Le second paramètre traité est la période pic $T_{p}$ . Les données représentatives sont cette fois directement calculées à partir de WW3 (cf. paragraphe 2). La moyenne de $T_{p}$ est de 9,59 s. Plus au nord (Fig. 1, même point que [5]), Dupuis et al. [6] trouvent 11,55 s par mesure in situ à 10 milles au large du cap Ferret.

Les trois dernières lignes du Tableau 2 présentent les statistiques de directions de pic, qui sont les premiers paramètres directionnels exploitables pour cette portion du littoral. Les seules données antérieures concernant la distribution angulaire de la houle étaient issues d'observations visuelles [9]. Les résultats concernant $D_{p}$ sont les paramètres non corrigés (WW3). Notons que ces statistiques n'ont pas de validation en périodes automnale et hivernale, puisque aucune mesure d'incidence n'a été réalisée durant ces saisons. La principale caractéristique de $D_{p}$ est sa répartition très étroite, avec 80 % des valeurs comprises dans un secteur angulaire de 40°. La moyenne de la direction de pic (301,9°) ne dépasse que très légèrement 300°, qui est approximativement la direction de la normale à la côte entre Biarritz et Capbreton. Au large du cap Ferret, Dupuis et al. [6] trouvent un $D_{p}$ moyen et un écart type très proches, respectivement de 301,21° et 33,37°.

Les statistiques présentées dans le Tableau 2 peuvent être utiles dans différents contextes d'applications (comparaison de sites entre eux, calculs de paramètres empiriques tels que la profondeur de fermeture [12]). La plupart du temps, cependant, la notion de scénarios représentatifs est plus adaptée pour des études précises. Dans ce cas, la connaissance des climats de houle définis par les relations entre les variables statistiques $H_{s}, T_{p}$ et $D_{p}$ est indispensable.

On va donc chercher les états de mer, ou climats de houle, les plus représentatifs sous forme de classes tenant compte des trois paramètres $H_{s}, T_{p}$ et $D_{p}$ et des barycentres de leur distribution. La méthode que nous avons mise en œuvre est la minimisation par recuit simulé [7]. Il s'agit d'un processus itératif ayant pour objectif la minimisation de la distance entre le barycentre et les points d'une classe donnée. Butel et al. [2] ont utilisé cette méthode qui apporte de bons résultats en terme de qualité de la classification.

Le Tableau 3 présente les classes obtenues en appliquant cette méthode aux données WW3 sur la période de 6 ans et 9 mois. L'algorithme montre une sensibilité importante aux nombres de classes imposées dans le processus de recherche des barycentres. Dans ce travail, ce nombre a été fixé à 12. Il s'agit d'un compromis permettant de faire apparaître les classes de tempêtes qui sont masquées pour des nombres inférieurs, tout en conservant un nombre limité d'états de mer. La probabilité d'occurrence d'une classe (colonne n° 2) est calculée par le poids statistique de cette classe sur l'ensemble des données. Les colonnes suivantes indiquent les coordonnées des barycentres dans l'espace $(H_{s}, T_{p}, D_{p})$ . $H_{s}^{*}$ est la hauteur significative des barycentres de classes modifiée a posteriori par la formule (1). Ce paramètre est plus représentatif que $H_{s}$ pour la zone côtière étudiée, compte tenu du gradient existant entre la côte et le large. Enfin, le type d'état de mer (houle ou mer du vent), la saison d'occurrence privilégiée et le secteur angulaire de provenance de la classe sont indiqués dans la dernière colonne.

Les cinq premières classes du Tableau 2 ont un poids total très élevé $(\sim 66 %)$ et correspondent à des houles (définies par une cambrure faible, la cambrure étant le rapport de la hauteur significative sur la longueur d'onde significative), d'énergie moyenne à élevée et une direction incidente proche du 300°. Les classes 6, 7, 8, 10 et 12 correspondent à des mers du vent définies par des cambrures plus importantes. Leurs directions incidentes privilégiées sont de 300° récurrent en annuel et du nord en période estivale ; elles représentent un poids total de 27 %. Enfin, la dernière catégorie, dans laquelle on trouve les classes 9 et 11, est constituée des houles de tempête (faible cambrure), qui ont un poids statistique limité (7,5 %), mais vraisemblablement une action importante sur l'évolution des fonds en zone côtière, compte tenu de leur énergie. La direction de pic de ces deux classes est toujours proche de 300°.

Il existe vraisemblablement des variations non négligeables du triplet $(H_{s}, T_{p}, D_{p})$ en se déplaçant parallèlement au rivage vers le nord. La quantification précise de ces variations n'a pas été abordée dans ce travail ; elle nécessiterait la comparaison de mesures et simulations en d'autres points. Les données des Tableaux 2 et 3 constituent donc une première approximation des paramètres directionnels de la houle en zone côtière sud-aquitaine, qu'il conviendra d'affiner ultérieurement.

4 Conclusion

Une première évaluation des paramètres statistiques de la houle directionnelle pour la zone côtière sud-aquitaine a été réalisée par comparaison de deux jeux de données : l'un issue de la mesure in situ, l'autre provenant de la simulation et couvrant une période plus représentative. La comparaison des jeux de données a permis de quantifier la corrélation qui existe pour les trois variables étudiées $(H_{s}, T_{p}, D_{p})$ . Cette corrélation est bonne en ce qui concerne $H_{s}$ $(R^{2} = 0, 86)$ et moyenne dans le cas de $T_{p}$ $(R^{2} = 0, 48)$ et $D_{p}$ $(R^{2} = 0, 47)$ .

Dans un deuxième temps, les statistiques de houle issues de la simulation corrigée par les mesures ont été présentées. La hauteur significative moyenne est de 1,57 m et l'écart type de 0,89. Les hauteurs de vagues sont ainsi légèrement plus importantes au sud de l'Aquitaine qu'environ 100 km plus au nord (Biscarosse).

Des classes statistiques ont enfin été calculées pour déterminer des états de mer représentatifs : 67 % des états de mer sont des houles océaniques d'énergie moyenne, 26 % sont des mers du vent d'énergie faible et 7,5 % des climats de tempête. Ces premiers résultats statistiques sur le littoral sud-aquitain, qui peuvent être affinés notamment par l'étude de la variabilité spatiale des paramètres de houle, devraient permettre de mieux comprendre la dynamique côtière dans cette zone active.

Acknowledgments

Les auteurs tiennent à remercier la Communauté d'Agglomérations Bayonne–Anglet–Biarritz, le conseil général des Pyrénées Atlantiques, le conseil régional d'Aquitaine et l'État français pour le financement d'une partie de ce travail ainsi que du houlographe Triaxys, le Bureau de recherches géologiques et minières (BRGM) pour avoir soutenu financièrement la réalisation de l'étude statistique et enfin le Centre d'études techniques maritimes et fluviales pour sa contribution au maintien technique des houlographes sur la côte aquitaine.

Bibliographie

[1] S. Abadie; C. Brière; J. Dubranna; P. Maron; D. Rihouey Étude préliminaire du comportement hydro-sédimentaire du littoral d'Anglet et de l'entrée du port de Bayonne. Rapport final d'étude, 2004 http://isabtp.univ-pau.fr (Disponible sur)

[2] R. Butel; H. Dupuis; P. Bonneton Spatial variability of wave conditions on the French Atlantic coast using in-situ data, J. Coast. Res., Volume 36 (2002) no. special issue, pp. 96-108

[3] R. Butel, H. Dupuis, S. Abadie, Paramètres statistiques de houles sur le plateau continental basque, Rapport d'étude pour le BRGM, novembre 2003

[4] CANDHIS, Base de données de houle réalisée par le Centre d'études maritimes et fluviales http://www.cetmef.equipement.gouv.fr/donnees/candhis/ (site Internet)

[5] H. Dupuis, G. Goasguen, L. Michel, B. Michard, P. Bretel, Inter-comparaisons de mesures de vagues au large du Cap Ferret, in : VIII^es Journées nationales Génie civil–Génie côtier, Compiègne, septembre 2004

[6] H. Dupuis, R. Butel, P. Bonneton, Statistics of directional waves on the north coast of Aquitaine, J. Coast. Res. (en préparation)

[7] S. Kirkpatrick; C.D. Gelatt; M.P. Vecchi Optimization by simulated annealing, Science, Volume 220 (1983), pp. 671-680

[8] H. Howa; J.N. Salomon; J.-P. Tastet Littoral aquitain, Acquis Sciences n° 20 (1999)

[9] Sogreah Ingénierie, Embouchure de l'Adour, amélioration des accès au port de Bayonne, Synthèse et actualisation des données existantes, rapport technique n° 5 1385 R0, octobre 1993, 48 p

[10] H.L. Tolman A third-generation model for wind waves on slowly varying, unsteady and inhomogeneous depths and currents, J. Phys. Oceanogr., Volume 21 (1991), pp. 782-797

[11] H.L. Tolman User manual and system documentation of WAVEWATCH-III version 1.18. NOAA/NWS /NCEP/OMB Technical Note 166, 110 pp., 1999 http://polar.wwb.noaa.gov/waves/wavewatch/wavewatch.html (Téléchargeable sur le site)

[12] US Army Corps of Engineers, Coastal Engineering Research Center, Shore Protection Manual, 1984

Commentaires - Politique

Ces articles pourraient vous intéresser

Modélisation du festonnage des barres sableuses d'avant-côte : application à la côte aquitaine, France

Bruno Castelle; Philippe Bonneton; Rémi Butel

C. R. Géos (2006)

Modélisation du courant sagittal induit par les vagues au-dessus des systèmes barre/baïne de la côte aquitaine (France)

Bruno Castelle; Philippe Bonneton

C. R. Géos (2006)

Contributions respectives des courants et de la houle dans la mobilité sédimentaire d'une plate-forme interne estuarienne. Exemple : le seuil interinsulaire, au large du pertuis d'Antioche, France

Déborah Idier; Rodrigo Pedreros; Carlos Oliveros; ...

C. R. Géos (2006)