Abridged English version
In Europe, the measurement of declination started in the 16th century, the measurement of inclination in the 17th century [1,7]. The measurements of the intensity – the force – of the field are more recent. The first measurement of the intensity of the horizontal component of the field is, legitimately, attributed to C.F. Gauss [4]. But the famous French geometer Poisson [11] also took interest in the problem, and proposed, in a remarkable paper dated 1825, a method for measuring the total intensity of the field as well as its horizontal intensity.
Poisson's method relies only on the measurement of the oscillation periods of two magnets, or needles, oriented along the same line of force of the magnetic field, in the case of the determination of the total intensity, along a horizontal line in the magnetic meridian in the case of the determination of the horizontal intensity. Poisson's ideas and paper are brilliant, based on the important work he had published previously on the theory of magnetism [10]. But it has never been seriously tested, and, eventually, never been applied.
The deviation–oscillation method of C.F. Gauss is well known and has been exposed up to now in physical textbooks as an exemplar experiment. It was systematically used in magnetic observatories till the introduction of atomic or nuclear resonance magnetometers at the end of the fifties.
Both Poisson's and Gauss methods rely on the mutual torque, exerted by two magnets one on the other. If it had been possible to compute accurately enough this torque given the locations of the magnets, their dimensions and weights and global magnetizations, the measurement would have been greatly simplified. But the computation of the torque requires the knowledge of the so-called magnetism distribution in both magnets, i.e. of the distribution of the equivalent magnetic mass density per unit volume, being the current point in the magnet. The needles being elongated barrels, it is enough in general to consider a one-dimensional distribution, being the distance along the barrel axis.
Coulomb was the first to investigate experimentally this distribution in elongated barrels and proposed an empirical law formalized by Biot. But it had never been possible to determine the two distributions precisely enough for the interaction torque to be computed from them. Painstaking experiments have been conducted in the Chambon-la-Forêt observatory (France) to determine, in various configurations, the mutual torque between magnetic needles made in the second half of the 19th century, and to derive the simplest distribution allowing us to account for the whole set of observations. This distribution appears to be of the form being reckoned from the centre of the needle axis, and is rather different from the one derived earlier by Coulomb. Such a distribution has peculiar properties; in particular, for each half of the needle, the point of the axis where the magnetic field of the needle vanishes divides the corresponding segment in two subsegments whose lengths ratio is equal to the golden number.
1 Introduction
En Europe, la mesure de la déclinaison remonte au XVIe siècle, celle de l'inclinaison , au XVIIe siècle [1,7]. Toutefois, les séries de mesures relativement précises et homogènes ne commencent, à Paris et à Londres, qu'au milieu du XVIIe siècle pour D, du XVIIIe pour I [1,7]. Les mesures de l'intensité – de la force – du champ magnétique terrestre sont plus récentes. En 1804, A. von Humbolt publie une carte « des zones isodynamiques » dans son mémoire intitulé Sur les variations du magnétisme terrestre à différentes latitudes, par M.M. Humboldt et Biot, lu par M. Biot à la classe des sciences mathématiques et physiques de l'Institut national, le 26 frimaire an 13. Cette carte représente les résultats de mesures faites, sur la suggestion de Borda, par Humboldt au cours de son voyage américain (1799–1803). Il s'agissait là de mesures relatives, consistant à compter le nombre d'oscillations d'une aiguille aimantée placée dans le méridien magnétique, mobile autour de son centre de gravité, se produisant pendant dix minutes, et de comparer les nombres obtenus à différentes latitudes. On attribue – justement – à C.F. Gauss (1832) [4] la première mesure absolue de la composante horizontale du champ par la fameuse méthode d'oscillation–déviation qui porte son nom. Cependant, dès 1825, Poisson [11] s'était penché sur ce problème de la mesure de l'intensité du champ magnétique de la Terre et en avait proposé une solution exposée dans un article de huit pages du Journal des savants, lu à l'Académie des sciences le 28 novembre 1825, intitulé Solution d'un problème relatif au magnétisme terrestre [11]. Cet article faisait suite à ses importants travaux consacrés à la théorie du magnétisme, publiés dans les nouveaux mémoires de l'Académie des sciences, en 1822 [10].
La mesure de la composante horizontale du champ par le jeu de l'interaction de deux aimants, due à Poisson et Gauss, a prévalu jusqu'en 1960. On s'est donc, au moins jusque là, beaucoup intéressé à la « distribution du magnétisme dans les aimants », tout spécialement dans les aimants en forme de barreaux cylindriques utilisés dans les mesures. Faute d'une théorie qui eût pu la donner avec une précision suffisante, on a dû se borner à quelques hypothèses générales et sûres sur cette distribution. C'est Poisson qui les a énoncées le premier.
Nous allons rappeler les méthodes de Poisson et de Gauss, montrer comment les expériences et les calculs étaient conduits, en l'absence d'une connaissance précise de la distribution de l'aimantation dans les barreaux. Puis, après avoir brièvement rappelé quelques travaux de savants français sur les aimants, nous donnerons les résultats d'expériences menées à l'observatoire de Chambon-la-Forêt pour y déterminer la distribution du magnétisme.
2 La méthode de Poisson
Nous garderons, pour l'essentiel, les notations de Poisson, et nombre de ses tournures ; elles ne présentent d'ailleurs aucune difficulté. « Supposons qu'on ait une aiguille d'acier A, librement suspendue par son centre de gravité, de sorte que sa longueur prenne la direction du magnétisme terrestre, à l'instant et au lieu d'observation. Soit la quantité de fluide libre contenue dans une tranche de cette aiguille, perpendiculairement à sa longueur, dont l'épaisseur infiniment petite est dx, et x la distance au centre de gravité ; selon que le fluide libre de cette tranche sera boréal ou austral, μ sera une quantité positive ou négative, qui variera avec x selon une loi que nous n'aurons pas besoin de connaître. Il nous suffira de savoir que l'intégrale prise sur toute la longueur de A devra être nulle. » Cependant, Poisson prend, pour simplifier les calculs, une distribution impaire, .
On voit donc que, d'entrée de jeu, Poisson ne cherche pas à connaître plus avant . Il note φ la mesure du pouvoir magnétique de la Terre (l'intensité du champ). Si l'aiguille est écartée d'un angle α de sa position d'équilibre – alignée selon le champ –, le moment des forces qui feront osciller l'aiguille aura pour expression :
Soit m son moment d'inertie par rapport à son axe de rotation passant par son centre de gravité. « Nous concluons, d'après la théorie du pendule, que si l'angle α est très petit et que t soit la durée de chaque oscillation entière (simple) », on aura :
| (1) |
Soit donc une seconde aiguille, B, pour laquelle :
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Dans le cas général :
L'article de Poisson n'est pas inconnu. Il est toutefois méconnu. Arago [2], dans sa très longue notice consacrée à Poisson, dit que ce dernier a imaginé une méthode de mesure du champ magnétique qui dispense complètement de l'invariabilité dans l'aimantation de l'aiguille de comparaison, et ajoute : « M. Gauss a perfectionné cette méthode, dont la première idée appartiendra toujours à Poisson, en substituant des mesures de déviations angulaires à la détermination de la durée des oscillations de diverses aiguilles ». E. Verdet [12], dans son cours de physique destiné aux élèves de l'École normale (1873), présente de façon succincte la méthode de Poisson, mais s'étend surtout sur celle de Gauss, dont il dit, justement, qu'elle a reçu de grands perfectionnements. E. Mascart [9], dans son traité de magnétisme terrestre (1900), dit « c'est à Poisson que l'on doit la première méthode pratique pour déterminer le rapport du champ magnétique d'un aimant au champ terrestre et en déduire la composante horizontale H en mesure absolue ». Il présente très brièvement la méthode, en évalue la précision par un calcul simple, et conclut : « Cette méthode ne semble pas avoir été employée et conduirait difficilement à des valeurs exactes ». Dans son article de 1892 consacré à la détermination du champ magnétique terrestre [8], Mascart ne cite pas Poisson. Dans le chapitre du traité classique de Chapman et Bartels Geomagnetism (1940) consacré à l'histoire de cette discipline [3], Poisson n'est pas cité pour sa méthode de mesure de l'intensité. Il est vrai que, comme le dit Mascart, cette méthode n'a jamais été employée. On peut se demander pourquoi. On a sûrement estimé délicate l'opération qui consiste à placer les centres de gravité des deux aiguilles selon une même droite parallèle à l'action magnétique de la Terre ; c'est là en effet une grande complication de la méthode, si l'on veut vraiment mesurer l'intensité (totale) du champ. Mais Poisson, bien averti de cette difficulté, ajoute : « On pourra aussi employer deux aiguilles horizontales placées dans le même méridien magnétique, et dans le prolongement l'une de l'autre. Toutes les formules précédentes subsisteront encore, en y remplaçant φ par la composante horizontale de cette force, , i étant l'inclinaison. C'est cette composante que mesurera Gauss. La raison est plutôt que Poisson, au contraire de Gauss, n'a jamais lui-même tenté de mettre en œuvre sa méthode, n'en a jamais présenté le mode opératoire, signalé les difficultés, estimé la précision atteignable. C'est demeuré une expérience de pensée. On ne saurait s'étonner de ce que Poisson n'ait pas monté lui-même cette difficile expérience. On a donné maints témoignages de sa maladresse. Mais le jugement de Mascart, rapporté plus haut, ne suffit pas à écarter définitivement la méthode de Poisson.
Il fut bien le premier à faire la théorie de l'interaction de deux aimants pour l'appliquer aux mesures de l'intensité du champ terrestre, en montrant de façon très générale comment traiter la distribution du magnétisme dans ces aimants.
3 La méthode de Gauss [4]
Cette méthode, utilisée depuis près de deux siècles (certains observatoires magnétiques l'emploient encore), a été largement exposée et discutée. On en trouve, par exemple, une présentation très détaillée dans l'article d'E. Mascart des Annales du Bureau central météorologique [8], et dans son traité Le champ magnétique terrestre [9], déjà cités. Nous n'en dirons ici que ce qui est nécessaire à notre propos.
Gauss se propose de mesurer l'intensité de la composante horizontale du champ ( avec les notations de Poisson), par deux opérations bien connues : (1) la durée d'oscillation, autour d'un axe vertical, d'un barreau soumis à l'action du champ terrestre donne la valeur du produit MH du moment magnétique du barreau par la composante horizontale H à mesurer ; (2) la déviation que ce même barreau imprime à l'aiguille d'un déclinomètre détermine le rapport . On en déduit H (et M).
La méthode de Gauss, toute simple dans son principe, exige « quelques corrections qui présentent des difficultés sérieuses et sur la détermination desquelles les physiciens ne sont pas entièrement d'accord » (E. Mascart). Nous nous limiterons à une présentation succincte de la correction des déviations, qui fait à nouveau appel au calcul de l'interaction de deux aimants pour lesquels la distribution de magnétisme est mal connue.
Le barreau déviant de moment M est d'abord orienté dans une direction perpendiculaire au méridien magnétique, c'est-à-dire à la direction initiale de l'aiguille (qui est aussi un barreau cylindrique dans la plupart des cas) de moment m du déclinomètre. Son centre C est placé sur une droite, soit perpendiculaire au méridien, soit contenue dans celui-ci. Dans la méthode originale de Gauss on mesure l'angle α dont dévie l'aiguille m, par rapport au méridien, dans l'une de ces configurations. Très tôt, Lamont [5] apporta une heureuse modification au montage de Gauss : on fait tourner M autour du centre O du déclinomètre (Fig. 1), de manière qu'il soit à nouveau perpendiculaire à m, c'est-à-dire, dans le cas de la figure, en première position de Gauss (par rapport à l'aiguille m). Soit ζ la déviation de m par rapport au méridien (Fig. 1). Le couple exercé par M sur l'aiguille équilibre le couple exercé par la composante horizontale H du champ :
| (10) |
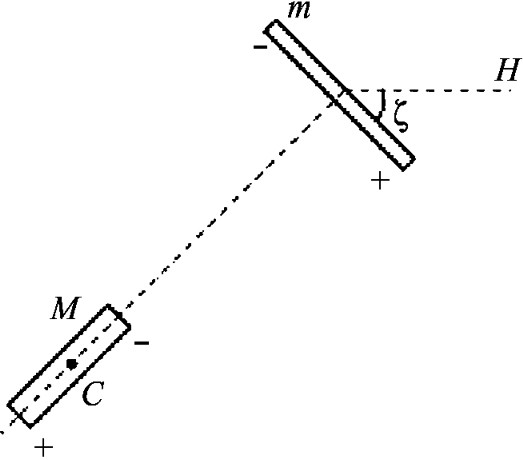
Position des aimants m et M dans l'expérience de Gauss–Lamont.
Location and orientation of the magnets m and M in Gauss–Lamont.
Le terme est dit « coefficient magnétométrique ». C'est aussi la correction de déviation. Beaucoup d'efforts, dans de nombreux observatoires, ont été consacrés à la détermination de ce coefficient, essentielle à une mesure précise de H. On a cherché quelquefois à calculer p en usant d'une hypothèse sur la distribution du magnétisme dans les aimants, mais en vain, comme nous l'avons vu plus haut. E. Mascart énonce que la méthode la plus exacte est de déterminer ce terme de correction dans un observatoire avec toutes les précautions nécessaires et d'en vérifier la valeur à intervalles réguliers dans les mêmes conditions. Nous procéderons plus loin de façon inverse : de la détermination expérimentale précise de p, nous déduirons la probable distribution de certains aimants anciens.
4 La distribution du magnétisme dans les aimants
Poisson, nous l'avons vu, note que, pour mesurer l'intensité du champ, « nous n'avons pas à connaître la loi » (à cela près qu'il faut supposer ). En effet, il détermine les différents moments de μ par l'expérience. De même, Mascart recommande-t-il de ne pas tenter de déduire par quelque théorie. Pourtant d'excellents savants se sont employés à établir cette loi de distribution. On admet toujours que le magnétisme du barreau est symétrique par rapport à son axe et à son plan équatorial (dans la pratique de la mesure, des retournements corrigent les effets des écarts à ces symétries). On admet aussi (dans la pratique de la mesure, la distance entre les aimants est grande devant leur diamètre) que le magnétisme de chaque section est concentré sur l'axe. Coulomb fut le premier à s'intéresser à la détermination de la distribution du magnétisme dans les aimants, . Pour cela il mesura l'action exercée par chaque tranche du barreau sur un même pôle d'aimant, qu'il plaçait successivement à une même distance de chacune d'elles. Cette action magnétique était supposée proportionnelle à la quantité de magnétisme , concentrée dans la tranche d'abscisse x. Coulomb utilisait des fils d'acier de 4 mm de diamètre, aimantés à saturation. La Fig. 2 présente un exemple de courbe . Biot calcula l'équation de ces courbes :
| (11) |
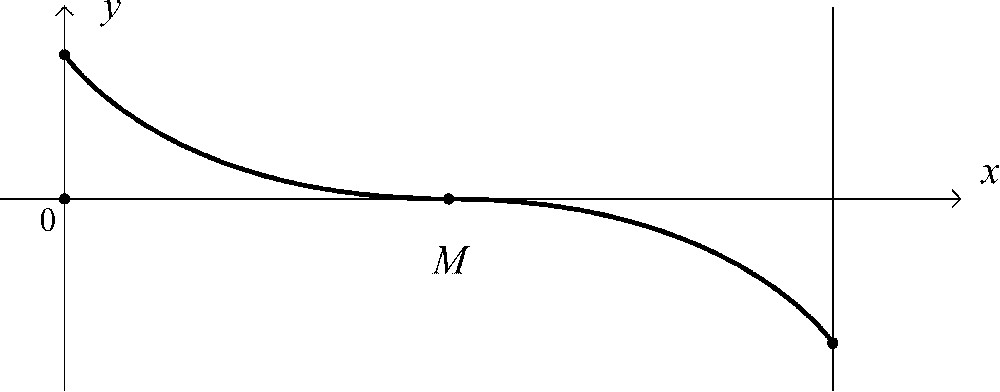
Distribution μ(x) selon Coulomb et Biot.
Distribution μ(x) according to Coulomb and Biot.
5 Les expériences de Chambon-la-Forêt
Elles ont été faites avec le théodolite des frères Brunner grand modèle, n° 3, construit vers 1880. Le but en était bien sûr de déterminer, aussi précisément que possible, la valeur du coefficient magnétométrique de l'appareil, mais aussi, par la multiplication des conditions expérimentales, d'en déduire la distribution la plus probable (il n'y a évidemment pas unicité de solution ; on aura recours à des arguments de simplicité). Les expériences de Chambon-la-Forêt sont décrites en détail dans [6]. Nous en rapportons ici seulement les résultats principaux.
Si l'on prend la distribution , dite souvent, abusivement d'après ce que nous venons de rappeler, distribution de Coulomb – x est compté ici à partir du milieu du barreau –, la valeur calculée de p s'écarte de façon irréconciliable de la valeur observée. Au contraire, si l'on choisit la distribution uniforme par moitiés :
| (12) |
Les distributions d'aimantation correspondant respectivement à μ et sont :
| (13) |
| (14) |
La distribution des charges magnétiques équivalentes (ou d'aimantation (14)) est moins régulière que la distribution de charges kx (ou d'aimantation (13)), à vrai dire seulement à l'origine (Fig. 3). La distribution est continue en , mais sa dérivée y présente une discontinuité . Deux masses magnétiques fictives, à l'origine, et , annulent leurs effets.

Intensités d'aimantation correspondant aux distributions μ (haut) et (bas).
Magnetization corresponding to distribution μ (top) and (bottom).
On peut se demander pourquoi les procédés d'aimantation des aiguilles en usage au XIXe siècle (frottement d'un aimant fort) donneraient cette distribution plutôt que celle, généralement admise, de Coulomb. Il est difficile de donner à cette question de réponse physiquement fondée. On peut cependant avancer quelques arguments, l'ordre géométrique – ou esthétique. Il est facile de calculer l'induction créée par la distribution de charges le long de l'axe de l'aimant. Soit P le point d'abscisse x. En retirant la contribution de la portion de barreau centrée en P de longueur (on fait le calcul pour ), il vient :
| (15) |
présente trois singularités de même ordre, en , , . doit s'annuler deux fois sur l'intervalle , à savoir pour :
6 Conclusion
La mesure absolue de l'intensité du champ magnétique terrestre, pratiquée seulement depuis le début du XIXe siècle, a présenté de redoutables difficultés pour les géomagnéticiens jusqu'en 1955, date à laquelle l'avènement des magnétomètres scalaires, à résonance atomique ou nucléaire, rendit cette mesure facile.
On ne se soucie guère aujourd'hui des mesures anciennes faites à l'aide d'appareils à aimants. Pourtant, l'intérêt historique de ce chapitre du géomagnétisme est considérable ; pour ne parler que des savants français, Coulomb, Biot, Poisson, Arago, Mascart s'y sont illustrés. Poisson, le premier, proposa une méthode de mesure absolue du champ ; son apport a été largement occulté par celui de Gauss.
Les méthodes de Poisson et de Gauss font intervenir les couples exercés l'un sur l'autre par des barreaux aimantés, les barreaux n'étant pas courts devant la distance qui sépare leurs centres. Les couples dépendent alors de la distribution du magnétisme dans les barreaux, étudiée au XIXe siècle, notamment par Coulomb, Biot, Jamin. Le sujet retient moins l'attention aujourd'hui, et pourtant il suscite des considérations qui ne sont pas triviales. Les expériences faites à l'observatoire de Chambon-la-Forêt sur les barreaux fabriqués par les frères Brunner vers 1880 indiquent qu'ils sont aimantés de la façon la plus simple possible : une distribution de masses magnétiques uniforme dans chaque moitié du barreau, antisymétrique par rapport à son centre. La distribution du champ magnétique créée par un tel barreau n'est toutefois pas aussi simple. Il est remarquable que la distance au centre des deux points où ce champ s'annule soit, avec leur distance à l'extrémité du barreau, dans un rapport égal au nombre d'or, nombre qu'on rencontre si communément dans les proportions d'objets naturels ou fabriqués par l'homme.
1 Il y a dans l'intégrale de la formule (3) une erreur assez visible (le facteur multiplicatif ). L'exemplaire du journal de la bibliothèque de l'Institut contient une note manuscrite de Poisson à la fin de son article, dans laquelle il reconnaît cette inexactitude « qu'on lui a fait remarquer », mais ajoute que les « changements qui en résultent » n'influent pas sur les formules importantes de la suite.
2 Dans les formules du mémoire de Poisson figure une constante physique f dont la valeur dépend des unités de mesure ; nous l'avons prise égale à 1 pour raison de simplicité.


