1 Introduction
Several hundred million people face the hazards of active volcanoes [9]. Much progress has recently been made in understanding what happens once a volcanic eruption has started [27]. Yet the stress conditions inside a volcano that must be satisfied for magma to reach the surface are still poorly understood. To assess hazards we must understand why periods of unrest in volcanic edifices are so much more common than volcanic eruptions; why so many dykes, inferred to be emplaced during unrest periods, never reach the surface to feed eruptions.
Major volcanic edifices and rift zones are composite; they are composed of numerous layers (strata) many of which have widely different mechanical properties (Fig. 1). The volcanic edifices themselves are referred to as stratovolcanoes, central volcanoes, or composite volcanoes. The last name is used here, both for individual stratovolcanoes and major rift zones, to emphasise the many mechanical similarities these volcanic structures have with composite materials [17,21].

Extinct Tertiary rift zone in Southeast Iceland (cf. [12,13]) composed mostly of stiff basaltic lava flows with softer scoria, sedimentary and soil layers between the flows. Many dykes are arrested or offset at the contacts between the soft and stiff layers. View northeast, the pile is about 400 m thick.
Élément d'une zone de rift éteint dans le Sud-Est de l'Islande [12,13] : alternance de coulées basaltiques mécaniquement résistantes et de niveaux de scories et de paléosols peu résistants. De nombreux dykes changent de parcours ou s'interrompent au contact entre ces deux types de matériaux. Vue vers le nord-est, affleurement épais d'environ 400 m.
This paper explores the effects of layering in composite volcanoes on dyke emplacement and volcanic hazards. The specific questions addressed are, first, why are dyke injections in volcanoes and rift zones so much more common than dyke-fed eruptions? Second, how does the layering affect the surface deformation induced by arrested dykes? And, third, how can the results of the field observations and numerical models presented here help to evaluate volcanic hazards?
2 Data on dykes
There are three main types of sheet intrusions: sills, inclined sheets, and dykes. Sills are parallel with the layering of the host rock. They do not normally supply magma to volcanic eruptions and tend to be comparatively rare in active rift zones and composite volcanoes. Inclined sheets, mostly dipping between 30° and 60°, are common in the vicinities of many shallow magma chambers [13,22]. Outside the stress-field effects of shallow crustal magma chambers, however, subvertical dykes are the most common magma-driven fractures in composite rift zones and volcanoes [1]. In this paper I use the word “dyke” in a generic sense, comprising both proper dykes and inclined sheets.
Most dykes become arrested on their way to the surface [13–15]; some in essentially homogeneous (and commonly thick) layers, others at contacts between layers (Fig. 2). Dykes that end in thick, stiff (high Young's modulus) homogeneous layers taper out to narrow tips. By contrast, many dyke tips arrested in soft (low Young's modulus) layers or at contacts between layers are round or blunt (Fig. 2). Many contacts in composite volcanoes are weak; they tend to form planes of separation (parting surfaces), reflecting the weak bonds between layers of contrasting mechanical properties.

Basaltic dyke tip arrested 5 m below the surface of the Holocene rift zone in Southwest Iceland cf. [12,14]. View northeast; the dyke is 34-cm thick at the bottom of the 8-m-tall exposure (a sea cliff) but gradually thins to about 8 cm where its tip is arrested, at the contact between the basaltic lava flow and the tuff layer below.
Extrémité d'un dyke basaltique s'étant arête à 5 m de la surface dans la zone de rift du Sud-Ouest de l'Islande [12,14]. Vue vers le nord-est ; affleurement épais de 8 m (falaise côtière). L'épaisseur du dyke, 34 cm en pied de falaise, diminue progressivement jusqu'à 8 cm en bout de dyke, au contact entre tufs et coulée.
Since dykes are commonly arrested or, more generally, offset at contacts between layers of contrasting mechanical properties [13–15], mechanical rather than thermal conditions appear to largely control whether a propagating dyke becomes arrested or reaches the surface. These mechanical conditions are primarily the local stress fields associated with individual layers and contacts [13–16].
3 Surface deformation
Surface deformation during volcanic unrest periods can be monitored using the Global Positioning System (GPS) and the Synthetic Aperture Radar interferometry (SAR) [3,7,23]. The geodetic data thus obtained have been mainly interpreted in terms of two basic models: magma chambers and dykes [3,6,8,11,19,24–26]. Large-scale inflation or deflation of the surface of a composite volcano is normally regarded as the result of expansion or contraction of an associated magma chamber.
An expansion is generally thought to be due to increased pressure in the chamber, when the inflow of magma exceeds the rate of outflow. Similarly, chamber contraction is thought to be due to decreased pressure, when the magma outflow rate exceeds the inflow rate. Other processes that may result in deflation, such as cooling of the magma in the chamber and subsidence related to extension of the crust hosting the chamber, are normally too slow to explain rapid deflation events. In particular, rapid deflation of the surface of a volcano is normally attributed to rupture of the magma chamber and related dyke injections.
The second basic model proposed to explain surface deformation during periods of volcanic unrest is dyke emplacement. Almost all eruptions in composite volcanoes are supplied through magma-driven fractures that on solidification become dykes. Many arrested dykes are associated with surface deformation that can be detected by geodetic measurements.
Inferring geometries of arrested dykes from surface-deformation data, however, is difficult for the following reasons. First, there is no unique solution when using two-dimensional surface deformation data to infer three-dimensional dyke geometry. Second, composite volcanoes are heterogeneous structures with many discontinuities where local stresses develop, and where individual rock bodies respond differently to the dyke-induced loading. The surface deformation during dyke emplacement may thus be a very complex result of stress concentrations and displacements generated by loading of a heterogeneous and anisotropic crust.
4 Model of dyke emplacement
Composite volcanoes are primarily composed of lava flows that alternate with beds of pyroclastics, often with weak contacts between the layers (Figs. 1 and 2). The lava flows are normally stiff, whereas the pyroclastic layers may be soft (such as young tuff layers) or stiff (such as many welded layers) depending on their age and mode of formation.
Nearly all dykes are extension fractures, so that they form in a direction perpendicular to the minimum compressive (maximum tensile) principal stress,
The potential pathways of dykes can thus be mapped using the trajectories (directions) of
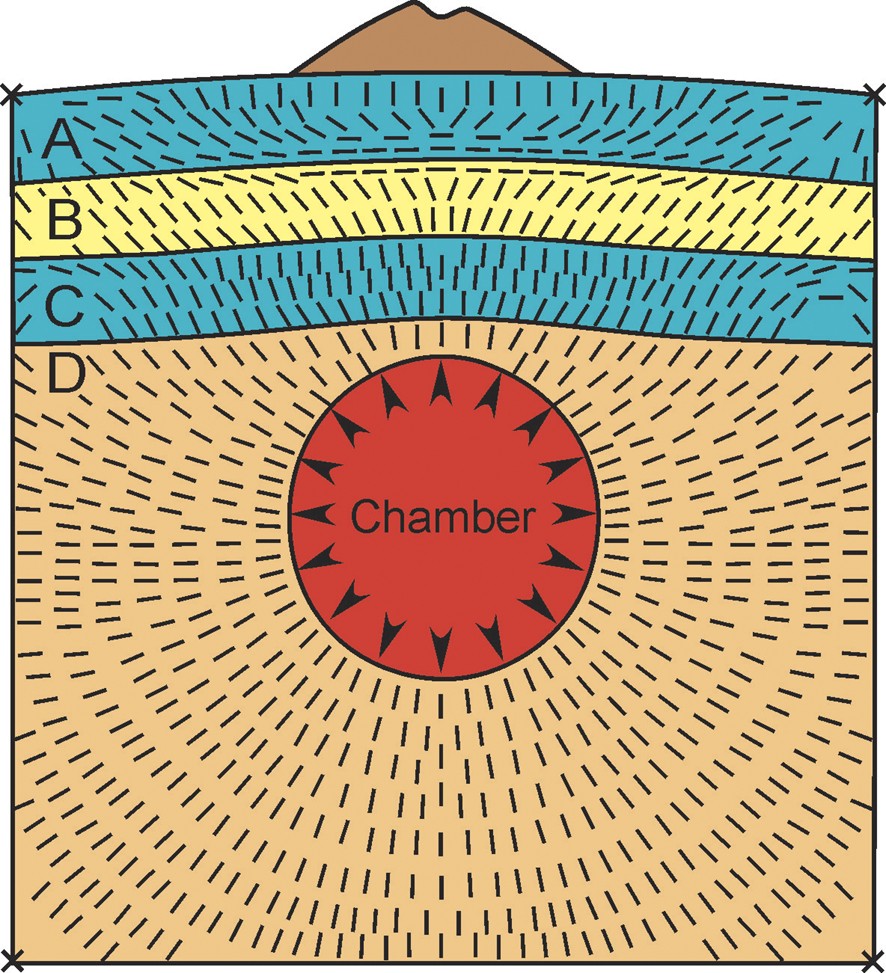
Rotation of the
La rotation des trajectoires de la contrainte principale maximum,
The only loading in the model is the chamber's internal magmatic excess pressure (pressure in excess of the lithostatic pressure at the depth of the chamber) of 10 mega-pascals (MPa). Before its elastic expansions resulting from the magma pressure, the chamber has a diameter of 0.25 units. The thickness of each of the layers A, B and C is 0.1 unit, while that of layer D is 0.7 unit. For a 10-km-thick crust, the diameter of the chamber in the model would be 2.5 km and the thickness of each of the mechanical layers A–C 1 km. The layer thickness in the models, however, may be regarded as arbitrary, since the contrasts in mechanical properties between layers, rather than the absolute layer thicknesses, determine the local stress fields.
In the model, layer D has stiffness of 40 GPa, layer C 100 GPa, layer B 1 GPa, and layer A 100 GPa. Layers A and C are thus very stiff and may represent piles (acting as mechanical units) of stiff basaltic lava flows. By contrast, layer B is very soft and may represent soft pyroclastic rocks or sediments [4,20]. Layer D is moderately stiff and corresponds to large parts of the crust of the rift zone in Iceland [13,14] and many common rock types [4].
In Fig. 3, the ticks show the trajectories (directions) of the maximum principal compressive stress
5 Model of surface deformation
Traditionally, surface deformations in composite volcanoes and rift zones have been interpreted in terms of models that assume the crust to be a homogeneous, isotropic half-space or a semi-infinite body [24–26]. Presumably, the main reason why such models continue to be used is that they are simple and easy to use [19].
A vertical extension fracture with an upper tip at a comparatively shallow depth below the free surface of an elastic half space and subject to internal fluid overpressure (or external tension) generates tensile stresses at the surface to either side of the projection of the fracture tip to the surface, and no tensile stress at the surface right above the tip itself [18]. Early developments of this model for arrested dykes indicated a significant graben subsidence at the surface above the upper tip of the dyke [25], but later studies indicate no such subsidence [26].
When a homogeneous, isotropic half-space model is used for composite volcanoes their fundamental mechanical property, namely the layering, is ignored. The mechanical effects of layering normally decrease with depth in the crust as the layers become more welded together at their contacts and form thicker units of essentially homogeneous properties. At shallow depths in active composite volcanoes, however, a homogeneous, isotropic half space is normally a poor model since there the crust consists of alternating soft pyroclastic layers (occasionally sedimentary layers) and stiff lava flows. In addition, the contacts between the layers at shallow depths are often weak.
The BEASY boundary-element program (http://www.beasy.com) was used to calculate the surface and tip stresses induced by at dyke arrested at 1-km depth below the surface of a 10-km-thick composite rift zone (Fig. 4). The stiffnesses of the layers are 40 GPa (A, C) and 100 GPa (B); they are thus stiff to very stiff and should magnify any dyke-induced tensile stresses. A weak contact between layers B and C is 8-km long, similar to the surface width of a typical Holocene volcanic system in the rift zone of Iceland [12]. Such weak contacts may occur between a pile of basaltic lava flows and either a pile of weaker lava flows or of pyroclastic layers.
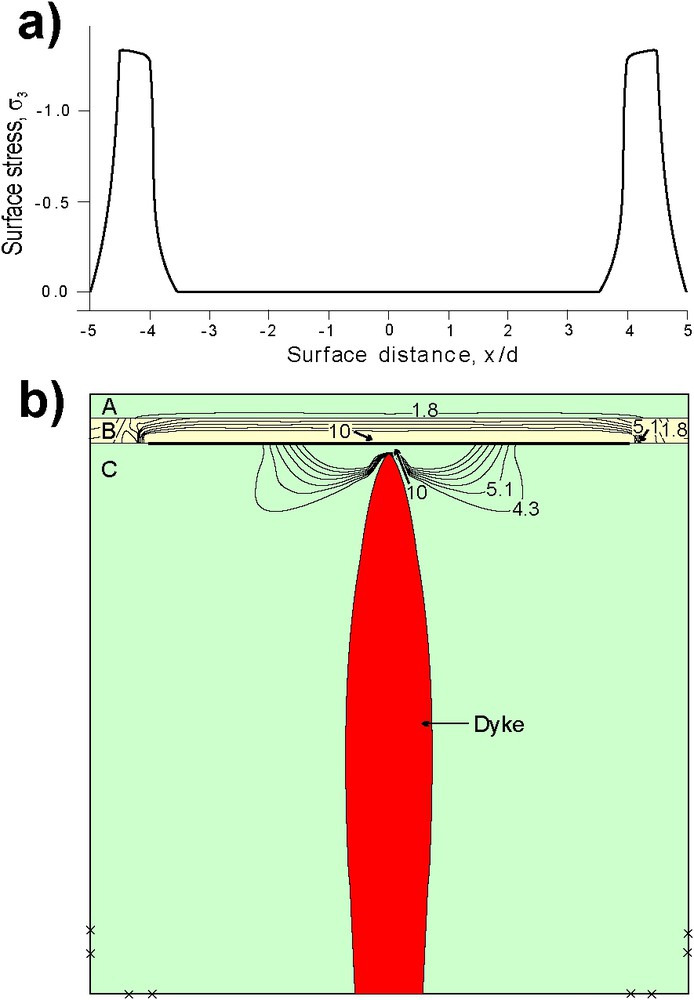
Surface (a) and tip (b) stresses induced by a dyke with a tip arrested at 1-km depth below the surface of a composite rift zone. At 800-m depth, there is a weak contact between layers B and C. The contours of the maximum principal tensile stress
Modélisation de la distribution des contraintes induites par un dyke dont la propagation est arrêtée à une profondeur de 1 km sous la surface d'une zone de rift composite. À 800 m de profondeur, un contact mécaniquement faible a été placé entre les niveaux B et C. Les iso-valeurs de la contrainte principale minimum,
The contact is modelled as an internal spring with a stiffness of 6 MPa m−1 in the vertical direction (opening) and 12 MPa m−1 in the horizontal direction (sliding) because of a possible anisotropy in stiffness depending on whether the loading is opening or sliding. This low stiffness takes into account the stiffnesses of rocks at the contact in the lava pile (Fig. 1); for example, weak tuff layers may have small-sample laboratory Young's moduli as low as 50 MPa and weak mudrocks as low as 3 MPa [4]. Models with zero discontinuity stiffness, corresponding to an open joint or a contact, yield similar results.
At the tip of the dyke, the theoretical tensile stress reaches 111 MPa (Fig. 4). Nevertheless, no tensile stresses are induced at the surface above the dyke. The peak surface stresses (1.3 MPa) occur above the ends of the 8-km-long weak contact, that is, at distances of 4 km to either side of the dyke tip. Thus, if there was any surface deformation (fractures), it would occur in these peak areas and have no simple relationship to the geometry, or depth to the tip, of the dyke.
6 Discussion
Most dykes injected from magma chambers during unrest periods become arrested at some crustal depths, indicating that the local stresses in composite volcanoes commonly prevent eruptions. The seismicity of a composite volcano (excluding dyke-induced earthquakes) may indicate whether or not its stress field has been homogenised. If the seismicity is evenly distributed throughout the volcano, the stress field is essentially homogenised, so that dyke propagation to the surface is likely. By contrast, if the seismicity is largely confined to specific rock bodies or layers, the stress field is heterogeneous and tends to arrest injected dykes and thereby prevent eruptions.
As an example, Campi Flegrei, a collapse caldera in Italy, was subject to dramatic crustal doming in two periods. From 1969 to 1972, the total maximum uplift of the ground reached 1.7 m; from 1982 to 1984, the maximum uplift of the ground reached 1.8 m [2,6,10,11]. The peak of the uplift occurred in the town of Pozzuoli, where the cumulative uplift for both periods was 3.3 m.
During the earlier period there was little seismicity, but in the later period most of the earthquakes were confined to a mechanical layer at the depth of 3–4 km. Thus, the stress field in crust of the Campi Flegrei area was heterogeneous during these unrest periods. Possibly as a consequence, and despite the dramatic uplift, there was no eruption.
Similarly, of 30–40 inflation–deflation events with dyke injections in the Krafla Volcano in Iceland in 1975–1984, only nine resulted in eruptions. Of these nine eruptions, six (and all the significant ones) occurred in the second half of the period (from 1980, [5]). Thus, in the early part of the period the stress field in the Krafla Volcano and the associated part of the rift zone was heterogeneous and unfavourable for dyke propagation to the surface.
Normal faulting in the early part of the 1975–1984 episode contributed to dyke arrest [14] and gradual homogenisation of the stress field. However, dyke injections in the early events were presumably the main contributors to the homogenisation of the stress field that encouraged frequent and larger eruptions in the later part of the period.
In conclusion, during magma-chamber inflation, many composite volcanoes develop local stress fields that prevent volcanic eruptions. The local stresses in the stiff mechanical layers may then favour dyke propagation while the stress fields in the soft layers favour dyke arrest. If the seismicity is uniformly distributed throughout a volcano, the stress field may be largely homogeneous and encourage dyke-fed eruptions. Conversely, if the seismicity is mostly confined to certain mechanical layers within the volcano, the heterogeneous stress field is likely to encourage dyke arrest and prevent eruptions.
Acknowledgements
This work was supported by grants from Norsk Hydro, Statoil, and the European Commission (EVG1-CT-2002-00073 PREPARED). I thank Sonja L. Brenner for running the model in Fig. 3 and help with the figures, and Kristjan Saemundsson and an anonymous referee for helpful comments.


