1 Introduction
The Little Ice Age (LIA) is understood to be one of the most important climatic fluctuations of the Holocene [16]. Since the northern-latitude glaciers were the first to have been described experiencing a considerable expansion beyond their present limits over a period lasting from ca. the 14th to the 19th centuries [27,28,60], the LIA was not believed to have been a global climatic event. With the result of numerous investigations identifying cooler temperature during this six-century period, the presence of this event in other regions of the world, including tropical mountains, is now completely ascertained [8,16,53]. However, many uncertainties persist concerning the timing of these fluctuations and the climatic changes that generated them. Did glacier fluctuations during the LIA occur in the tropics with magnitudes comparable to those determined in the mid-latitudes? Were these fluctuations synchronous on a world scale, suggesting that climate changes were similar and produced the same effects? The latter is a complex question, since glaciers in the tropics do not have the same response to climatic variations as glaciers in the mid-latitudes due to their different characteristics [14,25]. Moreover, different modes of climate variability can be present on a regional scale, with the influence of the North-Atlantic Oscillation (NAO) in Europe [50] and the effect of the El Niño Southern Oscillation (ENSO) in the Andes [12,13]. Thus, any evidence of the synchronicity/asynchronicity of glacier fluctuations in the tropics and in Northern Hemisphere mid-latitudes must be carefully examined and interpreted.
Many authors have identified the LIA between the 15th and the 20th centuries in the tropical Andes [17,32,47], but these dates were obtained using 14C, an isotope that includes important sources of error for this period. Unlike the Alps, where abundant historical documentation exists [27,37,60], archives describing glaciers in the Andes are rare. The only evidence comes from reports of voyagers and scientists in Peru and Ecuador [2,7,11,18] and from mining settlements of the colonial period [38,49]. These authors have reported that glaciers advanced considerably during the 16th–19th centuries, then began to retreat after 1860 AD in Peru [7] and 1880 AD in Ecuador [18]. Based on an analysis of stable isotope (O) and dust contents in the Quelccaya ice core (southern Peru), Thompson et al. [53] bounded the LIA between ca. 1500 AD and 1900 AD. Indeed a clear signal of the LIA exists from this marker, but its interpretation in terms of palaeotemperature has not yet been confirmed, since the O in the tropics seems to be more controlled by precipitation than temperature [19,46,57]. Thus, even if the potential of ice cores as a proxy of climate is well established, moraines attesting to glacier extents remain a valuable and complementary option to date glacier fluctuations and to reconstruct past climates. In the tropical mountains, moraines can be considered as reliable indicators of climate evolution at short-time scale because time-lag between mass balance fluctuations and snout response is reduced to few years, particularly for the small-sized glaciers [13]. Moreover, despite their high elevation, moraines are not significantly affected by frost and snow melting disturbance.
Recently several researchers used lichenometry in the tropical Andes for dating moraines over the last millennia [44] or the last centuries [51]. In the Cordillera Blanca (Peru), this technique revealed the presence of a clear glacier maximum between 1590 and 1720 AD and various minor advances between 1780 AD and 1880 AD [51].
The aim of this study is (1) to present a detailed chronology of glacier evolution during the LIA, (2) to compare this chronology with other results in the tropical Andes, and (3) to assess to what extent this chronology is similar or different from other existing in the Northern Hemisphere mid-latitudes.
In this respect, inferences will be made regarding the Central Andes' climate during this period.
2 Study area
Cerro Charquini (5392 m, 16°17′S, 68°06′W) is located 20 km northeast of La Paz in the Cordillera Real, close to the Zongo and Chacaltaya glaciers, which have been monitored for mass balance and energy balance for more than a decade [12,58]. Glaciers in this area are considered to be very similar in terms of their evolution: the strong ablation occurring year round at snout level for all exposures leads to a fast and concomitant response of glaciers to climate forcing [40]. Despite the low elevation of Cerro Charquini, glaciers are present on all its slopes but are small in size (<0.5 km2 in 1997 [41]). An important number of moraines reflecting past glacier extents are well preserved about 1 km downstream of current snouts (Fig. 1). As they have not yet been covered by vegetation, these moraines may be considered a priori as dating from the LIA. Cerro Charquini is geologically a batholith of granite bounded by siliceous metamorphic rocks (quartzite). Rhizocarpon geographicum, the lichen most used in lichenometric studies, grows regularly in this environment, since annual temperature variations are low, and snow cover is rare and does not persist for long periods. Furthermore, exposure does not significantly affect lichen growth [36], because at low latitude, radiation input is very strong on all slopes year round.
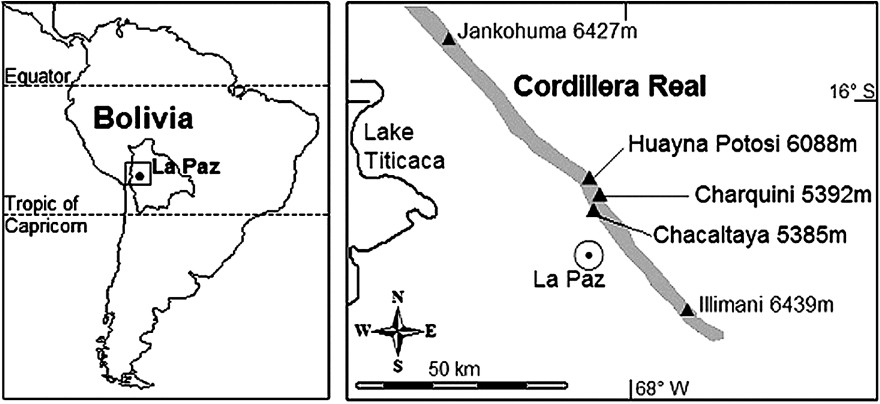
Study area: Cerro Charquini glaciers (Cordillera Real, Bolivia, 16°S). Glacier limit results from the 1997 IGM cover photogrammetric restitution.
Zone d'étude : glaciers du Cerro Charquini (Cordillera Real, Bolivie, 16°S). Les limites des glaciers sont issues de la restitution photogrammétrique des clichés IGM de 1997.
In the Bolivian eastern Cordillera, average precipitation is 800–1000 mm yr−1 on the glacier surface; 80% of the precipitation falls from October to April (austral summer) and 65% from December to February. The dry season extends from May to August, but ablation on glaciers is greatest during the wet season when snow accumulation occurs at high elevation. Falling mainly as snow on glaciers, precipitation controls ablation rates via the albedo [12,58]. Bolivian glaciers have retreated drastically since the beginning of the 1980s [56]. As the Equilibrium Line Altitude (ELA) is currently above 5250 m asl, the glaciers can be considered unbalanced with current climate and many of them could disappear in the near future [42].
3 Dating moraines by lichenometry
Lichenometry is a dating method, traditional in geomorphology, which can be used to date old monuments or periglacial landforms [21]. Developed in the 1950s to date glacial extension in the Alps [6], this method is based on diameter measurements of certain species of lichens that colonize a rock substrate. Rhizocarpon geographicum is the most frequently used, for several reasons: it can live in hard climatic conditions, its longevity is plurimillenary, and it develops a circular shape. Lastly, its colour, yellow punctuated of black, also makes it easily recognizable on siliceous rocks. This dating method is very efficient in high altitude or high latitudes environments where the vegetation scarcity makes other methods unusable, e.g., dendrochronology for example. Thus lichenometry can be used to date Holocene age surfaces, but is particularly efficient over these last centuries, when the classical 14C absolute dating method offers a weak precision. The principle proposed by Beschel consisted of first, determining a relationship between the diameter of thalli colonizing a surface and the time since which this surface has been exposed to colonization, and secondly applying this relationship on surfaces of unknown age. The link between the lichen diameter and the age can be obtained directly by measuring a growth rate during several years [24] or by measuring lichens on dated surfaces. However, it is specific to an environment, as the lichen growth depends on climate conditions [3,4], lithology [44], and exposition [36]; hence the growth rate must be determined for each specific area.
Since the pioneering works of Beschel [6], different approaches have been proposed to improve field measurements and statistical analysis. Supposing that the largest lichen diameters are among the first to colonize a surface, the most popular approaches have focused on the analysis of these extremes. Thus a mean of the largest lichens per block (classically the five largest) has been used both to determine the transfer function between the measured lichens and their age and to date the studied surfaces [20]. Despite numerous improvements, several problems remain with these ‘classical approaches’; the most important ones are:
- – it is assumed that the largest lichen diameters follow a normal distribution, but the probability theory dedicated to extreme values (the largest lichen in our case) dictates that the distribution of maxima cannot be normal but instead must follow a specific distribution called Generalized Extreme Value distribution (GEV), see Fig. 2;
- – confidence intervals, if included in the study at all, have been based on a Gaussian distribution rather than the appropriate extreme value distribution.
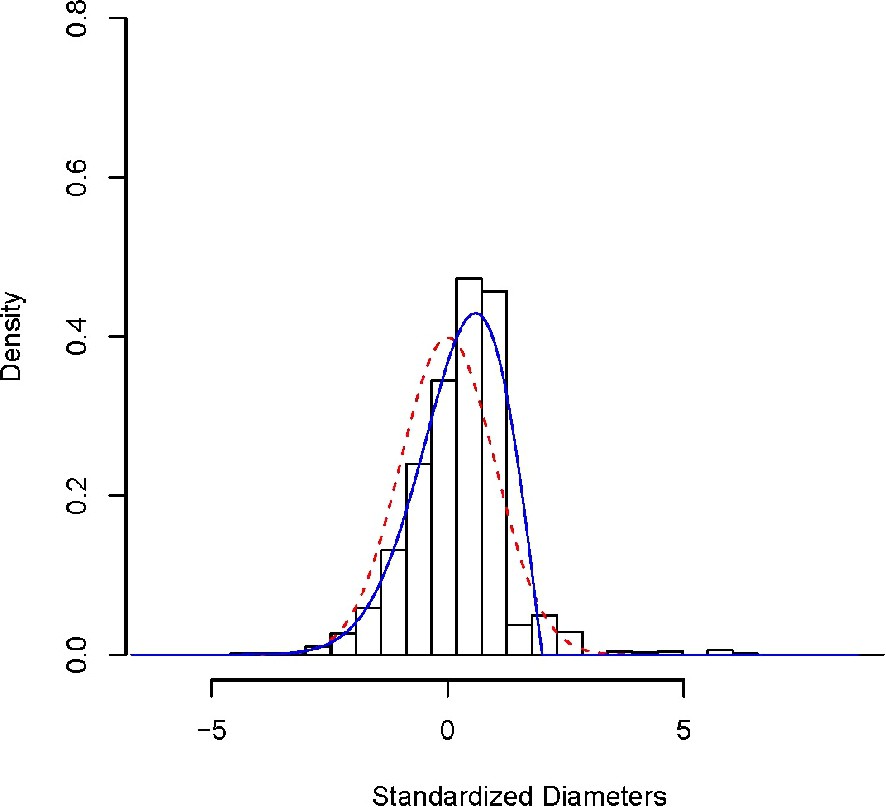
Distribution of standardized maxima lichen diameters (cm) measured on all the Charquini glaciers. The black boxes correspond to the histogram of the data. The dashed line shows the fit by a Gaussian density distribution. The solid line indicates the fit by a GEV density distribution.
Distribution des valeurs normalisées des diamètres maxima de lichen (cm) mesurés sur l'ensemble des glaciers du Charquini. Les histogrammes représentent les données. La courbe en tiret représente une distribution gaussienne, celle en trait continu une distribution GEV.
In the new conceptual approach used here and proposed recently by Naveau et al. [34], these difficulties are resolved by implementing the following two strategies. First, extreme value theory is applied to provide the adequate theoretical foundation for the modelling of maximum lichen diameter distributions (see Fig. 2). Second, all the measurements realized on both dated and undated surfaces are pooled into one data set. Consequently, this second point reduces the uncertainty associated with the construction of the link function between lichen diameters and their corresponding age distributions.
During fieldworks, the largest lichen diameter was measured on each boulder on dated and undated surfaces, repeating the experiment on at least 20 boulders. Then, as mentioned above, the distribution of lichen diameters measured on a given surface (dated or undated) is modelled by the GEV. This distribution can be summarized with its distribution function:
| (1) |
The three parameters () describing the GEV distribution are, respectively: the location parameter, the scale parameter, and the shape parameter. In our lichenometry application, the location parameter varies with the age of the feature on which the lichens are found, and both the scale and shape parameters are constant with time for a given study area, the Bolivian Eastern Cordillera in our case.
Thus each sample surface is characterised in time, by letting the GEV location parameter vary as a function of the moraine age, and in space, by fixing the GEV shape and scale parameters for a given region.
Even when the age of the lichen is supposedly known, i.e. lichens on the dated surfaces, there is still an uncertainty that has been represented in our statistical model. For example, a 14C dating procedure provides a mean and a standard deviation of a dated surface. These values correspond to the fact that the accuracy of the 14C sources is classically modelled by a normal distribution. Following this approach, we assume that the average age of dated or undated surfaces can be viewed as Gaussian-type random variables.
In summary, maximum lichen diameters and average surface ages are assumed to have two different distributions, a GEV and a normal distribution, respectively. This statement is based on probability theory for maxima (Extreme Value Theory) and for averages (Central Limit Theorem), respectively.
The following step is the construction of the relation between these two distributions. This relation is defined by a bivariate model in which the parameter μ, describing lichen diameters, is given by the GEV and dated surfaces' age α follows a Gaussian distribution. These two distributions are linked through the relationship , where the function f represents the temporal variation of μ.
In ‘classical approaches’, the authors carried out the moraines dating analysis in two steps. First they constructed a growth curve on the basis of the measurements realized on dated surfaces and then, with the equation of this curve, they computed the ages of the moraines.
In the approach used here, the protocol is different. First, a parameterisation of the function f is chosen. For example, a linear relationship is selected for our Bolivian data. As an initialisation step, the parameters μ for the dated surfaces are estimated and then the parameters of f, i.e. a and b in our linear example, are fitted with respect to these parameters μ.
In a second stage, the parameters μ of all surfaces (dated and undated) are estimated with the constraint of having the best likelihood for explaining our data.
The procedure is sequential, the values of μ and of the parameters describing f change at each iteration in order to maximize the probability of observing all our data. This step is possible because we can explicitly write the likelihood function of our statistical model (GEV and Gaussian distributions for maxima and averages, respectively). After a few iterations, the estimated parameters should converge to fixed values if the initial parameterisation of f is adequate and the data satisfy the assumptions of our model. If not, another parameterisation for f has to be proposed.
The optimisation algorithm allows one to estimate the variance of , which makes it possible to compute the error margin for the ages given for each moraine.
Thus, Fig. 3 does not depict a growth curve like the ones presented in classical lichenometric studies. Instead of linking raw diameters and date values through a growth curve, the distribution parameters of maxima diameters and average dates are now linked. This has the advantage of giving a relationship between distributions instead of values. Hence, conceptually and numerically, the uncertainties are better summarized with distributions than single values.
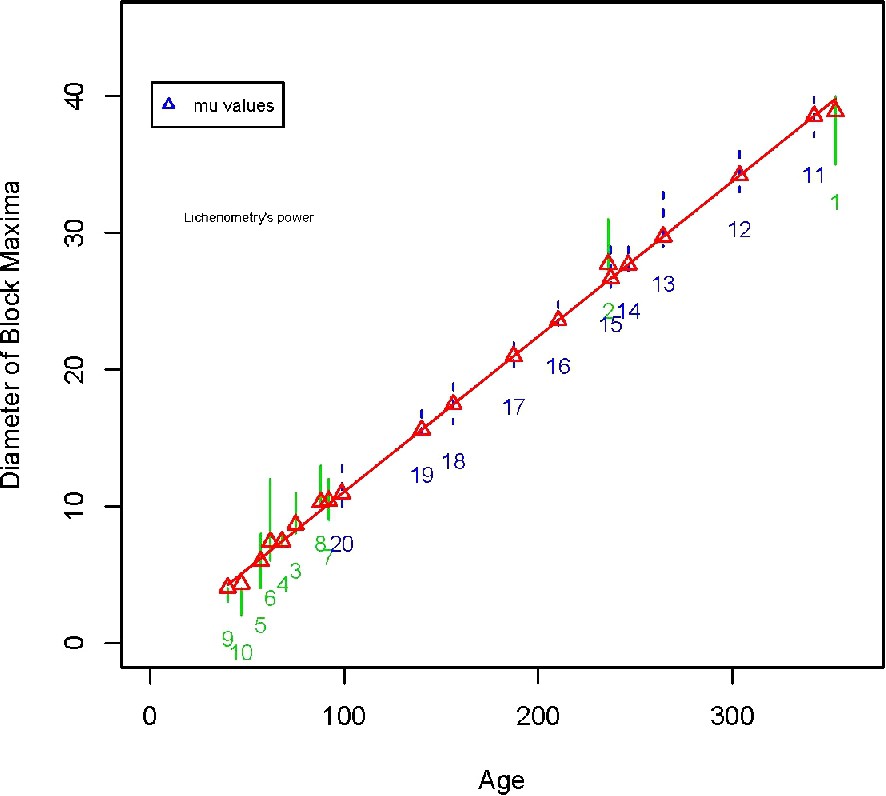
A new type of growth curve between the GEV parameters of block maxima and the mean parameter of the ages Gaussian distribution. Example for the Charquini northeastern glacier. Light grey numbers associated with a solid line represent the dated surfaces, dark numbers associated with dashed lines correspond to the ten moraines of the glacier. The length of the vertical lines indicates the measurements variability.
Un nouveau type de courbe de croissance entre les paramètres GEV décrivant la distribution des plus gros lichens par bloc et le paramètre moyen de la distribution gaussienne des âges. Exemple du glacier nord-est du Charquini. Les nombres en gris clair, associés à une ligne continue, représentent les surfaces datées, ceux en foncé, associés à une ligne en tirets, représentent les dix moraines du glacier. La longueur des lignes verticales correspond à la variabilité des mesures.
In the field, all measurements were taken with a flexible, transparent plastic rule with an accuracy of 1 mm. The smallest measured diameter was of 2 mm. Only lichens of circular shape were considered to reduce the risk of coalescence. Our dataset of lichenometric measurements of Rhizocarpon geographicum is composed of 10 dated and 48 undated surfaces. The surfaces of known age are presented in detail in Naveau et al. [34]; all were found in the Eastern Cordillera (up to 4500 m asl), and so are expected to be representative of lichen growth rate on the glacier forelands. Eight are included within the 20th century (between 1910 and 1965), one dates to the mid-18th century and one to the mid-17th century. Only the oldest one is based on a 14C dating, all the others are dated with documentary sources. The reduced size of the margin of error can be mostly attributed to the accuracy of the mid-18th century control point.
Undated surfaces correspond to the main moraines of each of the glaciers to be dated.
4 Results
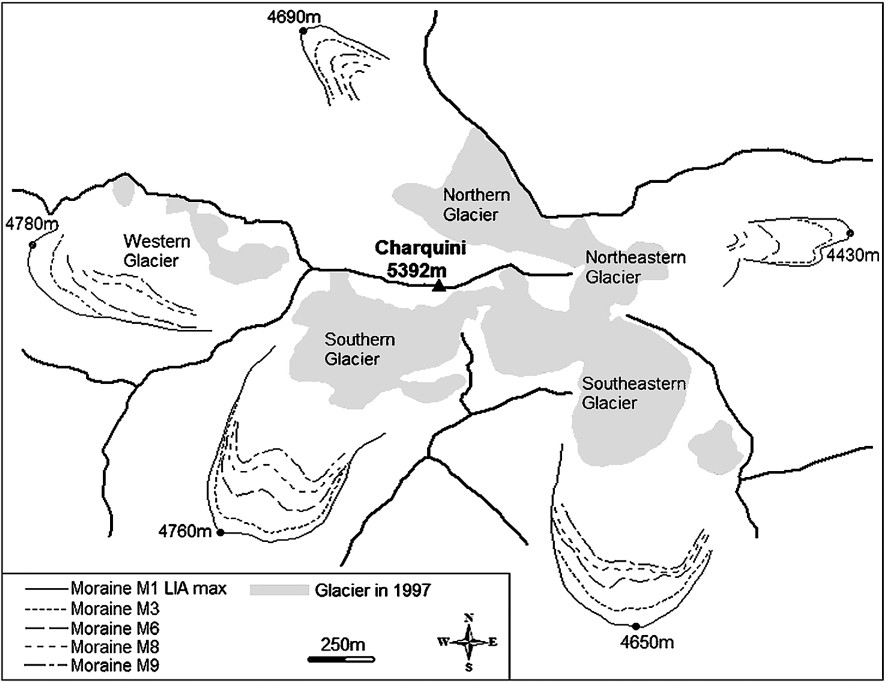
The moraines of respective glaciers show the same pattern (Fig. 1). On each of the five slopes corresponding to the Charquini glaciers, ten moraines can be identified between the furthest (located at 4430 to 4780 m asl depending on the glacier) and the present snout (situated at 4820 to 4960 m asl in 1997) over a horizontal distance varying from 1000 m (southern, southeastern and western glaciers) to 1400 m (northern glacier). On each site, the succession of moraines is homogeneous and is repeated from one slope to another. Five of these moraines, M1, M3, M6, M8 and M9 are always prominent and attest to phases of stabilisation or small advances, whereas the others, such as M2, M4, M5 and M7, are less marked and are believed to represent only short stops in a continuous recession process. The corresponding moraines on the different slopes present the same lichenometric pattern, i.e. the same diameter. Results from the five glaciers are shown in Table 1 and Fig. 4, whereas the chronology of moraines of the southern glacier is illustrated by a picture in Fig. 5.
Lichenometric dating of LIA moraines on Charquini glaciers. On the southeastern glacier, moraines M2 and M5 were too fine-grained to allow lichen measurements. Note that margins of error (M.E.) are computed on the basis of the variance of μ, see text
Datations lichénométriques des moraines PAG des glaciers du Charquini. Aucune mesure de lichen n'a pu être faite sur les moraines M2 et M5 du glacier sud-est, celles-ci étant uniquement composées de matériaux fins. Les marges d'erreur (M.E.) sont calculées à partir de la variance de μ, cf. texte
| Moraine | Southern glacier | Southeastern glacier | Northeastern glacier | Northern glacier | Western glacier | |||||
| Date | M.E. | Date | M.E. | Date | M.E. | Date | M.E. | Date | M.E. | |
| M1 | 1686 | 14 | 1664 | 14 | 1662 | 14 | 1663 | 14 | 1663 | 14 |
| M2 | 1703 | 12 | 1700 | 12 | 1706 | 12 | 1700 | 12 | ||
| M3 | 1734 | 12 | 1736 | 12 | 1740 | 12 | 1740 | 12 | 1739 | 12 |
| M4 | 1765 | 10 | 1755 | 10 | 1758 | 10 | 1755 | 10 | 1755 | 10 |
| M5 | 1802 | 10 | 1767 | 10 | 1769 | 10 | 1763 | 10 | ||
| M6 | 1808 | 10 | 1792 | 10 | 1794 | 10 | 1794 | 10 | 1791 | 10 |
| M7 | 1825 | 10 | 1819 | 10 | 1817 | 10 | 1817 | 10 | 1815 | 10 |
| M8 | 1843 | 9 | 1849 | 9 | 1848 | 9 | 1847 | 9 | 1852 | 9 |
| M9 | 1871 | 9 | 1868 | 9 | 1864 | 9 | 1870 | 9 | 1873 | 9 |
| M10 | 1912 | 9 | 1909 | 9 | 1905 | 9 | 1910 | 9 | 1907 | 9 |
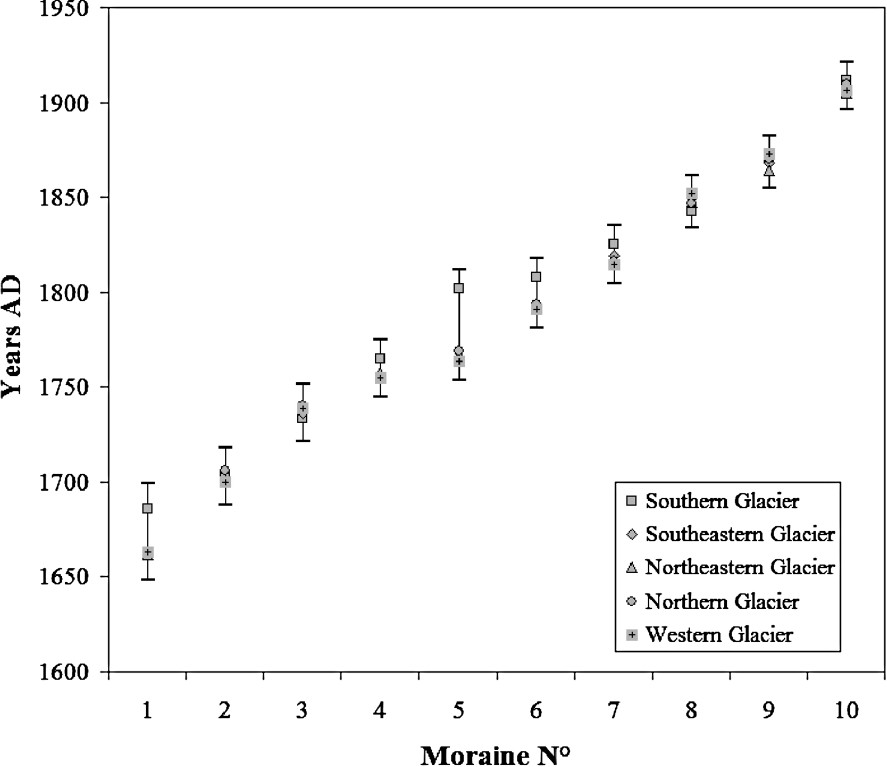
Dates obtained for the ten main moraines of the five Charquini glaciers. Dates obtained from lichen size measurements are generally consistent from one glacier to another. The discrepancy for the moraines M5 and M6 of the southern glacier can be attributable to insufficient sampling lichen measurements, since the moraines found in that sites are made up of fine-grained materials. For M1 moraine on the same glacier, although a problem in the lichen sampling cannot be ruled out, this glacier might reach its maximum size some decades later or stay in the same position for a longer period. Cumulative error margins are illustrated.
Dates obtenues pour les dix principales moraines de chacun des cinq glaciers du Charquini. Les écarts observés pour les moraines M5 et M6 du glacier sud peuvent résulter d'un échantillonnage insuffisant, ces moraines étant composées essentiellement de matériaux fins. Pour la moraine M1 de ce même glacier, bien qu'un problème d'échantillonnage ne puisse pas être totalement écarté, il est possible que ce glacier ait atteint sa position maximale plus tardivement ou qu'il soit resté à cette position pendant une période plus longue. Les marges d'erreur cumulées sont présentées.

The moraine pattern of the southern glacier with estimated dates. (Photo: V. Jomelli.)
Date estimée des moraines du glacier sud du Charquini. (Photo V. Jomelli.)
The dating of the moraines suggests the following glacier fluctuations:
- – the LIA maximum is attested by the large outer moraine M1, which dates from the second half of the 17th century. Considering the five slopes (moraine number 1 in Fig. 4), the date of the LIA maximum falls in the AD 1648–1700 period. On the southern glacier, M1 contains an interstratified peat dated by 14C to 1090–1220 cal. AD (Gif-11869). The presence of peat in the moraine proves that the glacier eroded the substratum constituted by a peat bog formed well before the LIA;
- – after this maximum, the very close moraine M2 dates from the late 17th–early 18th centuries attests to a short stop of glaciers and points out that during half a century they never moved away from their maximal extent;
- – the moraines M3 are very close to the outer moraines and date from the AD 1722–1752 period. From their morphology and as in the foreland of southern and southeastern glaciers, M3 has partially removed M2; it can be assumed that these moraines result from an advance which interrupted a period of retreat during the beginning of the 18th century;
- – the morphology and the small size of moraines M4 and M5 reflect only short stops of glaciers during a continuous retreating process all along the second half of the 18th century;
- – the recession was interrupted by a clear glacier advance in the late 18th century when the moraine M6 was formed during the AD 1781–1818 interval. But this event was limited and in no way allowed the previous moraines to be removed;
- – a continuous glacier recession took place throughout the first half of the 19th century; it was moderate (145 m between M6 and M9) and not interrupted by any important advance, because principally M7 and in a lesser extent M8 are small moraines in size which attests only to short stops of glaciers;
- – between the moraines M9 dated to be about 1870 AD, and M10, which marks snout position at the beginning of the 20th century (about 1910 AD), the glaciers receded by 250 m on the average. This retreat was fast compared to previous recessions. This accelerated retreat and the ‘break’ in the moraine deposition support the finding that the LIA ended between M9 and M10. However, since intermediate moraines are lacking, we cannot claim so far when the LIA ended in this part of the Andes.
In conclusion, this chronology makes it possible to state that the LIA maximum occurred in the second half of the 17th century. Henceforth, the overall pattern of glacier evolution is a continuous retreat since the mid-18th century with only minor advances or stops interrupting this trend during the late 18th and the mid-19th centuries, but these advances did not remove the previous moraines. The LIA ended between 1870 and 1910 AD.
It could be objected that glaciers could have retreated on large scale before the early 20th century, that moraines might have been removed by a later advance and that some stages would be missing in this chronology. Nevertheless, several arguments against this possibility can be pointed out: (1) on all the different slopes, moraines present exactly the same arrangement; (2) considering the short time interval existing between two consecutive moraines (about 25 years) and the small size of glaciers, these are expected to have not receded extensively between the morainic stages; (3) from the regularly decreasing glacier extent upstream, it can be assumed that climatic conditions within the LIA precluded glaciers to advance significantly and to bury or remove completely several previous moraines.
Glacier areas corresponding to the moraine contours were reconstructed and the ELA determined for each glacier and each period. For that, we used the Accumulation Area Ratio (AAR) method adjusted to 0.65, corresponding to the value measured on the nearby Zongo Glacier over the 1991–2004 period [52]. Assuming a similar AAR during the 17th century when the glaciers deposited M1, we find an ELA depressed by about 160 m (between 115 and 190 m depending on the slope) for this period compared to the present (1997), assuming glaciers being in equilibrium at this date.
5 Assessing synchronicity during the LIA of glacier fluctuations in the tropical Andes and in the Northern Hemisphere
The LIA was identified in the tropical Andes, generally in the cordilleras of Peru, by several authors [8,32,45], but these studies resulted in a poor description of glacier fluctuations over the recent centuries, because they focused on the long Holocene timescale and used only the 14C as dating method. Neither the LIA maximum nor the fluctuations of minor magnitude included in this period could thus be dated accurately. Rodbell [44] used lichenometry to date Holocene fluctuations, but the growth curve of Rhizocarpon sp. was calibrated on 14C-dated surfaces with only one control point within the last millennium. Consequently, the dates obtained in earlier studies on the LIA could not be improved. This author put the two morainic stages Gueshque 1 and 2 into the last millennium and dated these stages from the 1250 BP–400 BP period and the 19th century, respectively. We believe that the ages found by Rodbell for the outer ridges (i.e. Gueshque 1) are too old. Two arguments support this assertion: (1) Rodbell's Gueshque 1 stage includes both pre/early-LIA and LIA s.s. moraines; (2) the growth curve over-estimates the moraines' age because control points are too scarce and inaccurate. The first accurate dating of LIA glaciers was performed by Solomina et al. [51] in the Cordillera Blanca (Peru). Using lichenometry and improving the Rodbell's growth curve for the last centuries, the authors dated the outermost moraines within the 1590–1720 AD period. Later advances of weak magnitude are 1780 and 1880 AD old.
The results obtained on the Charquini glaciers are in good agreement with those from Solomina et al. [51], because both the maximal extent (M1) dated from the 17th century and the later minor advances (M6 and M9) from the late 18th–19th centuries fall into the same age ranges (Fig. 6, upper part). This leads to the conclusion that glaciers in Bolivia, as well as in Peru, have clearly retreated after the 17th century maximum and during the whole 19th century.
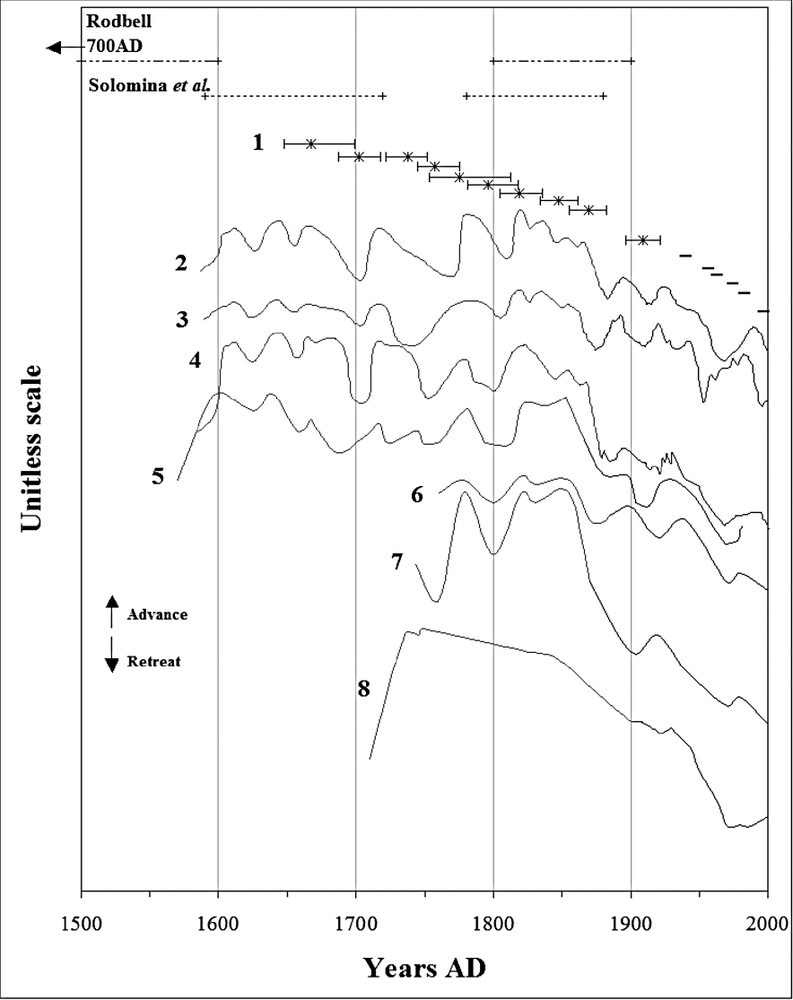
Fluctuations of Charquini glaciers compared with documented glaciers of the Peruvian Cordillera Blanca (upper part, results from Rodbell and Solomina showing only the time intervals within which the moraines are dated) and of the Northern Hemisphere over the last 500 years. 1 = Mean of the five Charquini glaciers (crosses and lines represent positions of glacier termini dated by lichenometry and aerial photographs, respectively), 2 = Glacier d'Argentière (French Alps), 3 = Glacier des Bossons (French Alps), 4 = Mer de Glace (French Alps), 5 = Grindelwald Gletscher (Swiss Alps), 6 = Rosenlaui Gletscher (Swiss Alps), 7 = Rhone Gletscher (Swiss Alps), 8 = Nigarsbreen Glacier (Norway). Curves 2 to 4 are from Vincent et al. [55], curves 5 to 7 are from Zumbühl and Holzhauser [60], curve 8 is from Nesje and Dahl [35].
Fluctuations des glaciers du Charquini comparées à celles de glaciers documentés en cordillère Blanche, Pérou (haut du graphe, les résultats de Rodbell et Solomina montrent uniquement les intervalles de temps au sein desquels sont datées les moraines) et de l'hémisphère nord sur les 500 dernières années. 1 = Moyenne des cinq glaciers du Charquini (les croix et les traits représentent les positions du glacier datées respectivement par lichénométrie et photographies aériennes), 2 = glacier d'Argentière (Alpes françaises), 3 = glacier des Bossons (Alpes françaises), 4 = mer de Glace (Alpes françaises), 5 = Grindelwald Gletscher (Alpes suisses), 6 = Rosenlaui Gletscher (Alpes suisses), 7 = Rhone Gletscher (Alpes suisses), 8 = Nigarsbreen Glacier (Norvège). Les courbes 2 à 4 sont tirées de Vincent et al. [55], 5 à 7 de Zumbühl et Holzhauser [60], et 8 de Nesje et Dahl [35].
The accelerated glacier retreat in Bolivia during the late 19th century is consistent with observations reported by scientist explorers, which suggest that glaciers were all receding after 1860 AD and particularly after 1880 AD in Peru [7] and Ecuador [11,18]. Consequently, the LIA ended after 1860 AD and probably after 1880 AD in these regions.
Such coincidences between these cordilleras allow us to state a synchronicity in the LIA evolution along the chain, at least in Bolivia and Peru, which is in favour of a common climatic signal at regional scale.
The concurrence of the glacier maximum in the tropics and the Maunder solar minimum (1645– 1715 AD) strengthens arguments that could link a low irradiance input to glacier expansion [9,15,43]. In accordance with the following Dalton minimum (1783–1830 AD), which was less significant than the former, the retreat of glaciers in the tropical Andes slowed down and a significant but limited advance marked by the moraine M6 took place, possibly linked to this decreasing solar activity. It is possible that glacier advances in the tropics could have been controlled by a slight decline in the solar irradiance, but at this stage of the investigation, it is not possible to link the −2.5 W m−2 Maunder Minimum irradiance decrease [43] with physical processes at the glacier surface.
However, it has to be stated that glacier advances during the Maunder Minimum are not a global phenomenon. Effectively, due to regional atmospheric circulation patterns, e.g., the NAO, the Alps were dry during the Maunder Minimum [30] and glaciers receded in many cases (Fig. 6).
Concerning the general retreat since the mid-18th century, solar activity cannot alone explain the glaciers' evolution. Furthermore, as shown in Fig. 6, many glaciers in the Northern Hemisphere experienced a strong re-advance during the first half of the 19th century [29,33,35,55,60]. Such a re-advance did not occur in the tropical Andes and this discrepancy in glacier evolution has to be linked with specific changes at the regional scale. Temperature was probably low in the tropical Andes during the first half of the 19th century, a reasonable assertion even if indicators from this region are scarce and not used in the current temperature reconstructions (e.g., [22]). On the other hand, precipitation might have been low and insufficient to allow a significant glacier expansion to occur. This hypothesis is consistent with glacier behaviour in this environment, as pointed out by recent studies in Bolivia, based on detailed energy balances at the glacier surface [10,48,58]. Precipitation appears to be a crucial factor governing mass balance evolution through the feedback existing with net radiation and albedo. When precipitation is abnormally scarce from October to March (i.e. during the Austral summer), melting rates increase dramatically and mass balance is strongly negative [59]. This situation is observed to occur nowadays during the ENSO warm phases (El Niño) [12]. Further studies using other climate proxies are needed to confirm this low precipitation trend in Bolivia during the 19th century, but the ice core retrieved by Thompson et al. [53] on the Quelccaya ice cap (southern Peru) brought some support to this finding. In the southern Peru, net accumulation rates were strong during the early LIA till about 1720 AD, which supports wet conditions, whereas a dry climate seems to have prevailed after ca 1720 till about 1880 AD. The dry 1720–1880 AD period [53] is in good agreement with our hypothesis that glacier mass balance were affected by general dry conditions during the 19th century.
As for glaciers in the Alps [16,55], an acceleration in the glacier recession occurred in the Andes after 1860 AD (Fig. 6). However, some doubts exist about the synchronicity and the causes of the LIA ending in the central Andes and in the Northern Hemisphere.
Since no reconstructed temperature dataset based on instrument records since 1860 AD, particularly in the Northern Hemisphere, shows an increasing trend before the first decades of the 20th century (e.g., [5,22,31]), we may suppose that environmental changes in the tropical Andes concerned mainly precipitation evolution. As mentioned before, the beginning of the 19th century is assumed to have been dry, based on the Quelccaya evidence [53]. Furthermore, we suppose that this climate regime lasted, even more drastically, during the second half of the 19th century. Recent evidence from the Bolivian Western Cordillera brings new arguments for an extension of the dry climate observed in Quelccaya ice cap till the beginning of the 20th century [54]. From ca. 1880 AD to 1905 AD, these authors have shown that the level of the Chungara Lake (18°15′S) was low, which implies low precipitation in a sector of Bolivia located relatively close to our study area. At the same time, according to the same authors, lake levels have been rather high in the subtropical Andes (23–26°S). This opposite situation between tropical and subtropical Andes can be observed currently and relates with the ENSO variability [1]. If we look at the long-term climatic cycles that play out in the Pacific Ocean, we observe that the Central/Eastern Tropical Pacific sea-surface temperature (SST) displayed long and intense warm anomaly periods after 1860 till the beginning of the 20th century [23,26]. Quinn and Neal [39] also claimed that the 1864–1891 period “was exceptional since the El Niño events occurred frequently and many of them were strong or very strong”. Thus, it can be assumed that the mechanisms linking the Central/Eastern Pacific SST anomaly and the glacier mass balance in the central Andes were of the same nature one century ago. Hence, it is probable that a succession of El Niño events could have precipitated the ending of the LIA in the central Andes. Recurrent low accumulation amounts and high ablation rates could have combined their effect to repeatedly provoke strong mass balance deficits on glaciers. Due to the very short time of response of these glaciers, the snout reacted immediately and retreated, as they did during the well-documented strong and frequent warm ENSO events occurring in the 1990s [12,13].
6 Conclusion
Dating of moraines of the Cerro Charquini glaciers by lichenometry has allowed us to propose the first detailed chronology of glacier fluctuations in a tropical area during the LIA. The glacier maximum occurred in the second half of the 17th century, as observed in many mountain areas of the Andes and the Northern Hemisphere. This expansion has been of a comparable magnitude to that observed in the Northern Hemisphere, with the ELA depressed by 100–200 m during the glacier maximum. The synchronisation of glacier expansion with the Maunder and Dalton minima supports the idea that the solar activity could have cooled enough the tropical atmosphere to provoke this evolution, but in the absence of a physical model linking solar activity and atmosphere, this assertion remains conjectural. Throughout the 18th–19th centuries, Charquini glaciers retreated continuously, whereas most glaciers advanced during the first decades of the 19th century in other mountain regions of the world. The most probable explanation for this discrepancy is related to regional-scale climate changes. Since tropical glaciers retreat significantly when precipitation decreases during the austral summer, it is proposed that the second part of the LIA could have been dry in the Andes. Evidence of decreasing precipitation in the second half of the LIA and during the late 19th century corresponding to the LIA ending exist on the Quelccaya ice cap, in palaeohydrological reconstructions and historical ENSO records.
Acknowledgements
The first phase of this work is part of the French ECLIPSE program of the INSU–CNRS (‘Institut national des sciences de l'univers’–‘Centre national de la recherche scientifique’). We thank Valérie Masson-Delmotte, from the ‘Laboratoire des sciences du climat et de l'environnement’ (LSCE, CEA–CNRS), for initiating this project involving a multiproxy study of the LIA in the Alps and the Andes. We are deeply grateful to G. de Marsily, who presented this paper, and to the two anonymous referees for their comments and suggestions.


