Gravity observations and 3D structure of the Earth

Yanick Ricard; Frédéric Chambat; Carolina Lithgow-Bertelloni

doi:10.1016/j.crte.2006.05.013

Internal Geophysics (Physics of Earth's Interior)

Gravity observations and 3D structure of the Earth
[Observations gravimétriques et structure tridimensionnelle de la Terre]

Yanick Ricard ¹ ; Frédéric Chambat ² ; Carolina Lithgow-Bertelloni ³

¹ Laboratoire de sciences de la Terre, UMR CNRS 5570, université Lyon-1, bd du 11-Novembre-1918, 69622 Villeurbanne cedex, France
² Laboratoire de sciences de la Terre, UMR CNRS 5570, École normale supérieure de Lyon, 46, allée d'Italie, 69364 Lyon cedex 07, France
³ Department of Earth Sciences, University of Michigan, Ann Harbor, MI 48109, USA

Comptes Rendus. Géoscience, Volume 338 (2006) no. 14-15, pp. 992-1001.

Résumés

Anglais
Français

The determination of Earth's gravity field has benefited from various gravity missions that have been launched recently (Champ and Grace) and a new quantitative jump should be made by the Goce mission in a few more years. For the first time, a global high-quality coverage of the Earth's gravity is available. In this paper, we review the results that have been obtained to explain Earth's gravity on a global scale. We show how we can separate the contributions due to shallow density variations (crust and lithosphere) to those related to the deep mantle. The geoid (or the first degrees of the gravity field) is very simply and well explained by ancient slabs subducting throughout the whole mantle. Such a density distribution is in agreement with tomographic results and qualitatively with what is expected from a convective mantle without a large amount of bottom heating. Although we can produce a simple model that correlates with observations for all degrees and explain most of the geoid, a significant improvement in the fit is possible and will need to take into account the details of the lithospheric structure.

La détermination du géopotentiel a bénéficié de récentes missions spatiales (Champ et Grace) et un nouveau saut quantitatif est attendu, dans le futur proche, avec la mission Goce. Pour la première fois, une couverture globale de qualité de la Terre est disponible. Nous synthétisons, dans cet article, les résultats permettant d'interpréter le champ de gravité global. Nous montrons comment séparer les contributions des variations superficielles de densité (croûte et lithosphère) des contributions du manteau plus profond. Le géoïde (ou les premiers degrés du champ de gravité) est simplement expliqué par les paléoplaques traversant tout le manteau. Ces variations de densité sont en accord avec les résultats de la tomographie sismique et, qualitativement, avec les résultats des modèles de convection à relativement faible chauffage par le bas. Bien qu'un tel modèle soit corrélé avec les observables à tous les degrés et explique une bonne part du géoïde, une amélioration substantielle de l'ajustement reste possible et devra être obtenue en tenant compte d'un modèle détaillé de la structure lithosphérique.

Métadonnées

Reçu le : 2006-05-17
Accepté le : 2006-05-31
Publié le : 2006-07-17

DOI : 10.1016/j.crte.2006.05.013

Keywords: Gravity, Geoid, Lithosphere, Earth's mantle, Density structure
Mot clés : Gravité, Géoïde, Lithosphère, Manteau terrestre, Structure en densité

Affiliations des auteurs :

Yanick Ricard ¹ ; Frédéric Chambat ² ; Carolina Lithgow-Bertelloni ³

¹ Laboratoire de sciences de la Terre, UMR CNRS 5570, université Lyon-1, bd du 11-Novembre-1918, 69622 Villeurbanne cedex, France
² Laboratoire de sciences de la Terre, UMR CNRS 5570, École normale supérieure de Lyon, 46, allée d'Italie, 69364 Lyon cedex 07, France
³ Department of Earth Sciences, University of Michigan, Ann Harbor, MI 48109, USA

@article{CRGEOS_2006__338_14-15_992_0,
     author = {Yanick Ricard and Fr\'ed\'eric Chambat and Carolina Lithgow-Bertelloni},
     title = {Gravity observations and {3D} structure of the {Earth}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {992--1001},
     publisher = {Elsevier},
     volume = {338},
     number = {14-15},
     year = {2006},
     doi = {10.1016/j.crte.2006.05.013},
     language = {en},
}

TY  - JOUR
AU  - Yanick Ricard
AU  - Frédéric Chambat
AU  - Carolina Lithgow-Bertelloni
TI  - Gravity observations and 3D structure of the Earth
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 992
EP  - 1001
VL  - 338
IS  - 14-15
PB  - Elsevier
DO  - 10.1016/j.crte.2006.05.013
LA  - en
ID  - CRGEOS_2006__338_14-15_992_0
ER  -

%0 Journal Article
%A Yanick Ricard
%A Frédéric Chambat
%A Carolina Lithgow-Bertelloni
%T Gravity observations and 3D structure of the Earth
%J Comptes Rendus. Géoscience
%D 2006
%P 992-1001
%V 338
%N 14-15
%I Elsevier
%R 10.1016/j.crte.2006.05.013
%G en
%F CRGEOS_2006__338_14-15_992_0

Yanick Ricard; Frédéric Chambat; Carolina Lithgow-Bertelloni. Gravity observations and 3D structure of the Earth. Comptes Rendus. Géoscience, Volume 338 (2006) no. 14-15, pp. 992-1001. doi : 10.1016/j.crte.2006.05.013. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.05.013/

Version originale du texte intégral

1 Forty years of gravity observations

Since the first artificial satellite orbited around the Earth (1957), the tracking of satellite orbits has been used to constrain the lateral variations of the gravity field of the Earth [12]. In this last 40 years, our knowledge of the Earth's gravity field has improved significantly in both accuracy and resolution [20]. The accuracy of the lowest degrees of the field has been increased by the addition of new and better data (a larger number of satellite orbits, some dedicated, with variable inclinations). At the same time, the resolution benefited from adding the constraints of satellite altimetry over ocean [2] and from expending the geographical coverage and the quality of direct gravity measurements at the Earth's surface. Combined models have been published up to degree and order 360 and in this paper we will use the Egm96 model [13].

However, the gravity community of scientists had been longing for years to have a direct satellite dedicated to the gravity field until these last years when, at last, various satellites have been launched or planned (Champ2000 [21], Grace2002 [22] and soon Goce2006 [29]). Of course, a direct measurement of gravity is impossible in orbits, but the derivatives of the gravity can be measured by monitoring the distances between two or more probes orbiting around the Earth. These probes can be two active satellites (Grace), an active satellite and a passive orbiting target, or two probes inside a single satellite (accelerometric concept, Champ).

The knowledge of satellite-only gravity models is necessary for various reasons. First, the direct surface gravity data that controls most of the present-day gravity models at, say, degree larger than 50, is very geographically uneven and of variable quality. The missing data are sometimes estimated from the topography itself, which bias further study of gravity–topography relationships. Second, the altimetric data assumes that the ocean topography is an equipotential surface, although surface currents are driven by the dynamic topography of the sea surface (i.e. the topography in excess of the equipotential). Third, the quality of the gravity models is now such that the time variations of the gravity of astronomical (tides), meteorological (annual perturbations), hydrological (variations of water table levels), and secular sources (post glacial rebound) must be taken into account.

The combined data of Champ and Grace have recently allowed geodesists to describe the gravity field using satellite only data up to degree ∼160, although it is probably safer to limit the expansion around degrees 100–120. This is already a striking progress, as the previous satellite-only solutions were probably only accurate up to degree 20–30. This decade should see a huge further progress in gravity observations.

As usual in the geodynamic community, we do not refer the geoid to a best-fitting ellipsoid, but to the shape that the Earth should have if gravity and rotation were in equilibrium [18]. This non-hydrostatic geoid and the corresponding free-air gravity only differ at even degrees and order 0 (practically, only at degrees 2 and 4) from those used by geodesists. The degree-2 order-0 density induces a gravity anomaly seen in the non-hydrostatic geoid of the geodynamicists, but would apparently have no effect when the best-fitting ellipsoid of the geodesists is used.

Here, we want to discuss a few simple ideas about the source of the gravity field and the implications for the solid-Earth geophysics. We only consider the global gravity field and all studies with local gravity measurements or with oceanic altimetry are beyond the scope of this paper. The gravity field is depicted in Fig. 1 as the geoid surface (top) and the free-air gravity (bottom) anomalies. The relationships between these quantities will be given in Section 2. The geoid undulations emphasize the long-wavelength components of the free-air anomalies. An unexpected feature of the geoid is its lack of correlation with the usual pattern of plate tectonics or surface topography.

Fig. 1
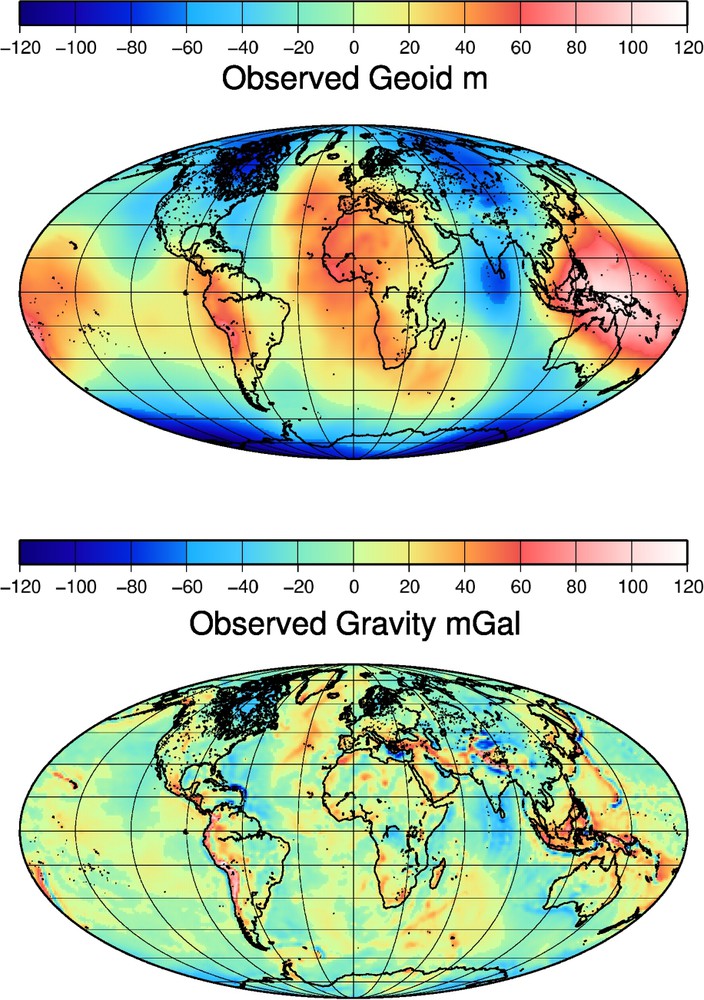
Non-hydrostatic geoid (in meters) and free-air gravity anomalies (in mGal). The pattern of the geoid with its band of equatorial maxima interrupted across India by a north–south band of minima is not correlated to any surface feature, like the topography.
Géoïde non hydrostatique (en mètres) et anomalies à l'air libre (en milligals). La structure du géoïde, avec sa bande de maxima équatoriaux, interrompue à la longitude de l'Inde par une bande nord–sud de minima, n'est pas corrélée avec les structures de la tectonique des plaques ou avec le relief terrestre.

2 A few basic equations

The gravitational potential outside the volume including all mass sources is simply harmonic and can be written as:

V (r, θ, ϕ) = \sum_{l = 0}^{\infty} \sum_{m = 0}^{l} {(\frac{a}{r})}^{l + 1} V_{l m} (a) Y_{l m} (θ, ϕ)

(1)

where

Y_{l m} (θ, ϕ)

are spherical harmonic functions and a the mean Earth's radius. Practically, the expansion is only performed up to a maximum degree

l_{\max}

that can be associated with a minimal wavelength

λ_{\min} = 2 π a / (l_{\max} + 1 / 2)

. The summation does not include the degree 1, which corresponds to an arbitrary shift of the center of mass and the degree 2 order 1, whose weak presence is associated with the more complex physics of true polar wander [24].

Two possible mappings of the gravity data can be done, either on the form of a geoid anomaly (see Fig. 1, top):

N (θ, ϕ) = \frac{V (a, θ, ϕ)}{g_{0}}

(2)

where

g_{0}

is the reference gravity (

g_{0} = 4 π G \bar{ρ} a / 3

, where G is the gravitation constant and

\bar{ρ}

is the average Earth density), or on the form of a free-air gravity anomaly

δ g (θ, ϕ)

(see Fig. 1, bottom) whose spherical harmonics coefficients

δ g_{l m}

are related to those of the geoid by

δ g_{l m} = (l - 1) \frac{V_{l m} (a)}{a}

(3)

The natural use of the spherical harmonic functions in the gravity representation suggests similarly to expand the topographies $h_{i} (θ, ϕ)$ (e.g., surface, Moho, core–mantle undulations...) and the internal density $ρ (r, θ, ϕ)$ on the same basis:

ρ (r, θ, ϕ) = \sum_{l, m} ρ_{l m} (r) Y_{l m} (θ, ϕ)

(4)

h_{i} (θ, ϕ) = \sum_{l, m} h_{l m}^{i} (r) Y_{l m} (θ, ϕ)

(5)

The coefficients $V_{l m} (a)$ are related to the density variations by

V_{l m} (a) = \frac{G}{(2 l + 1) a} \int_{E} ρ (r, θ, ϕ) {(\frac{r}{a})}^{l} Y_{l m} (θ, ϕ) d V

(6)

where E is the total Earth volume. The inverse gravitational consists of inferring the density from the observed potential. However, it is well known that Eq. (6) is non-invertible. There is an infinite number of density distributions that belong to the kernel of the external gravity field, i.e. that produce no gravity outside the planet. The mathematical description of this kernel and the identification of the subset of density models that generates an external gravity field is possible [3], but will not be discussed here.

By introducing the spherical harmonic expansion (4) into (6) and taking into account the density jumps $Δ ρ_{i}$ (here assumed uniform, and corresponding to the difference between the densities above and below the discontinuity) associated to each interface i located around the mean radius $a_{i}$ , one gets:

V_{l}^{m} (a) ≃ \frac{4 π G}{(2 l + 1) a^{l + 1}} (\int_{0}^{a} r^{l + 2} ρ_{l m} (r) d r - \sum_{i} Δ ρ_{i} h_{l m}^{i} a_{i}^{l + 2})

(7)

This equation is only valid to first order in

h^{i} (θ, ϕ) / a_{i}

, as we neglected higher-order terms. Second-order terms would include the integrals on the unit sphere of

h^{2} (θ, ϕ) Y_{l m} (θ, ϕ)

. A more elaborate and general discussion of these expansions can be found in [4], which also takes into account the fact that the reference shape of the Earth is ellipsoidal, not spherical.

An obvious but important implication of Eq. (7) is that the geoid undulations generated by the Earth topography alone are:

N_{l}^{m} = \frac{3}{2 l + 1} \frac{ρ_{c}}{\bar{ρ}} h_{l m}

(8)

(

ρ_{c}

is the crust density). We depict in Fig. 2 the spectrum of the geoid, of the topography, and of the geoid that an uncompensated Earth topography should generate (thin dashed line). This geoid would be basically one order of magnitude too large up to degree 20 and still a factor 3 too large at degree 250. The slope of the spectrum of this non-compensated geoid would also be too steep with respect to that observed. Trying to explain the observed gravity without modeling the processes of compensation is definitively hopeless.

Fig. 2
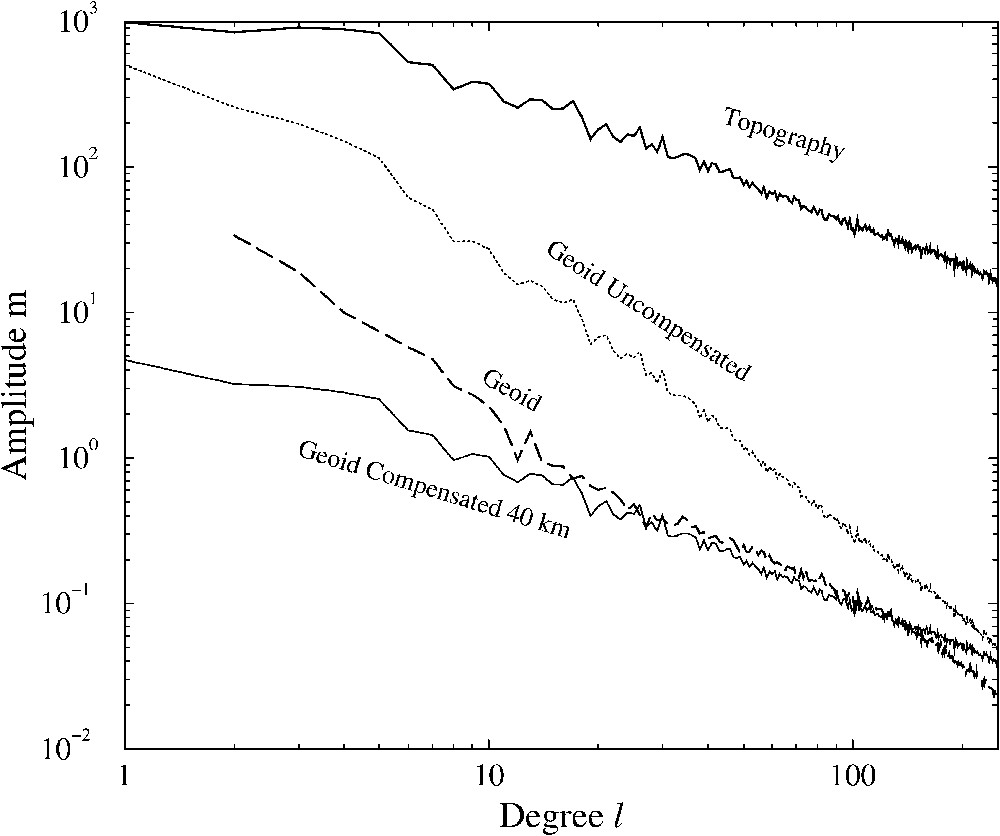
Amplitude spectrum (in meters) of the Earth's topography and geoid (thick solid and dashed lines) compared to the spectrum of the geoid signal due to an uncompensated topography (thin dotted line) and a topography compensated at 40-km depth (thin line).
Amplitudes spectrales (en mètres) de la topographie terrestre et du géoïde (traits continus, gras et tireté), comparées à celles de géoïdes synthétiques dues à une topographie non compensée (trait mixte) ou à une topographie compensée à 40 km de profondeur (trait continu fin).

Compensation means that as soon as density anomalies are present, they induce stresses that deflect all the density interfaces. It is only the total mass anomalies (i.e. density anomalies and interface deflections) that can be safely used in gravity modeling. Deflections of interfaces are generally computed assuming perfect compensation under each point (Airy model) or using elastic models of the lithosphere for shallow mass anomalies (e.g., [31]) and using viscous models for deep heterogeneities related to mantle convection. We do not want to develop here a complete model of viscous dynamic compensation that can be found in [26] and [23] (see also [7] in Cartesian coordinates), and we only summarize the results of these papers.

The general idea is to consider a model of the Earth where the rheology and the reference density are known, then from this mechanical model to compute the interface deformations (surface, CMB...) imposed by the presence of internal density loads. Only mass distributions (internal masses plus interface deformations) that are solutions of the mechanical problem are physically acceptable and it is only within these solutions that the 3D density structure of the Earth can be found. In other words, the models of Moho topography, CMB topography and mantle 3D tomography taken separately cannot be trusted, unless when taken together they satisfy the requirement of mechanical equilibrium.

From the interface deflections and from the internal loads the resulting gravity can be easily computed following (7). The results of this modeling are as follows:

• the presence of an internal mass of degree l induces an interface topography that reaches exponentially an equilibrium shape after a time constant of order $2 η l / (ρ_{m} g_{0} a)$ . This is the constant of post-glacial rebound, a few thousands of years for degrees ∼10. This is very short compared to most geological timescales. Except over the zones previously covered by the last glaciation, the long-wavelength topography is in steady equilibrium with internal loads;
• density anomalies close to the surface (between the radii $a - d$ and d) induce a topography that verifies the usual isostatic rule:
$ρ_{c} h_{l m} + \int_{a - d}^{a} ρ_{l m} (r) d r = ε (\frac{d}{a})$ (9)
with $ε (0) = 0$ , i.e. the departure from isostasy goes to zero with d. Under a stiff viscous lithosphere, $ε (d / a)$ varies as ${(d / a)}^{2}$ . Isostasy is even more closely verified when the elasticity of the lithosphere is also taken into account. In that case, the right-hand side of Eq. (9) varies as ${(d / a)}^{4}$ [30];
• in agreement with the previous point, masses located directly on interfaces (surface or Cmb) are exactly compensated and do not generate a gravity field at first order. This implies that we cannot understand the geoid by only considering compensated mass anomalies very close to the surface or very close to the Cmb;
• the resulting gravity has generally a sign opposite to that of the deep-density anomaly; e.g., a topographic high is associated with a crustal root (internal deficit of density), but a geoid high. A positive correlation between internal densities and geoid can however be obtained when the deep masses are close to a significant viscosity increase. This point will be discussed in Section 4.

To illustrate the role of compensation, we can consider the case where a density anomaly

δ ρ_{l m}

extending from the surface to the depth d induces a surface topography

h_{l m}

. We apply the isostatic rule (using (9) as a strict equality). An expansion of Eq. (7) shows that

N_{l}^{m} = \frac{3}{2} \frac{l + 2}{2 l + 1} \frac{ρ_{c}}{\bar{ρ}} \frac{d}{a} h_{l m} = - \frac{3}{2} \frac{l + 2}{2 l + 1} \frac{δ ρ_{l m}}{\bar{ρ}} \frac{d^{2}}{a}

(10)

The first line expresses the geoid as a function of the surface topography, the second line as a function of the internal density. The minus sign indicates that on top of dense mass anomalies we should expect a decrease of the gravity, a minimum of the geoid. The gravity that could be expected from the surface topography compensated at 40-km depth is depicted in Fig. 2 (thin dashed-dotted line). Although the first 20 degrees are much smaller than observed, a satisfactory amplitude and slope is predicted from degrees 15–150. This agreement suggests that isostasy is indeed very closely verified, although we have no mathematical or physical proof that it should be strictly valid (a right-hand member of order d in Eq. (9) would affect the expansion (10)).

The fact that the gravity perturbations induced by the surface topography and the internal loads tend to cancel each other strengthens the need to use the exact gravity equation in order to model the short-wavelength components. For the short-wavelength anomalies, we therefore represent the mass anomalies by parallelepipedic cells of uniform density (a volume limited by two longitudes, two latitudes and two radii). To compute the crustal field, we use for example a grid of 1024 longitudes and 512 latitudes. The computation of Eq. (6) for parallelepipedic units can be very precisely performed up to high order by recurrence relations [11] (here we use $l_{\max} = 250$ ). Notice however that although we compute exactly the gravity field from the crustal model, this model remains based on the isostatic rule that in principle is only valid to first order. For the lowest harmonic degrees that we will ascribe to the mantle and, in part, to the lithosphere, we can safely use the first-order expression (7).

3 Crustal and lithospheric sources of the gravity field

The most direct candidates for the sources of the gravity field are of course related to the density heterogeneities associated with the surface topography and the associated Moho undulation. However, we know that at least one major structure of the Earth's topography, namely the oceanic ridges, is not related to the crust, but to the cooling and contraction of the oceanic lithosphere (e.g., [30]).

Assuming that the topography is locally compensated (Airy compensation), we can estimate the Moho depth from the isostatic rule. We define the densities of ice, water, oceanic or continental crust by $ρ_{i}$ , $ρ_{w}$ , $ρ_{c}$ and their thicknesses by $h_{i}$ , $h_{w}$ and $h_{c}$ , respectively. These layers overlay a lithosphere of density $ρ_{L}$ with thickness L and a mantle of density $ρ_{m}$ . We define H as the external topography of the Earth, being zero over oceans and following the surface of the crust or the ice sheets on continents. Isostasy implies:

(ρ_{m} - ρ_{i}) h_{i} + (ρ_{m} - ρ_{w}) h_{w} + (ρ_{m} - ρ_{c}) h_{c} + (ρ_{m} - ρ_{L}) L - ρ_{m} H = C t e_{1}

(11)

where

C t e_{1}

is a constant. In this equation, we have two unknowns, the crustal and lithospheric thicknesses,

h_{c}

and L. Here, for simplicity, we treat the lithosphere as a layer of uniform density. A more accurate computation should include the depth dependence of the lithospheric density. Considering the lithosphere as limited by a density interface tends to overestimate the resulting gravity effect. To counterbalance this bias, we choose rather low lithospheric thicknesses.

To build an isostatic model of crustal thickness, $h_{c} (θ, ϕ)$ , we assume that the lithospheric thickness is only a function of the age of the sea floor, $L (age)$ . Therefore, using a compilation of sea-floor ages [19], we computed $h_{age}$ , the excess topography of the sea floor with respect to its depth far from the ridge. Our empirical fit, $h_{age}$ , reaches 2360 m over ridges, varies as expected with $\sqrt{age}$ at young lithospheric ages and flattens to zero near 120 Myr and under continents.

We assume that all this age-dependent excess sea-floor topography is related to the lithospheric thickening that we compute from:

- (ρ_{m} - ρ_{w}) h_{age} + (ρ_{m} - ρ_{L}) L (age) = C t e_{2}

(12)

We choose

C t e_{2}

so that the lithosphere under old ocean and continents is 80 km. Our model assumes that the continental lithosphere is uniform and rather thin, which is certainly oversimplified. The resulting lithospheric thickness

L (age)

is then introduced in Eq. (11) to derive a model of crustal thickness

h_{c} (θ, ϕ)

. We choose the arbitrary constant

C t e_{1}

so that the average oceanic crust is in the order of 7 km. In fact, with this choice, Eq. (11) cannot be verified with a positive

h_{c}

over some deep subduction trenches; when this is the case, we locally ascribe a minimum value to the crustal thickness (3 km) and leave the topography locally uncompensated.

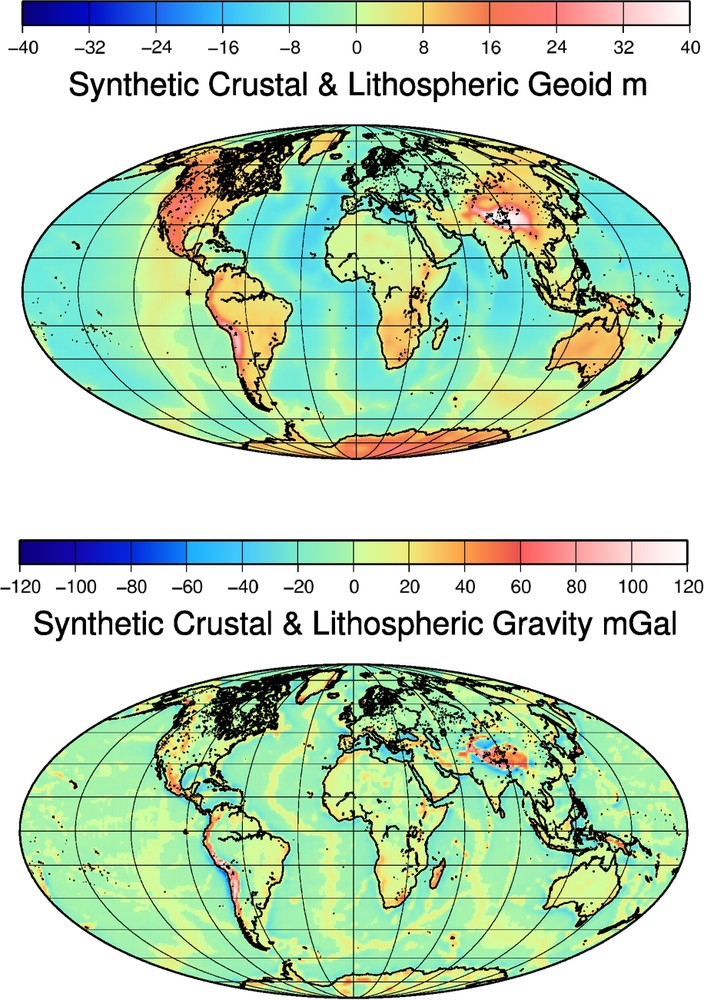
The resulting geoid and free-air gravity computed to degree and order 250 are depicted in Fig. 3 (using $ρ_{i} = 900 kg m^{−3}$ , $ρ_{w} = 1000 kg m^{−3}$ , $ρ_{c} = 2800 kg m^{−3}$ , $ρ_{L} = 3270 kg m^{−3}$ and $ρ_{m} = 3200 kg m^{−3}$ ). This degree of resolution should be attained within the next 10 years by satellite-only solutions. The predicted geoid has a rather low amplitude, about one third of that observed (compare with Fig. 1, top), and little resemblance to the observed pattern. The free-air gravity map, on the other hand, is highly correlated with the observations (compare with Fig. 1, bottom). Over trenches, our model that forces isostasy cannot explain the very local signal of non-isostatic origin.

Fig. 3
Crustal and lithospheric geoid and gravity models. The synthetic geoid of shallow density sources has an amplitude of about 30% of the total geoid (see Fig. 1). Its shape is rather different from that of the total geoid. An obvious signal with an amplitude of about 15 m can be associated with ridges. The free-air gravity is quite similar to observations.
Géoïde et anomalies à l'air libre d'origines crustales. Le géoïde synthétique dû aux sources peu profondes a une amplitude de l'ordre de 30% de celle du géoïde total (comparer avec la Fig. 1). Sa topologie est assez différente de celle du géoïde total. Un signal notable, d'une amplitude de l'ordre de 15 m, souligne les dorsales. Les anomalies à l'air libre sont assez semblables aux observations.

We quantify the misfit between model and observation in Fig. 4 where we plot the degree correlations, the degree amplitude ratio between model and observation and the variance reduction of the observed gravity. The thick lines correspond to our total-crust and lithospheric model. The thin dotted lines only include the crustal model. As expected from Section 2, for the lowest degrees, the isostatically compensated crustal signal is much lower in amplitude (middle panel) than the observations and not even correlated (top panel). 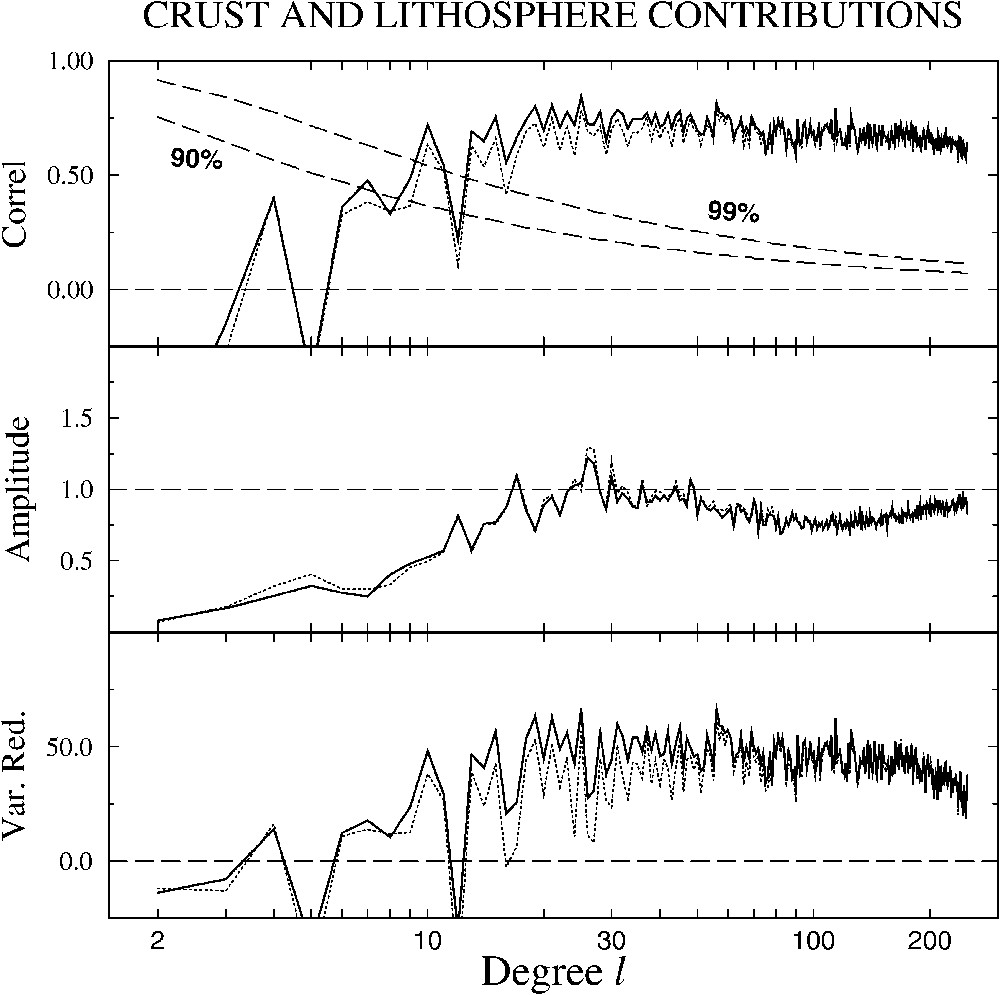However, for degrees larger than ∼15, a very signification correlation (top panel) is observed that leads to a $\sim 45 %$ variance reduction of the signal. Including the oceanic-lithosphere thickening improves moderately but uniformly the correlations and the variance reductions, particularly between degrees 8–40 (compare the thin and thick lines).

Fig. 4
Correlation between observed gravity field and the isostatic crustal and lithospheric contributions (top). Amplitude ratio of the shallow contribution to the observed gravity (middle). Variance reduction of the observed gravity by the crustal and lithospheric components (in %, bottom). The two dashed lines of the top panel depicts the 90 and 99% confidence levels. In each channel, we also plot the results for the crustal component only, without the lithospheric component (thin dotted lines).
Corrélations entre le champ de gravité observé et les contributions cumulées d'origines crustales et lithosphériques (en haut). Rapports des amplitudes entre la contribution d'origines crustales et lithosphériques et la gravité observée (au milieu). Réduction de variance de la gravité observée par la contribution crustale et lithosphérique (en bas). Les deux courbes en tiretés du graphique du haut représentent les niveaux de confiance à 90 et 99%. Dans chaque graphique, nous avons aussi reporté les résultats pour la contribution crustale sans la contribution lithosphérique (pointillés).

The elastic support of mass anomalies that exists at short wavelength [31] has not been considered in this modelling of gravity of crustal and lithospheric density anomalies. This does not seem to affect the fit of our synthetic gravity with observations, except maybe by a slight reduction of the variance for degrees 150–250 (Fig. 4, bottom panel). The presence of elasticity affects the compensating topography and the gravity by a term varying like ${(k E_{e})}^{4}$ (where $E_{e}$ is the elastic thickness of the lithosphere and k the wavenumber of the topography [30,31]). Replacing k by $(l + 1 / 2) / a$ , the good fit depicted on Fig. 4 implies that the average elastic thickness of the Earth is not larger than ∼30 km. Any attempt to explain the Earth's gravity for degrees larger than 200–250 will need to account for the lithospheric elasticity.

4 The long-wavelength mantle sources

The previous exercise clearly shows that the lowest wavelengths of the gravity field cannot be related to near-surface features: shallow anomalies would be compensated and would not generate much gravity anomaly and, at any rate, no obvious near-surface feature (geological structure, ocean–continent distribution...) correlates with the geoid. We must therefore look toward the 3D structure of the mantle to identify the large-scale density heterogeneities. Undulations of the CMB also affect the geoid, but are consequences of the general mechanical equilibrium. The liquid core cannot sustain large mass anomalies and the small inner core density heterogeneities, if they exist, are too far away to reasonably have a large influence on the surface gravity.

Starting in the mid-1980s (e.g., [6]), mantle tomography, i.e. the determination of the 3D structure of the mantle through seismic-wave propagation modeling has made enormous progress. Like the geoid observations, the quality of the models has improved both in precision and in resolution. To search for deep-mantle mass anomalies, we make use of the synthetic S model (‘Smean model’ of [1]), which is a weighted average of previously published models [9,17,28]. This model may not be a very good model for any of the dataset that have been used to construct it, but it should somewhat emphasize the common structures found by various tomographic approaches.

Although the relationship that relates seismic velocities and densities may not be so simple, we will consider these velocities as a proxy for densities, where faster velocities correspond to higher densities. The correlation between the observed gravity field and the Smean tomographic model is depicted in Fig. 5. This correlation is plotted as a function of degree (horizontal line) and depth (vertical axis). This correlation indicates very clearly that at long wavelength, the gravity is positively correlated with fast mantle zones from the transition zone to about ∼1000 km deep (red colors) and negatively correlated with fast mantle zones in most of the lower mantle and in the first ∼200 km (blue color).

Fig. 5
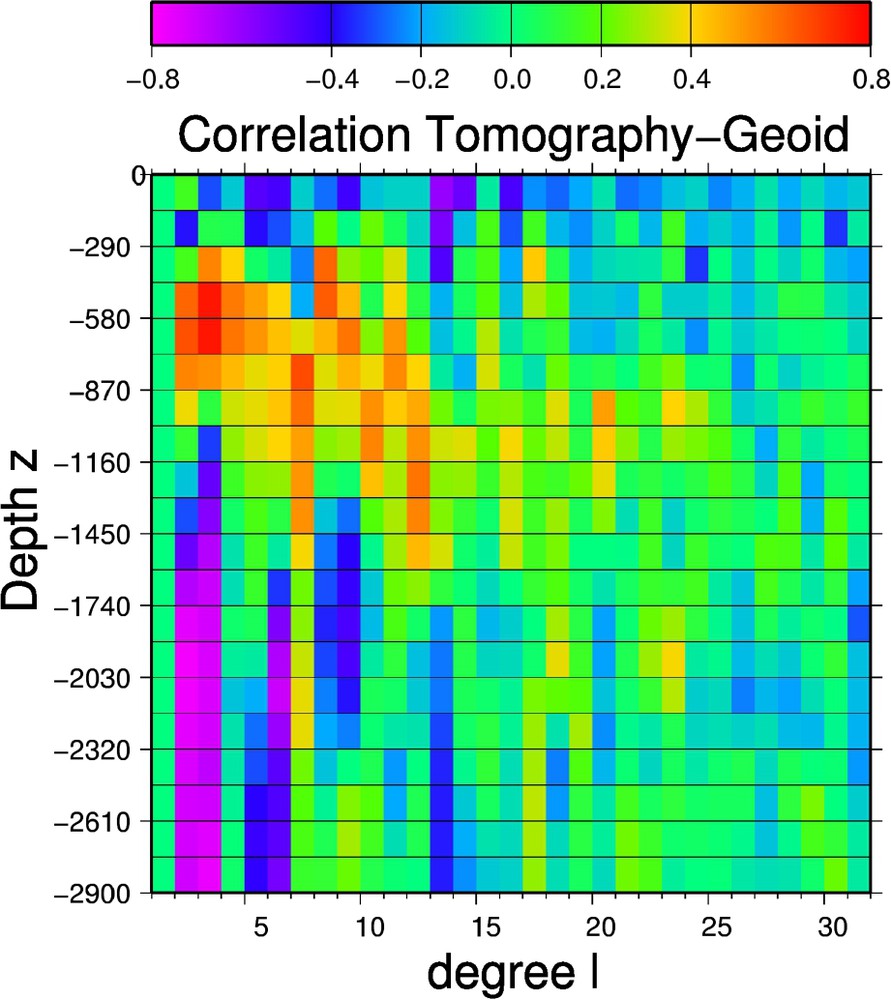
Correlation between gravity and the synthetic tomographic Smean model [1] as a function of degree l and depth. For the first ∼15 degrees, there is a clear pattern with a negative correlation between the seismic velocities near the surface and in the lower mantle, but a positive correlation between gravity and tomography in the transition zone and the top of the lower mantle.
Corrélations entre la gravité et la tomographie synthétique Smean [1], en fonction du degré l et de la profondeur. Pour les premiers ∼15 degrés, il y a une corrélation négative entre les vitesses sismiques et la tomographie, près de la surface et dans le manteau profond, mais une corrélation positive dans la zone de transition et le sommet du manteau inférieur.

The anti-correlation (blue color) is in fact in agreement with the isostatic rule: the dense lithosphere (fast velocities) should depress the surface topography and the resulting gravity anomalies should have the sign of the surface depression and be negative. It is in fact the depth range of positive correlations, across the upper–lower mantle interface that needs to be explained.

Since 1984 [23,26], an explanation for the change of sign of the correlation between mantle density and geoid has been proposed. In the case when the mantle viscosity increases rapidly with depth by a factor in the order of ∼30, a dense anomaly is supported by the stiffer underlying mantle, which results in a smaller surface deflection, larger CMB deflection and a positive correlation with the geoid. Away from a sharp viscosity increase, the induced surface deflection is larger, and imposes its sign to the gravity anomaly. The general theory also includes the dynamic topography induced by the flow at the CMB.

The geoid models based on this approach are well correlated with the observed geoid (e.g., [8,10]). Unfortunately, this approach does not constrain tightly the exact amount of viscosity increase that, according to various authors, ranges between one or two orders of magnitude and is localized across the transition zone, at 670-km depth, across the top of the lower mantle, with a discontinuous jump or a continuous increase. Rather than using a given tomographic model to derive the gravity contributions of the mantle heterogeneities, we can also use a somewhat different approach, maybe more speculative, but that brings the present structure of the mantle within the general paradigm of plate tectonics.

The general agreement on convection of fluids heated largely by internal radioactivity is that the regions of lithospheric downwellings (the subduction zones) should be underlain by cold descending plumes (the slabs). These structures should dominate the mantle heterogeneity structure. This view results in a testable consequence that the present-day mantle structure should, at first order, be the result of past subductions [27].

Starting from a compilation of plate reconstruction models spanning the last 200 Myr [16], we compute the position that subducted slabs could have in the mantle. This very simple model assumes that each piece of slab sinks vertically and that the slab excess density is conserved through the whole mantle [15,25]. The only free parameter of the model is the viscosity increase at 670 km depth that slows down the sinking velocity of slabs in the lower mantle.

The quality of this geodynamical model based on paleo-plate reconstructions lies in its robustness. Indeed there is only one parameter to adjust, the viscosity jump at 670 km depth. The age relationship for the slab density of the lithosphere at subduction is well known (e.g., [30]).

Using a very simple viscosity profile (a 100-km-thick lithosphere with a viscosity 13 times that of the upper mantle, and a lower mantle 30 times more viscous, the resulting density model is well correlated with the available tomographic models, and provides a remarkable fit to the lowest degrees of the Earth's gravity field [25]. We perform the computation up to degree 10 only as our slab model is too simplistic to be trusted at very high degrees. The computed geoid of Fig. 6 is strikingly similar to the observed one in Fig. 1. The correlations depicted in Fig. 7 (dotted lines) confirm that the fit of the degrees 2 and 3 is close to perfect, but the first 10 degrees are indeed highly correlated with observations. This confirms the general geodynamic findings that slabs are the major structures of the convective mantle and that the structure of the whole mantle records the last 200 Myr of plate tectonics [15]. Further complexities in the modelling can be added, related to the details of the rheology in the transition zone, to the lateral viscosity variations and to the nature of the lithospheric rheology, but the gain in fitting the observed long-wavelength gravity remains small.

Fig. 6
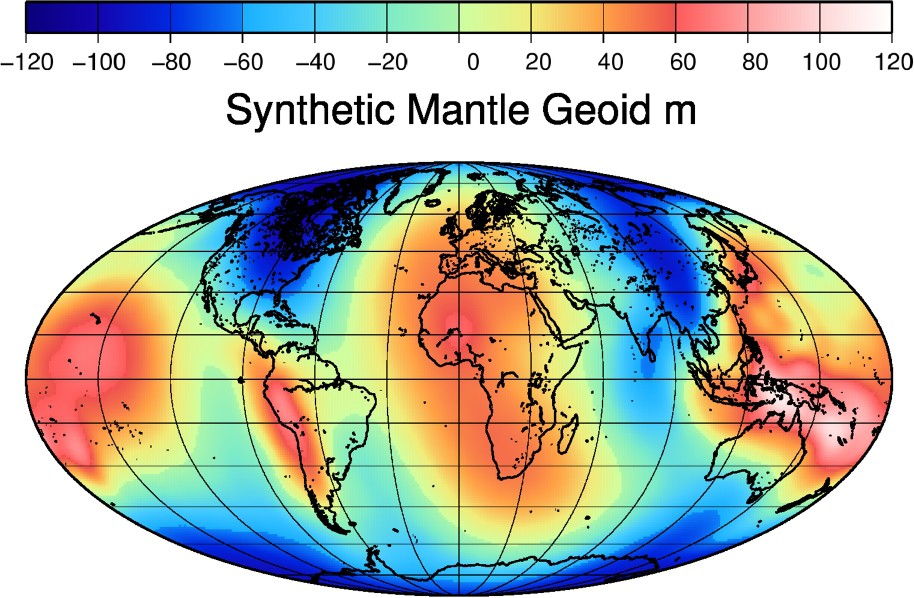
The slab derived mantle components yields to a computed gravity field strikingly similar to the observed geoid in pattern and amplitude (see Fig. 2).
Les anomalies de gravité d'origines mantelliques, calculées à partir des plaques en subduction, sont remarquablement similaires aux observations, en géométrie comme en amplitude (voir Fig. 2).

Fig. 7
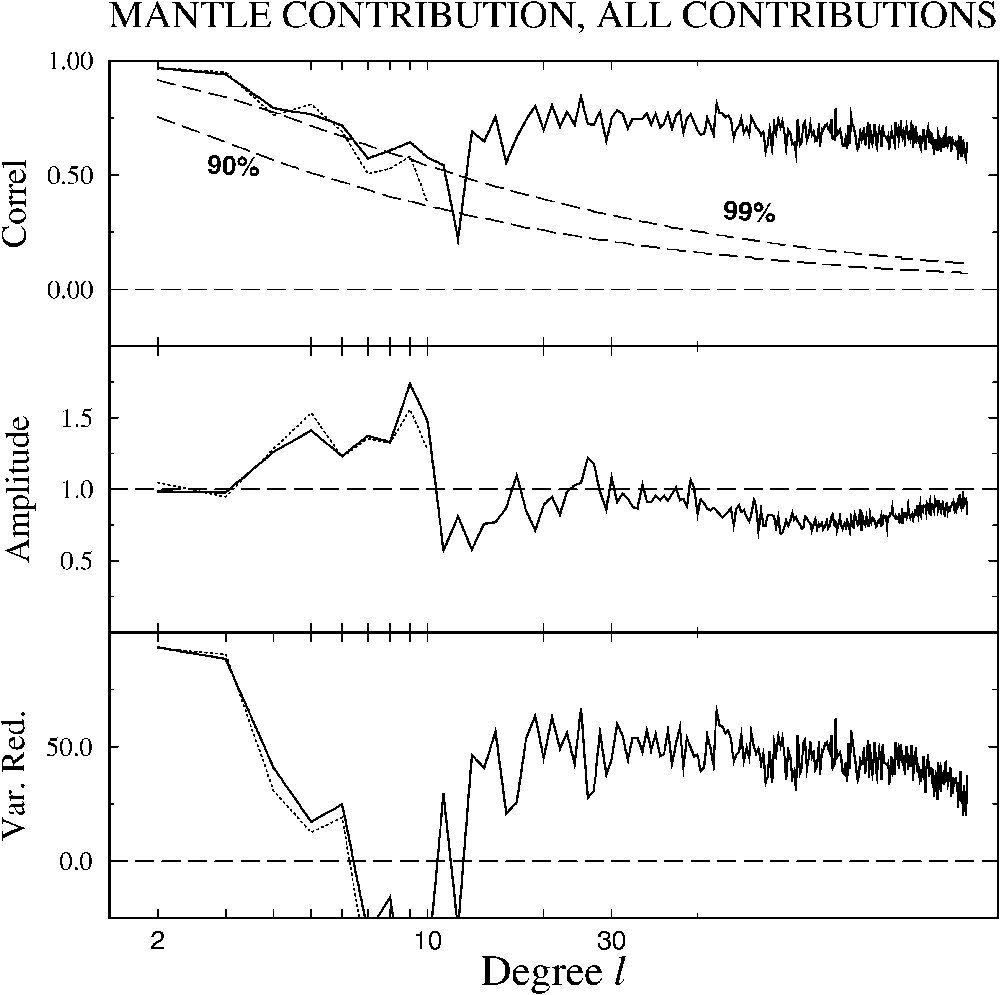
Same as in Fig. 4, we compare the synthetic mantle gravity field (thin dotted lines) and the total gravity field (solid line) with the observations (correlation on top, amplitude ratio, middle and variance reduction, bottom). The mantle component corresponds very well in correlation and amplitude to the observations at low degrees.
Cette figure, similaire à la Fig. 4, compare les gravités synthétiques d'origines mantelliques (traits pointillés) et totales (traits continus) avec la gravité observée (corrélations en haut, rapport d'amplitude au milieu et réduction de variance en bas). La composante mantellique correspond, en amplitude comme en corrélation, au signal observé, pour les premiers degrés.

5 Conclusion: present-day understanding of the static gravity field

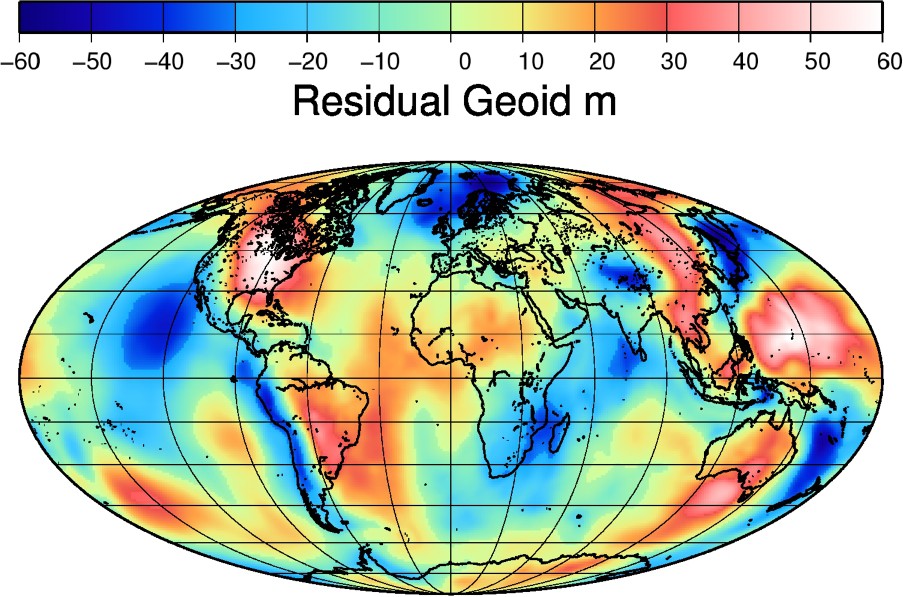
When the contributions of our crust, lithosphere and mantle sources are added together, the resulting gravity field is correlated at more than 99% with the observed gravity (see Fig. 7, solid line). The residual geoid (Fig. 8), has an amplitude reduced by ∼3 with respect of the original geoid. The total variance reduction is however not so good in the range $l = 6 – 15$ , where the two end-member models (deep mantle sources versus shallow crust and lithospheric sources) are both inaccurate.

Fig. 8
Residual geoid, difference between observed and computed geoid (crust, lithosphere and mantle). Its amplitude is less than 40% of the observed geoid, which corresponds to a total variance reduction of ∼85%. The residual bears correlation with subduction zones.
Géoïde résiduel, différence entre les observations et notre modèle incluant les sources crustales, lithosphériques et mantelliques. Son amplitude est de moins de 40% du signal initial, ce qui correspond à une réduction de variance de ∼85%. Ce résidu reste corrélé avec la distribution des zones de subduction.

Certainly the lithosphere under continents is not uniform and density heterogeneities are observed by surface wave tomography up to 200–250-km depth (e.g., [5]). However, the density anomaly due to the subcontinental lithosphere should be very low, as no major anomaly of the residual geoid seems to correlate to the ocean–continent distribution or even to the position of cratons [14].

The fact that the mantle contribution of the geoid is highly correlated with observations but does not lead to a major variance reduction except for the very first degrees could be improved. We select the viscosity profile in order to achieve the best total variance reduction, which is strongly dominated by the signal at degrees 2 and 3. Fitting the total gravity rather than the total geoid would certainly select a viscosity profile yielding a lower total variance reduction for the geoid, but a more uniform variance reduction over the first 10 degrees.

Although an isostatic density model provides a satisfactory modeling of the gravity field, it is clear that the processes of mechanical compensation only require isostasy approximatively. The existence of deviatoric stresses (viscous or elastic), even at long wavelength, forbids the existence of a strict Archimedean equilibrium. The fact that the new generation of geoid models will be obtained with accuracy and without the potential bias of using surface data will impose to re-discuss the small departure of the shallow masses from isostasy. In particular, it will be necessary to take into account the elastic support of the lithosphere to extend the gravity modeling toward higher degrees.

Bibliographie

[1] T.W. Becker; L. Boschi A comparison of tomographic and geodynamic mantle models, Geochem. Geophys. Geosyst., Volume 3 (2002) (2001GC000168)

[2] A. Cazenave The geoid and oceanic lithosphere (P. Vanicek; N. Christou, eds.), Geoid and its Geophysical Interpretations, CRC Press, 1994, pp. 255-283 (Ch. 13)

[3] F. Chambat; Y. Ricard Empirical 3D basis for the internal density of a planet, Geophys. J. Int. (2005), pp. 32-35 | DOI

[4] F. Chambat; B. Valette Earth gravity up to the second order in topography and density, Phys. Earth Planet. Inter. (2005), pp. 89-106 | DOI

[5] E. Debayle; B. Kennett; K. Priestley Global azimuthal seismic anisotropy and the unique plate-motion deformation of Australia, Nature, Volume 433 (2005), pp. 509-512 | DOI

[6] A. Dziewonski Mapping the lower mantle: Determination of lateral heterogeneity in p velocity up to degree and order 6, J. Geophys. Res., Volume 89 (1984), pp. 5929-5952

[7] L. Fleitout; C. Froidevaux Tectonics stresses in the lithosphere, Tectonics, Volume 2 (1983), pp. 315-324

[8] A.M. Forte; W.R. Peltier Plate tectonics and aspherical Earth structure: The importance of poloidal–toroidal coupling, J. Geophys. Res., Volume 92 (1987), pp. 3645-3679

[9] S.P. Grand; R. van der Hilst; S. Widiyantoro Global seismic tomography a snapshot of convection in the Earth, GSA Today, Volume 7 (1997) no. 4, pp. 1-7

[10] B.H. Hager; R.W. Clayton Constraints on the structure of mantle convection using seismic observations, flow models, and the geoid (W.R. Peltier, ed.), Mantle Convection, Gordon and Breach, New York, 1989, pp. 657-764

[11] K. Ilk, Y. Ricard, R. Rummel, M. Thalhammer, Application of spaceborne gravity to research on the interior of the Earth, Technical report, CIGAR IV, ESA Report, 1986

[12] W. Kaula A geoid and world geodetic system based on a combination of gravimetric, astrogeodetic, and satellite data, J. Geophys. Res., Volume 66 (1961), pp. 1799-1811

[13] F.G. Lemoine, D.E. Smith, L. Kunz, R. Smith, E.C. Pavlis, N.K. Pavlis, S.M. Klosko, D.S. Chinn, M.H. Torrence, R.G. Williamson, C.M. Cox, K.E. Rachlin, Y.M. Wang, S.C. Kenyon, R. Salman, R. Trimmer, R.H. Rapp, R.S. Nerem, The development of the NASA GSFC and NIMA joint geopotential model, in: J. Segawa, H. Fujimoto, S. Okubo (Eds.), Gravity, Geoid and Marine Geodesy, International Association of Geodesy Symposia, vol. 117, 1997, pp. 461–469

[14] Y. Lestunff; Y. Ricard Topography and geoid due to mass anomalies, Geophys. J. Int., Volume 122 (1995), pp. 982-990

[15] C. Lithgow-Bertelloni; M.A. Richards The dynamics of Cenozoic and Mesozoic plate motions, Rev. Geophys., Volume 36 (1998), pp. 27-78

[16] C. Lithgow-Bertelloni; M.A. Richards; Y. Ricard; R.J. O'Connell; D.C. Engebretson Toroidal–poloidal partitioning of plate motions since 120 Ma, Geophys. Res. Lett., Volume 20 (1993), pp. 375-378

[17] G. Masters; G. Laske; H. Bolton; A. Dziewonski The relative behavior of shear velocity, bulk sound speed, and compressional velocity in the mantle: Implications for chemical and thermal structure (S. Karato; A.M. Forte; R.C. Liebermann; G. Masters; L. Stixrude, eds.), Geophysical Monograph, Earth's Deep Interior, vol. 117, AGU, Washington, DC, 2000, pp. 63-87

[18] S.M. Nakiboglu Hydrostatic figure and related properties of the Earth, Geophys. J. R. Astron. Soc., Volume 57 (1979), pp. 639-648

[19] H.-C. Nataf; Y. Ricard 3-SMAC: An a priori model of the upper mantle based on geophysical tomography, Phys. Earth Planet. Inter., Volume 95 (1986), pp. 101-122

[20] R.S. Nerem; C. Jekeli; W. Kaula Gravity field determination and characteristics retrospective and prospective, J. Geophys. Res., Volume 100 (1995), pp. 15053-15074

[21] C. Reigber; G. Balmino; P. Schwintzer; R. Biancale; A. Bode; J. Lemoine; R. Koenig; S. Loyer; H. Neumayer; J. Marty; F. Barthelmes; F. Perosanz; S.Y. Zhu A high-quality global gravity field model from champ GPS tracking data and accelerometry (eigen-1s), Geophys. Res. Lett., Volume 29 (2002) no. 14, pp. 1692-1696

[22] C. Reigber; R. Schmidt; F. Fletchtner; R. König; U. Meyer; K.-H. Neumayer; P. Schwintzer; S.Y. Zhu An earth gravity-field model complete to degree and order 150 from grace: Eigen-grace02s, J. Geodyn., Volume 39 (2005), pp. 19-55

[23] Y. Ricard; L. Fleitout; C. Froidevaux Geoid heights and lithospheric stresses for a dynamic Earth, Ann. Geophys., Volume 2 (1984), pp. 267-286

[24] Y. Ricard; G. Spada; R. Sabadini Polar wander of a dynamic earth, Geophys. J. Int., Volume 113 (1993), pp. 284-298

[25] Y. Ricard; M. Richards; C. Lithgow-Bertelloni; Y.L. Stunff A geodynamic model of mantle density heterogeneity, J. Geophys. Res., Volume 98 (1993), pp. 21895-21909

[26] M.A. Richards; B.H. Hager Geoid anomalies in a dynamic earth, J. Geophys. Res., Volume 89 (1984), pp. 5987-6002

[27] M.A. Richards; D.C. Engebretson Large-scale mantle convection and the history of subduction, Nature, Volume 355 (1992), pp. 437-440

[28] J. Ritsema; H.J. van Heijst Seismic imaging of structural heterogeneity in Earth's mantle: Evidence for large-scale mantle flow, Sci. Progr., Volume 83 (2000), pp. 243-259

[29] R. Rummel; G. Balmino; J. Johannessen; P. Woodworth Dedicated gravity field missions, principles and aims, J. Geodyn., Volume 33 (2002), pp. 3-20

[30] D.L. Turcotte; G. Schubert Geodynamics: Applications of Continuum Physics to Geological Problems, Wiley, New York, 1982 (450 p.)

[31] A.B. Watts Isostasy and Flexure of the Lithosphere, Cambridge University Press, 2001 (472 p.)

Commentaires - Politique