1 Introduction
Ground deformation, and in particular subsidence, are major issues in terms of damage to infrastructures, implying remarkable costs for prevention and compensation. The causes of subsidence phenomena can be numerous, among others: ground settlement due to liquid/gas extraction [1,36–37], underground working like tunnelling [29], or mining [10,35]. Aiming at an effective risk management, monitoring techniques are required in order to allow a better knowledge of ground deformation phenomena and of their possible evolution. Crucial tasks are, in particular:
- • detection: where and when subsidence occurred (or is occurring);
- • assessment of the deformation;
- • evolution (past and future) of the deformation.
Techniques based on revisiting ground-based benchmarks, such as optical levelling or Global Positioning System (GPS), generally offer precise measurements, well recognised by the authorities in charge of the risk management. Nevertheless, the following shortcomings could appear:
- – difficulty and high costs of a wide-area (e.g., regional) coverage, foreseeing a reasonable spatial density (e.g. > 10 points/km2) of benchmarks to be visited at regular time intervals (e.g., a few times per year);
- – considerable variation of the precision of the measurements with the quality of the physical realisation of the benchmarks and with the care taken by the technicians during the measurement campaigns;
- – difficulty in accessing the monitoring sites (in particular in isolated areas);
- – the fact that often, in case of sudden deformations, ground-based networks are implemented only after a (or even the) relevant deformation event [10].
Deformation monitoring by remote sensing techniques and, in particular, Synthetic Aperture Radar interferometry (InSAR) could complement or, in certain cases, replace the ground-based techniques.
In this paper, we will present the principle and the domain of applicability (constrained by the limitations of the technique) of the InSAR techniques (conventional InSAR and Persistent Scatterers InSAR) and their application to the examples of the coal mining basin of Lorraine and of a ground settlement in the city of Paris.
2 Principles of InSAR and DInSAR
The principle of the SAR interferometry technique has been exposed by Graham [25]. It is based on the combination of two radar images, allowing either the retrieval of a Digital Elevation Model, i.e. a digital map of the local topography (InSAR), or the detection and quantification of the ground deformations that occurred between the two acquisitions (Differential InSAR, DInSAR).
Major applications of DInSAR concern different fields of ground-deformation investigation such as earthquakes [33], mining subsidence [4], landslides [21]. Presently, the existence of the 14-year (since 1992) data archive from the ERS-1 and ERS-2 sensors is a unique opportunity for studying the past evolution of uninstrumented phenomena.
A detailed review of the main principles of radar interferometry can be found in [3,26,32,39]; here we only wish to review briefly its basic concepts.
Synthetic Aperture Radars (SAR) are microwave imaging systems onboard of moving platforms (aeroplanes or satellites). Radar sensors are active (i.e. they emit their own radiation) and can, therefore, acquire data day and night. Furthermore, most of the remote sensing SAR systems operate in upper L band, in C band or in X band (i.e. within well-defined frequency bands comprised roughly between 1.2 and 10.9 GHz). At such frequencies, the electromagnetic radiation penetrates the cloud cover: SAR sensors can therefore acquire data regardless of the weather conditions.
SAR systems are coherent, they record a complex valued signal that is processed to generate two-dimensional complex matrices, usually represented in terms of amplitude and phase, and called SAR images.
The amplitude identifies the amount of electromagnetic field scattered back by the radar targets grouped within each SAR image-sampling cell (pixel).
The phase (actually the phase difference between transmitted and received signal), is an ambiguous (i.e. modulo 2π) measure of the distance between the SAR sensor and each area on the ground corresponding to an image pixel. It is worth remarking immediately that the phase sensitivity to a distance variation is very high: a phase shift of 2π corresponds to λ/2 (λ being the operating wavelength). For ERS-1/2, operating at 5.3 GHz in C-band, λ/2 = 2.8 cm.
The direction from the sensor to the individual radar targets on the ground is usually referred to as the Line of Sight (LOS), or slant range.
Phase measurements cannot be directly used to evaluate the sensor–target distance, because of an unknown reflectivity phase term, which represents the phase shift introduced by the scattering phenomenon and by the coherent sum of the contributions of all radar targets within each image cell.
Interferometry overcomes this problem by evaluating, on a pixel-by-pixel basis, the phase difference between two successive SAR images (called master and slave) acquired from very similar observation geometries. Assuming that the scattering phenomenon remains the same (i.e. at the time of the second acquisition, the cell still contains the same scatterers, in the same positions), the reflectivity term is cancelled out by the difference. This condition is referred to as absence of decorrelation or full coherence. The phase difference image is called interferogram (ϕInt).
Actually, also the interferometric phase ϕInt of a single pixel cannot be exploited directly, since this would require the orbits of the sensor to be known with a level of incertitude sufficiently lower than the operating wavelength (i.e. with subcentimetric precision). Once more, the way to circumvent this prohibitive requirement is to consider phase differences, in particular the difference between the interferometric phases of two distinct pixels P1 and P2 within the interferogram.
The difference between the interferometric phases relative to two pixels ϕInt,P1–P2 reflects both the differential topographic height of the two pixels (ϕtopo,P1–P2), i.e. the height of one of the pixels with respect to the other, and the LOS projection of possible differential deformations of the ground (ϕdisP1–P2), which could have occurred in the time span between the two images involved in the interferogram. Furthermore, the interferometric phase difference is affected by atmospheric terms (ϕaP1–P2), by noise due to decorrelation (ϕnoiseP1–P2), and by a flat-Earth component (ϕflat-EarthP1–P2). This latter term reflects the fact that (as long as the orbits of the master and slave acquisitions are not perfectly coincident), even in absence of topography (i.e. assuming that the Earth is flat), the interferometric phase varies as a function of the position of the pixel within the imaged scene.
Finally, as already mentioned, phase data are ambiguous: whenever, moving across an interferogram, a cumulative phase variation of 2π is exceeded, a new phase cycle starts, and a 2π discontinuity (‘phase jump’) is clearly visible.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
In Eqs. (1)–(5), δr is the differential displacement of the sampling cells P1 and P2 in the time span between master and slave acquisition projected along the LOS direction; R is the average sensor–target distance (845 km for ERS-1/2 data), B⊥ is the perpendicular baseline (further details provided in a few lines), i is the incidence angle (23° for ERS-1/2) and
It is worthwhile remarking that Eqs. (3)–(5) are simplified expressions obtained under the assumption of parallel master and slave orbits.
The topography phase term is directly proportional to the perpendicular baseline B⊥, which is the projection of the distance vector between the two satellite trajectories in the direction perpendicular to the line of sight (B⊥ is, therefore, a measure of how different the master and slave orbits are). Combinations of interferograms acquired with different baseline values can be used to compute accurate digital elevation models [13,45].
Aiming at the detection of ground deformation, the topographic and flat-Earth phase terms are estimated and removed from the interferometric phase; we obtain the so-called differential interferogram (Differential SAR Interferometry, DInSAR). This is accomplished using a Digital Elevation Model and precise sensor orbital data.
As already mentioned, only (spatial) differences in the differential interferometric phases of pixel pairs (or of any pixel with respect to a pixel assumed as reference) are actually exploitable. Anyway, for the sake of simplicity, we often omit the explicit mention of the two pixels P1 and P2 in the notation.
The phase of a differential interferogram (ϕDInt) gathers, therefore, only the term reflecting LOS deformation and the disturbing terms due to decorrelation noise (ϕnoise) and atmospheric distortion (ϕa).
Actually, a residual topographic term (ϕtopo–res) and a residual term due to the imprecision of the orbital data (ϕorb–res) also affect the differential interferograms as additional sources of disturbance:
| (6) |
Interferograms with small perpendicular baselines are particularly suitable for LOS deformation measurements, since they have a reduced sensitivity to topography (i.e. the residual topographic term is negligible), and are only slightly affected (at least) by the geometry-dependent part of the decorrelation noise.
Table 1 summarises the phase terms of a differential interferogram as a function of:
- – the temporal baseline ΔT (time between master and slave acquisition);
- – the difference in the imaging geometry relative to master and slave acquisitions (summarised in the core parameter normal baseline B⊥ of the interferogram);
- – the spatial distance of two arbitrary pixels P1 and P2 (within a single interferogram), in correspondence of which the interferometric phase is evaluated.
Differential interferometric phase terms and their behaviour as a function of time, acquisition geometry, and space
Tableau 1 Termes de la phase interférométrique différentielle et leur comportement en fonction du temps, de la géométrie d’acquisition et de l’espace
| Parameter/ Phase term | Temporal baseline ΔT | Perpendicular baseline, B⊥ | Spatial distance P1–P2 |
| ϕtopo–res | Uncorrelated | Proportional | Variable |
| ϕdis | Strongly correlated | Uncorrelated | Variable |
| ϕa | Uncorrelated | Uncorrelated | Strongly correlated |
| ϕorb–res | Uncorrelated | Uncorrelated | Strongly correlated/2nd order relationship |
| ϕnoise | Uncorrelated | Uncorrelated | Uncorrelated |
The phase terms and the correlation properties gathered in Table 1 will be referred to in the forthcoming sections, while discussing the limits of DInSAR and possible strategies to overcome them.
3 Limitations
The main limitations in the detection of motion by means of the radar interferometry technique are linked to the loss of coherence with time, to the influence of atmospheric artefacts, the presence of uncompensated topography, and to instrumental limitations, such as the orbital cycle or the pixel size.
3.1 Loss of coherence
Two types of decorrelation prevent the reflectivity phase term from being perfectly cancelled out while generating (differential) interferograms, thereby contributing to the phase noise affecting the interferometric or differential interferometric phase [46]:
- • geometrical decorrelation, which is a consequence of the slightly different imaging geometries of the master and slave image. The value of the normal baseline B⊥ of the interferogram is, therefore, an index of the level of geometric decorrelation that affects the interferometric phase. A quantitative assessment and a very elegant spectral interpretation of the phenomenon are provided in [22];
- • temporal decorrelation: when the physical/geometrical nature of the soil changes in the time span between master and slave acquisitions (vegetation, water, ploughed field...), the reflectivity phase term also changes and is no longer cancelled by computing the phase difference for generating the interferogram.
The ‘coherence’ level is a normalised index reflecting the amount of reflectivity variation (both due to geometric and temporal decorrelations) – see Fig. 1.

Average coherence level for the city of Paris derived from all 87 interferograms with perpendicular baselines lower than 250 m and average coherence larger than 0.4, obtained using a set of 30 SAR images covering the period 29/04/1992 to 02/12/2000.Vegetated areas are characterised by low coherence values, i.e. by a temporally decorrelated phase signal (e.g., the Jardin des Tuileries in the very centre of the image and a small part of the Bois de Boulogne on the left), as well as the Seine River [30]. Masquer
Average coherence level for the city of Paris derived from all 87 interferograms with perpendicular baselines lower than 250 m and average coherence larger than 0.4, obtained using a set of 30 SAR images covering the period 29/04/1992 to 02/12/2000.Vegetated areas ... Lire la suite
Fig. 1. Moyenne d’images de cohérence sur la ville de Paris obtenue à partir de 87 interférogrammes ayant des composantes perpendiculaires d’écarts orbitaux inférieurs à 250 m et une cohérence moyenne de plus de 0,4, issus d’un jeu de 30 images RSO couvrant la période 29/04/1992–02/12/2000. Les zones végétalisées sont caractérisées par une faible cohérence, c’est-à-dire par un signal de phase décorrélé dans le temps (par exemple, le jardin des Tuileries au centre de l’image et une partie du bois de Boulogne, à gauche de l’image), ainsi que la Seine [30]. Masquer
Fig. 1. Moyenne d’images de cohérence sur la ville de Paris obtenue à partir de 87 interférogrammes ayant des composantes perpendiculaires d’écarts orbitaux inférieurs à 250 m et une cohérence moyenne de plus de 0,4, issus d’un jeu de 30 images ... Lire la suite
Coherence maps can, therefore, be used as indicators of changes (such as forest damages after a storm or city destruction after an earthquake [19]) or to obtain information on ground characteristics (as land use information or ice typology [42]). Of course, for this kind of applications, low normal baseline pairs are used, so that geometric decorrelation is negligible and the coherence map entirely reflects the reflectivity variations of the ground.
A loss of coherence between two acquisitions corresponds to a dominating term ϕnoise in Eqs. (1) and (5). This hampers the identification of the other phase terms, in particular of topography and LOS deformation.
When the purpose is motion detection, in order to mitigate the effects of a loss of coherence, it is necessary to select interferometric pairs having close orbital characteristics (i.e. a low perpendicular baseline), so as to minimise the variation of the reflectivity phase term with geometry. If possible, it is useful to select pairs of images separated by a short time interval to try to minimise also the impact of temporal decorrelation. Short time spans are particularly necessary whenever the scattering characteristics of the observed areas are changing rapidly (like with agricultural fields). Of course, this implies that on areas affected by temporal decorrelation, a long-term systematic monitoring (e.g., several years) is not feasible, and slowly evolving (e.g., in the order of a few mm/yr) deformation phenomena can hardly be detected.
On the contrary, urban areas are particularly suitable for interferometry aimed at deformation measurement, due to the stability of the urban reflectors. Interferometric combinations covering as much as ten years can be computed without suffering from a significant loss of temporal coherence.
3.2 Atmospheric artefacts
Fluctuations within the tropospheric and ionospheric layers between the two acquisitions induce subtle phase variations, which can be misinterpreted as ground-deformation signatures [24,31]. The variogram of the tropospheric contribution, often dominating the ionospheric and vertical stratification contributions, can be described with a Kolmogorov model [26,44], highlighting a strong spatial correlation that can be rather similar to the one of subsidence bowls induced, e.g., by water or oil/gas extraction.
Atmospheric artefacts can be as high as one fringe (i.e. a full phase cycle) on a few kilometres. Since the level of atmospheric phase distortion depends strongly on the meteorological conditions (with winter images being less affected than summer images) as well as on the topography of the sites (isolated mountains overhanging the surrounding area, as often do volcanoes, are particularly affected), it is not possible to provide figures of general validity.
In conventional differential interferometry, the comparison between several independent interferograms (not sharing a common image) can be used to discriminate between ground deformations and atmospheric artefacts. Indeed, atmospheric structures are uncorrelated in time (and therefore the corresponding phase term varies from one image to the other), whereas ground deformations are spatially at the same location [47]. Of course, the various interferograms involved should, as far as possible, span similar temporal intervals so as to ensure that approximately the same LOS deformation is recorded in each interferogram. In alternative, assuming a constant LOS deformation rate (or any other deformation model), the phases of one (or more) interferogram(s) can be scaled with the ratio of the time spans so as to render them comparable with the phase of a reference interferogram. This last approach works only as long as the assumed model manages to provide a proper description of the occurring deformation.
3.3 Residual orbital component and uncompensated topography
A residual contribution (ϕorb–res), due to insufficient accuracy of the orbital information, affects the phase measurements. This term is composed by a flat-Earth-like component and by a further component depending on the topography. This latter is negligible unless the orbital data are highly imprecise (errors in the order of metres) and the imaged area includes high mountains (thousands of metres). For ESA ERS-1/2 data, the flat-Earth-like component of ϕorb–res can usually be assumed as quadratic with the distance among any couple of pixels considered within a full ERS scene interferogram, i.e. 100 × 100 km2 [26]. This behaviour allows one to correct the effect by estimating and removing a low-order phase polynomial from a differential interferogram. Of course, this implies separating low-spatial-frequency components from the other phase terms (e.g., from possible LOS deformation), and discarding them.
On the other hand, the magnitude of topographically related phase errors is a function of the quality of the DEM, of the precision with which the DEM is co-registered onto the interferograms, and of the separation between the satellite orbits (the perpendicular baseline |B⊥|).
Eqs. (3) and (4) allow one to evaluate the impact of residual topography depending on the perpendicular baseline. For ERS-1/2 data, given |B⊥| = 20 m, a DEM error of 50 m results in a negligible phase shift of 38°, whereas with |B⊥| = 700 m a DEM error of 15 m (i.e. a just four floor tall building) causes a full phase cycle.
3.4 Other instrumental limitations
3.4.1 Orbital cycle
The orbital cycle of existing satellites is 35 days (ERS and ENVISAT) and 24 days for Radarsat. The temporal spacing between successive acquisitions is, therefore, in the order of a couple of tens of days and cannot be selected freely, depending on the characteristics of the phenomenon to be monitored.
3.4.2 Deformation gradient
The modulo-2π (modulo-λ/2) ambiguity of displacement data can be solved via 2D spatial phase unwrapping. However, the sampling theorem states that it is impossible to solve unambiguously a phase gradient (and therefore a differential movement between two adjacent pixels), which is bigger than half a fringe per pixel, which corresponds to ∼1.5 cm/20 m for vertical movements with ERS data. The practical threshold is actually lower, since the signal is affected by noise.
3.4.3 Pixel size
For ERS satellites, the initial size of the resolution sampling cell is 4 × 20 m (which is usually transformed in 25 × 25 m after geocoding).
3.4.4 Archive
The data in the ERS archive start in the spring of 1992, with one image every 35 days and a gap during year 1994. Deformations older than 1992 cannot be derived.
As already mentioned, only the projection of the deformation vector along the line of sight of the satellite can be obtained by InSAR. In particular, given that the ERS incidence angle i = 23°, the system is very sensitive to vertical deformation. Therefore, whenever the deformation occurs mainly or exclusively in the vertical direction (e.g., in many cases of subsidence), this limit does not really penalise the performances of differential interferometry. Conversely, this can be problematic when 2D (e.g., to assess the rotational or translational character of a slowly evolving landslide) or 3D deformation data (e.g., for characterising the displacement dynamics across a seismic fault) are required. It is worthwhile mentioning that, if both ascending and descending datasets can be used, it is possible to obtain a second component of the deformation vector.
In order to reduce these drawbacks, different approaches can be used depending on the limiting aspect to be overcome and on the SAR data available. In the following sections, we show some examples:
4 Use of L-band interferometry in areas with vegetated land cover
To address the issue of the poor coherence where the land cover is characterised by vegetation or agricultural fields, the use of L-band data (as produced by the JERS-1 satellite until 1998 and now by the PALSAR sensor of the ALOS satellite) can be a valuable alternative.
The L-band signal penetrates deeper into the vegetation cover than the C-band one. Even over vegetated areas, a remarkable part of the backscattered L-band echo arrives from the ground, rather than from the vegetation. The L-band signal is, therefore, much less sensitive to the temporal decorrelation due to changes in the vegetation cover (e.g., with the seasons). These considerations agree with the observations by Strozzi et al. [40], who reported higher coherence in L-band over non-urban imaged areas.
On the other hand, because of its wavelength of about 23 cm, the phase is less sensitive to the deformation according to Eq. (2) (one fringe corresponds to about 11.5 cm instead of the 2.8 cm of ERS). Without specific processing (such as multi-interferograms approaches), L-band interferograms are, therefore, well suited for the detection of LOS deformations in the order of decimetres, while C-band serves best for LOS deformations of a few centimetres.
4.1 Mining subsidence in Lorraine (France)
The following example concerns the application of conventional SAR interferometry in the coal-mining basin of Lorraine (France), in the area of the cities of Forbach and Merlebach up to Saarbrücken (Germany). Subsidence is due to the mine exploitation and post-mining consequences. The test area is covered both by forests and by urban settlements. The deformation was assessed by C-band (ERS-1 data) and L-band (JERS-1 data). The following figures show the most relevant interferograms for assessing the occurring ground deformation.
On this example, we can observe that L-band interferometry is more suitable to the local context (fast deformation and vegetation cover) than C-band interferometry (Figs. 2 and 3). In this case, L-band data provided a good coherence even on a 1-year interferogram on areas where the two-month ERS-1 interferogram failed because of the forest and agricultural cover. The images were acquired during different months for the two interferograms, and of course, we could object that the difference in coherence could be due to this difference in acquisition dates. Due to the small amount of available JERS-1 data (the shown example is the only one available for the period of interest), a direct comparison is not really possible. However, on the vegetated areas, the presented interferogram has a better coherence than the interferograms (excepted 1-day interferograms, called Tandem interferograms) derived from the set of 15 ERS SAR images used previously.
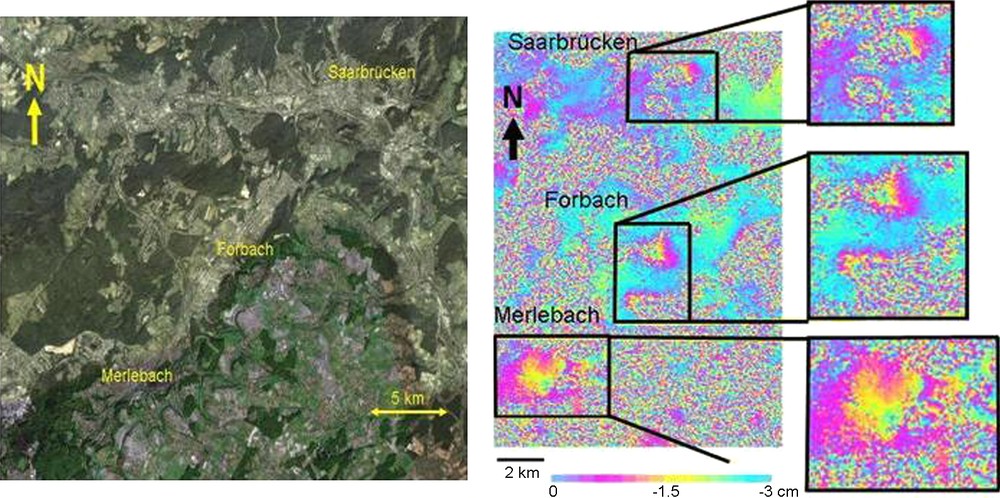
ERS-1 interferogram on the mining area of Lorraine and location of the site on a LandSat image. Acquisition dates: 14/06/1993 and 23/08/1993 (i.e. two-month time span). One fringe ∼ 3 cm of vertical deformation. Detected subsidence bowls are shown.
Fig. 2. Interférogramme ERS-1 sur une zone minière en Lorraine et image LandSat. Dates d’acquisition ERS-1 : 14/06/1993 and 23/08/1993 (c’est-à-dire des intervalles de temps de deux mois). Une frange ∼ 3 cm de déformation verticale. Les cuvettes d’affaissement détectées sont indiquées.
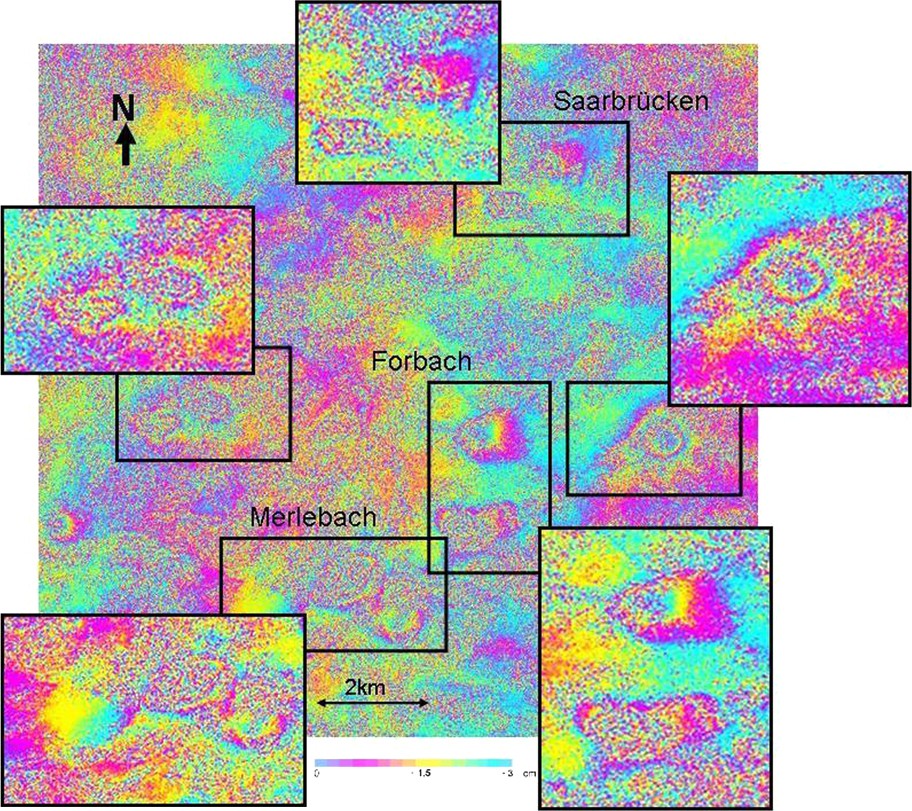
JERS-1 interferogram on the mining area of Lorraine. Acquisition dates 24/03/1993 and 11/03/1994 (i.e. one-year time span). One fringe ∼ 11.5 cm of vertical deformation. Additional subsidence bowls, undetected in Fig. 2, can be appreciated.
Fig. 3. Interférogramme JERS-1 sur la zone minière de Lorraine. Dates d’acquisition : 24/03/1993 et 11/03/1994 (c’est-à-dire un intervalle de temps d’un an). Une frange ∼ 11,5 cm de déformation verticale. Des cuvettes de subsidence non détectées sur la Fig. 2 sont indiquées.
L-band interferometry is, therefore, particularly interesting as a complementary tool to the widely used C-band interferometry.
5 Integration of a selection of interferograms
An alternative allowing one to enhance the performance of conventional interferometry consists in combining several interferograms. The possibilities that can be considered are:
- • summing several interferograms covering similar time spans;
- • estimating average LOS deformation rates from an interferogram;
- • deriving the full evolution of LOS deformation by a least-square optimisation.
Such approaches were proposed by Usai et al. [43] or Le Mouélic et al. [30].
The selection of interferograms can be made using quantitative criteria as the average coherence, the spatial and temporal baselines level, but a visual examination of the interferograms is generally very useful. A critical visual inspection allows one to remove promptly the interferograms affected by high decorrelation and by strong atmospheric artefacts (the comparison with other interferograms covering approximately the same time span allows one to identify spurious atmospheric fringe patterns appearing in a single interferogram).
5.1 Time uniform (linear) LOS deformation
Rather often, the deformation is well described by a single parameter, namely the average LOS velocity. Unwrapping the interferograms, converting them into deformation maps and merging the maps allows one to provide a unique velocity map relative to the period covered by the interferograms. Combining deformation data from a set of interferograms, the impact of the atmospheric artefacts can be reduced [47], since the atmospheric artefacts superimposed on the interferograms are uncorrelated.
In [30], we propose to use the following standard estimator for merging the deformation information into an average LOS velocity estimate (the expression leads a more robust estimate than a simple arithmetic mean of velocities obtained from each interferometric pair):
| (7) |
Fig. 4 shows the velocity map derived from the SAR information of the city of Paris. It highlights deformation effects on the Grand Palais and Montmartre areas. The phenomenon observed in Montmartre is related to old gypsum quarries, whereas the deformation is probably due to settlement of alluvia in the Grand Palais area.
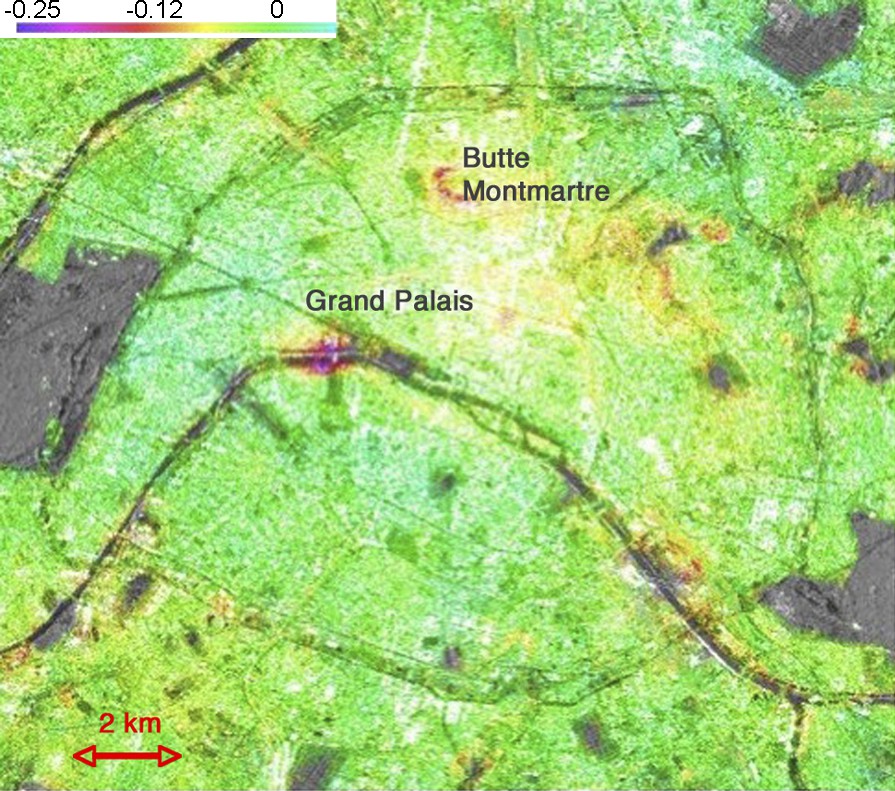
Example of the city of Paris. Assessed velocity on the period 1992–2000 using 30 SAR images. LOS deformation rates smaller than 1 mm/yr can be observed.
Fig. 4. Exemple sur la ville de Paris. Vitesse de déformation en ligne de visée estimée sur la période 1992–2000 à partir de 30 images RSO. Des déformations plus petites que 1 mm/an peuvent être observées.
5.2 Sudden deformation
The case of a sudden deformation taking place within a short period of time (i.e. shorter that the revisiting time) is also very interesting. Of course, in this case, the deformation is a non-linear function of time. A simple and effective description consists in locating the event in time and providing the total amount of deformation that occurred.
The visual interpretation of the set of interferograms helps locating temporally such a deformation. The linear combination of different unwrapped or wrapped interferograms [29,41] allows one to enhance the ratio between the deformation component and the atmospheric distortion. When using wrapped data, the phase noise adds up and therefore limits the number of usable interferograms. The LOS deformation value corresponding to one fringe (i.e. a full 2π-phase cycle) is of course reduced. Fig. 5 shows an example of well-known deformation [20,29] near the Gare Saint-Lazare (Paris) and related to underground works (subway construction).
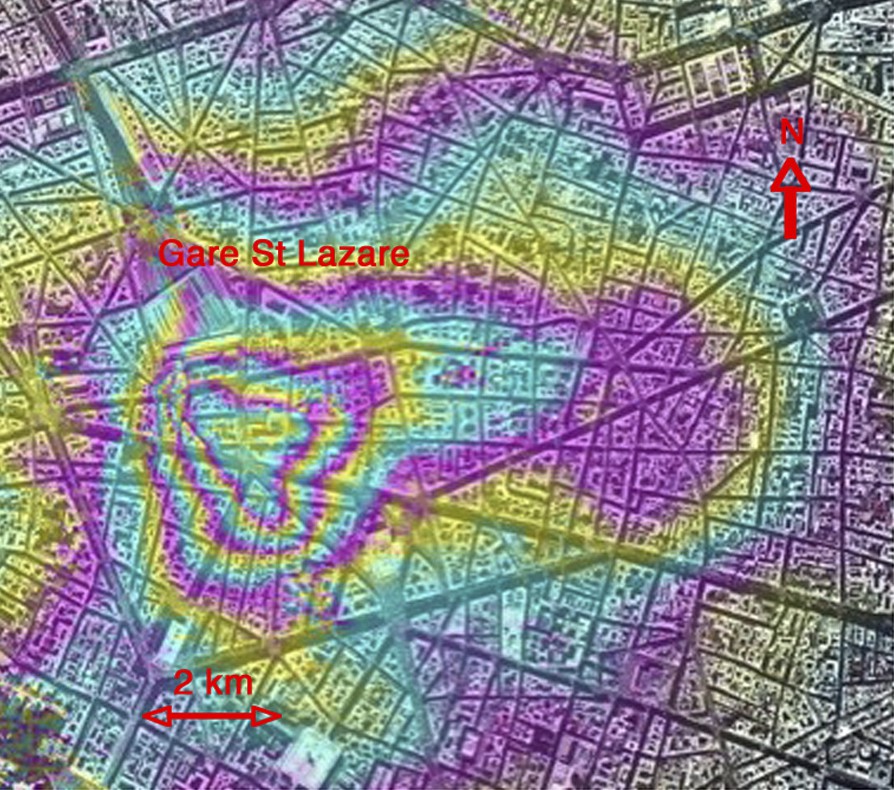
Example of the sum of five interferograms (one fringe corresponds to 3 mm) in the area of the Gare Saint-Lazare, affected by a 1.5-cm uplift during the summer of 1998 [29].
Fig. 5. Somme de cinq interférogrammes (sur la figure, 1 frange correspond à 3 mm) sur le secteur de la Gare Saint-Lazare, affecté par un soulèvement de 1,5 cm durant l’été 1998 [29].
5.3 Derivation of a temporal evolution of the deformation
By carrying out a least-square inversion [30,43] on the set of unwrapped interferograms, the sequence of the ground level motion with respect to the first acquisition date can be derived. Fig. 6 shows the result of the application of the procedure. In addition, low-pass filtering in time can be applied in order to reduce the atmospheric effects. As a matter of fact, the temporal high-frequency terms of atmosphere and decorrelation noise (both uncorrelated in time and, therefore, including high-frequency components in their temporal spectrum) are suppressed in this way. It should, however, be kept in mind that high temporal frequency components of the deformation pattern (e.g., the displacement due to a sudden collapse) are also suppressed, thereby smoothing the temporal evolution of the deformation.
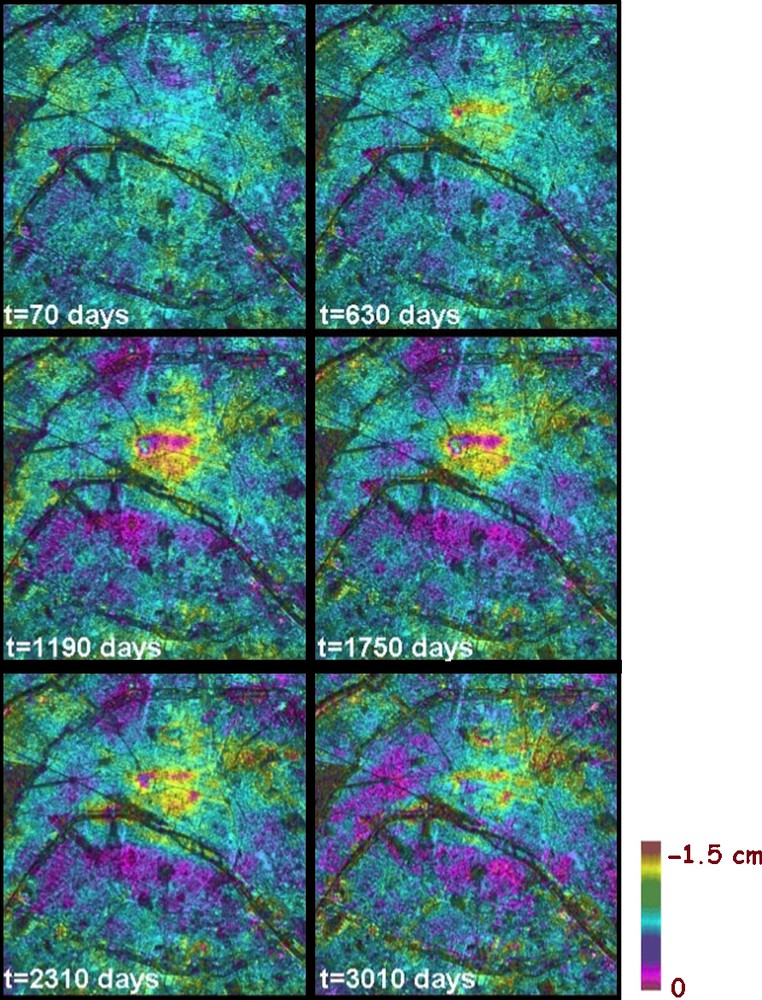
Set of representative phase screens (with respect to 3 June 1992) obtained after the least-square inversion and the temporal Lee filtering [28] performed on five dates. One cycle of colour represents a vertical deformation of 1.5 cm in these images. The mean amplitude image has been used as background [30].
Fig. 6. Ensemble d’images de phase significatives (la référence est le 03/06/1992) obtenues après inversion par moindres carrés et filtrage de Lee temporel [28] effectué sur cinq dates. Un cycle de couleur représente une déformation verticale de 1,5 cm. L’image d’amplitude moyenne apparaît en fond [30].
6 The Permanent Scatterers’ technique
6.1 Core ideas and hypotheses
The Permanent Scatterers’ technique, developed at the ‘Politecnico di Milano’ (Milan, Italy), is the first of a family of similar advanced interferometry techniques, presently known as Persistent Scatterers’ techniques.
The following core issues need to be tackled in order to address more effectively the drawbacks discussed in Section 3:
- (i) isolating the atmospheric contribution to the interferometric phase;
- (ii) coping with temporal and geometric decorrelation. As already mentioned, these phenomena are respectively due to the variability with time and with the acquisition geometry of the electromagnetic phase signature of each SAR image pixel, and result in a random noisy contribution to its interferometric phase.
A pixel-by-pixel analysis is carried out on a set of N > 10–15 SAR images in order to isolate the elementary contributions – listed in Eq. (6) – to the differential interferometric phase of individual image pixels.
Exploiting their different behaviour (see Table 1), the phase terms (in particular the LOS ground deformation) can be separated on a pixel-by-pixel basis. Details about how the processing is exactly carried out are provided in [7,8,14–15].
Of course, a first requirement for the approach to work is that the phase noise contribution (uncorrelated in all dimensions) of the image pixels under examination is not the dominating phase term.
Given N images, a set of N–1 differential interferograms is generated with respect to a single master. High temporal and normal baseline interferograms (affected by a high decorrelation noise) are, thus, part of the dataset. The approach has consequently to be focused on privileged image pixels that, even in these ‘extreme conditions’, still exhibit a low noise term (e.g., with a standard deviation σϕ < 0.66 rad).
Such a stringent condition is met by radar targets:
- (i) whose scattering contribution is well above the sum of the terms from all other objects within the same resolution cell;
- (ii) whose geometric extension amounts to a small fraction of a resolution cell.
These are the so-called Permanent Scatterers (PS), usually corresponding to parts of manmade structures or rocky outcrops.
As a second requirement, a minimum PS density (>3–4 PS/km2) is necessary in order to guarantee a sufficient spatial sampling to exploit the spatial correlation and isolate the atmospheric (and orbital error) phase terms.
In urban areas, the PS spatial density is in the order of several hundreds of benchmarks per square kilometres (up to more than 1000 PS/km2), thereby providing a fully unprecedented density of measurement points.
In non-urban areas, the PS density can exhibit very different values: in the typical Western European countryside and mountainous valleys, its value is usually in the order of a few tens (e.g., 10–50) PS/km2. However, in densely vegetated areas, in absence of individual exposed rocks and isolated manmade structures, the PS density drops to zero and the analysis becomes locally unfeasible.
The same happens on a wider scale in fully non-urbanised environments such as forests, rain forests, prairies, savannahs, etc.
Conversely, as long as the terrain conformation is characterised by scattered rocky outcrops, a PS analysis is usually feasible, and can lead to high benchmark densities (>100 PS/km2), even in total absence of manmade structures [12].
In practice, Permanent Scatterers can be thought of as ‘natural’ benchmarks (i.e. not deployed ad hoc) of a high spatial density geodetic network (in analogy with conventional GPS and/or optical levelling networks).
6.2 Output products
The main output results available for each individual PS are [8]:
- (i) a submetric precision (0.1 < σh < 1 m) estimate of the exact height of the object corresponding to the PS. This by-product (of the isolation of the residual topography interferometric phase term) is of crucial importance, since it allows one to geocode the position of individual PS with a precision well within 10 m. Permanent Scatterers can, therefore, be mapped on the corresponding structures. Single-building monitoring by means of interferometry becomes possible;
- (ii) the average LOS displacement rate of single PS is evaluated with a precision in the order of σv,LOS = 0.1–0.5 mm/yr;
- (iii) the whole LOS displacement time series of individual PS (as a function of time) is reconstructed. The precision on each measurement of the series amounts to σδ,LOS = 1 to 3 mm.
It is worth remarking that the precision figures supplied are achievable, provided that the atmospheric phase term is correctly estimated and removed.
The PS technique has been developed and used mostly on ESA ERS-1/2 data. Results have been obtained also on Radarsat [9] and JERS datasets [11,23]. Moreover, first results of coherent ERS-ENVISAT PS interferometry (sharing a unique ERS master) have also been already reported [2].
The PS approach provided precious results in a wide set of different scenarios: urban subsidence both affecting wide areas (e.g., [14]) and localised (e.g., [5]), creeping along active seismic faults (e.g., [7,8,17]), slope instability and/or failure (e.g., [8,27]), mining subsidence (e.g., [10]).
6.3 Potentials and limits
Having reviewed the basic ideas behind the PS approach as well as its output products, we can try to highlight its major advantages and limits.
6.3.1 Main advantages
- • No need to set up and maintain a network of benchmarks.
- • Whenever a SAR data archive is available (e.g., the ESA ERS-1/2 archive gathering images acquired over the whole world since early 1992), the investigation of past deformation phenomena is feasible (very relevant for responsibility assessment in case of litigations [16] and for studying precursors of critical events, e.g., collapses [10]).
- • Each result can be provided with reliability and precision figures, taking into account all terms contributing to the interferometric phase of each PS (e.g., the single-pixel multi-interferogram coherence [7,14]). A correct use and understanding of the results by technicians not having a direct expertise in interferometry is significantly simplified.
- • Suitability and unprecedented cost effectiveness for application at once on a wide-area basis (hundreds to thousands of square kilometres, like conventional interferometry) and on localised areas for investigating single-building effects (PS geocoding precision).
- • Millimetric precision coupled with regular revisiting (35 days for ERS, 24 for Radarsat).
- • Isolated PS, even if fully surrounded by incoherent pixels (e.g., single building or outcrop in a forest area), provide deformation data, as all other PS, since no spatial averaging is carried out. (As already mentioned, even though individual PS can be fully isolated, a local minimal PS density is necessary). This is a major advantage with respect to conventional interferometry, especially for non-urban monitoring applications.
6.3.2 Main limits and possible ways to tackle them
- • Displacement data represent the LOS projection of a deformation that can actually occur in all three dimensions. This limit can be at least partially circumvented by merging results from PS analyses carried out on distinct datasets (e.g., parallel tracks and ascending-descending datasets acquired by the same sensor as well as datasets from different platforms) [38]. Of course, this requires mapping PS grids independent of each other, taking also into account the fact that, most likely, different parts of the same object (e.g., building) behave as PS for different acquisition geometries and/or sensors [6,9].
- • The ambiguity of phase measurements implies the impossibility to track correctly and unambiguously a single PS LOS deformation exceeding λ/4 (= 1.4 cm for ERS) within one revisiting time interval (35 days for ERS). In practice, due to the presence of noise, more than 1 cm in 35 days (24 days for Radarsat) can hardly be interpreted correctly for deformation phenomena affecting single building. This limit is posed by the sampling theorem and can be overcome in two ways: (a) exploiting the possible spatial correlation of the ground deformation phenomenon at hand (as hinted in [10]) and/or (b) carrying out more than a single PS analysis involving SAR data acquired at different frequencies. For instance, L-band JERS data have a wavelength such as λ/4 = 5.9 cm and a revisiting time of 44 days. (Of course, as already mentioned, this implies also that the precision of JERS PS measurements is about four times worse than the one of ERS PS). Carrying out a PS analysis on both ERS and JERS datasets and merging the (geocoded) results allows one to profit at once from the reduced JERS sensitivity to phase ambiguity problems and of the higher precision of ERS PS measurements.
- • Limited versatility in terms of (a) position of the measurement points and (b) revisiting time. Both parameters (a) and (b) cannot be optimised as degrees of freedom while planning an analysis. Nevertheless, in correspondence with ‘strategic’ structures of particularly high importance, artificial corner or planar reflectors can be deployed ad hoc, so as to create additional ‘artificial’ PS (obviously, this has a high cost and implies that, for these artificial PS, the past archive cannot be exploited). Once more, the constraint on the revisiting time can be partially relaxed by merging results from PS analyses carried out on distinct datasets.
- • Despite the high geocoding precision, it is often unclear which part of a structure actually corresponds to a PS. This could become a limiting factor whenever it is important to discriminate the possible deformation of a building from the possible deformation of the ground surrounding it. The problem can often be solved, since the precision of the elevation estimate at PS generally allows one to discriminate PS corresponding to objects on the ground (e.g., a metallic pole, or the dihedral surface ground-wall of a building) from PS corresponding to features on the roof or on upper floors of a building. Furthermore, in this respect, it is worthwhile mentioning an ongoing research activity aiming at the systematic classification of individual PS into different typologies (e.g., mirror-like or trihedral, dihedral, pole-like, resonating structure, etc.). This is achieved by combining data acquired from different geometries, polarisations, and platforms. Remarkable results of PS classification in urban areas have already been reported [18,34].
6.4 Example – Paris, Grand Palais
The shown results are taken from a PS analysis carried out by TRE on Paris (18 × 18 km2) within the project Copeesat funded by ESA (ESRIN/Contract No. 16564/02/LG). Seventy-five ERS-1/2 images covering the time span April 1995 to January 2003 have been involved (Track 466, Frame 2691, Mode descending). The spatial density of PS guaranteeing a σδ,LOS ≤ 3 mm exceeds 300 PS/km2. (This threshold on σδ,LOS is rather conservative, suitable if the purpose is the extraction of high-precision LOS deformation time series. If the target is only the detection of reliable LOS velocities, looser constraints can be set – see false alarm probability, discussed in [7] – resulting in a very high PS density in the order of 2000 PS/km2).
Fig. 7 displays PS positions and (colour-coded) average LOS velocities relative to a 1.5 × 1.5 km2 area in the heart of the historical centre of Paris. PS results are superimposed on a 1-m-resolution orthorectified aerial photography.
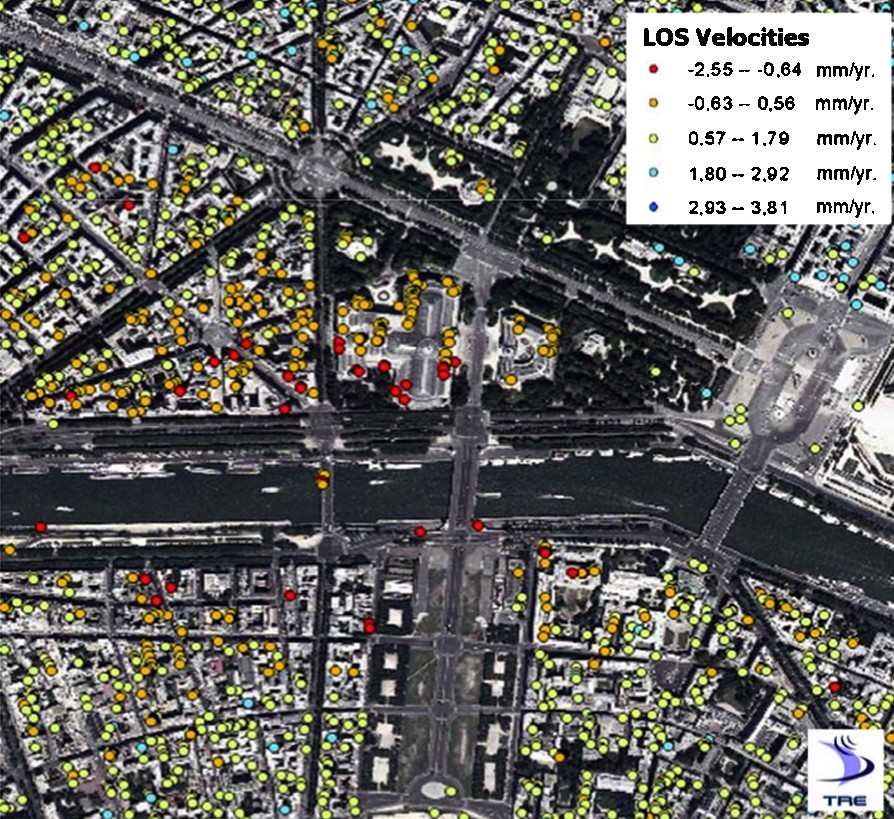
Position and average LOS displacement rate of Permanent Scatterers superimposed on a 1-m resolution orthorectified aerial photography of the area around the Grand Palais, in the city centre of Paris. The image covers approximately 1.5 × 1.5 km2.
Fig. 7. Position et vitesse de déplacement en ligne de visée de diffuseurs permanents (ou PS), superposées à une image aérienne orthorectifiée de 1 m de résolution autour du Grand Palais à Paris. L’image couvre environ 1,5 × 1,5 km2.
The velocities are relative to a PS chosen as reference and supposed motionless, located in the Place de la Nation, a few kilometres towards the east.
The precision of the PS georeferencing, allowing one to map the PS positions on the corresponding buildings, can be appreciated (see also Fig. 8). Slow-evolving ground-deformation phenomena have been identified in the area along the Seine River between the Place de la Concorde and the Place de l’Alma. Particularly interesting is the case of the Grand Palais (see close-up in Fig. 8). The PS results allow one to appreciate clearly a differential subsidence phenomenon affecting it: the northern wing is substantially stable, whereas the southern wing subsides with an average LOS deformation rate exceeding 2 mm/yr. Complete time series of two PS, within a 130-m distance from each other, are reported in Fig. 8.
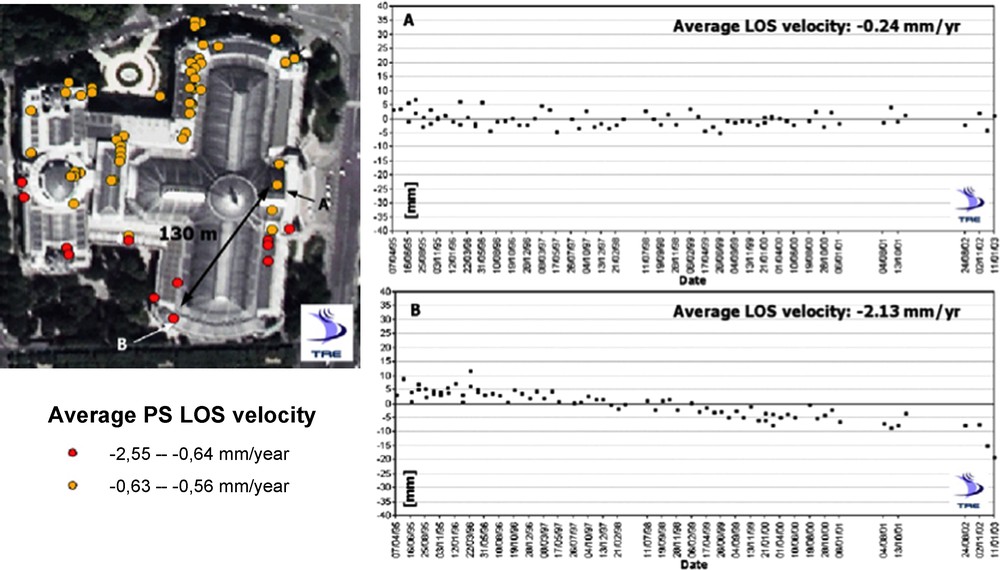
Close-up on the Grand Palais. The southern wing subsides with a rate of 2 mm/yr, whereas the northern wing is stable. Demonstrative LOS displacement time series of two PS (A and B) are reported.
Fig. 8. Agrandissement sur le Grand Palais. L’aile sud subside à un taux de 2 mm/an, tandis que l’aile nord est stable. Les séries temporelles de la déformation en ligne de visée de 2 PS significatifs (A et B) sont montrées.
Several isolated PS, corresponding to structures fully surrounded by incoherent vegetation, can also be recognised along the Avenue des Champs-Élysées (Fig. 8).
7 Conclusion
We have reviewed the basic principles of spaceborne SAR interferometry techniques, pointing out their advantages and limits. When used to track deformation phenomena with favourable characteristics (velocities from a few mm/yr to several dm/yr on spatial scales compatible with the resolution of the used sensors) and in suitable land use contexts, these technologies can provide valuable information that often cannot be accessed by other means (past ‘history’ of the deformation, spatial density of the measurements). For these reasons, InSAR techniques are well suited for complementing and enriching existent ground-based monitoring networks.
Application examples in the field of mining and urban subsidence showed the large spectrum of possible applications of InSAR techniques to ground-deformation assessment.
Acknowledgements
The results illustrating this paper have been obtained in the frame of the project RESUM (‘Réseau de suivi de subsidence urbaine et minière par interférometrie radar’), supported by the ‘Ministère délégué à la Recherche’, by the CNES (‘Centre national d’études spatiales’) and the Research Division of BRGM (France), the project Copeesat (Coherent Observation of PS with ERS and ENVISAT), funded by ESA (ESRIN/Contract No. 16564/02/LG) and within ESA-ESRIN contract No. 13557/99/I-DC. C. Colesanti gratefully acknowledges all the colleagues and friends working at Polimi and TRE – especially Dr. A. Ferretti – for the fruitful work carried out together. D. Raucoules and C. Carnec acknowledge Dr. S. Le Mouélic for the work carried out for the production of the conventional InSAR examples shown in this paper.



Vous devez vous connecter pour continuer.
S'authentifier