Abridged English version
Recent major floods in the French Mediterranean region prompted us to investigate if they are the consequence of a climate change. This study examined changes in monthly and annual maximum series from 92 precipitation gauges in the French Mediterranean region. Each station provided a minimum of 56 years of daily measurements. Missing data do not exceed 2% of the series. As the studied domain is not homogeneous from a climatic point of view, the stations were classified in homogeneous climatic zones by the method of the ascending hierarchical classification of Ward [15]. Seven zones were retained (Fig. 1). For each homogeneous region, the studied regional variables are the intensity and the occurrence of extreme events. The sampling threshold is arbitrary, it is chosen among the 0.99-quantiles of precipitation series forming the studied zone. The sensitivity of the test to the threshold choice was tested.
A peak-over-threshold series can be considered as a sample of the POT model if the series of occurrences is a Poisson process, and if the intensities of extremes follow a Generalized Pareto Distribution (GPD). Both processes (Poisson and GPD) are independent [13]. For the study of a possible trend, we use the POT model while supposing that the intensity of the Poisson law and the scale parameter of the GPD depend linearly on time. Then the likelihood ratio test [2] allows us to choose the best model (stationary or trend) and thus to determine the behaviour of the series. Then, the Fisher information matrices of both processes were analytically calculated in the stationary and non-stationary cases (Table 1), in order to define the confidence regions of the maximum-likelihood estimates (Figs. 2 and 3).
Table 2 presents the results of the POT methodology applied to each of the 14 regional variables (two variables per zone). The only significant results concern an increase of the occurrence and intensity of extreme daily rains in the North of the Lozère ‘departement’ and the southern part of the Auvergne, and an increase of the intensity of extreme rainfalls in Languedoc-Roussillon. Then, the precipitation quantiles were calculated at the beginning of the series, then at the end, at the term of the detected linear trends (Table 3). In zone 2, quantiles of frequency 0.90, 0.95, and 0.99 increase respectively of 14%, 16%, and 20%, and in zone 4 of 22%, 25%, and 31%. However, it is necessary to interpret with caution the evolution of these quantiles, because they depend on the persistence of the trend in the future, and also on the hypothesis made on the shape of the trend (linear).
An analysis of the meteorological factors at the origin of these non-stationarities must be led in parallel. Finally, we shall also note that only extreme daily precipitations were studied, because they are the longest series. It is however possible that a non-stationarity affects extreme events at timescales of less than 24 h.
1 Introduction
Parallèlement au contexte de changement climatique global, la vulnérabilité face aux événements hydrologiques extrêmes est en constante augmentation, notamment en France. Une urbanisation mal maîtrisée a conduit la population à être de plus en plus exposée au risque d’inondation. En outre, la surmédiatisation de tels événements au cours de ces dernières années, comme les inondations de novembre 1999 dans l’Aude [1,9] ou de septembre 2002 dans le Gard [10], a conduit à la perception d’une recrudescence des événements extrêmes. Cependant, si l’effet du changement climatique sur les températures maximales est avéré [3], son impact sur le régime des pluies extrêmes n’est pas établi. Ainsi, détecte-t-on une évolution des précipitations extrêmes depuis ces dernières années ? Un tel changement, s’il a lieu, ne peut être localisé en un point et a obligatoirement eu un impact à l’échelle régionale. C’est pourquoi une étude locale est limitée. Par exemple, si l’on détecte, à l’aide d’un test statistique local au risque 5 %, cinq stations non stationnaires sur 100 testées, est-ce le fait du hasard, ou peut-on l’interpréter comme une instationnarité significative ? Une approche régionale semble plus adaptée [14] à cette problématique. Pour contourner le problème lié à l’aspect multivarié de toute analyse régionale, une solution consiste à se ramener au cas univarié en calculant des variables définies régionalement. Le travail exposé ici porte sur une nouvelle adaptation du modèle Peaks Over Threshold (POT)[11] à la recherche d’instationnarité dans les séries. On se focalise ici sur la recherche d’une tendance linéaire, en raison de sa facilité de mise en œuvre. Pour cela, on considère le paramètre d’échelle du modèle comme dépendant du temps : le modèle non stationnaire ainsi créé est opposé au modèle stationnaire par le test de déviance statistique [2]. Il est alors possible de rechercher des tendances régionales en étudiant la stationnarité des variables régionales « occurrence » et « intensité » des dépassements de seuil. Une fois le zonage climatique du domaine effectué, les éventuels changements dans des séries issues de 92 pluviomètres du pourtour méditerranéen français sont examinés. La méthodologie a été programmée et mise en œuvre à l’aide du logiciel Matlab [6].
2 Données
Nous disposons de 92 longues séries pluviométriques de la banque PLUVIO de Météo France. Chacune fournit au moins 56 ans de mesures journalières, et les données manquantes n’excèdent pas 2 % dans les séries. Les changements métrologiques ont été vérifiés : les tests de rupture de Pettitt et Buishand [4] ont été appliqués aux séries maximales annuelles. Les résultats ont été mis en parallèle avec les fiches descriptives des stations consultées auprès de Météo France. Aucun changement de ce type n’a été détecté. Cela s’explique par le fait que les tests de rupture de Pettitt et de Buishand ont la capacité de détecter des tendances, le test de Buishand étant même parfois plus puissant que certains tests de détection de tendance [4]. En effet, on a observé que les stations admettant une rupture présentent toutes une tendance statistiquement significative des maxima annuels, selon le test de Mann–Kendall [12]. Ensuite, le domaine d’étude n’étant pas homogène d’un point de vue climatique, les stations ont été classées en zones climatiques homogènes par la méthode de classification hiérarchique ascendante de Ward [15], où l’on a tenu compte de la saisonnalité des maxima mensuels, de l’occurrence des événements de part et d’autre de la vallée du Rhône, de l’altitude et de la saisonnalité des cumuls mensuels. Sept zones ont été retenues (Fig. 1).
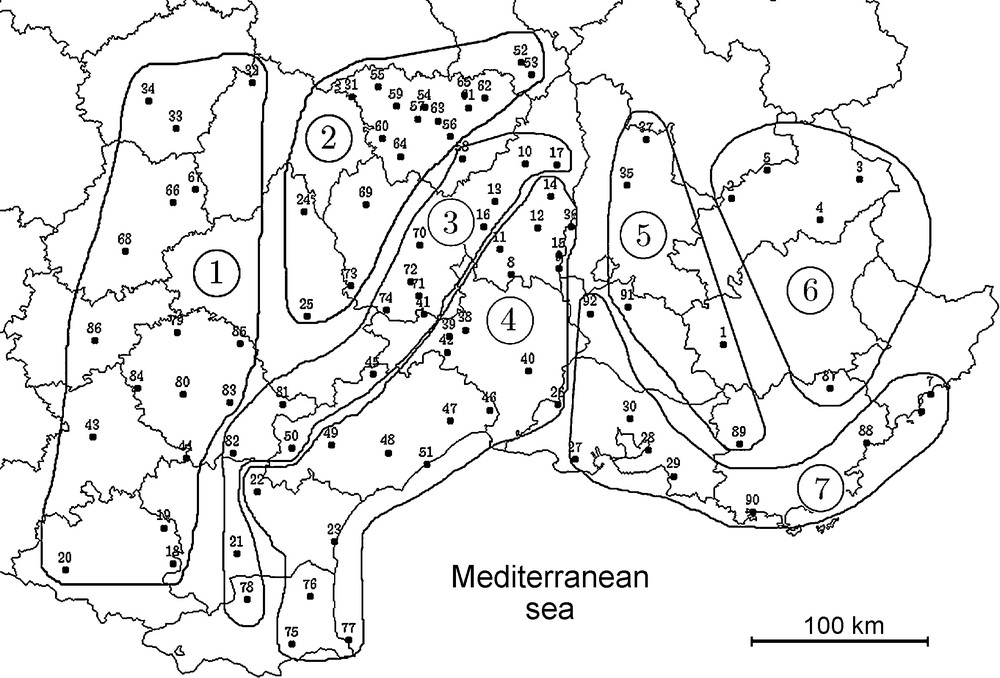
Localisation des stations (numérotées de 1 à 92) et des zones homogènes (numérotées de 1 à 7).
Fig. 1. Location of the stations (numbered from 1 to 92) and homogeneous zones (numbered from 1 to 7).
La dépendance spatiale entre les stations formant chaque région d’étude peut induire un biais dans le risque de première espèce des tests. En effet, il est très probable qu’un même événement pluvieux affecte plusieurs stations proches géographiquement. Il s’agit alors de ne pas considérer, dans l’analyse, plusieurs fois ce même événement, afin d’éviter toute redondance d’information. Un critère répondant à ce problème a donc été défini. Pour chaque région homogène, les variables régionales étudiées sont :
- • l’intensité des dépassements de seuil dans chaque zone d’étude. Lorsqu’ils ont lieu le même jour, on ne conserve que les événements distants d’au moins 60 km, afin de ne pas les compter plusieurs fois dans l’étude de stationnarité. Au-delà de cette distance, on peut admettre que les événements pluvieux journaliers sont indépendants [8] ;
- • l’occurrence des dépassements de seuil dans la zone d’étude.
On définit un seuil d’échantillonnage par zone. Nous le choisissons égal à la médiane des quantiles de pluies à 99 % des stations qui composent la zone étudiée, dans le but de ne retenir que des pluies extrêmes. Les seuils retenus pour les zones 1 à 7 sont respectivement, en millimètres, 42,4, 43,25, 83,55, 84,8, 57,1, 60 et 67,5.
3 Méthodologie
Dans toute la suite, on utilise les notations suivantes : (X1,…,Xn) représente la série des n événements pluvieux qui dépassent le seuil d’échantillonnage noté u (unités en mm). (t1,…,tn) représente la série des dates des événements, en jour. L’instant t = 1 correspond au premier jour de l’année civile du premier événement pluvieux X1, c’est-à-dire le 1er janvier de cette année-là, puis la date de chaque événement correspond alors au nombre de jours qui se sont écoulés depuis l’instant t = 0. On note N la variable occurrence des dépassements. Cette variable compte le nombre de dépassements ayant lieu sur un intervalle de temps [ti, tj] donné (1 ≤ i,j ≤ n). Par exemple, sur l’intervalle [0,365], N compte le nombre de dépassements de seuil ayant eu lieu la première année de mesure. A représente, en années, la longueur de la chronique, et L, en jours, la taille de chaque année de mesures. On note la vraisemblance du modèle POT et sa log-vraisemblance. Enfin, (X1,…,Xn) peut être considéré comme un échantillon du modèle POT si les hypothèses (H1), (H2) et (H3) qui suivent sont vérifiées. N suit une loi de Poisson non homogène d’intensité λ(t). La vraisemblance d’un processus de Poisson non homogène d’intensité λ dépendante du temps t ∈ [0,AL] est donnée par l’équation (1) [2]. Il en découle la log-vraisemblance (éq. (2)).Hypothèse (H1)
(1) (2)
Remarque : l’intensité du processus de Poisson représente ici un nombre moyen d’événements par jour. Notons que, dans le cadre de l’échantillonnage par valeurs supérieures à un seuil, il est fréquent de supposer que le nombre d’événements sélectionnés par unité de temps (l’année, en général) suit une loi de Poisson [5,13]. Les variables Xi sont indépendantes et identiquement distribuées suivant la loi de Pareto généralisée. La vraisemblance (éq. (3)) et la log-vraisemblance (éq. (4)) du processus sont données par [2] :Hypothèse (H2)
(3) (4)
Les paramètres σ et ξ sont respectivement les paramètres d’échelle et de forme de la GPD (Generalized Pareto Distribution). On note que, lorsque ξ = 0, la GPD est une loi exponentielle. Les processus (Xi)i=1…n et (ti)i=1…n sont indépendants [13]. Il découle de cette hypothèse que , et donc que .Hypothèse (H3)
Pour l’étude d’une éventuelle tendance, on utilise le modèle POT avec les paramètres λ et σ, qui sont des fonctions du temps. Nous nous focaliserons ici au cas tendance linéaire, avec les notations suivantes : λ(t) = λ0 + λ1t et σ(t) = σ0 + σ1t où λ0, σ0 > 0 et λ1, σ1 sont réels. En revanche, le paramètre ξ, qui caractérise la forme de la queue de distribution, est considéré stationnaire, du fait de la difficulté d’estimation de celui-ci, notamment en raison des incertitudes d’échantillonnage [14]. La log-vraisemblance totale du modèle POT devient alors :
| (5) |
Le test du rapport de vraisemblance maximale (RVM) [2] permet alors de choisir le meilleur modèle (stationnaire ou tendance) et donc de déterminer le comportement de la série. Ensuite, les matrices symétriques d’information de Fisher In (θ) des deux processus ont été calculées analytiquement dans les cas stationnaire et non stationnaire. Par souci de clarté, on ne définit dans le Tableau 1 que la partie triangulaire supérieure de chaque matrice, la partie triangulaire inférieure étant obtenue par symétrie.
Matrices d’information de Fisher des processus de Poisson et GPD, stationnaires et non stationnaires
Table 1 Fisher's information matrix of Poisson and GPD processes in stationary and non-stationary cases
| In (θ) | Stationnaire | Tendance linéaire |
| Poisson | n/λ2 | |
| GPD |
On rappelle que l’information de Fisher In (θ) évaluée en (l’estimateur de vraisemblance maximale – EVM – de dimension d), permet de définir une région de confiance RC1−α (θ) au risque α des estimateurs :
| (6) |
4 Application aux séries pluviométriques de l’arc Méditerranéen français
Le Tableau 2 suivant présente les résultats de la méthodologie POT appliquée à chacune des 14 variables régionales (deux variables par zone). Pour chaque zone, sont indiqués la taille de l’échantillon testé, le nombre moyen de dépassements de seuil par an, et le comportement des lois de Poisson et GPD, où les notations « stat » et « tend » signifient respectivement « stationnaire » et « tendance ». Dans le tableau, les cas de tendance correspondent aux cases grisées. Enfin, les EVM du meilleur modèle (stat ou tend) sont précisés. Le test RVM est réalisé au seuil de risque 5 %. Les changements détectés sont les suivants :
- • en zone 2, on observe une augmentation de l’occurrence et de l’intensité des dépassements de seuil. Ce résultat rejoint celui de Pujol et al. [12], qui soulignent la présence d’une augmentation significative régionalement, dans cette même zone, des cumuls et maxima annuels ;
- • en zone 4, on note une augmentation de l’intensité des dépassements de seuil.
Comportement des séries régionales de pluviométrie journalière de dépassement de seuil, et EVM des lois de Poisson et GPD (stat signifie stationnaire, et tend tendance linéaire)
Table 2 Behaviours of the regional peak-over-threshold series of daily precipitation, and maximum-likelihood estimators of the Poisson and GPD laws (stat means stationary, and tend linear trend)
Le choix du seuil du modèle POT est arbitraire, aussi a-t-on testé la sensibilité de ce seuil. Dans chacune des zones, nous avons créé quatre nouvelles séries de dépassements de seuil en abaissant et en augmentant les seuils de 10 % et 20 %. Le modèle POT a ensuite été appliqué à ces séries. Les changements précédemment détectés restent significatifs, pour des seuils de risque variant entre 1 % et 10 %. Il apparaît de plus que l’intensité des dépassements de seuil, en zone 3, n’est plus stationnaire.
Nous avons regardé les résultats du projet européen European Climate Assessment and Dataset [16], dans le cadre duquel ont été recherchées des tendances dans les extrêmes à l’échelle européenne. Aucun changement n’a été détecté sur le pourtour méditerranéen dans les pluies dépassant le seuil de 20 mm. Cela peut s’expliquer par le fait que le seuil de 20 mm, choisi pour toute la zone européenne correspond, dans cette région-là, à des pluies ordinaires et non à des pluies extrêmes.
Ensuite, les quantiles de pluie ont été calculés au début des chroniques, puis, enfin, au terme des tendances linéaires détectées (Tableau 3). En zone 2, les quantiles à 90 %, 95 % et 99 % progressent respectivement de 14 %, 16 % et 20 %, et en zone 4 de 22 %, 25 % et 31 %.
Quantiles de pluie à 90 %, 95 % et 99 % des séries régionales non stationnaires de pluviométrie journalière de dépassement de seuil, en début et en fin de période
Table 3 90%, 95% and 99%-quantiles of the non-stationary peak-over-threshold regional series of daily precipitation, at the beginning and at the end of period
| ZONE | 2 | 4 | ||
| Quantile | Début | Fin | Début | Fin |
| à 90% | 72,54 | 82,50 | 154,82 | 188,54 |
| à 95% | 81,72 | 94,80 | 179,47 | 225,06 |
| à 99% | 103,73 | 124,31 | 244,20 | 320,96 |
Pour chaque zone homogène, les intervalles ou régions de confiance des EVM déterminés par l’éq. (6) sont présentés sur la Fig. 2, pour les paramètres de la loi de Poisson, et sur la Fig. 3, pour ceux de la GPD. Dans le cas où la région de confiance est une ellipse centrée autour de l’EVM, les lignes en pointillés représentent les intervalles de confiance associés. On note qu’à chaque fois qu’une tendance est détectée, l’intervalle de confiance contenant le coefficient directeur de la tendance linéaire ne contient pas la valeur 0. Cela conforte le résultat du test RVM, qui rejette l’hypothèse de stationnarité de ces séries. Ensuite, concernant le paramètre de forme de la GPD, on note que l’incertitude d’estimation sur ce paramètre est forte (intervalle de confiance de grande amplitude). On observe en zones 1 et 4 que la valeur ξ = 0 n’appartient pas à l’intervalle de confiance. Cela corrobore le travail de Muller [7], qui a montré, via différents modèles et de longues séries de mesures, que le paramètre de forme des lois extrêmes est significativement non nul et correspond à une queue plus lourde que les lois de Gumbel ou exponentielle, soumises à l’hypothèse ξ = 0. Par conséquent, l’utilisation systématique de ces lois peut être risquée, car cela tend à sous-estimer les quantiles de pluies extrêmes lorsque le paramètre de forme est significativement non nul [7].
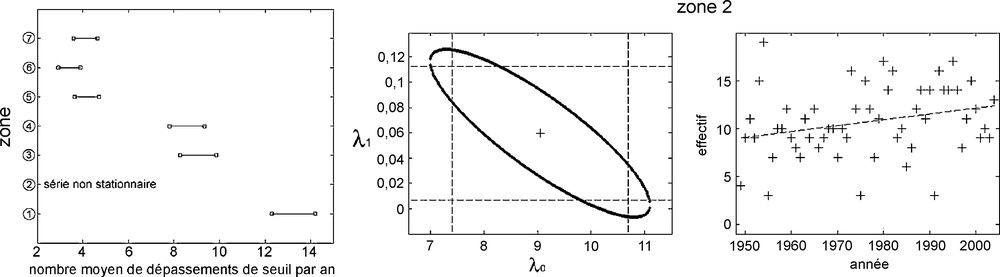
Intervalles de confiance à 95 % contenant l’intensité des lois de Poisson stationnaires. En zone 2, ellipse et intervalles (lignes en pointillés) de confiance à 95 % contenant les paramètres de la loi de Poisson non stationnaire, et représentation graphique de la tendance linéaire estimée sur la série des occurrences.
Fig. 2. Confidence intervals, with 5% risk, containing the intensity of the stationary Poisson laws. In zone 2, confidence ellipse and intervals (dotted lines), with 5% risk, containing the parameters of the non-stationary Poisson law, and representation of the linear trend estimated on the occurrence series.
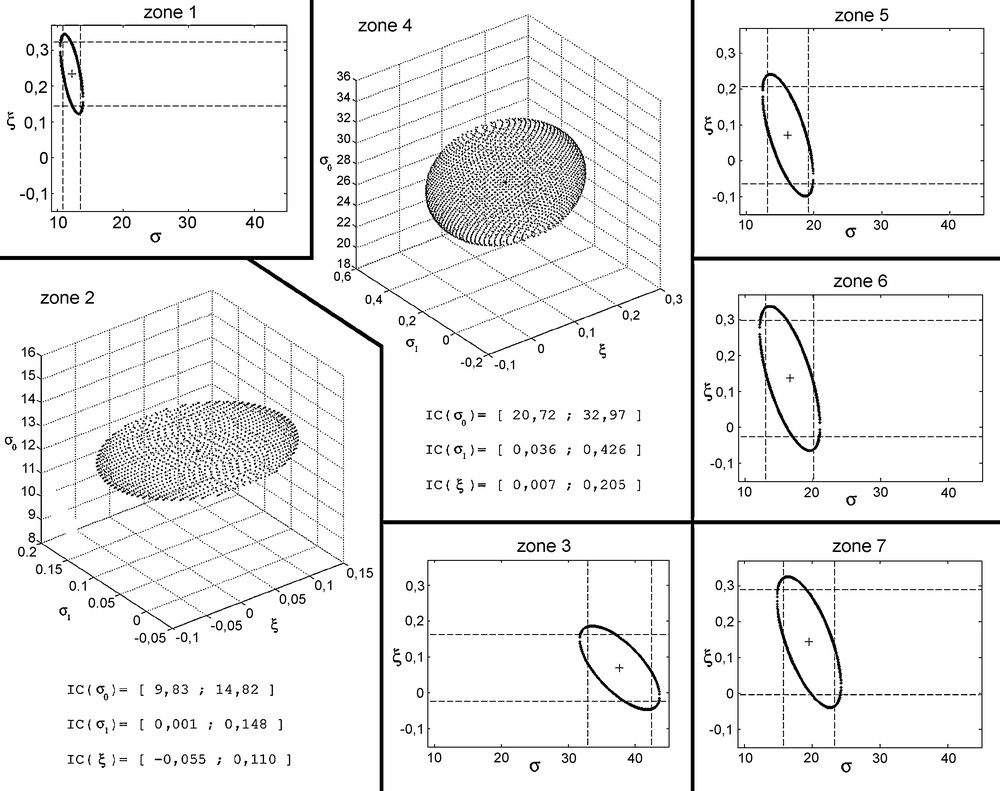
Ellipses et intervalles (lignes en pointillés) de confiance à 95 % des paramètres des lois GPD stationnaires. Ellipsoïdes et intervalles de confiance à 95 % contenant les trois paramètres σ0, σ1 et ξ lorsqu’une tendance a été détectée (zones 2 et 4).
Fig. 3. Confidence ellipses and intervals (dotted lines), with 5% risk, containing the GPD estimators in the stationary cases. Confidence ellipsoids and intervals, with 5% risk, of the three parameters σ0, σ1 and ξ when a trend was detected (zones 2 and 4).
5 Conclusion
Si le changement climatique observé au cours de ces dernières années a un effet sur les pluies extrêmes journalières, il est probable que cet effet concerne plusieurs stations. De plus, le caractère souvent local des pluies extrêmes milite en faveur d’une approche régionale pour étudier la stationnarité des extrêmes pluviométriques journaliers. L’application du modèle POT à des variables régionales de pluviométrie journalière nous a permis de réaliser une telle analyse, tout en évitant la prise en compte de la dépendance de l’approche multivariée. Seule la zone 2, correspondant au Nord de la Lozère et au Sud de l’Auvergne, se distingue par une augmentation en nombre et en intensité des dépassements de seuil. Plus au sud sur le littoral, on détecte une augmentation significative des dépassements de seuil. On observe également une tendance à la hausse de l’intensité des pluies fortes sur la frange montagneuse de la région Languedoc-Roussillon. En zone 2, ces changements se traduisent par une augmentation des pluies journalières de fréquence de non-dépassement 0,90, 0,95 et 0,99 de 14 %, 16 % et 20 %, et en zone 4, de 22 %, 25 % et 31 %, entre le début et la fin de la période 1949–2004. Cependant, il faut interpréter avec prudence l’évolution de ces quantiles de pluie, car ils dépendent de la persistance de la tendance dans le futur, mais aussi de l’hypothèse faite sur la forme de la tendance (linéaire). De plus, une analyse des facteurs météorologiques à l’origine de ces instationnarités doit être menée en parallèle. Enfin, on notera également que seules les pluies extrêmes journalières ont été étudiées, car elles constituent les chroniques les plus longues. Il est cependant possible qu’une instationnarité des extrêmes touche les intensités à un pas de temps infrajournalier.
Remerciements
Nous exprimons nos remerciements à Météo France pour la mise à disposition des données, dans le cadre de son accord avec l’université Montpellier-2.


