1 Introduction
Although a proper description of climate change cannot be based on temperature alone, temperature is often considered a useful index and is readily grasped by the general public. As a result, temperature curves are often the main data displayed in papers or reports readily accessible to the public and to policymakers. To give just a few recent examples, a special issue of Pour la Science dedicated to global warming featured a paper by Moisselin and Dubuisson [15] on warming in France that started with a figure displaying the mean variations in temperature in metropolitan France from 1901 to 2005, whereas a paper by Le Treut [14] on modelling “certainties and uncertainties” displayed the famous hockey-stick curve (basically the version from Mann, see for instance Jones and Mann, [11]) over the past 1000 years. The Summary for policymakers of Working Group 1 (part of its contribution to the IPCC Fourth Assessment Report, [10]) displays variations of the global average temperature from 1850 to 2005. One of the concluding figures (SPM-4) displays changes in the continental and global-scale decadal surface air-temperature anomalies for 1906–2005, measured relative to the corresponding averages for the 1901–1950 period, and compared with model simulations. Observations diverge from model simulations, starting around the mid-1970s, when greenhouse gases are not included.
An item for discussion, which we wish to emphasize, rests with actual temperature measurements and the way global average temperatures are derived. Whereas there are a rather large number of groups around the world studying the physical and chemical processes that affect climate and testing and inter-comparing numerical models (GCMs), the number of independent analyses of mean temperature data is not so large. Two main groups are involved in assembling a global data base of mean temperatures, one in the UK and one in the USA. A new data set from 1850 to the present day has been assembled by the Hadley Research Centre and is described in Brohan et al. [4]. The paper focuses usefully on uncertainty estimates and provides curves for mean temperature change from 1850 to 2005. Uncertainties in recent decades are claimed to be in the order of ±0.15 °C for the global land average, ±0.10 °C for the marine average. Corresponding values in the second half of the 19th century are ±0.40 °C and less than 0.15 °C. Because the surface covered by the oceans is two-thirds of the globe, the marine data dominate the final global average, which has an uncertainty of less than 0.10 °C in recent decades and less than 0.15 °C in the last half of the 19th century. This is the curve used in IPCC WG1 ([10], Figure SPM-3).
Global averages, which are derived from raw data in the Hadley Research Centre database, are faced with the problems of large temporal changes in data distribution, and to a lesser extent quality. The marine data in particular have been obtained using various bucket and thermometer techniques and automated engine cooling-water observations made from ships. Moreover, measurements are not made at the same instants, of course. Marine data are assigned their local time, whereas for land data the mean of the maximum and minimum daily temperatures is used. These mean daily values (in the case of continental measurements) or instantaneous values (in the case of marine data) are averaged over one month in a 5° square spherical cap, and the 1961–1990 mean is subtracted to define the temperature anomaly. Finally, adjustments are made to reduce the effects of land-use changes, changes in instruments, measurement site and missing data. Clearly, the amount of work involved in acquiring, collecting, analyzing, reducing these 3.7 million data is enormous and cannot easily be redone or checked independently.
We find it quite remarkable that the claimed uncertainties can be so small back to 1850. The marine data are the focus of a specific paper by Rayner et al. [16]. Both Rayner et al. [16] and Brohan et al. [4] discuss in detail the changes in the measurement techniques over these 150 years. Prior to 1900, the total number of observations was less than 5% of the number of data after 2000 and less than 15% of the number of data after 1950. Moreover, the number of 5° square boxes with any data (yielding monthly averages) prior to 1900 was less than 50% of the number of data after 1950. Before 1900, two thirds of the total oceanic surface had no data. It is quite remarkable that this enormous under-sampling hardly affects the uncertainties of the global temperature curves. P. Jones (pers. comm., 2007) informed us that attempting to reconstruct the global temperature means using post-1950 data, under-sampled in the way the pre-1900 data were distributed, hardly changed the global means. This would imply that the marine mean air surface temperature is a remarkably uniform field on the global scale.
We have not been able so far to obtain the files of data used by Brohan et al. [4], i.e. the actual monthly data in each 5° box prior to any processing, including computation of the ‘temperature anomaly’. P. Jones (pers. comm., 2007) writes, quite understandably, that “the aim with the global temperature grids and time series is to make the data easy for scientists to use”, but that “the monthly station data are not available. They have been routinely obtained from the Global Telecommunication System between national meteorological services (NMSs). They have been augmented over the years using data received from NMSs around the world and from scientists working in the climate field. To get much of the NMS data, the centre has signed agreements with NMSs saying they would not pass the raw data onto third parties.” Also, there is apparently no access to daily data (only monthly means). Being used to collecting and processing worldwide magnetic data, we are quite sympathetic with these difficulties. The database would therefore have to be reconstructed step by step from original observatory publications or partial databases and websites.
We have given ourselves the more modest objective to use regional data bases, starting with 153 US and 44 European observatories, where we could obtain essentially a century of daily (rather than monthly; this may be quite important, as will be seen below) data (minimum, mean and maximum temperatures). We have analyzed individual station data and averages at the regional and continental scales. We focused on long-term variations evidenced after 3-year averaging of the data, in order to eliminate the large annual cycle. We then looked for an index that would allow us to estimate long-term variations of the characteristics of higher frequencies (disturbances) in the signal, attempting to diminish the otherwise large effect of the annual variation. We have used both a rather classical tool, the mean-squared interannual variation, and a more novel nonlinear filtering technique involving the ‘lifetime’ of temperature curves (which is described in more detail in Le Mouël et al., 2008, a description not needed at the stage of this paper).
We first discuss the results for North America, where we illustrate changes in minimum temperature and temperature disturbances over six climate zones centred on the North Atlantic coast, the Great Lakes, the central US Atlantic coast, Florida, California and the North Pacific coast. We show that there is a quite significant correlation between long-term variations in temperature disturbances and indices related to long-term changes in solar activity. We then repeat the analysis for European stations, the detailed results being described elsewhere (Le Mouël et al., [13]). We also present some preliminary results from five Australian stations. In a final section, we discuss implications of our findings with respect to potential driving forces of climate change.
2 North American temperatures
The data from 153 stations in North America (Fig. 1) were analyzed. The data are extracted from the ECA&ECD database (available via http://eca.knmi.nl/). They consist in series of daily minimum, mean and maximum temperature values. In the present paper, we only show results for minimum temperatures in stations with the shortest possible gaps; the other two yield rather similar results. Based on analysis of individual station data and previous definitions of climate zones on the continent (e.g., Groisman and Easterling, [8]), we have used six distinct zones, for which the time evolutions of (3-year-averaged) temperatures are shown in Fig. 2. Whereas the spectral content of all series in the 3–15-year period range is similar and some correlations can be noticed between adjoining climate zones, the longer-term (decadal to secular) trends are clearly very different from one zone to the other. California displays a continuously increasing temperature trend, which can be broken down in three periods, two with a faster rise (1910–1940 and 1980 to the present) and one with a smaller average slope (1940–1980). The North Pacific has similar features with larger amplitude and a significant decrease after 1940. The Great Lakes display a jagged, zigzag-like trend, rising until 1935, decreasing to 1975 and rising since. The North Atlantic coastal area displays a sharp rise until the early 1950s, a strong cooling between 1950 and 1960. On the other hand, in the Central Atlantic coast and Florida regions, the zigzag-shaped curves and their most recent warming segments yield to a plateau when temperatures stabilize, as of ∼1985.
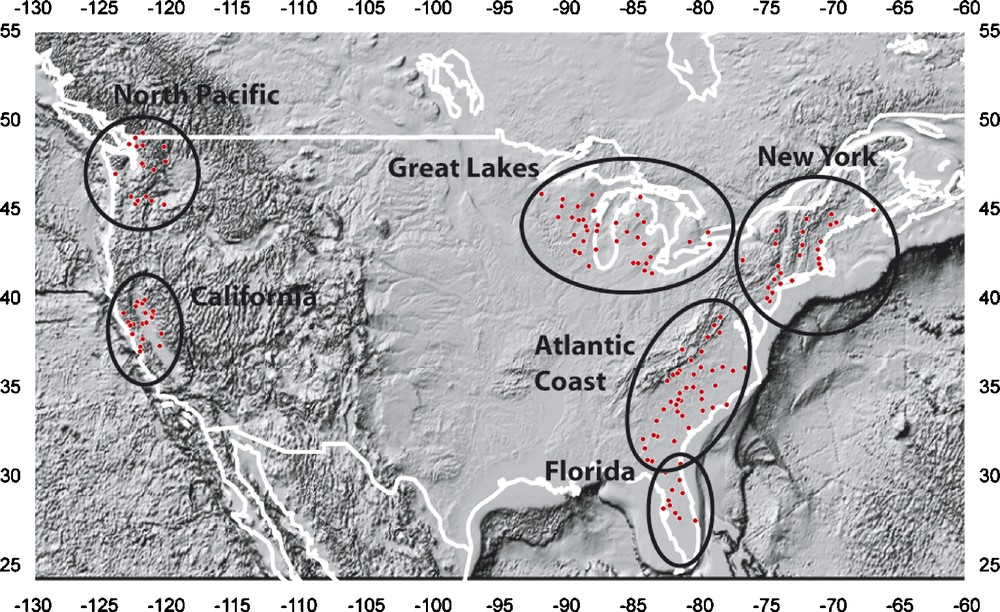
Climatological stations and climatic regions of the USA used for calculating regional averages. The numbers of stations used are 17 for the North Pacific, 37 for the Great Lakes, 25 for the North Atlantic (New York), 20 for California, 45 for the Atlantic Coast and 9 for Florida.
Stations climatologiques et régions climatiques des États-Unis utilisées pour calculer les moyennes régionales ; nombre de stations : 17 pour le Pacifique Nord, 37 pour les Grands Lacs, 25 pour l’Atlantique Nord (New-York), 20 pour la Californie, 45 pour la côte atlantique et 9 pour la Floride.
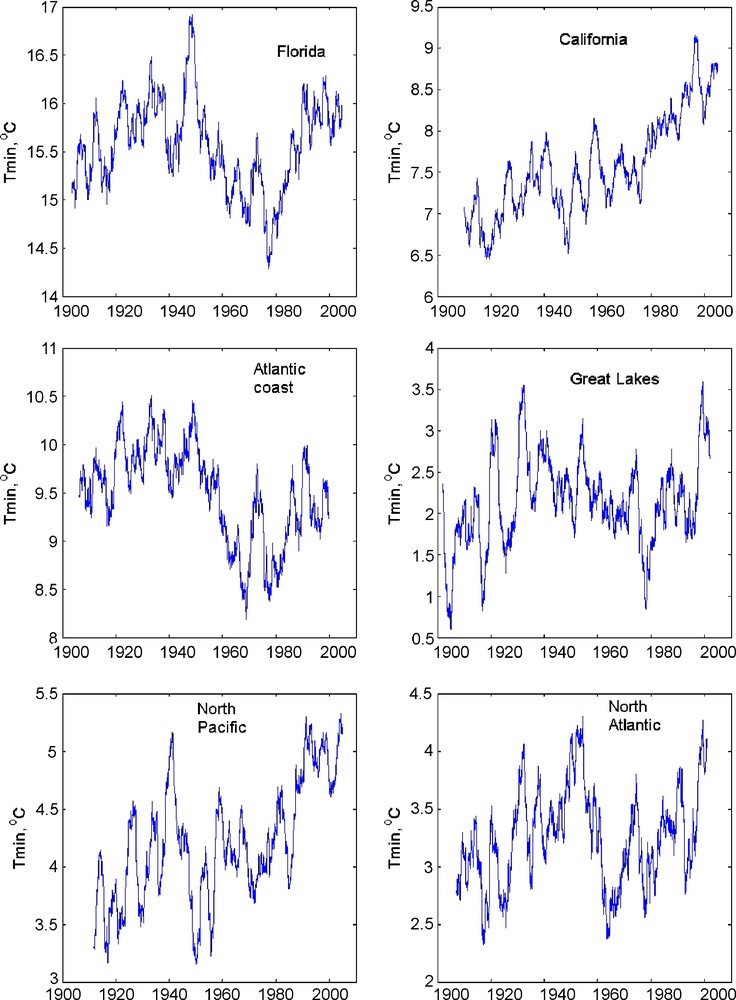
Three-year running mean minimum temperature curves for the six USA climatic zones shown in Fig. 1.
Courbes moyennes de température minimale journalière moyennée sur trois ans pour les six zones climatiques des États-Unis, indiquées sur laFig. 1.
The overall mean curve for 153 stations is shown in Fig. 3. It displays three main periods, two with a sharp rise between 1910 and 1935, and between the late 1970s and the present. This is interrupted by a long cooling period from 1930 to the late 1970s. Note that the slope and value reached in the most recent episode are no larger than in the one preceding 1940, and that the warmest temperatures may have been around 1930, as recently noted by the US weather service. There is therefore great similarity in the US (taken as an average) between the situation in the 1930s and at present. A North American mean temperature curve is given in Figure SPM-4 of the Working Group 1, part of the IPCC Fourth Assessment Report [10]. We note that this curve and ours are quite different. The overall increase from the beginning to the end of the 20th century is very significant in Figure SPM-4, but is found only in our western US regional curves (Fig. 2), not in the overall mean (Fig. 3). The two curves are based on somewhat different sets of data with very different resolution: one data point every ten years based on monthly averages for Figure SPM-4, vs. daily data with 3-year running mean filtering in our case. Yet, we do not see how these can be so different and wonder about the resolution and significance of the curves in the IPCC report [10].
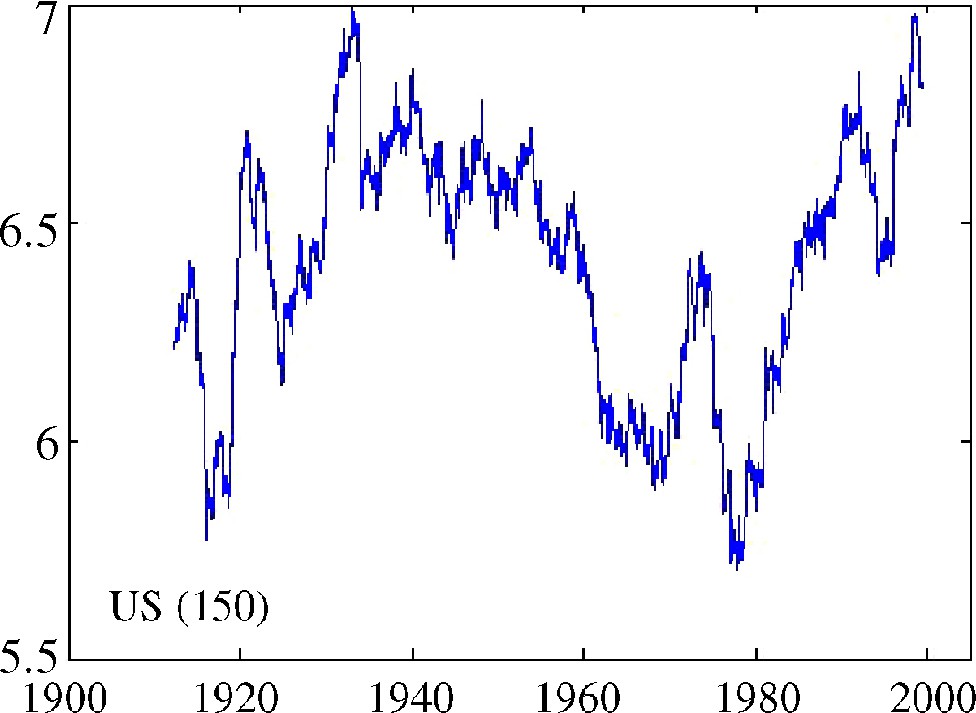
Overall mean curve (three-year running mean minimum temperature in ̊C) for the 153 USA stations shown in Fig. 1.
Courbe moyenne d’ensemble (température minimale moyenne sur trois ans en ̊C) pour les 153 stations des États-Unis indiquées sur laFig. 1.
3 Secular evolution of temperature disturbances in North America
When attempting to find long-term correlations, and possibly causal connections between observables linked to the climate system (here temperature) and potential driving factors (anthropogenic GHG, Sun, cosmic rays…), only the longer periods are relevant if the system is a linear one. But if it is nonlinear and moreover turbulent, cascades from the higher to the lower frequencies or the reverse can occur. In that sense, it is important to estimate the long-term behaviour of the higher frequencies (disturbances), a delicate task with many time series spanning several orders of magnitude in characteristic frequencies. In previous papers, we have used a nonlinear technique of analysis developed for time series whose complexity arises from interactions between different sources over different time scales. We have applied this technique to several geophysical time series [1,2,6]. In Le Mouël et al. [13], we apply it to European temperature time series and to several indicators of solar activity. The technique allows us to extract the ‘lifetime’ of (higher frequency) features from a time series (i.e. roughly the mean duration of temperature disturbances), and then to follow the time evolution of this higher-frequency component on the longer time scales. A more classical technique consists in computing simply the mean squared interannual variation, which is:
| (1) |
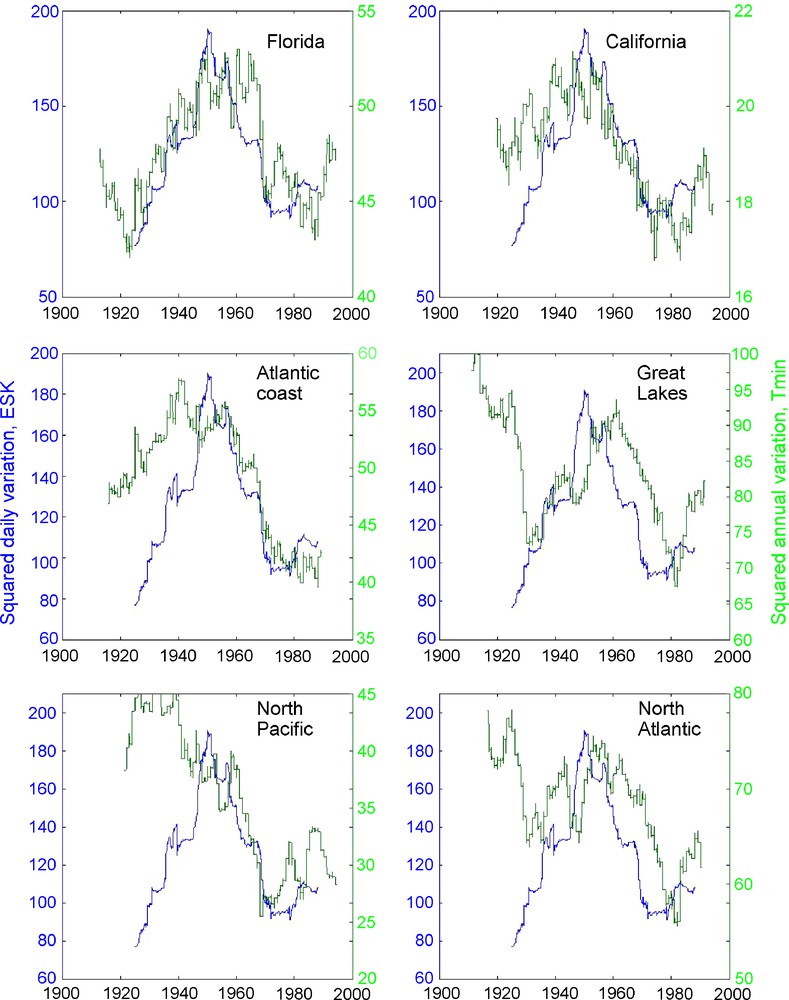
Mean-squared interannual variations (22-year averaged) of minimum temperature for the six USA climatic zones shown in Fig. 1 (green curves), compared to a magnetic index representing solar activity (the squared daily variation of the vertical component Z of the geomagnetic field at Eskdalemuir; blue curve).
Variations quadratiques moyennes interannuelles (moyennées sur 22 ans) de la température minimale pour les six zones climatiques des États-Unis indiquées sur laFig. 1(courbes vertes) comparées à un indice magnétique représentant l’activité solaire (variation quadratique interjournalière de la composante verticale Z du champ géomagnétique à Eskdalemuir : courbe bleue).
4 European temperatures
We have next analyzed (3-year running average) daily minimum temperature curves from 44 European climatological stations (Fig. 5) covering most of the past century. All individual station curves again display significant energy in the 3–15-year period range and correlate quite well, and so do country averages and the overall European average. So, much of the spectral content of the temperature curves is highly correlated at the continental scale (∼3000-km scale). This is discussed in more detail in Le Mouël et al. [13], but for the purpose of the present paper, it is sufficient to show this overall European average (Fig. 6).
Geographical distribution of 44 European climatological stations used in this study (see also [13]).
Répartition géographique des 44 stations climatologiques européennes utilisées dans cette étude (voir aussi [13] ).

Overall mean curve (three-year running mean minimum temperature in ̊C) for 44 European stations shown in Fig. 5.
Courbe moyenne d’ensemble (température minimale moyennée sur trois ans en ̊C) pour les 44 stations européennes de laFig. 5.
The ‘European’ trend that emerges would be positive if simple (first-order) least-squares linear fit over the entire time interval were used. But two particularly striking and sharp features emerge (Fig. 6), which are a brief and intense temperature drop (∼1.5 °C) with a minimum in 1940–1941 and a sharp temperature rise by almost 1 °C in ∼1987. Going back to the original station data, these two features are indeed found almost ubiquitously, though they become more pronounced with increasing averaging over the continent. We conclude from this curve that there was indeed warming in the 20th century in Europe, but that the characteristics of this warming are different from those shown again in Figure SPM-4 of Working Group 1, part of the IPCC Fourth Assessment Report [10]. There was almost no regional change in temperature between 1900 and 1987 and since then (although the series is a bit short to evaluate significantly the post-1987 trend; this is confirmed by the most recent and complete station data sets). Most temperature extremes of the 20th century have been reached in the past 20 years, due to the superimposition of the ∼±0.5 °C amplitude higher frequency changes (5–15-year period range) and the ∼1 °C step-like jump in 1987. The trend in the mean temperature in Europe has been essentially flat before and after 1987. The change occurred in an astonishingly short time and the situation appears to be stable since. That short intense events correlated at the continental scale can occur is well illustrated by the extreme cold event of 1940, which has no other equivalent in the 20th century.
A similar situation has been described for 17 Alaskan meteorological stations over the period 1951–2001 by Hartmann and Wendler ([9], their Fig. 5): when a linear trend is calculated over the 50-year period, it is found to be a warming one. But Hartmann and Wendler [9] show that this is a misrepresentation of the observations, which actually consist of two rather quiet, actually cooling periods separated by a quick positive jump in 1976 (that is ten years before the one we observe in Europe): “examining a trend in temperatures that straddles that 1976 shift generally yields an artificially high rate of warming over Alaska.”
5 Secular evolution of temperature disturbances in Europe
In the case of European data, we display both the mean-squared annual variation and the lifetime (see Section 3) for the mean minimum temperature curve of the 44 European stations (Fig. 7, lower row). These are all computed with a 22-year sliding window. Results are clearly similar using both methods. All curves display the same S-shaped variation with values rising from ∼1920 to ∼1950, then decreasing to a sharp minimum around 1975, and rising more or less since. The same analysis applied to solar indices (here again the mean squared daily variation of the vertical component of the geomagnetic field at Eskdalemuir observatory, an excellent solar indicator) yields a similar result. This S-shaped curve is indeed found to be the same for all components of all magnetic observatories [12]. We have analyzed a number of other indicators, such as long-term changes in the intensity of the 6-month spectral peak in magnetic observatories, or the energy content of the global temperature spectrum at periods less than 10 yr, and always found a similar overall shape.
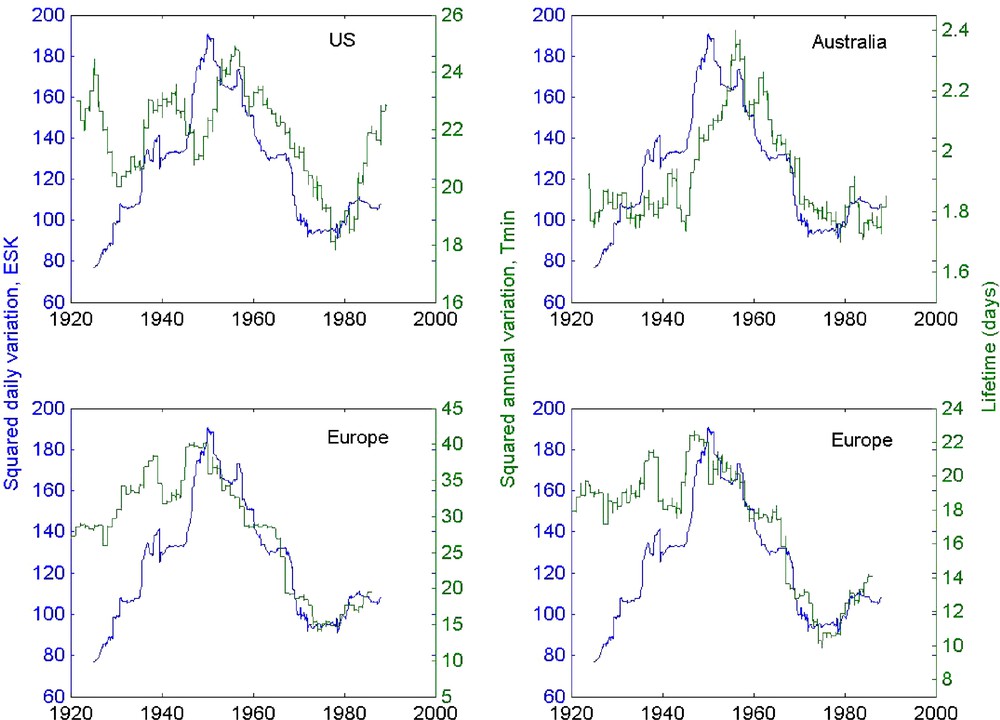
Comparison of the mean squared interannual variation (left column) and lifetime (right column) of the overall minimum temperature data from the US (153 stations), Australia (preliminary, 5 stations) and Europe (44 stations). Europe (bottom row) is shown for the two types of calculation for quick comparison (green curves), and also the magnetic index representing solar activity as in Fig. 4 (blue curve).
Comparaison de la variation quadratique moyenne interannuelle (colonne de gauche) et de la durée de vie (colonne de droite) pour les données de température minimale d’ensemble provenant des États-Unis (153 stations), d’Australie (étude préliminaire, cinq stations) et d’Europe (44 stations) (courbes vertes). Pour l’Europe (ligne du bas) les deux types de calculs sont comparés. Sur toutes les figures, un index magnétique représentant l’activité solaire est figuré en bleu comme sur laFig. 4.
Fig. 7 also displays the overall curves for the 153 US stations (shown by region in Fig. 4). A preliminary study of five Australian meteorological station data (using the ‘lifetime’ approach), also displayed in Fig. 7, confirms that the patterns that emerge from the analysis of European and North American data are likely to be global (there are three stations in the North and Northwest of Australia, including Darwin, and two in the Southwest, including Perth). The figure emphasizes the fact that the general features, sign of slopes of decadal trends and times of extremums of all lifetime and squared annual variation curves are very similar, though they may differ in amplitudes, slope values or higher-frequency details. The correlation of the Australian curve is actually the best. We point out that temperature variations in this subset of west-coast Australian stations are much smaller than in Europe or North America.
6 Discussion and conclusion
In geomagnetism, it is commonplace to use the adjective ‘secular’ to identify temporal trends in the range from decades to centuries. We use the term in the same way in the following. Figs. 2, 3 and 6 illustrate some similarities, but mainly the large differences between secular temperature trends. This naturally leads one to wonder about the significance of averaging them as part of building an even more global average. The various trends in the USA (Fig. 2) confirm the well-known fact that climate is strongly structured and organized in neighbouring areas with strong contrasts. Climate is easier to define at a regional rather than at a more global scale. The secular trend has been one of warming since 1950 in California and the North Pacific, since 1960–1970 in the US North Atlantic and Atlantic coast, since 1980 in Florida and the Great Lakes. But we note that recent decades do not appear to be as extreme or unusual in several regions (Great Lakes, North Atlantic, Atlantic coast, Florida) as is sometimes thought. As far as the regions we have examined are concerned, only in California and in Europe are temperatures significantly higher in recent decades than in the early 20th century; the signatures in both regions are very different. Europe, Florida and the Atlantic coast of the USA, and possibly the North Pacific, share the occurrence of a plateau in the last decade of the 20th century (too short to be considered a robust climatic trend?). In much of the USA, the secular trend was a significant cooling from 1930–1940 to 1960–1970, whereas there was already warming in California and a stable state in Europe.
Another point we wish to make on secular trends is that, however nonunique, a model consisting in no more than three or four rather linear segments would provide most mean temperature curves with a good fit. In the case of Europe, this even reduces to two flat segments separated by a step-like jump. These segments are often interrupted by rather sharp regime changes, giving an impression that in each region climate could be described as a succession of slowly, linearly evolving temperatures separated by sharp and short events of as little as 1- to 2-year duration. To the authors of this paper, this is of course reminiscent of the discovery that geomagnetic secular variation could be described in a similar way (e.g., [5]). This observation does not imply that mechanisms are the same, but emphasizes features that could be characteristic of chaotic nonlinear loosely coupled systems (see also [3]). It is not illegitimate to wonder about the significance and robustness of calculating a worldwide average for a disparate collection of trends. This question is of course addressed in the IPCC reports, in which regional averages are computed and compared to one another.
We have also shown that solar activity, as characterized by the mean-squared daily variation of a geomagnetic component (but equally by sunspot numbers or sunspot surface) modulates major features of climate. And this modulation is strong, much stronger than the one per mil variation in total solar irradiance in the 1- to 11-year range [7]: the interannual variation, which does amount to energy content, varies by a factor of two in Europe, the USA and Australia. This result could well be valid at the full continental scale if not worldwide.
We have calculated the evolution of temperature disturbances, using either the mean-squared annual variation or the lifetime. When 22-year averaged variations are compared, the same features emerge (Fig. 7), particularly a characteristic centennial trend (an S-shaped curve) consisting of a rise from 1920 to 1950, a decrease from 1950 to 1975 and a rise since. A very similar trend is found for solar indices (see also [5,12]). Both these longer-term variations, and decadal and sub-decadal, well-correlated features in lifetime (see [13]) result from the persistence of higher frequency phenomena that appear to be influenced by the Sun. The present preliminary study of course needs confirmation by including regions that have not yet been analyzed.


