1 Introduction
Over the years, the seismological picture of the Earth's inner core has become increasingly complex and enigmatic [22,23]. The observation of the difference of P wave travel times between equatorial and polar paths [21] is now well accepted, as is its interpretation in terms of a large scale cylindrical seismic anisotropy, roughly aligned with the Earth's rotation axis (see [23] and references therein). Variations with depth of anisotropy strength and geometry are still largely unconstrained, but observations seem to require the presence of an almost isotropic, hemispherically asymmetric, 100–300 km thick shallow layer [18] surrounding a more anisotropic region, and possibly an innermost inner core with different seismic properties [9]. The seismic anisotropy is usually believed to be due to the preferred orientation of iron crystals, the origin of which remains unclear. Most proposed mechanisms fall into two categories: solidification texturing at the inner core boundary [22], and large-scale plastic deformation [4,11–13,29], the latter possibly altering the texture acquired during crystallization. One of the difficulties in assessing the viability of the proposed deformation mechanisms comes from the fact that the solid viscosity of the inner core is virtually unknown, with estimates spanning a range of roughly ten orders of magnitude, from 1011 Pa s to 1021 Pa s [25,29]. This huge uncertainty reflects our poor knowledge of the rheology of iron in the inner core, which depends, among other factors, on the grain size.
Published estimates of grain size range from a few millimetres to the size of the inner core [3]. The latter estimate comes from calculations of the elastic properties of hcp iron at inner core pressure, but at 0 K, which were found to closely match the seismologically observed IC anisotropy, thus requiring an almost perfect alignment of crystals within the inner core, or alternatively the presence of a single crystal [24]. Subsequent work at more relevant temperatures (see [27] for a review) found a significantly higher iron elastic anisotropy, thus suggesting instead an imperfect alignment of a much larger grain population. This is, in addition, in much better agreement with the high seismic attenuation and the observation of seismic wave scattering [21,26], which strongly suggest the presence of small (∼1 km) scale heterogeneities, at least in the uppermost inner core. Interpretation of these heterogeneities in terms of an untextured aggregate of patches of aligned crystals suggests typical patch size of a few hundred meters [7]. Estimates of the grain size needed to explain the bulk seismic attenuation anisotropy by scattering of crystals elongated in the cylindrically radial direction yield similar values, ∼200 m [3].
2 Evolution of the grain structure
The evolution of the grain structure is computed with the classical model proposed by Burke and Turnbull [5]. The model is based on the decrease of the total grain boundary interfacial energy by motion of the boundaries due to atomic diffusion in their vicinity. According to these authors, the growth rate of a grain of radius R follows the relation:
| (1) |
In order to apply this simple model to the Earth's inner core, the following hypotheses are taken into account:
- • due to the high pressure and plasticity, there is no porosity likely to interact with the grain motion;
- • the inner core is isothermal, close to the melting temperature [25];
- • the grain boundary mobility does not depend on the grain disorientation.
- • the calculation is aiming at obtaining a maximum value of the grain size. Then the grain multiplication mechanisms, including plastic deformation, are not taken into account;
- • pure iron is considered, in spite of the fact that the core contains Ni and some light elements (Si, O, S …) [1]. Impurities or alloying elements, or precipitates, are likely to interact with the grain boundaries and decrease the grain motion. In this case the relation (1) becomes cubic instead of quadratic [6]. In order to get a maximum grain size, this effect is neglected;
- • it is considered that, after the first nucleation in the undercooled liquid, the inner core growth follows on in the equiaxed mode, by accretion of new grains nucleating in the liquid. The grain size is maximum at the core centre and minimum at the liquid–solid interface. Following the columnar-equiaxed transition model from Hunt [8], it might have happened that, for a low enough growth rate, solidification mode changed to the columnar. In this case, the number of grains would remain constant and their size should be the largest at the periphery. Only the equiaxed mode is studied here.
Table 1 gives the physical parameters of interest in the problem. The iron atomic volume, the grain boundary thickness and its interfacial energy are not subjected to great variations, in any case less than an order of magnitude. The critical parameter is then the diffusion coefficient in the grain boundary. Its value is unknown and an upper value will be estimated by the self-diffusion coefficient of pure iron. At high temperature and atmospheric pressure, it follows the relation (in m2/year) [10]:
| (2) |
Physical parameters of the Earth inner core [10,14].
Tableau 1. Paramètres physiques du noyau terrestre [10,14].
| Inner core temperature | T | 5500 K |
| Interfacial energy | γ J | 1 J m−2 |
| Molar volume | Ω = M/ρ*N | 7.4 × 10−30 m3 |
| Grain boundary thickness | 1.9 × 10−10 m | |
| Diffusion coefficient | D JT | 4 × 10−4 to 0.16 m2/an |
| Specific mass | ρ | 12,760 kg m−3 |
Poirier [20] shows that the transport properties of a metal, including the diffusion coefficient, do not vary, as long as the material remains close to the melting temperature. In this case, the diffusion coefficient of Fe at the melting point, 4 × 10−4 m2/year, gives a minimum value for the calculation, in good agreement with estimation in cubic Fe at the inner core temperature (DFe ≈ 10−4 m2/year) [25]. A maximal value could be obtained by using Eq. (2) at 5500 K, which gives 32.6 m2/year, but this value is much larger than most of the estimations of the self-diffusion of Fe in the liquid state, for example 0.16 m2/year in [28], and this is this last value that will be used in order to overestimate the grain growth rate. Eqs. (1) and (2) give an order of magnitude agreement with experimental values of grain coarsening in iron at high temperature and at atmospheric pressure [16,17].
Using these values, the growth velocity of the iron grains in the inner core is obtained:
| (3) |
The grain growth rate decreases with time. Indeed, when the grain size is large, the boundary curvature is low and the atomic diffusion decreases, then lowering the grain boundary motion. The final grain size depends on the integration constant, i.e. their initial size. According to Bergman [2,3], the initial size of the grains may range between 10 cm and 5 m. In practice, calculations show that the grain radius does not depend on the initial size after ∼106 years of growth.
In Fig. 1, the growth of the iron grains with time is shown for the low and high diffusivities considered above, and is compared with the evolution of the inner core radius with time. Models of the thermal evolution of the core suggest an inner core age of ∼0.5–2 Gy [15,19], with typical solidification rates of a few tenth of millimetres per year. To be explicit, we show here the result of one particular thermal evolution calculation by Labrosse et al. [14], which gives an inner core age of 1.7 Gy. The grain radius (R) is always lower than the inner core radius (c) and the growth rate of the inner core is always much larger than the grain growth rate, when their size gets closer to the core size. The present grain size is of the order of 12 km at the centre of the core when the largest diffusion coefficient is used. With the lower estimation of this coefficient, the grain size would be 560 m. However, it can be even lower, due to the phenomena aiming to decrease the grain boundary motion and that has not been taken into account here. The upper scale of the figure gives the position, inside the inner core, where the grains are located: the grain size, given by the plots (R, ●, ♦), does not vary significantly for depths larger than 100 km.
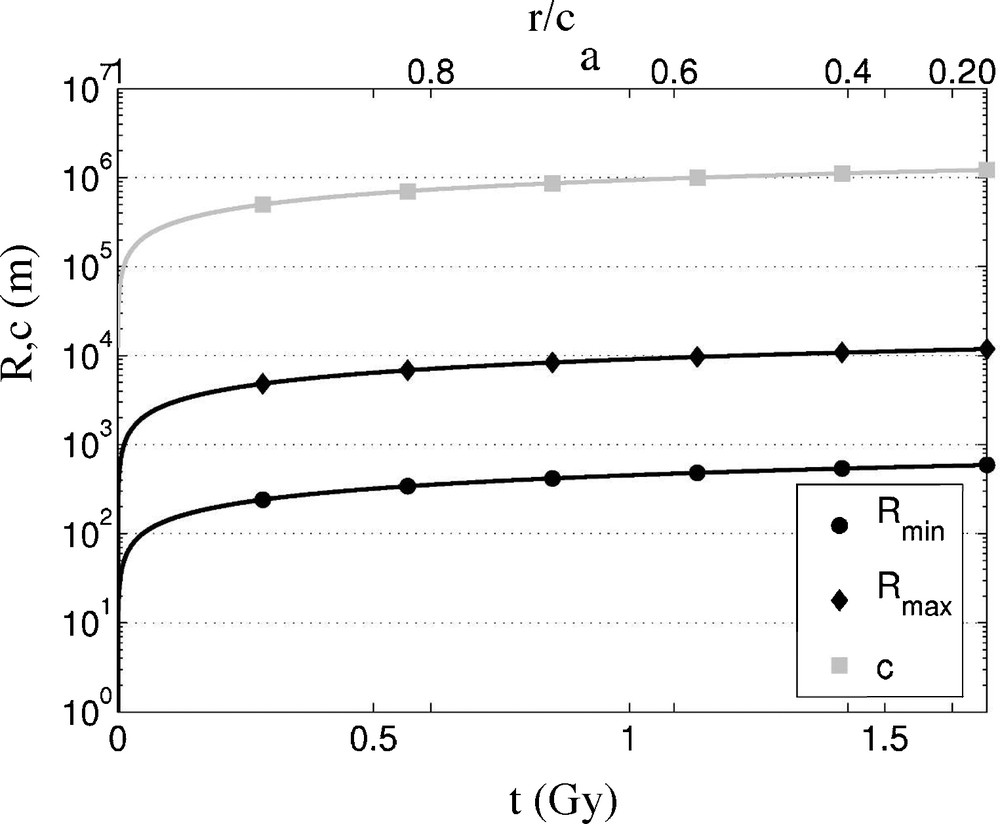
Evolution with time of the radii of the inner core (c, , from [14]) and of the iron grains (R, ●, ♦). The upper scale gives the present radial position of the grains, normalised by the present core radius, r/ca.
Fig. 1. Evolution du rayon de la graine (c, , repris de [14]) et des grains de fer (R, ●, ♦) en fonction du temps. La graduation supérieure donne le rayon, normalisé par le rayon actuel de la graine, r/ca, où se trouvent aujourd’hui les grains.
3 Conclusions
The evolution of a population of iron grains has been determined under the inner core conditions with a simple model of grain coarsening. As function of the value taken for the self-diffusion coefficient of iron in the core conditions, the grain size is estimated to be 0.6 to 12 km at the centre of the core. Results show that the grain-coarsening rate is always lower than the inner core growth rate: this mechanism cannot give a single crystal core. It is also shown that the grain size changes significantly during the 108 first years, and then reaches a stable value, so that the grain size is homogeneous for depths larger than 100 km. As can be seen on the Fig. 1, this depth is not significantly affected by the value chosen for the diffusion coefficient and it is easy to show that the calculation for an alloy, with a third power in Eq. (1), would also result in a stable grain size, but much smaller, after a small depth.
Acknowledgments
The authors are grateful to Drs. T. Alboussière and D. Brito, LGIT- St Martin d’Hères for their comments and encouragement.


