Abridged English version
The knowledge of climatic parameters is essential in order to understand the behaviour of vegetation, and particularly in the present-day context of climate change in which strata translation and flora drift are considered in response to climate warming and rainfall decrease. However, very often, data about study areas are not available. Thus we must have recourse to climatic reconstructions (spatial interpolation) from the existing meteorological network (269 base stations (Djellouli, 1991)). The purpose of our study consists in characterizing every sampled site (1035 phytoecological plottings) by a set of climatic parameters, the latter being of use for the definition of boundaries between vegetation strata (sensu Rivas-Martinez, 1982). A first non-exhaustive model of altitudinal vegetation zonation was proposed by Dahmani-Megrerouche (1997, 2002). The aim of this study is to extend this typology to the entire North Algeria (Fig. 1) by integration of the entire forest vegetation of Algerian mountains on its whole latitudinal scale.
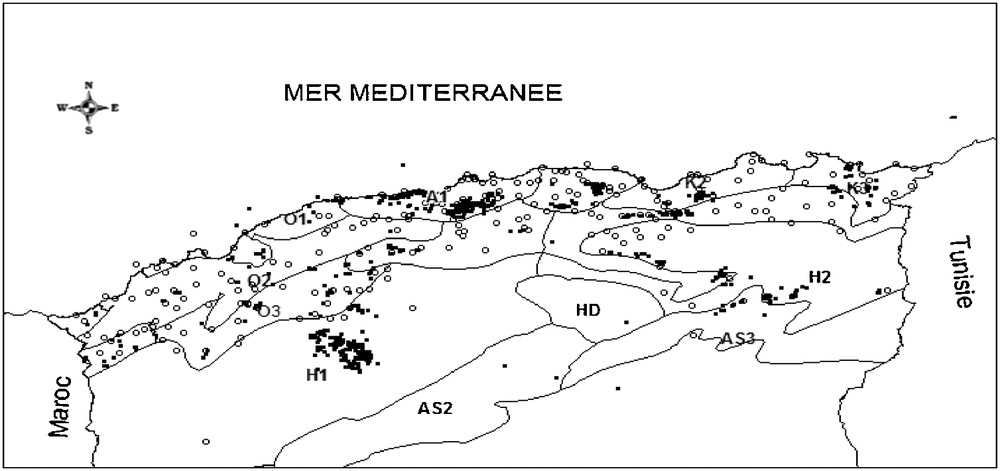
○ : localisation des stations météorologiques de référence ; ● : des sites échantillonnés.
○: meteorological reference stations localisation; ●: sampled sites localisation.
Here is presented the application of an automatic interpolation method, denominated neural network method (Guiot, 1991; Proulx, 1994). The latter is characterized by a great flexibility of non-linearity as well as by its capability to reconstruct information from partial and ill-defined indications, such as those provided by the meteorological network. This method is based on a “steps method” (multilayer perception) in which the different units are built on three layers, as follows: (i) input units which receive information (i.e. explicate variables, that is: longitude, latitude and altitude); (ii) intermediary units (three hidden neurones) whose activation function is sigmoidal; (iii) output units which plot information – the variables to be explained, such as rainfall (P) and temperatures (T, Tmax, Tmin, m, M and M′). As the signal must be close to a pilot signal, neural network proceeds to calibration. This consists of a supervised machine learning in two steps, that is, propagation and retro-progradation (retro-propagation algorithm with inertia moment) which proceeds by iteration up to the minimum of the error function (mean square error) between calculated and measured data. Calibration of the network was tested from climatic parameters considered globally (Table 1), or separately (Table 2), for the whole study zone (Table 1) or by geographic zone (Table 3).
Global treatment for the whole climatic parameters.
| Région d’étude Analyse globale |
Paramètres | P | T | m | M′ | T min | M | T max |
| −1°87 à 8°45 35°10 à 36°9 |
Corrélation calibrée | 0,784 | 0,873 | 0,893 | 0,853 | 0,942 | 0,545 | 0,515 |
| Corrélation vérifiée | 0,772 | 0,857 | 0,885 | 0,834 | 0,933 | 0,503 | 0,479 |
Partial treatment by geographical Sector.
| Secteurs | Paramètres | P | T | m | M′ | T min | M | T max |
| Est 1°87 à 8°45 35°10 à 36°9 |
Corrélation calibrée | 0,853 | 0,885 | 0,922 | 0,879 | 0,929 | 0,725 | 0,760 |
| Corrélation vérifiée | 0,836 | 0,864 | 0,915 | 0,860 | 0,930 | 0,698 | 0,717 | |
| Centre 2°02 à 4°47 35°87 à 36°08 |
Corrélation calibrée | 0,887 | 0,917 | 0,933 | 0,962 | 0,962 | 0,835 | 0,850 |
| Corrélation vérifiée | 0,856 | 0,904 | 0,927 | 0,940 | 0,956 | 0,765 | 0,773 | |
| Ouest 1°87 à 2°43 35°10 à 36°48 |
Corrélation calibrée | 0,787 | 0,830 | 0,623 | 0,807 | 0,781 | 0,826 | 0,831 |
| Corrélation vérifiée | 0,777 | 0,793 | 0,591 | 0,773 | 0,748 | 0,791 | 0,796 |
Total and partial treatment of parameters individually considered.
| Analyses | Paramètres | P | T | m | M′ | T min | M | T max | |
| Analyse globale | 35°10 à 36°9 −1°87 à 8°45 |
Corrélation calibrée | 0,359 | 0,884 | 0,888 | 0,355 | 0,936 | 0,601 | 0,413 |
| Corrélation vérifiée | 0,295 | 0,834 | 0,888 | 0,152 | 0,940 | 0,100 | 0,368 | ||
| Analyse partielle | Est 3°57 à 8°45 36°73 à 36°90 |
Corrélation calibrée | 0,890 | 0,890 | 0,925 | 0,877 | 0,937 | 0,677 | 0,770 |
| Corrélation vérifiée | 0,868 | 0,868 | 0,915 | 0,869 | 0,937 | 0,670 | 0,725 | ||
| Centre 2°02 à 4°47 35°87 à 36°08 |
Corrélation calibrée | 0,655 | 0,655 | 0,929 | 0,326 | 0,963 | 0,811 | 0,645 | |
| Corrélation vérifiée | 0,702 | 0,702 | 0,918 | 0,024 | 0,953 | 0,776 | 0,584 | ||
| Ouest 1°87 à 2°43 35°10 à 36°48 |
Corrélation calibrée | 0,683 | 0,683 | 0,903 | 0,803 | 0,802 | 0,681 | 0,687 | |
| Corrélation vérifiée | 0,646 | 0,646 | 0,896 | 0,741 | 0,761 | 0,611 | 0,649 |
The interpolation results are expressed through a cartography of climate parameters (rainfall (Fig. 2) and average minimal temperature of the coldest month (Fig. 5) automatically performed by MapInfo 8.0 software). Reliability of results provided is evaluated through mapping of estimation errors (Figs. 3, 4 and 6) by comparison with reference data (Aissani et al., 1995; Chaumont and Paquin, 1971; Lebane et al., 1995). These results roughly show a satisfactory reconstruction of climatic data for almost all of North Algeria. When associated to the in situ measurements of meteorological stations, these data lead to a spatial coverage sufficient to better apprehend the vegetation/climate inter-relations. It is obviously a static analysis, which represents a first aim to establish a typology of the vegetation–climate relations (vegetation strata). For a tentative dynamic analysis of the reply functions of flora and vegetation to global changes, or in the viewpoint of predictive models the appropriate predictors will be others than simply geographic. Promising methodological improvements are presently recorded in this sense, such as the use of neural networks in numerous application domains (Cannon, 2007; Dibike and Coulibaly, 2006; Guiot et al., 1995; Keller et al., 2000; Peyron et al., 1998).
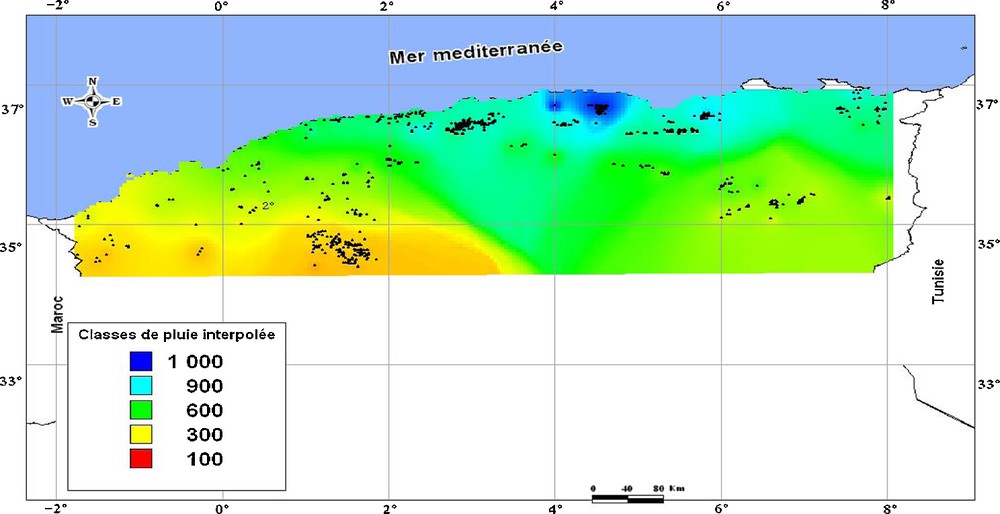
Carte pluviométrique (valeurs de pluviosité interpolées par les réseaux de neurones).
Pluviometric map (rain values interpolated by neural network method).
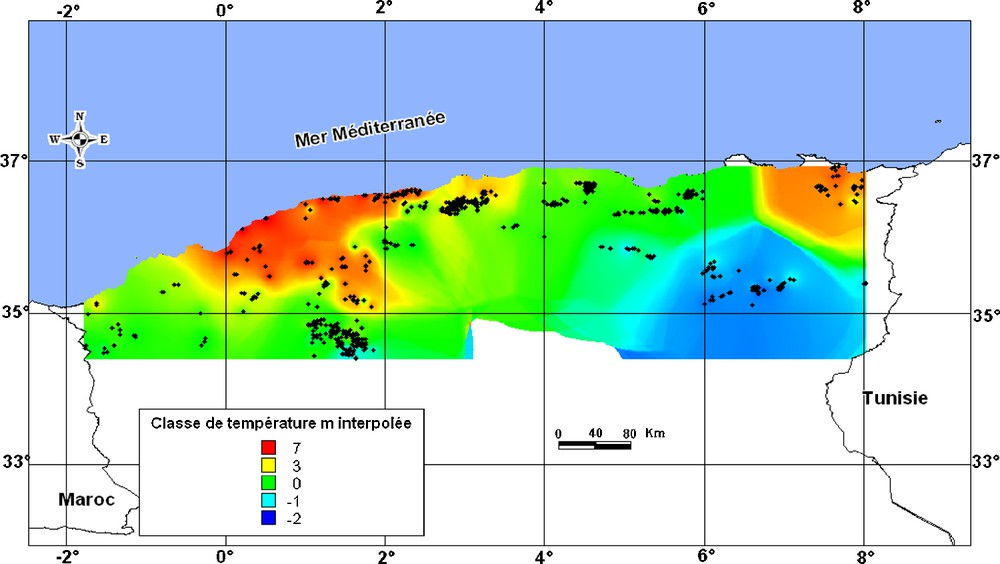
Carte des températures minimales interpolées par les réseaux de neurones.
Minimal temperature map interpolated by neural network method.
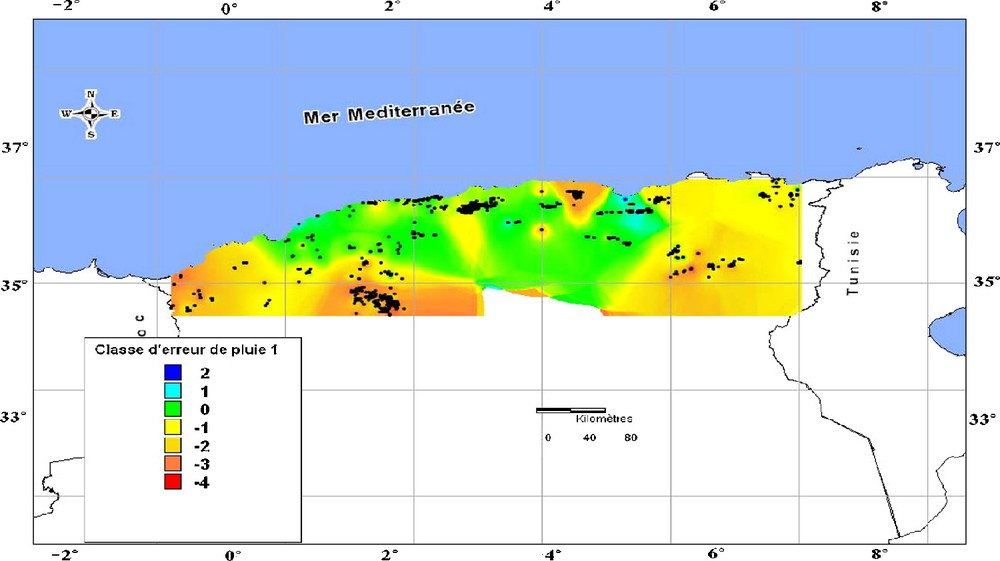
Classe des erreurs d’appréciation de la quantité de pluie par interpolation, comparée à celle donnée par la carte pluviométrique d’Algérie (Chaumont et Paquin, 1971).
Class of appreciate errors by interpolation of the rain quantity, by comparison with the pluviometric map of Algeria (Chaumont et Paquin, 1971).
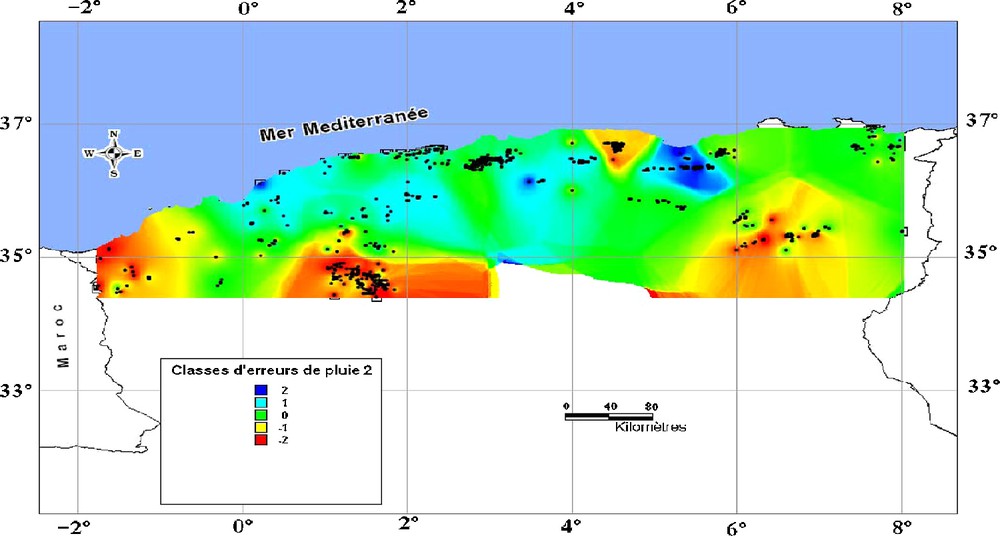
Classe des erreurs d’appréciation de la quantité de pluie par interpolation, comparée à celle donnée par la carte pluviométrique d’Algérie (Aissani et al., 1995 [ANRH])
Class of appreciate errors by interpolation of the rain quantity by comparison with the pluviometric map of Algeria (Aissani et al., 1995 [ANRH]).
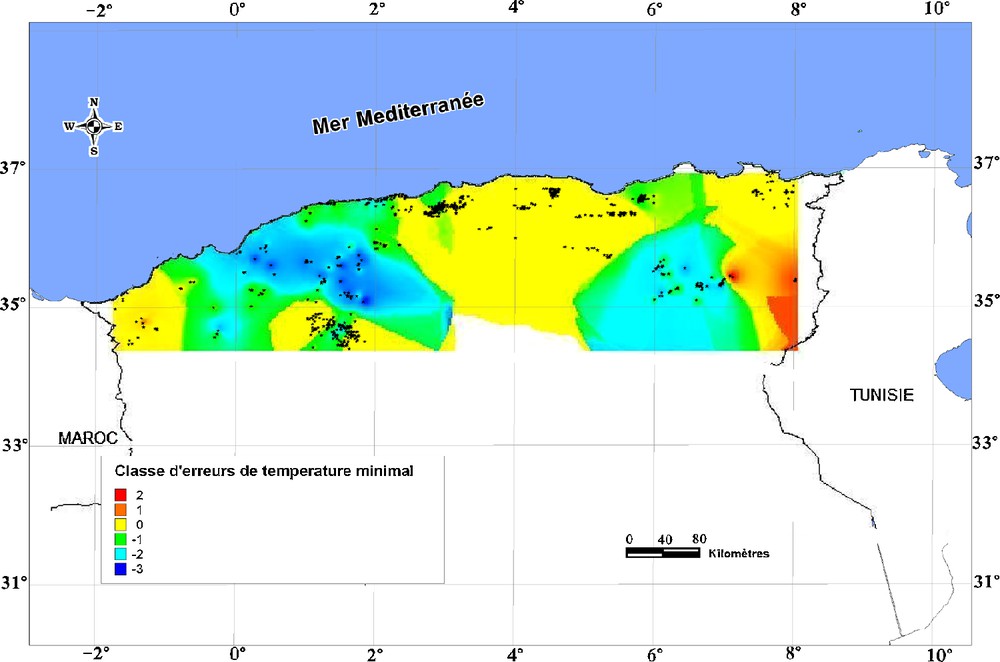
Cartes des erreurs d’estimation de la température minimale par référence à la carte bioclimatique d’Algérie (Lebane et al., 1995).
Class of appreciate errors of the minimal temperature, by reference to bioclimatic map of Algeria (Lebane et al., 1995).
1 Introduction
Le rôle du climat sur la répartition de la végétation est incontestable. L’intervention, notamment, des précipitations et de la température sur la zonation de la végétation est reconnue par l’ensemble des auteurs. Ces facteurs agissent aussi bien au niveau du macroclimat où ils déterminent la répartition des grandes formations végétales à la surface du globe, qu’au niveau du mésoclimat où ils régissent la distribution altitudinale et latitudinale des communautés végétales d’une région climatique donnée. La connaissance de ces paramètres est, par conséquent, indispensable pour comprendre le comportement de la végétation, notamment dans le contexte actuel de changement climatique où translation d’étage et dérive floristique sont envisagées, en réponse au réchauffement climatique et à la réduction des précipitations.
Mais très souvent, nous ne disposons pas de mesures au niveau des zones d’étude. Nous sommes donc contraints de recourir à l’interpolation des données climatiques. Cette opération permet de reconstituer, à partir du réseau météorologique existant, les données climatiques (pluviosité, température) au niveau des sites échantillonnés (relevés phytoécologiques). Par ailleurs, il existe différentes méthodes d’interpolation. Celles qui consistent à calculer un gradient altitudinal à partir de régressions linéaires, ont été les plus utilisées. Ces méthodes ont donné généralement de bons résultats quand elles ont été appliquées à de petites zones. Elles deviennent difficilement applicables à petite échelle, en raison vraisemblablement de la faible densité du réseau météorologique (Dahmani-Megrerouche, 1997). Des méthodes d’interpolation automatiques ont été également développées. Les premières qui ne prennent en compte que la situation géographique des postes météorologiques, ne semblent pas plus satisfaisantes. Une méthode plus élaborée « la méthode AURELHY » (Benichou et Le Breton, 1987) qui considère, en plus des coordonnées géographiques, l’altitude et la distance à la mer des stations, a été utilisée par Djellouli (1991) et semble donner de bons résultats, lorsque le réseau météorologique est assez dense. N’ayant pu accéder à l’utilisation de cette méthode, Dahmani-Megrerouche (1997, 2002) a testé deux nouvelles méthodes d’interpolation automatique mises au point par Guiot (1991).
La première méthode « CALINT » est basée sur une relation linéaire entre les paramètres géographiques (longitude, latitude et altitude) et climatiques. Elle rappelle celle décrite précédemment. Le principe de cette méthode est de calculer la moyenne des valeurs observées au niveau des stations environnant le point à estimer, en accordant plus de poids aux stations les plus proches. Ces stations sont préalablement ramenées au niveau de la mer. Le programme procède par la suite à une correction pour l’altitude voulue du gradient altitudinal obtenu.
La reconstitution des données climatiques est réalisée en tenant compte d’un nombre minimum (six) de stations disponibles sur un rayon spatial défini par l’utilisateur. À défaut, le rayon doit être augmenté. La fiabilité de l’interpolation dépendra d’une part de la qualité du réseau météorologique et, d’autre part, de la valeur du rayon considéré (plus le rayon est réduit, plus la valeur obtenue approcherait la réalité dans le cas d’un réseau météorologique suffisamment dense). Son application a posé des problèmes notamment au niveau des zones montagneuses, en relation vraisemblablement avec les faibles densité et représentativité des postes météorologiques.
La seconde méthode, celle des réseaux neuronaux, qui permet une grande souplesse de non-linéarité, a été plus efficace et c’est celle que nous adoptons pour la reconstitution climatique de notre zone d’étude (interpolation spatiale). Il s’agit plus précisément de caractériser chaque site échantillonné par un ensemble de paramètres climatiques devant servir à la définition des limites d’étage de végétation (sensu Rivas-Martinez, 1982). Un premier modèle, non exhaustif, de zonation altitudinale de la végétation a été proposé par Dahmani-Megrerouche (1996, 2002). L’objectif de ce travail est d’étendre cette typologie à l’ensemble de l’Algérie du Nord, en intégrant l’ensemble de la végétation forestière des montagnes algériennes et sur toute leur amplitude altitudinale.
Dans le domaine biologique, cette méthode a été également utilisée en dendrochronologie (Guiot et al., 1995 ; Keller et al., 1997) pour le calcul des fonctions de réponse entre croissance des cernes (variables dépendantes) et les paramètres climatiques et la pollution (variables explicatives), ainsi qu’en palynologie (Peyron et al. 1998) pour la reconstitution paléo climatique à partir de données polliniques ; ou encore dans l’élaboration de modèle prédictif de la croissance radiale des arbres dans un contexte de changement climatique. Plus récemment, elle a été appliquée dans la modélisation des impacts des changements climatiques sur l’hydrologie et les ressources en eau par Dibike et Coulibaly (2006) et sur le fonctionnement hydroécologique des bassins versants (Tisseuil, 2009). Son efficacité, par rapport aux autres méthodes de régression, a été également soulignée dans les prédictions climatiques (Cannon, 2007 ; Keller et al., 2000), ou encore les problèmes de pollution atmosphérique (caractérisation et prévision de la qualité de l’air, (Rude, 2008). Ces différents domaines d’application possible des réseaux neuronaux soulignent l’efficacité de cette méthode.
2 Méthodologie
La zone d’étude couvre l’ensemble de l’Algérie du Nord comprise entre la longitude 1°90 W et 8°45E et la latitude 35°00 et 36°90 (Fig. 1). Elle comprend plus précisément les zones sub-littorales, les massifs de l’Atlas tellien (Monts de Tlemcen, Monts des Daias, de Saida, l’Ouarsenis, l’Atlas blidéen, le Djurdjura, les Babors, l’Edough, les monts d’Annaba) et une partie de l’Atlas saharien (Aurès). La délimitation de cette zone d’étude est déterminée par la disponibilité des relevés phytoécologiques.
2.1 Récolte des données
Les données sont de nature phytoécologique et climatique. Les 1035 relevés phytoécologiques utilisés dans cette étude sont issus de la bibliographie (Abdessemed, 1981 ; Bouaoune, 1996 ; Brakchi, 1998 ; Dahmani-Megrerouche, 1984, 1997 ; Gharzouli, 1989 ; Habel, 1998 ; Hadjadj Aoul, 1999 ; Kheloufi, 1995 ; Khelifi, 1987 ; Laribi, 2000 ; Meddour, 1994 ; Sadki, 1988 ; Zeraia, 1981). Pour les besoins de l’étude, chaque relevé est renseigné par ses coordonnées géographiques (longitude, latitude et altitude). Les données climatiques au niveau des stations de référence sont extraites de Djellouli (1991). Chaque station comporte en plus des coordonnées géographiques, les paramètres climatiques suivants : P : pluviosité moyenne annuelle, T : température moyenne annuelle, m : moyenne des températures minimales du mois le plus froid, M’ : moyenne des températures maximales du mois le plus froid, Tmin : température moyenne minimale annuelle, M : moyenne des températures maximales du mois le plus chaud, Tmax : température moyenne maximale annuelle.
2.2 Analyse des données
2.2.1 Principe de la méthode des réseaux neuronaux
Il s’agit d’un « modèle connexionniste » de traitement de l’information. En effet, le principe à la base du fonctionnement du réseau s’inspire de celui des cellules nerveuses. Il est composé de plusieurs unités simples interconnectées, apparentées à des neurones dont l’arrangement détermine le type d’architecture spécifique (Proulx, 1994).
Dans notre cas, il s’agit d’un « modèle à plusieurs étages » (perceptron multicouches) dans lequel, les unités sont structurées en trois couches : les unités d’entrée qui reçoivent l’information (variables explicatives) ; les unités intermédiaires (neurones cachés) dont la fonction d’activation est sigmoïde et les unités de sortie qui restituent l’information.
Chaque unité du réseau est caractérisée par un état (quantité scalaire) qui varie en fonction des signaux reçus à travers l’ensemble de ses connexions. L’information dans le réseau est généralement, définie par l’état collectif (et non individuel) de ses unités.
Le signal-sortie (état final des unités) s’établit en fonction de la somme pondérée des informations reçues par le biais de leurs connexions. Ce modèle de traitement de l’information est caractérisé par sa capacité d’adaptation. De ce fait, le réseau procède à un apprentissage qui se traduit par une modification des poids des connexions entre les unités, de façon à minimiser l’écart entre le signal de sortie et le signal de référence.
L’intérêt de l’application de cette méthode réside surtout dans sa capacité de reconstruction d’une information à partir d’indices partiels et mal définis, tel que c’est le cas des données fournies par le réseau météorologique existant.
2.3 Application
Chaque unité de la couche d’entrée représente une variable explicative, longitude, latitude et altitude (variables géographiques bien corrélées aux paramètres climatiques pris en considération dans ce travail) dont elle utilise chaque valeur disponible et la transmet aux unités de la couche intermédiaire, qui sont au nombre de 3, nombre choisi, car donnant une bonne estimation et une dispersion raisonnable. En effet, quand le nombre total de neurones augmente, il y a risque de surestimation des variables météorologiques, et diminution de la capacité de généralisation du réseau. Le signal sortie (variables à expliquer : pluviosité et températures) devant être proche du signal de référence, le réseau neuronal procède à une calibration. Il s’agit d’un apprentissage supervisé, en deux étapes : propagation et rétro-propagation (algorithme de rétropropagation avec moment d’inertie) qui procède par itérations, jusqu’à atteinte du minimum de la fonction d’erreur (erreur quadratique moyenne) entre valeurs calculées et valeurs mesurées.
À ce niveau du traitement, le logiciel 3Pbase (Guiot et Goeury), initialement utilisé par Dahmani-Megrerouche (1996), a été amélioré par l’introduction de deux techniques :
- • l’arrêt prématuré de l’apprentissage (early stopping) : c’est une approche de régularisation de l’apprentissage, qui a pour but de déterminer le nombre optimal d’itérations pour éviter le surajustement par un entraînement du réseau. L’ajustement du réseau est considéré optimal lorsque l’erreur sur la vérification est minimale et que l’erreur de calibration continue à diminuer ;
- • le bootstrap, méthode qui contrôle la stabilité et la reproductibilité des résultats et de ce fait, valide le réseau. Elle consiste à extraire de manière aléatoire deux sous-ensembles à partir de l’ensemble des données ; le premier est utilisé pour effectuer l’apprentissage (base de calibration) et le second pour tester et déterminer les performances du réseau obtenu (base de validation du modèle). Le seuil minimal de simulations utilisées étant de 50, la calibration est réalisée sur 50 sous-ensembles et aboutit à autant de séries de sorties estimées. Pour chaque sous-ensemble, le logiciel calcule les moyennes, écarts type, corrélations et coefficients de régression. Le résultat est exprimé par la médiane et les 90 % d’intervalle de confiance. L’accord global entre valeurs mesurées et estimées permet de vérifier la significativité des résultats et de valider leur fiabilité.
La première phase du traitement a consisté en une calibration du réseau en se basant sur les données observées au niveau des 269 stations météorologiques de référence.
La deuxième étape est relative à une reconstitution des paramètres climatiques au niveau des 1035 sites échantillonnés. Pour définir l’approche la plus fiable pour la reconstitution climatique, plusieurs tests ont été réalisés :
- • estimation de l’ensemble des paramètres climatiques pour l’ensemble de la zone d’étude ;
- • estimation de l’ensemble des paramètres, par secteur géographique (Ouest, Centre et Est) ;
- • estimation de chacun des paramètres pris isolément, pour l’ensemble de la zone d’étude et par secteur géographique.
3 Résultat de la calibration du réseau
3.1 Traitement global de l’ensemble des paramètres géographiques et climatiques, pour l’ensemble de la zone d’étude
Les résultats de la calibration sont appréciés par un calcul de corrélation entre les valeurs observées et celles estimées. Le Tableau 1 montre dans l’ensemble, de bonnes corrélations calibrées et vérifiées pour l’ensemble des paramètres, excepté pour les températures maximales, M et Tmax pour lesquelles les corrélations restent moyennes.
3.2 Traitement partiel par secteur biogéographique
Dans une deuxième étape, nous avons procédé au traitement de tous les paramètres considérés, mais cette fois-ci pris par secteurs géographiques, Est, Ouest et Centre. Nous remarquons (Tableau 2) que pour M et Tmax, les valeurs des corrélations aussi bien calibrées que vérifiées sont, dans les trois secteurs considérés, meilleures que celles obtenues dans le traitement global. Pour le reste des paramètres étudiés l’estimation est dans l’ensemble moins bonne dans la région occidentale. Elle est, par contre, similaire ou légèrement améliorée pour les régions Centre et orientale.
3.3 Traitement global et partiel des paramètres pris individuellement
Pour la troisième partie, nous avons réalisé le même traitement pour l’ensemble des paramètres considérés, mais pris isolément. Nous pouvons noter (Tableau 3) globalement, des valeurs de corrélations plus faibles. Le traitement global ne donne de valeurs significatives que pour les paramètres T, m et Tmin. Quant aux traitements partiels, l’estimation reste bonne pour Tmin et m, quelle que soit la région, ainsi que P et M′, en région orientale et enfin pour M en région Centre. Le reste des estimations est peu significatif.
4 Résultat de l’estimation des paramètres climatiques
Les calibrations observées et estimées, des paramètres climatiques pris individuellement ou globalement, semblent donner des résultats légèrement améliorés par le traitement régional, mais pas de façon uniforme pour tous les paramètres. Aussi, pour notre étude des relations climat–végétation de l’Algérie du Nord, nous avons opté pour la reconstitution climatique par le traitement global des paramètres climatiques, pris globalement et pour toute la région d’étude. En effet, les résultats obtenus à cette échelle d’analyse, restent satisfaisants, notamment pour les principaux paramètres (P, T, m, M′) devant intervenir dans la définition des limites d’étages de végétation.
Une représentation cartographique des résultats de l’estimation des paramètres est tentée. Des cartes de la pluviosité et de la température moyenne minimale du mois le plus froid, sont ainsi élaborées, grâce à l’utilisation du logiciel de cartographie numérique MapInfo 8.0. La validité des résultats ainsi obtenus est appréciée par comparaison à des données de référence.
4.1 Pluviosité
Une première carte pluviométrique de l’Algérie du Nord a été réalisée en prenant en considération 5 classes pluviométriques à partir des valeurs interpolées. Elle montre (Fig. 2) une distribution des valeurs de pluviosité globalement croissantes d’ouest en est et du nord au sud, confirmant ainsi les principaux gradients pluviométriques, longitudinal et latitudinal, connus pour l’Algérie.
Pour vérifier la fiabilité de ces résultats, nous avons procédé à leur comparaison avec des cartes de référence préexistantes qui ont l’avantage de couvrir la même région d’étude. Il s’agit de la carte pluviométrique au 1/500 000 de Chaumont et Paquin (1971) qui a été élaborée avec des données de la période 1913–1963 et celle plus récente de Aissani et al. (1995), au 1/500 000, basée sur des données couvrant deux périodes, 1922–1960 et 1969–1989. L’évaluation de l’écart d’estimation a été faite, par la projection manuelle des stations pour lesquelles les données ont été interpolées sur ces cartes de référence. Sept classes de 100 mm d’intervalle ont été retenues pour évaluer, soit la conformité des résultats (0), soit la surestimation (+1, +2 et +3) ou la sous-estimation (−1, −2, −3 et −4).
La comparaison de la carte d’erreur ainsi obtenue à celle de Chaumont et Paquin (1971), montre (Fig. 3) que le paramètre pluviosité semble légèrement sous-estimé dans les parties méridionale, orientale et Extrême-Ouest de la région d’étude, alors que pour la partie septentrionale, Ouest, Centre et une partie de l’Est, l’estimation de ce paramètre est correcte. Par rapport à la carte (Fig. 4), en référence à celle d’Aissani et al. (1995), l’estimation semble globalement meilleure pour une plus grande partie du territoire étudié, bien que des valeurs sur ou sous-estimées soient encore observées. Ces écarts pourraient s’expliquer, d’une part, par la période d’observation des données climatiques, plus longue (70 ans) dans le cas de notre étude et, d’autre part, la densité des stations météorologiques de référence, considérées.
Par ailleurs, la comparaison de nos résultats avec ceux obtenus dans différents travaux monographiques indique généralement des concordances.
4.2 La température moyenne minimale du mois le plus froid
La même démarche a été suivie pour le paramètre température moyenne minimale du mois le plus froid (retenu en priorité, du fait de son importance et de son influence sur la répartition de la végétation). Le résultat est représenté par la carte (Fig. 5) qui montre une répartition assez cohérente de la température avec les valeurs les plus basses pour la région des Aurès (région montagneuse alticole) et les plus chaudes à l’Ouest correspondant aux zones littorales de basse altitude.
Par ailleurs, comme pour le paramètre pluviosité, nous avons essayé de comparer la carte des températures, obtenue à partir des données interpolées par la méthode des réseaux de neurones, à une carte de référence, afin d’estimer les écarts d’interpolation.
La seule carte disponible est la carte bioclimatique de l’Algérie du Nord au 1/500 000, réalisée à partir de données de la période 1913–1984 par Lebane et al. (1995). L’avantage de cette carte, est qu’elle présente, en plus des étages bioclimatiques, les isothermes de la température moyenne minimale. Pour faire l’estimation des erreurs d’interpolation, 5 classes de 0,5 °C d’intervalle ont été retenues (Fig. 6). La comparaison montre, soit une conformité entre les valeurs estimées par les réseaux de neurones et celles utilisées dans la carte bioclimatique (c’est le cas pour les régions Centre, et Extrême-Est et Ouest), soit une sous-estimation de 0,5 °C, pouvant atteindre 1 °C au niveau des Aurès et de l’Ouarsenis. Nous pouvons considérer, de ce fait, correcte l’estimation de ce paramètre.
5 Conclusion
La connaissance des données climatiques est souvent indispensable pour comprendre la répartition de la végétation et prédire ses réponses face aux changements climatiques actuels. Toutefois, l’absence de mesure au niveau des sites d’étude nécessite le recours aux méthodes d’interpolation. La méthode des réseaux de neurones, appliquée dans ce travail, semble offrir de nombreux avantages. En effet, comparée aux méthodes statistiques classiques, elle offre une grande souplesse de non-linéarité, ainsi qu’une efficacité d’ajustement et une relative rapidité de réalisation. Elle donne des résultats dans l’ensemble satisfaisants, comme l’attestent les faibles erreurs d’estimation observées par comparaison à des données de référence. Les légers écarts parfois observés pourraient s’expliquer par les différences de résolution spatiale et temporelle. Cette performance de la méthode des réseaux neuronaux par rapport à d’autres méthodes statistiques est également soulignée par de nombreux travaux relatifs aux paramètres climatiques.
Pour notre étude, elle a permis, malgré le manque considérable de postes météorologiques, notamment, pour les régions montagneuses, de reconstituer des données climatiques pour un nombre important de relevés, recouvrant la quasi-totalité de l’Algérie du Nord. Associées aux mesures in situ des stations météorologiques, ces données permettraient d’avoir une couverture spatiale suffisante pour mieux appréhender les relations climat-végétation.
Il s’agit évidemment d’une analyse statique répondant à un premier objectif d’élaboration d’une typologie des relations climat-végétation (étages de végétation). Dans l’optique d’analyse dynamique des fonctions de réponse de la flore et de la végétation aux changements globaux, ou encore dans la perspective d’élaboration de modèles prédictifs, les prédicteurs appropriés, seront autres que simplement géographiques. Des progrès méthodologiques prometteurs sont enregistrés actuellement dans ce sens, pour l’utilisation des réseaux neuronaux dans de nombreux domaines d’application.
Remerciements
Nous tenons à remercier Mrs les professeurs Guiot et Keller du Laboratoire de paléoclimatologie et paléoécologie, Aix-Marseille III, pour leur précieuse aide dans le traitement des données.


