1 Introduction
Deciphering the history of continental surfaces, unraveling the physical chemical mechanisms controlling their evolution, and predicting their transformation under human activities or climatic forcing conditions are important goals of environmental sciences. Considering these various aspects, the mineral phases that occur in low-temperature environments and sometimes coexist at the micrometer scale (Fig. 1), can bring major information, provided their reactivity and age (absolute or relative) be determined.

Scanning electron micrograph in backscattered mode of a lateritic kaolin sample (Manaus, Brazil). The section displays two types of kaolinite (grey contrast) with contrasted grain size (large booklets vs. sub-micrometric particles) surrounding a significantly older heterogeneous zircon grain (bright contrast).
Cliché en microscopie électronique à balayage (mode rétrodiffusé) d’un échantillon de kaolin latéritique. La section présente deux types de kaolinite (contraste gris), avec des tailles de particules contrastées (accordéons de grande taille vs. particules sub-micrométriques) entourant un grain de zircon (contraste clair) bien plus ancien, présentant une structure interne hétérogène.
Most of low-temperature secondary minerals display small grain sizes and significant surface reactivity, and these characteristics drive key processes such as adsorption, trace element incorporation, crystal growth and dissolution (Brown et al., 1999). Despite the importance of interfacial properties, the present article will focus on the bulk and defective structure of low-temperature minerals using approaches developed in mineral physics, mostly spectroscopic methods and quantum mechanical modeling. In a broad sense, the defective structure of these minerals encompasses any difference between real and ideal structures. It may include point defects, such as impurities and radiation-induced electronic defects, as well as extended defects, such as stacking faults in clay minerals or defect cascades in radioactive minerals. The variations of the isotopic composition of minerals is also an important feature of real minerals. The defective structure of minerals thus provides a record of their growth conditions and subsequent evolution (Allard et al., 1997; Muller and Calas, 1993; Muller et al., 1995). Here, we will provide some examples of this approach, illustrating potential directions for future research in low-temperature “mineral physics”.
2 Real structure of kaolinite-group minerals from infrared spectroscopy
Infrared (IR) spectroscopy provides information at the molecular level on the structure and properties of minerals (e.g. Farmer, 1974). The technique is based on the resonant interaction between the vibrational modes of crystal structures or molecules with the oscillating electric field of an incident IR light. Interatomic vibrations can thus be used as structural probes for determining subtle changes of structure or chemical bonding in minerals. The technique is not limited to periodic systems but is also widely used to investigate amorphous solids, disordered minerals and molecules in liquid and gas phase. The high-frequency vibrational modes observed in solids are usually related to the internal vibrations of specific molecular groups. In particular, the stretching vibrational modes of OH groups (see Figs. 2 and 3 for kaolinite) are commonly used to probe the structural order of hydrous minerals (Farmer, 1974). Ab initio modeling (Fig. 3) has provided a direct interpretation of the vibrational spectra of kaolinite-group minerals (Balan et al., 2001b, 2005a) This modeling was based on quantum mechanical calculation of the low-frequency dielectric tensor of crystals, using density functional theory within a planewave / pseudopotential scheme (Baroni et al., 2001). An important conclusion is that the interpretation of OH-stretching IR absorption bands in kaolinite-group minerals cannot be performed by assuming a straightforward relation between OH…O distance and OH stretching frequency. Frequencies above 3500 cm–1 weakly depend on “H-bond” lengths (Libowitzky, 1999) and likely involve other parameters, such as electrostatic interactions between OH groups and the surrounding crystal structure (e.g., Mitev et al., 2009). In fact, previous experimental observation of the polarization properties of OH-stretching bands in kaolinite (Farmer, 1974) and theoretical ab initio modeling show that, except for the inner-OH group, the OH stretching modes of kaolinite-group minerals involve the coupled motion of nonequivalent interlayer OH groups (Fig. 3). The combination of first-principles calculations with the electrostatic modeling of the absorption of IR light by small particles also makes it possible to quantitatively determine the influence of parameters, such as the shape of particles or the dielectric constant of the surrounding medium, on the IR powder spectra. This approach provides a robust quantitative basis to investigate kaolin-based materials and better understand their modifications under heavy irradiation (e.g., Fourdrin et al., 2009). It has also been applied successfully to other lateritic and low-temperature minerals such as aluminium hydroxides (Balan et al., 2006, 2008) and hematite (Blanchard et al., 2008). The nature of shape-related effects on the OH spectra of gibbsite and bayerite has been clarified, ruling out the previously proposed significant contribution of surface OH groups in the observed spectra (Phambu et al., 2000).
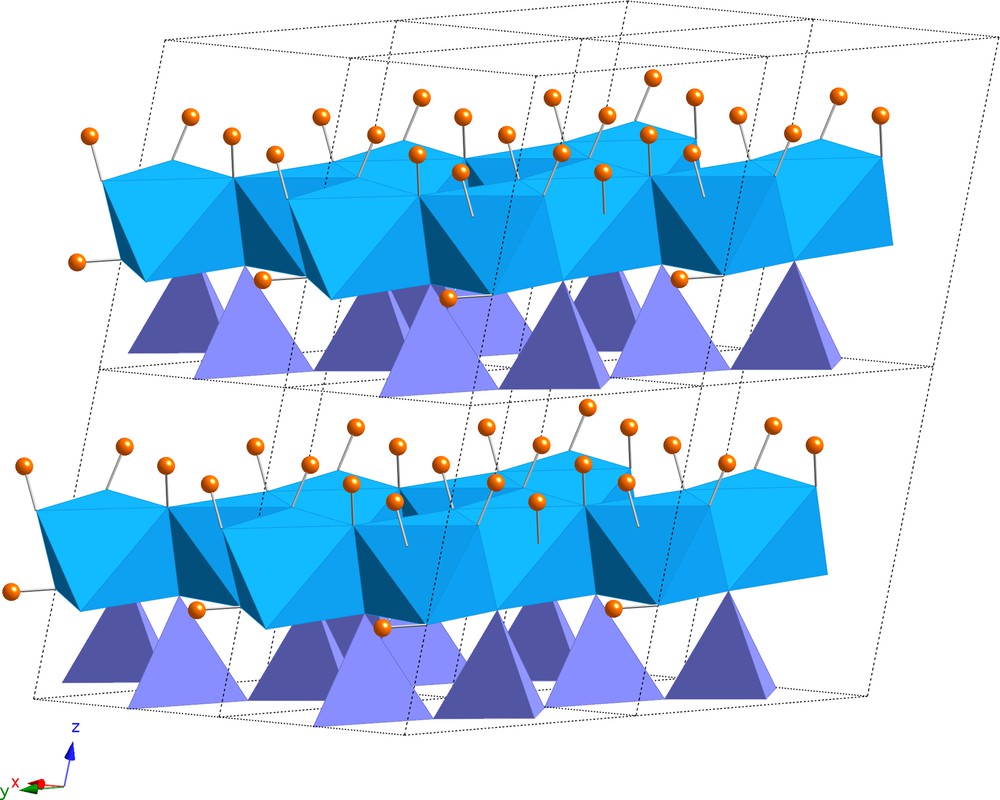
Kaolinite structure (Al2Si2O5(OH)4). The structure is made of a stacking of layers, each one containing a sheet of tetrahedral silicates (violet) and one of Al3+ ions in octahedral sites (blue). Note the three non-equivalent OH groups with an orientation sub-parallel to the c* direction (perpendicular to the layers) and sharing weak H-bonds with the next layer. In dickite, one of these OH groups (OH3) is inclined, leading to a weaker interaction with the next layer.
Structure de la kaolinite (Al2Si2O5(OH)4). La structure est constituée d’un empilement de feuillets, chacun contenant une couche de silicates tétraédriques (violet) et une couche d’ions Al3+ en site octaédrique (bleu). Noter les trois groupes OH non équivalents orientés sub-parallèlement à la direction c* (perpendiculaire aux feuillets) et partageant des liaisons hydrogène faibles avec le feuillet suivant. Dans la dickite, un des ces groupes OH (OH3) est incliné, impliquant une interaction plus faible avec le feuillet suivant.
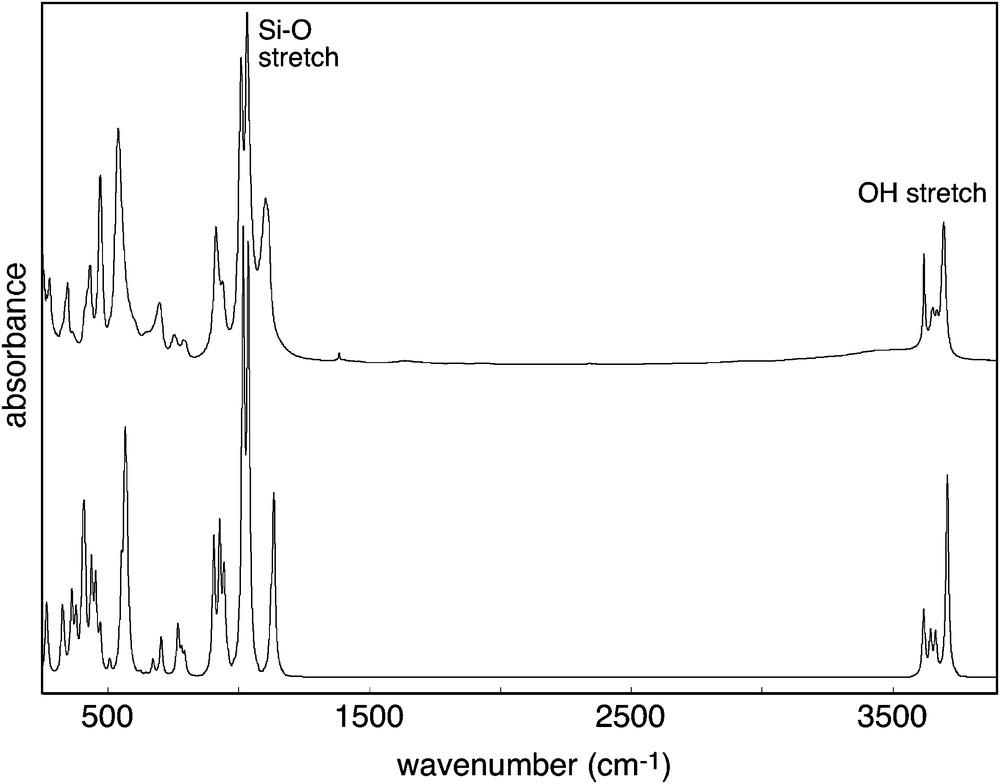
Powder infrared transmission spectrum of kaolinite using KBr pellet. Top: experimental spectrum (KGa-1 sample). Bottom: theoretical spectrum obtained from first-principles and considering platy kaolinite particles inserted in a homogeneous dielectric medium (after Balan et al. 2001b).
Spectre infrarouge en transmission de kaolinite (pastille de KBr). Haut : spectre expérimental (échantillon KGa-1). Bas : spectre théorique obtenu par des calculs de chimie quantique et en considérant des particules de kaolinite plates et insérées dans un milieu diélectrique homogène (d’après Balan et al. 2001b).
The OH-stretching spectrum of kaolinite-group minerals is also sensitive to the stacking sequence of the various polymorphs and to defects such as cationic substitutions and stacking faults. This property has been used to unravel the transformation of kaolinite-group minerals in natural environments (e.g., Balan et al., 2007a; Beaufort et al., 1998). As developed in the next section, coupling the structural information obtained from IR spectroscopy and electron paramagnetic resonance (EPR) on disordered lateritic kaolinite confirms the elevated proportion of a dickite-like configuration and the absence of a direct relationship between the kaolinite order and the amount of substituted Fe3+ ions (Balan et al., 2007a).
Low-temperature measurements significantly improve the usefulness of IR spectroscopy in the investigation of kaolinite-group minerals. The narrowing and differential shift of OH stretching IR absorption bands at low temperature leads to a better identification of stacking faults in disordered varieties of kaolinite-group minerals (Bish and Johnston, 1993; Brindley et al., 1986; Johnston et al., 2008; Prost et al., 1989). Low-temperature spectra of kaolinite-group minerals (Table 1) reveal a minor proportion of dickite-like configuration, even in well-ordered kaolinite samples, whereas ordered dickite samples display minor quantities of kaolinite-like defects (Fig. 4). Notably, the splitting of the high-frequency band ascribed to the inclined interlayer OH group (OH3; Fig. 3) in the IR spectrum of dickite is particularly well resolved at low temperature. This splitting is related to the doubling of the cell size and 2-layer stacking of dickite in the [001] direction. Disordered kaolinite from lateritic profiles and sedimentary deposits (Table 1) clearly exhibits a significant proportion of dickite-like and nacrite-like configurations (Fig. 4). Variations in the proportion and nature of the stacking faults in kaolinite-group minerals can be considered as a record of the growth conditions of kaolinite. Detailed low-temperature IR spectroscopic studies of natural kaolinite samples originating from well-characterized environments are however still required to obtain more quantitative relationships between stacking order and environmental parameters. In addition, the evolution of IR absorption bands as a function of temperature provides important information about the anharmonic character of vibrational modes and spectral broadening mechanisms (Balan et al., 2010a,b).
Liste des échantillons étudiés.
| Sample | Origin | Context | Reference |
| Reference samples | |||
| Kaolinite (Kga-1) | Georgia (USA) | Sedimentary | Balan et al., 1999, 2000 |
| Dickite | Nowa Ruda (Poland) | Hydrothermal | Balan et al., 2002 |
| Nacrite | Sweden | Unknown | |
| Variably ordered samples | |||
| A1 | Brazil | Sedimentary | Balan et al., 2005b |
| Kga-2 | Georgia (USA) | Sedimentary | Balan et al., 1999, 2000 |
| CHA2 | Charente (France) | Sedimentary | Balan et al., 2000 |
| Goy | Goyoum (Cameroon) | Soil | Balan et al., 2000 |
| FU7 | Charente (France) | Sedimentary | Balan et al., 2000 |
| I570N | Manaus (Brazil) | Soil | Fritsch et al., 2002; Balan et al., 2005b |
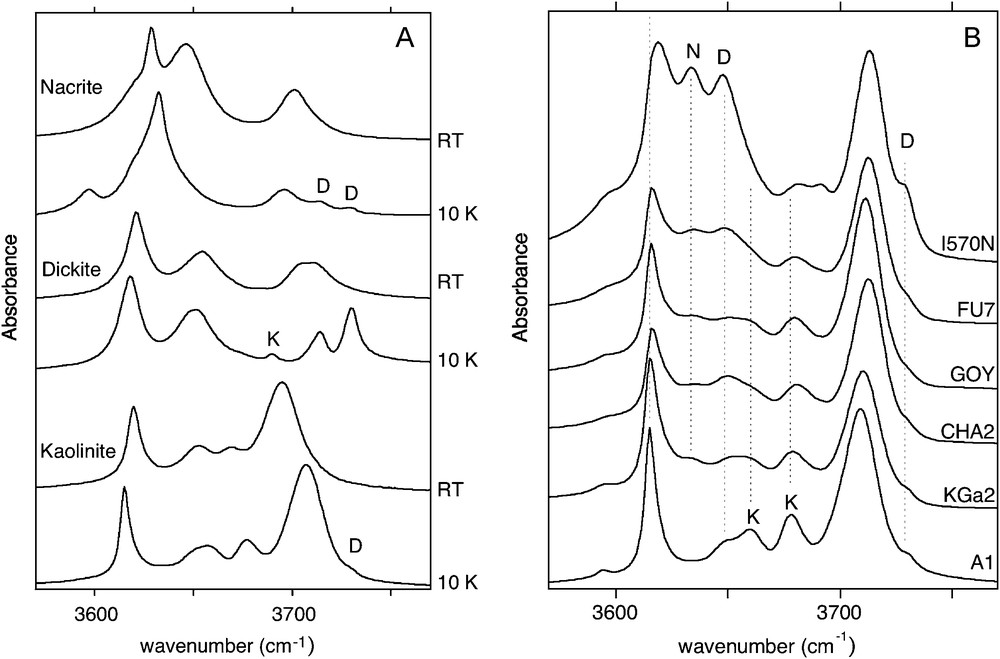
Powder infrared transmission spectra of reference kaolinite-group mineral samples in the OH-stretching range. A: well-ordered samples recorded at 10K and room temperature. Note that well-ordered nacrite and kaolinite samples display a minor proportion of dickite-like stacking faults (D); whereas well-ordered dickite sample displays kaolinite-like stacking faults (K); B: variably ordered kaolinite samples recorded at 10K. The kaolinite order decreases from bottom to top. Note the increasing contribution of dickite- and nacrite-like signals (referred to as D and N).
Spectres infrarouge en transmission d’une série de minéraux du groupe de la kaolinite dans la gamme des élongations OH. A : échantillons bien ordonnés enregistrés à 10 K et à température ambiante. Noter la présence de fautes d’empilement de type dickite (D) dans les échantillons de nacrite et de kaolinite bien ordonnés, tandis que l’échantillon de dickite bien ordonné présente une contribution liée à des fautes d’empilement de type kaolinite (K). B : Échantillons de kaolinite variablement ordonnés enregistrés à 10K. L’ordre d’empilement décroît de la base vers le sommet. Noter l’importance croissante des contributions de type dickite et de type nacrite (notes D et N).
Finally, we stress here that the use of effective medium theory makes it possible to extract physically meaningful vibrational mode parameters from absorbance spectra recorded on composite samples (Balan et al., 2010a,b; Salje and Bismayer, 1997; Yagil et al., 1995). Using this theory, the IR absorption properties of a composite sample, e.g., made of mineral particles and surrounding KBr matrix, can be related to the intrinsic properties of the pure mineral (Fig. 5). This approach is better suited to fit the IR spectra of mineral/KBr mixtures than simple decomposition procedures based on Gaussian or Lorentzian line-shape, because it accounts for the line shifts and intensity changes related to electrostatic interactions within the absorbing sample. Along the same line of arguments, the linewidth of complex spectra can be efficiently analyzed using an approach initially developed to investigate phase transitions in minerals using hard-mode spectroscopy (Salje et al., 2000). The self-convolution of the IR spectrum with a frequency offset ω’ leads to the autocorrelation function:
| (1) |
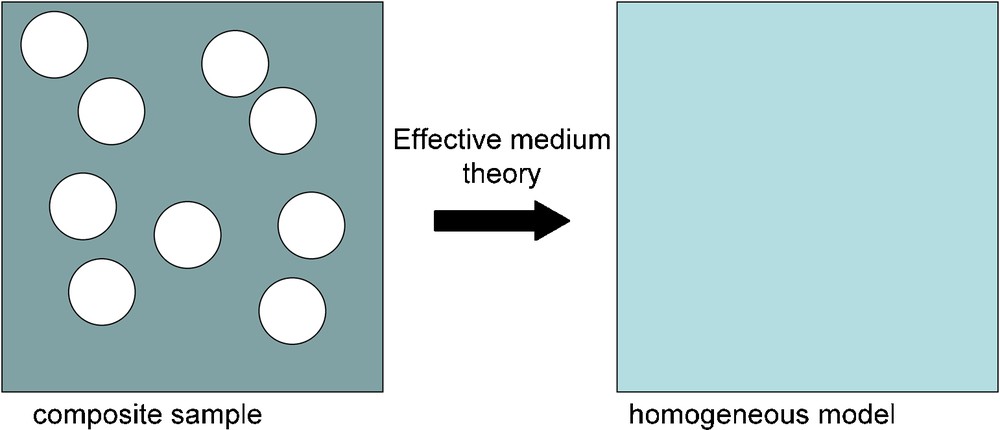
Effective medium theory makes it possible to link the properties of a composite sample to those of a homogeneous model. The 2D composite sample shown here is made of disk-shaped particles inserted in a homogeneous matrix. The properties of the homogenous model depend on the properties of the matrix and on those of the particles, including their shape, concentration and spatial arrangement. In the case of powder IR spectroscopy, this may lead to shifts, broadenings and intensity changes of absorption bands.
Les théories de milieu effectif permettent de relier les propriétés d’un échantillon composite à celles d’un modèle homogène. L’échantillon composite bi-dimensionnel présenté ici est constitué de particules en forme de disque, insérées dans une matrice homogène. Les propriétés du modèle homogène dépendent de celles de la matrice et de celles des particules, notamment de leur forme, de leur concentration et de leur organisation spatiale. Dans le cas de la spectroscopie infrarouge sur poudre, ce type d’effets conduit à des déplacements, des élargissements et des modifications de l’intensité des bandes d’absorption.
3 Paramagnetic defects and impurities in kaolinite-group minerals
A variety of paramagnetic defects and impurities can be detected using EPR. This technique is based on the splitting of the electronic spin levels of a paramagnetic impurity induced by an external magnetic field (Abragam and Bleaney, 1970). The splitting is proportional to the applied magnetic field (Fig. 6). Microwave absorption by the sample occurs when the resonance condition is met:
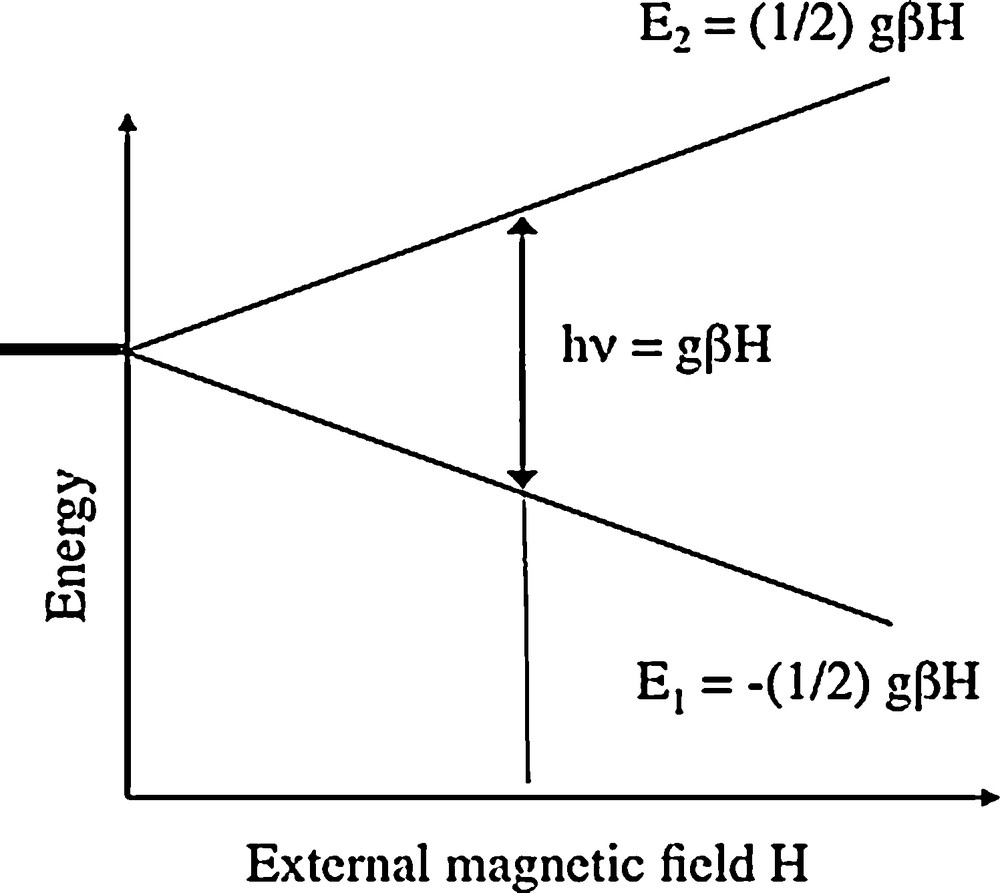
Basis of Electron Paramagnetic Resonance. The application of an external magnetic field (H) to a degenerated spin state (here, a doublet) leads to a splitting of the energy levels depending on the intensity of the applied magnetic field. When the splitting equal the energy quantum of an applied electromagnetic micro-wave, transition between the levels can occur leading to a detectable absorption of the microwave by the sample. The position of the transition is characteristic of the nature of the paramagnetic center, whereas its intensity depends on the center concentration.
Principe de la résonance paramagnétique électronique. L’application d’un champ magnétique externe (H) à un état de spin dégénéré (ici, un doublet) conduit à une séparation des niveaux d’énergie dépendant de l’intensité du champ magnétique appliqué. Quand la séparation des niveaux est égale au quantum d’énergie de l’onde électromagnétique (micro-onde) appliquée, une transition peut intervenir entre les niveaux d’énergie, conduisant à une absorption détectable de la micro-onde par l’échantillon. La position de cette transition est caractéristique de la nature du centre paramagnétique, tandis que son intensité dépend de leur concentration.
At room temperature, the most easily detected cations of transition elements in natural kaolinite-group mineral samples are Fe3+, Cr3+, Mn2+ and VO2+ (Balan et al., 1999, 2002; Delineau et al., 1994; Muller et al., 1995; Djemai et al., 2001; Gaite et al., 1993; Muller and Calas, 1993; Mosser et al., 1993). Combined with chemical concentration, EPR quantitatively deciphers among transition elements between ions occurring either as dilute ions in a specific valence state or occurring under other forms, including concentrated domains and other redox states. In addition, EPR spectroscopy is sensitive to the local geometry around substituted paramagnetic species, including site relaxation and charge compensation. The simulation of powder EPR spectra using spin Hamiltonian parameters, has improved the determination of the location of minor and trace elements in minerals (Morin and Bonnin, 1999). Concerning kaolinite-group minerals, well-resolved spectra of Fe3+ ions substituted for Al3+ (Figs. 7 and 8) have been identified in ordered kaolinite (referred to as the Fe(II) spectrum) and dickite (Balan et al., 1999). Cr3+ ions substituted for Al3+ in ordered kaolinite and dickite also lead to well-resolved spectra (e.g. Balan et al., 2002). In contrast, the fluctuation of local site symmetry in disordered kaolinite leads to an almost isotropic resonance at geff=4.3, referred to as the Fe(I) spectrum. Most kaolinite EPR spectra display both types of signal in various proportions (Fig. 9). The modeling of the Fe(I) signal shows that the distribution of site geometries is related to the occurrence of specific stacking faults leading to a dickite-like local geometry. This interpretation is consistent with the observation of an elevated proportion of dickite and nacrite-like OH configurations in the low-temperature IR spectrum of the more disordered kaolinite samples. The quantification of the intensity of Fe3+ EPR spectra in kaolinite, calibrated by an Fe3+-doped corundum sample annealed at high temperature, has provided a basis for determining the Fe3+ distribution between substitutional sites and concentrated domains, like nanometric iron oxides (Malengreau et al., 1994), in natural kaolinite (Balan et al., 2000). The occurrence of concentrated domains is evidenced by the presence of a broad super-paramagnetic signal in the EPR spectra (Fig. 7). The structural Fe3+ content is not directly related to the disordered character of kaolinite. This observation suggests that the increased disorder of kaolinite from iron-rich lateritic samples, is not related to the effect of Fe3+ substitution on the kaolinite structure but to other variables, such as crystal growth conditions. For example, in sediments and soils with a high porosity, where kaolinite occurs as highly ordered crystals with large grain size, the reduction and leaching of associated iron oxides could be more efficient. This increased efficiency might explain some broad correlation observed between lower total iron content and higher order of kaolinite in hydromorphic systems (Fritsch et al., 2002).
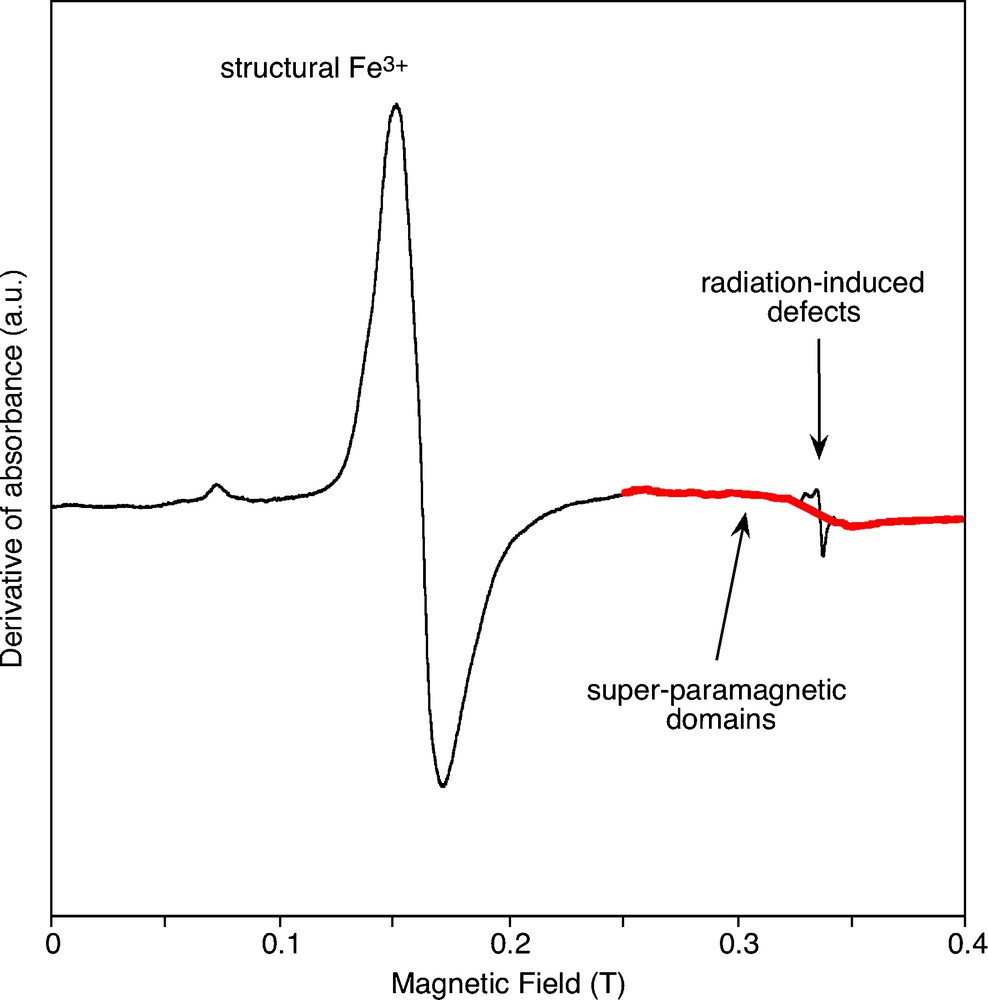
EPR spectrum of a disordered lateritic kaolinite sample. The spectrum displays signals characteristic of structural Fe3+ ions substituted for Al3+ ions, radiation-induced defects and a broad signal (in red) related to super-paramagnetic phases.
Spectre RPE d’un échantillon de kaolinite latéritique désordonnée. Le spectre présente des signaux caractéristiques d’ions Fe3+ structuraux substitués à des ions Al3+, de défauts électroniques induits par irradiation, ainsi qu’un signal large (surligné en rouge) attribué à des phases super-paramagnétiques.
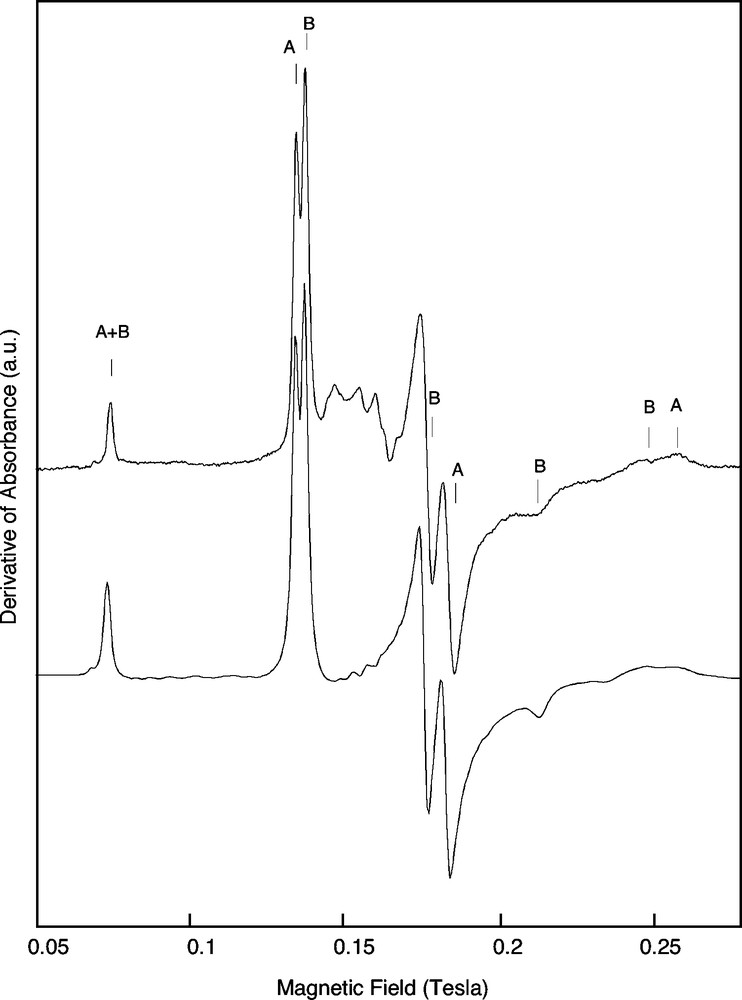
EPR spectrum of structural Fe3+ ions in ordered kaolinite (Fe(II) signal). The spectrum displays the signals arising from Fe3+ ions substituted for Al3+ in the two non-equivalent sites of the kaolinite structure (A and B). Top: Experimental spectrum of a very well ordered sample (DCV) Bottom: Theoretical spectrum obtained using a parameterized spin Hamiltonian (after Balan et al. 1999).
Spectre RPE d’ions Fe3+ structuraux dans une kaolinite ordonnée (signal de type Fe(II)). Le spectre présente les signaux provenant des ions Fe3+ substitués à Al3+ dans les deux sites non équivalents de la structure de la kaolinite (A et B). Haut : spectre expérimental d’un échantillon très bien ordonné (DCV). Bas : spectre théorique obtenu à l’aide d’un Hamiltonien de spin paramétré (d’après Balan et al. 1999).
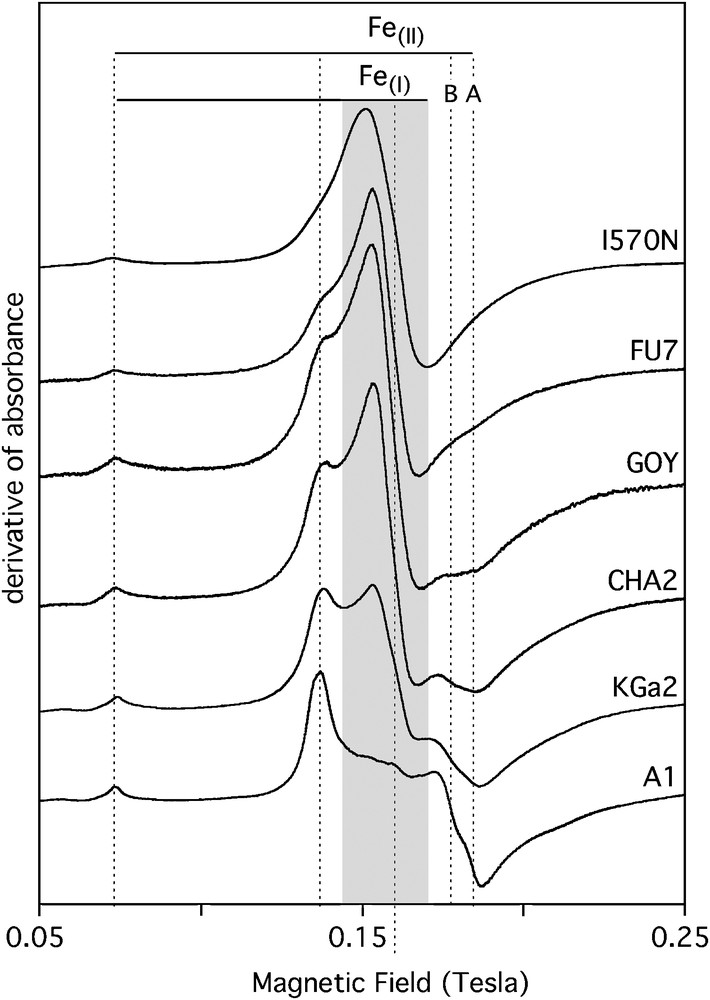
EPR spectrum of structural Fe3+ ions in reference kaolinite-group mineral samples. The kaolinite order decreases from bottom to top. The Fe(II) signal corresponds to Fe3+ substituted for Al3+ ions in the two non-equivalent octahedral sites of well-ordered kaolinite. Note the increasing proportion of the Fe(I) signal in poorly ordered samples. The Fe(I) signal is related to fluctuations in the distortion of octahedral sites related to the stacking disorder.
Spectres RPE d’ions Fe3+ structuraux dans des échantillons de référence de kaolinite. L’ordre d’empilement décroît du bas vers le haut. Le signal de type Fe(II) correspond à des ions Fe3+ substitués à Al3+ dans les deux sites non équivalents de la structure de la kaolinite ordonnée. Noter la contribution croissante du signal de type Fe(I) dans les échantillons désordonnés. Le signal de type Fe(I) est lié à une fluctuation de la distorsion des sites octaédriques, d’un site à l’autre et liée au désordre d’empilement.
All natural kaolinite samples examined so far contain paramagnetic native radiation-induced defects (Fig. 7). Different hole-centers located on oxygen atoms can be differentiated by their spectral signature and possess different production kinetics and thermal stability (Allard et al., 1994; Clozel et al., 1994). A-centers display a half-life of ≈1012 years at room temperature and are then stable over geological periods at the Earth's surface. The center concentration is related to the radiation dose experienced by kaolinite since its formation, thus to geochemical transfers of short-lived radionuclides and/or kaolinite age (Allard and Muller, 1998; Allard et al., 1997, 2003, 2007; Muller et al. 1995). Such applications rely on adequate calibrations using experimental irradiations (Allard and Calas, 2009). This approach has been recently applied to kaolinite samples from lateritic profiles of Brazil, leading to ages constraining the models of weathering processes in these tropical regions (Balan et al., 2005b).
4 Ab initio calculation of the isotopic fractionation properties of low-temperature minerals
Stable isotope geochemistry is increasingly used to investigate lateritic minerals (Giral-Kacmarcik et al., 1998; Girard et al., 2000; Poitrasson et al., 2008; Yapp, 2000; Vitali et al., 2001), providing information about past weathering conditions and element transfers. An essential basis for interpreting the isotopic composition of low-temperature minerals is to know the equilibrium isotopic fractionation factors between different minerals or between minerals and solutions. These fractionation factors can be obtained through different approaches: analysis of natural minerals, experimental studies and computational methods. For the first two approaches, the attainment of equilibrium may be difficult to demonstrate or even to achieve, particularly at low temperature. Theoretical methods thus represent an attractive approach able to provide equilibrium fractionation factors from vibrational properties of crystals or molecules. The theory of equilibrium isotopic fractionation has been firmly established for more than half a century (e.g. Bigeleisen and Mayer, 1947). The calculation of isotopic fractionation factors has been successfully carried out on small molecules for which almost complete sets of vibrational frequencies can be obtained from vibrational spectroscopies (e.g., Richet et al., 1977). In contrast, it is more difficult to determine the complete vibrational properties of crystals and their extrapolation to isotopic fractionation factors usually requires the use of simplified models (Kieffer, 1982). Based on the density functional perturbation theory, it is now possible to compute the phonon dispersion patterns of crystals and to obtain the corresponding reduced partition function ratio as a function of temperature, thus leading to isotopic fractionation factors at any temperature (e.g., Schauble et al., 2006). This approach, although based on the harmonic approximation, has been successfully applied to the stable isotope fractionation of H and O in the kaolinite-quartz-water system (Méheut et al., 2007, 2010). It is worth noting that the calculation of isotopic fractionation properties of liquids and solutions still involves major approximations. For example, the mineral-liquid water fractionation in Méheut et al. (2007) was obtained by combining the theoretical mineral-gas fractionation with the experimental liquid–gas water fractionation. Importantly, the modeling of “conventional” or “unconventional” isotopes can be performed with a similar precision (e.g., Méheut et al., 2009). Iron isotope fractionation between hematite, pyrite, siderite and aqueous iron species has also been investigated by Blanchard et al. (2009). Good agreement with experimental data was achieved for solid–solid equilibrium, confirming that experimental values correspond to the equilibrium isotopic fractionation of iron and allowing an extrapolation to any temperature. In contrast, significant discrepancies of unclear origin are still observed for iron fractionation factors between solid and aqueous species (Blanchard et al., 2009; Rustad and Dixon, 2009). Finally, this approach also permits assessment of the effect of incorporating impurities and minor elements in minerals on isotopic fractionation factors. In low-temperature environments, hematite, like other iron (hydr)oxides, can show substantial aluminum substitution. Modeling the equilibrium structure and vibrational properties of a series of hematites containing various amounts of Al and H defects (Blanchard et al., 2010) provides an explanation of the evolution of the lattice parameters of natural or synthetic aluminous hematite. In addition, the theoretical results show a linear dependence of the reduced partition function ratio of iron and oxygen isotopes on the aluminum content. This effect is sufficiently large to be measurable and to affect the interpretation of natural isotopic compositions. Through these few examples, it seems clear that the development of tools enabling an accurate modeling of the vibrational properties of molecules and solids will strengthen the relations between mineralogy and isotope geochemistry.
5 Future perspectives on low-temperature “mineral physics”
Traditionally, the scientific field referred to as “Mineral Physics” deals with the investigation of deep-Earth processes (e.g., Karato et al., 2000; Rubie et al., 2004). Under high temperature conditions, atomic diffusion provides an efficient attainment of equilibrium conditions and makes easier the use of equilibrium thermodynamic parameters in geophysical models. At low temperature, thermodynamic models based on bulk mineral properties can also be applied to environmental minerals. For example, calorimetric and solubility measurements provide important information on the stability of secondary minerals (e.g., Ligny and de Navrotsky, 1999; Fialips et al., 2001, 2003; Zotov et al., 1998). Reactive-transport models (e.g., Steefel et al., 2005) combining thermodynamic and kinetic parameters have also been applied to investigate weathering processes. Refined models have been developed to better take into account the nucleation of finely divided clay minerals (Fritz et al., 2009). However, extrapolation from laboratory to field is usually less straightforward than in high-temperature systems, for which the chemical composition and intensive parameters such as pressure and temperature already lead to relatively well-constrained systems. In comparison, the number of parameters required to describe low-temperature systems dramatically increases, e.g., accounting for the diversity of the interfaces between minerals and aqueous solutions, for the tremendous importance of porosity and hydrological parameters, for the role of living organisms, and for the long-term geological history of some weathering profiles (see e.g., Brantley et al., 2007).
Along the line of the examples given in this article, it is possible to identify some directions in which developments of mineral-physics investigations of low-temperature mineral phases could provide important information. Spectroscopic tools are widely used to investigate mineral phases sampled in the field, synthesized in the laboratory or probed with remote sensing techniques. Concerning this last aspect, it should be emphasized that such an approach is not limited to Earth environments but has provided major information on the mineralogy of other telluric planets. As an example, near-infrared spectra recorded by the Compact Reconnaissance Imaging Spectrometer for Mars (CRISM) have revealed the spectacular diversity of clay minerals, including kaolinite-group minerals and smectites, occurring at the surface of Mars (Bishop et al., 2008). Improvements in the modeling of spectroscopic signals from first-principles, in combination with appropriate averaging methods required by the powdered nature of environmental samples, should therefore represent an important direction for future research. In particular, much attention should be given to the extraction of physically meaningful parameters from the spectra, overcoming the use of empirical indices of disorder. Such an approach could also be a way to improve the links between our knowledge of the microscopic structure of minerals, including the presence of defects or interfaces, and the determination of other properties, e.g., those related to the chemical reactivity of minerals. Focusing on vibrational properties, the anharmonic character of some phases is still a major limitation to their modeling. Although simple models can be used to discuss anharmonic shifts in weakly H-bonded systems (e.g., Balan et al., 2007b; Pascale et al., 2004), the first-principles modeling of anharmonic effects, that includes temperature-dependent shift, spectral broadening and intensity changes can be properly done only on simple systems not relevant for environmental studies (e.g., Lazzeri et al., 2003); whereas parameterized models have been mostly developed for strongly H-bonded molecular systems (e.g., Henri-Rousseau and Blaise, 1999). The temperature-dependence of spectroscopic signals is, however, an important property that can be used to improve the identification of defects and other disorder parameters in real samples. In addition, the occurrence of diagnostic combination and overtone vibrational bands in the near-infrared range is also related to anharmonic properties of crystals or molecules. The modeling of (dynamic and anharmonic) liquid systems has still to be improved to obtain reliable liquid-solid isotopic fractionation coefficients and chemical reaction constants. The properties of water in confined environments (Mercury et al., 2003; Richard et al., 2007), the relation between the metastable phase diagram of water and mineral precipitation reactions, and the effect of oscillating physical-chemical conditions on the nature and properties of minerals are also promising directions of research to better understand the formation of soils and other porous media.
Finally, the evolution of primary minerals (Fig. 1) under weathering conditions was not treated in this article but has important environmental implications related to, e.g., the geochemical mobility of elements, the disposal of mine tailings, and the storage of waste elements. For example, the stability of zircon in lateritic soils critically depends on its degree of radiation-induced amorphization (Balan et al., 2001a; Delattre et al., 2007), thus limiting the use of Zr as an invariant element in the mass-balance calculations used to quantify weathering processes.


