1 Introduction
Multiple lines of evidence reviewed by Cartigny (2005) and Cartigny et al. (2004) show that diamond formation in the mantle is associated with carbon-bearing fluids. Oxygen fugacity () estimates of the subcratonic lithosphere of the Kaapvaal (e.g., Woodland and Koch, 2003) and Slave (McCammon and Kopylova, 2004) Cratons show that, generally, decreases with increasing depth relative to the Fayalite-Magnetite-Quartz (FMQ) oxygen buffer, e.g. is ∼FMQ − 1 at ∼100 km depth ∼FMQ − 4 at a depth of ∼220 km for the Kaapvaal Craton (e.g., Woodland and Koch, 2003). In such an environment, diamond may precipitate by reduction of a CO2-rich fluid/melt that reacts with the reduced host rocks (e.g., Haggerty, 1999) in the subcontinental lithosphere. Alternatively, which is the topic of this study, diamond may also precipitate by oxidation of reduced mantle fluid species including CH4 (Deines, 1980) and C2H6 as it rises (Taylor and Green, 1988, 1989).
The diamond precipitation reactions including CH4 + O2 → C + 2H2O and C2H6 + 1½O2 → 2C + 3H2O result in an increase of the H2O-activity, and subsequent (local) melting of the surrounding peridotitic mantle. This concept was introduced by Taylor and Green (1988, 1989) and referred to as redox melting, which is considered to be an important process in the cratonic mantle lithosphere (Foley, 2011). The redox melting proposition has gained significant support, based on the fact, as mentioned previously, that reduced fluid species are likely to exist in a mantle fluid, combined with a suitable (e.g. Galimov, 1991; Haggerty, 1999; Kadik, 2006; Stachel and Harris, 2009; Woodland and Koch, 2003). In addition, the chemistry of mineral inclusions in diamond (Jacob et al., 2004; Malkovets et al., 2007; Stachel and Harris, 1997) and stable isotope data of carbon and nitrogen (Thomassot et al., 2007) indicate that diamond precipitation from CH4 is a distinct possibility.
The purpose of this study is, by using thermodynamic calculations, to determine: (1) the diamond precipitation potential from a reduced rising C-O-H fluid in the Kaapvaal cratonic mantle (KM), and (2) the influence of changing P, T, and conditions on this process. Our aim is thus to test whether diamond precipitation, by means of redox melting, is feasible or not. So far, no quantitative study has been done before on mantle fluid oxidation and the associated diamond precipitation as a function of P, T, and . The recently published themodynamic model for C-O-H fluids at mantle conditions (Zhang and Duan, 2009, 2010) and the existence of high-quality data for the KM have created an ideal opportunity to perform this study.
2 Fluid composition of the Kaapvaal cratonic mantle (KM)
2.1 P, T, and data
As will be discussed in the section below, carbon-saturated C-O-H fluid compositions can be calculated if P, T, and are known. Here, we used KM P, T, and data obtained from garnet-olivine-clinopyroxene-orthopyroxene assemblages in non-metasomatised lherzolitic and harzburgitic xenoliths from different kimberlite localities in South Africa (Bultfontein, Finsch, Frank Smith, Jagersfontein, Kimberley, Monastery, Wesselton) and Lesotho (Letseng, Liqhobong, Matsoku) (Lazarov et al., 2009; McCammon et al., 2001; Woodland and Koch, 2003). For consistency, we only used P, T, and data that were calculated from the Al-in orthopyroxene barometer, the two-pyroxene thermometer (Brey and Köhler, 1990), and the Fe2+-Fe3+ redox reaction involving garnet, olivine and orthopyroxene (Gudmundsson and Wood, 1995; Luth et al., 1990), respectively. Only data in which Fe3+ in garnet was determined by Mössbauer spectroscopy were used. All values are reported relative to FMQ, which is calculated as follows:
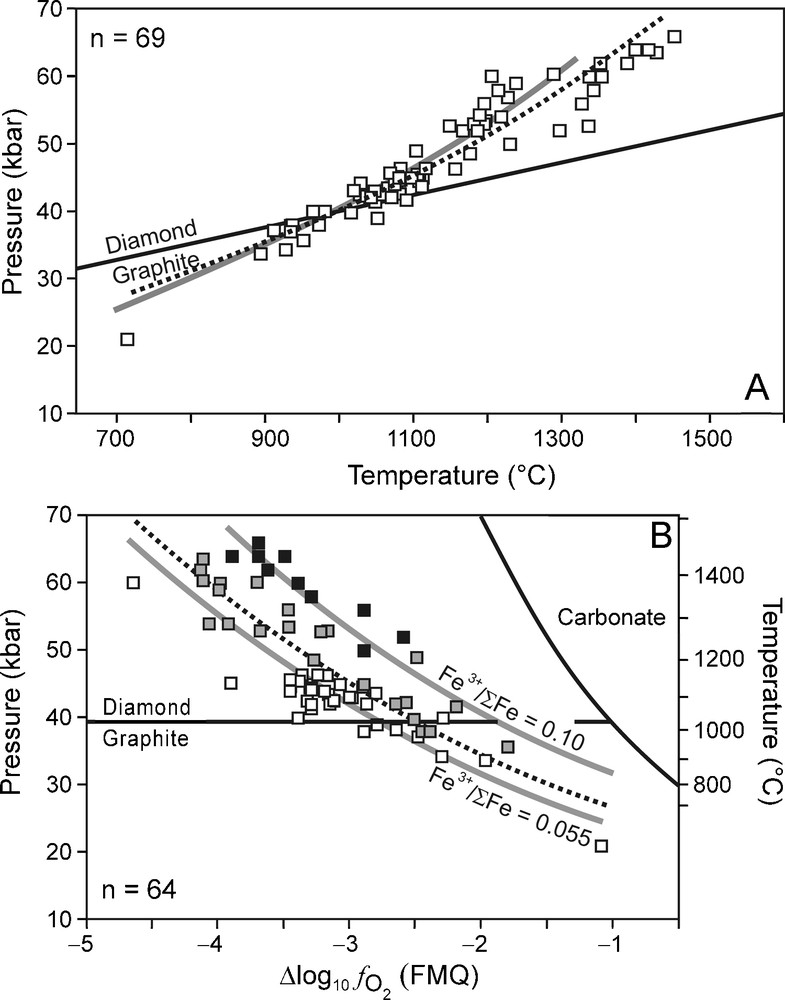
(A) Xenolith-based P-T data for the Kaapvaal mantle (KM) (Lazarov et al., 2009; McCammon et al., 2001; Woodland and Koch, 2003). The best fit line for the P-T data (dotted line) overlaps almost perfectly with that of the 43 mW/m−2 surface heat flow geotherm (grey line, after Pollack and Chapman, 1977) and is given by the equation: P (kbar) = 11.455 exp [0.0012 T (°C)]. (B) data for KM (Lazarov et al., 2009; McCammon et al., 2001; Woodland and Koch, 2003). Black squares: samples with Fe3+/ΣFe > 0.10; grey squares: samples of which 0.055 ≤ Fe3+/ΣFe ≤ 0.10; white squares: samples with Fe3+/ΣFe < 0.055. The best fit line for the data is given by the equation P (kbar) = 20.310 exp [−0.265 ΔFMQ]. Grey lines: relationship calculated for isochemical systems of which garnet Fe3+/ΣFe = 0.10 and 0.055 for the 43 mW/m−2 geotherm (grey lines) (Creighton et al., 2009). The carbonate stability field calculated from the enstatite-magnesite-olivine-graphite/diamond buffer (calculated for the best fit P-T curve) is indicated (Stagno and Frost, 2010). For both (A) and (B) the diamond-graphite boundary is calculated using GFluid (Zhang and Duan, 2010) from thermodynamic data by Fried and Howard (2000).
(A) Conditions P-T estimées d’après des xénolithes du manteau du Kaapvaal (Lazarov et al., 2009 ; McCammon et al., 2001 ; Woodland and Koch, 2003). La meilleure ligne de régression pour ces données P-T (pointillés) suit à peu près parfaitement le géotherme correspondant à un flux de chaleur en surface de 43 mW/m−2 (ligne grise, d’après Pollack and Chapman, 1977), d’équation : P (kbar) = 11,455 exp [0,0012 T (°C)]. (B) Données pour Kaapvaal mantle (KM) (Lazarov et al., 2009 ; McCammon et al., 2001 ; Woodland and Koch, 2003). Carrés noirs : échantillons dont Fe3+/ΣFe > 0,10 ; carrés gris : échantillons pour lesquels 0,055 ≤ Fe3+/ΣFe ≤ 0,10 ; carrés vides : échantillons dont Fe3+/ΣFe < 0,055. La meilleure ligne de régression pour les données est fournie par l’équation P (kbar) = 20,330 exp [-0,265 FMQ]. Lignes grises : relation calculée pour les systèmes isochimiques dont le grenat Fe3+/ΣFe = - 0,10 et 0,055 pour le géotherme 43 mW/m-2 (lignes grises) (Creighton et al., 2009). Le champ de stabilité du carbonate, calculé à partir du tampon enstatite-magnésite-olivine-graphite/diamant (calculé pour la meilleure courbe de régression P-T) est indiqué (Stagno et Frost, 2010). Pour A et B, la limite diamant/graphite est calculée en utilisant Gfluid (Zhang et Duan, 2010) à partir des données thermodynamiques et Fried et Howard (2000).
2.2 C-O-H fluid composition calculations
A carbon-saturated (i.e., diamond or graphite present) C-O-H fluid generally comprises H2O, CO2, and CH4 as the most dominant fluid species (e.g., French, 1966; Ohmoto and Kerrick, 1977). For such a system, the carbon activity in the fluid phase () is 1 and becomes invariant if is known. Due to the reduced nature and relatively high P of KM, additional fluid species such as H2 and C2H6 may also be present in significant quantities. The Gibbs energy minimisation method as proposed by Zhang and Duan (2009, 2010) is an appropriate thermodynamic model available for the calculation of the fluid composition at KM conditions. Here, the fluid composition is calculated by establishing the minimum Gibb's energy for the system using an equation of state that is valid for all relevant fluid species at mantle P-T conditions. All calculations were carried out using the Excel spreadsheet GFluid (Zhang and Duan, 2010). The details of the calculations and the equation of state used are given in Zhang and Duan (2009, 2010).
The GFluid model has been compared with experimental results within the P-T range of 5–30 kbar and 1000–1500 °C, respectively, showing differences generally within ±5% (Zhang and Duan, 2009). At P > 30 kbar, however, experimental data (Sokol et al., 2009) show significant quantities of C2H6 and H2, at the expense of CH4, in contrast to the calculated fluid compositions (Sokol et al., 2009). Both C2H6 and H2 are the products of the partial dissociation of CH4 (e.g., Scott et al., 2004; Spanu et al., 2011). The GFluid model appears to underestimate the effect of partial dissociation of CH4 (Sokol et al., 2009). However, a molecular dynamics study performed by Spanu et al. (2011) appears to solve this contradiction. This study shows that the actual dissociation of CH4 requires transition metals (in particular noble metals such as Ir) and that CH4 occurs in metastable conditions if these metals are absent. As mantle metal saturation is only to be expected at P > ∼80 kbar (Frost and McCammon, 2008, Rohrbach et al., 2011), CH4 is expected to exist in a metastable condition (Spanu et al., 2011) at P < ∼80 kbar. Consequently, the GFluid thermodynamic model can be used for the purpose of this study if P < 80 kbar.
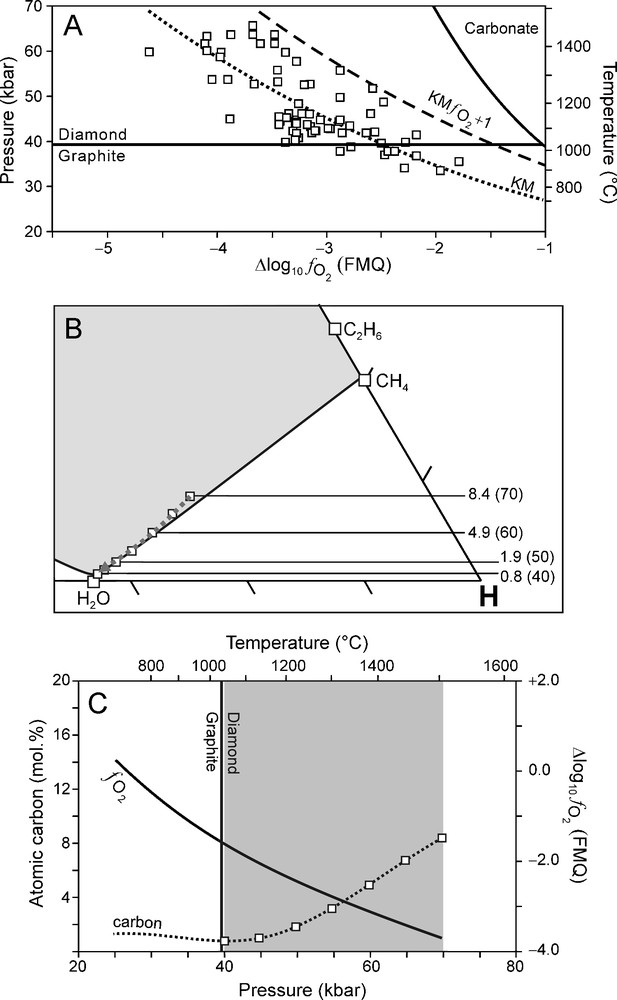
Using the correlations between P and T (Fig. 1A), and P and (Fig. 1B), the composition of a C-O-H fluid in KM can be calculated (Fig. 2A) as a function of pressure. The calculation results are summarised as follows (Fig. 2A): (1) An ambient C-O-H fluid in KM will be dominated by H2O, CH4 and C2H6 whereas CO2 will be absent; (2) The concentrations of CH4, C2H6 and H2 increase with depth at the expense of H2O; (3) The atomic carbon content of the fluid phase increases with pressure (Fig. 2B). (4) Not only CH4, but also C2H6 is a potential fluid species from which diamond can precipitate by oxidation. These results are in good agreement with those from other studies (e.g. Kadik, 2006; Saxena, 1989; Simakov, 1998; Wood et al., 1990; Zhang and Duan, 2009).
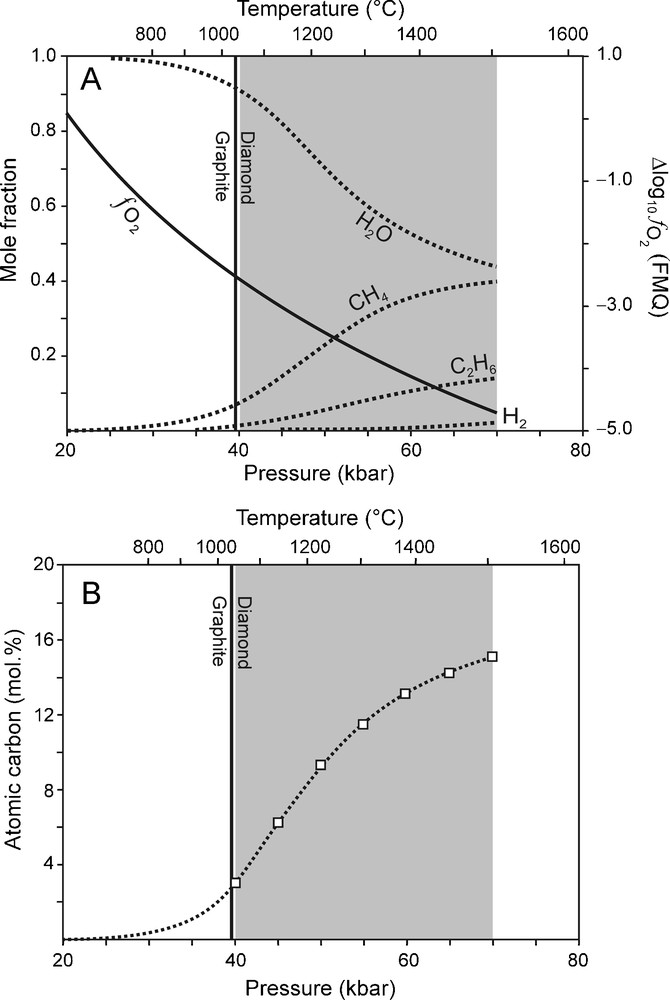
(A) Carbon-saturated fluid compositions calculated as a function of P for Kaapvaal mantle (KM), using the best fit equations between P-T and (Fig. 1) illustrating that the main fluid species at P between 40 and 70 kbar (grey area) are H2O, CH4 and C2H6. (B) Variation of the fluid atomic carbon content (dotted line) for the carbon-saturated fluid compositions calculated as a function of P for KM (see A). Squares: fluid atomic carbon content at 70 to 40 kbar (5 kbar interval).
(A) Compositions de fluides saturés en carbone, calculées en fonction de P pour Kaapvaal mantle (KM), en utilisant les meilleures courbes de régression entre P-T and (Fig. 1), illustrant le fait que les espèces les plus importantes pour P entre 40 and 70 kbar (surface grise) sont H2O, CH4 and C2H6. (B) Variation de la teneur en carbone atomique du fluide (ligne pointillée) pour des compositions saturées en carbone, calculées en fonction de P pour KM (voir A). Carrés : teneur du fluide en carbone atomique de 70 à 40 kbar (intervalles de 5 kbar).
3 Thermodynamic modelling of a rising reduced fluid through Kaapvaal cratonic mantle (KM)
3.1 Kaapvaal cratonic mantle (KM) conditions
The thermodynamic factors involved in the precipitation of diamond from an upwards percolating reduced fluid in the subcratonic lithosphere, include changes in ambient pressure and temperature, as well as changes in of the fluid phase (which is controlled by of the surrounding mantle lithosphere with which it equilibrates). Isobaric-isothermal C-O-H ternary diagrams are appropriate for visualising and assessing the process of diamond crystallisation from such an upward moving mantle fluid.
Fig. 3A shows a C-O-H ternary diagram that is calculated at an arbitrarily chosen fixed P and T of 50 kbar and 1227 °C, respectively, that plots on the best fit P-T curve (Fig. 1A). The C-O-H ternary diagram is characterised by a fluid-only region (white area in Fig. 3A) and a field of fluid + diamond (grey area in Fig. 3A). These are separated from each other by the carbon saturation surface (black line in Fig. 3A). The carbon saturation surface represents the variation of carbon-saturated () C-O-H fluid compositions as a function of (Fig. 3B, C). Fluids situated on the carbon saturation are in dynamic equilibrium with diamond, i.e. there is no net consumption or production of diamond. However, any changes of P, T and/or disturbs this equilibrium and may result in either the crystallisation of diamond from the fluid or in the resorption of diamond by the fluid. Fluid compositions that are situated in the grey field (Fig. 3A) are supersaturated in carbon. Studies for the graphite-C-O-H fluid system have shown that in such a case the graphite that precipitates is poorly crystalline (Ziegenbein and Johannes, 1989). Therefore, it is expected that, in the diamond stability field, carbon supersaturated fluids will probably result in the precipitation of poor quality diamond such as polycrystalline aggregates (Bureau et al., 2012; Sunagawa, 1990). Carbon undersaturated fluids, on the other hand, are situated in the white field in Fig. 3A, and these fluids will have the ability to dissolve diamond if present.
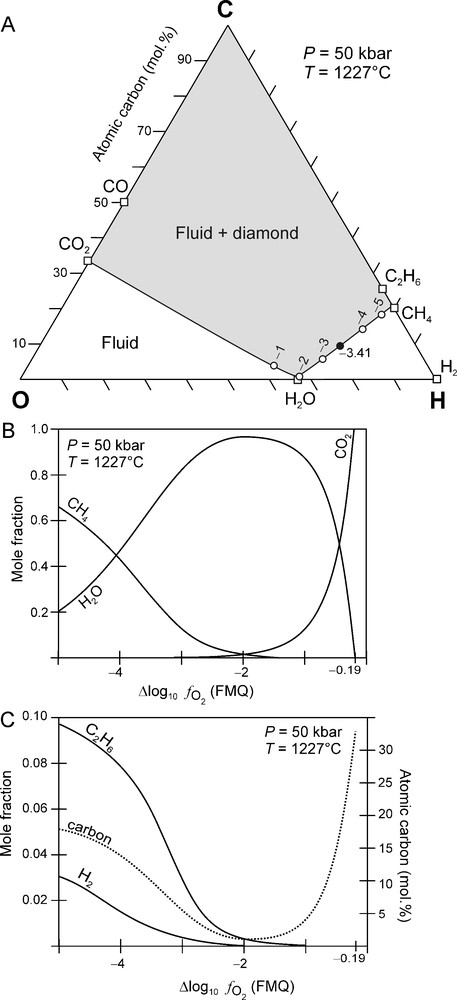
(A) C-O-H ternary diagram constructed at 50 kbar and 1227 °C. Solid line: carbon saturation surface, i.e. all fluid compositions in equilibrium with diamond are located on this surface. Open circles: values relative to FMQ. Black circle: carbon-saturated fluid composition for Kaapvaal mantle (KM) at 50 kbar and 1227 °C: FMQ − 3.41. See text for further explanation. (B) and (C) Variation of a C-O-H fluid composition and the fluid atomic carbon content along the carbon saturation surface (see A) as a function of at 50 kbar and 1227 °C.
(A) Diagramme ternaire C-O-H à 50 kbar et 1227 °C. Trait continu : surface de saturation en carbone, i.e. toutes les compositions de fluides en équilibre avec le diamant sont situées sur cette surface. Cercles vides : valeurs de relativement à FMQ. Cercle noir : composition du fluide saturé en carbone pour Kaapvaal mantle (KM) à 50 kbar et 1227 °C : FMQ − 3,41. Voir le texte pour plus d’explications. (B) et (C) Variation de la composition d’un fluide C-O-H et de la teneur en carbone atomique le long de la surface de saturation en carbone (voir A) en fonction de à 50 kbar et 1227 °C.
For the specified P-T conditions, a C-O-H fluid is dominated by H2O and CO2 if it is relatively oxidised (i.e., (Fig. 3B) whereas, when more reduced , it will comprise predominantly of H2O and CH4, and, to a lesser extent, also C2H6 and H2 (Fig. 3B, C). The fluid is carbon undersaturated if , in which case diamond cannot coexist with the fluid.
The carbon saturation surface in a C-O-H ternary diagram will move downwards towards the O-H binary with isobaric cooling (i.e., increasing the diamond stability field) whereas it will move upwards towards the C apex with isothermal decompression (i.e., decreasing the diamond stability field). This is an important fact that must be emphasised; the diamond stability field in a diamond-C-O-H fluid system may either increase or decrease during cooling and decompression, depending on ΔT/ΔP of the geotherm. If the diamond stability decreases, diamond precipitation from a rising C-O-H fluid would be impossible as the fluid becomes carbon undersaturated. Alternatively, the diamond stability field of a diamond-C-O-H fluid system may also increase during cooling and decompression, in which case the rising C-O-H fluid becomes carbon supersaturated. Therefore, in order to evaluate the possibility of diamond precipitation from a rising reduced fluid caused by oxidation, both ΔT/ΔP and must be taken into consideration.
We considered a pressure interval of 70 to 40 kbar (5 kbar intervals) for the thermodynamic calculations, which is based on the total range of reported diamond crystallisation pressures (Phillips et al., 2004; Stachel and Harris, 2008). For each P we: (1) calculated the corresponding T and from the best fit equations (Fig. 1), (2) determined the carbon saturation surface in a C-O-H ternary diagram at the specified P and T, and (3) determined the unique C-O-H fluid composition for the given conditions. The results of these calculations are shown in Fig. 4A–G and combined into one (Fig. 4H) for interpretative purposes.
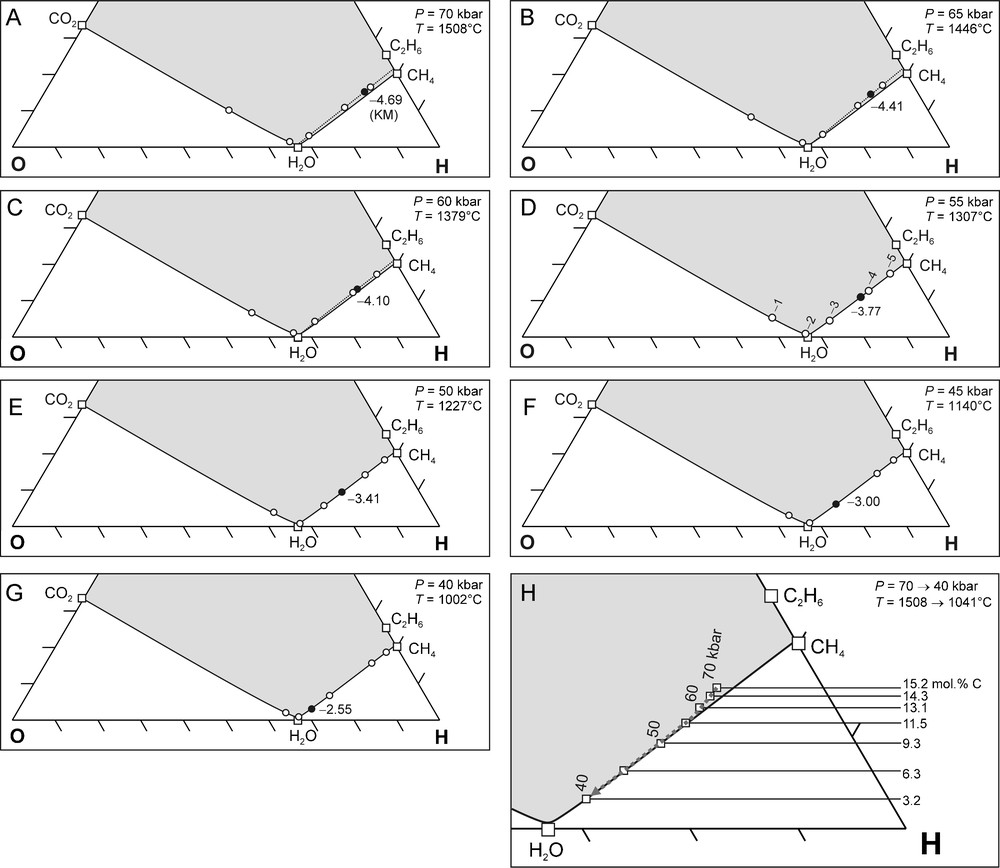
(A–G) C-O-H ternary diagrams showing carbon saturation surfaces calculated for P = 70 to 40 kbar (5 kbar interval), and corresponding T calculated from the best fit P-T equation (Fig. 1A). The of Kaapvaal mantle (KM) (black circles) are indicated at each pressure and calculated from the best fit equation (Fig. 1B). Open circles: values relative to FMQ as indicated in D. (H) Compilation of (A–G). The carbon saturation surfaces for 55, 50, 45, and 40 kbar, and their corresponding temperatures overlap completely. The 70, 65 and 60 kbar carbon saturation surfaces are situated slightly above the others (dotted lines). The compositional evolution of an upward migrating fluid in KM is shown by the grey dashed arrow. The decrease in the fluid atomic carbon content with decreasing pressure (15.2 mol.% at 70 kbar to 3.2 mol.% at 40 kbar) is caused by diamond precipitation. See text for further discussion.
(A–G) Diagrammes ternaires C-O-H indiquant les surfaces de saturation en carbone, calculées pour P = 70 à 40 kbar (intervalles de 5 kbar), ainsi que T correspondant, calculé d’après les courbes de régression P-T (Fig. 1A). Les de Kaapvaal mantle (KM) (cercles noirs) sont indiquées pour chaque pression et calculées en fonction de la courbe de régression de l’équation (Fig. 1B). Cercles blancs : valeurs de relativement à FMQ, ainsi qu’indiqué en D. (H) Compilation de (A–G). Les surfaces de saturation en carbone pour 55, 50, 45, and 40 kbar, et leurs températures correspondantes, se recouvrent complètement. Les surfaces de saturation en carbone pour 70, 65 and 60 kbar sont situées légèrement au-dessus des surfaces précédentes (lignes pointillées). L’évolution de la composition d’un fluide migrant vers le haut dans KM est indiquée par la flèche grise tiretée. La décroissance des teneurs en carbone atomique à pression décroissante (de 15,2 mol.% à 70 kbar à 3,2 mol.% à 40 kbar) est provoquée par la précipitation de diamant. Voir le texte pour une discussion plus détaillée.
The carbon saturation surfaces at 40, 45, 50, and 55 kbar are at the exact same position in a C-O-H ternary diagram, whereas at 60, 65 and 70 kbar the carbon saturation surface is positioned slightly above the others (Fig. 4H). This implies that a rising KM C-O-H fluid is carbon saturated or becomes slightly supersaturated. In other words, the KM geothermal conditions allow diamond precipitation from a rising C-O-H fluid as the condition of carbon saturation is met. Further, the fact that the fluid is only slightly carbon supersaturated implies that the diamonds that precipitate from such a fluid are likely to be highly crystalline (Ziegenbein and Johannes, 1989), i.e. typical of that utilised in the gem industry (single crystals or simple twins of good transparency) as opposed to industrial quality boart (Bureau et al., 2012; Sunagawa, 1990).
During migration over a depth interval corresponding to an ascent from 70 to 40 kbar pressure, the fluid H2O concentration increases whereas the concentrations of CH4 and C2H6 decrease (grey dashed arrow in Fig. 4H). Consequently, the atomic carbon content of the fluid phase decreases, which is due to the precipitation of diamond. This change in atomic carbon content can thus be used as an indication of the diamond precipitation potential of the fluid. The overall change in fluid atomic carbon content between 70 and 40 kbar is 12.0 mol.% (Fig. 4H). A comparison of the relative differences in fluid atomic carbon content for each 5 kbar interval (Fig. 2B, Fig. 4H) shows a gradual increase with decreasing P (Fig. 2B, Fig. 4H): from 0.9 mol.% (between 70 and 65 kbar) to 3.1 mol.% (between 45 and 40 kbar). This implies an increase of the diamond precipitation potential with decreasing P.
The reactions that are responsible for the change in the fluid composition can be deduced from the direction of the arrow in the C-O-H ternary diagram (cf. Fig. 4H and Fig. 5) and include the net oxidation reaction (direction 1 in Fig. 5):
| (1) |
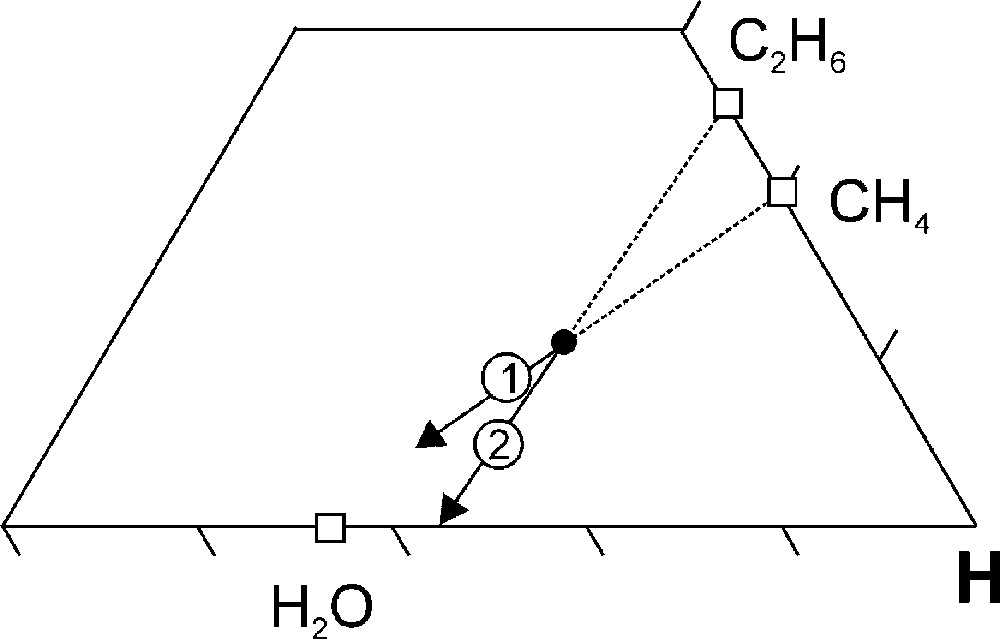
C-O-H ternary diagram showing the expected compositional change (indicated with the arrows) for a H2O-CH4-C2H6 fluid as a result of the following net diamond precipitation reactions: 1, CH4 + O2 → 2H2O + C; 2, C2H6 + 1½O2 → 3H2O + 2C.
Diagramme ternaire C-O-H indiquant les variations de composition (indiquées par les flêches) d’un fluide H2O-CH4-C2H6 lors de la précipitation de diamant, d’après les réactions : 1, CH4 + O2 → 2H2O + C ; 2, C2H6 + 1½O2 → 3H2O + 2C.
and (direction 2 in Fig. 5):
| (2) |
Comparing Fig. 4H and Fig. 5 indicates that both reaction (1) and (2) take place at P > 60 kbar, whereas at P < 60 kbar reaction (1) dominates. The oxygen that is required for the reactions is extracted from the surrounding lithosphere, i.e. the lithosphere acts as an oxygen source. Alternatively, the reactions can also be written in an oxygen-absent manner:
| (3) |
| (4) |
in which case the surrounding lithosphere acts as a hydrogen reservoir. In presence of water, reactions (1) and (2) are thermodynamically equivalent to reactions (3) and (4), respectively (Eugster, 1959).
The calculation results can be compared with diamond crystallisation pressures, using Brey and Köhler's (1990) Al-in orthopyroxene barometer, based on non-touching garnet-orthopyroxene inclusion pairs in diamonds from the De Beers Pool kimberlites in Kimberley (Phillips et al., 2004) (Fig. 6). Some care should be taken with comparing the model calculations with the data by Phillips et al. (2004) (Fig. 6). First, Phillips et al. (2004) calculated temperatures with the garnet-orthopyroxene thermometer (Harley, 1984) and not the two-pyroxene thermometer (like all the other data used in this study) as clinopyroxene was absent. Second, the crystallisation pressures are slightly higher compared to the best fit geotherm (Fig. 6A). Lastly, a few of the Kimberley samples deviate from the best fit curve (Fig. 6B). However, despite these limitations, we feel that the comparison of our results with those of Phillips et al. (2004) will give some indication on whether diamond precipitation from a reduced fluid can be supported or should be rejected outright. The data by Phillips et al. (2004) show that more diamonds tend to crystallise as the pressure decreases (Fig. 6 C). This is in reasonable good agreement with the model calculations (Fig. 6 C).

(A) P-T data of Kimberley xenoliths (open squares) and Kimberley diamond inclusions (solid squares). Dotted line: best fit line obtained from xenolith data (Fig. 1A). (B) data of Kimberley xenoliths (open squares). Dotted line: best fit line obtained from xenolith data (Fig. 1B). (C) Histogram (black outlined bars) showing crystallisation pressure estimations of Kimberley diamonds (Phillips et al., 2004). The grey bars indicate the expected frequency of crystallisation pressures based on the calculation results (Fig. 4H). These results were converted into frequencies for different pressure intervals by normalising the differences in fluid atomic carbon content for each 5 kbar interval against the total change (from 70 to 40 kbar) of the fluid atomic carbon content.
(A) Données P-T des xénolithes de Kimberley (carrés vides) et des inclusions dans les diamants de Kimberley (carrés pleins). Ligne pointillée : courbe de régression d’après les données des xénolithes (Fig. 1A). (B) Données des xénolithes de Kimberley (carrés vides). Ligne pointillée : courbe de régression à partir des données des xénolithes (Fig. 1B). (C) Histogramme (barres soulignées en noir) des pressions estimées de cristallisation des diamants de Kimberley (Phillips et al., 2004). Les barres grises indiquent les fréquences attendues des pressions lors de la cristallisation, d’après les résultats des calculs (Fig. 4H). Les fréquences pour les différents intervalles de pression ont été obtenues en normalisant les différences de teneur en carbone atomique du fluide par intervalle de 5 kbar par rapport à la variation totale entre 70 et 40 kbar.
3.2 Variable Kaapvaal cratonic mantle (KM) redox conditions
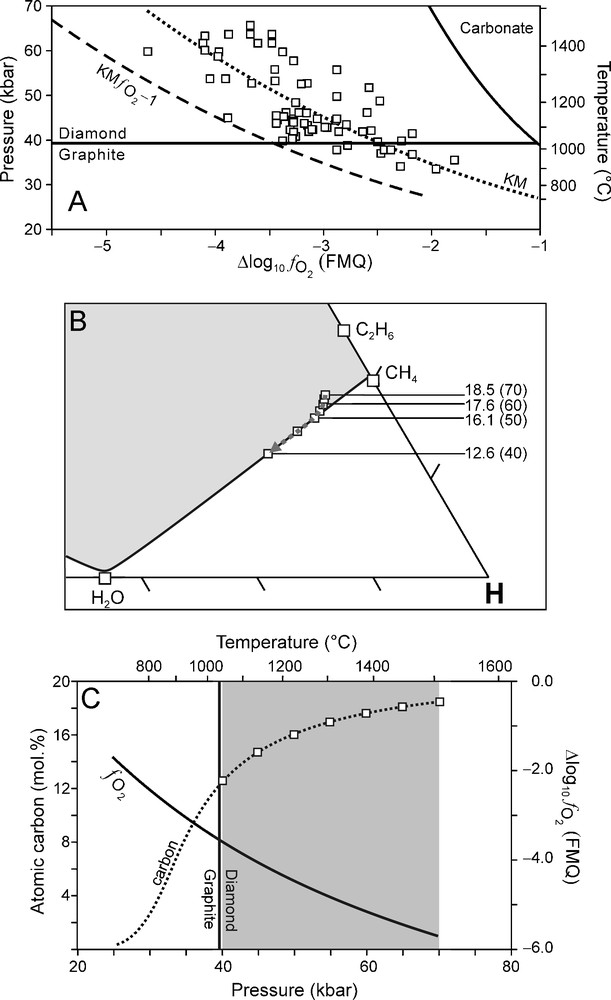
Although a reasonable good correlation was found between it is to be expected (as shown by the scatter of data points in Fig. 1B) that there are lateral variations within KM (Luth, 1999). In order to evaluate the effect of varying redox conditions on the composition of an ascending C-O-H fluid and the crystallisation of diamond, we have performed calculations of C-O-H fluid compositions for two possible scenarios. In the first scenario, we assume that of the surrounding mantle (over the entire depth interval of interest) is one log10 unit higher (i.e., more oxidised) than for KM (KM Fig. 7). In the second scenario is considered to be one log10 unit lower than KM (KM Fig. 8). These two scenarios were chosen so that the entire scatter of the data points are accommodated for (Fig. 7A, Fig. 8A).The results of these two scenarios are compared to that of KM (Fig. 9).
(A) relationship (Kaapvaal mantle (KM) ) used for modelling calculations (dashed line) of which the results are illustrated in (B) and (C). (B) C-O-H ternary diagram showing fluid compositions calculated for 70 to 40 kbar (5 kbar interval) and corresponding T calculated from the best fit P-T equation (Fig. 1A). Fluid atomic carbon content is indicated for 70–40 kbar (10 kbar interval). (C) Variation of (solid line) and the fluid atomic carbon content (dotted line) as a function of pressure. Squares: fluid atomic carbon content at 70 to 40 kbar (5 kbar interval).
(A) Relation (Kaapvaal mantle (KM) ) utilisée pour la modélisation (ligne tiretée), dont les résultats sont donnés en (B) and (C). (B) Diagramme ternaire C-O-H indiquant les compositions calculées du fluide entre 70 et 40 kbar (intervalles de 5 kbar) et les T correspondantes, calculées d’après la courbe de régression de l’équation P-T (Fig. 1A). La teneur du fluide en carbone atomique est donnée pour 70-40 kbar (intervalles de 10 kbar). (C) Variation de (ligne continue) et de la teneur en carbone atomique (ligne tiretée) en fonction de la pression. Carrés : teneur du fluide en carbone atomique de 70 à 40 kbar (intervalle de 5 kbar).
(A) relationship (Kaapvaal mantle (KM) ) used for modelling calculations (dashed line) of which the results are illustrated in (B) and (C). (B) C-O-H ternary diagram showing fluid compositions calculated for 70 to 40 kbar (5 kbar interval) and corresponding T calculated from the best fit P-T equation (Fig. 1A). Fluid atomic carbon content is indicated for 70-40 kbar (10 kbar interval). (C) Variation of (solid line) and the fluid atomic carbon content (dotted line) as a function of pressure. Squares: fluid atomic carbon content at 70 to 40 kbar (5 kbar interval).
(A) Relation (Kaapvaal mantle (KM) ) utilisée pour la modélisation (ligne tiretée), dont les résultats sont donnés en (B) and (C). (B) Diagramme ternaire C-O-H indiquant les compositions de fluide calculées entre 70 et 40 kbar (intervalles de 5 kbar), ainsi que les T correspondantes, calculées d’après la courbe de régression de l’équation P-T (Fig. 1A). La teneur en carbone atomique du fluide est indiquée entre 70- et 40 kbar (intervalles de 10kbar). (C) Variation de (ligne continue) et teneur en carbone atomique du fluide (ligne pointillée) en fonction de la pression. Carrés : teneur en carbone atomique du fluide entre 70 et 40 kbar (intervalles de 5 kbar).

Decrease in fluid atomic carbon content for different pressure intervals for the different scenarios as explained in the text. The decrease in atomic carbon content is the result of diamond precipitation and thus a reflection of the diamond precipitation potential.
Décroissance de la teneur en carbone atomique du fluide pour les différents intervalles de pression, d’après les différents scénarios indiqués dans le texte. La décroissance des teneurs en carbone atomique résulte de la précipitation de diamant et indique donc le potentiel de formation de diamant.
For the oxidised scenario (KM Fig. 7A), the fluid is generally H2O rich (Fig. 7B). The dominant net reaction for diamond precipitation in this instance is the oxidation of CH4 according to reaction (1) (cf. Fig. 5 and Fig. 7B). Compared to KM, this scenario favours diamond crystallisation at P > 60 kbar (Fig. 9). However, at P < 60 kbar, the diamond precipitation potential is significantly less compared to KM (Fig. 9).
A more reduced environment (KM Fig. 8A) results in a systematic shift of the fluid compositional evolution towards a more CH4-rich starting composition (Fig. 8B). The change in the fluid atomic carbon content between 70 and 40 kbar (Fig. 8B, C) is significantly less compared to that for KM (Fig. 9). The net diamond precipitation reaction at high P (70 to 60 kbar) is dominated by the oxidation of C2H6 according to reaction (2) (cf. Fig. 5 and Fig. 8B) whereas at P < 60 kbar the oxidation of CH4 (reaction (1)) is the dominant net diamond precipitation reaction (cf. Fig. 5 and Fig. 8B).
3.3 Effect of redox melting on diamond crystallisation
As mentioned previously, the increase of the H2O activity results in partial melting of the mantle due to a decrease of the mantle solidus temperature (Foley, 2011; Taylor and Green, 1988, 1989). The H2O will subsequently be removed from the fluid phase as it is concentrated in the melt phase (Foley, 2011). The elimination of H2O from the fluid phase has an interesting effect on diamond crystallisation (Fig. 10). The removal of H2O will “push” the fluid composition back along the carbon saturation surface to become more reduced relative to the host rock. As a result, diamond crystallisation will occur according to reaction (1) and/or (2) as the C-O-H fluid re-equilibrates towards the redox state of the host rock. Obviously, this process is dependent on the amount of H2O that is removed, which is directly related to efficiency of the redox melting to physically remove H2O from the fluid phase. It is important to note that the H2O concentration in the fluid phase will increase again during diamond crystallisation, i.e. the entire process may repeat itself. The limiting factor to this repetition is the possibility to oxidise CH4 and C2H6, which depends on the ability of the host rock to act either as an O2 source or H2 reservoir. In other words, the process will cease if the immediate surroundings of diamond crystallisation site cannot supply O2 or absorb H2.
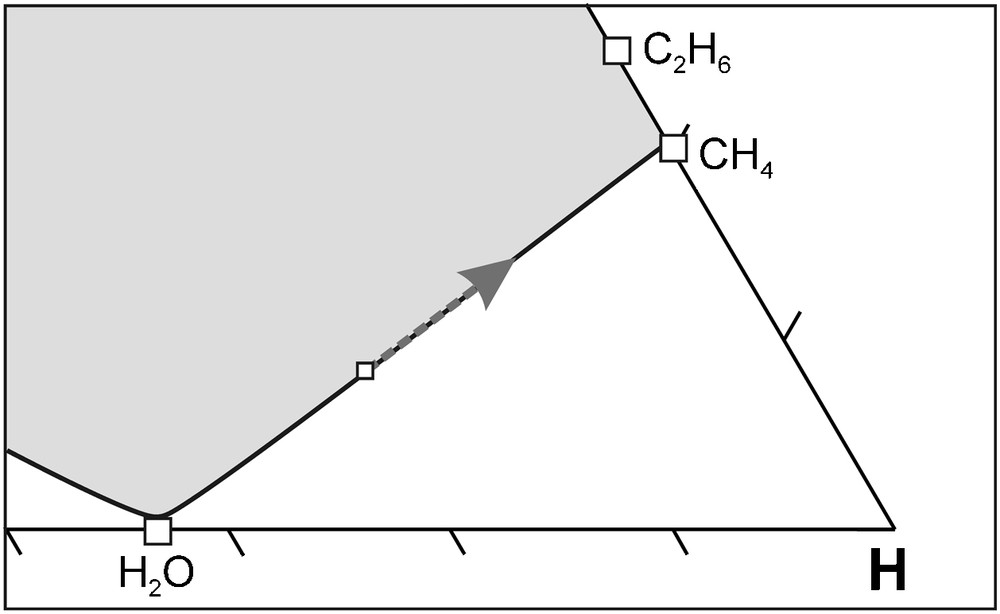
Illustration of water removal from a carbon-saturated C-O-H fluid at isobaric-isothermal conditions. Removal of H2O causes the fluid composition to move “back” along the carbon saturation surface to become more reduced relative to the host rock . As a result, diamond crystallisation will occur by CH4 oxidation. See text for further discussion.
Illustration de l’effet de l’élimination de l’eau dans un fluide C-O-H saturé en carbone, à des conditions isobares-isothermes. L’élimination de l’eau fait se déplacer la composition du fluide “en arrière” le long de la surface de saturation en carbone, la rendant plus réduite par rapport à la de la roche encaissante. Il en résulte une cristallisation de diamant par oxydation de CH4. Voir le texte pour une discussion plus détaillée.
4 Conclusions
The results of this study show that redox melting along with diamond precipitation is possible in the Kaapvaal lithospheric mantle because of its suitable environment. The calculations show that in such a case, crystallisation of diamond occurs of a carbon-saturated or slightly supersaturated C-O-H fluid, i.e. the diamonds that crystallise from such a fluid should be highly crystalline and of good quality. The removal of H2O from the fluid phase by redox melting is an additional factor that would stimulate diamond crystallisation as it would result in a relative increase of CH4 and C2H6 and thus fluid reduction. In this case, the redox difference between the fluid and the host rock is not caused by an ascending fluid into a more oxidised environment but by isobaric-isothermal reduction of the fluid due to H2O removal. This effect, however, cannot be quantified as it depends on the exact amount of water that is removed.
The calculations demonstrate that diamond precipitation from a rising reduced fluid becomes less favourable when: (1) the environment is either more reduced or oxidised relative to the KM best fit curve, and (2) the cratonic lithosphere shows a cooler geotherm in comparison to the KM P-T best fit curve. In this case, the diamond stability field may actually decrease with decreasing P and T, i.e. the ascent of the reduced C-O-H fluid will render it to become carbon undersaturated and thus prohibit diamond precipitation.
Generally, it can be concluded that even if a reduced mantle fluid exists and decreases with a depth, redox melting and the associated diamond precipitation may be insignificant or not possible. This might be in particular the case if lateral variations disturb the general trend of decreasing with increasing depth. Only high-quality data of the relevant region and thermodynamic calculations as done in this study can determine whether redox melting along with diamond crystallisation is a viable option.
Acknowledgements
This project was supported with funds from the DST Research Chair in Geometallurgy, administered by the National Research Foundation of South Africa (FV). Comments on a previous version of this manuscript by Katie Smart and Jeff Harris are highly appreciated. We would like to thank Pierre Cartigny and an anonymous reviewer for their detailed and constructive reviews.


