1 Introduction
With the advent of high-precision multicollection-inductively coupled plasma-mass-spectrometry (MC–ICP–MS), high-precision measurement (< 50 ppm per atomic mass unit) of “non-traditional” stable isotopes of alkali earth elements and transition metals became possible. Owing to its omnipresence in rocks and minerals, and its central role in biochemistry, Fe has received much of the attention, both in experimental and theoretical studies. For example, Beard et al. (1999) found that the bacterium Shewanella algae fractionates Fe isotopes by 0.7 permil/amu (atomic mass unit) during the reduction of FeIII to FeII and that isotopic exchange between different Fe complexes and oxidation states, as well as adsorption of Fe onto inorganic particles, can generate isotopic fractionations of the same magnitude as bacterium reduction (Anbar, 2004; Anbar et al., 2000, 2005; Brantley et al., 2001, 2004; Dideriksen et al., 2008; Fujii et al., 2006; Hill et al., 2009; Johnson et al., 2004; Mandernack et al., 1999; Welch et al., 2003; Wiesli et al., 2004) and biologically induced Fe isotopes fractionation made by higher animals (Hotz et al., 2011; Ohno et al., 2004; Walczyk and von Blanckenburg, 2002, 2005).
Following the discovery of biologically induced isotopic fractionation, metal stable isotopes have been used to trace metal transport in the soil/plant system [see the recent review by von Blanckenburg et al. (2009) and Schmitt et al. (2012)] and isotopic fractionation induced by higher plants has been detected for Zn (Arnold et al., 2010a,b; Aucourt et al., 2011; Caldelas et al., 2011; Moynier et al., 2009; Viers et al., 2007; Weiss et al., 2005), Cu (Jouvin et al., 2012; Weinstein et al., 2011), Mg (Black et al., 2008; Bolou-Bi et al., 2010), Ca (Cenki-Tok et al., 2009; Cobert et al., 2011; Schmitt et al., 2013), Si (Opfergelt et al., 2006; Keller et al., 2012); and Fe (Guelke and von Blanckenburg, 2007; Kiczka et al., 2010).
Only three studies report high-precision Fe isotopic composition in higher plants (Guelke and von Blanckenburg, 2007; Guelke-Stelling and von Blanckenburg, 2012; Kiczka et al., 2010). Guelke and von Blanckenburg (2007) suggest that the discrepancies in the behavior of Fe isotopes observed between graminaceous (grasses) and other higher plants were a consequence of distinct Fe uptake mechanisms. In soils, Fe is mostly in its oxidized form, Fe(III), which is poorly soluble, depending on the pH conditions, and therefore hardly available for plants. In order to respond to this problem, higher plants have developed two different strategies to acquire Fe (Hell and Stephan, 2003). Strategy-I plants (dicots and non-graminaceous monocots) solubilize Fe(III) by releasing protons to decrease the pH of the rhizosphere (Fe(III) becomes soluble at acidic pH) and the enzyme ferric chelate reductase contained in the membrane of the root cells reduces Fe(III) to Fe(II) (Marschner and Romheld, 1994; Romheld and Marschner, 1986). Strategy-II plants (graminaceous monocots) secrete an iron-chelating mugineic acid phytosiderophore complexant, which solubilizes Fe by chelating Fe3+ (Marschner and Romheld, 1994; Romheld and Marschner, 1986; Takagi et al., 1984). Therefore, Fe enters the plant as Fe2+ (after reduction of the Fe(III) of the soil) in strategy-I plants and as Fe3+-phytosiderophore in strategy-II plants.
Guelke and von Blanckenburg (2007) found that seven strategy-I plants fractionate Fe isotopes such that different components of the plant become isotopically lighter from stem to seed. On the other hand, three strategy-II plants exhibit almost no fractionation and all components have the same Fe isotopic composition as the growth medium. The authors suggested that this discrepancy was the direct consequence of the difference in Fe uptake and transport mechanisms between the two groups of plants. They proposed that strategy-I plants reduce Fe prior to uptake through the roots and during transport within the plant, resulting in isotopic fractionation. Strategy-II plants do not reduce Fe, which remains mostly in the ferric state during its adsorption and transport, complexed to a phytosiderophore (Charlson and Shoemaker, 2006; Grotz and Guerinot, 2006); no isotopic fractionation takes place.
However, Kiczka et al. (2010) studied the Fe isotopic composition of three wild plants from the Alps and found that leave and flowers from the graminaceous Agrostis gigantea was isotopically fractionated compared to the growth medium by the same order of magnitude as non-graminaceous plants. These results suggest that the difference between graminaceous and non-graminaceous plants is not as universal as what could be inferred from Guelke and von Blanckenburg (2007), and that the distribution and availability of Fe in the soil may affect the conditions of uptake and translocation. Fe isotopic fractionation in Strategy-II plants was further confirmed by Guelke-Stelling and von Blanckenburg (2012) in oat grown on a nutrient solution supplemented by Fe(III)–EDTA, which suggests that Fe mobilization by strategy-II plants is controlled by Fe abundance in soils or in nutrient solutions. When there is no Fe deficit, Fe mobilization is similar to that of strategy-I plants and Fe taken up by the plants is isotopically light. When Fe is in deficit, the plant mobilizes Fe with the Fe-siderophore and Fe isotopes are not fractionated during the uptake.
More work is needed to better understand the source of iron isotopic fractionation in higher plants in order to trace Fe uptake and translocation. In particular, Fe isotopic fractionations induced by the change of ligands and therefore of bonding environments involved in the uptake and transport of Fe in plants (citrates, phytosiderophore, nicotianamine) have never been evaluated. Such fractionation should be known in order to interpret the isotopic data.
Here, we set out to calculate by the ab initio techniques Fe isotope fractionation for Fe(II)-citrate, Fe(III)-citrate, Fe(II)-nicotianamine and Fe(III)-phytosiderophore. Ab initio calculations determine the vibrational frequencies for the different bonds (Fujii and Albarède, 2012; Fujii et al., 2009, 2010, 2011a,b, 2013; Moynier et al., 2011; Schauble, 2004; Schauble et al., 2001). From the vibrational frequencies, we have calculated the reduced partition functions (lnβ; Table 1), which are finally used to predict isotopic fractionation between the different Fe species.
Logarithm of the reduced partition function, lnβ (‰), for the isotope pair 56Fe/54Fe.
| Species | Temperature (°C) | |||
| 0 | 25 | 50 | 100 | |
| (a) [Fe(II)(H2O)6]2+ | 6.27 | 5.32 | 4.56 | 3.46 |
| (b) [Fe(III)(H2O)6]3+ | 8.82 | 7.50 | 6.45 | 4.91 |
| (c) [Fe(II)(cit)(H2O)3]− | 6.46 | 5.48 | 4.71 | 3.58 |
| (d) [Fe(III)(cit)(H2O)3]0 | 10.06 | 8.56 | 7.36 | 5.61 |
| (e) [Fe(II)H(cit)(H2O)4]0 | 6.42 | 5.45 | 4.68 | 3.56 |
| (f) [Fe(III)H(cit)(H2O)4]+ | 10.05 | 8.55 | 7.35 | 5.61 |
| (g) [Fe(II)(cit)2]4− | 4.92 | 4.15 | 3.55 | 2.68 |
| (h) [Fe(III)(cit)2]3− | 8.33 | 7.06 | 6.05 | 4.59 |
| (i) [Fe(II)-nicotianamine]− | 6.20 | 5.25 | 4.49 | 3.40 |
| (j) [Fe(III)-phytosiderophore]0 | 9.99 | 8.49 | 7.29 | 5.54 |
In addition, we measured the Fe isotopic composition of different components of six plants in order firstly, to confirm the potential Fe isotopic fractionation during its translocation in graminaceous plants by analyzing the different components of five different common Missouri graminaceous (all strategy-II plants) (Johnsongrass: Sorghum halepense; Kentucky bluegrass: Poa pratensis, river oats: Uniola latifolia; Indian goosegrass: Eleusine indica; Virginia wild rye: Elymus virginicus) grown in the same soil, secondly, to test the isotopic fractionation induced by the mobilization of the reserve from a seed on a dicot (a strategy-I plant) (lentil: Lens culinaris) that is grown on the reserve of the seed with no additional nutrient. We already used the same experimental protocol to measure the Zn (Moynier et al., 2009) and Cu (Weinstein et al., 2011) isotopic composition of plants.
2 Material and methods
2.1 Samples
The Lentil and Virginia wild rye samples are the Fe fractions saved from our previous study (Weinstein et al., 2011). Lentils were cultivated in large Petri dishes lined with high-purity Kimwipes in a class 10,000 clean chemistry laboratory at Washington University in St Louis (WUSTL) following the same protocol described in Weinstein et al. (2011). The room temperature was 25 °C. No nutrient solution was added, and therefore the lentils grew on their own nutrient reserves with only the addition of 18.2-MΩ water for 15 days. The reproducibility was tested by conducting two identical experiments (Exp. A1 and A2). Then, the germinated seeds, and shoots (stems and leaves) were separated, weighed, dissolved (see protocol below) and prepared for Fe isotopic measurements.
The graminaceous (strategy-II plants) Virginia wild rye, Johnsongrass, Kentucky bluegrass, river oat, and Indian goosegrass plants were harvested in a field in Saint-Louis, MO (Fig. 1). The plants were simply cut with scissors, placed in plastic bags and brought back to the clean lab. In order to avoid any possible post-harvest redistribution of the Fe isotopes, the different components of the plants were separated later that same day. A soil sample was also collected from a depth of 10 cm where the plants were harvested. The soil was an Alfisol of silt loam texture developed in loess and had a pH as measured in 0.01 M CaCl2 of 6.42 (17). For the Virginia wild rye, the different components (leaves, stems, and seeds) of four to five plants were separated (Exp. B1, Fig. 1B). The exact same protocol was applied to another group of four to five plants of Virginia wild rye to test the reproducibility of the experiment (Exp. B2). For the Johnsongrass (Exp. F), two individual plants (F1 and F2) were used in order to compare the Fe isotopic evolution between two similar plants. For the three other specimens, only one single plant was used for each experiment.
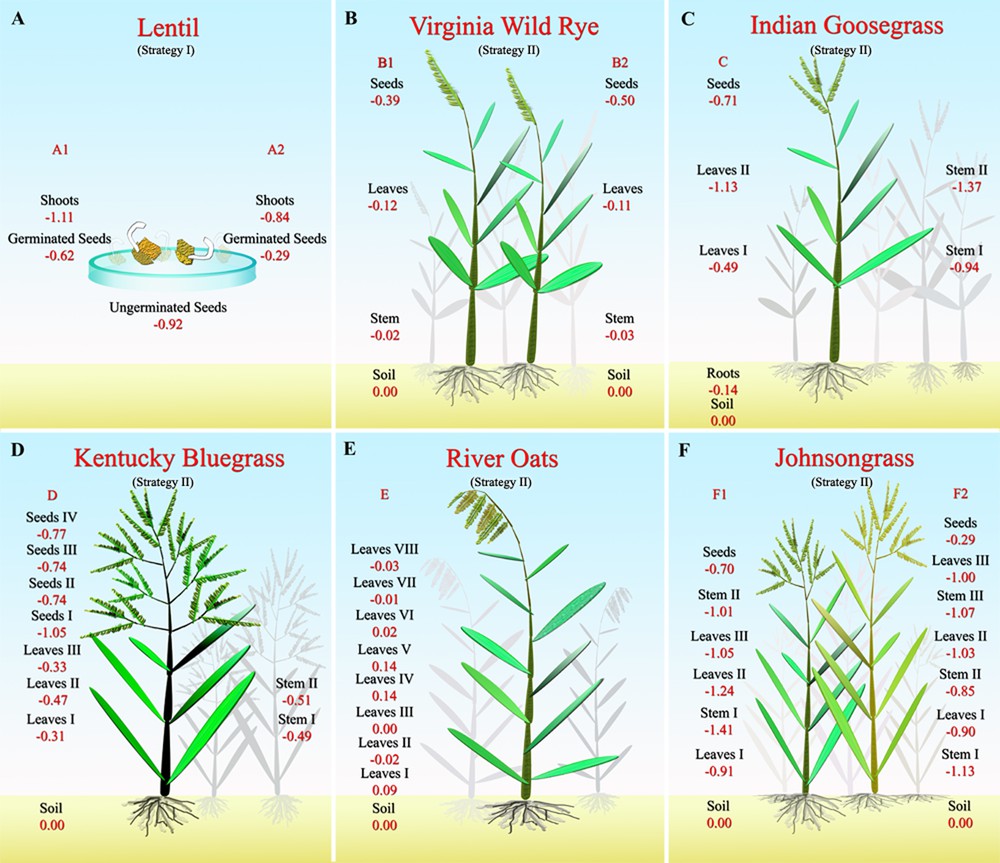
Sampling strategy for the different experiments. The Fe isotopic composition is reported in permil δ notation with IRMM14 as the reference material.
For all the plants, we have separated stems, leaves and seeds at different heights to test whether Fe isotopic composition changes with height, as was observed for Zn isotopes (Moynier et al., 2009). The river oats experiment (Exp. C) was specifically designed to test the correlation between the heights of the leaves with the magnitude of the Fe isotopic composition and we separated eight different leaves at heights between 6.5 and 69 cm from the bottom of the plant.
A terrestrial basalt, BCR-2, from the Columbia River, OR, USA, has been processed and run many times while we were analyzing the plant samples in order to check the stability of our measurements and estimate the external reproducibility of our procedure.
2.2 Theoretical background
A reaction of isotopic exchange between AX and AY, where A and A′ are the heavy and light isotopes of the element A, and X and Y represent ligands can be written as:
| (1) |
The isotope separation factor α between AX and AY is defined as:
| (2) |
Deviations of isotopic ratios from a reference value in parts per 1000 are conventionally defined as:
| (3) |
If AX (and A′X) is the major component in the system, Σ[A]/Σ[A′] is approximated to be ([A]/[A′])X such that an approximation expression δ ≈ 103 lnα is suitable.
The standard theory of chemical isotope fractionation is based on mass-dependent isotopic differences in vibrational energies of isotopologues (Bigeleisen and Mayer, 1947; Urey, 1947). The isotope enrichment factor is proportional to:
The isotope enrichment lnα due to intramolecular vibrations can be evaluated from the reduced partition function ratio (RPFR) β = (s/s′)f defined as:
| (4) |
| (5) |
In this equation, νi stands for vibrational frequencies, s for the symmetry number of the molecule, and ui = hνi/kT. The isotope enrichment factor due to the molecular vibration can be evaluated from the frequencies summed over all the different modes. The partition function ratio (s/s′)f for isotopologues A′X and AX (A′Y and AY, respectively) is noted βX (βY, respectively). In the isotopic exchange reaction 3, isotope fractionation can be estimated from the relation lnα ≈ lnβY–lnβX. An adequate approximation of fractionation factors between different Fe species may be obtained by the conventional mass-dependent theory. All the calculations were made for the 56Fe/54Fe ratio.
In the present study, the optimized structures of Fe species were first determined for 54Fe. The intramolecular vibrational frequencies νi were calculated for each complex. lnb(ui′) was determined by substituting νi into Eq. (7). Then 54Fe was replaced by 56Fe and the vibrational frequencies were calculated again for the same molecular structures to obtain lnb(ui), from which lnβ was then determined.
2.3 Computational details
Orbital geometries and vibrational frequencies of aqueous Fe(II) and Fe(III) species were computed using density functional theory (DFT) as implemented by the Gaussian09 code (Dennington et al., 2009; Frisch et al., 2009). The DFT method employed here is a hybrid density functional consisting of Becke's three-parameter non-local hybrid exchange potential (B3) (Becke, 1993), with Lee-Yang and Parr (LYP) (Lee et al., 1988) non-local functionals. Similar to our previous study (Fujii et al., 2006), the 6-31+ + G(d,p) basis set was chosen for H, C, N, and O, and LanL2DZ (Dunning and Hay, 1976; Hay and Wadt, 1985a, b; Wadt and Hay, 1985) was chosen for Fe. The former is an all-electron basis set, while the latter is an effective core potential basis set. The geometry optimization and intramolecular vibrational frequency analysis were performed for the hydrated Fe(II) and Fe(III) ion, Fe(II)-H and Fe(III)-H citrates, Fe(II) and Fe(III)-citrates, Fe(II)-nicotianamine and Fe(III) phytosiderophore. Molecules were modeled without any forced symmetry. An “ultrafine” numerical integration grid was used and the SCF convergence criterion was set to 10−9.
2.4 Chemical purification and mass-spectrometry
Plant and soil samples were first cleaned twice using 18.2-MΩ water and then dissolved using a 1:1 mixture of 15 N HNO3 (four times sub-boiled) and concentrated Seastar© optima grade H2O2 in closed Teflon beakers for several days. They were subsequently dissolved with first a concentrated 5:1 HF/HNO3 mixture (∼20 mL) and then aqua regia (∼10 mL) to ensure a complete dissolution of all the sample material, including the siliceous matter. The terrestrial standard was dissolved in a concentrated 5:1 mixture of HF/HNO3, followed by a treatment by 6 N HCl.
Prior to the mass-spec analysis, Fe was purified by ion exchange chromatography following procedures described previously (Dauphas et al., 2009; Moynier et al., 2006; Wang et al., 2011, 2012a, b, 2013), so that elements producing interferences at the masses of Fe isotopes or degrading the stability of the instrument by inducing matrix effects were removed.
Fe isotopic data were measured using the MC–ICP–MS (Thermo-Finnigan Neptune Plus) at the Isotope Geochemistry Laboratory at Washington University in Saint-Louis. A 1-ppm solution of purified Fe was introduced into the mass-spectrometer using an Apex-Q + Spiro inlet system and a 100-μL/minute PFA nebulizer. The measurements were done in medium-resolution mode on the peak shoulder in order to resolve the isobaric interferences of 40Ar14N with 54Fe, 40Ar16O with 56Fe and 40Ar16OH with 57Fe. The intensities of masses 53, 54, 56, and 57 were measured on the Faraday cups L3, L2, central, and H1, respectively. Concentrations (Table 2) were calculated by comparing the sample solutions Fe signal intensity to that of a known-concentration standard. The sample dilutions were then adjusted (to ∼5%) to match the concentration of the standard.
Fe isotopic composition and elemental abundance (ppm) from experiments A (lentils), B (Virginia wild rye), C (Indian goosegrass), D (Kentucky bluegrass), E (river oats), and F (Johnsongrass) as well as for the soil from which the plants have grown.
| Sample names | δ56Fe | δ54Fe | [Fe] ppm wet matter | Height |
| BCR-2 | 0.07 ± 0.04 (2σ) | 0.06 ± 0.07 (2σ) | ||
| Ungerminated lentil seed | –0.92 | –1.34 | 32 | |
| Lentil experiment A1 | ||||
| Shoots A1 | –1.11 | –1.62 | 7 | |
| Germinated seeds A1 | –0.62 | –0.90 | 0.6 | |
| Lentil experiment A2 | ||||
| Shoots A2 | –0.84 | –1.21 | 2 | |
| Germinated seeds A2 | –0.29 | –0.41 | 0.2 | |
| Soil (growth media for exp. B–F) | 0.00 | 0.03 | 146 | |
| Virginia Wild Rye (Elymus virginicus) B1 | ||||
| Stem B1 | –0.02 | 0.00 | 1 | |
| Leaf B1 | –0.12 | –0.18 | 17 | |
| Seeds B1 | –0.39 | –0.57 | 12 | |
| Virginia Wild Rye (Elymus virginicus) B2 | ||||
| Stem B2 | –0.03 | 0.00 | 2 | |
| Leaf B2 | –0.11 | –0.15 | 27 | |
| Seeds B2 | –0.50 | –0.74 | 13 | |
| Indian goosegrass (Eleusine indica) C | ||||
| Root C | –0.14 | –0.19 | 0 | |
| Stem C I | –0.94 | –1.39 | 30 | |
| Stem C II | –1.37 | –2.06 | 50 | |
| Leaf C I | –0.49 | –0.71 | 30 | |
| Leaf C II | –1.13 | –1.68 | 50 | |
| Seed C | –0.71 | –0.93 | ||
| Kentucky Bluegrass (Poa pratensis) D | ||||
| Stem D I | –0.49 | –0.71 | 1 | 0–20 |
| Stem D II | –0.51 | –0.95 | 0.5 | 20–55 |
| Leaf D I | –0.31 | –0.42 | 15 | 19 |
| Leaf D II | –0.47 | –0.70 | 16 | 55 |
| Leaf D III | –0.33 | –0.49 | 20 | 85 |
| Seed D I | –1.05 | –1.53 | 9 | 90 |
| Seed D II | –0.74 | –1.14 | 11 | 100 |
| Seed D III | –0.74 | –1.08 | 14 | 110 |
| Seed D IV | –0.77 | –1.04 | 14 | 120 |
| River oats (Uniola latifolia) E | ||||
| Leaf E I | 0.09 | 0.14 | 23 | 6.5 |
| Leaf E II | –0.02 | 0.00 | 49 | 18 |
| Leaf E III | 0.00 | –0.05 | 12 | 28 |
| Leaf E IV | 0.14 | 0.19 | 21 | 38 |
| Leaf E V | 0.14 | 0.23 | 14 | 46 |
| Leaf E VI | 0.02 | 0.04 | 17 | 59 |
| Leaf E VII | –0.01 | –0.03 | 11 | 65 |
| Leaf E VIII | –0.03 | 0.00 | 7 | 69 |
| Johnsongrass (Sorghum halepense) F1 | ||||
| Stem F1 I | –1.41 | –1.95 | 6 | 0–30 |
| Stem F1 II | –1.01 | –1.48 | 8 | 30–60 |
| Leaf F1 I | –0.91 | –1.28 | 26 | 17 |
| Leaf F1 II | –1.24 | –1.83 | 23 | 30 |
| Leaf F1 III | –1.05 | –1.50 | 38 | 42 |
| Seed F1 | –0.70 | –0.98 | 46 | 82.3 |
| Johnsongrass (Sorghum halepense) F2 | ||||
| Stem F2 I | –1.13 | –1.49 | 7 | 0–18.5 |
| Stem F2 II | –0.85 | –1.27 | 5 | 18.5–40 |
| Stem F2 III | –1.07 | –1.51 | 5 | 40–55 |
| Leaf F2 I | –0.90 | –1.30 | 21 | 18.5 |
| Leaf F2 II | –1.03 | –1.48 | 29 | 40 |
| Leaf F2 III | –1.00 | –1.45 | 40 | 69 |
| Seed F2 | –0.29 | –0.43 | 11 | 210 |
The total yield of Fe was checked before starting the first chemical purifications and was found to be greater than 98%. The blank of the full procedure is less than 1 ng, which is negligible in comparison to the amount of Fe present in each sample (> 1 μg).
Replicate analyses of the same samples carried out during different analytical sessions define an external reproducibility of ± 0.04‰ (2 sd) for δ56Fe and 0.07‰ for δ57Fe. In addition, the good reproducibility of the two different sets of Virginia wild rye (B1 and B2) for two pools of stems (δ56Fe = –0.02‰ and–0.03‰), leaves (δ56Fe = –0.12‰ and –0.11‰) and seeds (δ56Fe = –0.39‰ and–0.50‰) confirms the external reproducibility of the full procedure (dissolution, chemical purification and mass-spec measurements).
3 Results
3.1 Ab initio calculations
The different possible molecular structures of the Fe species are shown in Fig. 2 and the lnβ values obtained are shown in Table 1 and reported in Fig. 2. The structure and lnβ values of six citrate species, Fe(II)(cit)(H2O)3−, Fe(III)(cit)(H2O)30, Fe(II)H(cit)(H2O)40, Fe(III)H(cit)(H2O)4+, [Fe(II)(cit)2]4−, [Fe(III)(cit)2]3−, as well as [Fe(II)-nicotianamine]−and Fe(III) phytosiderophore, were calculated.
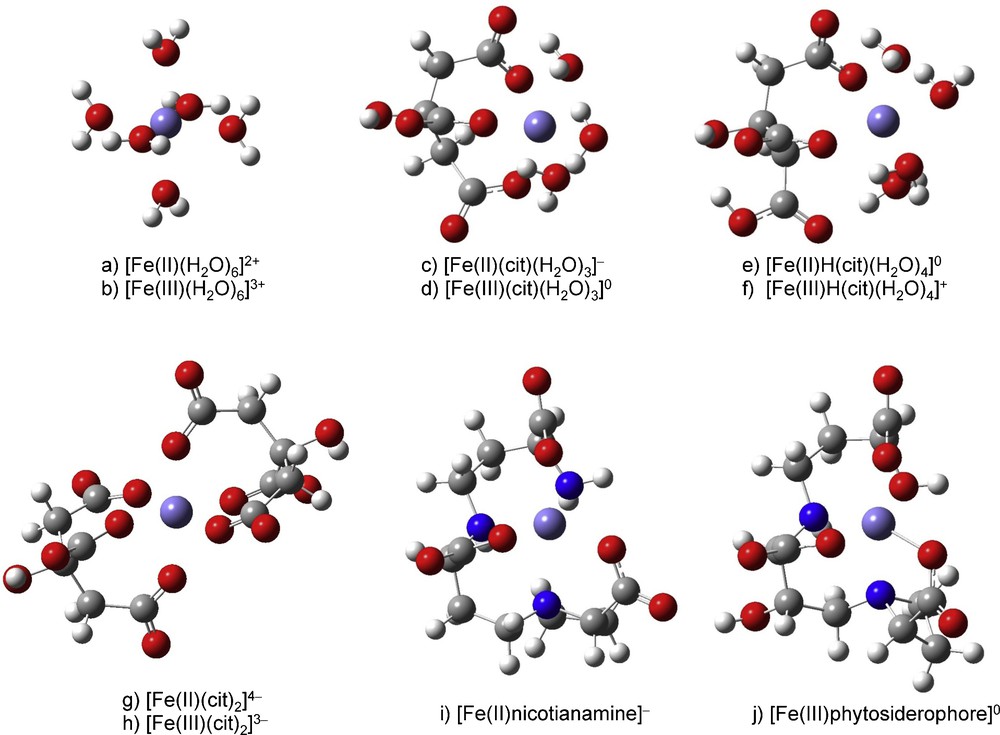
Molecular structure of Fe(II)(cit)(H2O)3−, Fe(III)(cit)(H2O)30, Fe(II)H(cit)(H2O)40, Fe(III)H(cit)(H2O)4+, Fe(II)H(cit)(H2O)30, Fe(III)H(cit)(H2O)3+, [Fe(II)-nicotianamine]− and Fe(III)-phytosiderophore.
The optimized structure Cartesian coordinates are given in Appendix A. The hydrated Fe2+ and Fe3+ ion possess six H2O molecules in its first coordination shell. In the present study, we therefore assumed that the coordination number of Fe species is six. Coordination with multidentate ligands, however, sometimes decreases the coordination number due to stereochemical restriction.
These calculations show that at 25 °C relatively large (∼1‰) 56Fe/54Fe fractionation values are expected between different Fe species without change in the redox state of Fe (Fig. 3). In particular, Fe(II)-nicotianamine has a 56Fe/54Fe ratio ∼1‰ higher than that of Fe(II)-(citrate)2. Fe(III) phytosiderophore has a 56Fe/54Fe ∼1.5 ‰ higher than that of Fe(III)-(citrate)2.
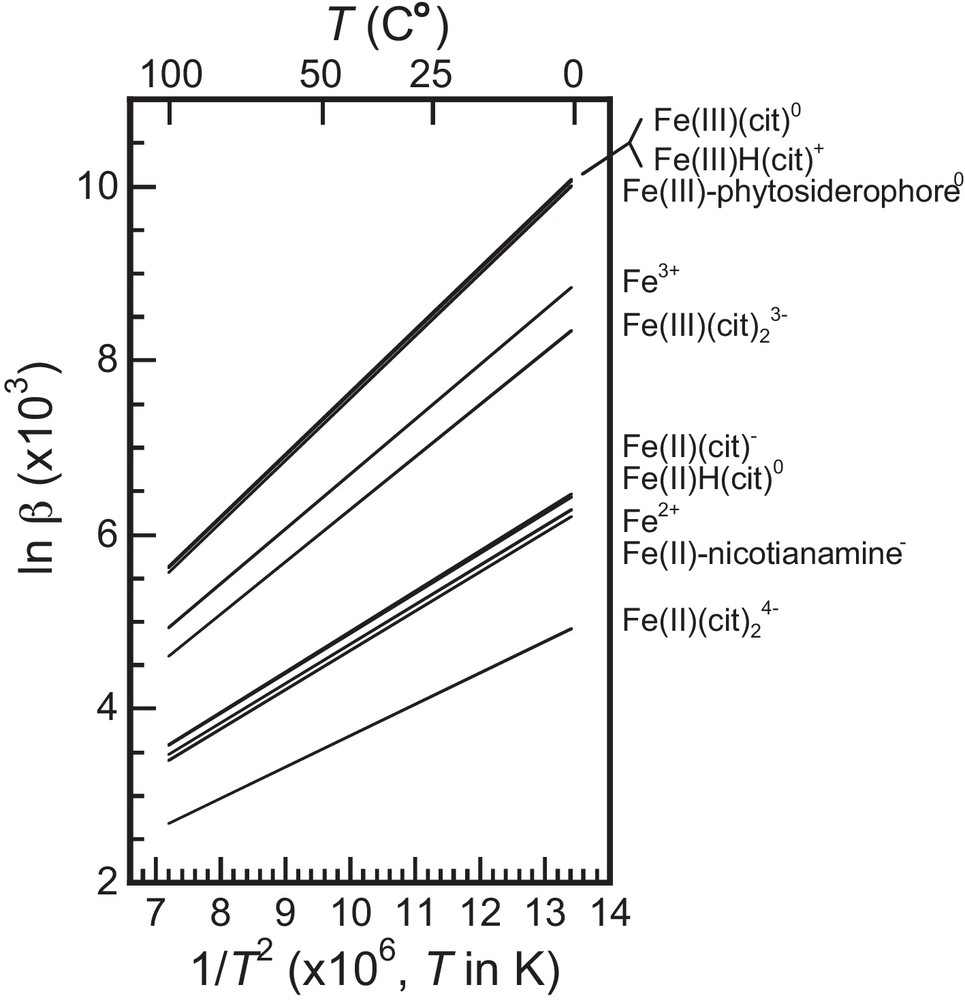
Temperature dependence of lnβ, using lnβ values reported in Table 1. The calculated lnβ(T) values are shown as functions of 1/T2.
In addition, we show that Fe(II)-nicotianamine is ∼3‰ isotopically lighter than Fe(III)-phytosiderophore.
3.2 Isotopic measurements
Isotope ratios of the samples measured in this study are expressed as parts per 1000 deviations relative to a standard:
| (6) |
The isotopic fractionation between two components i and j is defined as:
| (7) |
The Fe isotopic compositions of the geostandard and plant samples are reported in Table 2 and plotted in Figs. 1 and 4. The geostandard BCR-2 that we have replicated six times (δ56Fe = 0.04, 0.07, 0.08, 0.08, 0.09, and 0.09 ‰) shows the typical value for terrestrial basalt with an average of 0.07 ± 0.04 ‰ (2 sd) (Craddock and Dauphas, 2011).
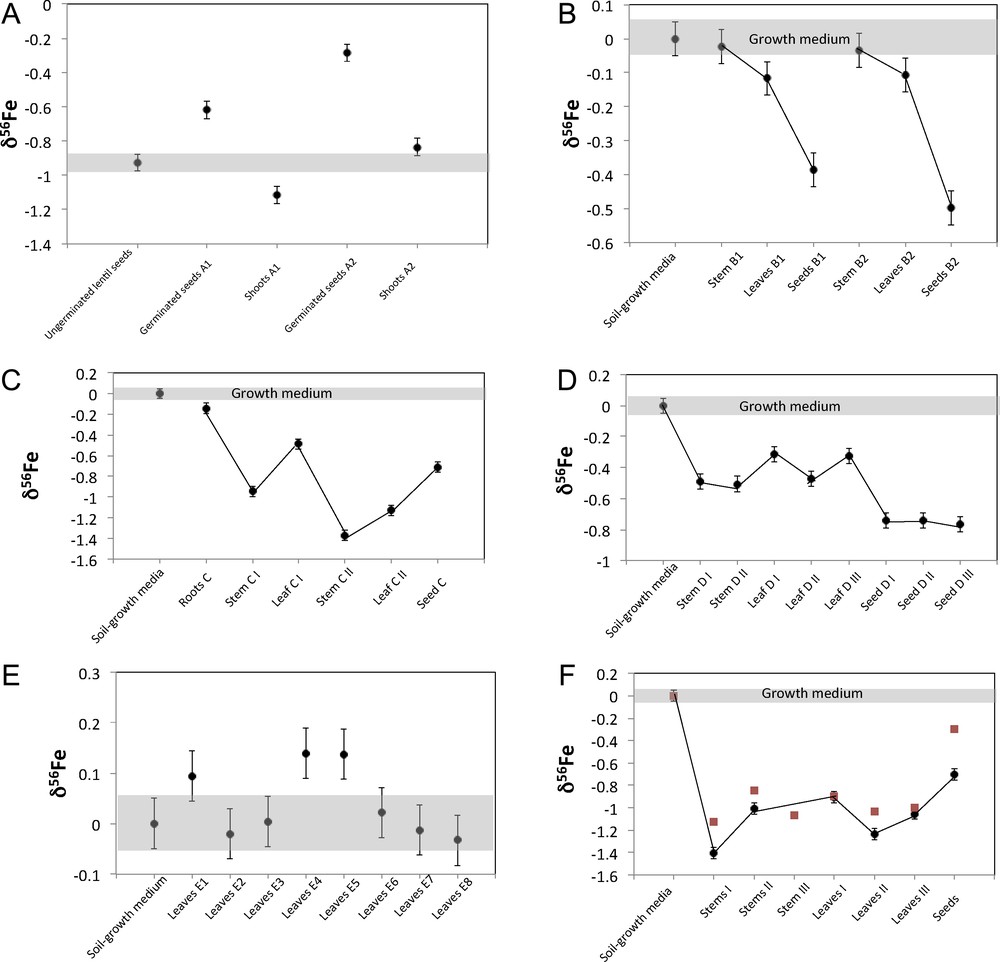
Fe isotopic composition for experiment A (lentil) (panel A), experiment B (Virginia wild rye, panel B), experiment C (Indian goosegrass, panel C), experiment D (Kentucky bluegrass, panel D), experiment E (river oats, panel E) and experiment F (Johnsongrass, panel F). For the experiment F, the black circles correspond to the experiment F1 and the red squares to the experiment F2. The isotopic composition is reported in permil δ deviation from the IRMM14 standard.
The lentil experiments A1 and A2 give similar results (Table 1 and Fig. 1A): shoots (–1.11‰ < δ56Fe < –0.84‰) are lighter than the germinated seeds (–0.62‰ < δ56Fe < –0.29‰) and Δ56Fegerminated seeds–shoots = +0.50‰ and +0.55‰ and are similar in both experiments. The isotopic composition of the lentil seeds before germination (δ56Fe = –0.92) lies in between those of shoots and those of germinated seeds for experiment A1, while it is slightly lighter than the germinated seed in experiment A2. This suggests that some Fe might have been leached from the plant by the culture medium.
The soil sample has a typical continental crust Fe isotopic composition with δ56Fesoil ∼ 0.00‰. All the graminaceous plants but one (the river oats) analyzed here show enrichments in the lighter isotopes of Fe compared to the soil with a maximum of Δ56Fesoil–plant of 1.40‰ for the stem F1 I.
4 Discussion
The Virginia wild rye experiments B1 and B2 (Figs. 1 and 4 panel B) both show the same trend, with δ56Fesoil ∼ δ56Festem > δ56Feleaves > δ56Feseedsor Δ56Fesoil–stems = –0.02‰ and –0.03‰; Δ56Festem–leaves = 0.09‰ and 0.07‰ and Δ56Feleaves–seeds = 0.36‰ and 0.46‰.
The Indian goosegrass (Exp. C), which is the only plant for which we have analyzed the roots, shows a clear enrichment in light isotopes of Fe between the root and the shoots (0.80‰ < Δ56Feroot–stem < 1.23‰; 0.35‰ < Δ56Feroot–leaves < 0.99‰ and Δ56Feroot–seeds = 0.57‰; Fig. 1C). The roots are slightly enriched in light isotopes when compared to the soil (Δ56Fesoil–root = 0.14‰).
The different parts of the stem and different leaves and seeds from the Johnsongrass (Exp. F; Fig. 1F) are fractionated in comparison to the soil: –0.85‰ < Δ56Fesoil–stem < –1.41‰; 0.90‰ < Δ56Fesoil–leave < 1.24‰ and 0.29‰ < Δ56Fesoil–seeds < 0.70‰ but with no clear trend, except that the new grown seeds are slightly heavier than the leaves and the stem.
The Kentucky bluegrass (Exp. D; Fig. 1D) also shows a clear enrichment in light isotopes of the stem (0.49‰ < Δ56Fesoil–stem = 0.51‰), leaves (–0.47‰ < Δ56Fesoil–leaves < –0.31‰) and seeds (–1.05‰ < Δ56Fesoil–seeds < –0.74‰) with the new grown seeds slightly lighter than the stem and leaves, but with no relation with height.
River oats experiment E, for which we analyzed eight single leaves collected at different heights, show a very homogeneous isotopic composition, which scatters around the composition of the soil (Figs. 1 and 4, panel E). These results for eight leaves as well as for the other plants for which two or three leaves were collected at different heights show that, contrary to Zn and Cu, the Fe isotopic composition of leaves is not correlated with the height. The absence of fractionation in the leaves from the graminaceous river oat confirms the observation that leaves from some strategy-II plants do not exhibit any isotopic fractionations in comparison to the growth medium (Guelke and von Blanckenburg, 2007).
The lentils (Exp. A) that were grown only on their seeds reserves with no external addition of nutrients show enrichment in light isotopes of Fe between shoots and germinated seeds. This is exactly what is predicted if Fe isotopes are fractionated only during the mobilization of Fe from the seeds reserve and confirm that Fe isotopes are fractionated in strategy-I plants (Guelke and von Blanckenburg, 2007; Guelke-Stelling and von Blanckenburg, 2012).
The origin of the fractionation between the seed and the leave of the lentils is consistent with a difference of speciation of Fe between the different components. In the seed, Fe is stored as Fe(II)-nicotianamine, while in the leaves it is in citrate form (Hell and Stephan, 2003). The ab initio calculations show that, at 25 °C, Fe-(citrates)2 are isotopically lighter than nicotionamine with Δ56Fe(nicotianamine-citrate2) up to 1‰ (Table 1). Therefore, the isotopic fractionation observed between the germinated seeds and the shots of the lentils is best explained by the difference of bonding configuration of Fe between the different components.
The large Fe isotopic variations measured in different components of four graminaceous plants of different genera confirms that the absence of isotopic fractionation observed by Guelke and von Blanckenburg (2007) for three strategy-II plants is not universal. When taken together, the data from Guelke and von Blanckenburg (2007), Kiczka et al. (2010), Guelke-Stelling and von Blanckenburg (2012) as well as the present study show that four strategy-II plants do not show any isotopic fractionation, while six are isotopically fractionated by the same magnitude as strategy-I ones.
This dichotomy between different graminaceous plants suggests that the Fe isotopic fractionation mechanism for strategy-II plant may depend on the growing conditions rather than on the Fe absorption pathways (strategy-I vs. strategy-II).
It has actually been observed that rice, a strategy-II plant, possess the Fe(II) specific transporter (IRT1) and has therefore the ability to uptake Fe2+ from the soil (Bughio et al., 2002; Cheng et al., 2007; Ishimaru et al., 2006) in the same way as strategy-I plants. The fact that graminaceous plants are also able to uptake Fe2+ from the soil and hence can potentially produce an isotopic effect would explain the discrepancies between the results of Guelke and von Blanckenburg (2007) and those of the present study, as well as those of Kiczka et al. (2010). If some graminaceous plants (e.g., Agrostis gigantea, Kiczka et al., 2010; Eleusine indica; this study) have the possibility to acquire Fe in the same way as strategy-I plants, Fe isotopic fractionation could occur and it would be impossible to use Fe isotopes as a mean to understand the difference of translocation mechanisms between strategy-I and strategy-II plants.
In addition, most of the Fe isotopic fractionations observed for strategy-II plants seem to be limited to the upper part of the plants (stems, leaves and seeds) and therefore in this case the fractionation must be controlled by the translocation mechanism from roots to shoots. Therefore it appears to be critical that both fractionation-producing mechanisms, uptake and translocation, are considered when studying the iron isotopic composition of plants.
After the uptake of Fe(III) as Fe(III)-phytosiderophore by the root system of strategy-II plants, the mechanism of translocation of the Fe(III) from the root to the leaves is still uncertain. However, it has been suggested that the transport of Fe for both uptake strategy is similar and transported by both the xylem and phloem sap. In the xylem sap, which has a pH less than 7, Fe is transported as a Fe(III)-citrate complexes (Pich et al., 1994). In the phloem sap, which has a pH more than 7, Fe is chelated to a ligand nicotianamine (NA) (Stephan and Scholtz, 1993) during its transport within the phloem sap.
While NA has the ability to chelate both Fe2+ and Fe3+, the Fe(II)-NA complex is kinetically favored over the Fe(III)-NA, which is why most Fe is in the form of Fe(II) in the phloem (von Wiren et al., 1999).
Our calculations show that Fe isotopes could be fractionated by up to 1.5‰ between Fe(III)-phytosiderophore (in the roots) and Fe(III)-citrate (in the xylem) (Table 1). This would explain part of the light isotopic composition observed in the upper part of the plant in comparison to the roots if Fe is in the form of Fe(III)-citrate. Reduction of Fe(III)-phytosiderophore (roots) to Fe(II)-nicotianamine (phloem) would create an isotopic fractionation of ∼3‰, much larger than anything observed in the plant. Therefore, the isotopic composition of the upper parts of the plant is best explained by a mixing between Fe transported by the phloem and the xylem. This mixing between Fe received by the phloem and the xylem could also explain the observation from Guelke-Stelling and von Blanckenburg (2012) that younger leaves are isotopically lighter than older leaves.
5 Conclusion
In this study, we show that Fe isotopes are highly fractionated during the translocation in higher plants. We have calculated the isotopic fractionation between several Fe species relevant to the soil–plant system (Fe(II)-citrate, Fe(III)-citrate, Fe(III)-phytosiderophore, and Fe(II)-nicotianamine). These new ab initio calculations show that Fe isotopes can be fractionated up to 1.5‰ in the absence of redox changes. The fractionation observed between the root and the shoots of strategy-II plants (graminaceous plants) could be explained by isotopic fractionation between Fe(III)-phytosiderophore (in the root) and Fe(III)-citrate (xylem) Δ56Fe ∼ 0.5‰ and between Fe(III)-phytosiderophore and Fe(II)-nicotianamine Δ56Fe ∼ 3‰.
Acknowledgments
We thank Minore Abe, Masaaki Musahi, Nathalie Vigier, as well Derek Vance and four anonymous reviewers for careful reviews which have greatly improved the quality of this manuscript. We also thank Francois Chabaux for his efficient edition of the paper.FM acknowledges funding from NASA EXO #NNX12AD88G.


