1 Introduction
One of the major unresolved problems in the Earth Sciences remains the pattern of convection in the mantle. The peculiar difficulty of this question is not that evidence to decide it is lacking, but rather that the framework to reconcile evidence from the different sources is still missing. For example, fast present-day seismic velocity anomalies, imaged all the way down to the core-mantle boundary and associated with subducted plates [57], have often been interpreted as a proof of whole-mantle convection. However, analysis of the composition of erupted lavas demonstrates the survival of isotopically distinct reservoirs for billions of years [28]. Since thermal convection in a homogeneous mantle would mix the mantle too rapidly to preserve those heterogeneities [10,27], it has therefore been proposed that the mantle was convecting in two superimposed homogenous layers (e.g., [2]). But this seems to contradict the seismic data. As the quality and the variety of the observations improve, both one-layer and two-layers models fail to explain an increasing number of data, which calls for the existence of chemical heterogeneities in the mantle on a wide range of scales: while the geochemical ‘DUPAL’ anomaly is encountered in a huge area, comprising a large part of the southern hemisphere, the whole spectrum of MORB compositions can be found within mm-scale fluid inclusions [28]; at the base of the lower mantle, the magnitude of the seismic heterogeneities indicate a chemical and/or partial melt component, which would be consistent with the high ambient-temperature gradient [34]; forward geodynamic modelling shows a reduced mass transfer at mid-lower mantle depths [19]; although subducted plates are imaged all the way down to the core-mantle boundary, the tomographic image in the mid-lower mantle changes significantly [57]; and scattered seismic energy throughout the whole mantle is probably due to 8-km-thick chemically heterogeneous filaments [24]. Furthermore, neither model can fully explain the origins of the principal manifestations of intraplate volcanism, ‘hot spots’ and ‘superswells’ [14].
More complicated models and pedagogic cartoons have been proposed to interpret the new data, such as two layers with a highly deformed interface [32], three layers [3], ‘blobby’ convection (with small [25] or big [5] blobs)... – see [55] for a recent review. Out of this wealth of studies, several ingredients emerge: (a) thermal convection in an homogeneous mantle is not sufficient to reconcile the various lines of evidence from geochemistry, seismology, and geodynamics [41], (b) the mantle is chemically heterogeneous, (c) different data probe different length- and time-scales of the dynamical processes occurring in the mantle. The compositional heterogeneities could be created by slabs remnant (e.g., [12,43]), delaminated continental material, relics of a primitive mantle (e.g., [21,32,54]) enriched, for example, in iron [30], chemical reactions or infiltration from the core (e.g., [22]). However, the density contrast associated with those heterogeneities, as well as their sizes, remains unknown, and the influence that they may have on the convective pattern in the Earth's mantle is not clear. Hence we need a better understanding of the physics governing the interaction of thermal convection with chemical heterogeneities. This paper is therefore an attempt to (1) summarize and classify what we now know about ‘thermochemical’ convection, and (2) see to what extent this ‘messy’ convection can explain the geological observations. In particular, we shall see that, because of entrainment and mixing, convection in a heterogeneous fluid is never steady but can continuously describe the different cartoons already mentioned, i.e. evolve through time from 2-layer to blobby to 1-layer convection.
2 Thermal convection in an initially stratified fluid
2.1 Problem set-up
Since a mantle initially stratified in density is the simplest case of a heterogeneous mantle, we study convection in two superimposed layers of viscous fluids of different viscosity and density, cooled from above and heated from below at constant temperature. The two fluids are miscible in the sense that there is no surface tension and chemical diffusion is negligible (see [15] for a detailed discussion of those two aspects of the experiments). The viscosity can depend on composition and/or temperature. In our discussion, the subscript ‘b’ designates the initial lower layer, ‘u’ the initial upper layer and ‘i’ either of them. The dynamics of the system is characterized by five dimensionless numbers:
- – the Rayleigh number, ratio of the driving thermal buoyancy forces to the resisting effects of thermal diffusion and viscous dissipation: , where d is the total fluid depth, ΔT is the temperature difference applied across it, g is the gravitational acceleration, α is the thermal expansivity at the tank mean temperature, κ is the thermal diffusivity and νu is the kinematic viscosity of the upper layer at its mean temperature;
- – the Prandtl number, Pr=νi/κ;
- – the viscosity ratio, γ=νb/νu, where νb is the kinematic viscosity of the bottom layer at its mean temperature;
- – the depth ratio a=db/d;
- – the buoyancy ratio, ratio of the stabilizing chemical density anomaly Δρ to the destabilizing thermal density anomaly: .
Convection in two superimposed fluid layers has been studied by a number of authors, using a range of analytical (e.g., [47]), numerical (e.g., [9,11,13,22,23,38,48,51,54]) and experimental techniques (e.g., [13–16,20,35,36,42,43,48]). The domain of parameters investigated is therefore large, with 102<Ra<109, 10−2<γ<6·104, 0.05<a<0.95, 0.04<B<10.
2.2 Stability to convective motions
For low Rayleigh numbers, the equations of motion can be linearized and marginal stability curves can be derived analytically [35,47]. Fig. 1 shows the stability diagram of the system calculated for given viscosity and depth ratios. The stability of the system to convective motions depends on the Rayleigh number Ra, which must be greater than a critical value. Then, depending on the buoyancy ratio B, two different regimes, set in [48], can occur: (a) for B greater than a critical value Bc, stratified convection develops, in which both layers convect above and below the interface; the critical Rayleigh number for convection Rac is therefore independent of the compositional gradient at the interface, i.e. is independent of B; (b) for B smaller than Bc, the whole tank is involved in one motion, causing overturn, because the density at the heated bottom of the lower layer is smaller than the density in the cooled top of the upper layer, despite the stabilizing jump across the interface. Therefore, the critical Ra depends on B. In this regime, the interface between the two fluids becomes highly distorted and two different modes of motions are predicted, either oscillatory (Fig. 1a) or steady (Fig. 1b). Laboratory [35,44] and numerical [49] experiments agree well with these theoretical predictions.
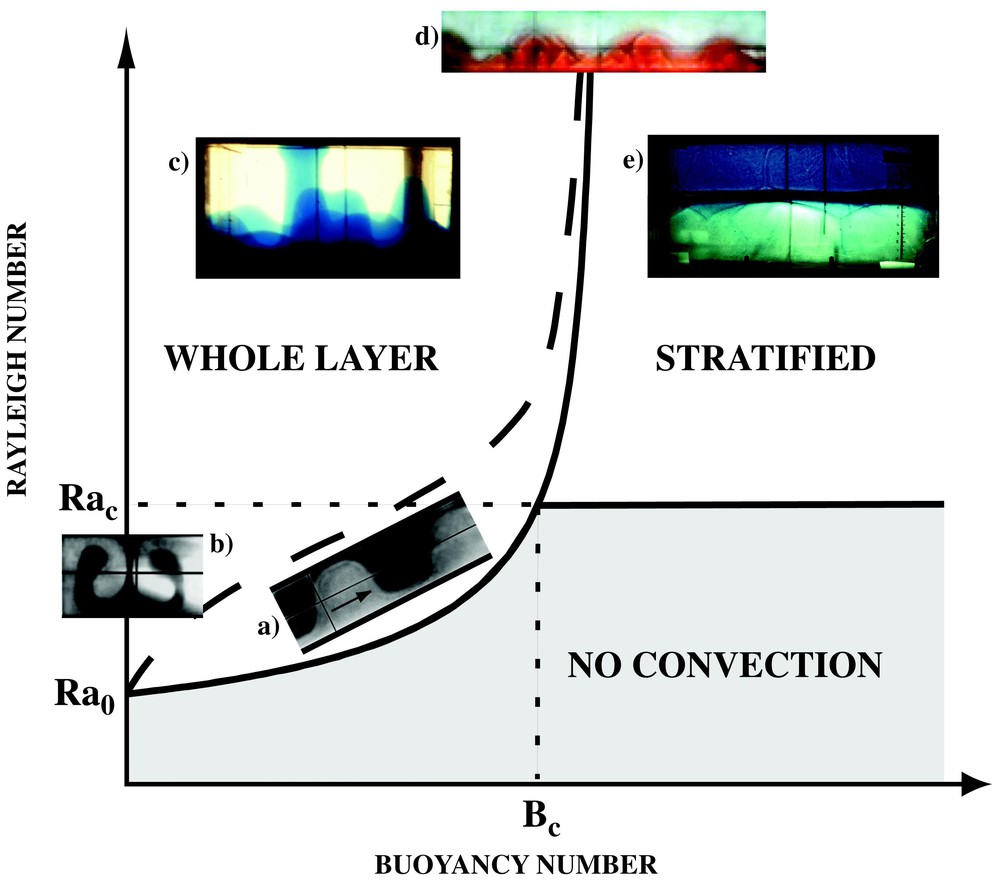
Marginal stability curves separating the different regimes shown in the photographs. The curves correspond to the case γ=6.7 and a=0.5, where Ra0=5430, Rac=38227 and Bc=0.302. For B<Bc, the whole-layer regime develops under the form of (a) travelling waves at low Rayleigh number (here B=0.20; Ra=1.8×104; a=0.5; γ=6.7), (b) overturn for γ around 1 and/or low B (here B=0.048; Ra=6.7×103; a=0.44; γ=1.1), (c) pulsating diapirs or cavity plumes at high Ra and γ>5 or γ<1/5. For B>Bc, stratified convection takes place, above and below (d) a deformed interface for Bc<B<1 (here B=0.33; Ra=4.6×105; a=0.25; γ=170), or (e) a nearly flat interface (here B=1.72; Ra=8.4×107; a=0.5; γ=1336).
Diagramme des régimes.
For much higher Rayleigh numbers, i.e. away from marginal stability, laboratory experiments [14,35,48] showed that the marginal stability analysis predicts well the different regimes for 0.01<γ<100 and 0.2<a<0.8. Bc is a weak function of a and γ, and typical values of Bc are between 0.2 and 0.5. For more extreme values of γ and a, the marginal stability does not predict correctly Bc, but it is found experimentally to range between 0.3 and 0.5 (Fig. 2).
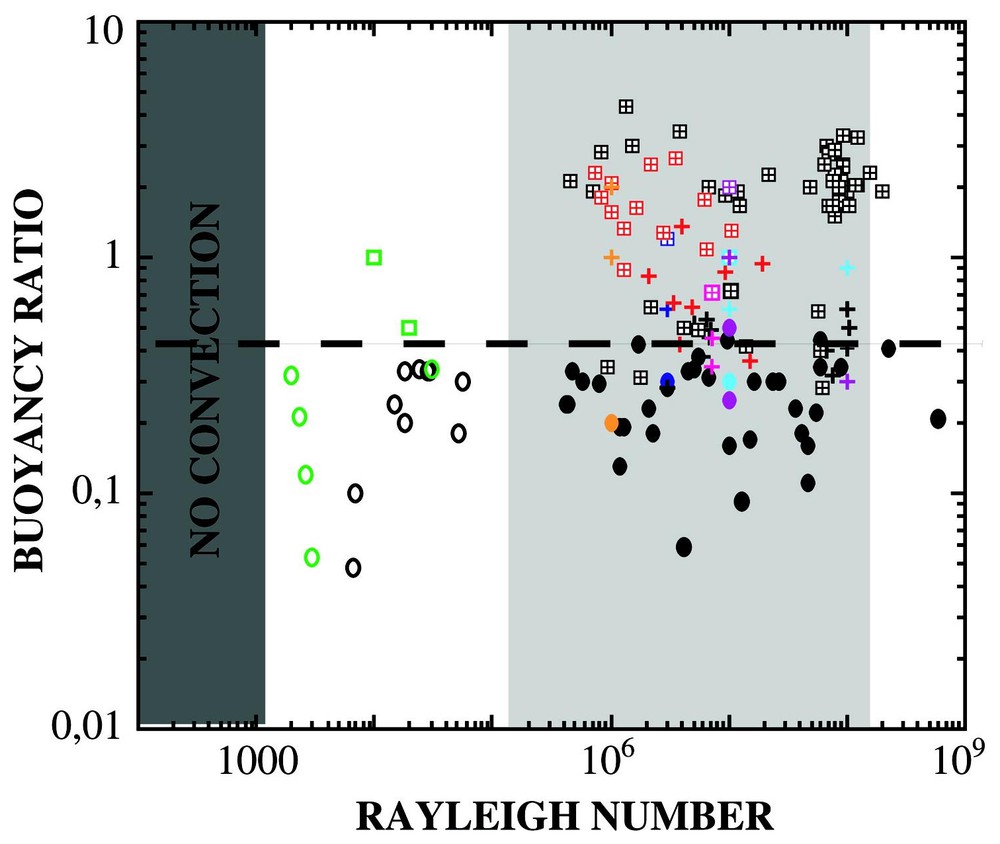
Different regimes of thermochemical convection as a function of Rayleigh number and buoyancy ratio. Circles: whole layer regime; squares: stratified regime throughout the whole duration of the experiment; crosses: convection initially stratified with strong deformation of the interface, which eventually becomes unstable. Open symbols designate experiments where only one scale of convection (thermochemical mode) is observed, while filled symbols stand for experiments where the purely thermal mode is superimposed on the thermochemical mode. In green, numerical data by Schmeling [44], in purple by Tackley [54,56], in pink by Samuel and Farnetani [50], in light blue Kellogg et al. [32,38], in orange by Hansen and Yuen [23]; in red, lab experiments by Richter and McKenzie [48], in dark blue by Olson and Kincaid [43], in black, by Davaille et al. [14–16,35,36]; in dark grey, the parameter space where convection does not occur. The light-grey shaded area represents the domain of parameters relevant for the Earth's mantle.
Les différents régimes de convection thermochimique en fonction de Ra et de B.
If the individual Rayleigh number of each initial layer is big enough (typically greater than 104), another scale of convection, superimposed on the large-scale thermocompositional modes just described, develops from the outer boundaries under the form of small and short-lived thermal plumes [15]. This small-scale thermal mode corresponds to classical Rayleigh–Bénard convection in a homogeneous fluid.
We shall now characterize the different regimes of convection.
2.3 ‘Stratified’ regime
When B>1, thermal convection develops in two superimposed layers (Fig. 3a), separated by a thermal boundary layer at a relatively undeformed interface (Fig. 3b). For high Rayleigh numbers, two scales of motion are observed, (a) small-scale plumes driven by the temperature gradient imposed at the copper plates (‘thermal’ mode), and (b) a large-scale motion originating at the interface, due to the non-linear interaction of the unstable thermal and stable chemical density gradients. This ‘thermochemical’ mode is responsible for the entrainment and for the thermal structure of the tank.

Stratified regime. (a) Composite snapshot showing a direct view of the entrainment in the bottom more viscous layer and a shadowgraph of the top layer. The interface (dark blue line) remains flat and sharp. Two scales of motions are visible: a large-scale circulation generated at the interface and a small-scale thermal mode with plumes coming from the two outer boundaries (arrow in the upper layer). Entrainment only occurs through the interfacial mode, comprising in the lower layer the blue cusps (arrow in the lower layer) and the thin sheets of blue, light, low viscosity fluid (one can distinguish three cells), and in the upper layer, the very thin conduit centred on top of a cell (indicated by the vertical arrow above the upper layer), which is not distorted until it encounters the upper cold thermal boundary layer. (b) Vertical thermal structure associated with the cold descending currents in the cusps (blue) and with the hot narrow plume conduit (red). (B=1.72; Ra=8.4×107; a=0.5; γ=1336.)
Convection stratifiée.
2.3.1 Pattern
The convective pattern is asymmetrical between the two layers, depending on the viscosity ratio and the Rayleigh numbers: narrow cylindrical plumes usually develop in layer 2 (higher Ra), and 2-D sheets in layer 1 (Fig. 3a). If one layer is too thin to convect – as may be the case for the D″ layer at the base of the mantle –, a conductive thermal gradient develops across it. The system then has only two thermal boundary layers, one of them (the lower, say) being thicker since stratified in density. Hot cylindrical plumes rise from it (Fig. 4a) and create cusps in the interface, through which entrainment occurs. They involve temperature fluctuations much bigger than those of purely thermal convection [15], because, since the layers are miscible, any instability starting from one side of the interface must entrain by viscous coupling a film of more stable material from the other side. Hence, for instabilities to occur at the interface, the temperature there must increase to overcome the stable chemical gradient. These strong thermal heterogeneities create lateral and temporal heat flux variations of up to a factor of three. Moreover, these instabilities induce a topography at the interface, which acts further to anchor the thermochemical plumes: coupled with the strong plume thermal anomaly, the cusp localizes the instability and forces the lateral flow in the thermal boundary layer along the cusp (Fig. 4b) [15,16,40]. The thermochemical plumes therefore form a stable polygonal pattern. Compared to classical thermal convection, in which plumes arise randomly, the effect of a strong stratification is thus to focus heat and stabilize features.

Thermochemical plumes: (a) generation from a stratified thermal boundary layer, where the thin denser layer is dyed with fluoresceine (B=0.41; Ra=9×106; a=0.06; γ=30); (b) sketch of a thermochemical plume.
Panaches thermochimiques.
2.3.2 Entrainment
The entrainment occurs in two steps [15,16,42]: first, the thermal heterogeneities at the interface induce circulations in the two layers; then the viscous drag due to those convective motions becomes sufficient to overcome the negative buoyancy forces due to the stable chemical density gradient, and thin tendrils of material are entrained (Fig. 4). After a while, the two superimposed convecting layers will therefore look like ‘marble cakes’ [4]. The entrainment rate and the filament thickness depend on the intensity of convection, the viscosity ratio and the buoyancy ratio: the more stable the fluid, the harder it is to entrain. Scaling laws have been derived [14–16,31,52], which explain the data well [14,16,20,31].
2.3.3 Thermal structure
At very low Rayleigh numbers and small viscosity ratios (1/5<γ<5), mechanical coupling is predicted [47] and observed in numerical (e.g., [13]) and laboratory experiments [44] with cold sinking currents above hot rising currents. At large Rayleigh numbers, and/or large viscosity ratios (γ>5 or γ<1/5), thermal coupling is observed throughout the tank (Fig. 3b) [13,15,42], with large-scale, high-amplitude temperature anomalies that are maximum at the interface, and correlated throughout the whole depth (Fig. 5). However, the small-scale, small-amplitude, anomalies associated with the ‘thermal’ mode are largest in the outer thermal boundary layers, but are suppressed at the interface by the stratification (Fig. 5b).
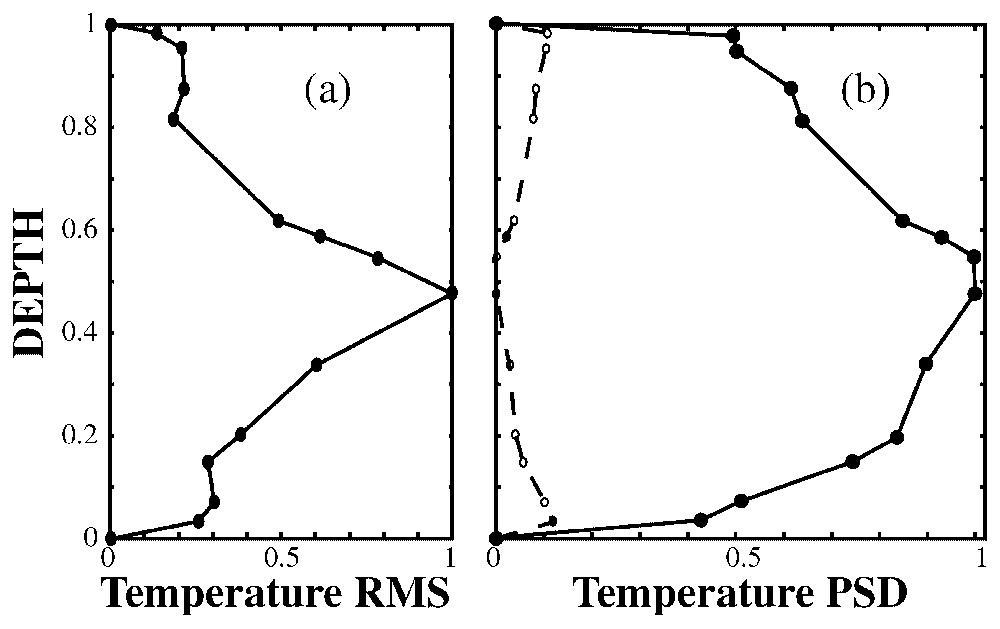
Stratified regime: temperature fluctuations. (a) Root-mean square amplitude of the temperature fluctuations as a function of depth. (b) Relative proportion of energy contained in a given frequency band as a function of depth. The dashed line is due to the small periods (<50 min) fluctuations created by the purely thermal instabilities out of the top and bottom thermal boundary layer. The solid line is due the long-period (>50 min), large-amplitude fluctuations generated by the thermochemical mode at the interface. The small-scale signal has been multiplied by 10 (B=3.95; Ra=1.6×108; a=0.5; γ=17).
Fluctuations de température en régime stratifié.
2.3.4 Topography of the interface
For B⩾1, the interface remains flat (Fig. 3a). When the buoyancy ratio becomes lower than about 1, the interface begins to deform substantially under the action of the thermal features coming from both convecting layers (Figs. 1d and 6b). The topography amplitude increases with the viscosity ratio, and/or when B decreases [36]. When one of the layer is thin enough compared to the other one, it can even become discontinuous (Fig. 1d), and form stable piles [54,56].
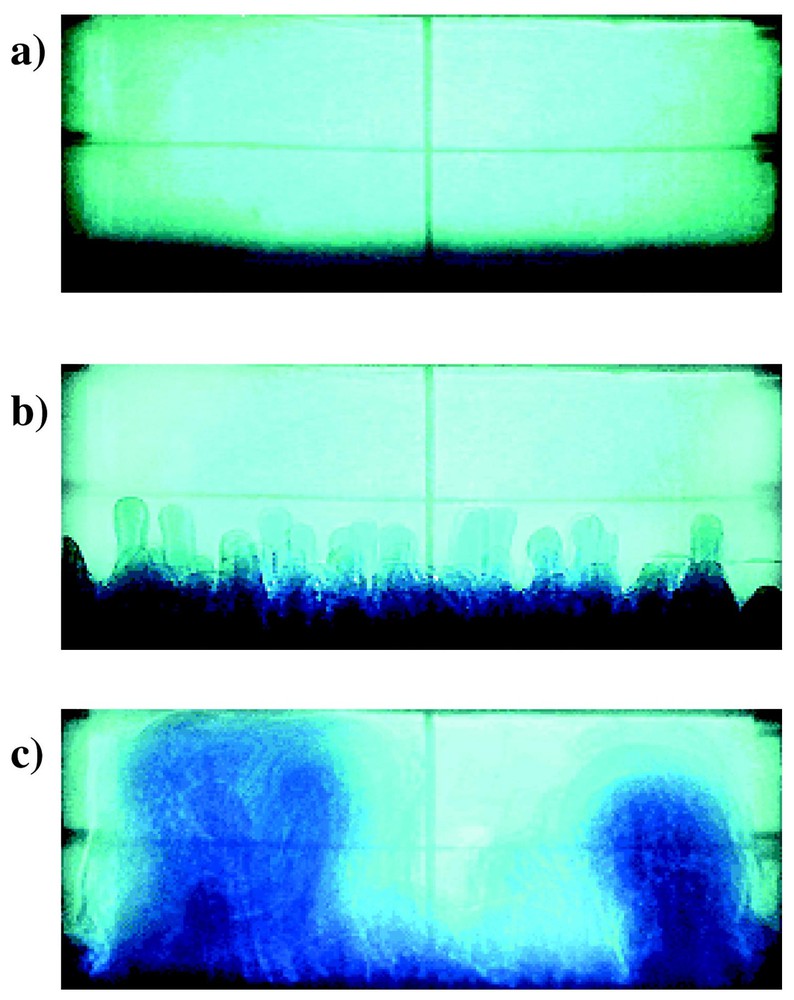
Whole layer regime at high Rayleigh numbers when the hot less viscous layer invades the more viscous layer. Salt-sugar syrup solutions (the viscosity strongly depends on temperature and not on composition). Ra=3×107; B=0.3; a=0.155; γ=0.18. (a) t=0; (b) t=2 min; (c) t=4 min.
Convection sur toute la couche avec dômes moins visqueux montants.
2.3.5 Evolution through time
Because of entrainment, a steady stratified state is never obtained and the buoyancy ratio slowly decreases through time, until B=0 and complete mixing is achieved. Scaling laws allow predictions of the evolution of the densities and thicknesses of the two initial layers [15].
2.4 ‘Whole-layer’ regime
This regime is characterized by large deformations of the interface. However, two modes are observed, either ‘oscillatory’ or ‘overturning’. Fig. 1a and 1b show the convective patterns developed in each case close to marginal stability, i.e. at very low Rayleigh numbers. In the oscillatory mode, the interface deforms following the push of the rising hot and descending cold domes and a travelling pattern develops, which can last for weeks (Fig. 1a). No mixing across the interface is observed, so that the two reservoirs constituted by the two initial layers remain pristine. This regime is best observed for B close to Bc and γ>5 or γ<1/5. In the overturning mode, when the rising and descending domes reach respectively the upper cold and lower hot boundaries, overturn occurs. Although the temperature distribution remains steady, the two fluids describe a spiral (Fig. 1b) and the layers mix slowly. Away from marginal stability, i.e. at high Rayleigh numbers, the pattern becomes more complicated.
2.5 Pattern
When the lower layer (or the upper layer) is heated (respectively cooled), by conduction or convection, to the point where its thermal buoyancy counterbalances the stable chemical stratification and the viscous forces, the interface deforms in large domes (Figs. 6 and 7). When such a dome reaches the top (or the bottom) of the tank, it cools (warms) and loses its thermal buoyancy. Being compositionally denser (lighter), it falls back to the bottom (rises back to the top). At high Ra, it may even detach from its base before sinking (rising) again. When thermal convection exists in the layer before doming (Fig. 6b), each dome collects several smaller scale instabilities (Fig. 6c). The wavelength of doming is controlled by the more viscous layer [26,36]. The direction of doming is determined by the balance between tendencies to penetrate the less viscous layer and the thicker layer [45]. Thus, less viscous domes sometimes invade the more viscous layer when the latter is thicker (Fig. 8). When one of the layers is thin (typically a⩽0.3 or a⩾0.7) and/or when the Rayleigh number is high, the invading layer becomes discontinuous once the domes are well developed (Figs. 6c and 9). When the interlayer viscosity ratio γ is close to unity, the dome breaks up into smaller-scale blobs upon overturning and the two layers are very quickly mixed [43]. When γ is greater than 10, the domes collapse on themselves (Fig. 7e), and the two initial layers are reconstituted, ready for another cycle to begin. The number of observed cycles depends strongly on the viscosity and depth ratios (Fig. 8), and more weakly on the Rayleigh number. As many as eight cycles can be observed before mixing of the two ‘reservoirs’. After one cycle, the domes may contain encapsulated ‘blobs’ of the other fluid (Figs. 7e and 9), which will eventually burst through the domes as Rayleigh–Taylor instabilities. For γ>10 and high Rayleigh numbers, hot thermochemical plumes typically form on the rising domes (Fig. 10).
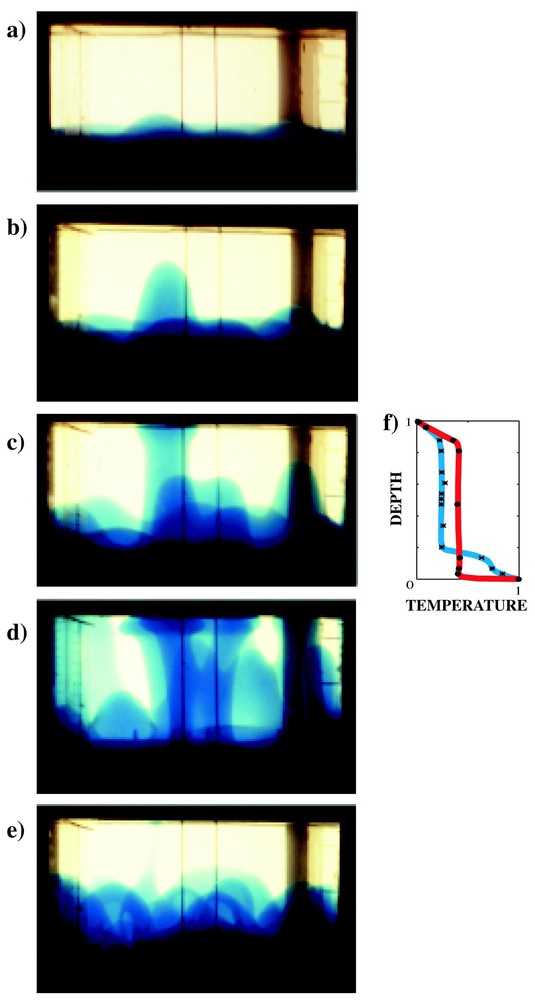
Whole layer regime at high Rayleigh number when the hot more viscous layer invades the less viscous layer. Salt–Natrosol solutions (the viscosity depends mainly on Natrosol content and not on temperature): Ra=1.6×107; B=0.2; a=0.30; γ=33. (a) t=21 min; (b) t=22.5 min; (c) t=24 min; (d) t=27 min; (e) t=37 min; (f) vertical temperature profiles within a rising dome (in red) and out of a dome (in blue) for case (c).
Convection sur toute la couche avec dômes plus visqueux montants.
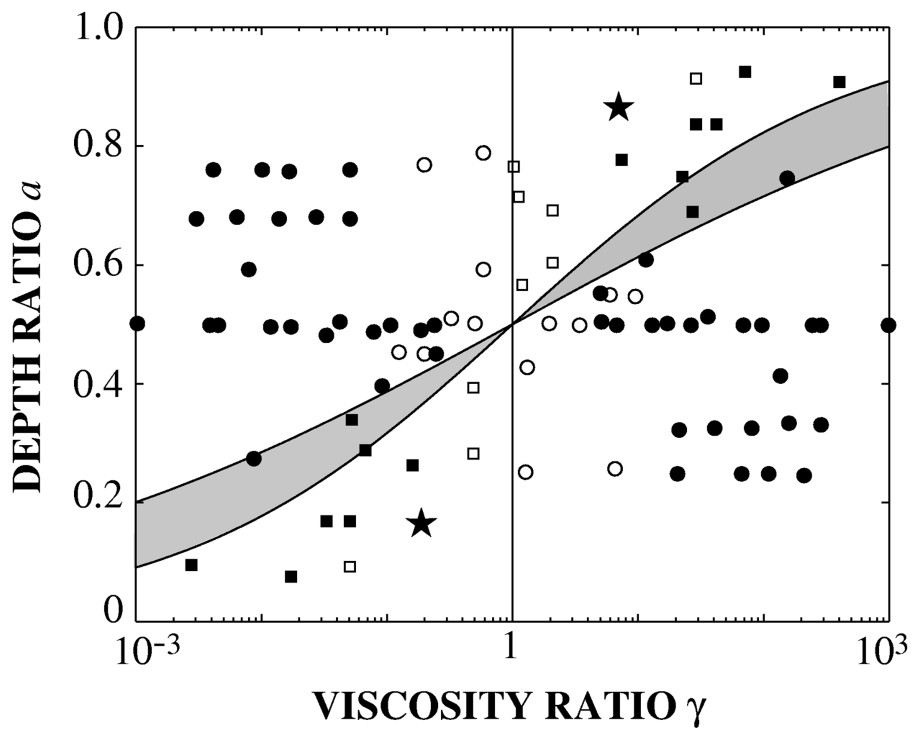
Spouting direction as a function of γ and a. Circles: experiments where more viscous diapirs invade a less viscous mantle; squares: experiments where less viscous cavity plumes invade a more viscous mantle. Filled symbols designate cases where at least two pulsations were observed (data from [36]). The star designates the experiment run with sugar syrup (Fig. 6). Above the shaded area, the top layer invades the bottom layer; below the shaded area, the bottom layer invades the top layer.
Direction d'invasion en fonction de γ et a.

Pattern of mixing. The lower layer, initially denser and more viscous, is dyed with fluoresceine. The experimental tank is illuminated by a laser sheet. After three cycles, the two layers are still not mixed, but one can distinguish filaments and blobs of dark, light fluid within the viscous domes. The thin filaments were entrained by viscous coupling while the blobs were encapsulated when the viscous dome collapsed upon cooling. Since the blobs are lighter, they are bursting up through the viscous fluid as Rayleigh–Taylor instabilities. (B=0.30; Ra=2.7×107; a=0.3; γ=175).
Figures de mélange.

Thermochemical plume out of the top of a dome. B=0.2; Ra=1.1×107; a=0.6; γ=18 (shadowgraph).
Panache thermochimique issu d'un dôme.
2.6 Thermal structure
At a given position, the local thermal structure (Fig. 7f) oscillates between ‘stratified convection’ with two outer boundary layers and one interfacial one when the two initial reservoirs are re-constituted (Fig. 7a, b and e), and ‘whole-layer’ convection with only the two outer boundaries and a thermally homogeneous core when a dome has formed (Fig. 7c and d). As a result, the bottom and surface heat flows are very heterogeneous in space and time, with heat-flow fluctuations that can reach a factor of four (Fig. 11).
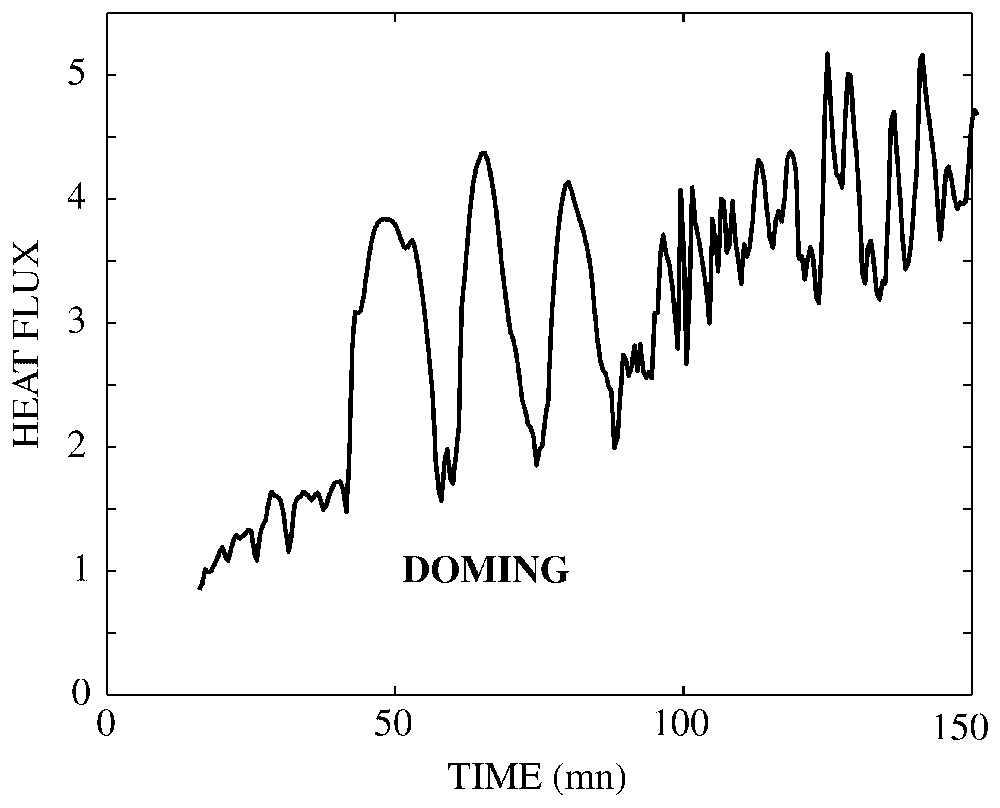
Surface heat flux (in arbitrary units) measured at one location as a function of time. The three peaks correspond to the three cycles where a dome reached the surface at this location (B=0.22; Ra=1.48×108; a=0.4; γ=146).
For doming to occur, thermal effects have to overcome the stabilizing compositional effects and the thermal and mechanical diffusion. The large-scale temperature anomalies θ (Fig. 7f) are therefore of the form [26,36]:
| (1) |
2.7 Mixing
The mixing pattern in this regime is complicated (Fig. 9), since convection creates compositional heterogeneities with two different typical size and topology: (a) thin filaments are generated by mechanical entrainment through viscous coupling, either in the thermochemical plumes on top of the domes (Figs. 5 and 10), or during the doming sequence (Fig. 9) – the two initial reservoirs therefore quickly become ‘marble cakes’ [4], even though they remain dynamically separated for a long time –; (b) domes, and blobs encapsulated in the domes, are generated by instabilities (Figs. 6, 7 and 9).
3 Convection in a heterogeneous mantle
3.1 Stability
Although the experimental system is greatly simplified (no plate tectonics, no radioactive heating, no pressure-dependence of ν, κ, and α), it can give important clues to the behaviour of a heterogeneous planetary mantle. From the definition of the buoyancy ratio, the critical density contrast separating the stratified and doming regimes is:
| (2) |
Fig. 12 shows Δρc/ρ as a function of the temperature difference applied to the system ΔT for typical values of Bc=0.4, and αint=3×10−5 K−1 (typical for the transition zone), and 1×10−5 K−1 (deep mantle) [8]. Therefore, it allows us to estimate under which conditions the mantle would be wholly in the stratified regime, wholly in the doming regime, or in different regimes at different lateral positions.

Critical density contrast as a function of the temperature difference driving convection. The thin line dividing the two regimes is obtained for α=10−5 K−1 and the thick line for α=3×10−5 K−1. ‘A’: whole mantle in the stratified regime; ‘B’: locally stratified D″ layer (the shaded area shows the range of temperature differences across the D″ layer [34]; ‘C’: whole mantle doming regime; : locally stratified on top of a dome generated in ‘C’.
Régime du manteau terrestre en fonction du contraste de densité et de la différence de température.
For a typical ΔT across the mantle around 2500 K, the transition between ‘stratified’ and ‘whole-mantle’ convection occurs when Δρc/ρ is of the order of 2% (Fig. 12). However, because Δρc/ρ depends linearly on α and α decreases with depth [8], Δρc/ρ will also decrease with depth. Thus a given density contrast Δρ/ρ and temperature difference ΔT can generate whole-mantle convection and doming if the interface is in the mid-mantle, or stratified convection if it is near the bottom of the mantle (Fig. 12). This suggests a unified physical explanation for two important features of convection in the present-day mantle: superswells and hot spots.
3.2 How to generate a superswell
‘Superswells’ are regions of anomalously shallow sea-floor several thousands of kilometres in extent with unusually dense concentrations of hot spots (for a review, see [37]). At present, two have been identified: one under Africa and the other beneath French Polynesia in the South Pacific. Modelling based on the correlation of seismic tomography, geoid and topography concludes that both superswells are caused by dynamic upwelling of hot material in the mantle [37]. Seismic studies further suggest that the hot material is also chemically distinct at the bottom of the mantle, and that the edges of the chemical anomaly are sharp [7]. Moreover, the lavas produced are radiogenically enriched. It has been suggested that such ‘superplumes’ are oscillatory phenomena related to surges in ocean–crust production and periods of magnetic quiescence [33]. If true, this indicates strong core/mantle coupling and suggests that superplumes originate at the core-mantle boundary.
Now, consider an interface in the mid-mantle. The appropriate value of α at this depth is about 2×10−5 K−1. Fig. 12 then shows that for Δρ/ρ<2%, a mid-mantle interface would deform into large sharp-edged domes (Figs. 6, 7, 9, and 10) crowned by several small hot plumes (Fig. 10). According to the scaling laws [14,36], they would be 1000–4000 km in lateral extent and oscillating up and down on a 100 Ma–1 Ga time scale. We propose that those domes are the ‘superplumes’ identified by the geophysical data. Thus the two present-day ‘superplumes’ would represent two different stages of the same phenomenon: the African superswell would correspond to the early stage of dome formation and ascent, while the Polynesian superswell would correspond to a more mature dome, which has already gone through a whole cycle.
According to the experiments, each dome would be composed of several smaller-scale instabilities (Fig. 6b), and, after a cycle, this situation would be enhanced by mixing (Fig. 9). A ‘dome’ is therefore most certainly a patchwork of different mantle components, which could explain the complex shapes of the superplumes revealed recently by seismic tomography [49]. Moreover, since the mantle viscosity strongly decreases with temperature, the hot rising domes are expected to be less viscous. According to Fig. 8, that several pulsations occur (as under the Pacific) implies that γ<0.1. And that less viscous domes spout into a more viscous mantle implies that a<0.3, i.e. that the average thickness of the less viscous bottom reservoir is less than 800 km [36]. This small thickness further implies that the lower layer would become discontinuous upon doming.
3.3 Four deep ways to generate hot spots
A ‘hot spot’ [58] is characterized by a localized source of volcanism, which can produce flood basalts and/or a volcanic track. It usually samples mantle geochemical reservoirs distinct from those sampled by mid-ocean ridges [28]. Morgan [39] proposed that it occurs where a hot, narrow (<100 km) and relatively fixed plume rising from a deep mantle boundary layer impinges on the moving lithosphere. Since a plume is mushroom-shaped with a large cap or ‘head’ and a thin stem or ‘tail’, the flood basalts would correspond to the impingement of the head and the volcanic track to the impingement of the tail [46]. Several hot spots follow well this sequence of events (e.g., La Réunion, Tristan, Louisville...). Considering the diameter of the traps/head (which can be >1000 km), it seems unlikely that they should come from the transition zone at 660-km depth [46]. However, mantle plumes are too cold [1,18] and many are too long-lived [16] to have arisen from a purely thermal core/mantle boundary layer having the expected temperature jump (∼1000 °C). Besides, some (e.g., Crozet) are too weak to have traversed the entire depth of the mantle [1].
Section 2 shows that long-lived thermochemical plumes are a feature of the stratified regime, which occurs whenever the buoyancy ratio is locally greater than a critical value Bc. According to Eq. (2) and Fig. 12, thermochemical plumes can therefore be produced for the following density heterogeneities:
- (a) greater than 2% (e.g., point ‘A’ in Fig. 12) if the mantle is completely stratified with an interface in the mid-mantle (e.g., 670-km depth, Fig. 3a);
- (b) greater than 0.2–0.3% (e.g., point ‘B’ in Fig. 12) if the interface lays in the D″ layer just above the core-mantle boundary (Fig. 4a);
- (c) around 0.1–1% (e.g., point ‘C’ in Fig. 12) if plumes form on top of a thermochemical ‘dome’ in the mid-mantle (Fig. 10). This can happen since the temperature difference across the interface (Fig. 12, C′) is less than that over the whole mantle (Fig. 12, C). Therefore, the ‘local’ buoyancy ratio at the upper surface of a dome will be higher than the ‘global’ B for the whole mantle. Because the stratification at the top of a dome then is locally ‘strong’, thin hot plumes entraining dome material are expected.
This suggests that ‘weak’ hot spots are produced by plumes out of a thermochemical boundary layer in the mid-mantle, either due to a global and strong stratification (case a), or to a local stratification on top of a dome (case b). And in the three cases a, b, and c, part of the temperature gradient applied to the mantle will be absorbed by the lower, denser layer [1,18,54], so that plumes rising out of the interfacial thermal boundary layer will always generate ‘cold’ hot spots. Moreover, if plumes arise from a stratified D″ layer (case b), they will generate huge lateral variations in heat flow out of the core-mantle boundary. It is important to note that these three types of hot spots will mainly sample the unstable part of the stratified boundary layer, i.e. the lower part of the upper reservoir, with at most 10% of entrained material from the lower reservoir [14,16].
The experiments reported here suggest yet another possibility for intraplate volcanism (d), when encapsulated lighter blobs spout from the thermochemical domes (Fig. 9) and reach the lithosphere: they will then generate short flood basalts with no subsequent volcanic track. A number are found in the ‘Darwin Rise’ area, which is thought to be the first cycle of the Polynesian superswell.
3.4 Signatures of a stratified mantle
For density contrasts greater than 2% and an interface somewhere in the mid-mantle, the mantle would be stratified and convection would occur in two superimposed layers. According to Section 2.2, it would be characterized by thermal coupling, anchored thermochemical plumes, and a ‘marble-cake’ chemical structure in both layers.
3.4.1 Thermal structure
A horizontally averaged vertical temperature profile would give a stratified temperature structure, with two external thermal boundary layers and an interfacial boundary layer and two isothermal cores (Fig. 3b). However, the pattern of lateral thermal heterogeneities (i.e. the total temperature field minus the lateral average) would strongly depend on wavelength. For the small wavelength (<200 km) due to purely thermal instabilities from the outer boundaries of each layer, the heterogeneities would be maximum in the outer boundaries and completely vanish at the interface. By contrast, the long wavelength heterogeneities would be largest at the interface and correlated over the whole mantle.
3.4.2 Anchored plumes
Cylindrical, narrow and quite stable thermochemical plumes (Fig. 3a) would be produced in the less viscous, top layer and their characteristics have already been summarized in case (a) of Section 3.3. They would entrain a mass flux from the lower reservoir to the upper reservoir ranging from 1011 to , depending on the parameters chosen.
3.4.3 Marble cake
Considering the Earth's parameter values (especially viscosity), both layers would be convecting. Therefore, both layers would rapidly incorporate 2D or 3D filaments of the other layer by mechanical entrainment. According to the scaling laws [15], the thickness of those filaments would probably be of the order of 10 km, and it would subsequently decrease by stirring [27]. Objects of this size are expected to scatter seismic energy [24]. Moreover, one expects to obtain a wide spectrum of geochemical compositions from random sampling of those filaments at the surface [4,10,21,25,27].
3.5 Temporal evolution and geochemical reservoirs
Because of entrainment and mixing, all the experiments evolve towards single layer convection, even if they started in the stratified regime. The typical duration of the stratified regime is a function of the buoyancy and viscosity ratios, and of the respective intensity of convection in each layer [15]. Fig. 13 shows the typical evolution through time of the interface depth and the averaged densities of both layers, for a very simple model where viscosity depends only on composition. It is interesting to note that (1) both densities are changing through time, so that no ‘pristine’ reservoir remains, and (2) the interface depth can vary. Running those kinds of models shows that the mantle may be capable of erasing a 2% density contrast within the age of the Earth. Moreover, the occurrence of the doming regime today would require an initial density contrast, 4.5 Byr ago, not greater than 4%. Such an evolution would also imply huge changes in the heat flow out of the core, both in time, and in space. And we would expect the changes to be much more frequent in the doming regime.
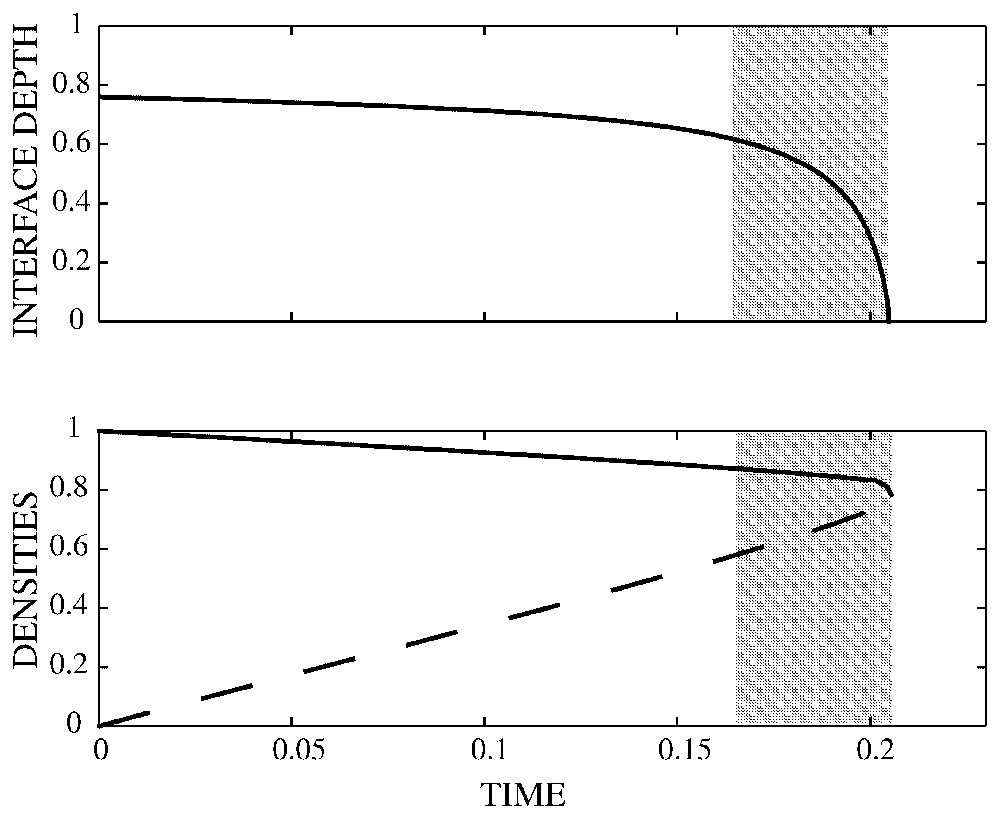
Typical time evolution of the interfacial depth and of the densities of the two initial layers, calculated with the scaling laws of Davaille [13] using as initial values Ra=108; γ=100 and . The dashed line stands for the less dense, less viscous top layer, while the solid line stands for the more viscous, denser bottom layer. The interface was originally at the transition zone. The shaded area represents the ‘doming’ regime domain.
Évolution temporelle d'un système initialement stratifié.
3.6 The Earth's mantle from a fluid mechanics point of view
Both seismic Earth models [17] and mineral physics studies [29] suggest that any present-day planet-wide stratification in density of chemical origin cannot exceed a few percent [6]. As we have seen in previous sections, neither the correlation of the large-scale seismic heterogeneities across the mantle, nor the scattering of seismic energy throughout the whole mantle, are good criteria to discriminate between whole-mantle and stratified convection.
Strongly stratified convection with a nearly flat interface in the mid-mantle would require a chemical density contrast greater than 5% (i.e. B⩾1). Such a density jump would act as a strong reflector for seismic waves, which is not observed in the mid-mantle [17]. It has sometimes been argued that such a chemical boundary could be hidden at the 660-km discontinuity and that thermal coupling in the lower mantle could explain the cold material imaged by seismic tomography below the 660 discontinuity and the sinking slabs. However, since heat transfer across the 660 discontinuity would then be conductive, it would take more than 100 Myr to establish such thermal coupling. Hence, although thermal coupling is expected in stratified convection (see previous section), it cannot explain that young slabs can be imaged through and below the 660 discontinuity. Therefore, strong stratification with a flat interface seems precluded in the mantle today.
For planet-wide density stratification between 2 and 5% (i.e. Bc⩽B⩽1) with an interface in the mid-mantle, our study shows that stratified convection would occur but with a highly distorted interface. In a careful study of the seismic signatures produced in that case, Tackley [56] showed that the thermal boundary layer at the interface would retain a strong signature that should be detected seismically, unless the lower reservoir is thin enough to become discontinuous under the action of convection. The signature of the latter case would be more consistent with seismic observations. Piles of denser material at the bottom of the mantle could therefore exist in the present-day mantle. Those piles would be located under lower mantle uprisings, and would remain quite stable through time [56].
If present-day density anomalies were smaller than 2%, the mantle would be in the whole-layer, ‘doming’ regime. As described in previous sections, this regime is characterized by its periodicity and its motion over the whole mantle depth. This is consistent with the occurrence of pulsatory superswells (e.g., under the Pacific) and hot spots with large ‘head’ event (e.g., Réunion) that crosses the whole mantle. But locally, strong stratification could persist, as, for example, in D″, where denser ‘piles’ could develop below superswells, or thermochemical plumes could develop out of a stratified thermal boundary layer. Hence, hot spots and superswells can coexist on Earth (Fig. 14), depending on the magnitude of the density heterogeneities and of the depth dependence of thermal expansion.
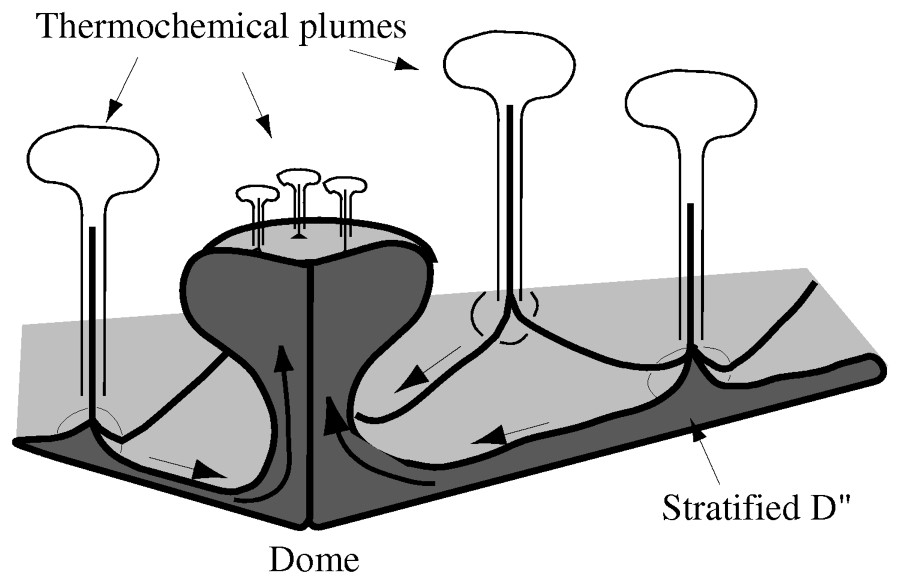
Superposition of plumes and domes in the Earth's mantle. Motions of the sources of the thermochemical plumes are induced by lateral motions in the stratified boundary layer. All plume sources are drifting towards the rising dome.
Superposition de panaches et de dômes dans le manteau terrestre.
The mantle may have evolved from a strong stratification 4.5 Byr ago with an interface, for example, initially located at the 660-km discontinuity, to a doming regime today. This would be a way to reconcile the survival of geochemically distinct reservoirs with the small amplitude of present-day density heterogeneities inferred from seismology and mineral physics. However, the notion of ‘reservoir’ has to be used with caution: from a fluid mechanics point of view, primitive material certainly exists today in the mantle under the form of km-thick filaments, but no ‘reservoir’ can have remained pristine because of entrainment by convection. Hence, evidence for the existence and persistence of different materials in the mantle does not require stratified convection.
Finally, although the physics of the phenomena described here is robust, several important ingredients of the Earth's mantle, such as Plate Tectonics, phase transition, floating continents, internal heating, variable properties or partial melting, are missing. No scenario of the mantle's evolution will be realistic until we understand how they influence the dynamics. For example, it may be reasonable to think that the first cratons were generated by an instability coming from deep in the mantle (superswell or thermochemical plume). This would prove that the early mantle was not strongly stratified, or that it was stratified only for small wavelengths (a endothermic phase transition could have this effect [53]). Because of differentiation and plate tectonics, the mantle could also, from nearly homogeneous initially, evolves toward stratification. Considering the complexity of mantle material, the reality is probably in between all these models.
4 Conclusions
Thermal convection in a heterogeneous mantle can produce very complex time-dependent patterns. To deduce the dynamical state of the mantle from the observations is therefore difficult. For example, our results show that (a) ‘whole-mantle’ convection does not mean convection into a homogeneous mantle and compositional density heterogeneities as small as 0.1% can change the convective pattern, (b) convection in a chemically heterogeneous mantle does not mean convection in two superimposed reservoirs, (c) it is important to consider the time- and length-scales of the observations when we interpret them. Given all those caveats, thermochemical convection provides a promising framework to account for both present-day mantle features (hot spots and superswells, seismic observations) and the existence of long-lived reservoirs inferred from geochemical data.
Thermochemical convection is also likely to have a strong influence on the dynamics of the core. Domes and hot spots generate heat flux variations at least as large as the mean heat flux value, which will result in a strongly inhomogeneous and time-dependent thermal boundary condition at the CMB. This spatiotemporal variability may induce changes of regimes in the dynamo.
Further questions remain to be answered. From a pure fluid mechanics point of view, the two most challenging questions for the future are probably (1) to understand Plate Tectonics, which will give us more constraints on the time-evolution of the Earth, and (2) to characterize (time- and length-scales) the mixing in a heterogeneous convecting fluid, which will clarify our interpretation of the geochemical data. From the observational point of view, we can ask (3) when seismology will be able to distinguish small chemical density heterogeneities from thermal anomalies and to resolve non-horizontal interfaces? (4) and how dependent are geochemical inferences on the time-history of the reservoirs, and on the filter of partial melting?
Acknowledgements
This work benefited from discussions with Dave Bercovici, Alain Bonneville, Vincent Courtillot, Claude Jaupart, Marc Javoy, Manuel Moreira, Neil Ribe, Barbara Romanowicz, Eléonore Stutzmann, George Veronis, and Steve Grand. The manuscript was improved thanks to the reviews of Dan McKenzie and Marc Monnereau.


