Solid-state mantle convection coupled with a crystallising basal magma ocean

Stéphane Labrosse; Adrien Morison; Paul James Tackley

doi:10.5802/crgeos.275

Article de recherche

Solid-state mantle convection coupled with a crystallising basal magma ocean
[Convection dans le manteau solide couplée à la cristallisation d’un océan de magma basal]

Stéphane Labrosse ¹ ; Adrien Morison ² ; Paul James Tackley ³

¹ LGLTPE, ENS de Lyon, Université de Lyon, 46 allée d’Italie, 69003 Lyon, France
² Univ Exeter, Phys & Astron, Exeter, Devon, England
³ Department of Earth and Planetary Sciences, ETH Zürich, Sonneggstrasse 5, Zürich, 8092, Switzerland

Comptes Rendus. Géoscience, Online first (2024), pp. 1-17.

Résumés

Anglais
Français

Fractional crystallisation of a basal magma ocean (BMO) has been proposed to explain the formation of large scale compositional variations in the mantle and the persistence of partially molten patches in the lowermost mantle. We present a complete set of equations for the thermal and compositional evolution of the BMO and show that it can be implemented in a mantle convection code to solve the long term mantle evolution problem. The presence of the BMO modifies the dynamics of the mantle in several ways. The phase equilibrium at the bottom of the solid mantle implies a change of mechanical boundary condition, which helps solid state convection. The net freezing of the BMO implies a change of computational domain, which is treated by mapping the radial coordinate on a constant thickness domain. Fractional melting and freezing at the boundary makes the composition of the BMO and the solid mantle evolve, which is treated using Lagrangian tracers. A sample calculation shows that the persistence of the BMO and its long term evolution drastically changes the dynamics of the solid mantle by promoting downwelling currents and large scale flow. The gradual increase of the FeO content in the BMO and in the solid that crystallises from it leads to the stabilisation of large scale thermo-compositional piles at the bottom of the mantle, possibly explaining the observations from seismology.

La cristallisation fractionnée d’un océan de magma basal (OMB) a été proposée pour expliquer la formation de variations de composition à grande échelle dans le manteau et la persistance de zones partiellement fondues à la base du manteau inférieur. Nous présentons un ensemble complet d’équations pour l’évolution thermique et compositionnelle de l’OMB et montrons qu’il peut être implémenté dans un code de convection du manteau pour résoudre le problème de l’évolution du manteau à long terme. La présence de l’OMB modifie la dynamique du manteau de plusieurs façons. L’équilibre de phase à la base du manteau solide implique un changement des conditions limites mécaniques, ce qui favorise la convection à l’état solide. La cristallisation nette de l’OMB implique un changement de domaine de calcul, qui est traité en utilisant un changement de variable pour la coordonnée radiale pour garder une épaisseur constante. La fusion et la cristallisation fractionnés à la frontière font évoluer la composition de l’OMB et du manteau solide, ce qui est traité à l’aide de traceurs lagrangiens. Un exemple de calcul montre que la persistance de l’OMB et son évolution à long terme modifient radicalement la dynamique du manteau solide en favorisant les courants descendant focalisés et les écoulements à grande échelle. L’augmentation progressive de la teneur en FeO dans l’OMB et dans le solide qui cristallise à partir de celui-ci conduit à la stabilisation de piles thermo-compositionnelles à grande échelle en base de manteau, ce qui pourrait expliquer les observations sismologiques.

Métadonnées

Reçu le : 2024-05-21
Révisé le : 2024-10-03
Accepté le : 2024-10-07
Première publication : 2024-11-12

DOI : 10.5802/crgeos.275

Keywords: Thermal evolution, Mantle convection, Core cooling, Basal magma ocean
Mot clés : Évolution thermique, Convection mantellique, Refroidissement du noyau, Océan de magma basal

Affiliations des auteurs :

Stéphane Labrosse ¹ ; Adrien Morison ² ; Paul James Tackley ³

¹ LGLTPE, ENS de Lyon, Université de Lyon, 46 allée d’Italie, 69003 Lyon, France
² Univ Exeter, Phys & Astron, Exeter, Devon, England
³ Department of Earth and Planetary Sciences, ETH Zürich, Sonneggstrasse 5, Zürich, 8092, Switzerland

Licence :

CC-BY 4.0

Droits d'auteur : Les auteurs conservent leurs droits

@article{CRGEOS_2024__356_S1_A6_0,
     author = {St\'ephane Labrosse and Adrien Morison and Paul James Tackley},
     title = {Solid-state mantle convection coupled with a crystallising basal magma ocean},
     journal = {Comptes Rendus. G\'eoscience},
     publisher = {Acad\'emie des sciences, Paris},
     year = {2024},
     doi = {10.5802/crgeos.275},
     language = {en},
     note = {Online first},
}

TY  - JOUR
AU  - Stéphane Labrosse
AU  - Adrien Morison
AU  - Paul James Tackley
TI  - Solid-state mantle convection coupled with a crystallising basal magma ocean
JO  - Comptes Rendus. Géoscience
PY  - 2024
PB  - Académie des sciences, Paris
N1  - Online first
DO  - 10.5802/crgeos.275
LA  - en
ID  - CRGEOS_2024__356_S1_A6_0
ER  -

%0 Journal Article
%A Stéphane Labrosse
%A Adrien Morison
%A Paul James Tackley
%T Solid-state mantle convection coupled with a crystallising basal magma ocean
%J Comptes Rendus. Géoscience
%D 2024
%I Académie des sciences, Paris
%Z Online first
%R 10.5802/crgeos.275
%G en
%F CRGEOS_2024__356_S1_A6_0

Stéphane Labrosse; Adrien Morison; Paul James Tackley. Solid-state mantle convection coupled with a crystallising basal magma ocean. Comptes Rendus. Géoscience, Online first (2024), pp. 1-17. doi : 10.5802/crgeos.275.

Version originale du texte intégral (Proposez une traduction )

1. Introduction

The long term evolution of the Earth is paced by convection in the solid mantle, which is much slower than the dynamics of the underlying liquid core. The present day structure of the mantle is rather well constrained, thanks to the tremendous progress of seismic tomography over the last few decades [e.g. Fichtner et al., 2024], and is generally well understood in the context of mantle convection in a plate-tectonic regime [e.g. Coltice et al., 2019]. Paleogeographic reconstructions have been used to constrain models of mantle convection going back 1 Gyr [Flament et al., 2022] although, of course, the uncertainties regarding paleogeography increase drastically with ages larger than about 200 Myr, the age of the oldest oceanic plate. These studies generally consider the presence of chemically denser material in the form of thermochemical piles at the bottom of the mantle as a way to explain the seismically imaged large low shear velocity provinces (LLSVPs) [e.g. Hernlund and McNamara, 2015, for a review].

If we accept the chemical interpretation of LLSVPs, the question of their formation remains. Several scenarios have been proposed. The formation of the Earth could make the mantle initially chemically stratified in two layers and the slow erosion of the stratification by mantle convection could lead to the present state [e.g. Le Bars and Davaille, 2004]. Instead of gradually mixing an initial stratification, dense material produced by the extraction of the oceanic crust could accumulate at the bottom of the mantle after being subducted [Christensen and Hofmann, 1994, Nakagawa et al., 2010, Li and McNamara, 2013]. A last scenario, which is the topic of the present paper, proposes that the fractional crystallisation of a basal magma ocean (BMO) can lead to the stabilisation of chemically different piles at the bottom of the mantle [Labrosse et al., 2007].

In addition to LLSVPs, seismological studies of the deep mantle have uncovered regions of very reduced seismic velocity, on a much smaller scale than LLSVPs, termed ultra low velocity zones (ULVZs). These regions, that can be tens to hundreds of km wide, have seismic velocities about 30% (for S) and 10% (for P) smaller than the surrounding mantle, and a density a few percent larger [Rost et al., 2005], while typical variations of the seismic velocities on the large scale are of the order of a few percent. These extreme velocity reductions, and the fact that the velocity of S waves is more reduced than that of P waves, has been used to imply the presence of partial melt [Williams and Garnero, 1996]. If indeed the mantle in contact with the core is currently partially molten, more melt should have been present in the past when the core was hotter. Indeed, we know that the Earth has been cooling down [Jaupart et al., 2015] and the possibility of the core to be cooling faster than the mantle has been invoked [Driscoll and Bercovici, 2014, Labrosse, 2016, Patočka et al., 2020] to solve the long standing thermal catastrophe problem for the thermal evolution of the Earth [Christensen, 1985]. The rapid core cooling is also a consequence of the necessity to maintain a convective dynamo with a large thermal conductivity of the core [Labrosse, 2015, Patočka et al., 2020]. All these arguments together led to the scenario of a basal magma ocean [Labrosse et al., 2007].

The aim of this paper is to present a first step toward including a basal magma ocean in a fully dynamical model of mantle evolution. Starting with a mantle convection model, in this case StagYY [Tackley, 2008], a first ingredient to add is the possibility of a solid-melt phase change at the boundary with the underlying magma ocean. Compositional changes associated with the phase change are also required. Both aspects have already been reported and the implications of such a boundary have been explored [Labrosse et al., 2018, Agrusta et al., 2019, Bolrão et al., 2021, Lebec et al., 2023, 2024]. The possibility of melting and freezing at one of the horizontal boundaries helps convection in the solid. This effect is included by applying a phase change boundary condition [Alboussière et al., 2010, Mizzon and Monnereau, 2013, Deguen et al., 2013, Deguen, 2013, Labrosse et al., 2018] controlled by a single dimensionless parameter, the phase change number 𝛷. For small values of this parameter (𝛷 ≲ 10), the phase change is fast and the critical Rayleigh number for the onset of convection is reduced compared to the situation without phase change or with a slow phase change (𝛷 ≳ 10³). The heat and mass transfer is also enhanced by the phase change at the boundary.

These previous studies on the effect of a solid–liquid phase change at the boundary did not include the net evolution of the planet, with the possibility of volume change of the basal magma ocean. Including this effect requires several important modifications of the model, which are presented below. Firstly, a numerical treatment of the moving boundary at the bottom of the solid mantle is necessary and this is the topic of Section 2.1. This requires knowing the moving rate of the boundary, which can be determined from the energy balance of the BMO. The relevant theory is presented in Section 2.2. An example calculation is then presented in Section 3 before discussing the implications and limitations of the model in Section 4.

2. Physical and numerical model

2.1. Convection in the solid mantle

We start with a mantle convection numerical code, StagYY, which can solve the equations for mass, composition, energy and momentum balances in an infinite-Prandtl-number fluid, like planetary mantles, in various geometries and with many complexities [Tackley, 2008]. This code is widely used in the geodynamics community and needs not be detailed here; only features directly relevant to the present study are presented. The code uses a finite volume approach for the mass, energy and momentum balances and a particle-in-a-cell (PIC) approach for composition [Tackley and King, 2003, Gerya and Yuen, 2003, Ismail-Zadeh and Tackley, 2012]. In the present study, we use the spherical annulus geometry [Hernlund and Tackley, 2008] since the sphericity is important for a proper surface to volume scaling in an evolving planet. In order to keep the study as simple as possible, we consider an incompressible mantle using the Boussinesq approximation, with all physical quantities uniform. With these assumptions, the solid part of the model is controlled by three dimensionless numbers, the Rayleigh number Ra, the internal heating rate H and the buoyancy number B, their usual definition being,

Ra = \frac{𝛼 g Δ T d^{3}}{𝜅 𝜈}, H = \frac{𝜌 h d^{2}}{k Δ T}, B = \frac{𝛽}{𝛼 Δ T},

(1)

with 𝛼 and 𝛽 the thermal and compositional (FeO) expansion coefficients, respectively, g the gravity, 𝜅 the thermal diffusivity, 𝜈 the kinematic viscosity, ΔT the temperature scale, d the thickness of the whole mantle (solid and BMO), 𝜌 the density and h the time-evolving radioactive heating rate. Among the parameters entering the definition of the dimensionless numbers, ΔT and d deserve a special discussion since the actual temperature drop across the solid mantle and its thickness, which are normally used as scales to define the dimensionless numbers, vary with the progressive crystallisation of the BMO. We use fixed values (see Appendix) and take into account the variations of the actual values as time-varying factors in the balance equations emerging from our way of dealing with the moving boundary, which is the main modification of the numerical model as presented in previous studies. The solid mantle shell is bounded by two spheres, the basal ocean-mantle boundary (BOMB) with dimensionless radius r_BOMB(t), and the Earth surface with dimensionless radius R_E. We can map the time-varying spherical shell to a constant one, between rescaled radii 1 and 2, by using as radial coordinate

z = 1 + \frac{r - r_{BOMB}}{R_{E} - r_{BOMB}} .

(2)

This change of radial coordinate implies a change of both radial and temporal derivatives, obtained using the chain rule. Considering a function

f (r, t) = \tilde{f} (z, t)

, we get

\frac{\partial f}{\partial r} = \frac{\partial z}{\partial r} \frac{\partial \tilde{f}}{\partial z} = \frac{1}{R_{E} - r_{BOMB}} \frac{\partial \tilde{f}}{\partial z},

(3)

and so on for higher order derivatives. Consider now the time derivative,

\frac{\partial f}{\partial t} = \frac{\partial \tilde{f}}{\partial t} + \frac{\partial z}{\partial t} \frac{\partial \tilde{f}}{\partial z} = \frac{\partial \tilde{f}}{\partial t} - ṙ_{BOMB} \frac{R_{E} - r}{{(R_{E} - r_{BOMB})}^{2}} \frac{\partial \tilde{f}}{\partial z},

(4)

the overdot standing for time derivative. Therefore, the change of BMO radius implies an additional advection term in the equation of energy balance when mapping the domain to a constant one. This additional advection is also applied to tracers. Introducing the time-dependent scaled solid mantle thickness, 𝛤 = R_E − r_BOMB, the dimensionless balance equations for mass, momentum, energy, FeO mass fraction 𝜉 and concentration c_HPE of heat producing elements (HPE) become

\begin{matrix} 0 & = & 𝛻 \cdot u, \end{matrix}

(5)

\begin{matrix} 0 & = & - 𝛻 p + 𝛻^{2} u \\ + Ra 𝛤^{3} [(T - B 𝜉) - ⟨T - B 𝜉⟩] e_{z}, \end{matrix}

(6)

\begin{matrix} 𝛤^{2} \frac{\partial T}{\partial t} & = & - u \cdot 𝛻 T - \dot{𝛤} 𝛤 (2 - z) \frac{\partial T}{\partial z} + 𝛻^{2} T \\ + H c_{HPE} 𝛤^{2} exp (- \frac{t ln 2}{𝜏_{HPE}}), \end{matrix}

(7)

\begin{matrix} 𝛤^{2} \frac{\partial 𝜉}{\partial t} & = & - u \cdot 𝛻 𝜉, \end{matrix}

(8)

\begin{matrix} 𝛤^{2} \frac{\partial c_{HPE}}{\partial t} & = & - u \cdot 𝛻 c_{HPE}, \end{matrix}

(9)

with u the flow velocity, T the temperature, p the dynamical pressure. For simplicity, we consider only one heat producing element with a unique half life parameter 𝜏_HPE that represents a mean of the four main ones in the Earth, ²³⁵U, ²³⁸U, ²³²Th and ⁴⁰K. The time derivative

{\dot{𝛤}}_{BOMB}

is computed from the balance equations for the BMO, which are explained in the next section. This calculation requires knowing the fluxes of heat and FeO, which are directly computed in StagYY from the temperature field and tracers, respectively. The change with time of bottom temperature, T_BOMB(t), does not appear directly in the equations above but is applied as boundary condition at the bottom of the solid mantle. Therefore, the effective Rayleigh and buoyancy numbers at any given time are

{Ra}_{eff} = Ra 𝛤^{3} T_{BOMB}, B_{eff} = B \frac{(⟨ 𝜉_{bot} ⟩ - ⟨ 𝜉_{top} ⟩)}{T_{BOMB}},

(10)

where the actual FeO mass fraction difference across the layer is introduced in the definition of the effective buoyancy number.

An important feature of the model, already included in StagYY for a few previous studies [Agrusta et al., 2019, Bolrão et al., 2021, Lebec et al., 2023, 2024], is the solid–liquid phase change boundary condition at the bottom of the solid shell [e.g. Labrosse et al., 2018],

2 \frac{\partial u_{r}}{\partial r} - p - 𝛷 u_{r} = 0,

(11)

u_r being the radial velocity, p the dynamic pressure and 𝛷 the phase change number. This dimensionless parameter is the ratio of two timescales, 𝛷 =𝜏 _𝜙/𝜏_𝜂, with 𝜏_𝜂 the timescale to create a topography from viscous stress in the mantle and 𝜏_𝜙 the timescale to erase it by convection in the liquid layer. The boundary condition, initially derived for the dynamics of the inner core [Deguen et al., 2013], expresses the competition between the generation of a topography by viscous stress in the solid and its removal by melting and freezing. With this equation, the boundary condition can be the classical no-penetrative one for 𝛷 →∞, in which case the phase change is effectively prohibited (u_r = 0), or of the flow-through type for small values of 𝛷. This boundary condition strongly affects convection: for small values of 𝛷, convection is easier to start [i.e. the critical Rayleigh number for the onset of convection is reduced, see Deguen, 2013, Labrosse et al., 2018, Morison et al., 2024], heat and mass transfer are increased and the wavelength of convection is increased compared to the situation usually considered in mantle convection [Agrusta et al., 2019]. For a purely thermal problem [Deguen et al., 2013], the phase change number can be expressed as

𝛷 = \frac{𝜌_{s} (𝜌_{l} - 𝜌_{s}) L d}{𝜌_{l}^{2} C_{pl} (m_{ad} - m_{p}) u_{l} 𝜂_{s}},

(12)

with 𝜌_s and 𝜌_l the density of the solid and the liquid, respectively, L the latent heat of fusion, C_pl the heat capacity of the liquid, u_l the typical flow velocity in the magma ocean, 𝜂_s the viscosity of the solid and (m_ad − m_p) the difference between the adiabatic gradient in the liquid and the Clapeyron slope. Several parameters are rather uncertain but reasonable estimates give 𝛷 ∼ 10⁻⁸ (see Appendix). With such a very small value, we are clearly in the flow-through regime. In that regime, down-welling currents reaching the boundary do not turn and, instead, melt to reach the BMO. For this to happen, the temperature has to reach the boundary temperature, which happens on a short length-scale. Resolving that thin boundary layer can be challenging at large Rayleigh number and we use here the technique introduced by Agrusta et al. [2019]: the fixed temperature boundary condition is replaced by a laterally varying Robin boundary condition representing the behaviour on the inner edge of the boundary layer:

𝓗_{s} (u_{r} + u_{0}) 𝜃 + [1 - 𝓗_{s} (u_{r} + u_{0})] \frac{\partial 𝜃}{\partial r} = 0,

(13)

with

𝓗_{s}

a smooth approximation of the Heaviside function, 𝜃 the temperature anomaly, and u₀ the reference velocity at which the boundary condition switches behaviour. For u_r < −u₀, in downwelling regions, the outflow of solid material toward the BMO makes

𝓗_{s} = 0

and therefore leads to an imposed zero gradient. Conversely, where u_r > −u₀,

𝓗_{s} = 1

and the value of the temperature is set to the freezing one. See Agrusta et al. [2019] for more details and benchmark comparisons.

The PIC method consists of using Lagrangian tracers in the domain to carry various quantities as they are transported by the flow, and averaging the relevant quantities on the finite volume grid to compute the flow solution. In the context of the present study, we use a unique compositional information, representing the FeO content of the mineral assemblage. A complexity added to this approach by the phase change boundary condition and already treated by Bolrão et al. [2021] comes from the fact that the flow crossing the phase change boundary implies exchange of FeO with the BMO. In practice, when solid material crosses the boundary by melting, the associated tracers are removed while new tracers are added to regions where crystallisation occurs. These new tracers are given the information associated with their FeO content according to a simple phase diagram model (Equation (19)) [Bolrão et al., 2021]. The net flux of FeO is computed by compiling the information carried by both removed and added tracers. The composition acts on the density through a linearised equation of state to give the last term on the right-hand-side of the momentum equation (6). The buoyancy number B measures the tendency of FeO entering from the BMO to stabilise against entrainment by thermal convection.

Note that this approach assumes a spherical boundary between the solid mantle and the BMO, i.e. a negligible topography of that boundary. The dynamic topography associated to convection in the solid mantle is in fact included in the theory that leads to the phase change boundary condition Equation (11) [see Labrosse et al., 2018, for a full development], which assumes it to be small. This assumption is consistent with the fact that it is limited by convection in the liquid ocean that tends to erase it by mixing laterally solute and energy.

In addition to the phase change at the bottom boundary of the solid mantle, partial melting could in principle occur anywhere in the bulk, depending on the local temperature and the solidus of the local composition. This possibility is already implemented in StagYY [e.g. Nakagawa and Tackley, 2012], the melt being then extracted to the surface to form a crust, but has not been used in the present paper to focus on the phase change at the bottom boundary.

2.2. Evolution of the BMO

The flow of heat and FeO across the boundary between the solid mantle and the BMO makes the boundary move by melting or freezing according to the phase diagram and the conservation of heat and solute in the BMO. The phase diagram prescribes the temperature of the liquidus, T_L, and the solidus, T_s, as function of composition and pressure. At the boundary between the solid and the liquid, the temperature equals the solidus of the solid composition and the liquidus of the liquid composition. This dependence on composition makes this evolution depend also on the net flux of FeO between the solid and the liquid, which is due to the partitioning between the two phases upon crystallisation and melting. The heat flow out of the BMO controls the rate of cooling and crystallisation of the BMO to form the solid mantle and the rate of cooling and crystallisation of core. The evolution of the BMO follows from the global energy balance in much the same way as the evolution of the core. The equations are therefore similar and we follow the theory presented by Labrosse [2015].

2.2.1. Evolving reference state

We consider the BMO to be composed of an entirely liquid magma, whose composition can evolve between two end-members, an MgO-rich one and an FeO-rich one. The composition is quantified by the mass fraction of FeO, 𝜉_l, the corresponding one in the solid mantle being 𝜉_s.

Fractional crystallisation at the top of the BMO releases FeO at the top, which drives compositional convection. Cooling from the top and heating by the underlying core also favor convection. Since both temperature and composition promote convection, we assume that the BMO stays well mixed at all times, such that $\partial {\bar{𝜉}}_{l} / \partial r = 0$ , and that it is also isentropic on average. Alternatively, the BMO could start stably stratified [Laneuville et al., 2018] but we neglect this possibility in the present study.

We therefore consider a well-mixed isentropic magma ocean whose reference profile of density, temperature, chemical potential, mass fraction of FeO, etc., are linked by the phase equilibrium occurring at the top of the layer. The system is characterised by three state variables, the specific entropy s, the mass fraction of FeO in the magma 𝜉_l and pressure P. The reference state is well mixed, ∂𝜉_l/∂ r = 0, isentropic, ∂ s/∂ r = 0, and hydrostatic, ∂ P/∂ r = −𝜌g. For the sake of simplicity, the density 𝜌 is kept constant, and so is the gravitational acceleration g. In the reference state, the radial derivatives of the temperature T and chemical potential 𝜇 come only from the pressure variation. The chemical potential can be obtained using thermodynamic identities by integration of [e.g. Braginsky and Roberts, 1995, Lister and Buffett, 1995, Labrosse, 2015]

\frac{\partial 𝜇}{\partial r} = {(\frac{\partial 𝜇}{\partial P})}_{s, 𝜉} \frac{d P}{d r} = - 𝛽 g,

(14)

𝛽 being the coefficient of chemical contraction

𝛽 \equiv - \frac{1}{𝜌} {(\frac{\partial 𝜌}{\partial 𝜉_{l}})}_{P, s} = 𝜌 {(\frac{\partial 𝜇}{\partial P})}_{s, 𝜉} .

(15)

Note that for FeO in a magma, 𝛽 here defined is negative. This is opposite to the case of light elements in the core. Assuming, for simplicity, 𝛽 and g to be constant, Equation (14) can readily be integrated to give

𝜇 = 𝜇^{BOMB} + 𝛽 g (r_{BOMB} - r) \equiv 𝜇^{BOMB} + 𝜇^{'}

(16)

with 𝜇^BOMB the chemical potential at the top of the BMO and 𝜇′ the deviation from that value in the BMO.

Similarly, for the temperature we get the classical isentropic gradient:

\frac{\partial T}{\partial r} = {(\frac{\partial T}{\partial P})}_{s, 𝜉} \frac{d P}{d r} = - \frac{𝛼 g T}{C_{p}},

(17)

with 𝛼 the thermal expansion coefficient and C_p the heat capacity at constant pressure. We know that 𝛼 generally decreases with pressure and therefore depth [Anderson et al., 1992, Chopelas and Boehler, 1992, Duffy and Ahrens, 1993, Ricard, 2007, Ricard et al., 2022] but since we consider here a magma ocean whose total thickness is a few 100 km only, we consider the assumption of a constant 𝛼 as sufficient. Therefore, Equation (17) can be integrated to give

T = T^{BOMB} exp [\frac{𝛼 g (r_{BOMB} - r)}{C_{p}}],

(18)

with T^BOMB the temperature at the top of the BMO. This equation can be safely linearised if that simplifies the expressions. T^BOMB is equal to the liquidus corresponding to the composition of the magma ocean, which evolves with time. The liquidus also depends on pressure and, for simplicity, we assume a linear dependence of the liquidus on both pressure and mass fraction of FeO, yielding

\begin{matrix} T^{BOMB} & = & T_{L} (r_{BOMB}) = T_{L} (r_{0}) - \frac{\partial T_{L}}{\partial P} 𝜌 g (r_{BOMB} - r_{0}) \\ + \frac{\partial T_{L}}{\partial 𝜉} (𝜉_{l} - 𝜉_{l 0}), \end{matrix}

(19)

with r₀ the initial position of the freezing front, 𝜉_l0 the initial FeO mass fraction of the magma ocean and T_L(r₀) the corresponding liquidus value. This equation can be time differentiated to give

\frac{d T^{BOMB}}{d t} = - \frac{\partial T_{L}}{\partial P} 𝜌 g \frac{d r_{BOMB}}{d t} + \frac{\partial T_{L}}{\partial 𝜉} \frac{d 𝜉_{l}}{d t} .

(20)

The two time derivatives on the right-hand-side can be related to each other using the equation for FeO conservation. This and other balance equations are derived in the next subsection.

The different profiles obtained above are only strictly valid in the well mixed isentropic bulk of the magma ocean and are complemented by boundary layers on both top and bottom. However, as soon as the magma ocean is unstably stratified, which we assume here from the start, the Rayleigh number is enormous and convection is very efficient, which makes the super-isentropic temperature difference across the BMO very small [Labrosse et al., 2007, Ulvrová et al., 2012]. Therefore, we neglect the thickness of boundary layers and their associated temperature, composition and chemical potential jumps.

2.2.2. Balance equations

The mass fraction 𝜉_l of FeO in the BMO is assumed to be uniform, owing to the high efficiency of convective stirring in the liquid. However, it evolves with time due to interaction with the solid mantle due to fractional crystallisation at the boundary, and possibly exchange by diffusion through the core mantle boundary. The equations describing the evolution of 𝜉_l are derived for their introduction in StagYY. The integrated fluxes over the CMB and top surface of the BMO are denoted I^CMB and I^BOMB, respectively, and are counted positive upward. The global balance equation for the FeO content is

\frac{d M_{BMO} 𝜉_{l}}{d t} = I^{CMB} - I^{BOMB},

(21)

M_BMO being the mass of the BMO in the 𝜉_l = 0 limit. For the time being, we will neglect I^CMB since its treatment would require constraints on the partitioning between the liquid metal and the liquid silicate at the relevant pressure and temperature and a model for the vertical transfer of light elements at the top of the core. This could be a target for future developments.

With this assumption, Equation (21) can be developed to give

M_{BMO} \frac{d 𝜉_{l}}{d t} + 4 π r_{BOMB}^{2} 𝜌_{0} 𝜉_{l} ṙ_{BOMB} = - I^{BOMB} .

(22)

The flux to the solid mantle, I^BOMB, is due to the phase change happening at the boundary, with a crystallisation mass rate w associated with the solid radial velocity u_r at the boundary as computed in StagYY, u_r, by $w = u_{r} - ṙ_{BOMB}$ since, in StagYY, the boundary is kept fixed by a continuous adjustment of the computation domain thickness (Section 2.1). We get

I^{BOMB} = \int_{Ω_{BOMB}} 𝜌_{0} 𝜉_{s} (u_{r} - ṙ_{BOMB}) d Ω,

(23)

with Ω_BOMB the surface of the boundary and 𝜉_s the mass fraction of FeO on the solid side of the boundary:

𝜉_{s} = \{\begin{matrix} D 𝜉_{l}, & u_{r} ⩾ 0 \\ 𝜉_{s}, & u_{r} < 0 . \end{matrix}

(24)

In regions of solid upwelling, fractional crystallisation occurs, producing a solid with a mass fraction 𝜉_s = D𝜉_l with D < 1 the partition coefficient of FeO between the solid and the liquid. Note that D depends on the composition and is related to the distribution coefficient K of the phase change, as detailed by Bolrão et al. [2021]. In regions of downwelling, the solid with a mass fraction 𝜉_s arrives in contact with the liquid and melts. Note that the composition of this solid may be different from that for equilibrium with the liquid at its liquidus temperature but melting can still proceed by pumping FeO from the liquid, which acts to reduce the mass fraction FeO in the liquid. This effect is balanced by the release of FeO in regions of crystallisation. The lateral transfer of FeO in the liquid occurs on a timescale, 𝜏_𝜙, much shorter than the timescale for convection in the solid and the same timescale applies to the transfer of latent heat from regions of freezing to regions of melting. This is taken into account in the dimensionless number 𝛷 =𝜏 _𝜙/𝜏_𝜂 which parameterises the boundary condition applied for convection in the solid, 𝜏_𝜂 being the viscous timescale on which a topography is built as a result of viscous stress in the solid [Labrosse et al., 2018].

Combining Equations (22) and (23) gives, after rearrangement:

\begin{matrix} (4 π r_{BOMB}^{2} 𝜌_{0} 𝜉_{l} - \int_{Ω_{BOMB}} 𝜌_{0} 𝜉_{s} d Ω) ṙ_{BOMB} \\ + \frac{4 π}{3} 𝜌_{0} (r_{BOMB}^{3} - r_{CMB}^{3}) {\dot{𝜉}}_{l} \\ = - \int_{Ω_{BOMB}} 𝜌_{0} 𝜉_{s} u_{r} d Ω . \end{matrix}

(25)

The two integrals in Equation (25) are computed in StagYY at each time-step and that gives the relationship between

ṙ_{BOMB}

and

{\dot{𝜉}}_{l}

. Equation (20) then allows us to express the rate of change of T^BOMB as a function of

ṙ_{BOMB}

only.

Note that in the case u_r = 0, which is obtained for 𝛷 = ∞, 𝜉_s = D𝜉_l is uniform and the mass flux of FeO to the solid mantle is $I^{BOMB} = - 4 π r_{BOMB}^{2} D 𝜉_{l} 𝜌_{0} ṙ_{BOMB}$ . This flux is positive for $ṙ_{BOMB} < 0$ , i.e. when crystallisation occurs. Equation (25) leads to

{\dot{𝜉}}_{l} = - \frac{3 r_{BOMB}^{2} Δ 𝜉}{r_{BOMB}^{3} - r_{CMB}^{3}} ṙ_{BOMB}

(26)

with Δ𝜉 =𝜉 _l −𝜉_s. This equation was used in the original BMO paper [Labrosse et al., 2007] but the general Equation (25) accounting for flow through the boundary is used in the present study.

The flux i of FeO across both boundaries contributes to the total heat flux density q as

q = - k 𝛻 T + 𝜇 i

(27)

and we note the thermal part as

q_{T} \equiv - k 𝛻 T .

(28)

Integrated over a surface Ω (BOMB or CMB), we get

Q^{Ω} = Q_{T}^{Ω} + 𝜇^{Ω} I^{Ω}

(29)

with 𝜇^Ω the average value of 𝜇 over the surface Ω.

The long term thermal evolution of the BMO is controlled by the integrated energy balance equation, which is written as [e.g. Braginsky and Roberts, 1995, Lister and Buffett, 1995]

\begin{matrix} \int_{V_{BMO}} 𝜌 (T \frac{\partial s_{l}}{\partial t} + 𝜇 \frac{\partial 𝜉_{l}}{\partial t}) d V \\ = \int_{Ω_{BOMB}} 𝜌 L (u_{r} - ṙ_{BOMB}) d Ω \\ + Q_{R} + Q^{CMB} - Q^{BOMB}, \end{matrix}

(30)

with Q_R the radiogenic heat production in the BMO and L the latent heat of melting, which contains two contributions:

L = T_{L} Δ s + 𝜇 Δ 𝜉

(31)

Δs = s_l − s_s being the entropy of melting. The surface integral on the right-hand-side of Equation (30) is the total latent released or consumed by phase change at the boundary and is related to the crystallisation change rate

u_{r} - ṙ_{BOMB}

. The entropy contribution to the latent heat, T_LΔs, is uniform along the phase change boundary and, since 𝜌u_r averages to 0 at the interface, only the net crystallisation rate

ṙ_{BOMB}

contributes to that part. Combining Equation (30) with the global balance in FeO Equation (21) and the expressions for the BOMB and CMB fluxes Equation (29) gives

\begin{matrix} Q_{T}^{BOMB} & = & - \int_{V_{BMO}} 𝜌 T \frac{\partial s}{\partial t} d V \\ - T_{L} (r_{BOMB}) Δ s 4 π r_{BOMB}^{2} ṙ_{BOMB} + Q_{R} + Q_{T}^{CMB} \\ + (𝜇^{CMB} - 𝜇^{BOMB}) I^{CMB} - \frac{d 𝜉_{l}}{d t} \int_{V_{BMO}} 𝜌 𝜇^{'} d V \\ + \int_{Ω_{BOMB}} 𝜌 𝜇^{BOMB} (Δ 𝜉 u_{r} + 𝜉_{s} ṙ_{BOMB}) d Ω . \end{matrix}

(32)

This equation has a simple interpretation: the heat flow out of the BMO has contributions from secular cooling, latent heat of freezing (positive for

ṙ_{BOMB} < 0

), radiogenic heating, heat flow at the CMB, the flux of compositional energy due to the chemical flux at the CMB and the change of compositional energy content in the BMO. Note that the CMB flux term has a sign opposite to I^CMB, which is expected since mixing any dense component from the core would require energy.

This equation can be used to compute the thermal and compositional evolution of the BMO and the core for a given heat flow at the bottom of the solid mantle. Each term of the equation needs to be expressed as function of a minimum number of parameters, which is the next task here.

As stated above, we will neglect I^CMB, for now. $Q_{T}^{BOMB}$ is provided at each time step by the convection model of the solid mantle, StagYY. Computing Q_R is straightforward for a given value of the partition coefficient of heat producing elements at the top of the BMO and their decay constants. The compositional energy term, the one involving 𝜇′ in Equation (32), is easily related to rate of change of r_BOMB using Equations (16):

\begin{matrix} E_{𝜒 1} & \equiv & - \frac{d 𝜉_{l}}{d t} \int_{V_{BMO}} 𝜌 𝜇^{'} d V = - 𝜌_{0} 𝛽 g [r_{BOMB} V_{BMO} \\ - π (r_{BOMB}^{4} - r_{CMB}^{4})] \frac{d 𝜉_{l}}{d t} . \end{matrix}

(33)

Using Equation (25), this term can be related to

ṙ_{BOMB}

.

The second compositional term (last on the right-hand-side of Equation (32)) can be simplified assuming 𝜇^BOMB, 𝜌 and 𝜉_l to be constant and using the fact that u_r is 0 on average on the boundary. This gives

E_{𝜒 2} = 𝜌_{0} 𝜇^{BOMB} \int_{Ω_{BOMB}} 𝜉_{s} (ṙ_{BOMB} - u_{r}) d Ω .

(34)

The secular cooling term is expressed as

Q_{C} \equiv - \int_{V_{BMO}} 𝜌 T \frac{\partial s}{\partial t} d V = - \int_{V_{BMO}} 𝜌 C_{p} \frac{\partial T}{\partial t} d V,

(35)

which can be computed using the Equations (18) and (20):

\begin{matrix} Q_{C} & = & - 4 π 𝜌_{0} C_{P} L_{M}^{3} [\frac{d T^{BOMB}}{d t} + \frac{𝛼 g T^{BOMB}}{C_{p}} ṙ_{BOMB}] \\ \times \int_{r_{CMB} / L_{M}}^{r_{BOMB / L_{M}}} x^{2} exp [\frac{𝛼 g L_{M}}{C_{P}} (\frac{r_{BOMB}}{L_{M}} - x)] d x . \end{matrix}

(36)

Using Equation (20) and (26), this term can be expressed as an afine function of

ṙ_{BOMB}

.

The last term to deal with is the CMB heat flow. The thermal evolution of the core can be parameterised using the CMB temperature [Labrosse, 2015] and we therefore have all the equations needed to solve the coupled evolution of the solid mantle, the BMO and the core. For a liquid core (only situation implemented for the moment), the core cooling term is related to the rate of change of the CMB temperature by

Q_{T}^{CMB} = - \frac{4 π}{3} 𝜌_{N} C_{p N} L_{𝜌}^{3} \frac{f_{C} (\frac{r_{CMB}}{L_{𝜌}}, 𝛾)}{{(1 - \frac{r_{CMB}^{2}}{L_{𝜌}^{2}} - A_{𝜌} \frac{r_{CMB}^{4}}{L_{𝜌}^{4}})}^{𝛾}} \frac{d T^{CMB}}{d t},

(37)

with 𝜌_N the density at the center of the core, C_{p N} the assumed constant heat capacity of the core, L_𝜌 and A_𝜌 the structure parameters describing the density variation with radius in the core, 𝛾 the Grüneisen parameter of the core and

\begin{matrix} f_{C} (r, 𝛾) & = & 3 \int_{0}^{r} x^{2} {(1 - x^{2} - A_{𝜌} x^{4})}^{1 + 𝛾} d x \\ = & r^{3} [1 - \frac{3}{5} (𝛾 + 1) r^{2} \\ - \frac{3}{14} (𝛾 + 1) (2 A_{𝜌} - 𝛾) r^{4} + O (r^{6})] . \end{matrix}

(38)

The boundary layers on both sides of the CMB are tiny, with temperature differences across them that are negligible compared to the temperature differences across the whole layers due to compressibility effects. Therefore, the cooling of the core must follow that of the BMO. More precisely, the CMB temperature is related to that at the top of the BMO using Equation (18):

T^{CMB} = T^{BOMB} exp [\frac{𝛼 g}{C_{p}} (r_{BOMB} - r_{CMB})] .

(39)

Therefore, the rate of change of T^CMB is

\begin{matrix} \frac{d T^{CMB}}{d t} & = & [\frac{d T^{BOMB}}{d t} + \frac{𝛼 g T^{BOMB}}{C_{p}} ṙ_{BOMB}] \\ \times exp [\frac{𝛼 g}{C_{p}} (r_{BOMB} - r_{CMB})] . \end{matrix}

(40)

The equations for the evolution of the BMO and the core presented in this section have been made dimensionless (see Appendix) and implemented in StagYY. In practice, at each time step, the temperature and composition fields in the solid mantle are used to compute the body force responsible for convection. The velocity and pressure fields resulting from the momentum balance are computed, which permits to compute the evolution of the temperature and composition fields, using tracers for the latter. The heat flow at the bottom of the solid mantle is also used to compute the evolution of the BMO and core.

3. Example of dynamical evolution

The model is controlled by many input parameters, the classical ones for mantle convection using StagYY [Tackley, 2008] and the additional ones for the BMO evolution, so that the parameter space is effectively enormous. Although we have run many cases, the goal of the present paper is not to provide a comprehensive study of this complex system but to show with one example a possible evolution of the Earth with a basal magma ocean. As will appear clearly, the model results are in some ways encouraging, in the sense that we obtain some of the expected features, in particular thermo-chemical structures that might explain some of the current seismological observations. On the other hand, some of the outcomes point toward strong limitations of this model, at least with the choice of parameters of this specific calculation. Future developments to solve these issues will then be discussed. Even though all the complexities of mantle convection that are included in the numerical code StagYY are also accessible with the BMO model, we restrict ourselves here to the simplest case, notably with a constant viscosity and compositional variations only due to the fractional crystallisation of the BMO.

The parameters specific to the basal magma ocean and its evolution are as follows: the initial thickness is taken to be 30% of the total mantle, the partition coefficients for FeO and the heat producing element are K_FeO = 0.3, K_HPE = 10⁻², respectively and the phase change parameter is 𝛷 = 3 × 10⁻². The initial composition of the solid mantle and the BMO are uniform in both FeO and HPE and in equilibrium with each other according to these partition coefficients. The mean mass fraction of FeO is 0.1 while that for HPE makes the mean dimensionless internal heating rate equal to 5, which is somewhat smaller than the expected value for the bulk silicate Earth. The internal heating rate decays exponentially with a dimensionless half-life time of 10⁻². The nominal Rayleigh and buoyancy numbers are Ra = 3 × 10⁷, B = 5, respectively. These are defined using, as a temperature scale, ΔT_m, an estimate for the melting temperature difference between the top and the bottom of the mantle, so that the dimensionless temperature accross the solid ΔT/ΔT_M is of order one. The chosen value is ΔT_M = 4000 K. The compositional range implied by the definition of B is 1, which corresponds to the density difference between the MgO and FeO end-members. Since the range of temperature and composition actually encountered in the model are different from these defining values, a rescaling needs to be performed after the calculations, as discussed below. Other parameters are detailed in the Appendix.

Figure 1 shows the evolution of several key fields with time, the temperature (top row), mass fraction of FeO (middle row) and HPE (bottom row). The time of each snapshot is written at the top of each column. The BMO is depicted by a uniform pink layer to visualise its shrinking by crystallisation. The total duration of this calculation, which lasts until nearly full crystallisation of the BMO, is about t = 6.4 × 10⁻³ (dimensionless), which is nearly half the dimensionless age of the Earth. This duration clearly depends on the value of several input parameters, and, in particular, is expected to decrease with an increase of the Rayleigh number, since this makes the heat flow increase, and decrease with the buoyancy number, since FeO buoyancy goes against thermal convection.

Figure 1.
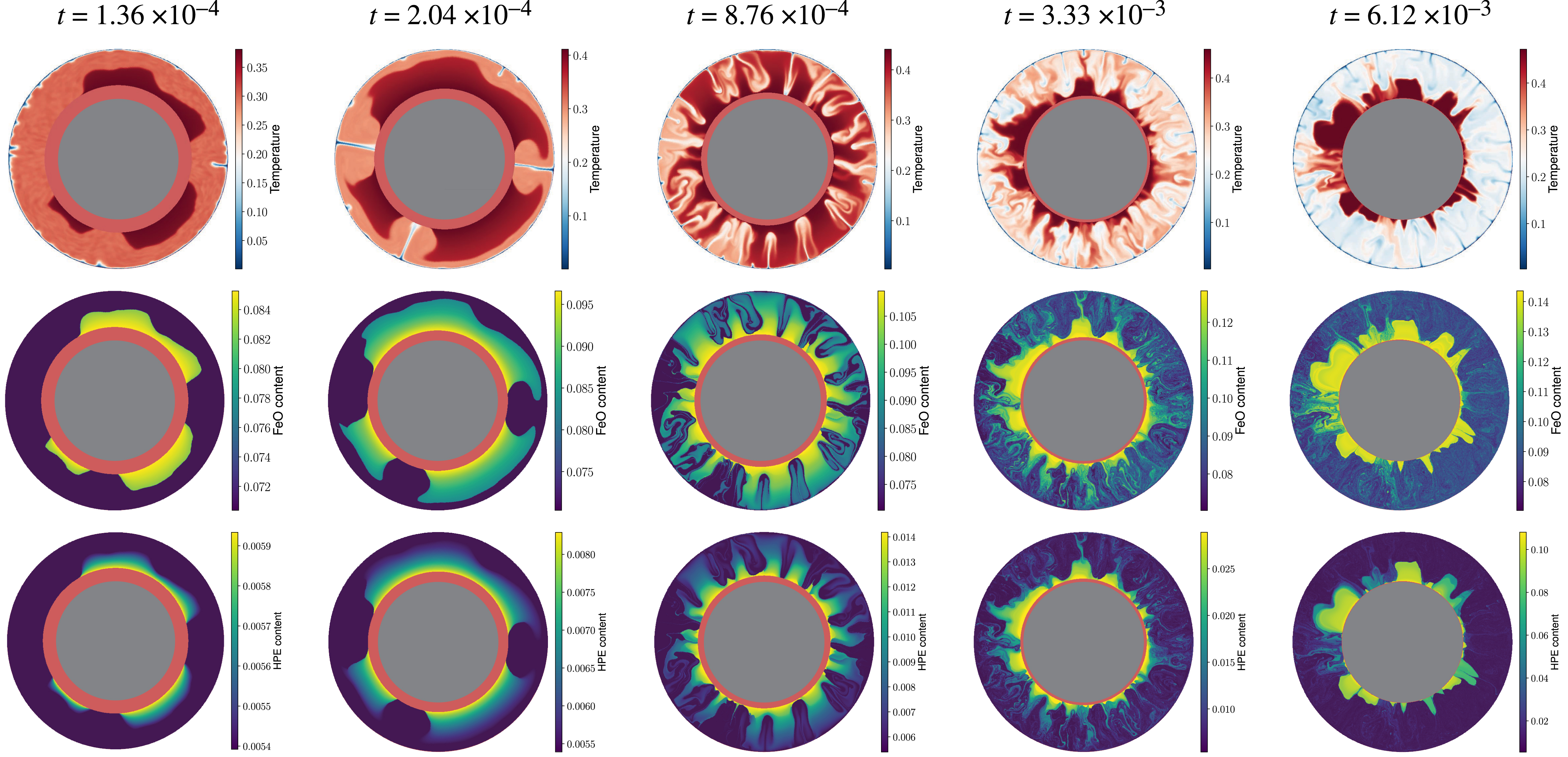
Evolution of the temperature (top row), FeO content (middle row) and concentration in heat producing elements (bottom row) as function of time, as indicated on the top. Note that the colorbar is adapted to each snapshot for maximum lisibility.

Convection first sets in at large scale (Figure 1), which is usual for convection with a phase change at the bottom boundary [Labrosse et al., 2018, Morison et al., 2019, 2024]. Starting from a compositionally uniform mantle, variations of concentrations in FeO and HPEs soon develop from fractional crystallisation of the BMO. In the first three snapshots of Figure 1, variations in FeO content do not seem to affect the dynamics, which is controlled by cold plumes that reach the bottom boundary with the BMO and melt, as expected from previous studies of purely thermal convection with solid–liquid phase change [Agrusta et al., 2019, Lebec et al., 2023]. In the last two snapshots, FeO-enriched regions start forming dome-like structures from which hot plumes depart. This behaviour, that was predicted in the original BMO model [Labrosse et al., 2007], happens when the FeO concentration contrasts become sufficient to compete with the thermal buoyancy.

To better understand the evolution, it is useful to study the mean temperature and composition profiles, as shown on Figure 2. The radius is scaled with the total thickness of the mantle (solid and magma ocean) so that the figure shows the crystallisation of the magma ocean with time.

Figure 2.
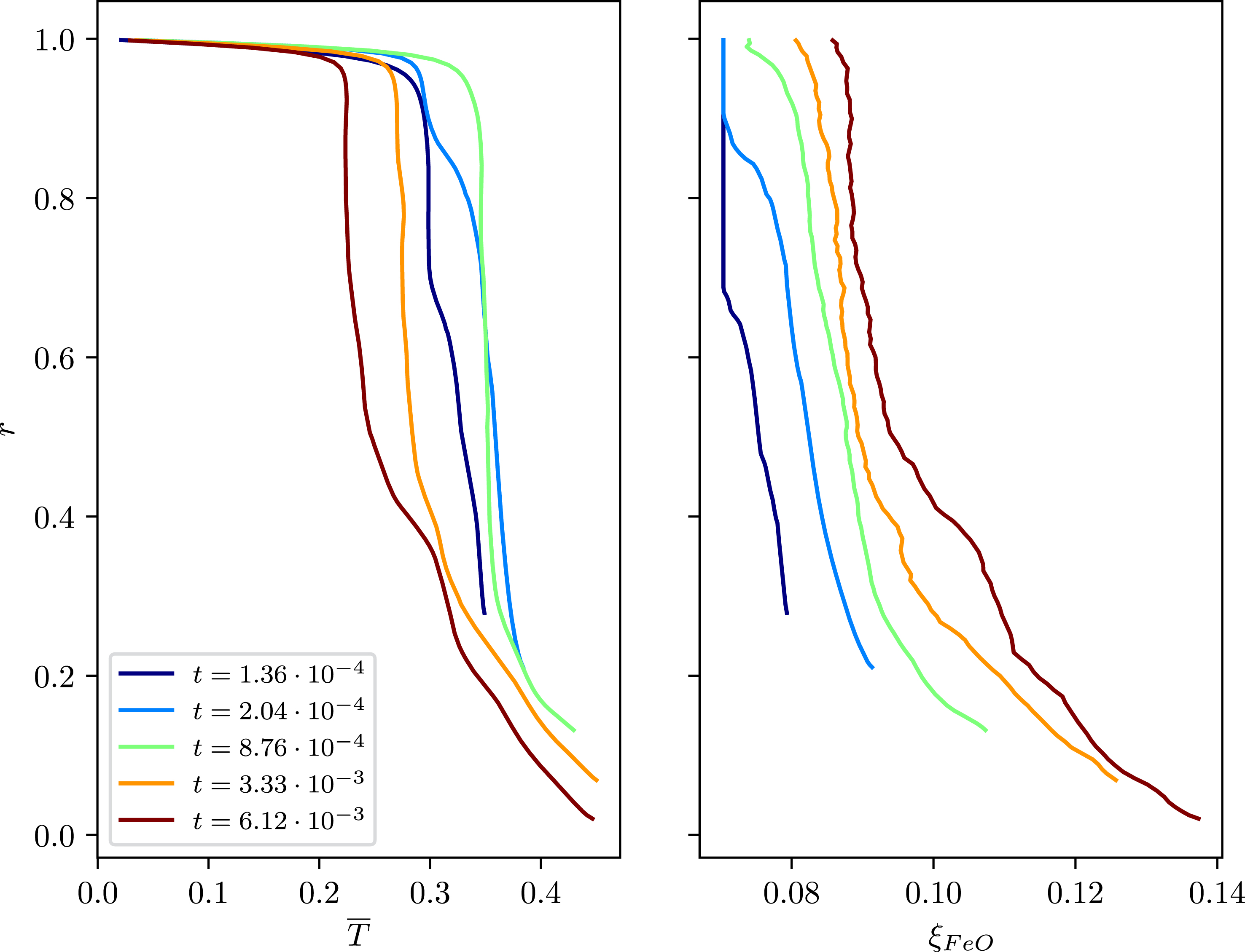
Temperature (left) and composition (right) mean profiles for the time steps corresponding to those of Figure 1. The radial position reflects the crystallisation of the BMO with time.

The FeO mass fraction profiles show a gradual increase with time and, more importantly for the dynamics, an increase of radial contrast. As the BMO concentration in FeO becomes larger, the solids that form from it become enriched and therefore denser, which leads to the partial stratification observed on Figure 1. Figure 3 shows the evolution of the minimum FeO mass fraction at the upper boundary, min(𝜉_FeO,top), and the maximum at the bottom boundary, max(𝜉_FeO,bot). The minimum value is stable, expressing the fact that no diffusion is allowed in this model, while the maximum value, after a rapid increase in the early evolution, increases with an almost constant time rate. The Buoyancy number in this calculation is set to a nominal value of B = 5 but this corresponds to a change of composition between the MgO and FeO end-members and a dimensionless temperature change between 0 and 1. Since the model is evolving with time with fixed temperature and composition scales, the effective buoyancy number at each time is given by Equation (10). The value obtained is also shown on Figure 3. Comparison with the snapshots of Figure 1 suggests that a critical value of B_eff ∼ 0.5 makes the convective regime transition between the well mixed situation to the stratified one. Determining the dependence of that number on other parameters of the problem, in particular the Rayleigh number, falls beyond the scope of the present paper. It is however grossly consistent with the value of the buoyancy number needed to get partial entrainment or a doming regime in convection with a compositionally layered initial condition [Tackley, 1998, Davaille, 1999, Le Bars and Davaille, 2004].

Figure 3.
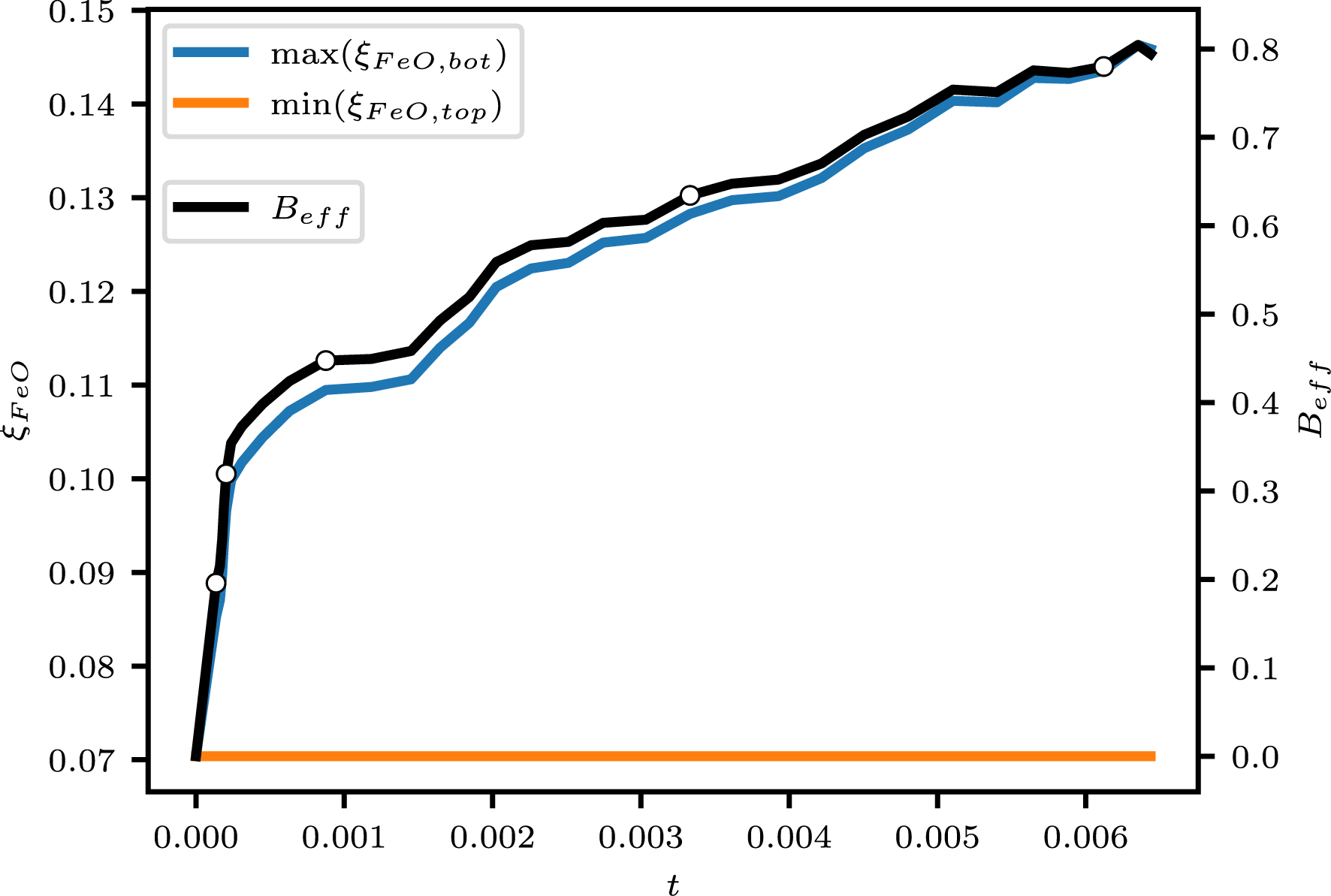
Time evolution of the minimum FeO mass fraction at the upper boundary, min(𝜉_FeO,top), the maximum at the bottom boundary, max(𝜉_FeO,bot) (left axis) and the effective buoyancy number B_eff, right axis. Empty circles on the black line gives the position of the snapshots presented on Figure 1.

The bottom temperature, equal to the liquidus, also varies with time because of the combined effect of the pressure (depth) and composition of the magma. With the choice of parameters made for this calculation, the pressure effect dominates over that of FeO mass fraction, which implies an increase of the liquidus with time. At the end of the calculation, the mass fraction of FeO increases faster than pressure at the BMO boundary (BOMB) which makes the liquidus decrease with time. Other choice of parameters would change this evolution and a more realistic phase diagram could be implemented in the future.

A striking feature of the temperature profiles shown on Figure 2 is that, for the long early period where the solid stays well mixed, the mean temperature is nearly independent of the radius and varies significantly only in the upper boundary. Therefore, no boundary layer exists at the bottom and, consequently, no focused hot plumes. This behaviour has already been observed from both linear and non-linear models [Labrosse et al., 2018, Agrusta et al., 2019] in cartesian geometry and results from the phase change boundary condition. In this scenario, hot plumes can only develop once the basal magma ocean gets crystallised enough to get 𝛷 ≳ 10³ or, as in the present case, when a compositional stratification separates the phase change boundary from the bulk of the convecting mantle. It is worth recalling here that this model assumes an incompressible solid mantle within the Boussinesq approximation and the development with time of a significant temperature gradient at the bottom of the solid shell is due here solely to the stabilisation of dense thermo-chemical piles, not to any compressibility effect. To convert these temperature profiles to realistic ones for the Earth requires to add an isentropic temperature gradient.

The concentration in HPE, depicted on the bottom row of Figure 1, is somewhat similar to that of FeO since both come from fractional crystallisation of the BMO. However, because the partition coefficient is much smaller, the enrichment is slower and the mean concentration becomes significant only at the very end of the crystallisation process. Moreover, comparing the various FeO-enriched domes, we can see that their concentrations are not uniform: at the latest stages of their formation, small differences in crystallisation time result in large concentration variations, a phenomenon much less visible for the concentration in FeO which increases in a more gradual manner. Finally, the enrichment in HPEs of the domes makes them warm up and, in some calculations (not shown here), they become unstable at the end of the calculation.

4. Discussion and the way ahead

The model presented in the previous section is the first application of the complete set of equations coupling the evolution of a basal magma ocean to convection in the solid mantle. As such, it provides some interesting results but has some limitations when application to Earth are considered.

First of all, this model is a proof of concept for the possibility of forming large scale compositional variations in the lower mantle from fractional crystallisation of the BMO, as can be seen on Figure 1. The fact that this situation arises at the end of this calculation is linked to the shrinking of the BMO, which is necessary to make its FeO mass fraction increase sufficiently for solids that crystallise from it to be dense enough. Our calculation stops when the BMO crystallises almost entirely. In the present model, the BMO is imposed to fully freeze when a minimum thickness is reached, while it is assumed to be fully liquid before. In reality, we expect that, at some point, a transition should occur toward a two-phase layer, the present interpretation of ULVZs as partially molten being the last remnant pockets of it. The present model does not include the physics necessary to deal with this transition. This two-phase situation could last quite a long time, the last melt getting enriched in all the incompatible elements, in particular volatiles, which significantly depress the freezing point of the magma [Nomura et al., 2014].

On the other hand, the thermal structure shown in Figures 1 and 2 may be difficult to reconcile with observations constraining the early Earth. Indeed, the absence of boundary layer at the bottom of the solid mantle implies that, except for thin downwelling plumes, the whole solid mantle in our model is at the same temperature as the bottom boundary. This situation, which results from the presence of phase change boundary condition at the bottom [Labrosse et al., 2018, Agrusta et al., 2019, Lebec et al., 2023], is difficult to sustain when applied to the mantle of the Earth since it would lead to very high temperature below the lithosphere, possibly making most of the upper mantle liquid. We expect that such a state would lead to massive eruptions and the associated rapid cooling would not allow it to persist for the length of time implied here [Davies, 1990, Sleep, 2000]. One way to avoid that problem is to increase the value of the phase change parameter, 𝛷. Indeed, for 𝛷 > 10³, the dynamics is similar to that obtained for a non-penetrative boundary condition [Agrusta et al., 2019] with a well-developed boundary layer on the solid side. However, the value of 𝛷 is expected to be on the low side, similar to the value used here, although it is difficult to estimate it precisely.

In the present model, the situation with a high upper mantle temperature persists as long as the solid stays well mixed but once a compositional stratification develops, the bulk of the mantle can cool down compared to its bottom boundary (Figure 2). The main problem therefore comes from the initial condition of the calculation. The one shown here starts from a compositionally uniform solid mantle and the variations of composition only arise from fractional crystallisation of the BMO, since testing the feasibility of this mecanism is one of the goals of this paper. The freezing of the surficial magma ocean is, however, likely to produce a compositional stratification of the solid that could be included as initial condition of our calculations. For example, models of fractional crystallisation of the lunar or martian magma oceans [e.g. Hess and Parmentier, 1995, Elkins-Tanton et al., 2003, Elkins-Tanton, 2012] suggest a gradual densification of the solid that make it prone to overturn and that should produce a solid mantle that is initially stably stratified. The degree of initial stratification can be rather extreme if the overturn happens after full crystallisation but several overturns are expected to occur during crystallisation [Ballmer et al., 2017, Maurice et al., 2017, Boukaré et al., 2018, Morison et al., 2019]. This initial stratification should therefore be considered as an input parameter whose effect should be quantified in future studies.

Alternatively, it could be desirable to run a model coupling the crystallisation of the surficial magma ocean to convection in the solid in order for the initial condition to result directly from this process. This means writing a set of equations similar to the one developed in Section 2.2 for the surficial magma ocean and including phase change boundary condition. Some progress has been donc in that direction [Morison, 2019] but a systematic exploitation of this model is still needed and will be the topic of a future study.

5. Conclusions

This paper presents, for the first time, a complete set of equations for the evolution of a basal magma ocean coupled to a convecting mantle and a cooling core. This theory has been used to build a model, starting from the mantle convection code StagYY [Tackley, 2008], for the evolution of the whole Earth that tracks the fractional crystallisation of the BMO and the implied compositional evolution of the mantle. The BMO is treated as a well-mixed layer whose evolution is controlled by general energy and composition balance equations. The solid mantle is treated with a full convection model that includes the possibility of melting and freezing at its bottom boundary as a phase change boundary condition [Labrosse et al., 2018].

The parameter space for this model is very large and, in this paper, we have only considered one typical case. It shows, for the first time in a self-consistent dynamical model, the feasibility of the scenario for the generation of large compositionally dense and heterogenous anomalies proposed by Labrosse et al. [2007].

The phase change boundary condition at the bottom of the solid mantle has profound implications on its dynamics and thermal structure: as long as it is well mixed, its bulk temperature follows an isentropic upward extrapolation of the BMO liquidus. This would likely imply large amounts of melting in the upper mantle although, of course, a more thorough exploration of the parameter space is necessary to confirm that implication. In any case, that points toward the necessary discussion of the initial conditions, in particular concerning the compositional structure of the solid mantle, that results from the crystallisation of a surficial magma ocean. Models integrating that aspect in the evolution would help decipher this question.

Another interesting addition to this model would be to include a treatment of volatiles, and in particular water. Assuming water to be incompatible at high pressure, we can expect its concentration to increase in the basal magma ocean as it crystallises, which would help to maintain partial melt to the present day by decreasing the solidus [Nomura et al., 2014]. The solid forming from it would gradually see its H content increase, with important implication on its viscosity and possibly on the melting and degassing of the mantle near the surface.

Declaration of interests

The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.

Acknowledgments

We gratefully acknowledge two very constructive reviews that pushed us to improve and clarify the presentation of our paper. The calculation was performed on the cluster of PSMN (Pôle Scientifique de Modélisation Numérique) of the ENS de Lyon.

Bibliographie

[Agrusta et al., 2019] R. Agrusta; A. Morison; S. Labrosse; R. Deguen; T. Alboussière; P. J. Tackley; F. Dubuffet Mantle convection interacting with magma oceans, Geophys. J. Int., Volume 220 (2019), pp. 1878-1892 | DOI

[Alboussière et al., 2010] T. Alboussière; R. Deguen; M. Melzani Melting-induced stratification above the Earth’s inner core due to convective translation, Nature, Volume 466 (2010), pp. 744-747 | DOI

[Anderson et al., 1992] O. L. Anderson; H. Oda; D. Isaak A model for the computation of thermal expansivity at high compression and high temperatures: MgO as an example, Geophys. Res. Lett., Volume 19 (1992) no. 19, pp. 1987-1990 | DOI

[Ballmer et al., 2017] M. D. Ballmer; D. L. Lourenço; K. Hirose; R. Caracas; R. Nomura Reconciling magma-ocean crystallization models with the present-day structure of the Earth’s mantle, Geochem. Geophys. Geosyst., Volume 18 (2017) no. 7, pp. 2785-2806 | DOI

[Bolrão et al., 2021] D. P. Bolrão; M. D. Ballmer; A. Morison; A. B. Rozel; P. Sanan; S. Labrosse; P. J. Tackley Timescales of chemical equilibrium between the convecting solid mantle and over-/underlying magma oceans, Solid Earth, Volume 12 (2021.), pp. 421-437 | DOI

[Boukaré et al., 2018] C.-E. Boukaré; E. Parmentier; S. Parman Timing of mantle overturn during magma ocean solidification, Earth Planet. Sci. Lett., Volume 491 (2018), pp. 216-225 | DOI

[Braginsky and Roberts, 1995] S. I. Braginsky; P. H. Roberts Equations governing convection in Earth’s core and the geodynamo, Geophys. Astrophys. Fluid Dyn., Volume 79 (1995), pp. 1-97 | DOI

[Chopelas and Boehler, 1992] A. Chopelas; R. Boehler Thermal expansivity in the lower mantle, Geophys. Res. Lett., Volume 19 (1992) no. 19, pp. 1983-1986 | DOI

[Christensen and Hofmann, 1994] U. R. Christensen; A. W. Hofmann Segregation of subducted oceanic crust in the convecting mantle, J. Geophys. Res., Volume 99 (1994) no. B10, pp. 19867-19884 | DOI

[Christensen, 1985] U. R. Christensen Thermal evolution models for the Earth, J. Geophys. Res., Volume 90 (1985), pp. 2995-3007 | DOI

[Coltice et al., 2019] N. Coltice; L. Husson; C. Faccenna; M. Arnould What drives tectonic plates?, Sci. Adv., Volume 5 (2019) no. 10, eaax4295 | DOI

[Davaille, 1999] A. Davaille Simultaneous generation of hotspots and superswells by convection in a heterogeneous planetary mantle, Nature, Volume 402 (1999), pp. 756-760 | DOI

[Davies, 1990] G. F. Davies Heat and mass transport in the early earth, Origin of the Earth (H. E. Newsome; J. H. Jones, eds.), Oxford University Press, New York, 1990, pp. 175-194

[Deguen, 2013] R. Deguen Thermal convection in a spherical shell with melting/freezing at either or both of its boundaries, J. Earth Sci., Volume 24 (2013), pp. 669-682 | DOI

[Deguen et al., 2013] R. Deguen; T. Alboussière; P. Cardin Thermal convection in Earth’s inner core with phase change at its boundary, Geophys. J. Int., Volume 194 (2013), pp. 1310-1334 | DOI

[Driscoll and Bercovici, 2014] P. Driscoll; D. Bercovici On the thermal and magnetic histories of Earth and Venus: Influences of melting, radioactivity, and conductivity, Phys. Earth Planet. Inter., Volume 236 (2014), pp. 36-51 | DOI

[Duffy and Ahrens, 1993] T. S. Duffy; T. J. Ahrens Thermal expansion of mantle and core materials at very high pressures, Geophys. Res. Lett., Volume 20 (1993) no. 11, pp. 1103-1106 | DOI

[Elkins-Tanton, 2012] L. T. Elkins-Tanton Magma oceans in the inner solar system, Ann. Rev. Earth Planet. Sci., Volume 40 (2012), pp. 113-139 | DOI

[Elkins-Tanton et al., 2003] L. T. Elkins-Tanton; E. M. Parmentier; P. C. Hess Magma ocean fractional crystallization and cumulate overturn in terrestrial planets: Implications for Mars, Meteorit. Planet. Sci., Volume 38 (2003) no. 12, pp. 1753-1771 | DOI

[Fichtner et al., 2024] A. Fichtner; B. L. N. Kennett; V. C. Tsai et al. Seismic tomography 2024, Bull. Seism. Soc. Am., Volume 114 (2024), pp. 1185-1213 | DOI

[Fiquet et al., 2010] G. Fiquet; A. L. Auzende; J. Siebert; A. Corgne; H. Bureau; H. Ozawa; G. Garbarino Melting of peridotite to 140 GigaPascals, Science, Volume 329 (2010), pp. 1516-1518 | DOI

[Flament et al., 2022] N. Flament; Ö. F. Bodur; S. E. Williams; A. S. Merdith Assembly of the basal mantle structure beneath Africa, Nature, Volume 603 (2022) no. 7903, pp. 846-851 | DOI

[Gerya and Yuen, 2003] T. V. Gerya; D. A. Yuen Characteristics-based marker-in-cell method with conservative finite-differences schemes for modeling geological flows with strongly variable transport properties, Phys. Earth Planet. Inter., Volume 140 (2003), pp. 293-318 | DOI

[Hernlund and McNamara, 2015] J. Hernlund; A. McNamara 7.11 – the core–mantle boundary region, Treatise on Geophysics. Mantle Dynamics (G. Schubert, ed.), Elsevier, Oxford, 2015, pp. 461-519 | DOI

[Hernlund and Tackley, 2008] J. W. Hernlund; P. J. Tackley Modeling mantle convection in the spherical annulus, Phys. Earth Planet. Inter., Volume 171 (2008) no. 1–4, pp. 48-54 | DOI

[Hess and Parmentier, 1995] P. C. Hess; E. M. Parmentier A model for the thermal and chemical evolution of the Moon’s interior: implications for the onset of mare volcanism, Earth Planet. Sci. Lett., Volume 134 (1995), pp. 501-514 | DOI

[Ismail-Zadeh and Tackley, 2012] A. Ismail-Zadeh; P. J. Tackley Computational Methods for Geodynamics, Cambridge University Press, Cambridge, 2012

[Jaupart et al., 2015] C. Jaupart; S. Labrosse; F. Lucazeau; J.-C. Mareschal 7.06 – temperatures, heat, and energy in the mantle of the Earth, Treatise on Geophysics. Mantle Dynamics (G. Schubert; D. Bercovici, eds.), Elsevier, Oxford, 2015, pp. 223-270 | DOI

[Labrosse, 2015] S. Labrosse Thermal evolution of the core with a high thermal conductivity, Phys. Earth Planet. Inter., Volume 247 (2015), pp. 36-55 | DOI

[Labrosse, 2016] S. Labrosse Thermal state and evolution of the Earth core and deep mantle, Deep Earth: Physics and Chemistry of the Lower Mantle and Core (H. Terasaki; R. Fischer, eds.) (AGU Geophysical Monograph Series), American Geophysical Union, Washington DC, 2016, pp. 43-56

[Labrosse et al., 2007] S. Labrosse; J. W. Hernlund; N. Coltice A crystallizing dense magma ocean at the base of Earth’s mantle, Nature, Volume 450 (2007), pp. 866-869 | DOI

[Labrosse et al., 2018] S. Labrosse; A. Morison; R. Deguen; T. Alboussière Rayleigh–Bénard convection in a creeping solid with a phase change at either or both horizontal boundaries, J. Fluid Mech., Volume 846 (2018), pp. 5-36 | DOI | Zbl

[Laneuville et al., 2018] M. Laneuville; J. Hernlund; S. Labrosse; N. Guttenberg Crystallization of a compositionally stratified basal magma ocean, Phys. Earth Planet. Inter., Volume 276 (2018), pp. 86-92 | DOI

[Lebec et al., 2023] L. Lebec; S. Labrosse; A. Morison; P. J. Tackley Scaling of convection in high-pressure ice layers of large icy moons and implications for habitability, Icarus, Volume 396 (2023), 115494 | DOI

[Lebec et al., 2024] L. Lebec; S. Labrosse; A. Morison; P. J. Tackley Effects of salts on the exchanges through high-pressure ice layers of large ocean worlds, Icarus, Volume 412 (2024), 115966 | DOI

[Le Bars and Davaille, 2004] M. Le Bars; A. Davaille Whole layer convection in a heterogeneous planetary mantle, J. Geophys. Res., Volume 109 (2004), B03403 | DOI

[Li and McNamara, 2013] M. Li; A. K. McNamara The difficulty for subducted oceanic crust to accumulate at the Earth’s core–mantle boundary, J. Geophys. Res., Volume 118 (2013) no. 4, pp. 1807-1816 | DOI

[Lister and Buffett, 1995] J. R. Lister; B. A. Buffett The strength and efficiency of the thermal and compositional convection in the geodynamo, Phys. Earth Planet. Inter., Volume 91 (1995), pp. 17-30 | DOI

[Maurice et al., 2017] M. Maurice; N. Tosi; H. Samuel; A.-C. Plesa; C. Hüttig; D. Breuer Onset of solid-state mantle convection and mixing during magma ocean solidification, J. Geophys. Res.: Planets, Volume 122 (2017) no. 3, pp. 577-598 | DOI

[Mizzon and Monnereau, 2013] H. Mizzon; M. Monnereau Implication of the lopsided growth for the viscosity of Earth’s inner core, Earth Planet. Sci. Lett., Volume 361 (2013), pp. 391-401 | DOI

[Morison, 2019] A. Morison Convection dans le manteau primitif en interaction avec des océans de magma globaux, PhD thesis, Université de Lyon, ENS de Lyon (2019)

[Morison et al., 2019] A. Morison; S. Labrosse; R. Deguen; T. Alboussière Timescale of overturn in a magma ocean cumulate, Earth Planet. Sci. Lett., Volume 516 (2019), pp. 25-36 | DOI

[Morison et al., 2024] A. Morison; S. Labrosse; R. Deguen; T. Alboussière Onset of thermal convection in a solid spherical shell with melting at either or both boundaries, Geophys. J. Int., Volume 238 (2024), pp. 1121-1136 | DOI

[Nakagawa and Tackley, 2012] T. Nakagawa; P. J. Tackley Influence of magmatism on mantle cooling, surface heat flow and urey ratio, Earth Planet. Sci. Lett., Volume 329–330 (2012), pp. 1-10 | DOI

[Nakagawa et al., 2010] T. Nakagawa; P. J. Tackley; F. Deschamps; J. A. D. Connolly The influence of MORB and harzburgite composition on thermo-chemical mantle convection in a 3-D spherical shell with self-consistently calculated mineral physics, Earth Planet. Sci. Lett., Volume 296 (2010) no. 3–4, pp. 403-412 | DOI

[Nomura et al., 2014] R. Nomura; K. Hirose; K. Uesugi; Y. Ohishi; A. Tsuchiyama; A. Miyake; Y. Ueno Low core-mantle boundary temperature inferred from the solidus of pyrolite, Science, Volume 343 (2014) no. 6170, pp. 522-525 | DOI

[Patočka et al., 2020] V. Patočka; O. Šrámek; N. Tosi Minimum heat flow from the core and thermal evolution of the Earth, Phys. Earth Planet. Inter., Volume 305 (2020), 106457 | DOI

[Ricard, 2007] Y. Ricard Physics of mantle convection, Treatise of Geophysics. Mantle Dynamics (D. Bercovici; G. Schubert, eds.), Volume 7, Elsevier, Oxford, 2007, pp. 253-303

[Ricard et al., 2022] Y. Ricard; T. Alboussière; S. Labrosse; J. Curbelo; F. Dubuffet Fully compressible convection for planetary mantles, Geophys. J. Int., Volume 230 (2022) no. 2, pp. 932-956 | DOI

[Rost et al., 2005] S. Rost; E. J. Garnero; Q. Williams; M. Manga Seismological constraints on a possible plume root at the core-mantle boundary, Nature, Volume 435 (2005), pp. 666-669 | DOI

[Sleep, 2000] N. H. Sleep Evolution of the mode of convection within terrestrial planets, J. Geophys. Res., Volume 105 (2000), pp. 17563-17578 | DOI

[Stixrude et al., 2009] L. Stixrude; N. de Koker; N. Sun; M. Mookherjee; B. B. Karki Thermodynamics of silicate liquids in the deep Earth, Earth Planet. Sci. Lett., Volume 278 (2009), pp. 226-232 | DOI

[Tackley and King, 2003] P. J. Tackley; S. D. King Testing the tracer ratio method for modeling active compositional fields in mantle convection simulations, Geochem. Geophys. Geosyst., Volume 4 (2003) no. 4, 8302 | DOI

[Tackley, 1998] P. J. Tackley Three-dimensional simulations of mantle convection with a thermochemical CMB boundary layer: D”?, The Core-Mantle Boundary Region (M. Gurnis; M. E. Wyession; E. Knittle; B. A. Buffett, eds.), American Geophysical Union, Washington DC, 1998, pp. 231-253 | DOI

[Tackley, 2008] P. J. Tackley Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid, Phys. Earth Planet. Inter., Volume 171 (2008) no. 1–4, pp. 7-18 | DOI

[Ulvrová et al., 2012] M. Ulvrová; S. Labrosse; N. Coltice; P. Raback; P. J. Tackley Numerical modeling of convection interacting with a melting and solidification front: application to the thermal evolution of the basal magma ocean, Phys. Earth Planet. Inter., Volume 206–207 (2012), pp. 51-66 | DOI

[Williams and Garnero, 1996] Q. Williams; E. J. Garnero Seismic evidence for partial melt at the base of earth’s mantle, Science, Volume 273 (1996) no. 5281, pp. 1528-1530 | DOI

Commentaires - Politique