Abridged English version
Obtaining rainfall averages in Sahelian regions is problematic, because of low rain-gauge density and of the predominant type of rainfalls in the region (convection). Using satellite infrared measurements might be the solution but present results are still disappointing [3,12].
This paper shows the changes in the estimation error due to a decrease in the number of stations belonging to a dense network of rain-gauge stations in the Niamey region (Niger, Fig. 1), on a 12 000 km2 area [9], studied for 6 years from 1991 to 1996. Over the last fifteen years, other studies on Niger rainfall statistics have been conducted [1,2,5,8–11], most of them in the context of the EPSAT–Niger Experiment.

Localisation de la zone d'étude, du réseau complet de pluviographes du programme EPSAT–Niger et des deux réseaux de 12 stations.
Location of the study area, the total network rain gauge of EPSAT–Niger and the two networks of 12 stations.
In this study, kriging is used as the spatialisation method, because it seems to fit particularly well the calculation of rainfall spatial means and estimation errors [4,6]. Kriging uses the variogram:
The variogram modelling allows the calculation of rainfall means and of a standard deviation of estimation error – ECTE. Hereafter, we will use the standard estimation error (ESE), which is ECTE divided by the mean estimate.
For one year, a network of ten stations regularly distributed over an area of 12 000 km2 is sufficient to estimate the mean with an error below 10%, in comparison with the rainfall mean calculated from a network of 67 stations [13]. At the smaller scale of one month or one period of ten days, a regularly distributed network of 12 stations (two such networks were tested for 1993 and 1994) is necessary to determine a rainfall mean over the same area with an error below 20% (99% and 97% of the total rainfall are under this error threshold). And over the six-year study, 82% of the periods stay below the 20% error threshold (Fig. 2, Tables 1 and 2).
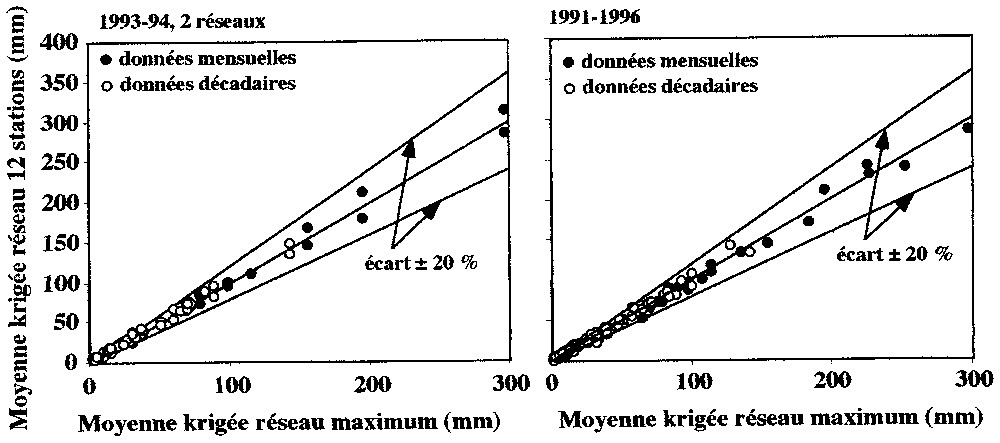
Moyenne pluviométrique krigée mensuelle et décadaire calculée en fonction du réseau de référence et du réseau de 12 stations sur le degré carré (saisons 1991–1996). En 1993–1994, deux réseaux différents de 12 stations sont utilisés.
Kriged mean rainfall for a monthly and a ten days period depending on the reference network and 12 stations network over the 1°×1° square (period 1991–1996). For 1993–1994, two different networks with 12 stations each are used.
Minimum et maximum pluviométrique saisonnier, moyenne krigée saisonnière et mensuelle sur le degré carré en fonction du réseau pour les saisons 1991–1996 (en mm)
Minimum and maximum seasonal, seasonal and monthly kriging mean over the degree square according to network for 1991–1996 season (mm)
| Année | Nombre | Minimum | Maximum | Moyenne krigée | M | J | J | A | S | O |
| de stations | annuel | annuel | sur le degré carré | |||||||
| 1991 | 52 | 340,9 | 745,3 | 533,0 | 114,5 | 85,5 | 98,3 | 184,5 | 15,4 | 29,2 |
| 12 | 413,2 | 667,3 | 517,4 | 118,6 | 88,5 | 88,2 | 170,4 | 17,1 | 28,1 | |
| 1992 | 98 | 389,0 | 782,1 | 516,2 | 15,5 | 74,8 | 136,4 | 226,5 | 59,9 | |
| 12 | 432,4 | 705,7 | 541,2 | 19,9 | 72,6 | 133,3 | 240,0 | 65,8 | ||
| 1993 | 55 | 314,5 | 613,9 | 465,2 | 6,0 | 79,0 | 114,6 | 195,4 | 68,5 | 3,1 |
| 1–12 | 314,5 | 613,9 | 454,2 | 4,0 | 72,0 | 109,8 | 210,8 | 63,2 | 2,1 | |
| 2–12 | 317,9 | 548,1 | 547,5 | 5,7 | 83,2 | 110,6 | 178,7 | 73,1 | 3,4 | |
| 1994 | 46 | 491,9 | 835,7 | 666,9 | 14,0 | 70,5 | 155,7 | 297,6 | 98,5 | 29,9 |
| 1–12 | 491,9 | 813,3 | 643,7 | 17,0 | 71,3 | 144,0 | 283,9 | 95,2 | 26,1 | |
| 2–12 | 493,8 | 835,7 | 704,7 | 15,1 | 74,2 | 167,7 | 312,3 | 99,9 | 32,7 | |
| 1995 | 38 | 323,1 | 602,4 | 494,7 | 7,4 | 67,0 | 108,6 | 253,0 | 57,4 | |
| 12 | 361,2 | 558,4 | 484,6 | 8,3 | 66,3 | 99,7 | 237,8 | 65,3 | ||
| 1996 | 37 | 374,3 | 593,3 | 504,9 | 10,4 | 91,4 | 83,3 | 227,7 | 64,7 | 20,6 |
| 12 | 416,3 | 571,8 | 503,9 | 14,0 | 91,7 | 89,4 | 230,2 | 53,4 | 22,7 |
Moyenne krigée pluviométrique décadaire sur le degré carré en fonction du réseau choisi pour les saisons 1991–1996 (en mm). Réf.: réseau complet de référence, dont le nombre de stations chaque année est donné dans le Tableau 1; 12: réseau à 12 stations; 1–12 et 2–12: deux réseaux à 12 stations différents en 1993–1994
Ten-day-period kriging mean over the degree square for the selected network for the 1991–1996 season (mm). Ref. : reference network, the number of stations for each year is given in Table 1 ; 12 : network with 12 stations ; 1–12, 2–12 : two different networks with 12 stations for 1993–1994
| 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | |||||||||
| Réf. | 12 | Réf. | 12 | Réf. | 1–12 | 2–12 | Réf. | 1–12 | 2–12 | Réf. | 12 | Réf. | 12 | |
| 1 avril | 7,6 | 7,8 | 6,3 | 6,4 | ||||||||||
| 2 avril | 10,0 | 8,8 | 5,4 | 6,1 | 4,3 | 2,1 | 2,7 | 2,9 | 2,7 | |||||
| 3 avril | 3,4 | 4,2 | 2,3 | 1,8 | 2,0 | 1,4 | 0,7 | |||||||
| 1er mai | 28,9 | 30,3 | 6,6 | 5,9 | 7,4 | 4,4 | 4,0 | 3,4 | 3,8 | |||||
| 2 mai | 7,7 | 10,1 | 8,6 | 5,2 | 4,5 | 4,5 | 5,8 | 0,9 | 0,6 | 2,7 | 4,3 | |||
| 3 mai | 92,5 | 97,3 | 12,9 | 11,0 | 5,9 | 3,8 | 5,8 | 4,0 | 6,6 | 3,1 | 1,6 | 3,9 | 4,6 | 5,5 |
| 1er juin | 18,2 | 19,5 | 31,7 | 34,9 | 30,4 | 23,1 | 36,8 | 26,6 | 26,9 | 29,5 | 3,7 | 3,4 | 57,4 | 54,5 |
| 2 juin | 28,9 | 29,0 | 18,9 | 18,1 | 30,0 | 28,8 | 29,4 | 31,6 | 32,6 | 30,5 | 30,8 | 30,4 | 4,9 | 6,5 |
| 3 juin | 39,4 | 42,5 | 24,4 | 21,5 | 18,7 | 18,2 | 17,7 | 12,8 | 12,2 | 13,2 | 32,7 | 32,5 | 28,6 | 33,5 |
| 1er juillet | 20,7 | 21,4 | 8,9 | 9,4 | 38,1 | 36,8 | 38,7 | 33,2 | 30,2 | 31,2 | 37,5 | 42,6 | 32,1 | 29,8 |
| 2 juillet | 50,4 | 45,4 | 46,6 | 44,0 | 29,2 | 27,5 | 27,3 | 30,6 | 27,4 | 35,9 | 39,9 | 32,1 | 9,0 | 9,4 |
| 3 juillet | 28,2 | 29,1 | 79,5 | 80,5 | 51,0 | 50,6 | 46,0 | 89,0 | 81,5 | 95,1 | 33,0 | 26,3 | 47,8 | 50,5 |
| 1er août | 68,6 | 61,4 | 63,5 | 67,8 | 64,5 | 63,2 | 64,5 | 142,9 | 134,1 | 146,7 | 100,9 | 91,7 | 48,1 | 50,1 |
| 2 août | 69,6 | 65,5 | 30,7 | 31,0 | 70,2 | 72,2 | 66,6 | 82,9 | 85,5 | 88,7 | 84,3 | 78,2 | 100,7 | 107,1 |
| 3 août | 46,2 | 42,0 | 128,5 | 42,2 | 59,1 | 65,4 | 51,7 | 71,6 | 69,5 | 72,4 | 68,8 | 69,6 | 71,1 | 71,5 |
| 1er septembre | 11,6 | 12,5 | 24,8 | 28,0 | 20,8 | 22,4 | 20,3 | 70,0 | 68,8 | 73,6 | 7,0 | 7,2 | 24,9 | 21,9 |
| 2 septembre | 3,7 | 1,5 | 32,2 | 32,8 | 37,3 | 34,4 | 40,9 | 24,4 | 25,5 | 21,2 | 21,3 | 22,8 | 31,7 | 22,7 |
| 3 septembre | 2,7 | 4,6 | 10,3 | 7,4 | 12,7 | 5,4 | 5,7 | 5,7 | 31,2 | 34,5 | 8,7 | 8,4 | ||
| 1 octobre | 27,9 | 26,2 | 1,1 | 0,9 | 3,1 | 2,4 | 3,1 | 13,6 | 12,9 | 14,6 | 7,4 | 9,2 | ||
| 2 octobre | 14,8 | 10,6 | 18,2 | 12,4 | 13,1 |
The chosen 12-station network is then systematically reduced, N decreasing from 12 to one station, with a combination of stations in order to evaluate the mean standard estimation error distribution as a function of N.
As shown in the 1993 study on two different 12-station networks, which were progressively reduced, the variation of the estimation error does not depend very much on the choice of the 12-station network (Table 3). At seasonal and monthly time-scales, the estimation error variation is the same for both networks except for the lowest rainfall (3 mm in October 1993). At the scale of the ten-day period, there is a difference between the two networks, but it only concerns rainfalls below 10 mm, which is negligible, in comparison with the total seasonal rainfall.
Comparaison pour l'année 1993 (pas de temps saisonnier et mensuel (a), puis décadaire (b)) des ESE pour les réseaux dégradés (N=1 à 12 stations) pour deux réseaux de 12 stations
Comparison (year 1993, seasonal and monthly time step (a) and ten-day-period time step (b)) of the ESE for the reduced networks (N=1 to 12 stations) from two networks of 12 stations
| (a) | saison | mai | juin | juillet | août | septembre | octobre | |
| 12 | 3,9–3,9 | 42,5–29,8 | 6,0–5,0 | 7,6–7,4 | 3,8–4,3 | 8,9–7,5 | 47,6–26,5 | |
| 11 | 4,2–4,1 | 44,7–29,8 | 6,4–5,4 | 8,4–8,2 | 4,2–4,8 | 9,4–8,0 | 48,4–29,5 | |
| 10 | 4,4–4,4 | 46,2–31,6 | 6,9–5,8 | 9,3–9,0 | 4,6–5,3 | 9,9–8,5 | 53,0–31,7 | |
| 9 | 4,7–4,6 | 49,6–34,7 | 7,4–6,3 | 10,3–10,0 | 5,0–5,8 | 10,6–9,0 | 53,2–32,5 | |
| 8 | 5,1–5,0 | 52,1–36,8 | 8,1–6,8 | 11,5–11,1 | 5,6–6,5 | 11,4–9,7 | 58,0–35,6 | |
| 7 | 5,5–5,4 | 55,6–38,6 | 8,8–7,5 | 12,9–12,4 | 6,2–7,2 | 12,3–10,5 | 63,0–38,5 | |
| 6 | 6,01–5,9 | 59,9–42,1 | 9,7–8,3 | 14,6–14,0 | 7,0–8,1 | 13,4–11,5 | 68,0–41,5 | |
| 5 | 6,6–6,6 | 66,8–47,4 | 10,8–9,2 | 16,8–16,0 | 8,0–9,2 | 14,8–12,7 | 76,5–46,0 | |
| 4 | 7,5–7,4 | 74,2–52,6 | 12,4–10,6 | 19,6–18,6 | 9,2–10,7 | 16,7–14,4 | 85,7–51,4 | |
| 3 | 8,7–8,6 | 86,4–61,4 | 14,6–12,4 | 23,7–22,4 | 11,0–12,8 | 19,5–16,8 | 98,0–59,4 | |
| 2 | 10,8–10,7 | 106,2–75,5 | 18,2–15,6 | 30,2–28,5 | 14,0–16,2 | 24,1–20,8 | 121,8–74,0 | |
| 1 | 15,5–15,3 | 150,5–107,8 | 26,2–22,4 | 44,5–41,7 | 20,3–23,7 | 34,4–29,7 | 175,6–106,9 | |
| (b) | 3 avril | 3 mai | 1er juin | 2 juin | 3 juin | 1er juillet | 2 juillet | 3 juillet |
| 12 | 9,5–17,4 | 42,1–27,6 | 13,0–7,9 | 12,5–11,9 | 17,0–17,5 | 11,1–10,3 | 16,0–16,1 | 10,7–11,5 |
| 11 | 12,2–22,0 | 44,8–29,1 | 14,2–8,6 | 14,3–13,1 | 19,2–19,7 | 12,6–11,7 | 16,7–16,8 | 11,2–12,1 |
| 10 | 14,1–24,6 | 48,6–30,9 | 15,5–9,4 | 16,3–14,7 | 21,6–22,1 | 14,1–13,2 | 17,4–17,6 | 12,0–13,0 |
| 9 | 16,1–28,2 | 52,0–33,2 | 16,9–10,2 | 18,4–16,4 | 24,3–24,9 | 15,8–14,9 | 18,5–18,7 | 12,8–13,8 |
| 8 | 18,5–32,0 | 55,4–36,2 | 18,5–11,2 | 20,9–18,3 | 27,3–28,0 | 17,8–16,8 | 19,8–19,8 | 13,7–14,9 |
| 7 | 21,4–36,6 | 60,0–39,6 | 20,3–12,3 | 23,9–20,6 | 30,7–31,7 | 20,2–19,0 | 21,2–21,2 | 14,8–16,1 |
| 6 | 24,5–42,0 | 65,3–4,20 | 22,6–13,0 | 27,6–23,0 | 34,7–36,0 | 23,0–22,0 | 22,9–23,0 | 16,2–17,0 |
| 5 | 29,0–50,1 | 72,5–48,4 | 25,5–15,4 | 32,3–27,0 | 39,7–41,6 | 26,6–25,0 | 25,3–25,4 | 18,0–19,5 |
| 4 | 34,7–60,0 | 81,9–55,0 | 29,2–17,0 | 38,5–32,0 | 46,2–48,0 | 31,3–28,0 | 28,3–29,0 | 20,3–22,0 |
| 3 | 42,8–72,9 | 95,3–64,4 | 34,6–20,8 | 47,3–38,4 | 55,3–59,1 | 37,9–35,5 | 32,8–33,0 | 23,7–25,8 |
| 2 | 56,2–98,5 | 117,9–79,4 | 43,5–26,3 | 61,6–49,5 | 70,0–75,4 | 48,4–45,6 | 40,3–40,9 | 29,4–31,9 |
| 1 | 86,1–138,0 | 168,1–115,8 | 62,9–37,3 | 93,3–75,3 | 101,9–109,4 | 70,77–66,6 | 57,3–57,8 | 42,0–45,7 |
| 1er août | 2 août | 3 août | 1er septembre | 2 septembre | 3 septembre | 1er octobre | ||
| 12 | 7,7–7,4 | 4,1–4,5 | 8,4–10,2 | 17,8–19,2 | 10,2–8,6 | 28,4–15,8 | 37,5–29,0 | |
| 11 | 8,5–8,2 | 4,6–4,8 | 9,0–11,0 | 19,6–21,3 | 11,0–9,1 | 30,4–17,1 | 42,2–31,0 | |
| 10 | 9,4–9,0 | 5,0–5,3 | 9,7–11,9 | 21,6–23,5 | 11,9–9,9 | 32,5–18,4 | 42,4–32,3 | |
| 9 | 10,3–9,8 | 5,4–5,8 | 10,5–12,9 | 23,9–25,8 | 12,9–10,7 | 35,0–19,9 | 46,6–35,5 | |
| 8 | 11,3–10,8 | 6,0–6,4 | 11,3–14,0 | 26,5–28,6 | 14,0–12,0 | 37,7–21,7 | 50,9–38,7 | |
| 7 | 12,6–11,9 | 6,6–7,1 | 12,4–15,3 | 29,6–31,8 | 15,4–12,8 | 41,1–23,8 | 55,2–41,9 | |
| 6 | 14,1–12,5 | 7,3–8,2 | 13,7–16,5 | 33,3–36,0 | 17,1–13,5 | 45,1–26,0 | 58,6–45,0 | |
| 5 | 15,9–14,9 | 8,3–8,9 | 15,3–18,9 | 38,0–40,5 | 19,2–15,7 | 50,2–29,5 | 64,0–48,4 | |
| 4 | 18,3–16,0 | 9,5–10 | 17,4–21,0 | 44,1–47,0 | 22,0–17,0 | 57,0–34,0 | 72,3–56,0 | |
| 3 | 21,8–20,2 | 11,2–12,2 | 20,5–25,4 | 53,0–55,9 | 26,0–21,4 | 66,8–39,7 | 84,3–64,5 | |
| 2 | 27,4–25,4 | 14,1–15,4 | 25,6–31,7 | 67,5–70,2 | 32,6–26,8 | 82,9–49,5 | 105,2–79,4 | |
| 1 | 39,7–36,8 | 20,4–22,2 | 36,8–45,7 | 99,4–103,8 | 47,3–38,5 | 118,9–71,8 | 151,6–116,1 |
For all three time-scales (seasonal, monthly and ten day periods), the standard estimation error follows an almost exponential increase when the number of stations decreases. The smaller the time-step, the larger the estimation error, which agrees with many other studies [7].
For a seasonal time-step (Fig. 3a), there is not much difference from one year to another, and five stations in a network seem to be enough to estimate the rainfall spatial mean with a standard estimation error below 7% over the degree square area.
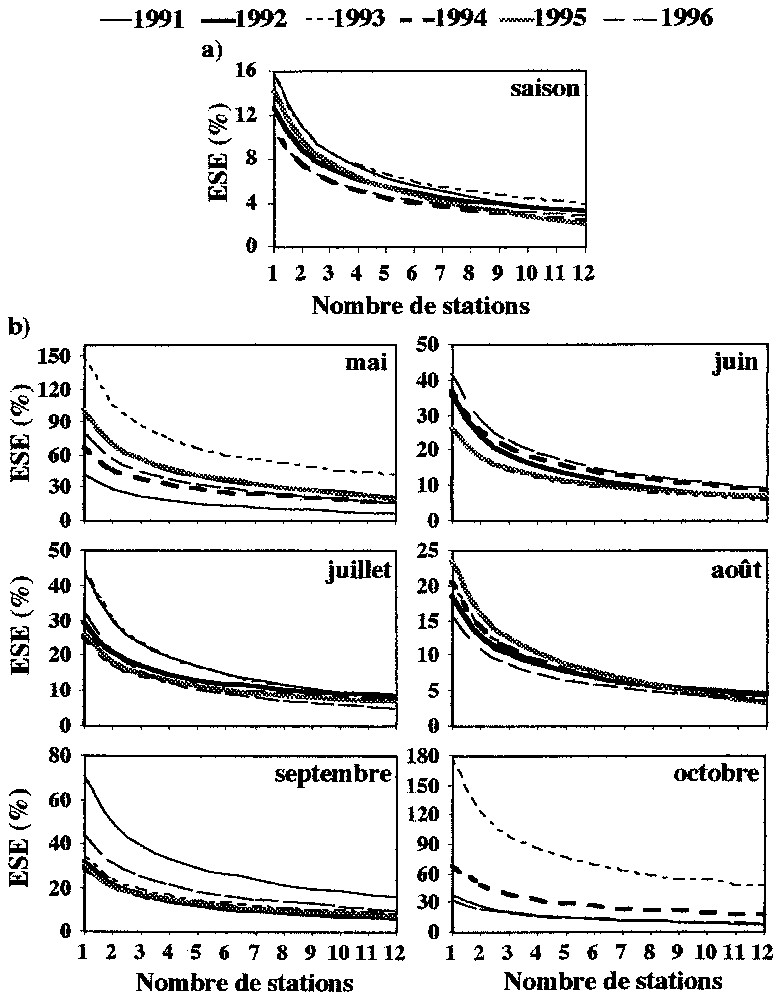
ESE moyen en fonction de la densité du réseau (saison 1991–1996): (a) échelle saisonnière; (b) échelle mensuelle.
Mean ESE according to the network density (period 1991–1996) : (a) season scale ; (b) monthly scale.
For a monthly time-step (Fig. 3b), there is a great difference between the core of the rainy season on the one hand, and both the beginning and the end of the season on the other hand. In May, September and October, there is a great variation of the standard estimation error from one year to the other and these months show the largest values. For the other months, graphs are rather homogeneous and the standard estimation error stays below 45%; this is due to the homogeneous structure of the rain field during this period. August (50% of the total annual rain) has the lowest standard estimation error variation. For June, July, August and September, which receive 91% of the total seasonal accumulation, a five-station network is sufficient to stay below the 20% error threshold.
Fig. 4 represents the standard estimation error for the different periods of ten days of each month for the seasons 1991 to 1996. It shows a very large scattering for all months, except July and August, with a great divergence of the estimation error when the number of stations is below five. Some ten-day periods in July show larger estimation errors. This is due to an intra-seasonal drought that occurred systematically during the six studied years.

ESE moyen en fonction de la densité du réseau à l'échelle décadaire (saison 1991–1996).
Mean ESE according to the network density (period 1991–1996) at ten-day-period scale.
There is a strong correlation between the rainfall variability of the rain field, the rain depth and the number of stations, this allows us to compare directly the rainfall spatial means with the estimation error, and this for each network type and for different time steps. Hence, we can use these curves as abacuses (Fig. 5).

Abaques annuelles, mensuelles et décadaires de l'erreur standardisée d'estimation en fonction de la hauteur moyenne de pluie sur le degré carré.
Annual, monthly and period of ten days abacus of the standard estimation error versus mean rainfall over the 1°×1° square.
For a monthly time-step and for a maximum standard error of 20%, it is possible to evaluate rain fields larger than 8 mm with 12 stations, rain fields larger than 15 mm with nine stations and rain fields larger than 30 mm with six stations. As the climatology between Mali and Chad (band 300–600 mm) is similar, we can reasonably extend the results to this area.
1 Introduction
La pluviométrie au Sahel est caractérisée, à l'échelle annuelle, par un gradient sud–nord de décroissance de la pluie d'environ 1 mm km−1. Il est, en revanche, difficile de passer de cette analyse à grande échelle spatiale à une analyse plus fine, car l'extrapolation de la mesure ponctuelle des précipitations en Afrique sahélienne a toujours été entachée d'une erreur importante en raison du type de précipitation dominant (convection) et du réseau de mesures, en général trop lâche (de l'ordre de un à cinq postes pour 10 000 km2) par rapport à la variabilité spatiale des pluies.
Bien qu'ayant une résolution assez fine dans l'espace et dans le temps, d'autres méthodes d'estimation de la pluie, telle l'utilisation des indices satellitaires infrarouges, ne présentent pas, à l'heure actuelle en région sahélienne, une bonne corrélation avec le cumul pluviométrique, d'autant plus qu'il n'est pas possible d'obtenir une validation parfaite avec les données sol en raison de la forte variabilité des pluies et de la faible densité de postes [3,12].
Cette étude a pour but de calculer une moyenne pluviométrique sur environ 12 000 km2, à partir de la méthode du krigeage, à différentes échelles de temps, en fonction d'un réseau très dense. Cette forte densité permet le calcul d'une valeur moyenne surfacique se rapprochant de la valeur statistiquement vraie et permet, de même, de mesurer l'erreur sur la mesure en fonction du nombre de postes. Six années de suivi, comportant des années extrêmes sèches et humides, ont été analysées pour avoir un échantillon statistique le plus complet possible de la variabilité des champs de pluie sahéliens.
2 Site d'étude et méthodologie
L'étude se situe dans la région de Niamey (Niger), dans une zone ne présentant pas de relief marqué, afin de s'affranchir des renforcements de convection liés à l'orographie. Ces quinze dernières années, plusieurs études sur les précipitations (statistique, géostatistique, estimation...) ont déjà été menées dans cette zone [1,2,5,8–11], la plupart dans le cadre de l'expérimentation EPSAT–Niger. Ce dispositif expérimental comprend un réseau dense de pluviographes, régulièrement distribué sur une surface d'environ 16 000 km2 (Fig. 1), comprenant une zone de référence de 12 000 km2 (13°–14°N ; 2°–3°E), le degré carré, et une zone d'extension à l'ouest d'environ 4000 km2 [9]. Le maillage du réseau a évolué durant l'étude, d'un appareil pour 156 km2 (1991–1992) à un appareil pour 400 km2 (1993–1996) ; le Tableau 1 donne le nombre maximum de postes pour chaque année.
Pour le calcul de moyennes pluviométrique surfaciques, le krigeage apparaı̂t particulièrement bien adapté [4,6]. Cette méthode considère le champ pluvieux comme une variable régionalisée z(x), réalisation d'une fonction aléatoire Z(x). Si cette fonction aléatoire est stationnaire d'ordre 2, ou intrinsèque, une fonction variogramme peut être alors définie par l'équation suivante :
Dans cette étude, on a modélisé indépendamment chaque champ pluvieux annuel, mensuel et décadaire à partir du nombre maximum de stations disponibles pour chaque année, pour d'abord déterminer le variogramme de chaque champ, qui varie beaucoup, puis conduire l'estimation par krigeage.
Le krigeage permet de calculer des valeurs ponctuelles ou des moyennes surfaciques et un écart type d'estimation associé (ECTE). Par la suite, on utilisera l'ESE (erreur standardisée d'estimation) qui représente l'ECTE divisé par l'estimation de la moyenne. L'intérêt de cette méthode est de minimiser, par le krigeage, la variance d'estimation, et de s'affranchir par cette standardisation de la vraie moyenne qui, en l'absence d'un réseau dense, ne peut pas être évaluée.
Le calcul d'une moyenne pluviométrique sur une surface donnée nécessite d'avoir un nombre suffisant de stations pour se rapprocher le plus possible de la valeur vraie, qui reste inconnue, mais ce nombre de stations ne peut être étendu indéfiniment et doit tenir compte des contraintes économiques. Une étude préliminaire sur l'ensemble du réseau dense d'EPSAT–Niger a montré qu'à l'échelle annuelle, une dizaine de postes (dont on prend la moyenne arithmétique) disposés régulièrement sur une surface donnée sont suffisants pour estimer la moyenne avec une erreur inférieure à 10 % par rapport à celle calculée par krigeage à partir d'un réseau maximum de 67 stations [13]. À l'échelle mensuelle et décadaire, la variabilité à laquelle on peut s'attendre étant plus importante, on a déterminé un réseau régulier minimal, nécessaire pour obtenir par moyenne arithmétique à cette échelle de temps des écarts inférieurs à 20 % par rapport au calcul par krigeage sur le réseau maximum (le chiffre de 20 % d'écart toléré est évidemment arbitraire, mais semble un critère d'estimation satisfaisant à l'échelle de la décade ou du mois). Les deux années extrêmes de la série, 1993 et 1994, ont été testées, et il s'est avéré que, pour 80 % des périodes observées (99 % du cumul total des pluies à l'échelle mensuelle et 97 % à l'échelle décadaire), un réseau régulier de 12 stations (deux réseaux réguliers ont été testés pour chaque année) était nécessaire pour déterminer une moyenne pluviométrique sur le degré carré respectant la valeur d'écart de 20 % retenue. Les périodes où l'écart est supérieur à 20 % présentent généralement des cumuls faibles inférieurs à 15 mm, où l'on peut tolérer un écart plus important. On a ensuite choisi un réseau régulier commun de 12 stations pour les six années d'étude (103 décades, 34 mois), 82 % des périodes restant bien sous le seuil d'écart de 20 %, et les périodes restantes présentant des cumuls inférieurs à 15 mm, à l'exception de deux décades d'environ 30 mm (première décade de juin 1993 et seconde décade de septembre 1996), où l'écart atteint respectivement 24 et 28 % (Fig. 2, Tableaux 1 et 2).
Le réseau de 12 stations choisi est ensuite dégradé systématiquement, N variant de 12 à une station(s), avec combinaison des stations, soit au total la création de 4095 réseaux (une station, 12 réseaux ; deux stations, 66 réseaux ; trois stations, 220 réseaux ; quatre stations, 495 réseaux ; cinq stations, 792 réseaux ; six stations, 924 réseaux...), ceci afin d'étudier la répartition de l'erreur d'estimation en fonction de N. L'estimation est toujours calculée en prenant la moyenne arithmétique des N stations. Vu le nombre de résultats acquis, on raisonnera en terme de moyenne, c'est-à-dire que l'ensemble des ECTE calculés pour un nombre de station donné sera représenté par sa moyenne.
3 Résultats et discussion
3.1 Comparaison des erreurs standardisées d'estimation obtenues sur les réseaux dégradés à partir de deux réseaux différents de 12 stations
Dans le but de généraliser les résultats obtenus pour établir des abaques d'erreur d'estimation, il était nécessaire de connaı̂tre l'influence du choix du réseau de base de 12 stations dans la variation des erreurs d'estimation que cela engendre pour les réseaux dégradés. L'étude a porté sur les deux années extrêmes de notre série, 1993 et 1994. La comparaison de la variation des ESE des deux réseaux en 1993 (année déficitaire à plus forte ESE), en fonction de la hauteur moyenne de pluie calculée à partir de chaque réseau de 12 stations, est donnée dans le Tableau 3 et montre que le facteur de variation va dépendre bien évidemment du nombre N de stations, mais surtout de la hauteur de pluie. Au pas de temps de la saison et du mois (Tableau 3a), la variation de l'ESE avec N pour les deux réseaux est pratiquement identique, sauf pour la valeur de pluie la plus faible (3 mm en octobre 1993) où l'on note un écart plus grand, mais sans réelle importance du point de vue hydrologique. À l'échelle décadaire, l'écart de variation de l'ESE avec N entre les deux réseaux est plus fréquent, mais cela ne concerne que les pluies inférieures à 10 mm, où cet écart reste là aussi négligeable en terme de différence sur l'erreur faite sur le calcul de la lame d'eau. Au vu des résultats, il semble donc que le choix du réseau de 12 stations, s'il peut dans certains cas influencer le calcul de la moyenne surfacique, n'entraı̂ne pas de variations importantes sur le calcul de l'erreur d'estimation, du moins sur les hauteurs de pluie significatives. La mise en place d'abaques pourra donc s'affranchir de ce paramètre.
3.2 Calcul d'erreur d'estimation et proposition d'abaques
Aux trois échelles de temps, l'erreur d'estimation croı̂t à peu près exponentiellement en fonction de la diminution du nombre de stations. Plus le pas de temps est petit, plus l'erreur d'estimation est grande. Ces résultats sont conformes aux différentes études traitant ce sujet [7]. À l'échelle saisonnière (Fig. 3a), il y a peu de variations d'une année sur l'autre ; on remarque surtout que l'ensemble des courbes est encadré par les saisons 1994, la plus excédentaire (plus faibles valeurs d'ESE), et 1993, la plus déficitaire (plus fortes valeurs d'ESE). Pour la surface considérée (degré carré), la faible variation de l'ESE montre qu'un réseau de cinq stations suffit pour estimer la moyenne surfacique avec une erreur standardisée d'estimation inférieure à 7 %. Au pas de temps mensuel (Fig. 3b), on note un contraste important entre, d'une part, le début et la fin de la saison des pluies et, d'autre part, le cœur de cette saison. Mai, septembre et octobre montrent une variation importante de l'ESE d'une année sur l'autre et regroupent les plus fortes valeurs de l'ESE. Pour les autres mois, les courbes sont bien groupées et l'ESE reste inférieure à 45 %, ces caractéristiques étant dues à l'homogénéité de la structure du champ pluvieux pendant cette période. Le mois d'août (50 % du cumul saisonnier des pluies) présente la plus faible variation de l'ESE d'une année sur l'autre. Pour un seuil de tolérance de l'estimation de 20 %, on remarque que, pour la plupart des années, l'erreur d'estimation des mois de mai et octobre est le plus souvent au-dessus de ce seuil, quel que soit le nombre de postes (limité à 12). Néanmoins, pour juin, juillet, août et septembre, qui représentent 91 % du total pluviométrique saisonnier, un réseau de cinq stations est suffisant pour rester sous le seuil d'estimation de 20 %. À l'échelle décadaire, la capacité d'avoir des estimations fiables est importante, car c'est l'échelle de temps de référence des agronomes pour le suivi des cultures. La Fig. 4, qui représente l'ESE pour les différentes décades de chaque mois des saisons 1991 à 1996, montre une très forte dispersion des courbes pour tous les mois, mis à part juillet et août, avec une divergence de l'erreur d'estimation importante quand le nombre de stations est inférieur à cinq. Sur quelques décades de juillet, on peut noter des erreurs d'estimation plus importantes, liées à la présence d'une sécheresse intra-saisonnière observée systématiquement au cours des six années d'étude.
L'utilisation de telles courbes comme abaques est bien sûr fastidieuse. On peut essayer de regrouper les différents critères qui vont influencer l'erreur d'estimation, telle la hauteur de pluie et le nombre de stations. On obtient ainsi des courbes expérimentales au pas de temps annuel, mensuel et décadaire qui apparaissent d'un emploi plus pratique pour déterminer directement une erreur d'estimation standardisée moyenne en fonction du nombre de postes disponibles et de la hauteur moyenne pluviométrique recueillie sur ces différents postes (Fig. 5). Ainsi, à l'échelle mensuelle, pour une erreur standardisée moyenne maximum de 20 %, 12 stations permettent d'évaluer les champs de pluie supérieurs à 8 mm, neuf stations les champs supérieurs à 15 mm, six stations les champs supérieurs à 30 mm. Cette étude intéressant seulement la région de Niamey, il est difficile d'extrapoler spatialement la validité de ces abaques ; néanmoins, la climatologie sur la bande 300–600 mm, entre le Mali et le Tchad, étant homogène, on peut raisonnablement étendre ces résultats à l'ensemble de cette zone.
4 Conclusions
Le réseau dense d'EPSAT–Niger a permis de mesurer l'erreur d'estimation sur la pluie moyenne pour une surface d'un degré carré en fonction du nombre de stations et à différentes échelles de temps. La faible densité du réseau pluviométrique dans les régions sahéliennes ne permet pas de calculer des moyennes spatiales correctes, même sur des surfaces très grandes, en raison de la forte variabilité des champs de pluie aux petites échelles, induisant une erreur d'estimation qui est d'autant plus importante que le nombre de stations est faible. À partir de la méthode d'interpolation du krigeage, des courbes d'erreur standardisée d'estimation ont pu être établies en fonction du nombre de stations. Au vu de ces résultats, neuf stations, réparties régulièrement sur un degré carré, sont nécessaires pour estimer la moyenne pluviométrique spatiale à moins de 20 % d'erreur pour au moins 90 % du cumul de la pluie à l'échelle décadaire. En corollaire, sont proposées des abaques d'erreurs standardisées d'estimation, fonction de la hauteur moyenne de pluie, pouvant permettre d'optimiser le réseau pluviographique en fonction des objectifs fixés (suivi agricole, étude hydrologique...). Ces abaques sont valables pour la région du Niger étudiée, mais vraisemblablement aussi pour toute la bande sahélienne de précipitations 300–600 mm/an, entre le Mali et le Tchad.



