Abridged English version
Introduction
Modelling of argillaceous minerals elastic properties in porous medium shows a great interest for the understanding of argillaceous sediments-mechanical behaviour. This behaviour depends on the clays’ mineralogy and porosity. The paper gives the theoretical background of the present experimental modelling and a new approach to model clays and shale elastic behaviours.
Theoretical background
Elastic-behaviour boundaries
Fig. 1 shows Hashin–Shtrikman boundaries for elastic moduli: effective bulk modulus K1 and effective shear modulus μ1 following these relationships:
| (1) |
| (2) |
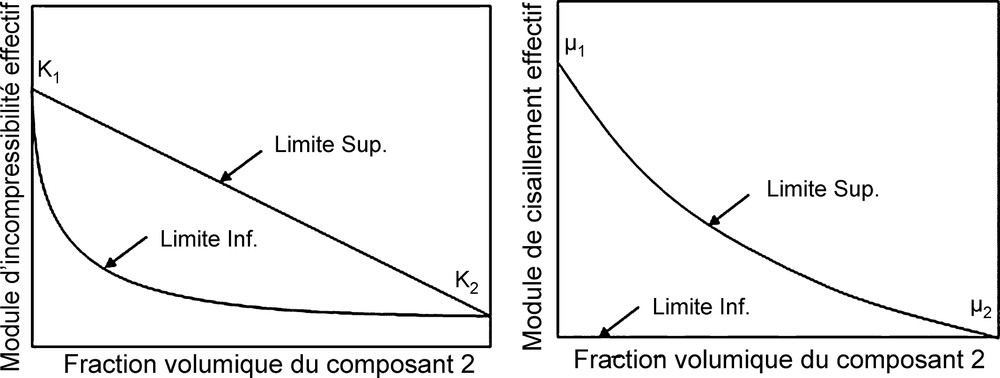
Limite des modules élastiques établis par une limite de Hashin-Shtrikman.
Fig. 1. Hashin–Shtrikman boundaries for elastic moduli.
Clay-porosity evolution as a function of effective pressure
Many authors have observed a progressive modification of the shale density with burial. Athy [1] and Korvin [7] have shown that it exists a density exponential decreasing with burial increase. Korvin [7] has shown that in a normally compacted sequence, clay density increases exponentially with burial depth, with effective pressure. So, with a description of effective pressure as a linear function of burial, it is possible to express clays porosity as:
| (3) |
Clay porosity from density tool
It is possible to express the clay porosity from shales density obtained from density tool:
| (4) |
Results and discussions
Fig. 2a and b show the clay compaction evolution and the water drainage, causing density increase. We observe that clay is initially put in suspension in water and then arranges itself progressively to raise a laminated structure. The ultimate stage of compaction tends to form a mineral block of a much-reduced porosity in which anisotropy tends to disappear. Several studies have proposed elastic moduli for dry clays. From these results and laboratory studies, hydrated-argillaceous mineral elastic moduli have been estimated. These moduli are specified in Table 1.
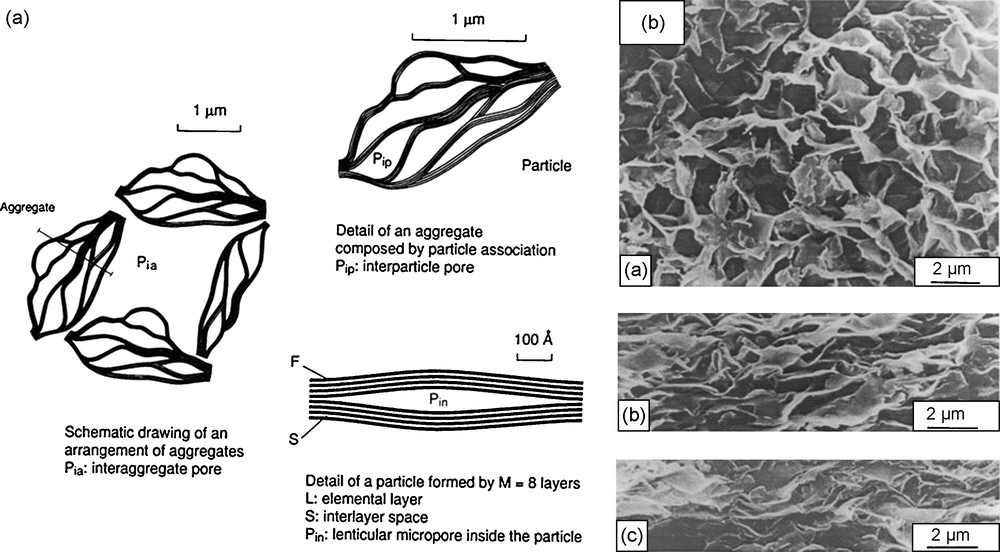
Structure des argiles et compaction avec l’augmentation de pression.
Fig. 2. Clay structure and compaction evolution with pressure increasing.
Example of P and S velocities modelling in argillaceous sediments
Fig. 4 and Table 2 give the results of clay-mineral determination from two methods: X-ray diffraction on plugs and gamma-ray spectroscopy. Fig. 5 gives clay porosity determined as a function of effective pressure.
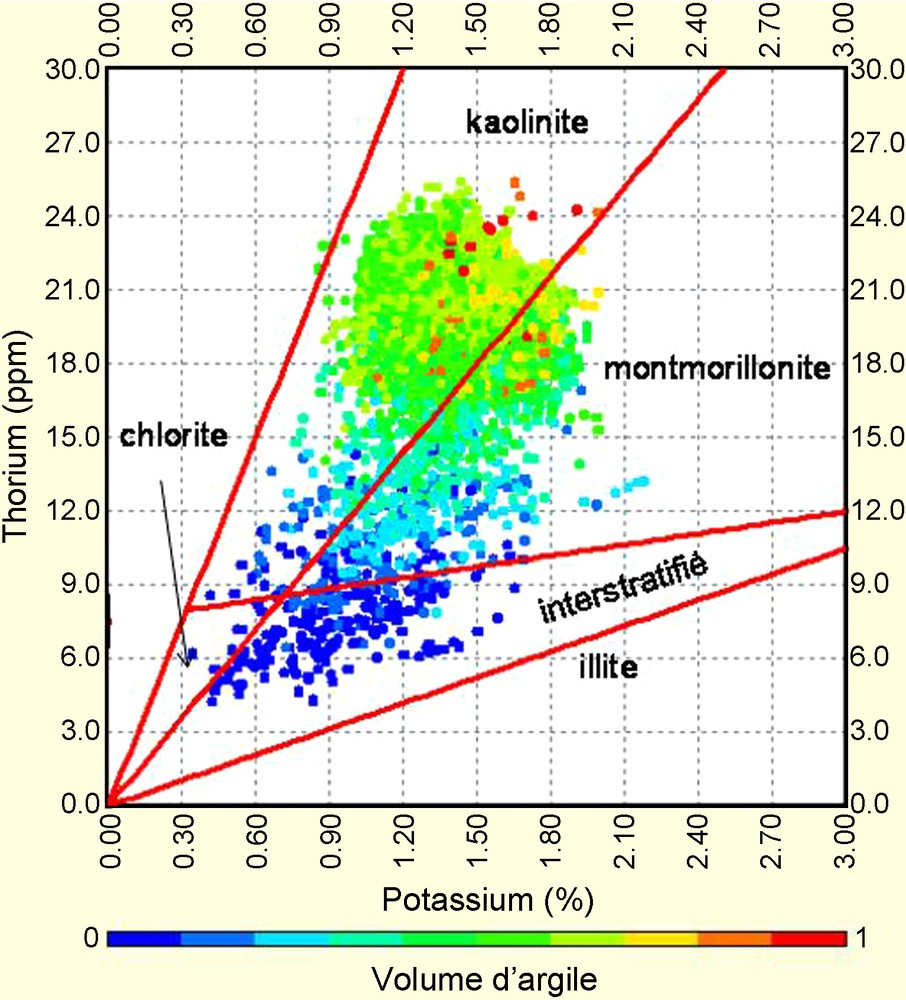
Diagramme thorium versus potassium pour la caractérisation minéralogique des argiles.
Fig. 4. Thorium versus potassium diagram in clays for clay-mineralogy definition.
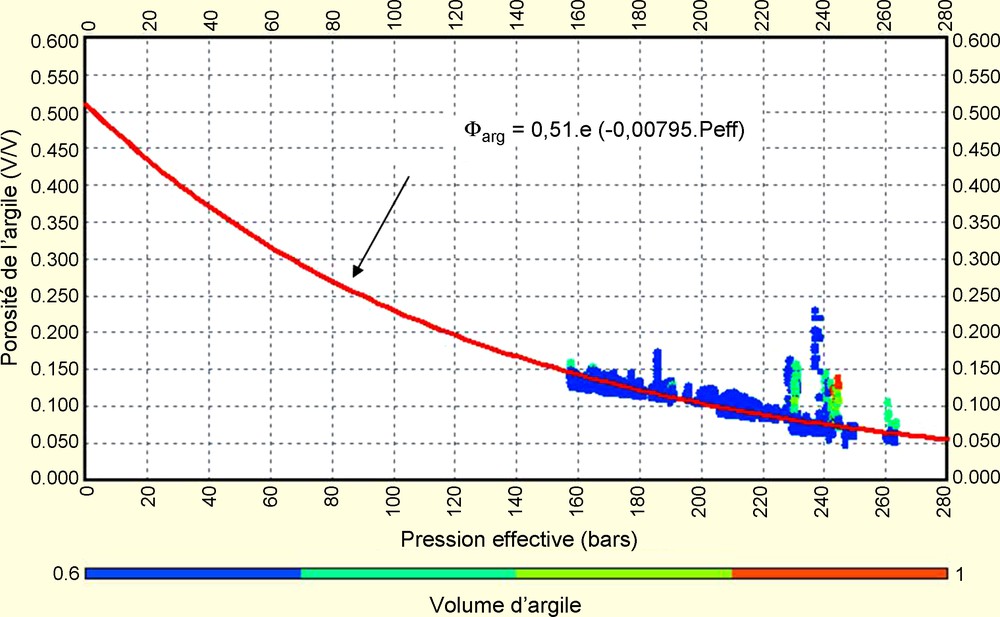
Évolution de la porosité de l’argile en fonction de la pression effective.
Fig. 5. Clay-porosity evolution in function of effective pressure.
P and S velocities calculation is realised with the process described in part 3. We will determine clay-elastic moduli with:
- • rock-petrophysical parameters from a classical log study;
- • clay-mineralogical parameters from XRD study and spectrometry gamma-ray tool results;
- • laws established and present in this paper. The results of modelling are presented in Fig. 6.
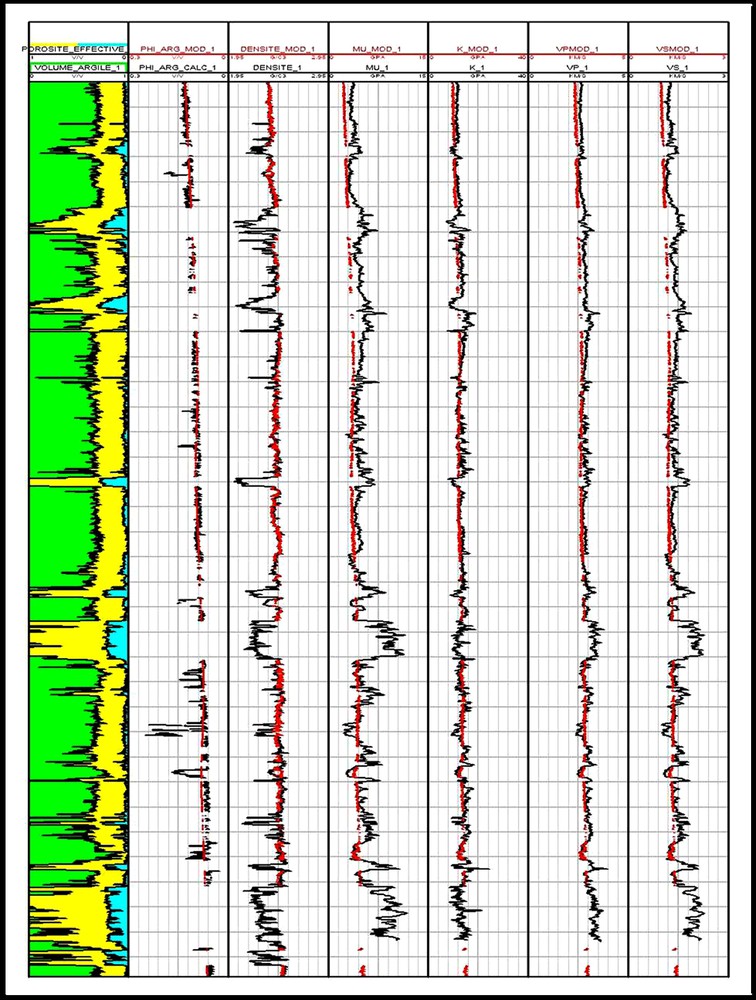
Résultats de la modélisation des vitesses P et S dans les sédiments argileux.
Fig. 6. P and S wave-propagation velocities modelling results in shales.
1 Introduction
La modélisation des propriétés élastiques des minéraux argileux présente un grand intérêt pour la caractérisation et la définition du comportement mécanique des formations sédimentaires argileuses. A ce jour, la compréhension de ce comportement reste mal connue, compte tenu de la diversité en terme de structure et de nature minérale des argiles, ainsi que de la grande complexité du matériel étudié. Elle demeure pour autant essentielle, attendu que les minéraux argileux sont présents dans la majorité des environnements sédimentaires et qu’ils influencent de manière non négligeable les propriétés physiques et mécaniques des roches auxquelles ils sont associés.
Il n’existe, à ce jour, que quelques modèles empiriques [2,4,5,10] et les limites proposées par Voigt et Reuss [8], d’une part et Hashin-Shtrikman [6], d’autre part, pour apprécier les modules élastiques des argiles et d’un mélange de minéraux argileux. Le comportement élastique des argiles est fortement dépendant de leur porosité et de la minéralogie. En estimant l’évolution de la porosité en fonction de la pression effective, pour chaque type d’argile, et en combinant l’évolution structurale associée à l’augmentation de pression, il est possible de modéliser le comportement élastique d’une formation argileuse en fonction des modules du minéral argileux proprement dit et de la pression.
Ainsi, l’article présente successivement, dans la Section 2, des considérations théoriques sur les modèles existants ; dans la Section 3 un nouveau modèle de comportement acoustique des formations argileuses et dans la Section 4 les résultats et discussions issus d’un cas d’application du modèle proposé.
2 Considérations théoriques
Pour prédire le module élastique effectif d’un mélange de grains et de pores, théoriquement, il est généralement nécessaire de préciser les fractions volumiques des différentes phases, les modules élastiques des différentes phases, ainsi que l’arrangement géométrique des phases les unes par rapport aux autres. En indiquant uniquement les fractions volumiques des constituants et leurs modules respectifs, il est au mieux possible de prédire les limites inférieures et supérieures du mélange. Quelle que soit la fraction volumique des constituants, le module effectif du mélange est compris entre ces limites. Cependant, la valeur précise du module effectif de ce mélange dépend de l’arrangement géométrique des constituants entre eux.
2.1 Limites de comportement élastique
La limite supérieure du module effectif d’un mélange de N phases est donnée par la formule de Voigt [8] :
| (1) |
La limite inférieure du module effectif d’un mélange de N phases est donnée par la formule de Reuss [8] :
| (2) |
La valeur du module effectif du mélange pourra être considérée comme la moyenne du module de Voigt MV et du module de Reuss MR. Cette moyenne est appelée moyenne de Hill et elle s’exprime sous la forme suivante :
| (3) |
Les limites, reconnues comme donnant les valeurs les plus proches des modules élastiques effectifs d’un mélange, sans apport d’information sur l’arrangement géométrique des constituants, sont les limites de Hashin-Shtrikman [6], définies par :
| (4) |
| (5) |
Les limites supérieures et inférieures sont obtenues en intervertissant les composants 1 et 2 (Fig. 1). De manière générale, la limite supérieure est obtenue quand la phase la plus résistante est le composant 1 et la limite inférieure quand la phase la plus résistante est le composant 2 (Fig. 1). L’écart entre les limites inférieure et supérieure dépend de la différence existant entre les constituants. Il est usuel, dans le cas d’un mélange considéré homogène, de représenter le module moyen du mélange comme la moyenne des limites supérieure et inférieure. Cela est couramment utilisé quand les caractéristiques des composants du mélange sont proches. En revanche, lorsque les constituants sont très différents l’un de l’autre, comme dans les mélanges minéral/fluide contenu dans les pores, le grand écart entre les limites ne permet pas de prédire avec une grande fiabilité les modules effectifs des mélanges. Dans le cas d’un sédiment argileux, la composition élémentaire du système est une matrice minérale argileuse et sa porosité (eau libre et eau liée), associée à un certain nombre d’autres constituants (quartz, minéraux lourds…) dispersés dans cette matrice. Afin de prédire l’évolution de la fraction volumique de chacune des phases, il est nécessaire de connaître la variation de la porosité de l’argile avec l’enfouissement et la variation de pression effective. On ne considèrera pas ici les transformations minéralogiques diagénétiques au sein de la matrice argileuse.
2.2 Évolution de la porosité des argiles en fonction de la pression effective
De nombreux auteurs ont observé un changement progressif dans la densité des shales avec l’enfouissement. Plusieurs modèles mathématiques assez différents ont été proposés pour décrire ces changements. Un modèle de décroissance exponentielle de la densité avec l’enfouissement, proposé par Athy [1] et démontré par Korvin [7] pour la compaction d’une séquence d’argiles pures, a été largement accepté :
| (6) |
| (7) |
À une profondeur z donnée, on peut écrire :
| (8) |
Korvin [7] prouve que dans une séquence normalement compactée, la densité de l’argile augmente exponentiellement avec la profondeur d’enfouissement, soit avec la pression, par une élimination systématique de l’eau contenue dans la porosité. En égalisant les deux équations (6) et (8), on obtient la relation suivante :
| (9) |
En exprimant la pression effective linéairement en fonction de l’enfouissement, on peut écrire :
| (10) |
On obtient :
| (11) |
Le paramètre α correspond à la porosité de l’argile quand la pression effective est nulle. Cette porosité est appelée porosité initiale et le paramètre α sera donc désormais nommé Φ0. L’équation (11) peut s’écrire sous la forme :
| (12) |
Le paramètre Φ0 est fonction de la nature minérale de l’argile. En effet, la porosité initiale d’une argile est fonction de la structure et de l’arrangement des minéraux constitutifs de cette argile. Chaque argile va donc avoir une porosité initiale caractéristique de sa minéralogie. Le coefficient β traduit, quant à lui, la rapidité de décroissance de la porosité avec l’augmentation de la pression effective et l’enfouissement.
2.3 Calcul de la porosité de l’argile à partir de l’outil diagraphique densité
L’outil diagraphique densité permet de connaître une mesure de la densité d’une formation sédimentaire argileuse traversée par un forage. La densité mesurée par l’outil traduit la moyenne des densités de chaque constituant, pondérée par leur fraction volumique.
| (13) |
Il est possible de décomposer la fraction argileuse en deux phases : une phase minérale et une phase poreuse. On exprime donc la densité de la fraction argileuse pondérée par le volume d’argile comme une fonction du volume d’argile, de la porosité de l’argile Φargile, de la densité du minéral argileux et de la densité de l’eau contenue dans la porosité.
| (14) |
En combinant les équations (12) et (13), il est possible d’exprimer la porosité de l’argile, en fonction des densités de la roche et de ses constituants et de sa composition volumique :
| (15) |
La mesure de la densité des formations argileuses est assez délicate et peut être affectée par la formation de cave dans les puits. L’utilisation de cette méthode nécessite donc l’utilisation de diagraphies de densité, corrigées des effets liés à l’environnement du trou de forage.
3 Considérations empiriques
Afin de modéliser la porosité de l’argile, il est nécessaire d’estimer les paramètres Φ0 et β de l’équation (12). L’évaluation des ces paramètres a été réalisée de manière empirique. Le détail de la détermination de ces paramètres est décrit ci-après.
3.1 Expression de la porosité initiale Φ0 de l’argile
La porosité initiale Φ0 a été déterminée pour trois types d’argiles (kaolinite, illite et montmorillonite), à partir des travaux menés en laboratoire par Chillingar and Knight [3] et des résultats de mesures de plusieurs études de sol. Les valeurs moyennes de Φ0 pour chaque type d’argile sont répertoriées dans le Tableau 1.
Les valeurs de porosité et de modules élastiques (exprimées en gigapascal), associées à trois types d’argiles pures (Montmorillonite, Illite, Kaolinite).
Table 1
Porosity values and elastic-moduli values related to three pure clays (Montmorillonite, Illite, Kaolinite).
| Minéral | Φ0 | Densité minéral | Kmin | γ | μmin |
| Kaolinite | 0,45 | 2,63 | 20 | 15 | 9,2 |
| Illite | 0,55 | 2,75 | 17,9 | 10 | 8,5 |
| Montmorillonite | 0,65 | 2,42 | 14,1 | 7 | 6,4 |
3.2 Expression du paramètre β
Le coefficient β peut être déterminé à partir des équations (12) et (15). Une étude de la variation du coefficient β a été réalisée sur 19 puits provenant de diverses régions du globe.
Le coefficient β a été déterminé par calage de la courbe définie par l’équation (12), sur un graphique représentant la porosité de l’argile déterminée à partir de l’équation (15), en fonction de la pression effective exprimée en bars pour chacun des 19 puits. La valeur de β, ainsi calculée, est comprise entre 0,007 et 0,0085.
La variation du coefficient β traduit la vitesse de décroissance de la porosité de l’argile avec l’augmentation de la pression effective ou de l’enfouissement et traduit donc la variation du régime de compaction des argiles dans les différents puits. Attendu que dans une argile, la dilatabilité du fluide dans la porosité est beaucoup plus grande que la dilatabilité de la matrice minérale, l’hypothèse retenue est la suivante : plus la température de la roche argileuse augmente rapidement avec l’enfouissement, plus l’élimination du fluide de la porosité se fait rapidement. Par voie de conséquence, la roche se compacte d’autant plus rapidement, que le gradient de température est grand.
La comparaison du coefficient β avec le gradient de température dans chaque puits a permis de relier la valeur de β au gradient de température GradT dans le puits sous la forme de l’équation linéaire suivante :
| (16) |
avec GradT exprimé en degré Celcius par 100 m (°C/100 m).
4 Résultats et discussions
Les formations argileuses sont constituées par des feuillets argileux associés sous forme de particules, elles-mêmes regroupées sous forme d’agrégats (Fig. 2a) [11]. La diminution de la porosité, associée à la compaction de l’argile, résulte d’une réorientation des agrégats suivant une direction perpendiculaire à la contrainte maximum. Les minéraux argileux sont d’abord mis en suspension dans l’eau, puis s’arrangent, au fur et à mesure, pour arborer une structure laminée (Fig. 2b) [9]. Le stade ultime de compaction tend à former un bloc minéral de porosité très réduite, au sein duquel l’anisotropie tend à disparaître.
4.1 Lois d’évolution des modules élastiques de l’argile en fonction de la pression
4.1.1 Module d’incompressibilité
Afin d’obtenir la loi d’évolution du module d’incompressibilité, on considère dans un premier temps, un milieu composé d’un fluide et de feuillets d’argile hydratés. La structure laminée de l’argile et l’alternance eau/argile dans les shales impliquent de considérer une formule de Reuss. On peut alors écrire :
| (17) |
| (18) |
En utilisant les équations (12), (16) et (18), on obtient donc :
| (19) |
4.1.2 Module de cisaillement
En considérant le même système, on exprime le module de cisaillement à partir du modèle de Voigt, compte tenu que la direction de cisaillement est perpendiculaire à la direction de propagation de l’onde S.
| (20) |
La valeur du module de cisaillement du fluide est nulle, attendu que l’onde S ne se propage pas dans les fluides. La valeur de module de Voigt est la valeur maximale théorique du module de cisaillement. Le module effectif est donc inférieur au module de Voigt. On exprime le module de cisaillement de l’argile en introduisant un coefficient γ, sous la forme :
| (21) |
Cette fonction est équivalente à la fonction :
| (22) |
L’onde S ne se propageant pas dans les fluides, la propagation de cette onde ne sera physiquement possible que s’il existe un contact entre les minéraux argileux ; donc si la porosité de l’argile est inférieure à la porosité Φ0.Si Φarg > Φ0, le module de cisaillement de l’argile est nul. Cette hypothèse est vérifiée en calculant le coefficient γ en fonction de la minéralogie. Le coefficient γ n’est calculé que pour μarg = 0,01 quand Φarg = Φ0. Les valeurs des coefficients γ pour chacune des trois argiles considérées (kaolinite, illite et montmorillonite) sont détaillées dans le Tableau 1.
| (23) |
4.2 Loi d’évolution des vitesses P et S de l’argile en fonction de la pression effective
À partir des modules Karg et μarg, modélisés pour chaque type minéral d’argile, il est possible de calculer les modules Karg et μarg d’un mélange de plusieurs argiles, en réalisant une moyenne de Hill des modules de chaque argile. Pour ce faire, il est nécessaire de connaître la composition volumique de la fraction argileuse.
| (24) |
| (25) |
L’argile ne se trouve jamais à l’état pur dans la nature et on la rencontre souvent associée à d’autres minéraux, tels que des grains de quartz ou des silts, dont la présence va jouer sur les vitesses. Il convient donc de prendre en compte ces minéraux dans le calcul de la vitesse. Le modèle qui semble le plus approprié est celui d’une matrice argileuse avec des minéraux flottants. Il convient également de tenir compte du résidu de porosité effective, aussi faible soit-il, associé à la présence des minéraux flottants. On utilise alors une moyenne harmoniques pour modéliser les minéraux flottants dans la matrice argileuse.
| (26) |
| (27) |
À partir de ces μ et K calculés, il est dès lors possible de calculer les vitesses des shales constitués par une formation majoritairement argileuse, au sein de laquelle on trouve d’autres minéraux qui flottent dans la matrice argileuse.
| (28) |
On considérera que le milieu est élastique et que l’équilibre des pressions est effectif dans la matrice argileuse lors du passage des ondes de compression et de cisaillement, de manière à pouvoir appliquer les deux formules ci-dessus.
4.3 Modules élastiques des minéraux argileux hydratés
Afin d’utiliser les lois préalablement établies, il convient de connaître les modules élastiques Kmin et μmin du minéral argileux hydraté, à savoir, le minéral argileux et son eau liée. Plusieurs études menées par Castagna et al. [2], Tosaya et al. [10], Vanorio et al. [12], et Wang [13] ont permis de déterminer les valeurs des modules élastiques de formations argileuses. En utilisant les résultats de ces études et des résultats de mesure en laboratoire à très haute pression où la porosité de l’argile tend vers le volume d’eau liée, on peut estimer les modules élastiques des minéraux argileux hydratés. Les valeurs recalculées à partir de ces différents travaux sont présentées dans le Tableau 1.
Les différentes valeurs de modules élastiques sont exprimées en gigapascal. Une représentation graphique des modules élastiques K et μ, pour chaque type d’argile, est présentée en Fig. 3. Le module K du fluide considéré est de 2,5 GPa.
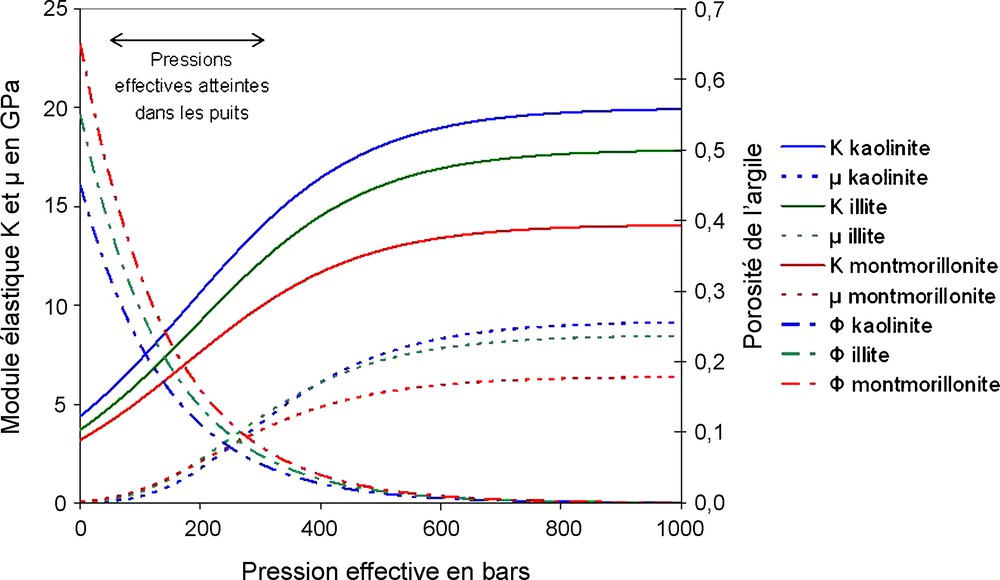
Évolution des modules élastiques K et μ des argiles en fonction de la pression effective.
Fig. 3. Evolution of argillaceous-elastic moduli K and μ versus effective pressure.
4.4 Incertitudes liées au modèle
Le modèle développé dans cette étude fait appel à plusieurs hypothèses et à plusieurs variables. Ces dernières sont source d’incertitudes sur les résultats de la modélisation. Il est possible de regrouper les incertitudes de ce modèle sous trois grands types :
- • l’utilisation de résultats d’interprétation quantitative des diagraphies conventionnelles dans le modèle et les incertitudes liées au calcul des volumes des différentes fractions élémentaires dans le puits (argile, sable, porosité) ;
- • les incertitudes liées aux paramètres empiriques utilisés dans le modèle ;
- • enfin, l’adéquation entre les hypothèses structurales et la réalité structurale des argiles dans le puits.
Le premier type d’incertitude concerne les volumes des différentes fractions argile, sable et porosité dans le puits. Le modèle d’estimation quantitative utilise une matrice biminérale (argile/sable). La fraction argileuse est généralement déterminée à partir des diagraphies Gamma Ray et Neutron/Densité. Le calcul du volume est basé sur l’hypothèse que les zones les plus argileuses contiennent 75 % de minéraux argileux et 25 % de sable. Le modèle biminéral ne tient pas compte de la présence d’autres minéraux lourds ou de carbonates, ce qui induit une incertitude sur le calcul du volume d’argile VCL.
Le deuxième type d’incertitude concerne les paramètres utilisés pour l’estimation de la porosité de l’argile Φ0 et β.
Ces paramètres sont estimés à partir d’une méthode empirique. Dix-neuf puits ont été utilisés de manière à réduire statistiquement l’erreur, mais une incertitude demeure sur ces paramètres. En ce qui concerne le paramètre Φ0, ce paramètre va principalement jouer sur l’estimation de la porosité des argiles à faible enfouissement. C’est dans cette zone que l’on trouve le plus de dispersion dans les porosités d’argiles. La dispersion de la porosité des argiles est nettement plus réduite lorsque la pression effective augmente et donc l’impact direct de la porosité initiale sera de moins en moins fort avec l’enfouissement. Le nombre d’études et le nombre d’enregistrements à très faible enfouissement étant réduits, il est difficile de réduire statistiquement l’incertitude sur ce paramètre.
De la même manière, le paramètre β va avoir une influence importante sur les zones de faible enfouissement, puisque c’est ce paramètre qui guide la vitesse de décroissance. Ce paramètre est contrôlé par une hypothèse forte qui est que, plus la température augmente rapidement, plus la décroissance de porosité de l’argile est rapide. Cette hypothèse est directement coordonnée à une autre hypothèse qui est que les gradients de température mesurés dans les puits, qui ont servi au calage du paramètre β, ont un gradient de température qui ne se trouve pas perturbé par des mouvements verticaux des couches dans le temps (surenfouissemment/désenfouissement) ou par la présence de sources de chaleur extérieure nouvelle (remontée de diapir de sels…).
L’influence conjointe des paramètres Φ0 et β est non négligeable et elle est responsable de deux types d’erreur facilement identifiable, un léger shift général de la courbe de porosité modélisée par rapport aux valeurs calculées à partir de la densité (paramètre Φ0), ou une déviation progressive des courbes modélisées dans les faibles enfouissements, due à l’incertitude sur le coefficient β.
Le troisième type d’incertitude concerne les hypothèses structurales sur la réorientation des feuillets argileux, en fonction des directions des contraintes et de déformations maximums, à partir des formules de Voigt et de Reuss. Cette hypothèse repose sur la propagation de l’onde dans la formation et le trajet préférentiel de l’onde, ainsi que sur les directions préférentielles de cisaillement et de compression. Une incertitude est liée à cette hypothèse, à savoir, que toutes les argiles n’arborent pas obligatoirement la structure en paillettes qui se réorientent régulièrement, même si cela reste le comportement général. Par conséquent, l’évolution des modules d’incompressibilité et de cisaillement peut légèrement varier par rapport au modèle général proposé.
5 Exemple de reconstruction des vitesses P et S dans les sédiments argileux
5.1 Utilisation des outils Gamma Ray spectraux pour apprécier la nature minérale de l’argile
Pour obtenir la bonne loi d’évolution des modules, il est essentiel de connaître ou, du moins, d’avoir une bonne approche de la nature minérale de l’argile à une profondeur donnée. La détermination de la nature de l’argile peut se faire suivant deux méthodes, soit par des mesures de diffraction des rayons X (DRX) sur échantillons, soit en utilisant les résultats de mesure des radioactivités naturelles spectrales. La première méthode présente l’avantage d’être fiable mais très onéreuse, compte tenu de l’échantillonnage conséquent à réaliser pour avoir une connaissance multiminérale de l’argile sur un puits. La seconde méthode, diagraphique, permet, quant à elle, d’avoir une vision globale sur un puits, mais est nettement moins précise que les mesures DRX. Elle ne permet d’avoir qu’une idée de la nature minérale de l’argile dominante au point de mesure. Nous utiliserons pour modéliser la nature de l’argile, les résultats des mesures de spectrométrie, validés au préalable par les mesures de DRX sur échantillon. Les résultats de cette interprétation sont présentés dans la Fig. 4 et dans le Tableau 2.
Résultats de diffraction X sur six échantillons.
Table 2
X-ray diffraction results on six samples.
| Échantillon | Minéraux détritiques (%) | Kaolinite (%) | Illite (%) | Smectite (%) | Pourcentage d’argile dans l’échantillon |
| A | 33,6 | 42,8 | 10,4 | 13,2 | 66,4 |
| B | 38,7 | 37,1 | 11,1 | 13,0 | 61,3 |
| C | 27,4 | 43,4 | 14,8 | 14,5 | 72,6 |
| D | 37,8 | 37,4 | 13,9 | 10,9 | 62,2 |
| E | 33,2 | 41,4 | 11,1 | 14,3 | 66,8 |
| F | 31,2 | 40,6 | 13,2 | 15,0 | 68,8 |
À partir des résultats des mesures de DRX et des mesures spectrales de radioactivité, on considère donc que les formations argileuses sont constituées par les trois fractions minérales suivantes (kaolinite 60 %, illite 20 % et montmorillonite 20 %).
5.2 Modélisation des vitesses en intégrant la minéralogie
Le calcul des vitesses P et S des ondes de compression et de cisaillement est réalisé à partir du processus présenté dans les parties 3.1 et 3.2. On calcule, dans un premier temps, les modules élastiques de l’argile à partir :
- • des paramètres pétrophysiques de la roche déterminés par une étude des diagraphies conventionnelles (Gamma Ray, neutron, densité…) ;
- • des paramètres minéralogiques de l’argile, déterminés à partir des résultats de spectrométrie de radioactivité naturelle et validés par mesure DRX ;
- • des lois établies et présentées dans cet article (porosité de l’argile : on recalcule une porosité initiale moyenne en fonction de la composition minéralogique de 0,51 – le gradient de température dans le puits est de 3,95 °C/100 m – Fig. 5)
Les résultats de la modélisation sont présentés en Fig. 6. Les zones modélisées correspondent aux niveaux où le volume d’argile est supérieur à 0,6 pour former une structure avec des minéraux flottants dans une matrice argileuse.
6 Conclusions
Les méthodes présentées dans cet article permettent de modéliser avec une bonne fiabilité les vitesses de propagation des ondes acoustiques P et S dans les sédiments argileux. Les résultats de la modélisation présentés en Fig. 6, montrent que dans les continuums argileux, les vitesses modélisées sont proches des vitesses mesurées par les outils soniques en forage. Il existe cependant des secteurs où la méthode ne permet pas de concilier les vitesses modélisées et les vitesses mesurées. Ces erreurs de modélisation proviennent de trois sources. La première raison est qu’il peut y avoir des erreurs d’interprétation des diagraphies courantes. En effet, l’essentiel de la méthode repose sur une interprétation quantitative des diagraphies conventionnelles. Cette interprétation ne fait pas intervenir les résultats des mesures de lenteur des ondes acoustiques. Or les zones mal reconstruites se situent toujours dans des niveaux où la densité de la roche chute, sans que, pour autant, l’interprétation quantitative en tienne compte par des variations de volume des différentes phases. La deuxième raison est que certaines zones se situent face à des zones cavées dans le puits, détectées par l’outil diamétreur, qui peuvent expliquer une mauvaise lecture des outils. La troisième raison provient de la modélisation à part entière, à savoir que la modélisation de Φargile, à partir de l’outil densité, et la mise en équation de cette porosité en fonction de la pression effective, peut induire de la perte d’information ou être biaisées sur des zones réduites, qui ne sont pas compactées de manière analogue. L’intérêt premier de cette méthode est de modéliser les vitesses P et S dans les sédiments argileux, en cas d’absence de mesure. Par ailleurs, un second intérêt de la méthode réside dans l’inversion du processus de calcul des vitesses. Cette inversion permet d’avoir une bonne estimation de la pression effective dans les zones de continuums argileux. La notion de pression effective dans les argiles n’est pas évidente à définir, compte tenu du fait que la pression fluide y est difficile à mesurer dans les puits. De plus, via les données de pression, cette modélisation fournit un outil pour la détection des régimes de compaction et des zones en surpression.


