1. Introduction
The chemical and isotopic effects of evaporation from molten silicates, and their cosmochemical consequences, have been widely studied under nebular conditions [Davis et al. 1990; Hashimoto 1990; Tissandier et al. 2002; Tsuchiyama et al. 1999; Yu et al. 2003]. Under these conditions where the total gas pressure is extremely low (<10−4 bar), vacuum or near-vacuum evaporation experiments are pertinent, because the conditions are applicable to numerous cosmochemical processes taking place in the early stages of the evolution of the solar nebula [Mendybaev et al. 2021; Richter et al. 2002].
As planetary accretion proceeds and primitive condensates agglomerate to form larger bodies, gravity enables them to retain an atmosphere [Massol et al. 2016], whether captured from the nebula [Olson and Sharp 2019] or more likely generated by the molten body’s (magma ocean) evaporation itself [Young et al. 2019]. The evaporation rate of a species i from a spherical surface of radius r is quantitatively described by the Hertz–Knudsen–Langmuir (HKL) equation,
| (1) |

(a) Detailed view of the conical nozzle in the custom-built gas-mixing aerodynamic levitation laser furnace (ALLF) at IPGP (Paris, France) used in these experiments. The inset is a closeup view inside the nozzle, showing the molten spherical sample levitating in the gas stream. (b) and (c) Imaging of the evaporative (SiO and Mg gases) trail mimics that of a burning incense stick; the gas stream starts laminar around the sample inside the nozzle, and turns turbulent as it lifts away, due to the increasing Reynolds number. Masquer
(a) Detailed view of the conical nozzle in the custom-built gas-mixing aerodynamic levitation laser furnace (ALLF) at IPGP (Paris, France) used in these experiments. The inset is a closeup view inside the nozzle, showing the molten spherical sample levitating in ... Lire la suite
2. Experimental setup
The ALLF is a contactless furnace where samples are heated and melted by an infrared CO2 laser, and float in a conical nozzle where they are supported by a gas stream flowing vertically (upwards) from underneath, so as to counteract gravity [Hennet et al. 2011]. Gas compositions can be changed by mixing (using multiple gas flow controllers) H2, CO2, and Ar gases, so as to allow variation in the oxygen fugacity of the surrounding gas. Some key advantages of this furnace are (i) the capability to perform contactless melting experiments, eliminating contamination from container materials, (ii) the production of homogeneous glassy samples resulting from a combination of ultrafast quenching rates (on the order of 1000 °C/s) and the absence of nucleation sites for crystals in a levitating spherical sample, and (iii) the ability to reach very high temperatures, in excess of 3000 °C (Figure 2).
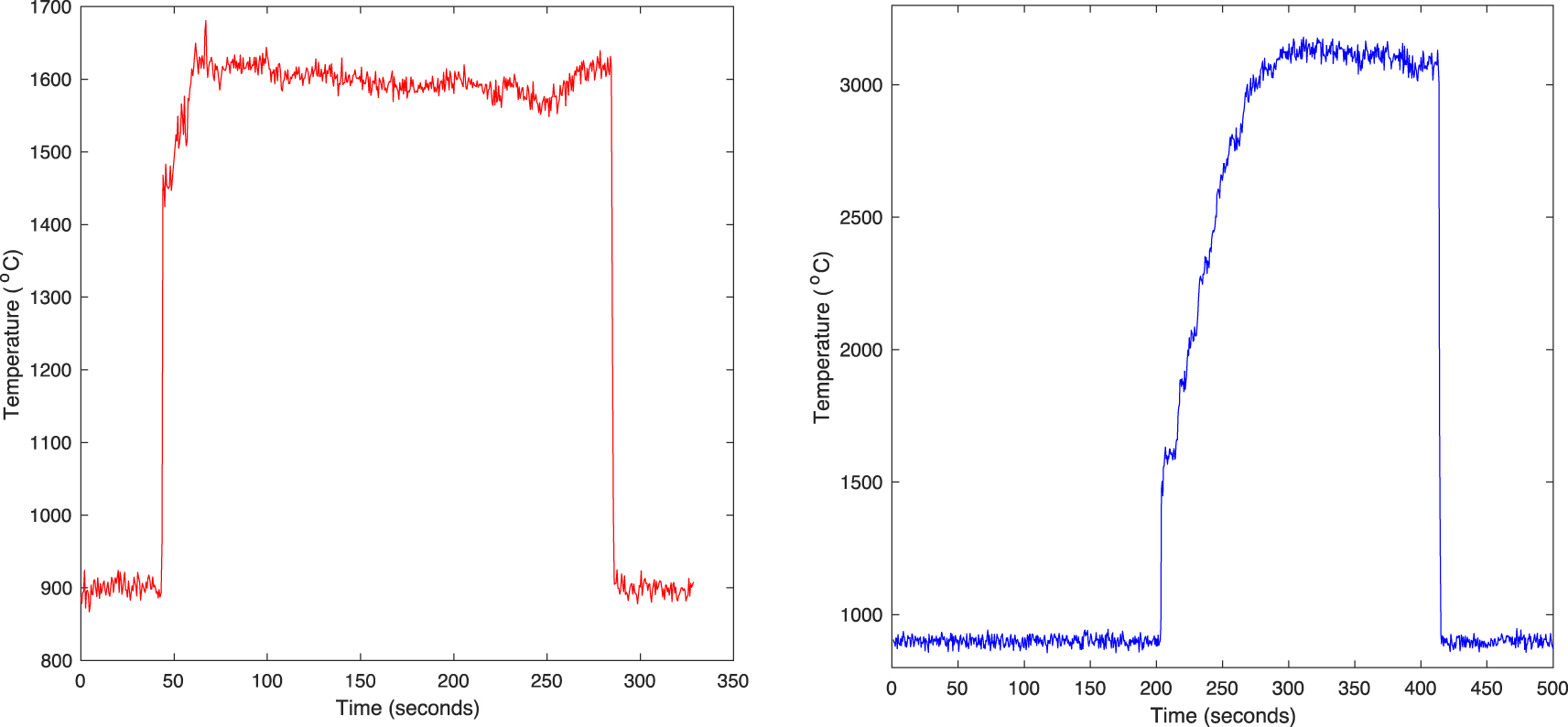
(Left) Typical heating runs (temperature versus time) of samples produced for this paper (shown here is that of sample VP4, Table 1). Note that the pyrometer only measures temperatures above 900 °C, and returns a baseline of 900 °C below that. (Right) The same starting composition, stably heated to 3100 °C for over 120 s demonstrating the temperature capability of the furnace.
The high velocity of the gas stream that levitates the sample gives rise to an advective hydrodynamical regime relative to the ones found in vacuum and 1-atm furnaces. In our experiments, the gas flow is in the range of 800–1000 sccm (14–18 cm3/s) through a 1.5 mm diameter hole in the nozzle, yielding an advective velocity on the order of 8–10 m/s. These values of gas advection provide the force to counter gravity and levitate the sample; stable levitation is achieved when the upwards drag force of the gas on the spherical sample exactly counters the downwards gravitational pull, Fdrag = Fgrav. For a gas with specific mass 𝜌gas at a velocity U, the force on a sphere of radius r is Fdrag = Cx((1∕2)𝜌gas U2)πr2 where Cx is the drag coefficient. The gravitational force on a melt of density 𝜌melt and radius r is Fgrav = ((4∕3)πr3)𝜌melt g, where g = 9.8 m/s2 is Earth’s gravity. Therefore, when stable levitation is achieved the gas velocity is given by:
| (2) |
Elemental and isotopic composition of the evaporated samples from this study (top) in the levitation furnace, along with the elemental data from evaporated samples in a vacuum furnace [Richter et al. 2007] carried out on the same starting melt composition (B-type CAI) and at the same temperature (1873 K)
| This study | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | MgO (wt%) | SiO2 (wt%) | Al2O3 (wt%) | CaO (wt%) | MgO/Al2O3 | SiO2/Al2O3 | f(Mg) | f(Si) | d26Mg-BHVO-2G ‰ | 2se ‰ | d25Mg-BHVO-2G ‰ | 2se ‰ | d30Si-BHVO-2G ‰ | 2se ‰ | d29Si-BHVO-2G ‰ | 2se ‰ |
| Starting | 12 | 46 | 19 | 23 | 0.6316 | 2.4211 | ||||||||||
| VP1 | 11.61 | 37.62 | 22.99 | 27.78 | 0.5050 | 1.6364 | 0.800 | 0.676 | −3.78 | 0.19 | −1.98 | 0.12 | −1.73 | 0.04 | −0.78 | 0.02 |
| VP2 | 12.05 | 40.03 | 21.74 | 26.18 | 0.5543 | 1.8413 | 0.878 | 0.761 | −4.39 | 0.21 | −2.29 | 0.12 | −2.63 | 0.17 | −1.27 | 0.08 |
| VP3 | 11.9 | 41.45 | 21.16 | 25.49 | 0.5624 | 1.9589 | 0.890 | 0.809 | −4.80 | 0.22 | −2.49 | 0.14 | −2.68 | 0.31 | −1.17 | 0.30 |
| VP4 | 11.94 | 41.68 | 21.08 | 25.31 | 0.5664 | 1.9772 | 0.897 | 0.817 | −4.62 | 0.22 | −2.40 | 0.13 | −2.79 | 0.07 | −1.33 | 0.05 |
| VP5 | 11.9 | 39.08 | 22.25 | 26.77 | 0.5348 | 1.7564 | 0.847 | 0.725 | −4.22 | 0.28 | −2.19 | 0.15 | −2.26 | 0.28 | −0.97 | 0.26 |
| VP6 | 10.77 | 34.81 | 24.51 | 29.92 | 0.4394 | 1.4202 | 0.696 | 0.587 | −2.27 | 0.14 | −1.15 | 0.10 | −1.04 | 0.11 | −0.40 | 0.06 |
| Richter et al. [2007] | ||||||||||||||||
| Sample | MgO (wt%) | SiO2 (wt%) | Al2O3 (wt%) | CaO (wt%) | MgO/Al2O3 | SiO2/Al2O3 | ||||||||||
| R2-13 | 4.55 | 29.40 | 30.21 | 35.84 | 0.1506 | 0.9732 | ||||||||||
| R2-15 | 5.24 | 30.16 | 29.53 | 35.11 | 0.1774 | 1.0213 | ||||||||||
| R2-14 | 0.04 | 20.86 | 36.10 | 43.00 | 0.0011 | 0.5778 | ||||||||||
| R2-9 | 0.02 | 16.29 | 39.28 | 44.41 | 0.0005 | 0.4147 | ||||||||||
| R2-8 | 0.03 | 8.54 | 45.21 | 46.22 | 0.0007 | 0.1889 | ||||||||||
| R3-2 | 12.22 | 46.36 | 19.31 | 22.11 | 0.6328 | 2.4008 | ||||||||||
| R3-1 | 9.62 | 33.93 | 26.24 | 30.21 | 0.3666 | 1.2931 | ||||||||||
| R3-20 | 6.43 | 31.01 | 29.11 | 33.45 | 0.2209 | 1.0653 | ||||||||||
| R3-21 | 9.44 | 33.69 | 26.32 | 30.54 | 0.3587 | 1.2800 | ||||||||||
| R3-4 | 4.60 | 30.84 | 30.20 | 34.36 | 0.1523 | 1.0212 | ||||||||||
| R3-7 | 0.20 | 22.40 | 36.01 | 41.39 | 0.0056 | 0.6220 | ||||||||||
| R3-19 | 6.70 | 31.34 | 28.86 | 33.11 | 0.2322 | 1.0859 | ||||||||||
| R3-18 | 4.34 | 29.39 | 30.81 | 35.46 | 0.1409 | 0.9539 | ||||||||||
| R3-8 | 1.65 | 26.73 | 33.21 | 38.40 | 0.0497 | 0.8049 | ||||||||||
| R3-5 | 0.12 | 17.74 | 38.36 | 43.78 | 0.0031 | 0.4625 | ||||||||||
The Reynolds number characterising the flow around a sphere is:
| (3) |
The relative magnitude of the two transport mechanisms, chemical diffusion and advection, in stripping the evaporating species away from the evaporation surface can be evaluated by the nondimensional Péclet (Pe) number (dimensionless ratio of advection/diffusion), which is the product of the Reynolds number (Re, inertia/viscosity) and the Schmidt (Sc, viscosity/diffusion) number:
| (4) |
| (5) |
These terms are combined in the Sherwood number (Sh), which is the ratio of mass transfer by convection to diffusion (the mass transfer equivalent of the Nusselt number for heat), and is defined as:
| (6) |
| (7) |
3. Experiments and analyses
A B-type CAI composition (Table 1) powder mix (identical to the one used in Knight et al. [2009] and Richter et al. [2007]) was made by mixing and milling high purity powders (SiO2, MgO, Al2O3, CaCO3), firing them at 900 °C overnight, and pressing them to a pellet. At first, six 15-mg chunks of the pellet were loaded in the conical nozzle of the ALLF, and fused at 1600 °C using pure O2 levitating gas for 30 s, to ensure full melting and homogenisation. Oxygen was used in this preliminary step so as to minimise the evaporation of Si and Mg, which have a very low evaporation rate at that temperature in an oxidising gas [Sossi et al. 2019]. The samples were then rapidly quenched to spherical glass samples ( ∼2 mm diameter) with a cooling rate of 850 °C/s. These six identical samples were then fused a second time at 1600 °C, using an Ar–CO2–H2 gas mixture, with a fixed molar ratio of 92% Ar, 1.6% CO2, and 6.4% H2. At 1873 K, the oxygen fugacity of that mixture is logfO2 = −9.1, corresponding to 0.5 log unit below the iron–wüstite buffer ( logfO2 = −8.6). The samples were evaporated for durations varying between 180 and 900 s, with a typical thermal history shown in Figure 2. The samples were once again rapidly quenched to glass by shutting down laser power.
The samples were then cut in two halves using a diamond saw, mounted in epoxy, diamond-polished on the flat (equatorial) side, and imaged and chemically analysed using a Zeiss Auriga 40 field-emission gun scanning electron microscope (SEM) equipped with a windowless Bruker Quantax XFlash EDX detector. Inspection using back-scattered electron imaging (Figure 3) confirmed that the samples were glassy and homogeneous at all scales, with no sign of crystal nucleation. Quantitative elemental analyses were performed by standardised EDX using the K-lines of Mg, Si, Ca, and Al (which with oxygen, are the only elements in our synthetic sample); large window scans, line scans, and point analyses again confirmed chemical homogeneity at all scales (millimetric to sub-micron). The compositions of the six evaporated samples are reported in Table 1.

Back-scattered SEM image of run VP6; the spherical sample was cut in half and polished on the flat (equatorial) side prior to being imaged and compositionally analysed on the SEM.
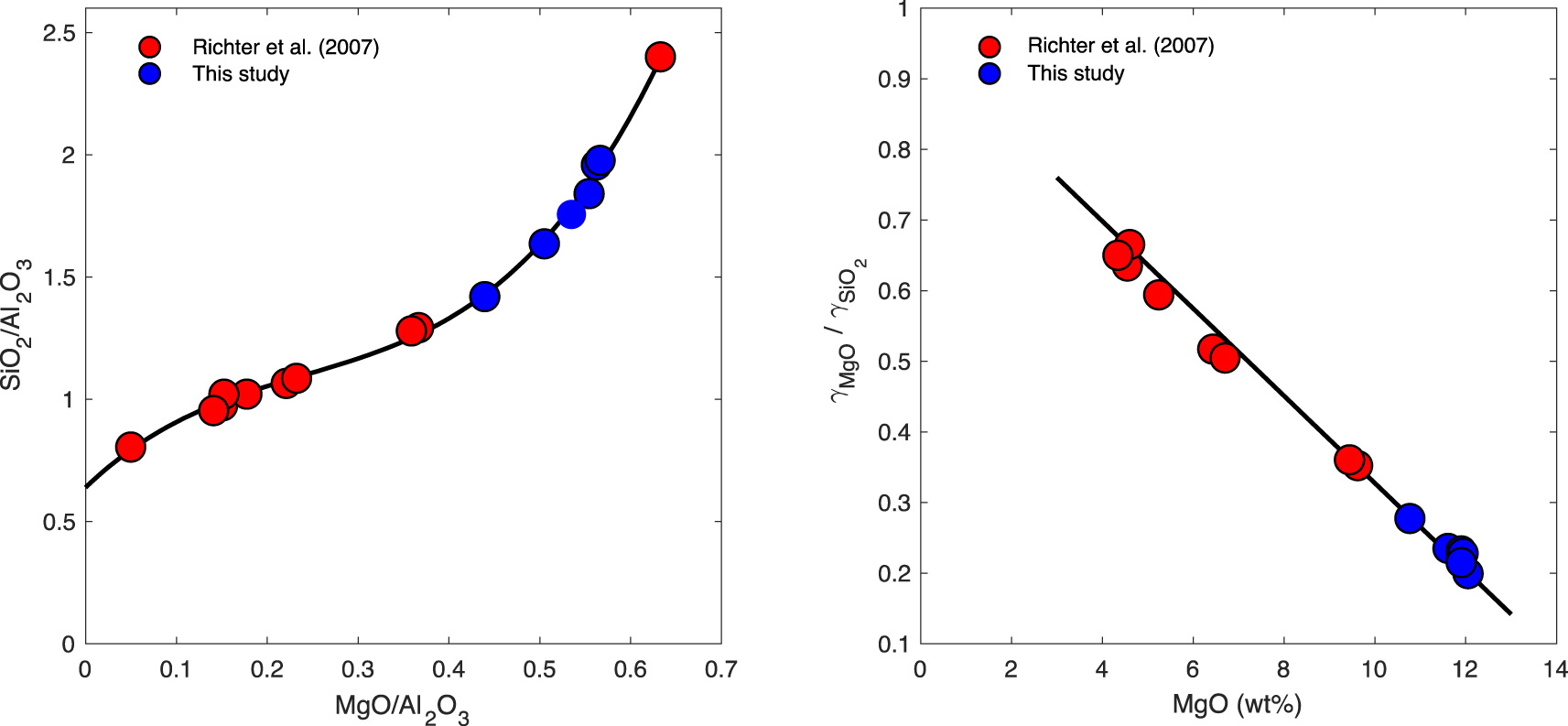
(Left) Compositional evolution of the evaporating melt (Si and Mg). Our data (blue circles) were plotted alongside the data (red circles) from Richter et al. [2007] that were gathered on the same melt composition and at the same temperature, albeit in a different evaporative regime (vacuum evaporation versus 1-atm evaporation in an advective flow). The path is identical, and the black curve fitting the evaporative path was fitted only to the Richter et al. [2007] data, illustrating the remarkable agreement with our data. This is expected, due to the fact that MgO and SiO2 evaporation have the same dependence on the composition of surrounding gas (i.e. fO2), see main text. The uncertainties on the analytical data are on the order of symbol size. (Right) The ratio of activity coefficients of evaporating components (MgO and SiO2) in the melt, plotted as a function of residual melt composition. Masquer
(Left) Compositional evolution of the evaporating melt (Si and Mg). Our data (blue circles) were plotted alongside the data (red circles) from Richter et al. [2007] that were gathered on the same melt composition and at the same temperature, albeit ... Lire la suite
The Mg and Si isotopic compositions of the evaporated glasses were measured [Deng et al. 2021] by laser ablation multi-collector inductively-coupled-plasma mass spectrometry (MC-ICP-MS) combining a 193-nm ultra-short ATLEX 300si excimer laser system with a Thermo-Scientific NeptunePlus at IPGP (Paris, France). To monitor matrix-induced Mg and Si isotopic effects, four CaO–Al2O3–MgO–SiO2 (CMAS) glasses were synthesised from the starting powders of the evaporation experiments, and were analysed along with the evaporated glasses and two other glasses (BCR-2G and TB-1G). To correct for instrumental fractionation, a basaltic glass BHVO-2G was analysed after every three or four analyses of the samples. The measurements were carried out with an ablation spot size of 110 μm, a repetition rate of 4 Hz and a He gas flow rate of 1.2 L/min. The typical laser fluence was 4.05 J/cm2, and each ablation spot contained 400 laser burst shots. The washout time was 10 s after the end of ablation, and the pause time after each ablation spot was 60 s. The mass spectrometer was operated in medium mass resolution mode (M∕𝛥M ≈ 5000), which is sufficient to resolve the major isobaric inferences from 12C14N+ on 26Mg+, and from 14N16O+ on 30Si+. For Mg isotopes, the measurements were conducted on the lower masses of the 24Mg+ (L3-F), 25Mg+ (C-F) and 26Mg+ (H2-F) peaks to avoid 12C14N+. As this cup configuration and resolution cannot prevent the interference of 48Ca2+ on 24Mg+, the central mass was moved from 25 to 23 a.m.u. to simultaneously measure the intensities of 44Ca2+ (mass 22, L4-F) and 24Mg+ (mass 24, H2-F), which were used afterwards to correct for the 48Ca2+ interferences. Since all the analysed materials are terrestrial, mass-independent effects on the raw Mg isotopic ratios can only arise from 48Ca2+ interferences on 24Mg+. This allows for precise determination of the instrumental 44Ca2+/48Ca2+ ratio (10.25 ± 0.37) and thus a reliable correction of 48Ca2+ interferences. For Si isotopes, the measurements were carried out on the lower masses of 28Si+ (L3-F), 29Si+ (C-F) and 30Si+ (H3-F) peaks to avoid 14N16O+ interferences. Using these instrumental settings, each laser ablation spot measurement consists of 13 cycles with an integration time of 4 s per cycle for Mg isotope analyses, whereas 21 cycles with the same integration time were used for Si isotope measurements. Data reduction was carried out by integrating these cycles excluding the transient cycles with intensity varying more than 25% from the plateau intensity at the start or the end of ablation. The background subtraction was conducted after a polynomial fit to the background cycles before ablation. The Mg and Si isotopic data of the evaporated glasses and the other glasses are given in Table 1, in per mil notation (‰) relative to the bracketing standard BHVO-2G.
4. Results and discussion
4.1. Elemental fractionation
The chemical homogeneity of Mg and Si observed for all samples indicates that diffusion of these elements though the melt to the surface did not inhibit their ability to evaporate. The elemental composition (MgO and SiO2) of the evaporated samples is plotted in Figure 4, alongside those from the study of Richter et al. [2007] which were performed on the same melt composition and at the same temperature, but under vacuum conditions (i.e. in a diffusive evaporative regime versus an advective evaporative regime for the levitation runs). This shows that the compositional evolution follows the same path, regardless of the difference in pressure and therefore evaporation regime. Both MgO and SiO2 concentrations are normalised to Al2O3 concentration, a component that does not readily evaporate, so as to correctly describe their evaporation from the melt. The standard method consists of plotting MgO and SiO2 mass loss, which requires measurement of the total mass of the glass samples, both before and after evaporation. With masses in the 10-mg range and mass losses in the sub-mg range, the uncertainties on these measurements are so large, if at all resolvable, that they disqualify the use of this method.
The noteworthy consistency of the evaporation trends observed in vacuum experiments and those presented herein is due to the fact that both Mg and Si evaporate with the same change in speciation between liquid and vapour phase (i.e., two electrons are exchanged). Therefore their relative partial pressures are independent of that of oxygen (fO2) around them. This is best expressed by the equilibrium constants of the evaporation reactions; with Mg and SiO the dominant gas species at the (P, T, fO2) conditions of the experiments, the evaporation reactions of MgO and SiO2 from the melt are (liquid species on the left, gas species on the right):
| (8) |
| (9) |
| (10) |
| (11) |
The residual silicon and magnesium content of the melt can be obtained by integrating the evaporation flux (Equation (1)) over time [Sossi et al. 2020], and is given by:
| (12) |
| (13) |
In principle, the evaporation constant 𝛼ec could be different for MgO and SiO2, and has indeed been shown to vary if evaporation were to take place from the solid state (such as from forsterite, e.g., [Wang et al. 1999]); but experiments and theory have shown that 𝛼ec during evaporation from liquids is indistinguishable from unity (see [Burns 1966; Shornikov 2015; Sossi et al. 2019], and references therein). Integrating the HKL equation to yield (12) and (13) assumes that all the terms inside the exponential are constant during evaporation. This is not formally true for activity coefficients and molar volume which depend on composition, nor for sample radii that decrease with evaporation. Using the integrated equations as shown here assumes that any changes occurring during evaporation are sufficiently smooth or vary slowly enough to justify brute-force integration. This is clearly the case during evaporation of minor components or trace elements for which the equation was developed [Sossi et al. 2019], but we stress that these equations should be used with great caution when considering the evaporation of major components in the melt.
The relative depletion (by evaporation) of Si and Mg from the sample is then described by the ratio:
| (14) |
Note that (14) is only formally correct in the ideal case where the evaporating species does not interact with the melt and is instantly removed from the surface (i.e. kinetic theory). In a realistic system, a gaseous boundary layer builds up around the sample, limiting the evaporating flux by chemical diffusion. This introduces a scaling factor to (Equations (12)–(14)), a function of the pressure saturation factor [Sossi et al. 2020; Young et al. 2019], and (14) becomes:
| (15) |
Equation (14) (or (15)) can be inverted to express the activity coefficients of the components evaporating from the melt as a function of measurable parameters, hence allowing a direct measure of these activity coefficients in temperature ranges that are unreachable using standard furnaces. Equation (14) becomes:
| (16) |
4.2. Isotopic fractionation
Isotopic analysis (Si and Mg isotopes) of the samples show that they are fractionated, following a mass-dependent fractionation law, as seen on three-isotope plots (Figure 5). Our experimentally derived slope for magnesium (𝛿 25Mg–𝛿 26Mg) is 0.531 ± 0.006 and that for silicon (𝛿 29Si–𝛿 30Si) is 0.522 ± 0.16. These values are consistent, within uncertainties, with the theoretically expected slopes for equilibrium and kinetic fractionation lines [Young et al. 2002], given by ((1∕m1) − (1∕m2))∕((1∕m1) − (1∕m3)) and (lnm1 −lnm2)∕(lnm1 −lnm3), respectively. With Mg being the predominant gas species for magnesium evaporation, the theoretical equilibrium slope is 0.520 and the theoretical kinetic slope is 0.510. For silicon, with SiO as the predominant gas species, the theoretical equilibrium slope is 0.511 and the theoretical kinetic slope is 0.506.
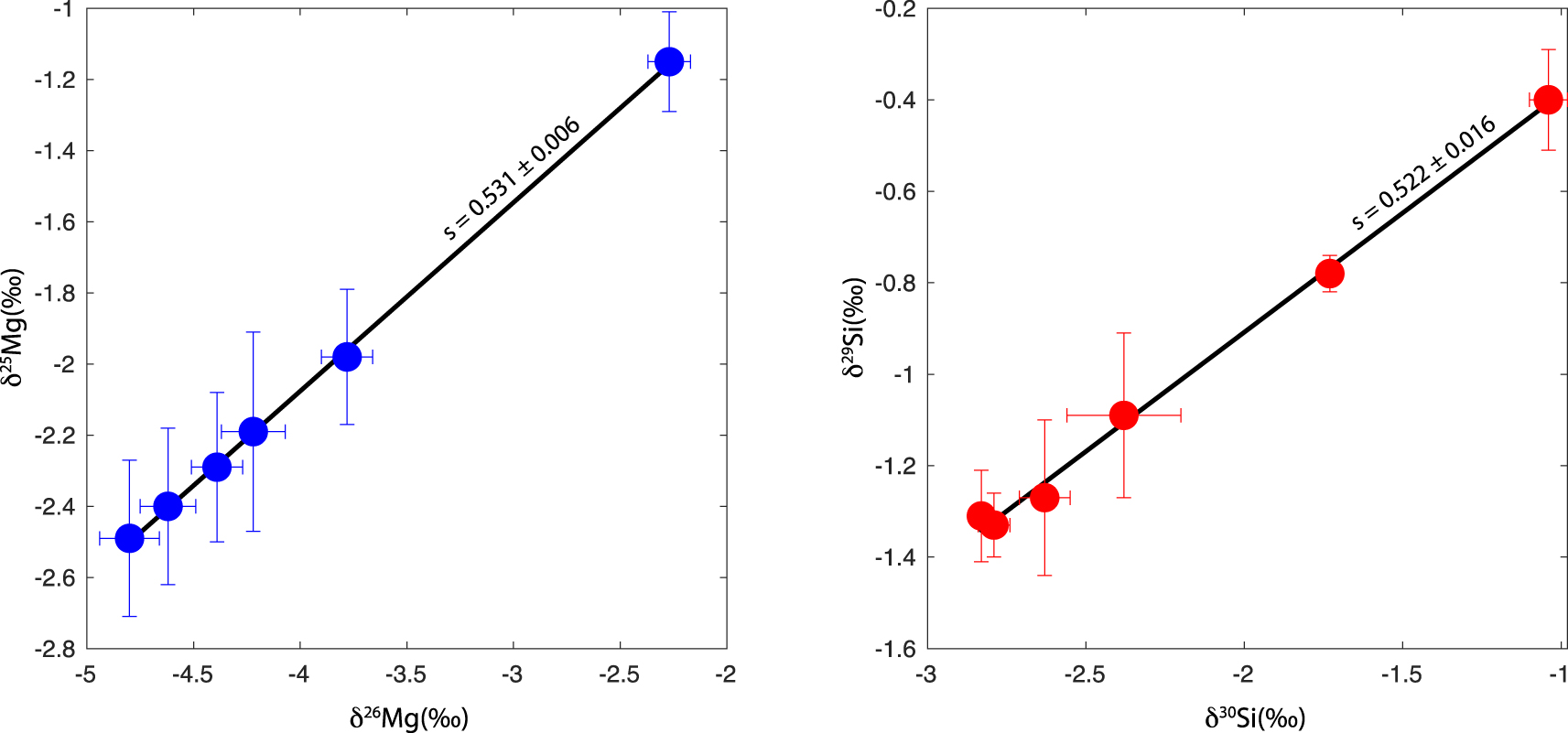
Isotopic composition of the evaporated samples shown in a three-isotope plot. Delta values are calculated with respect to the terrestrial BHVO-2G standard (Table 1). Both Mg (left) and Si (right) isotopes show quasi-perfect, straight lines consistent with mass-dependent isotopic fractionation. The slopes are consistent, within uncertainties, with theoretically calculated slopes for equilibrium and kinetic fractionation (see main text).
Accurate isotopic fractionation factors (𝛼) from our experimental runs can be obtained directly by comparing the isotopic fractionation to the evaporative loss f of each element (i.e. Si/Siinitial and Mg/Mginitial), which are reported in Table 1. Our data for Mg and Si is plotted in Figure 6, and shows a linear dependence on ln f (Rayleigh fractionation) defined by:
| (17) |
| (18) |
Firstly, we verify that for each element, the ratio of slopes (1-a) of the lighter versus heavier isotope in Figure 6 is equal (within uncertainties) to the slope found in the 3-isotope plot (Figure 5).
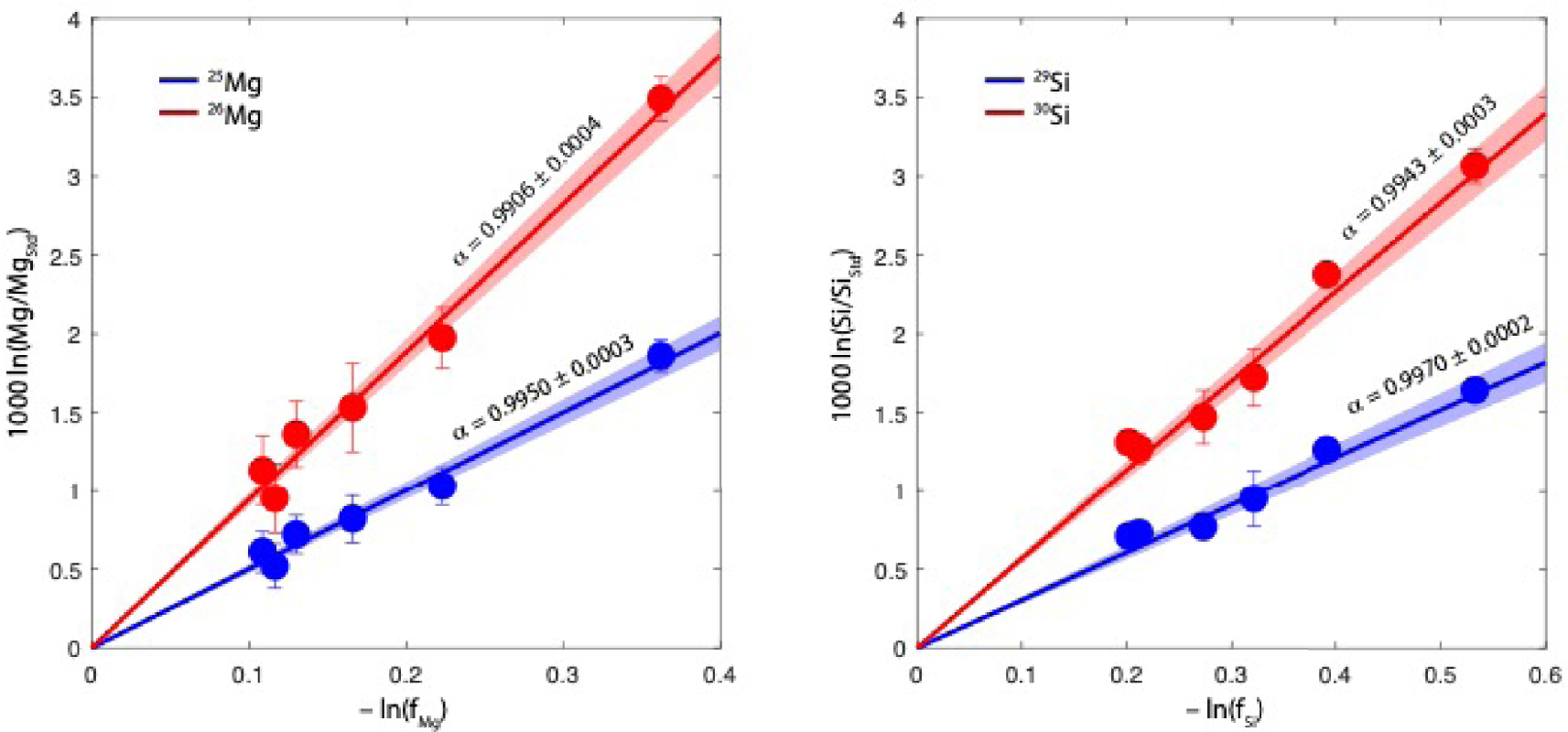
Isotopic composition of the evaporated samples as a function of evaporative loss. Magnesium is shown on the left and silicon on the right panels. The blue and red lines correspond to the lighter (
Isotopic composition of the evaporated samples as a function of evaporative loss. Magnesium is shown on the left and silicon on the right panels. The blue and red lines correspond to the lighter (
Isotopic fractionation factors from this study in the levitation furnace, compared with those obtained on the same composition and at the same temperature in a vacuum furnace [Richter et al. 2007], and to those expected at 1 bar for a diffusive transport mechanism recalculated from Sossi et al. [2020]
| Advective (this study) | 2SD | Vacuum [Richter et al. 2007] | 1-atm [Sossi et al. 2020] | |
|---|---|---|---|---|
| 𝛿 30Si | 0.9943 | 0.0006 | 0.9780 | 0.9933 |
| 𝛿 29Si | 0.9970 | 0.0004 | 0.9888 | 0.9966 |
| 𝛿 26Mg | 0.9906 | 0.0008 | 0.9608 | 0.9841 |
| 𝛿 25Mg | 0.9950 | 0.0006 | 0.9798 | 0.9918 |
The isotopic fractionation factors 𝛼 observed in our experiments can be compared to those measured in purely kinetic (vacuum) evaporation experiments. The isotopic fractionation factors in our experiments are much higher (closer to unity), indicating less isotopic fractionation for an otherwise constant degree of elemental evaporation (Table 2). Our data can also be compared to those expected in a 1-atm tube furnace [Sossi et al. 2020] in which diffusion through the gas phase is the limiting variable, and again, our isotopic fractionation factors are also closer to unity.
This important difference in isotopic fractionation factors between previous experiments (vacuum or 1 bar) and ours must be due to the fundamental difference in the mass transport mechanism involved. While chemical diffusion away from the sample (in a self-sustained chemical gradient) is the main mode of transport in vacuum or tube furnaces because the gas flow around the evaporating sample has Pe < 1, advective transport dominates in the levitation furnace where Pe > 1 as seen on its effect on the Sherwood number (Equation (7)). Empirically this change in mode of mass transport has a strong effect on isotopic fractionation, and we argue here it is the reason for our observation of isotopic fractionation factors that tend closer to unity than predicted. Indeed, in the limit where diffusion is overrun by advection, the difference in the diffusion constants of two evaporating isotopic species tends to vanish, and their effective values converge, e.g. their ratio (Di∕Dj)→1. In this case, the formalism of ideal isotopic fractionation in vacuum (purely kinetic) can be applied to the isotopic fractionation factors so that:
| (19) |
Because pi and pi,eq cannot be measured, we considered the ratio pi∕pi,eq (the saturation factor) appearing in (19) as a variable that can be constrained from our data. For both 𝛿 26Mg and 𝛿 25Mg (with Mg as the gas species), we find pi∕pi,eq = 0.74 ± 0.02, a value indistinguishable from that obtained for both 𝛿 30Si and 𝛿 29Si (with SiO as the gas species) where pi∕pi,eq = 0.76 ± 0.04. It is noteworthy that this value of 0.74 ± 0.01 was found recently for Cu evaporation conducted in a levitation furnace [Ni et al. 2021]. The fact that the saturation factor is the same for Si, Mg, and Cu despite their differing evaporation rates from the melt and differing diffusion rates through the gas implies that this factor is controlled by a property common to all systems. We argue that this property is the effective pressure reduction due to increased mass transport in a flow with a high Sherwood number. While in principle this pressure reduction could be calculated from (7), we note that flows in which Re > 200 are inherently unstable (i.e., transitional) and require detailed hydrodynamic treatment to fully resolve [Michaelides 2003], and hence cannot be applied in a quantitative manner in this work. It shows that advection is acting more quickly than the timescale for which a diffusive gradient can be established around the melt, and hence, the flow conditions around the sample are imposing a steady state transport rate.
5. Conclusions
These experiments demonstrate that the levitation furnace is an effective tool to study elemental and isotopic evaporation of silicate melts. Because this furnace is capable of reaching temperatures in excess of 3400 K, which are well beyond the limits of traditional (vacuum or tube) furnaces, it is well adapted to the study of the evaporation of refractory elements. Moreover, it would allow the measurement of activity coefficients of melt components at extreme temperatures (using (16)), and because the experiments are quick (on the order of minutes) and have a rapid turnover, could facilitate the gathering of large amounts of highly reproducible data to provide accurate measurements of these coefficients over a large range of previously unattainable temperatures.
Isotopic fractionation shows that the evaporation process here is controlled by advection instead of diffusion. Such a regime is relevant in certain astrophysical environments, and these experiments can help constrain evaporation processes occurring in such conditions [Macris et al. 2018; Schlichting et al. 2015; Saxena et al. 2017; Nguyen et al. 2020; Jackson et al. 2010; Charnoz et al. 2021]. The possibility of reaching a diffusive regime that is relevant to other planetary processes could be envisioned by increasing the evaporation rates so as to restore a diffusive boundary, either by working at higher temperature, or more effectively so by operating at lower oxygen fugacity to increase the net evaporating flux. With a square root dependence of the flux of Mg and Si on fO2 (Equations (10)–(11)) and with the capability to scan ten orders of magnitude in fO2, we can achieve in principle a five orders of magnitude change in the evaporation rate, which could eventually re-establish diffusive boundary condition, which remains to be tested by further experiments.
Acknowledgements
James Badro expresses his infinite gratitude to the Bourcart–Gentil Foundation of the French Academy of Science for their award, and to the editors of the proceedings of that noble society (Comptes Rendus Géosciences) for the invitation to contribute this work in recognition of this honour. Paolo A. Sossi thanks the SNSF through Ambizione Fellowship grant 180025. We thank Maylis Landeau, Sébastien Charnoz, Marc Chaussidon, and Frank Richter for invigorating and refreshing discussions. We acknowledge the financial support of the UnivEarthS labex program at the University of Paris (ANR-10-LABX-0023 and ANR-11-IDEX-0005-02). This work was supported by IPGP multidisciplinary program PARI, and by Paris–IdF region SESAME grant no. 12015908.




 CC-BY 4.0
CC-BY 4.0
Vous devez vous connecter pour continuer.
S'authentifier