Mettre la physique en équations : un problème de mathématiques ?
« En 1900, lors du Second Congrès International des Mathématiciens, David Hilbert a énoncé une liste de 23 défis mathématiques pour le siècle à venir, connus sous le nom de "problèmes de Hilbert". Le sixième de ces problèmes* concerne les fondements de la mécanique classique. Ce problème était alors motivé par les travaux récents de Ludwig Boltzmann qui ont introduit une description des gaz intermédiaire entre les modèles atomiques basés sur la mécanique de Newton, et les modèles fluides continus.
Une question naturelle est de savoir si ces différents modèles donnent des prédictions cohérentes, et Hilbert a suggéré d'utiliser des méthodes basées sur l'idée de "passage à la limite" pour apporter une réponse mathématique à cette question.
Malgré plus d'un siècle d'efforts, le problème soulevé par Hilbert reste en grande partie non résolu. » (Laure Saint-Raymond)
L’exposé du 23 mai 2023 de Laure Saint-Raymond (Rencontre 5 à 7) a pour objectif d'expliquer les difficultés rencontrées dans cette quête et de montrer comment elles peuvent apporter un éclairage intéressant sur la physique.
Cette collection propose de rassembler une partie des notes publiées sur ce sujet transverse dans les Comptes Rendus Mathématique, Physique et Mécanique.
*VI. Le traitement mathématique des axiomes de la Physique. Les recherches sur les principes fondamentaux de la Géométrie nous conduisent à envisager ce problème : traiter sur ce modèle les branches de la Physique où les Mathématiques jouent aujourd'hui un rôle prépondérant; ces branches de la Science sont, avant toutes autres, le Calcul des Probabilités et la Mécanique.
Quant aux axiomes du Calcul des probabilités (2 ), il me semblerait très désirable que l'on en fit la discussion logique en même temps qu'en Physique mathématique on développerait parallèlement d'une manière rigoureuse et satisfaisante la méthode des valeurs moyennes, et cela tout particulièrement dans la théorie cinétique des gaz.
Quant aux principes de la Mécanique, nous possédons déjà au point de vue physique des recherches d'une haute portée; je citerai, par exemple, les écrits de MM. Mach, Hertz, Boltzmann et Volkmann. Il serait aussi très désirable qu'un examen approfondi des principes de la Mécanique fût alors tenté par les mathématiciens. Ainsi le Livre de M. Boltzmann sur les Principes de la Mécanique nous incite à établir et à discuter au point de vue mathématique d'une manière complète et rigoureuse les méthodes basées sur l'idée de passage à la limite, et qui de la conception atomique nous conduisent aux lois du mouvement des continua.
Inversement on pourrait, au moyen de méthodes basées sur l'idée de passage à la limite, chercher à déduire les lois du mouvement des corps rigides d'un système d'axiomes reposant sur la notion d'états d'une matière remplissant tout l'espace d'une manière continue, variant d'une manière continue et que l'on devra définir paramétriquement.
Quoi qu'il en soit, c'est la question de l'équivalence des divers systèmes d'axiomes qui présentera toujours l'intérêt le plus grand quant aux principes. Pour que l'exemple de la Géométrie soit applicable au traitement des axiomes de la Physique, nous devons chercher à renfermer une classe aussi générale que possible de phénomènes physiques dans un nombre restreint d'axiomes; puis, au moyen de l'addition de nouveaux axiomes, il faut parvenir successivement aux théories plus particulières. Peut-être pourrait-on ici emprunter un principe de subdivision à cette profonde Théorie des groupes infinis de transformations de Lie. Le mathématicien, de même qu'en Géométrie, devra ici aussi avoir égard, non seulement aux théories qui se rapprochent de la réalité, mais encore en général à toutes celles qui sont logiquement possibles, et il devra toujours soigneusement chercher à obtenir une vue d'ensemble complète sur toutes les conséquences qu'entraîné le système d'axiomes choisi.
Enfin, pour compléter les théories physiques, le mathématicien devra attaquer le problème qui consiste en chaque cas à examiner si le nouvel axiome ajouté n'est pas en contradiction avec les précédents. Le physicien se voit souvent obligé, par le résultat de ses expériences, de faire de nouvelles hypothèses, et cela même pendant le développement de ses théories, et il invoque alors au sujet
de la non-contradiction des nouvelles hypothèses avec les précédentes, ces expériences précisément, ou encore un certain sentiment physique. Ce sont là des procédés qui ne sont pas admissibles dans l'édification rigoureusement logique d'une théorie. La démonstration requise de la non-contradiction de toutes les hypothèses faites me semble encore d'une grande importance par la raison
que l'effort nécessité par cette démonstration conduit toujours de la manière la plus effective à un énoncé exact des axiomes mêmes.
Jusqu'ici nous avons exclusivement examiné les principes fondamentaux des diverses branches de la Science mathématique. Il est certain que l'étude et la discussion des principes d'une science
possèdent un charme particulier et l'examen de ces principes sera toujours un des plus importants sujets de recherches. "Le but final", a dit Weierstrass, "que l'on doit avoir devant les yeux est la recherche d'un jugement exact sur les principes fondamentaux de la science. Pour pénétrer dans le domaine de la Science il est, sans doute, indispensable aussi de s'occuper de problèmes particuliers". En effet, pour pouvoir examiner avec fruit les principes d'une science, il faut être familiarisé avec ses théories particulières; seul, l'architecte qui connaît à fond, dans tous leurs détails, les diverses destinations d'un bâtiment, sera capable d'en poser sûrement les fondations. Nous allons donc maintenant passer en revue des problèmes spéciaux dans les diverses branches de la Mathématique, et nous commencerons par l'Arithmétique et l'Algèbre.
 | Linear diffusive limit of deterministic systems of hard spheres Bodineau, Thierry; Gallagher, Isabelle; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 352 (2014) no. 5, pp. 411-419 |
 | Solutions du système de Vlasov–Maxwell–Boltzmann avec interactions à longue portée Arsénio, Diogo; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 351 (2013) no. 9-10, pp. 357-360 |
 | Moyennisation en vitesse dans L1 pour l'équation de transport Golse, François; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 334 (2002) no. 7, pp. 557-562 |
 | Pseudodifferential calculus in large dimension and thermodynamic limits Royer, Christophe Comptes Rendus. Mathématique, Volume 336 (2003) no. 5, pp. 413-418 |
 | La limite de Boltzmann–Grad du gaz de Lorentz périodique en dimension deux d'espace Caglioti, Emanuele; Golse, François Comptes Rendus. Mathématique, Volume 346 (2008) no. 7-8, pp. 477-482 |
 | Bodineau, Thierry; Gallagher, Isabelle; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 353 (2015) no. 7, pp. 623-627 |
 | Paquets d'ondes et distance quadratique de Monge–Kantorovich en mécanique quantique Golse, François; Paul, Thierry Comptes Rendus. Mathématique, Volume 356 (2018) no. 2, pp. 177-197 |
 | Justification de l'équation de Schrödinger–Poisson à partir du problème quantique à N corps Bardos, Claude; Erdös, Laszlo; Golse, François; Mauser, Norbert; Yau, Horng-Tzer Comptes Rendus. Mathématique, Volume 334 (2002) no. 6, pp. 515-520 |
 | Une vision microscopique de la loi de Fourier Bodineau, Thierry; Gallagher, Isabelle; Saint-Raymond, Laure Comptes Rendus. Physique, Volume 20 (2019) no. 5, pp. 402-418 |
 | Rôle des quantités conservées dans la loi de Fourier pour les systèmes mécaniques diffusifs Olla, Stefano Comptes Rendus. Physique, Volume 20 (2019) no. 5, pp. 429-441 |
 | Bardos, Claude; Titi, Edriss S.; Wiedemann, Emil Comptes Rendus. Mathématique, Volume 350 (2012) no. 15-16, pp. 757-760 |
 | Inégalité d'observation pour des équations cinétiques linéaires par l'approximation de diffusion Bardos, Claude; Phung, Kim Dang Comptes Rendus. Mathématique, Volume 355 (2017) no. 6, pp. 640-664 |
 | Un formalisme pour la dérivation des lois de conservations Bardos, Claude; Pironneau, Olivier Comptes Rendus. Mathématique, Volume 335 (2002) no. 10, pp. 839-845 |
 | Existence globale de solutions faibles a quelques modèles micro-macro Lions, Pierre-Louis; Masmoudi, Nader Comptes Rendus. Mathématique, Volume 345 (2007) no. 1, pp. 15-20 |
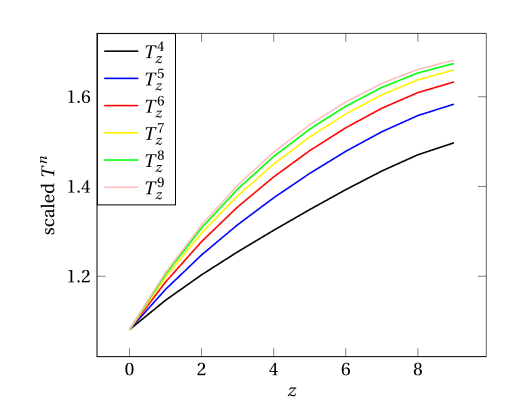 | Transfert radiatif stratifié couplé aux equations de la mécanique des fluides Golse, François; Pironneau, Olivier Comptes Rendus. Mécanique, Volume 350 (2022) no. S1, pp. 1-15 |
 | Régularité de solutions pour l'équation de Boltzmann sans angulaire cutoff Alexandre, Radjesvarane; Morimoto, Yoshinore; Ukai, Seiji; Xu, Chao-Jiang; Yang, Tong Comptes Rendus. Mathématique, Volume 347 (2009) no. 13-14, pp. 747-752 |
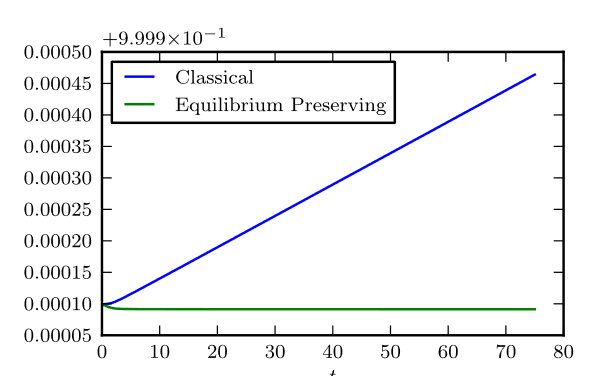 | Sur des méthodes spectrales préservant les équilibres de l'équation de Boltzmann homogène Filbet, Francis; Pareschi, Lorenzo; Rey, Thomas Comptes Rendus. Mathématique, Volume 353 (2015) no. 4, pp. 309-314 |
 | À propos du programme de Kac en théorie cinétique Mischler, Stéphane; Mouhot, Clément Comptes Rendus. Mathématique, Volume 349 (2011) no. 23-24, pp. 1245-1250 |
 | Lattice Fluid Dynamics: Thirty-five Years Down the Road Succi, Sauro Comptes Rendus. Mécanique, Volume 350 (2023) no. S1, pp. 1-12 |
 | Assous, Franck; Furman, Yevgeni Comptes Rendus. Mécanique, Volume 348 (2021) no. 12, pp. 969-981 |
 | Schémas dʼordre élévé et préservant lʼasymptotique pour lʼéquation de Boltzmann Dimarco, Giacomo; Pareschi, Lorenzo Comptes Rendus. Mathématique, Volume 350 (2012) no. 9-10, pp. 481-486 |
 | An ES–BGK model for gas mixtures Brull, Stéphane Comptes Rendus. Mathématique, Volume 351 (2013) no. 19-20, pp. 775-779 |
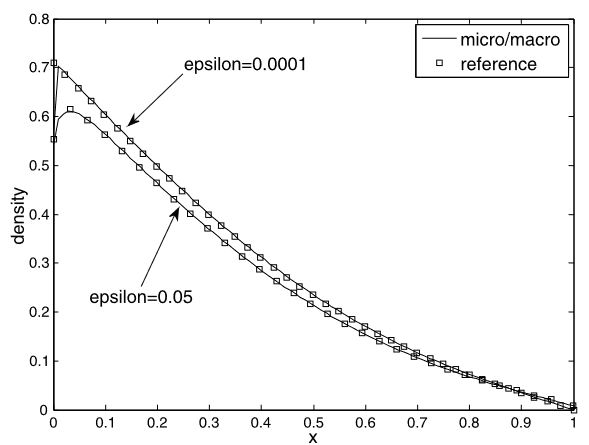 | Une nouvelle décomposition micro/macro adaptée au bord pour les équations cinétiques Lemou, Mohammed; Méhats, Florian Comptes Rendus. Mathématique, Volume 349 (2011) no. 7-8, pp. 479-484 |
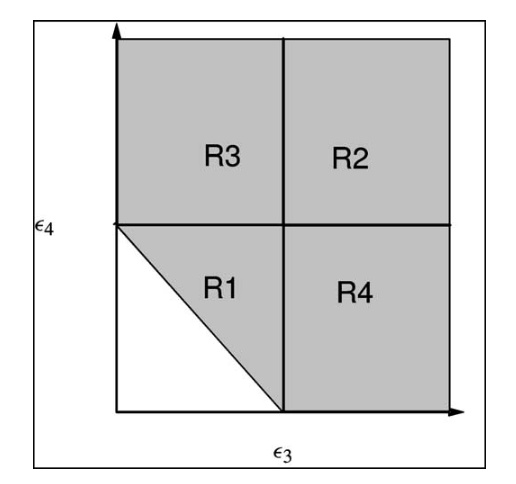 | La théorie cinétique et les condensats de Bose–Einstein Connaughton, Colm; Pomeau, Yves Comptes Rendus. Physique, Volume 5 (2004) no. 1, pp. 91-106 |