Putting physics into equations: a problem of mathematics?
"In 1900, at the Second International Congress of Mathematicians, David Hilbert set forth a list of 23 mathematical challenges for the coming century, known as the "Hilbert problems." The sixth of these problems concerns the foundations of classical mechanics. This problem was motivated by the recent work of Ludwig Boltzmann who introduced a description of gases intermediate between atomic models based on Newtonian mechanics, and continuous fluid models.
A natural question is whether these different models give consistent predictions, and Hilbert suggested using methods based on the idea of "boundary crossing" to provide a mathematical answer to this question.
Despite more than a century of effort, the problem raised by Hilbert remains largely unsolved." (Laure Saint-Raymond)
The presentation of May 23, 2023 by Laure Saint-Raymond (Meeting 5 to 7) aims to explain the difficulties encountered in this quest and to show how they can bring an interesting light on physics.
This collection proposes to gather a part of the notes published on this transverse subject in the Comptes Rendus Mathématique, Physique et Mécanique.
*VI. The investigations on the foundations of geometry suggest the problem: To treat in the same manner, by means of axioms, those physical sciences in which mathematics plays an important part; in the first rank are the theory of probabilities and mechanics.
As to the axioms of the theory of probabilities, it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases.
Important investigations by physicists on the foundations of mechanics are at hand; I refer to the writings of Mach, Hertz, Boltzmann and Volkmann. It is therefore very desirable that the discussion of the foundations of mechanics be taken up by mathematicians also. Thus Boltzmann's work on the principles of mechanics suggests the problem of developing mathematically the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua. Conversely one might try to derive the laws of the motion of rigid bodies by a limiting process from a system of axioms depending upon the idea of continuously varying conditions of a material filling all space continuously, these conditions being defined by parameters. For the question as to the equivalence of different systems of axioms is always of great theoretical interest.
If geometry is to serve as a model for the treatment of physical axioms, we shall try first by a small number of axioms to include as large a class as possible of physical phenomena, and then by adjoining new axioms to arrive gradually at the more special theories. At the same time Lie's a principle of subdivision can perhaps be derived from profound theory of infinite transformation groups. The mathematician will have also to take account not only of those theories coming near to reality, but also, as in geometry, of all logically possible theories. He must be always alert to obtain a complete survey of all conclusions derivable from the system of axioms assumed.
Further, the mathematician has the duty to test exactly in each instance whether the new axioms are compatible with the previous ones. The physicist, as his theories develop, often finds himself forced by the results of his experiments to make new hypotheses, while he depends, with respect to the compatibility of the new hypotheses with the old axioms, solely upon these experiments or upon a certain physical intuition, a practice which in the rigorously logical building up of a theory is not admissible. The desired proof of the compatibility of all assumptions seems to me also of importance, because the effort to obtain such proof always forces us most effectually to an exact formulation of the axioms.
So far we have considered only questions concerning the foundations of the mathematical sciences. Indeed, the study of the foundations of a science is always particularly attractive, and the testing of these foundations will always be among the foremost problems of the investigator. Weierstrass once said, "The final object always to be kept in mind is to arrive at a correct understanding of the foundations of the science. ... But to make any progress in the sciences the study of particular problems is, of course, indispensable." In fact, a thorough understanding of its special theories is necessary to the successful treatment of the foundations of the science. Only that architect is in the position to lay a sure foundation for a structure who knows its purpose thoroughly and in detail. So we turn now to the special problems of the separate branches of mathematics and consider first arithmetic and algebra.
 | Limite de diffusion linéaire pour un système déterministe de sphères dures Bodineau, Thierry; Gallagher, Isabelle; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 352 (2014) no. 5, pp. 411-419 |
 | Solutions of the Vlasov–Maxwell–Boltzmann system with long-range interactions Arsénio, Diogo; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 351 (2013) no. 9-10, pp. 357-360 |
| Velocity averaging in L 1 for the transport equation Golse, François; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 334 (2002) no. 7, pp. 557-562 |
| Calcul pseudodifférentiel en grande dimension et limites thermodynamiques Royer, Christophe Comptes Rendus. Mathématique, Volume 336 (2003) no. 5, pp. 413-418 |
| The Boltzmann–Grad limit of the periodic Lorentz gas in two space dimensions Caglioti, Emanuele; Golse, François Comptes Rendus. Mathématique, Volume 346 (2008) no. 7-8, pp. 477-482 |
| Bodineau, Thierry; Gallagher, Isabelle; Saint-Raymond, Laure Comptes Rendus. Mathématique, Volume 353 (2015) no. 7, pp. 623-627 |
| Wave packets and the quadratic Monge–Kantorovich distance in quantum mechanics Golse, François; Paul, Thierry Comptes Rendus. Mathématique, Volume 356 (2018) no. 2, pp. 177-197 |
| Derivation of the Schrödinger–Poisson equation from the quantum 𝐍-body problem Bardos, Claude; Erdös, Laszlo; Golse, François; Mauser, Norbert; Yau, Horng-Tzer Comptes Rendus. Mathématique, Volume 334 (2002) no. 6, pp. 515-520 |
 | A microscopic view of the Fourier law Bodineau, Thierry; Gallagher, Isabelle; Saint-Raymond, Laure Comptes Rendus. Physique, Volume 20 (2019) no. 5, pp. 402-418 |
 | Role of conserved quantities in Fourier's law for diffusive mechanical systems Olla, Stefano Comptes Rendus. Physique, Volume 20 (2019) no. 5, pp. 429-441 |
| The vanishing viscosity as a selection principle for the Euler equations: The case of 3D shear flow Bardos, Claude; Titi, Edriss S.; Wiedemann, Emil Comptes Rendus. Mathématique, Volume 350 (2012) no. 15-16, pp. 757-760 |
| Observation estimate for kinetic transport equations by diffusion approximation Bardos, Claude; Phung, Kim Dang Comptes Rendus. Mathématique, Volume 355 (2017) no. 6, pp. 640-664 |
| A formalism for the differentiation of conservation laws Bardos, Claude; Pironneau, Olivier Comptes Rendus. Mathématique, Volume 335 (2002) no. 10, pp. 839-845 |
| Global existence of weak solutions to some micro-macro models Lions, Pierre-Louis; Masmoudi, Nader Comptes Rendus. Mathématique, Volume 345 (2007) no. 1, pp. 15-20 |
 | Stratified radiative transfer for multidimensional fluids Golse, François; Pironneau, Olivier Comptes Rendus. Mécanique, Volume 350 (2022) no. S1, pp. 1-15 |
| Regularity of solutions for the Boltzmann equation without angular cutoff Alexandre, Radjesvarane; Morimoto, Yoshinore; Ukai, Seiji; Xu, Chao-Jiang; Yang, Tong Comptes Rendus. Mathématique, Volume 347 (2009) no. 13-14, pp. 747-752 |
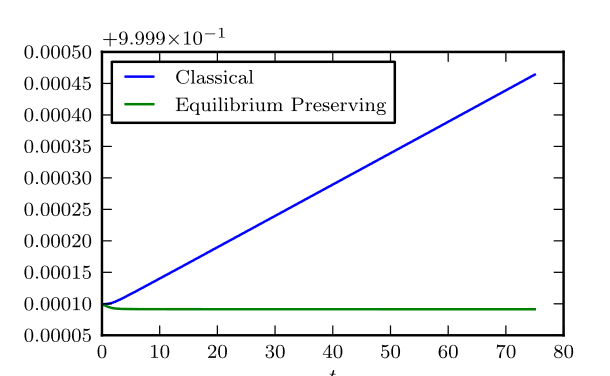 | On steady-state preserving spectral methods for homogeneous Boltzmann equations Filbet, Francis; Pareschi, Lorenzo; Rey, Thomas Comptes Rendus. Mathématique, Volume 353 (2015) no. 4, pp. 309-314 |
| About Kacʼs program in kinetic theory Mischler, Stéphane; Mouhot, Clément Comptes Rendus. Mathématique, Volume 349 (2011) no. 23-24, pp. 1245-1250 |
 | Lattice Fluid Dynamics: Thirty-five Years Down the Road Succi, Sauro Comptes Rendus. Mécanique, Volume 350 (2023) no. S1, pp. 1-12 |
 | A hierarchy of reduced models to approximate Vlasov–Maxwell equations for slow time variations Assous, Franck; Furman, Yevgeni Comptes Rendus. Mécanique, Volume 348 (2021) no. 12, pp. 969-981 |
 | High order asymptotic-preserving schemes for the Boltzmann equation Dimarco, Giacomo; Pareschi, Lorenzo Comptes Rendus. Mathématique, Volume 350 (2012) no. 9-10, pp. 481-486 |
| Un modèle ES–BGK pour des mélanges de gaz Brull, Stéphane Comptes Rendus. Mathématique, Volume 351 (2013) no. 19-20, pp. 775-779 |
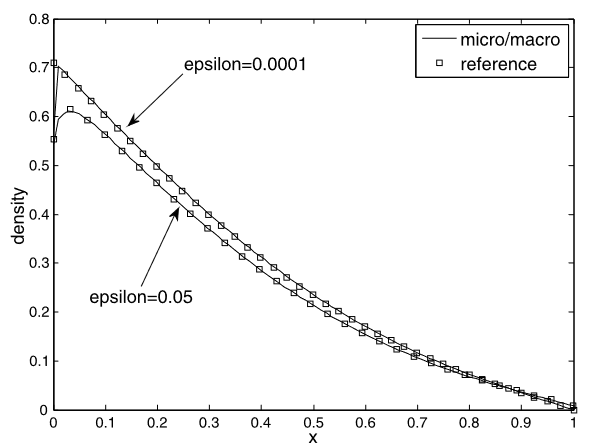 | A boundary matching micro/macro decomposition for kinetic equations Lemou, Mohammed; Méhats, Florian Comptes Rendus. Mathématique, Volume 349 (2011) no. 7-8, pp. 479-484 |
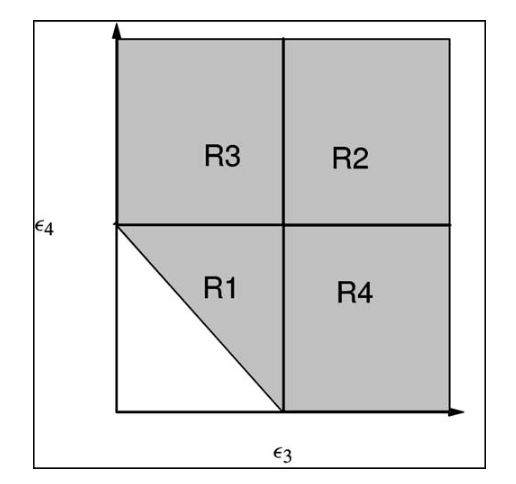 | Kinetic theory and Bose–Einstein condensation Connaughton, Colm; Pomeau, Yves Comptes Rendus. Physique, Volume 5 (2004) no. 1, pp. 91-106 |