1 Introduction
Dans le domaine biomédical, la mise en œuvre d’études dynamiques permet de caractériser des phénomènes physiologiques liés aux fonctions d’un organisme. Ces études peuvent êtres classés selon différents objectifs et, en particulier, celui du diagnostic, qui vise à identifier une pathologie par les altérations fonctionnelles qu’elle provoque.
Il existe différentes techniques pour effectuer des études dynamiques in vivo, chez l’animal et chez l’homme ; en particulier, l’utilisation de techniques de détection externes non invasives, faisant intervenir des traceurs.
Dans notre cas, nous nous sommes intéressés aux troubles du transport du glucose. Le glucose est un substrat énergétique essentiel pour l’organisme humain. Son transport est facilité dans les cellules grâce à une famille de protéines transmembranaires, les GLUTs (1 à 5), qui sont exprimées et régulées de façon « tissu spécifique » 〚1〛. De nombreuses pathologies sont associées à des anomalies de son transport – maladies neurodégénératives, cancers, diabète non insulino-dépendant (DNID)... Des techniques de détection permettent d’apprécier in vivo ces perturbations, comme l’utilisation d’analogues marqués du glucose (traceurs de son transport), associée à l’imagerie en médecine nucléaire. On peut ainsi observer leur répartition dans les différents organes intéressés grâce à des images scintigraphiques. Pour estimer l’insulino-résistance 〚2〛, il semble préférable, selon Bonadonna 〚3〛, d’utiliser un traceur pur du transport du glucose. Un nouvel analogue du glucose, le 〚123I〛-6-déoxy-6-iodo-d-glucose (6-DIG), a été proposé comme traceur du transport du glucose in vivo 〚4〛. Il a été montré sur différents modèles cellulaires que son comportement était voisin du 3-OMG (3-O-méthyl-d-glucose) 〚5〛, le traceur de référence du transport du glucose 〚6〛. Une première étude, réalisée in vivo sur des souris génétiquement diabétiques db/db, présentant des caractéristiques du DNID, a permis de mettre en évidence des anomalies de transport du glucose avec le 6-DIG 〚7, 8〛. La mesure du transport du glucose en clinique est d’un intérêt majeur, bien avant l’apparition du diabète, lors du stade dit « pré-diabétique », caractérisé par une insulino-résistance. C’est la raison pour laquelle nous avons choisi de tester le 6-DIG sur un modèle in vivo de rats présentant une insulino-résistance modérée, due à un régime enrichi en fructose (« rats fructose »), ainsi que sur une population de rats témoins. Une injection de ce traceur dans le sang permet d’obtenir des mesures du transport basal du glucose, ainsi que des mesures du transport induit par la présence d’insuline vers les différents organes.
La modélisation mathématique permet une synthèse quantitative des données biomédicales issues d’études dynamiques 〚9, 10〛.
Les modèles compartimentaux sont les plus fréquemment utilisés en médecine. En effet, les phénomènes physiologiques (diffusion, métabolisme, excrétion...) se prêtent bien à l’approche compartimentale et les équations de ces modèles sont relativement simples en regard de la complexité des systèmes biologiques. L’avantage de cette approche est d’apporter une compréhension globale du déroulement des phénomènes mis en jeu.
Fondé sur la théorie du transport transmembranaire du glucose, un modèle multicompartimental à coefficients invariants en fonction du temps peut être proposé pour décrire les cinétiques du glucose marqué (6-DIG), lors de son transport du sang vers les différents organes.
Le travail réalisé ici a ainsi eu quatre objectifs principaux :
- • élaborer un modèle mathématique capable de décrire le transport du glucose du plasma vers différents organes, en utilisant un modèle multicompartimental ;
- • identifier les paramètres d’échange du système étudié à partir de mesures réalisées sur celui-ci ; l’outil qui nous a permis d’identifier les paramètres du modèle est le logiciel SAAM II (Simulation Analyze And Modelling) 〚11–13〛 ;
- • démontrer, à l’aide du modèle mathématique, l’existence d’une différence significative dans le transport du 6-DIG entre la condition basale et la condition sous insuline chez les rats témoins et d’une faible différence de ce transport entre les mêmes conditions chez les « rats fructose » ;
- • déterminer comment le modèle mathématique pourrait nous aider à mieux élaborer les manipulations expérimentales sur différents aspects, comme la durée d’acquisition et les temps d’échantillonnage.
2 Matériels et méthodes
2.1 Expérimentations biologiques
Le but de cette expérimentation était de mettre en évidence les propriétés essentielles du transport du 6-DIG à l’échelle de l’organisme, mais aussi à l’échelle de l’organe, afin de montrer des variations pathologiques du transport du glucose in vivo chez le rat. Pour atteindre cet objectif, le moyen utilisé fut de tester ce traceur sur un modèle de rat présentant une pathologie du transport du glucose, l’insulino-résistance, dans deux conditions expérimentales différentes, l’une basale (normale) et l’autre sous perfusion d’insuline. Ce protocole a, par ailleurs, été appliqué à une population de rats témoins. Les rats, utilisés dix semaines après leur naissance, ont un poids de 300 g en moyenne et ont été nourris avec un régime UAR témoin (rats témoins) ou UAR fructose (dont 58% des sucres sont remplacés par du fructose), entraînant une insulino-résistance.
2.1.1 Méthode du clamp euglycémique hyperinsulinémique
Un jour avant l’expérience, la veine jugulaire droite est dégagée et cathétérisée, ainsi que la carotide gauche. Cette procédure est réalisée sous anesthésie générale de l’animal ; le clamp est effectué le lendemain matin sur l’animal éveillé. Sur chacun des groupes de rats (fructose et témoin), deux protocoles sont mis en œuvre : un clamp euglycémique hyperinsulinémique 〚14〛, avec perfusion d’insuline de 2 mUI min–1 et un protocole normoglycémique normo-insulinémique, avec perfusion de sérum physiologique, réalisée dans les mêmes conditions. L’injection en bolus du 6-DIG a lieu après 1 h, lorsque le plateau d’euglycémie est atteint. L’incorporation tissulaire du 6-DIG est mesurée aux temps suivants : 2, 3, 5, 7, 10, 15 et 20 min après son injection par le cathéter carotidien. Les animaux sont sacrifiés par décapitation. Des organes sont prélevés et pesés ; ces organes ont été choisis pour êtres répartis en deux groupes : le premier groupe correspond aux organes insulino-sensibles (cœur, muscle, diaphragme, graisse abdominale et graisse épididymale), tandis que le deuxième groupe correspond aux organes non sensibles à l’insuline (poumon, foie, duodénum, reins, cervelet et hémisphères cérébraux). Du sang est aussi prélevé aux mêmes temps, afin de déterminer l’évolution temporelle de l’activité sanguine. Ensuite, la radioactivité présente dans les organes et dans le sang est comptée.
Les valeurs obtenues pour chaque organe, pour chaque condition et pour les deux groupes de rats, nous ont été fournis par Perret 〚8〛 ; les activités du 6-DIG captées par ces différents organes, ainsi que les activités sanguines mesurées, ont été utilisées pour établir le modèle mathématique et identifier les paramètres des trois premiers modèles.
Il n’y a pas de différence de glycémie entre les rats témoins et les rats fructose : celle-ci est comprise entre 0,8 et 1,1 g l–1. Le GIR (Glucose Infusion Rate) représente le paramètre clé du clamp, c’est-à-dire la quantité de glucose qui doit être perfusée pour maintenir la glycémie constante, malgré la perfusion continue d’insuline. Sa valeur est, avec un clamp à 2 mUI min–1, de 18,2 ± 2,8 mg(min kg)–1 chez les rats témoins et de 11,0 ± 1,9 mg(min kg)–1 chez les rats fructose. La différence des GIR indique que les rats fructose sont bien insulinorésistants.
2.1.2 Détection externe
Cette expérience a été réalisée comme suite aux résultats obtenus dans l’expérience du clamp, montrant que l’organe qui a fourni les résultats les plus discriminants était le cœur. Nous avons donc choisi de réaliser une étude en détection externe fondée sur ce seul organe.
Dans cette étude, chaque rat a été utilisé comme son propre témoin et, tout comme dans l’étude précédente, nous avons observé la captation du 6-DIG en condition basale et sous insuline sur les deux population de rats. Environ 80 μCi de 6-DIG sont injectés dans la veine saphène de l’animal à t = 0 ; l’acquisition de l’activité du traceur se fait au niveau sanguin (artère fémorale) et au niveau du cœur de l’animal. La première partie de l’acquisition entre 0 et 40 min concerne la condition basale. Ensuite, 5 min avant une deuxième injection du 6-DIG (≈ 80 μCi), une injection d’insuline (3,0 UI kg–1) est réalisée. Cette deuxième étape de l’acquisition, entre 45 et 85 min, représente la condition sous insuline. En fin de manipulation, le cœur de l’animal est prélevé et la radioactivité (réelle) présente dans celui-ci est comptée afin de normaliser l’activité mesurée pendant toute la durée de la détection externe. L’activité résiduelle, due à la première injection, est présente dans la deuxième partie de l’expérience. La décroissance de l’activité résiduelle, due à la première injection, est simulée à partir du modèle entre 45 et 85 min. Celle-ci est retranchée à la cinétique mesurée entre 45 et 85 min, afin d’obtenir la cinétique réelle due à la deuxième injection.
2.2 Outil informatique
L’estimation des paramètres, faisant appel à des calculs numériques dont la complexité augmente avec l’ordre du modèle, nécessite l’utilisation de l’outil informatique. Nous avons donc, pour ce faire, utilisé un logiciel conçu pour l’analyse de données biomédicales à l’aide de modèles compartimentaux, le logiciel SAAM II, qui permet la création de modèles compartimentaux et des équations différentielles qui en découlent, ainsi que la résolution du modèle et son ajustement aux données, en utilisant des méthodes statistiques et mathématiques élaborées 〚15〛. SAAM II propose un choix de trois méthodes d’optimisation numérique. La méthode choisie pour notre étude est celle de Rosenbrock, qui permet de résoudre une large classe de modèles. L’estimation des paramètres repose sur la minimisation itérative d’une fonction du maximum de vraisemblance des moindres carrées étendues. L’optimiseur est une modification de la méthode de Gauss–Newton ; la convergence vers les paramètres optimaux est atteinte quand un des deux critères de convergence est satisfait, le premier critère concernant la fonction objective et le second le nombre maximum d’itérations spécifié.
2.3 Analyse statistique
Pour la méthode du clamp, les comparaisons entre la condition basale et la condition sous insuline ont été effectuées par le test t de Student pour séries non appariées, au niveau de signification de 5%.
Pour vérifier la normalité de la répartition des résidus obtenus après l’ajustement du modèle aux données, nous avons utilisé le test de Kolmogorov–Smirnov 〚16〛, fondé sur la comparaison de la fonction de répartition de la loi normale N(μ,σ) avec la fonction de répartition observée pour les résidus. L’hypothèse de normalité de la distribution, au niveau de signification de 5%, est acceptée si la statistique observée pour le test est inférieure à la valeur critique (lue dans la table appropriée) et rejetée dans le cas contraire.
Pour la détection externe, les comparaisons entre la condition basale et la condition sous insuline ont été effectuées par le test t de Student pour séries appariées au niveau de signification de 5%.
2.4 Identifiabilité du système
2.4.1 Identifiabilité globale du système
L’identifiabilité structurelle définit l’aspect théorique de l’identifiabilté d’un modèle, permettant de déterminer le nombre de solutions admissibles en fonction du système d’équations définissant le modèle et des mesures effectuées 〚9, 17, 18〛. L’identifiabilité globale d’un modèle est une tâche extrêmement difficile, puisqu’elle consiste en la résolution d’un système d’équations algébriques non linéaires, dont le nombre de termes et le degré de non-linéarité augmentent avec l’ordre du modèle 〚19〛. Des études sur l’identifiabilité globale des modèles linéaires et non linéaires, ainsi que la mise au point de programmes de résolution, ont été faites par Cobelli et Saccomani 〚20, 21〛. En ce qui concerne notre étude, le volume du compartiment plasmatique (V) ainsi que les masses des organes (m2, m3,..., mn) sont fixés, de manière à aboutir à une identifiabilité unique des paramètres de transfert kij du modèle.
2.4.2 Identifiabilité numérique
L’estimation des paramètres a été réalisée en considérant que les mesures de radioactivité effectuées étaient décrites par l’équation :
Le modèle mathématique appliqué aux données cinétiques expérimentales a permis de quantifier indirectement les paramètres physiologiques, c’est-à-dire les coefficients de transfert fractionnels (kij), qui ne sont pas accessibles par des mesures directes, ceci en utilisant le logiciel SAAM II, qui est très performant pour le développement des modèles multicompartimentaux à injection unique et sorties (mesures) multiples 〚22〛.
2.4.3 Précision sur les paramètres 〚15〛
Les résultats de l’identification du modèle ont été jugés par l’évaluation des erreurs résiduelles (resij), qui ont été calculées aux différents temps comme étant la différence entre la mesure et la valeur prédite par le modèle :
3 Modèles compartimentaux étudiés pour l’expérience du clamp
3.1 Premier modèle
Le modèle mathématique est symbolisé (pour chaque organe étudié séparément) par trois compartiments (Fig. 1). Le compartiment 1 représente le plasma où a lieu l’injection (ex1) du traceur, ainsi qu’une fuite irréversible (k(0,1)). Entre ce compartiment plasmatique et le compartiment espace interstitiel (compartiment 2), nous avons supposé l’existence d’un flux bidirectionnel et linéaire. En revanche, entre l’espace interstitiel et l’espace intracellulaire (compartiment 3), nous avons considéré un flux bidirectionnel non linéaire (de type Michaëlien 〚17〛).
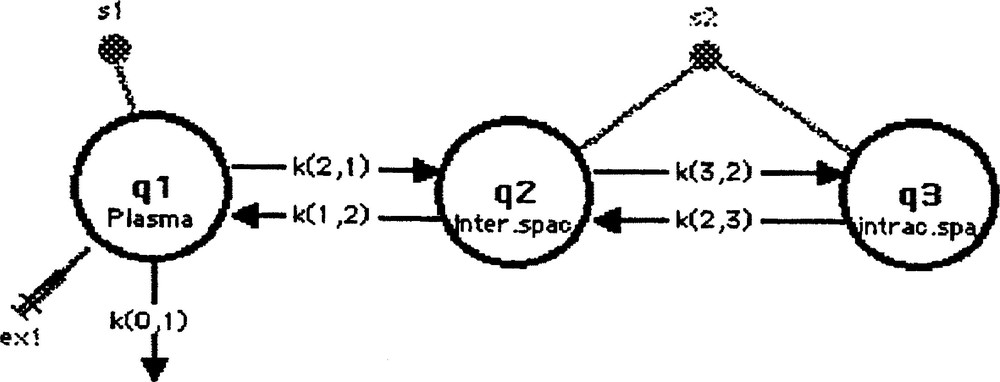
Premier modèle.
Le schéma d’acquisition de données comprenait six temps de mesure à 2, 3, 5, 7, 10 et 15 min après l’injection en bolus du traceur, pour le sang et les différents tissus. Sur la Fig. 1, ces mesures sont symbolisées par s1 (mesure de l’activité sanguine) et s2 (mesure de l’activité du tissu).
Les sept paramètres du modèle (trois coefficients de transfert fractionnels, deux Vmax et deux Km), qui devaient être estimés à partir de 12 points expérimentaux (à raison de n = 3 mesures, pour chaque point), n’étaient pas identifiables de façon unique et possédaient, par ailleurs, des coefficients de variation (CV) supérieurs à 100%. D’après Novotny 〚23〛, quand de grands écarts types et de grands coefficients de variation sont associés aux paramètres, le nombre de mesures expérimentales doit être augmenté, le nombre de compartiments diminué et, par conséquent, le nombre de paramètres diminué aussi.
Cette mauvaise précision sur les paramètres nous a alors conduits à une approche différente pour l’élaboration du modèle, à savoir un modèle simplifié à deux compartiments, avec suppression du compartiment extracellulaire, d’une part, et un affinement de l’échantillonnage temporel ainsi qu’une augmentation de taille de la population de rats étudiés à chaque temps, d’autre part.
3.2 Deuxième modèle
Le modèle est représenté par deux compartiments (Fig. 2), le compartiment 1 symbolisant le plasma où a lieu l’injection du traceur et une fuite irréversible (k(0,1)). Ce compartiment plasmatique réalise des échanges bidirectionnels linéaires avec le compartiment 2, qui symbolise, quant à lui, le tissu (ou l’organe étudié).
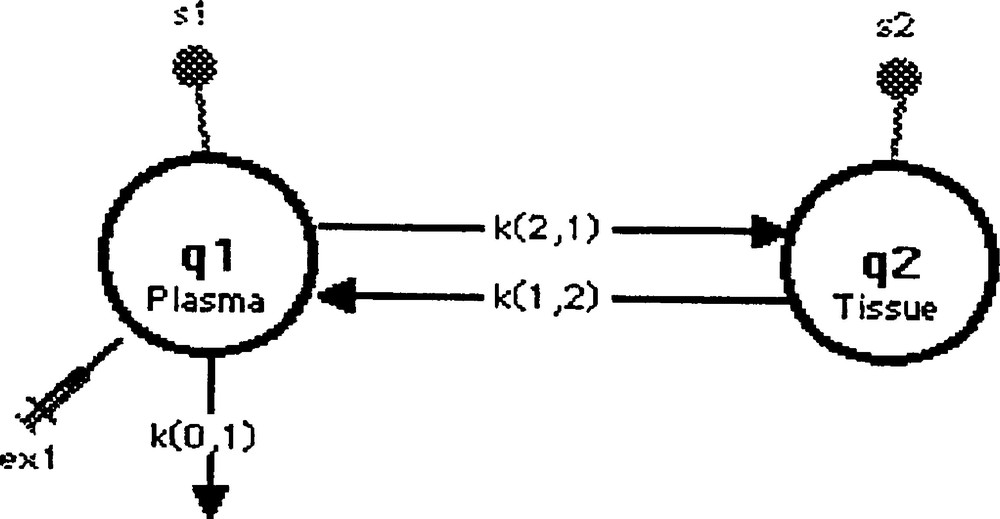
Second modèle.
Le schéma d’acquisition de données comprenait sept temps de mesure à 2, 3, 5, 7, 10, 15 et 20 min après l’injection en bolus du traceur, pour le sang et chacun des différents tissus.
Ce modèle était identifiable de façon unique et les trois paramètres cinétiques du modèle étaient donc estimés à partir de 14 points expérimentaux (à raison de quatre mesures pour chaque point), avec des coefficients de variation demeurant très élevés pour certains organes. Par ailleurs, l’estimation de la fuite au niveau du compartiment d’injection s’avérait différente selon l’organe considéré, ce qui n’était évidemment pas satisfaisant.
3.3 Troisième modèle
Le modèle mathématique finalement adopté pour l’étude du transport de l’analogue du glucose par la méthode du clamp est un modèle mamillaire linéaire illustré sur la Fig. 3. Il s’agit d’un modèle multicompartimental, inspiré de celui développé pour interpréter les cinétiques de distribution du 〚18F〛-FDG (fluoro-déoxy-d-glucose) dans le corps entier 〚24〛 et qui permet de suivre le devenir du 6-DIG après injection chez le rat in vivo. Le compartiment central représente le plasma, où a lieu l’injection du traceur et à partir duquel se produit une fuite irréversible (seulement une fraction de la dose injectée diffuse en dehors de ce site 〚9, 25〛). Ce compartiment central est en relation avec 11 autres compartiments, représentant les différents organes étudiés : cœur, muscle squelettique, diaphragme, graisse abdominale, cerveau, foie, graisse épididymale, cervelet, poumons, reins et duodénum (notés respectivement de q2 à q12). Des mesures de la radioactivité sont réalisées au niveau de tous les compartiments (plasma et organes) ; elles sont notées de S1 à S12 respectivement.
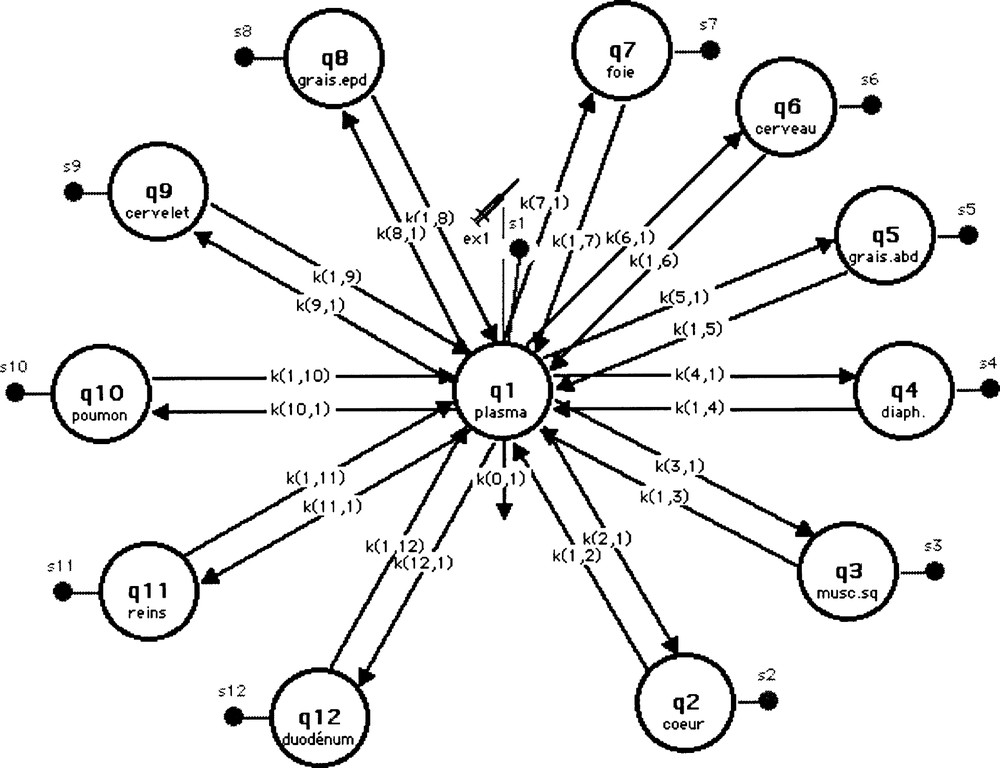
Modèle adopté pour l’étude du transport du 6-DIG.
4 Modèle compartimental pour l’étude en détection externe
Le modèle comporte trois compartiments (Fig. 4) : le compartiment 1 symbolise le plasma où a lieu l’injection du traceur et une fuite irréversible (k(0,1)). Ce compartiment plasmatique réalise des échanges bidirectionnels linéaires avec le compartiment 2 qui symbolise, quant à lui, le tissu cardiaque. Le compartiment 3 représente le pool des autres tissus, périphériques au compartiment 1, qui captent le 6-DIG ; tout comme pour le compartiment 2, nous avons supposé des flux bidirectionnels linéaires entre le plasma et ce pool.
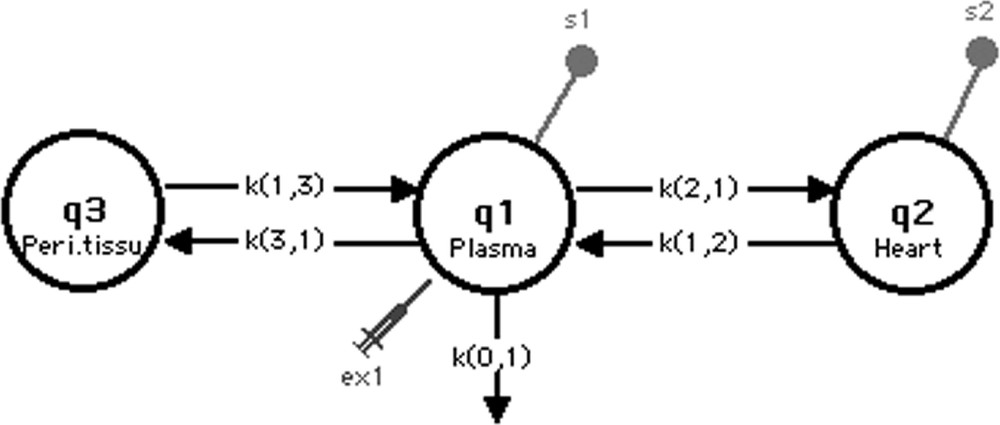
Modèle de l’étude en détection externe.
Le plan d’expérience a été élaboré parallèlement au développement de ce modèle à trois compartiments, afin d’obtenir un schéma d’acquisition optimal, ce dernier étant défini comme le schéma pour lequel le maximum de précision sur les paramètres estimés est atteint 〚26–28〛.
5 Résultats
5.1 Étude utilisant le clamp
5.1.1 Analyse compartimentale des cinétiques du 6-DIG
Les données obtenues au cours du temps au niveau du sang et des différents organes ont été analysées en utilisant le modèle multicompartimental de la Fig. 3. Dans ce modèle, on suppose que l’élimination du 6-DIG dans l’organisme du rat se fait par excrétion, représentée dans le modèle par un flux irréversible, k(0,1), au niveau du compartiment 1. Ce compartiment représente l’espace où le traceur est distribué immédiatement après son injection 〚9〛. On a supposé que cet espace était égal au volume du plasma, soit 4,7% (volume/poids) du poids total du rat 〚29–31〛. Les compartiments 2 à 12 représentent les différents organes étudiés ayant capté (au niveau tissulaire) le 6-DIG. Les échanges de 6-DIG entre le compartiment plasmatique et l’ensemble des compartiments organes compris dans le modèle sont représentés par des constantes de vitesse du 1er ordre. Les paramètres du modèle (kij, kin et kout) ont été estimés en ajustant le modèle aux données expérimentales.
L’ajustement du modèle aux données expérimentales obtenues pour les rats témoins sous insuline et en condition basale sont représentés sur les Figs. 5–7. Seuls les ajustements aux données des organes choisis pour chaque groupe insulino-sensible (Fig. 5) et non insulino-sensible (Fig. 6) sont présentés, ainsi que l’ajustement aux activités plasmatiques (Fig. 7). On peut constater que le modèle s’ajuste de façon satisfaisante aux données, ce qui témoigne de sa bonne qualité concernant les cinétiques de transport du 6-DIG pour ces différents organes et le plasma.
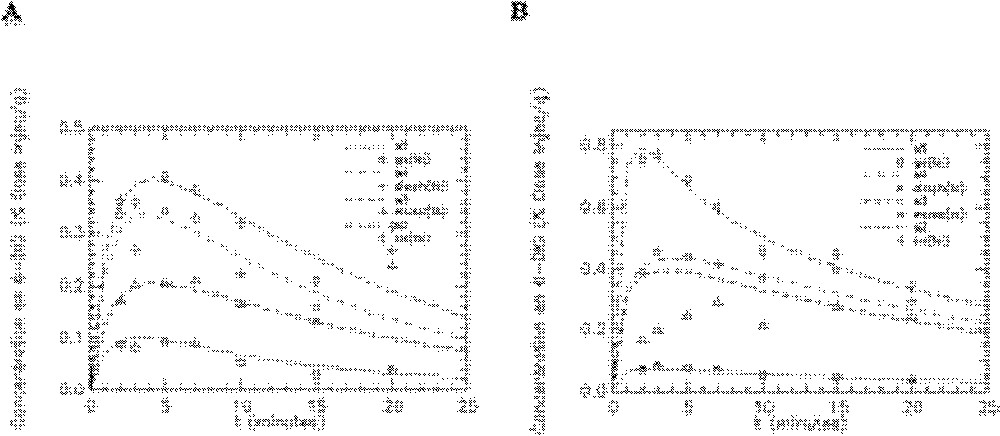
Ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour les compartiments cœur, muscle, diaphragme et graisse abdominale chez le rat témoin en condition basale (A) et sous insuline (B). s2, s3, s4 et s5 représentent les cinétiques simulées par le modèle respectivement pour le cœur (co), le muscle (musc), le diaphragme (diaph) et la graisse abdominale (ga). Unité pour l’axe des ordonnées : % dose injectée/gramme d’organe.
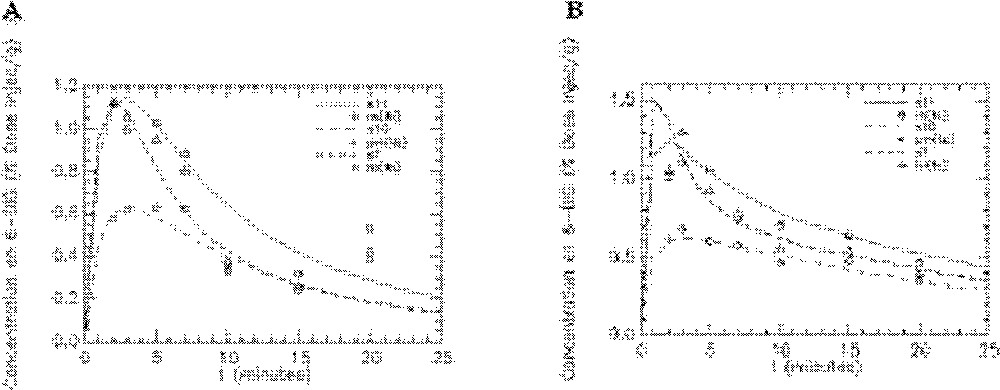
Ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour les compartiments reins (re), poumons (pm) et foie (fo) chez le rat témoin en condition basale (A) et sous insuline (B). s7, s10 et s11 représentent les cinétiques simulées par le modèle respectivement pour le foie, les poumons et les reins. Unité pour l’axe des ordonnées : % dose injectée/gramme d’organe.
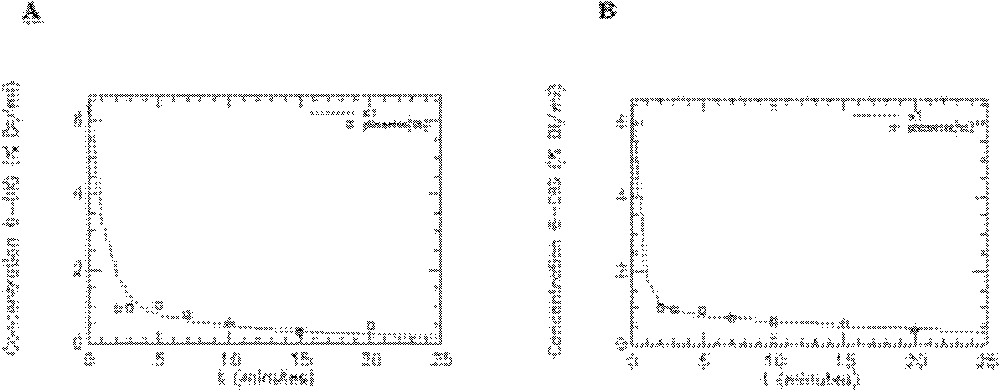
Ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour l’activité plasmatique (compartiment 1) chez le rat témoin en condition basale (A) et sous insuline (B). S1 représentant la cinétique simulée par le modèle. Unité pour l’axe des ordonnées : % dose injectée/millilitre de sang.
Les résultats de l’estimation des paramètres, ainsi que leur précision après l’ajustement aux données du modèle, sont présentés dans les Tableaux 1 et 2. Dans ces tableaux, nous avons rapporté les valeurs des coefficients de transfert fractionnel pour chaque famille de rats (témoin et fructose) dans les deux conditions expérimentales. Nous avons classé les résultats en deux groupes, insulino-sensibles et non insulino-sensibles, plus la valeur de la fuite au niveau du plasma. Par souci de clarté, seulement quatre organes représentatifs du groupe insulino-sensible (cœur, muscle squelettique, diaphragme et graisse abdominale) et trois organes du groupe non insulino-sensible (foie, poumon et reins) seront discutés, ainsi que la valeur de la fuite au niveau du plasma. Tous les paramètres du modèle ont été estimés avec une assez bonne précision (coefficient de variation inférieur à 50%, sauf pour la graisse abdominale chez les rats fructose).
Valeurs des coefficients de transport fractionnels (min–1) estimés chez les rats témoin et chez les rats fructose pour quatre organes insulino-sensibles : cœur, muscle squelettique, diaphragme et graisse abdominale. Les valeurs entre parenthèses représentent la précision des paramètres estimés exprimée comme un coefficient de variation , avec .
Comparaison basale en fonction de l’insuline : * p < 0,05, † p < 0,01, ‡ p < 0,001.
| Rats témoin | Rats fructose | |||||||
| Basale | Hyperinsulinémie | Basale | Hyperinsulinémie | |||||
| Organes | k in | k out | k in | k out | k in | k out | k in | k out |
| Cœur | 0,003 | 0,102 | 0,015† | 0,383*(29) | 0,004 | 0,145 | 0,012 | 0,364 |
| (13) | (27) | (31) | (21) | (32) | (44) | (46) | ||
| Muscle | 0,244 | 0,068 | 0,855‡ | 0,239† | 1,578 | 0,478 | 0,918 | 0,188 |
| (21) | (46) | (21) | (21) | (28) | (23) | (11) | (20) | |
| Diaphragme | 0,0018 | 0,079 | 0,005‡ | 0,217* | 0,002 | 0,128 | 0,002 | 0,097 |
| (22) | (42) | (16) | (17) | (14) | (16) | (33) | (55) | |
| Graisse abdominale | 0,0028 | 0,177 | 0,0036 | 0,287 | 0,0031 | 0,258 | 0,012 | 1,335 |
| (15) | (22) | (19) | (18) | (21) | (24) | (132) | (124) | |
| Sang (fuite) | — | 0,329 | — | 0,236 | — | 0,214 | — | 0,149 |
| (18) | (6) | (6) | (18) |
Valeurs des coefficients de transport fractionnel (min–1) estimés chez les rats témoin et chez les rats fructose pour trois organes non insulino-sensibles : le foie, les poumons et les reins. Les valeurs entre parenthèses représentent la précision des paramètres estimés exprimée comme un coefficient de variation , avec .
| Rats témoin | Rats fructose | |||||||
| Basale | Hyperinsulinémie | Basale | Hyperinsulinémie | |||||
| Organes | k in | k out | k in | k out | k in | k out | k in | k out |
| Foie | 0.175 | 0.359 | 0.468 | 0.723 | 0.379 | 0.607 | 0.147 | 0.248 |
| (13) | (19) | (72) | (67) | (42) | (41) | (27) | (28) | |
| Poumons | 0.0086 | 0.173 | 0.014 | 0.255 | 0.016 | 0.280 | 0.012 | 0.202 |
| (29) | (36) | (18) | (18) | (18) | (18) | (21) | (23) | |
| Reins | 0.029 | 0.205 | 0.058 | 0.380 | 0.073 | 0.554 | 0.031 | 0.239 |
| (9) | (20) | (28) | (27) | (37) | (36) | (12) | (14) |
Quelques exemples de représentation des résidus pour les rats témoins sont donnés sur les Figs. 8–10. On peut observer les résidus moyens de l’ajustement du modèle aux données expérimentales pour l’ensemble des points aux différents temps pour les compartiments cœur, muscle squelettique, diaphragme et graisse abdominale (Fig. 8) et pour les compartiments foie, poumons et reins (Fig. 9). Les résidus de l’ajustement du modèle aux activités plasmatiques sont présentés sur la Fig. 10. On peut voir que les résidus se distribuent autour de la ligne centrale zéro, ce qui indique que notre modèle est correct pour la description des données expérimentales du 6-DIG. De plus, les résidus sont en moyenne inférieurs à 0,6% ; leur distribution au cours du temps se fait de manière aléatoire et suit une loi normale (ceci a été vérifié par le test de Kolmogorov–Smirnov).
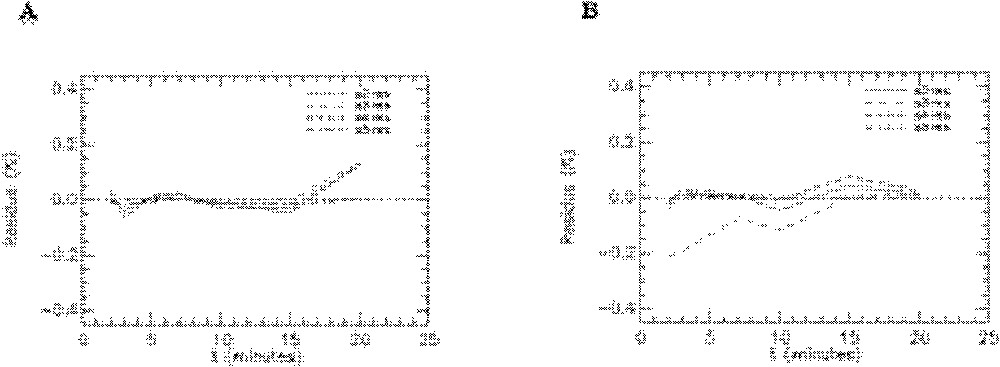
Résidus de l’ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour les compartiments cœur, muscle squelettique, diaphragme et graisse abdominale chez le rat témoin en condition basale (A) et sous insuline (B). s1-res : plasma, s2-res : cœur, s3-res : muscle squelettique, s4-res : diaphragme, s5-res : graisse abdominale.
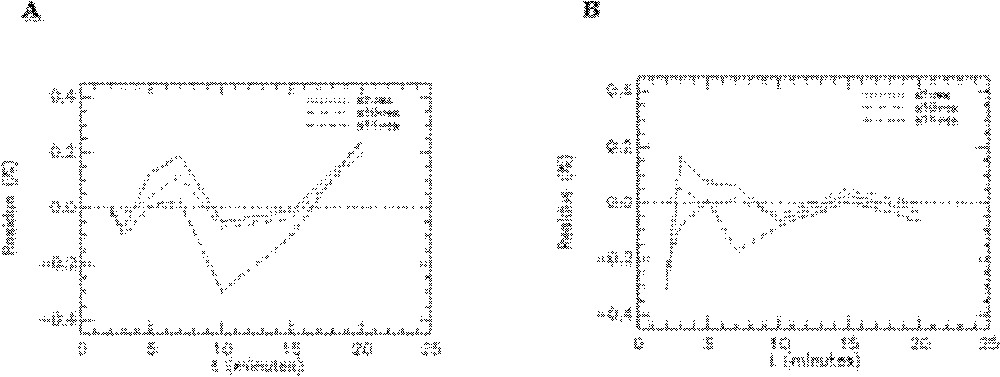
Résidus de l’ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour les compartiments foie, poumons et reins chez le rat témoin en condition basale (A) et sous insuline (B). s7-res : foie, s10-res : poumons et s11-res : reins.
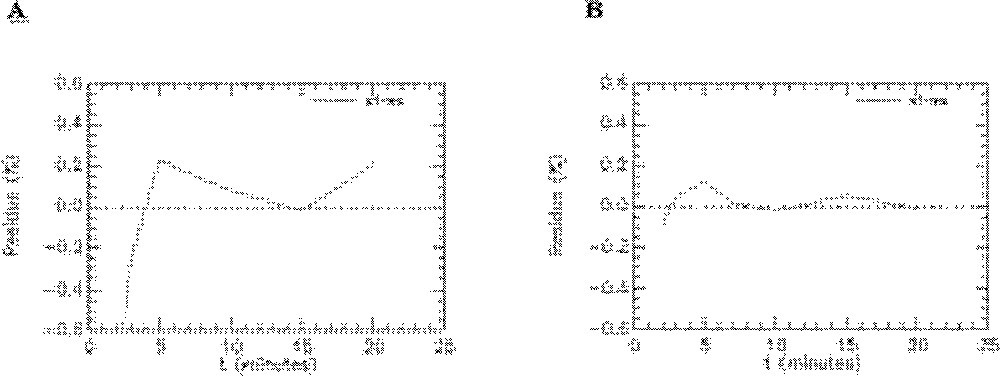
Résidus de l’ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour le compartiment plasmatique chez le rat témoin en condition basale (A) et sous insuline (B).
5.1.2 Comparaison entre les expériences en condition basale et sous insuline chez les rats témoins
Au niveau du compartiment plasmatique, sous l’effet de l’insuline, on observe une diminution de 28%, diminution significative de la fuite irréversible vers les urines : k(0,1) passe de 0,329 (18%) min–1 en condition basale à 0,236 (6%) min–1 sous insuline (p = 0,04) – cf. Tableau 1.
Au niveau des organes insulino-sensibles, on observe une augmentation significative dans le transport du 6-DIG en présence d’insuline. En effet, les valeurs des coefficients de transfert fractionnel d’entrée sont multipliées par 3 (ou 5 pour certains organes), ce qui est en accord avec ce qui était attendu. Au niveau du cœur, le kin (k(2,1)), est multiplié par 5 (0,015 min–1 (31%) sous insuline contre 0,003 (18%) en condition basale ; p = 0,01). Dans le compartiment muscle squelettique, k(3,1) est multiplié par 3,5 (0,244 min–1 (21%) sous insuline contre 0,855 (21%) en condition basale ; p < 0,001). Au niveau du diaphragme, cette captation est également augmentée, le kin (k(4,1)) est multiplié par 3 (0,0018 min–1 (22%) sous insuline contre 0,005 (16%) en condition basale ; p = 0,001). En revanche, dans la graisse, on n’observe pas d’augmentation significative du transport en présence d’insuline.
En ce qui concerne les organes non insulino-sensibles, pour presque tous, l’insuline est sans effet sur la captation du 6-DIG. Il n’y a pas d’augmentation significative du transport vers ces organes, sauf pour le compartiment duodénum, où le transport du 6-DIG est multiplié par 2 sous insuline.
5.1.3 Comparaison entre les expériences en condition basale et sous insuline chez les rats fructose
Dans le compartiment plasmatique, on observe une diminution significative de 30% de la fuite irréversible, k(0,1), sous l’effet de l’insuline. Le coefficient passe de 0,214 min–1 (6%) en condition basale à 0,149 (18%) sous insuline (p = 0,04) – cf. Tableau 2.
Pour les organes insulino-sensibles, l’insuline n’exerce qu’un effet très faible sur la captation du 6-DIG. On n’observe qu’une faible augmentation du transport entre les deux conditions, qui, de plus, est non significative pour la majorité des organes. Par exemple, au niveau du cœur, la valeur de k(2,1) est multipliée par 2,5 (0,012 min–1 (44%) sous insuline contre 0,0046 (21%) en condition basale ; p = 0,18, augmentation non significative).
En ce qui concerne les organes non insulino-sensibles, on n’observe pas de différence significative entre la condition basale et la condition sous insuline. Les valeurs estimées des paramètres sont pratiquement identiques, entre les deux conditions, pour la majorité des organes. Par exemple, au niveau du foie, on a, pour la valeur de k(6,1), 0,147 min–1 (27) sous insuline contre 0,379 (42) en condition basale, avec p = 0,15 (différence non significative).
Il est à préciser que les rats fructose sont hyperinsulinémiques : il est donc normal d’observer un transport de 6-DIG pratiquement identique à celui des témoins en condition basale.
5.2 Modèle de l’étude par détection externe
Les paramètres du modèle ont été estimés avec des coefficient de variation inférieurs à 5% (Tableau 3), cette excellente précision étant la conséquence de l’augmentation dans la durée de l’acquisition (40 min au lieu de 20 dans les précédentes études). Mais celle-ci est aussi due à l’échantillonnage temporel beaucoup plus fréquent (1 point toutes les 30’’, soit 80 points de mesures), pour le sang et le cœur. L’ajustement du modèle aux données, ainsi que les résidus, montrent la bonne qualité du modèle (Figs. 11 et 12).
Valeurs des coefficients de transport fractionnel moyen estimés chez les rats témoin et chez les rats fructose pour le cœur. Les valeurs entre parenthèses représentent la précision des paramètres estimés exprimée comme un coefficient de variation , avec .
Comparaison basale versus insuline : * p < 0,05, ‡ p < 0,001.
| Rats témoin (n = 7) | Rats fructose (n = 6) | |||||||
| Basale | Hyperinsulinémie | Basale | Hyperinsulinémie | |||||
| Organes | k in | k out | k in | k out | k in | k out | k in | k out |
| Cœur (min–1) | 0,085 | 0,53 | 0,110‡ | 0,308 | 0,071 | 0,354 | 0,087‡ | 0,311 |
| (2,97) | (3,05) | (2,26) | (2,18) | (2,20) | (2,36) | (1,80) | (1,84) | |
| Sang (fuite) (min–1) | — | 0,036 | — | 0,051 | — | 0,045 | — | 0,047 |
| (2,5) | (2,83) | (2,28) | (3,27) | |||||
| Tissu périphérique (min–1) | 1,61 | 0,283 | 2,73‡ | 0,212 | 1,9 | 0,227 | 2,81* | 0,269 |
| (2,73) | (2,95) | (2,55) | (2,17) | (2,62) | (2,72) | (3,22) | (3,26) |
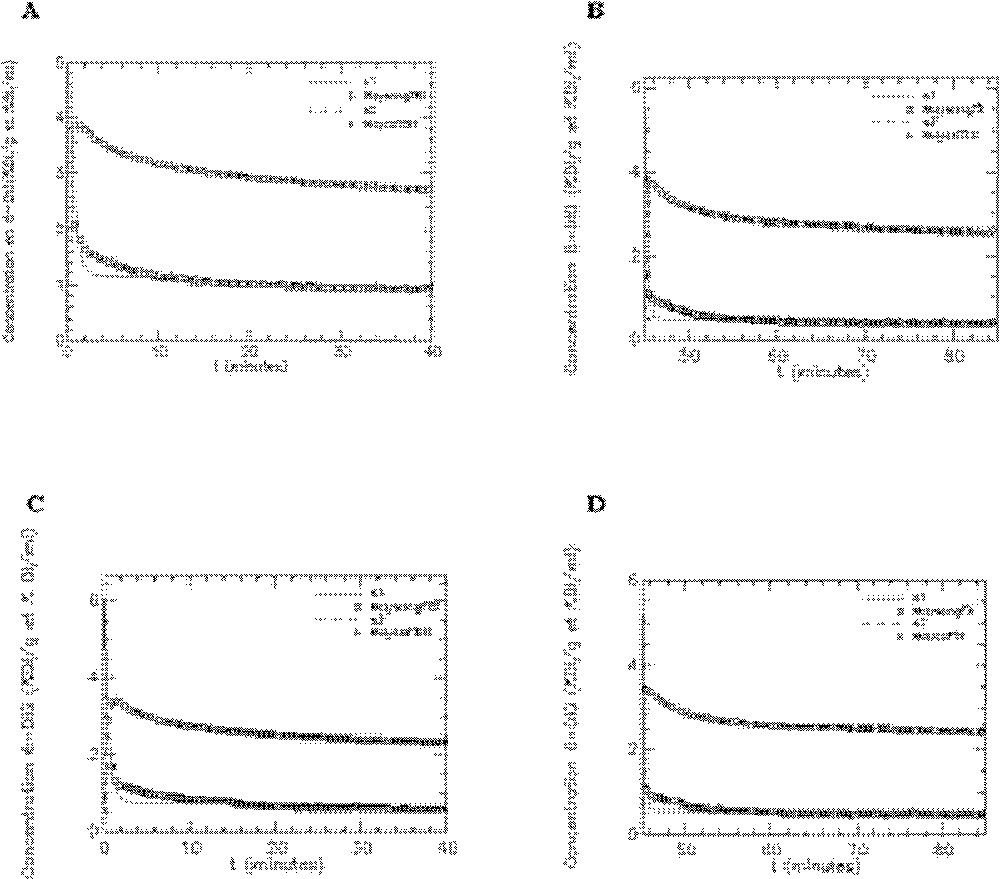
Ajustement du modèle aux données expérimentales obtenues avec le 6-DIG pour l’activité plasmatique (s1) et l’activité cardiaque (s2) (courbes moyennes). A. Rats témoins en condition basale (n = 7). B. Rats témoins sous insuline (n = 7). C. Rats fructose en condition basale (n = 6). D. Rats fructose sous insuline (n = 6). Unité pour l’axe des ordonnées : % dose injectée/gramme d’organe (cœur) et % dose injectée/millilitre (plasma).
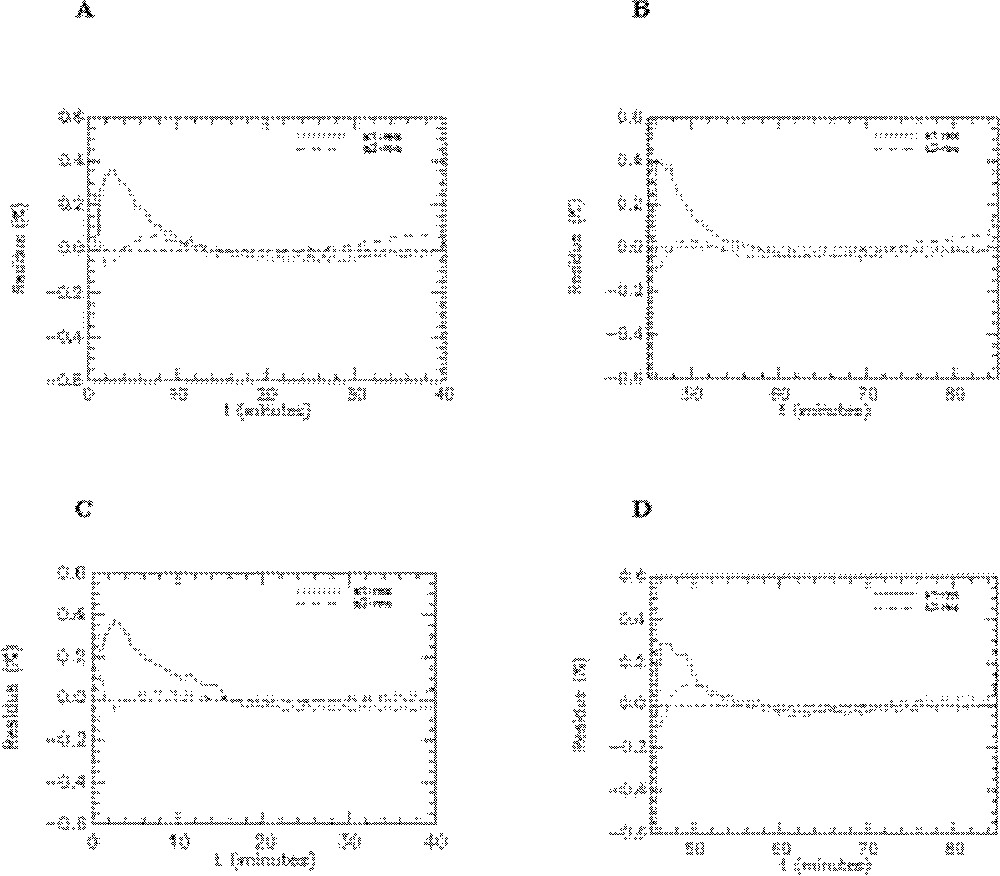
Résidus de l’ajustement du modèle aux données pour l’activité plasmatique (res-1) et l’activité cardiaque (res-2). A. Rats témoins en condition basale (n = 7). B. Rats témoins sous insuline (n = 7). C. Rats fructose en condition basale (n = 6). D. Rats fructose sous insuline (n = 6).
L’approche combinée de l’expérimentation biologique et du modèle mathématique développé dans cette dernière étude permet l’obtention de paramètres ayant des coefficients de variation très petits. Les résultats présentés dans cette étude sont préliminaires. En effet, l’échantillon reste encore trop petit pour qu’on puisse se prononcer de façon définitive, mais ces premiers résultats sont très encourageants.
5.2.1 Comparaison entre les expériences en condition basale et sous insuline chez les rats témoins
Au niveau du compartiment plasmatique, sous l’effet de l’insuline, on observe une augmentation non significative de la fuite irréversible vers les urines : k(0,1) passe de 0,036 min–1 (2,5%) en condition basale à 0,051 (2,83%) sous insuline (p = 0,07) – cf. Tableau 3.
Au niveau du cœur, organe insulino-sensible, on observe une augmentation significative dans le transport du 6-DIG en présence d’insuline : le kin (k(2,1)) passe de 0,085 min–1 (2,97%) en condition basale à 0,11 (2,26%) sous insuline (p = 0,003). La ressortie, kout, montre une diminution significative en présence d’insuline, le kout passant de 0,53 à 0,308.
Les coefficients estimés pour le compartiment 3 montrent une augmentation significative du transport du 6-DIG vers ce compartiment, le kin passant de 1,61 en condition basale à 2,73 sous insuline (p < 0,005). La ressortie, kout, n’augmente que très faiblement et de façon non significative en présence d’insuline.
5.2.2 Comparaison entre les expériences en condition basale et sous insuline chez les rats fructose
Dans le compartiment plasmatique, on observe une diminution non significative de la fuite irréversible, k(0,1), sous l’effet de l’insuline – cf. Tableau 3. Le coefficient passe de 0,046 (2,28%) min–1 en condition basale à 0,032 (3,27%) min–1 sous insuline (p = 0,6).
Pour le compartiment cœur, l’insuline n’exerce qu’un effet faible sur la captation du 6-DIG. On n’observe qu’une faible augmentation du transport entre les deux conditions. La valeur de k(2,1) passe de 0,071 (2,2%) min–1 en condition basale à 0,087 (1,8%) min–1 sous insuline (p = 0,003). Cette faible augmentation demeure quand même significative.
Un test t sur séries appariées a été réalisé sur le rapport k(2,1)/k(1,2) pour les deux populations de rats et pour les deux types de conditions expérimentales. Pour les rats témoins, on a observé une différence significative du rapport entre condition basale et condition sous insuline, le rapport passant de 0,16 à 0,35 (p = 0,0012), ce qui correspond à une augmentation de la captation nette du 6-DIG sous insuline par le cœur chez le rat témoin. Chez les rats fructose, l’insuline n’augmente que très faiblement ce rapport (0,20 en absence d’insuline contre 0,28 en présence de l’hormone, augmentation non significative avec p = 0,11).
6 Discussion
Dans cet article, nous présentons les résultats de notre étude concernant la quantification du transport du glucose à l’aide de mesures in vivo de la concentration d’un traceur, le 6-DIG. Dans ce but, deux approches expérimentales ont été réalisées, ainsi que le développement d’une modélisation mathématique, permettant de mieux étudier les cinétiques du transport vers différents organes.
La modélisation mathématique a posé au départ quelques problèmes. Ainsi, le modèle initialement proposé était de type caténaire à trois compartiments (plasma où a lieu la fuite irréversible, espace interstitiel et espace cellulaire) avec un échange linéaire de matière entre les compartiments plasmatique et interstitiel et un échange non linéaire (michaëlien) entre les compartiments interstitiel et cellulaire. Ce modèle, où sept paramètres étaient à évaluer, ne pouvait pas donner satisfaction, compte tenu du nombre de points de mesure, trop faible pour qu’on puisse aboutir à une identification numérique satisfaisante. Nous avons donc envisagé un modèle, toujours à deux compartiments, mais avec échanges uniquement linéaires, ce qui se justifiait par l’utilisation de faibles concentrations de traceur. Dans la cinétique du transport transmembranaire du glucose de type michaëlien, entre deux compartiments i et j, on a, entre les coefficients de transferts (kij) et (kji), les quantités de traceur (qi) et (qj), les constantes de Michaëlis (Kmi) et (Kmj) et les vitesses maximum VMi et VMj, les relations 〚12〛 :
Dans le cas d’une utilisation de faibles concentrations de traceur, la quantité de traceur étant négligeable devant le Km, on peut donc effectuer une approximation linéaire du modèle 〚9〛. De plus, nous supposons aussi que le métabolisme de la substance « tracée » (le glucose) est à l’état stationnaire (voir annexe). Dans ce cas, les coefficients de transfert fractionnels sont donnés par :
Finalement, nous avons adopté un modèle plus global, tenant compte de tous les organes étudiés, afin d’être le plus proche possible de la réalité biologique. Le modèle mathématique proposé est ainsi un modèle multicompartimental mamillaire et linéaire, qui décrit le transport du 6-DIG (entrée et sortie) entre le compartiment plasmatique et les compartiments des différents organes impliqués dans l’étude expérimentale.
La simplicité d’un tel modèle s’explique par le fait que le nombre de points par organes (compartiments) était faible (sept points), ce qui nous a donc limités dans la structure du modèle. Ce modèle a fourni un ajustement aux données qui était très satisfaisant, puisqu’il tenait compte de l’ensemble des 84 points expérimentaux (sept pour chacun des 11 organes étudiés et sept pour le sang). Le résultat de l’ajustement du modèle aux valeurs expérimentales nous a donné une estimation précise des paramètres (kij) du modèle, c’est-à-dire avec des coefficients de variation inférieurs à 50%. Afin d’obtenir une identifiablité globale du modèle, nous avons imposé quelques contraintes au modèle, en supposant connus le volume du compartiment central ainsi que la masse de chaque organe (compartiments 2 à 12). Ce compartiment central est censé représenter le plasma, mais c’est en réalité un pool où ont lieu des échanges rapides entre plasma et érythrocytes 〚25〛. Dans notre modèle, nous ne tenons pas compte de ces flux de matière extrêmement rapides ; on les néglige face aux flux entre plasma et compartiments intracellulaires des différents tissus impliqués dans l’étude qui ont, quant à eux, des cinétiques un peu moins rapides. Il faut bien comprendre que ce modèle a été utilisé dans un but précis, la mesure du transport fractionnel du traceur entrant et sortant des différents compartiments tissulaires. Les compartiments extracellulaires sont supposés compris dans le pool organe ; ainsi chaque compartiment organe contient l’epace extracellulaire (ou interstitiel) plus l’espace intracellulaire. Une telle contrainte a été imposée au modèle pour des questions d’identifiabilité numérique. En effet, si, pour chaque organe, on sépare l’espace extracellulaire de l’intracellulaire, on a un compartiment de plus, qui réalise des échanges de matière (flux bidirectionnels), donc deux coefficients de transfert de plus pour chaque organe à estimer, ce qui rend le modèle non identifiable numériquement, puisqu’on lui demande d’estimer 22 paramètres en plus, chose impossible, compte tenu du nombre insuffisant de points expérimentaux.
Une étude du transport du 6-DIG faite sur l’adipocyte a fourni des valeurs de Km et VM pour la condition basale et la condition sous insuline 〚5〛. De notre côté, à partir de la constante d’entrée k(2,1) obtenue au niveau du cœur et du Km (adipocytes tiré de la littérature 〚5〛), nous avons déterminé les valeurs de VM et nous les avons comparées aux mêmes valeurs pour les adipocytes. Les résultats obtenus sont les suivants :
- • condition basale, VM = 1,2×10–8 mol (min ml)–1 contre 1,1×10–8 mol (min ml)–1 pour les adipocytes ;
- • condition sous insuline (VM = 6×10–8 mol (min ml)–1 contre 9,1×10–8 mol (min ml)–1 pour les adipocytes).
Les valeurs calculées semblent raisonnablement en accord avec les valeurs obtenues pour les adipocytes. Le modèle linéaire permet donc de retrouver des valeurs de VM et de Km de même ordre de grandeur que celles trouvées dans la littérature.
L’aspect le plus original du modèle est qu’il prend en compte le transport du 6-DIG dans pratiquement la totalité de l’organisme, à travers les mesures réalisées au niveau de 11 organes simultanément, plus le sang. Ce modèle global est meilleur que 11 modèles différents à deux compartiments, tant au point de vue de la structure que du point de vue de l’estimation. L’ajustement du modèle aux données a fourni une assez bonne estimation des paramètres avec des coefficients de variation, ainsi que des écarts types et des intervalles de confiance à 95%, globalement satisfaisants.
Notre analyse montre une augmentation significative de la distribution du 6-DIG dans les tissus insulino-sensibles (cœur, muscle squelettique et diaphragme). En effet, les coefficients de transfert fractionnel sont multipliés par trois au minimum pour le coefficient d’entrée et par deux au minimum pour le coefficient de ressortie chez le rat témoin sous insuline, par rapport au rat témoin en condition basale. En revanche, une augmentation du transport est observée chez le rat fructose entre condition basale et condition sous insuline pour les tissus insulino-sensibles, mais de manière non significative.
Les cinétiques d’équilibre du 6-DIG, entre le plasma et les tissus, observées pour l’ensemble des organes de notre étude sont très rapides, sauf pour le muscle et le cerveau. Nous avons observé que notre modèle s’ajustait mal aux données obtenues pour le muscle squelettique : ce résultat pourrait venir du fait que les cinétiques de transport au niveau du tissu musculaire s’effectuent de façon très hétérogène. Un modèle régional très complexe, faisant intervenir 15 compartiments a été utilisé, par l’équipe de Bonadonna et Cobelli 〚32–34〛, pour étudier le transport d’analogues du glucose au niveau du tissu musculaire squelettique. Notre modèle est certainement mal adapté à ce type d’étude, puisqu’il ne tient pas compte de l’hétérogénéité de ce tissu.
L’organe discriminant de cette étude, c’est-à-dire celui qui montre la plus grande différence entre condition basale et condition sous insuline, est le cœur. Nous avons donc sélectionné le cœur (insulino-sensible) pour réaliser une étude en détection externe. Pour cette nouvelle étude, un nouveau modèle mamillaire à trois compartiments adapté a été proposé. La stratégie d’échantillonnage, améliorée dans cette expérience, a été réalisée conjointement à la mise au point du modèle. Une expérience doit être planifiée pour faciliter l’estimation des paramètres du modèle 〚35〛. L’acquisition de données s’est faite de manière à obtenir une très bonne précision sur les paramètres estimés du modèle, c’est-à-dire en utilisant le nombre de points expérimentaux nécessaire au bon ajustement du modèle aux données.
Une tentative de modélisation non linéaire a été réalisée, mais les résultats obtenus ont été très décevants quant à la précision des paramètres estimés. En effet, nous avons considéré dans ce modèle que les coefficients de transfert fractionnel étaient décrits par une équation de Hill, de la forme :
Le modèle linéaire a fourni de meilleurs résultats que le modèle non linéaire, même si ce dernier semblait être le plus approprié pour l’étude en détection externe, car l’hypothèse de quasi-stationnarité n’était pas réellement vérifiée pour ce protocole.
7 Conclusion
Ce travail montre les différentes étapes par lesquelles nous sommes passés pour aboutir à un modèle mathématique décrivant les cinétiques de transport du 6-DIG in vivo, ainsi que la mise en place d’un nouveau modèle pour une étude en détection externe. La précision de l’estimation des paramètres du modèle, l’ajustement du modèle aux données expérimentales et les résidus calculés sont très satisfaisants, mais ce modèle peut encore être amélioré. En effet, la mise au point d’un modèle régional (situé uniquement au niveau du cœur) tenant compte du compartiment espace interstitiel, associée à une étude de détection en imagerie SPECT (Single-Photon Emission Computed Tomography) est en préparation sur le petit animal.
Abridged version
The mathematical modelling of experimental data could be an excellent method to explore the mechanisms implied in the perturbations of glucose metabolism. Thus, starting from a symbolic formulation like compartmental modelling, it could be possible to develop a theoretical basis for the observation and to consider the best-adapted experiments for the study.
Our work concerns the development of a compartmental model able to highlight in vivo pathological variations of glucose transport by the intermediary of a tracer, the 〚123I〛 6-deoxy-6-iodo-d-glucose (6-DIG).
The experimental protocol consisted in a bolus injection of the tracer in a population of rats presenting such disorders of glucose transport (fructose rats) and in a population of reference rats. The activity of the tracer was measured in several tissues (eleven) and plasma at different times.
Various studies on the estimation of 6-DIG kinetics parameters were realised. A first, study was carried out with a three-compartment model, including plasma, extracellular space and intracellular space, with linear bi-directional flows between the plasma compartment and the interstitial compartment and non-linear bi-directional flows between interstitial space and intracellular space. The seven parameters of the model that we had to estimate from 12 experimental points were not uniquely identifiable and provided coefficients of variation higher than 100%. This over-parameterisation suggested a new approach: first, the introduction of a simplified model with only two compartments; second, a refinement in temporal sampling joined to an increase in size of the rats population studied at each time. Then, a second study on a uniquely identifiable model with two compartments provided significant variation coefficients but an over-estimate of the leak at the level of the injection compartment. Finally, we have chosen a global mamillary model close to biological reality, taking into account the results obtained with the 11 tissues, model obviously simplified (without interstitial space), which enabled us to uniquely identify the parameters. This model had the advantage to increase the number of freedom degrees of the system (84 experimental items against 14 for the regional model) and thus to improve the precision of the estimations of the model’s parameters.
A fourth study, whose suitable experimental design was elaborated simultaneously with the development of a three-compartment regional model for external detection, without extracellular compartment and with measurement on two compartments (blood and heart), provided parameters estimated with variation coefficients lower than 5%. And also, we obtained a good fit, as a consequence of the increase in the duration of acquisition (40 min instead of 20) and of a temporal sampling definitely more significant (a point every 30 s and a total of 80 measurement points). This last model allowed us to extract discriminating parameters between the reference and insulin-resistant rats, then in- and out- fractional transfer coefficients of the cardiac tissue comportment.
This study has pointed out the role of the heart as marker of the glucose transport disorder and will permit a further project, consisting in building a regional model applicable to SPECT (Single Photon Emission Computed Tomography) imaging. This model would take into account, in addition to an input function and an intracellular compartment, an extracellular compartment. Starting from this regional model, it will be necessary to set up a measurement procedure and a more complete data acquisition procedure taking into account this new compartment.
Annexe
État stationnaire
Un état stationnaire existe dans un système contenant un mélange de substances si, malgré les phénomènes de transport ou de transformation, et parce que les vitesses d'élimination sont égales aux vitesses de remplacement, la concentration de ces substances dans tout compartiment reste constante dans l'intervalle de temps considéré 〚36〛.
Nous avons considéré dans ce travail le système étudié à l'état stationnaire. La fonction d'entrée (injection en bolus du traceur) introduite dans le système n'exerce a priori aucun effet perturbateur sur l'équilibre pour l'expérience du clamp, puisqu'elle ne prend effet qu'une heure après le début de la perfusion d'insuline. Afin de déterminer l'équation de stationnarité du glucose, on considère un système constitué de N compartiments ; notons Qi0 la quantité de glucose présente naturellement dans le compartiment i (l'indice supérieur 0 signifie que la grandeur est prise à l'état stationnaire).
Si f0ij désigne la quantité de substance passant, à l'état stationnaire, du compartiment j au compartiment i, par unité de temps, l'équilibre au niveau de chaque compartiment implique :
Formalisme général utilisé
Si on applique les équations de base d'un modèle à n compartiments 〚18, 37〛 :
(où fij représente le flux de matière du compartiment j au compartiment i).
Pour notre modèle supposé linéaire et stationnaire, on obtient le système différentiel suivant :
où kij est le paramètre définissant le transfert fractionnel de matière du compartiment j au compartiment .
Les erreurs de mesure additives et non corrélées sont supposées de moyenne nulle et n'apparaissent donc pas dans ces équations.
La notation vectorielle 〚9〛 de l'ensemble de ces équations différentielles décrivant les cinétiques du système dynamique étudié est la suivante :
- • équation d'état,
- • équation d'observation,
- • vecteur de commande,
- • matrice d'état,
- • vecteur des n-variables d'état du système
- • vecteur des réponses radioactives mesurées pour le plasma et les organes, .
K, la matrice d'état (constante), de terme général kij, égal au transfert fractionnel de matière du compartiment j au compartiment ) et de terme diagonal kii, qui vérifie :
C est une matrice d'observation constante et diagonale et mesure la concentration dans le compartiment i ; c11 est donc égal à l'inverse du volume de distribution pour le compartiment plasmatique, tandis que les autre éléments sont égaux à l'inverse de la masse de chaque organe intégré dans le modèle.



