1 Introduction
It is well known that complexity in biology results in kinetics of numerous mechanisms, which involve high intrinsic non-linearities. For example, enzymatic reactions far from equilibrium may lead to steady and unsteady unstable states with, however, either local organization such as space structures, limit cycles and multistates transitions or deterministic chaos [1,2]. The same situation may also arise when more simple kinetics take place in particular conditions: presence of curved interfaces [3], effects in electric fields [4], transition critical point [5]. The coupling with hydrodynamic processes in models of fluid biological membranes was also taken into account [6]. On the basis of the bifurcation theory, the fundamental background of all these fascinating phenomena was formulated and developed by the Brussels school of Prigogine, Glansdorff, Nicolis and co-workers at the end of the last century [7,8]. They enter the frame of the so-called order by fluctuations, which creates local dissipative structures in far-from-equilibrium conditions.
Another kind of unexpected situations, however, not resulting from the non-linear character of the chemical mechanisms, may arise from the complexity of the space environment in which the chemical reactivity takes place. In other words, in addition to the intrinsic role of the chemical reactivity, we have now to analyse the geometric aspect of the domain concerned and the nature of the boundary conditions. This justifies the interest in the study of reactions and matter transfers in strong confinement encountered in disperse media containing micro (1–10 μm) and nano (10−2–10−3 μm) objects, droplets, bubbles, solid crystals or particles. All these small systems are, nevertheless, still considered as macroscopic entities, according to the magnitude of the fluctuations. They behave as chemical reactors submitted to very high internal pressures (102–104 atm) compared to the external pressure. Hence, we then expect that thermodynamic and kinetic properties should be significantly influenced by the smallness of the size of the object. This was shown in detail in our previous papers through numerous examples from atmosphere, sonochemistry and metallurgy [9,10]. One of the main interests, among other points, is that small objects give the potentiality to obtain products of reactions that would not be formed in large reservoirs. We will summarize in the next two sections the main theoretical results obtained for the influence of the confinement on some thermodynamic and kinetic properties, and then put the emphasis on applications to living systems in the last section.
2 Influence of the size of an object on the equilibrium constant
Among the thermodynamic and kinetic properties we shall restrict our final result to the chemical equilibrium and kinetic constants, by comparing the same reaction at the same temperature and the same external pressure, for small and large non-deformed objects. We first start with uncharged systems.
2.1 Uncharged systems
As well known from classical thermodynamics, the chemical equilibrium constant K is defined by:
| (1) |
| (2) |
In a liquid or in a solid phase, the standard chemical potential reads:
| (3) |
In a vapour phase, the standard chemical potential reads
| (4) |
At the surface of tension of a spherical object and under mechanical equilibrium conditions, the classical Laplace law may be applied:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Remark
When dealing with chemical reactions (including matter transfers) in multiphase systems, the ratio appears only through the reactive components inside the confined region.
2.2 Charged systems
When a reaction occurs in a spherical charged droplet in the presence of a vapour phase, the induced electric field polarizes the vapour, the hydrostatic pressure and the surface tension being then dependent on the intensity of the field [9,12]. The ratio reads then:
| (14) |
| (15) |
The predictions to be obtained from equations (7)–(11), (14) and (15) are the following:
- (i) high values of surface tension or of surface stress and high curvature influence the equilibrium constant, the effect being, however, much more important for bubbles than for droplets, and also important for small solid particles according to their high surface stress;
- (ii) charges on droplets reduce this effect (equation (14));
- (iii) the equilibrium constant of reaction taking place in the vapour in contact with a charged droplet depends on the electric field pressure and weakly on the polarization term (equation (15));
- (iv) the expansion (or shrinkage) contribution ( plays a significant role only in very viscous media (equation (9));
- (v) the role of the global stoichiometry of the reaction is important for reactions in bubbles (equations (8) and (9)) or in vapour around droplets (equation (15)) as well as the reactional dilatation in droplets and solid particles (equations (7), (10), (11) and (14)).
For a charged droplet in the presence of an insoluble liquid phase, we must take into account the thickness of the double layer established in the presence of ionic amphiphilic molecules. The prediction on should be qualitatively identical to those obtained for the droplet in presence of vapour.Remark
3 Influence of the size of a bubble on the kinetic constant
In the Eyring–Polanyi theory of the activated complex, it is assumed that the activated complex X is in equilibrium with the initial components.
A reaction between molecules M may be decomposed in two reactions involving the formation of an activated complex: a direct reaction of formation of the complex and the reversed reaction where and are the direct and antagonist kinetic constants related to the standard affinities of and . The kinetic constants read then:
| (16) |
| (17) |
Comparing, for the same reaction of activation, at the same temperature and external pressure, the direct kinetic constant in a small bubble and in a non confined gas, we get from equations (2), (4), (5) and (16):
| (18) |
| (19) |
| (20) |
4 Reactions in living system
4.1 Influence of the size of a pulmonary alveola on typical reactions
A pulmonary alveola is formed by one layer of epithelial cells separated from the gas by a layer of 1 μm, called hypophase (Fig. 1). Phosphoglyceric components and particularly lecithins are adsorbed at the interphase air–hypophase. In practice, for human newborn children and adults, the typical radii lie between 5 and 70 μm. As lecithin is a surfactant, during compression–depression cycle of the interfacial film [13,14], the surface tension varies from a very weak value close to 0 to 50 mJ m−2 (Fig. 2).
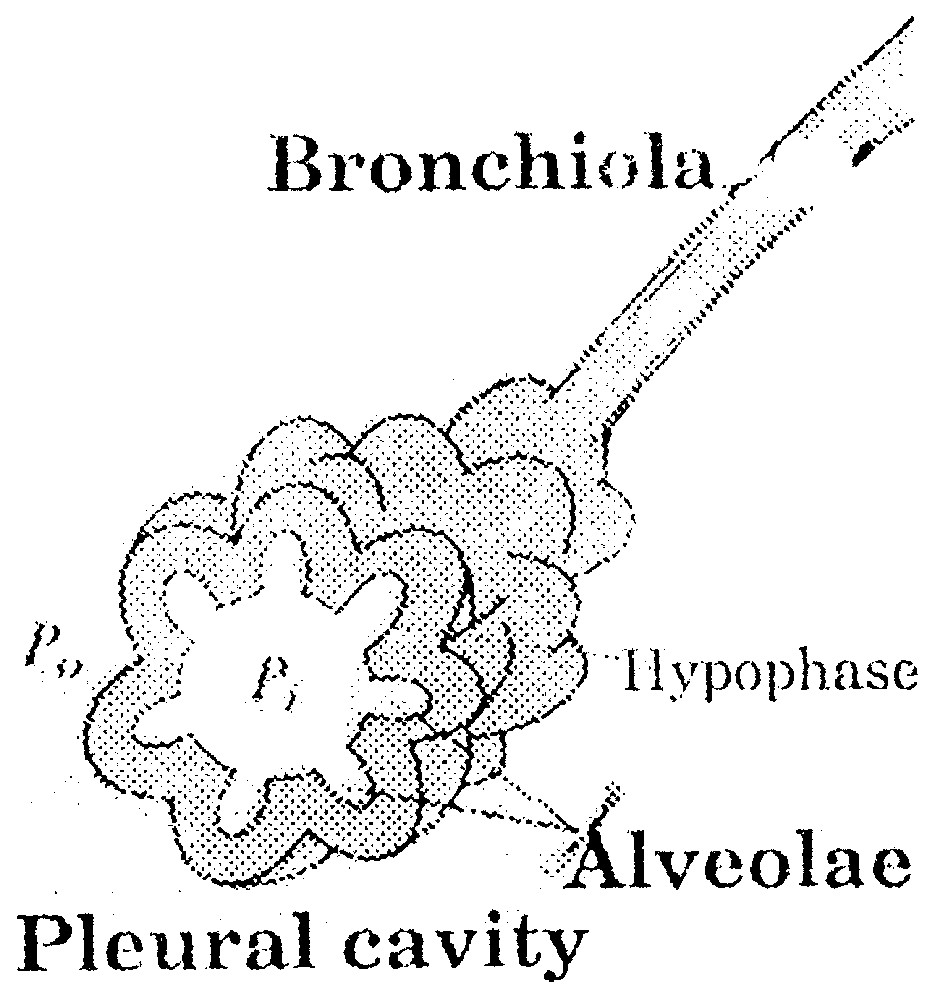
Pulmonary alveola.
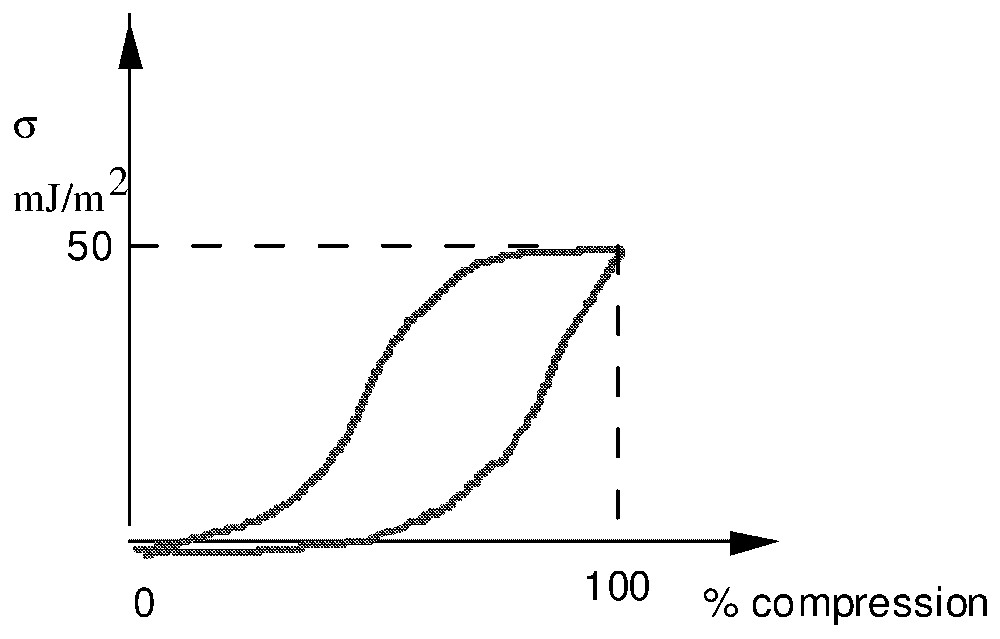
Surface tension in compression cycle.
Decomposition of the nickel carbonyl accidentally present in the atmosphere may occur in the pulmonary alveolæ following the stoichiometric scheme:
Considering as a first approximation that the alveola is a sphere, we calculate from equation (8). Taking σ=50 mJ m−2 and atm, we obtain for different values of the radius R (Table 1).
Ratio of equilibrium constant versus radius of alveolæ for nickel carbonyl decomposition
| R (μm) | |
| 5 | 0.58 |
| 10 | 0.75 |
| 50 | 0.94 |
| 100 | 0.96 |
Hence, the smallest the size of the alveola, the less efficient is the nickel carbonyl decomposition.
4.2 Role of the size of a solid dust in pulmonary alveola
Let us now draw our attention to the influence of the size of Ni particle on the equilibrium constant of the Ni carbonyl decomposition. Due to the breaking of the lattice of Ni, which creates vacancies and thus an increase of atomic volume, we may reasonably assume that v0Ni≅13 cm3 mol−1. In a vacuum, SNi≅2500 mJ m−2. However, in the alveola, Ni is oxidised, so that SNioxidised≅1500 mJ m−2. Due to the interactions with proteins present in the alveolar hypophase, the surface stress of Ni may be considerably lowered and SNicoated≅130 mJ m−2. In the presence, however, of proteases that destroy the proteins, one could expect that 500<SNicoated+protease<800 mJ m−2. Let us chose SNi≅600 mJ m−2 and T=310 K. Under these conditions, we obtain the values of displayed in Table 2 by using equation (10).
Influence of the size of a Ni particle on the equilibrium constant of decomposition of Ni carbonyl in the lung alveola
| R (μm) | |
| 1 | 0.99 |
| 0.1 | 0.94 |
| 0.01 | 0.54 |
| 0.005 | 0.30 |
In conclusion, the presence of large Ni particles in the pulmonary alveolæ favours the decomposition of Ni carbonyl.
4.3 Gallstones dissolution
As shown by Houton et al. [15], cholesterol particles are solved in a mixture water–lecithin and form micelles.
The reaction reads:
Role of the size of a cubic crystal of gallstones on the dissolution equilibrium constant
| l (μm) | |
| 1 | 1 |
| 0.1 | 1.1 |
| 0.01 | 2.5 |
| 0.005 | 6.4 |
As expected, small crystals are more soluble than large ones.
4.4 Role of the size of a gas vacuola on the kinetic constant
Consider a binary elementary collision leading to an activated complex. The reaction of formation of H2S in a vacuola of a sulphur bacteria (Fig. 3) [18] might proceed by such a mechanism.
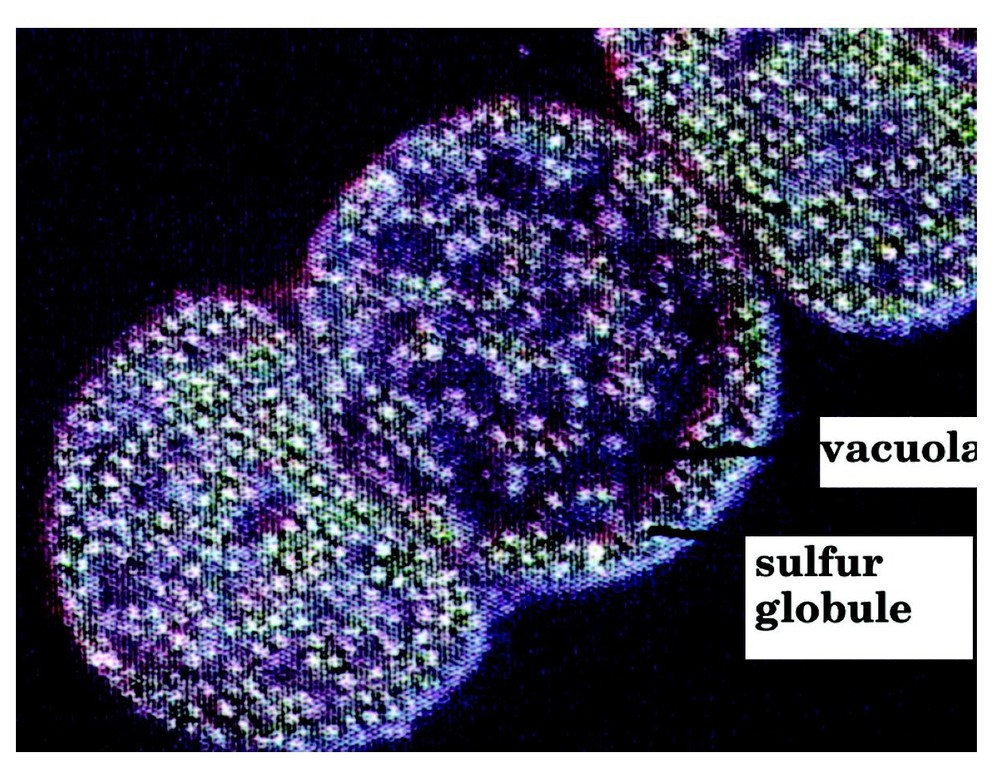
Vacuolæ and sulphur globules in Thiomargarita (from [18]).
For a reasonable value of σ=30 mJ m−2 and atm, values of are obtained from equation (20) for any kind of binary activation process in a perfect gas phase (Table 4).
Role of the size of a gas vacuola on the kinetic constant for any binary activation process
| R (μm) | |
| 10 | 1.1 |
| 5 | 1.25 |
| 1 | 2.6 |
| 0.5 | 4.9 |
| 0.1 | 50 |
The smallness of the alveola has thus an important influence on the kinetic constant. In agreement with the Eyring's theory, high confinement increases significantly the activation process.
5 Conclusion
Whether the biologist is concerned with the properties of a system, with an equilibrium constant, or with a reaction rate, the solution of the problem requires not only a knowledge of the intrinsic mechanisms but also of the confinement in which they take place. To understand such a problem, one must know the nature of the space environment, which, in living systems, is usually a very complex region. In particular, the existence of micro- and nano-subsystems like organelles in which numerous biochemical reactions occur, may significantly influence thermodynamic and kinetic properties. One must also know fundamental relations that come under statistical mechanics, electrostatics and capillarity. As it is not yet possible to carry out such a programme in every detail, as already presented in previous papers [10,11], we have restricted our goal to give in a concise form a brief comprehensive survey of the equations we need. They clearly show the influence of the size of objects (droplets, bubbles, solid particles) and of surface tension (or surface stress) on equilibrium and kinetic constants. To illustrate the interest of our theoretical approach, we have presented examples of biological interest: reaction in pulmonary alveolæ, dissolution of gallstones and reactions in gas vacuolæ of bacteria. It appears that the confinement may significantly influence chemical constants. Other examples in living systems are at present under investigation and shall be submitted to publication later on. According to our results, attention must also be drawn on experiments performed in tubes as the replicas of real processes that occur in living systems. In addition, artefacts may be also induced by external effects. For example, by sonication and depending on the frequencies imposed, cavities are created, which modify the chemical reactivity, as shown in our previous paper [9].
Acknowledgements
The authors thank Prof. J. Ricard for his invitation to the meeting on ‘Complexity in Biology’ at the ‘Institut Jacques-Monod’, Paris, France. We are extremely grateful to our colleagues J. Ricard, R. Verger, H. Lafont, J. Claverie, P. Gontrand, and A. Zamora for very stimulating discussions. This work was sponsored by the ‘Institut Jacques-Monod’ and the CNRS.



