1 Introduction
Conflicts with human populations remain the major threat to carnivore persistence [1–4]. Carnivore may kill domestic and game animals as well as threaten humans and, as a consequence, many carnivore species have been facing widespread persecution. Protected areas often offer insufficient protection, as they may be too small to encompass full home ranges, and substantial mortality is caused by contact with people at reserve borders [2]. Large carnivore conservation may be successful in the long term only if people can accept free ranging predators in their area [5,6]. This can be achieved if adequate conservation strategies maintaining viable populations while allowing removal of individuals are implemented [7].
Focusing on the recent expansion of the wolf Canis lupus in Western Europe, this paper addresses the dual nature of the conservation problem raised by large carnivores: regulating the population to address public concern, while maximizing population viability. The wolf is one of the most studied and well known of all wild mammal species [8]. Many aspects of its biology have been documented: sociality, reproduction, dispersal, effects of predation, activity patterns, diseases, genetics, population management (see [9] for a synthesis of our knowledge of wolf biology). This should be conducive to efficient design and implementation of management plans.
After centuries of persecutions, wolves have been expanding in Europe and USA over the last decade, leading to raging conflicts with livestock farming activities [7]. In Europe, wolf populations show significant growth, particularly in the Western Alps [10] and Scandinavia [11,12], where respectively extensive sheep and reindeer farming were not prepared to face the return of these predators. Government action plans [13,14] must deal with wolf protection under the Bern Convention and the European Council Directive 92/43/EEC (‘Habitat Directive’), which forbid wolf killing to prevent serious damage to livestock but allow for some derogations, provided that there is no other satisfactory solution and that the exception will not be detrimental to the survival of the population concerned. As Mech [15] pointed out, the question is no longer ‘Will we ever hear the howl of the wolf again?’ but ‘How many howls are enough?’ In fact, management plans should allow elimination of individual wolves or packs without threatening the population persistence, and should provide visible actions addressing public concerns. Many failures in carnivore conservation can be ascribed to lacking consideration of the human dimension [16,17]. For example, wolves reintroduced in Michigan Upper Peninsula in 1970 were all killed eight months after being released, and Hook and Robinson [18] found that ‘the wolf's future in Michigan depends upon the attitudes of Michigan residents’. In this most conflictive context, the wolf (Canis lupus) crystallizes several key issues of ecological sciences: the conservation of an endangered species, the control of a biological invader, and the design of harvesting strategies that can achieve both objectives. Conservation, control and harvesting are three aspects of the same general problem: population management [19]. The traditional dissociation of these disciplines is pervasive, and the wolf case shows the potential of a synthetic paradigm. Designing effective conservation and management plans is a task that requires the development of specific demographic models. Conservation biology owes much of its credibility to modelling [20–22]. Insights gained from modelling should never be dissociated from the model's assumptions [23] and conservation biologists must be aware that for conflictive species, such as large carnivores, population model conclusions are likely to be contested in a court [24].
In this paper, we develop stochastic models to study the dynamics of a recolonizing wolf population and compare several management strategies, with an emphasis on the wolf population in the Western Alps. We model a zoning strategy where wolves are tolerated in a restricted area only, and an adaptive management strategy where some wolves are removed whenever the annual population growth rate reaches a given threshold. We examine whether such strategies would make it possible to maintain a viable population while allowing for population control to minimize depredation on livestock.
2 Methods
2.1 Wolf biology
The unit of a wolf population is the pack, consisting of a breeding pair and their offspring (from one or more generations [25,26]). The dominant adult female in each pack breeds every year, usually producing a single litter. Subordinates rarely become dominant in their natal pack [27]. Pups reach their adult size by winter, and most of them disperse as yearlings [28–30]. A dispersing wolf may colonize a vacant territory, or it may join another pack and replace a missing breeding member [29,31–33]. When both breeding adults die, the pack usually disintegrates, leaving the territory vacant and creating an opportunity for recolonization [33]. Wolves are not habitat-specific and can live wherever they have sufficient food resources and are tolerated by humans [7,34]. There is no simple relationship between human density and wolf persistence in a given area [35]. For example, in the Abruzzi region, in Italy, wolves survive alongside 29 people/km2, whereas they have been exterminated amongst 1.33 people/km2 in Sweden [36].
2.2 Life cycle modelling
Our models are based on the wolf life cycle described in previous individual-based model papers [37,38] and refined with the few available demographic data on European wolves [12,39]. The population is divided into several stages defined by age and breeding status. The algorithms allow an individual-based approach. Wolves present in packs are pups (0–6 months), juveniles (6–18 months), subadults (18–30 months), adults (> 30 months) and pack leaders that are at least 18 months old. Wolves outside packs are juveniles that have dispersed from their packs and stay one year as lonely wolves since they are too young to reproduce.
All our population projections involve the same sequence of events. (i) Winter mortality affects the whole population and accounts for annual mortality. (ii) Dispersal of subordinates is conditional to the survival of the breeding pair: if the breeding pair disappears (both partners die), remaining pack members disperse, but if at least one breeder survives, subordinates disperse with some probability specific to their class. (iii) Dispersing wolves search for a vacant territory and a partner. We neglect the probability that a dispersing wolf joins an extant pack where no breeder is missing. (iv) Reproduction takes place in spring if a breeding pair is present. Age at first reproduction is always 22 months (dispersing juveniles must wait one year before looking for a mate). Only one litter is produced per year. (v) Pup mortality takes place in summer and accounts for infectious diseases that are often deadly for pups. In autumn, the distribution of wolves in the population is censused and then updated according to the following scheme (see also Fig. 1).
- 1. Surviving pups become juveniles.
- 2. Surviving juveniles that have not dispersed become subadults.
- 3. Surviving juveniles that have dispersed become dispersing wolves.
- 4. Surviving subadults that have not dispersed become adults.
- 5. Surviving subadults that have dispersed and found a territory and a mate become pack breeders.
- 6. Surviving adults that have not dispersed remain in the adult class.
- 7. Surviving adults that have dispersed and found a territory and a mate become pack breeders.
- 8. Dispersing wolves that found a territory and a mate become pack breeders.
- 9. Surviving pack breeders keep the same status.
- 10. Surviving pack breeders give birth to pups.

Life cycle graph for a wolf stage-structured population. P: Pups, J: Juveniles, S: Subadults, Di: Dispersers, A: Adults, Do: Dominants. All stages are in packs except dispersers. See text for arrow details.
Dispersing wolves that fail to find a territory and a mate leave the population and are no longer modelled. All analyses and simulations are performed with the computer program ULM (Unified Life Models [40,41]) that allows one to handle any time-discrete stage-structured population model. ULM has already been used to model the population dynamics of several carnivore species such as grizzly bears Ursus arctos horribilis [42], arctic foxes Alopex lagopus [43] and Iberian lynxes Lynx pardinus [44].
2.3 Parameters
We defined five scenarios, denoted by S0 to S4, from pessimistic to optimistic, that involve different combinations of parameter values (Table 1). Parameter estimates come from several European and North American studies. Fecundity refers to mean litter size and lies usually between 4 and 7 pups [25]. In France a review of several decades of capture and bounty records prior to wolf extirpation in the mid 19th century gave a mean of 5.13 pups per litter (N=2.271) [45]. Sex ratio in wolf population appears to be highly variable. Data from the former French wolf population indicate that over 16 000 adult individuals, female to male ratio was 0.483, but was larger than 0.5 at den [45]. Mech [25] reviewed demographic studies and concluded that sex ratio may range from 0.4 to 0.8. We keep the primary sex ratio fixed at 0.5 and do not differentiate male and female demographic parameters. Survival probabilities for each stage of wolves in packs (except pups) are difficult to measure. In order to keep the number of parameters as low as possible, we use the same value for juvenile, subadult and adult survival probabilities. No accurate estimate of pup survival is available. Fuller [28] gives a range of 0.48–0.89 from three studies, and Mech [25] a range of 0.06–0.43. We use values slightly lower than the older stage survival probabilities to account for the effect of infectious diseases on litters. Survival probabilities of dispersing wolves appear to be lower than those of wolves in packs [46]: dispersing wolves travel through unknown areas, are not familiar with prey distribution and can be killed by resident wolves [34]. Dispersal probabilities for juveniles, subadults and adults when breeders survived are respectively 0.25, 0.5 and 0.9. Therefore, the probability that a surviving non breeding wolf stays in its pack up to 4 year old (conditional on pack breeder survival) is: (1−0.25)×(1−0.5)×(1−0.9)×(1−0.9)=0.0375, a low value that is consistent with the observation that most non-breeding wolves disperse before age 4 [29].
Model parameters for various scenarios based on literature review
| Parameter | Scenario | |||||
| S0 | S1 | S2 | S3 | S4 | ||
| φ p | Pup survival | 0.55 | 0.6 | 0.65 | 0.7 | 0.75 |
| φ j | Juvenile survival | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 |
| φ s | Subadult survival | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 |
| φ a | Adult survival | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 |
| φ d | Dominant survival | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 |
| φ di | Dispersing wolf survival | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 |
| f | Breeding female fecundity | 5 | ||||
| d j | Dispersal probability for juveniles when at least one breeder survives | 0.25 | ||||
| d s | Dispersal probability for sub adults when at least one breeder survives | 0.5 | ||||
| d a | Dispersal probability for adults when at least one breeder survives | 0.9 |
2.4 Spatial structure
Subordinate dispersal probabilities are not equal between packs as they depend upon the actual survival of pack leaders. Therefore, our model describes explicitly the spatial arrangement of territories and individual movements between them. We assume that any territory may be either empty, or occupied by one pack. We fix the environment carrying capacity to K=20 territories. One pack can occupy only one territory and this induces a ceiling-type density dependence on pack numbers. Territories are numbered from 1 to K and may be viewed as aligned along a one dimension spatial axis that mimics the spatial pattern of the wolf northward expansion through the western Alps from central Italy. At each time step, subordinate wolves in any pack i disperse and start searching nearby for a territory and a mate to reproduce. A dispersing wolf is assumed to settle on the first territory where there is no breeder of the same gender (i.e. on a vacant territory or in a pack missing a breeder). Gese and Mech [29] found that 75–85% of juvenile and yearling dispersers crossed one to three territories while the others moved more than 200 km and crossed more than ten territories. Dispersing wolves from territory i (i.e. subadults and adults that just dispersed, and surviving dispersing juveniles from the previous year) are divided into two groups according to their direction of movement: one group explores territories i−1,…,i−D, while the other explores territories i+1,…,i+D, where D represents a maximum dispersal distance measured in number of territories; in our study D is fixed to an intermediate value D=6 [38]. The fact that we exclude long distance dispersal is not inconsistent with the situation in the Alps, where long-distance dispersers would likely leave the population. In accordance with the findings of Smith et al. [27], dispersing wolves cannot settle on their native territory to replace a missing breeding member. The number of wolves present in each of the two groups is proportional to the number of territories in either direction (this reflects the classical mechanism of diffusion, see [47]). Wolves leaving territory i=1 try to settle on territories i=2,…,7 consecutively, whereas for wolves leaving territory i=3, 2/(2+6) of this group explore territories i=2 and 1 and 6/(6+2) explore territories i=4,…,9. We arbitrarily assumed that pack 1 sends its dispersers first. This search sequence is the same for males and females and is performed for each pack present in the population.
2.5 Stochastic simulations
Reproduction occurs in territories containing a male and a female breeder. Survival and fecundity are treated as binomial and Poisson variates, respectively. Our Monte Carlo simulations involve 250 runs each. We tested on a restricted number of simulations that a higher number of runs did not change result precision. A population qualifies as extinct once all classes are empty.
If the species life cycle description and modelling are accurate, predicted population trends should match real observations. Fuller [28] reviewed several wolf population field studies [32,46,48–51] and based on parameter estimations obtained from these field studies, we calculate the growth rate over a five-year period for populations where all stages have the same survival rate and confront our results with those of Fuller [28].
Our simulations are intended to identify which parameters exert a predominant influence on the dynamics of a recolonizing wolf population, and to assess alternative management strategies. To this end, elasticities [52] of the population growth rate are computed by varying demographic parameters one at a time while holding the other parameters constant [53].
We study the effect of a zoning management strategy whereby wolves are allowed to settle on some territories but are systematically removed outside. A population zoned at N territories is modelled assuming an initial settlement on territories i=1 to N, whereas settlement is precluded on territories i=N+1 to K. We seek thresholds on the number of packs above which it is possible to remove every wolf in excess without threatening population persistence. An alternative to strict zoning is adaptive management, whereby there is no limit on pack number, but population control is operated whenever some predefined demographic conditions are met. We model wolf removals by considering that each individual wolf older than 6 months has a probability c to be removed, where c is given by the ratio (targeted number of wolves removed)/(wolf population size). Survival probabilities of wolves older than six months are therefore multiplied by (1−c). This accounts for the uncertainty in achieving the targeted number of removals, since the percentage of individuals removed each year is a stochastic variable. The strategy is defined as removing wolves following any year of population growth exceeding a given threshold (ranging from 0 to 10% in annual growth). We consider a population as being viable if its probability of extinction over 50 years is less than 0.02. Management simulations are started with populations that contained enough packs to ensure their viability under the assumption of no removal. We ask whether, for a population under a given scenario, there is a strategy that would allow for some removals without increasing markedly the probability of extinction.
3 Results
3.1 Wolf demography
Calculating the growth rate over a five-year period for populations where all stages have the same survival rate reveals that populations start declining when yearly mortality rate reaches 0.32, matching Fuller's estimate of 0.35 [28] (Fig. 2). Juveniles form the most frequent stage in packs, followed by dominants and subadults (Table 2). Elasticities are largest for dominant survival probability and somewhat lower for pup and juvenile survival probabilities as well as fecundity (Fig. 3a) and dispersal probabilities have the lowest elasticities (Fig. 3b). Probabilities of extinction within 50 years for populations starting at different pack numbers and under various ecological scenarios are shown in Fig. 4. Irrespective of the initial number of packs, a population under scenario S0 goes extinct within 50 years with certainty, whereas a population under scenario S4 never goes extinct. For intermediate scenario S1, S2, S3, probabilities of extinction decreases with pack number and mortality rates, but a population with many packs under scenario S1 could have a lower extinction probability than one with few packs under the more favourable scenario S3. Trajectories go extinct mostly during the first three decades of the simulations.

Exponential growth rates calculated for populations over a five-year simulation when mortality rates of wolves of all stages are equal. Field data come from Fuller's [28] review of North American wolf population dynamics.
Stable stage structure computed for a population under median scenario S2 and calculated once population had stabilized to its carrying capacity
| Stable stage structure (males and females) | |
| Juveniles | 0.42 |
| Subadults | 0.22 |
| Adults | 0.08 |
| Dominants | 0.27 |
| Dispersing wolves | 0.08 |

Extinction probabilities as a function of changes of parameters under median scenario S2.
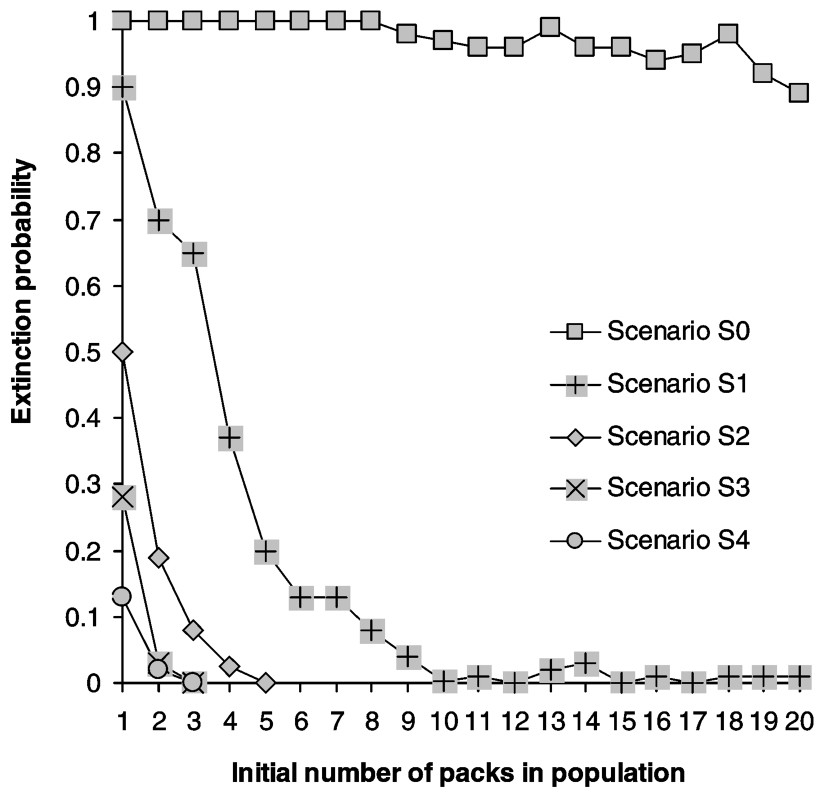
Extinction probabilities as a function of initial population size (in packs). Carrying capacity is 20 packs.
3.2 Zoning management
We calculate probabilities of extinction for a population zoned at 1 to 20 packs and under all scenarios (Fig. 5). The probability of extinction of a zoned population is always greater than that of a non-zoned population (Fig. 4). For the optimistic scenarios (S3 and S4), a few packs are sufficient to ensure a very low probability of extinction (S4, four packs, Pext=0.02). In contrast, for scenario S1, more than 12 packs are needed. Our results show that, for a given scenario, the probability of extinction is extremely sensitive to zone size (i.e. the number of packs allowed). For example, under scenario S2, a population zoned at six packs yields a probability of extinction of 0.08, whereas zoning at four packs results in a probability of extinction of 0.9. Furthermore, the effect of zoning at a given number of packs is most sensitive to slight changes in demographic parameters. For example, zoning at four packs under scenario S4 leads to a probability of extinction of 0.02, whereas scenario S3 results in a probability of extinction of 0.28. Fig. 5 shows that, in order to reduce the extinction probability P of a zoned population, it is more efficient to slightly increase survival of all classes than to increase the zone size (i.e. increase allowed pack number). For example, starting with a population zoned at six packs under scenario S1 (P=0.9), one could increase the probability of survival of all classes by 5% to reach scenario S2 (P=0.08), but the same effect could be achieved only if the zone size could be increased from 6 to 11 packs.
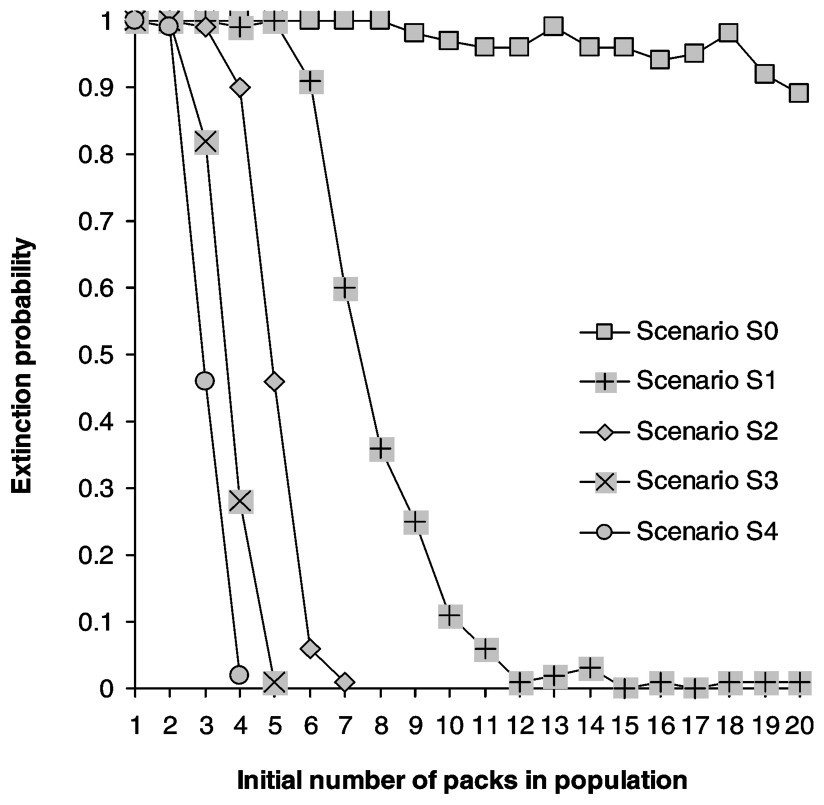
Extinction probabilities calculated when population (in packs) is prevented for exceeding its initial size. This corresponds to a zoning management strategy.
3.3 Adaptive management
We evaluate adaptive management strategies by first identifying strategies that result in a low probability of extinction (Fig. 6a) and then by selecting among them strategies that lead to a high number of removals (Fig. 6b). We borrowed this approach from the theory of optimal harvesting [54], traditionally developed in fisheries and forestry, to delineate management rules – how to act in response to demographic signals – targeting maximum yield along with minimal negative impact on population viability. Results suggest that a growing wolf population could sustain yearly removals without being seriously threatened. For all scenarios and for the same number of removed wolves over the simulation period, removing a fixed percentage of the population leads to lower probabilities of extinction than removing a fixed number. For a given harvest percentage, the number of culled wolves is a non-monotonic unimodal function of the harvest threshold. For optimistic scenarios, there is an optimal strategy that minimizes the extinction probability and maximizes the number of removals: removing a moderate percentage of the population (10%) whenever the population has grown by more than 5% in the previous year. Removing a low percentage of wolves after any year of positive growth, or removing larger percentages with a higher threshold on the growth rate, leads to fewer removals or increased extinction risk.

Extinction probabilities (a) and total number of removed wolves (b) calculated for populations under adaptive management (scenario S3, initial population of 3 packs). A given fraction of the population (5–20%) is harvested following years of annual population growth exceeding a given threshold (λ=1.0 to 1.1).
4 Discussion
Our analysis shows that a wolf population has a high potential growth rate under favourable ecological conditions, but can decline dramatically in response to reduced survival. The wolf is a species sensitive to high killing rates, as exemplified by its eradication from many areas, in contrast with smaller, more versatile species such as the red fox (Vulpes vulpes). However, the wolf shows a strong ability for recolonization once persecutions are stopped. Maximum annual growth rates obtained from field studies can reach 43% [55]. Our model does not lead to such high values, but scenarios more optimistic than S4 can probably occur during particularly favourable years. Population projections based on our model are in agreement with Fuller's review of wolf population dynamics, which reached the conclusion that a 0.35 mortality probability was a threshold value for growth versus decline [28]. Population growth is more sensitive to the survival probability of dominants (Fig. 3a). This result is not surprising, because wolf complex social structure results in a lower number of reproductive units in the population compared to other solitary species, thereby implying a high sensitivity to the survival of breeders.
Our analysis relies on several important assumptions. Individuals in a given class all have the same demographic parameters and could not be differentiated. Pup survival is independent of pack structure and parents' age and senescence is not explicitly considered. Taking a pack breeder survival rate of 0.75 yields an expected leadership of four years. We ignore environmental and genetic stochasticity because data are too scarce to incorporate these factors into our model. Our stage-structured approach did not allow us to incorporate genetic factor, because all individuals in a class were considered identical. As a consequence, all our probabilities of extinction were probably underestimated. Although dispersal is a fundamental and complex process [56], our model assumes simple dispersal rules. Here, dispersal is condition-independent, except for the case where both members of the breeding pair die, which triggers the dispersal of subordinates. Models considering condition-independent dispersal underestimate the persistence of harvested sink populations [57], but overestimate the persistence of metapopulation [58,59]. In our stochastic model, dispersing wolves move in the direction where most territories are located, an assumption that has been rarely tested in the field [60], but which was necessary to avoid many wolves leaving the modelled population with empty territories still available, in agreement with the conspecific attraction hypothesis [47]. The cost of dispersal incurred by subadults and adults is neglected: individuals that leave their packs and those that stay have the same winter survival rate. Only juveniles suffer a cost to disperse as they stay one year as solitary individuals with a lower survival rate. Elasticities of stage-specific dispersal probabilities are the lowest; therefore, we expect model projections to be robust to changes in these parameters.
Recent studies have shown that packs in expanding populations could have several litters per year [61]. Such a pattern is thought to be associated with large prey base, large territories and low human control [62] or may on the contrary act as a compensatory natality in heavily exploited populations [50]. However, some field studies showed that heavily harvested populations did not respond through increasing litter size or frequency; in fact mean pack size and territory size were reduced, with creation of new vacant territories as a possible consequence [46]. There is presently no evidence that multiple litters occur mostly in wolf populations that are substantially below their carrying capacities. Although we did not explicitly model the possibility of multiple litters, they can be accounted for by increasing female fecundity. Increasing fecundity does not markedly decrease the probability of extinction (Fig. 3a), suggesting that multiple litters may have little impact on population resilience.
The incorporation of density dependence has been advocated for modelling culling [63]. Our model does include a ceiling on the number of available territories, and therefore on the life expectancy of floaters, but we did not include density dependence functions on other survival rates as Miller did [64]. There is no available data on the form of density dependence, and it remains unknown how culling could act as a compensatory mortality. We therefore kept a conservative approach by modelling it in an additive way.
Our model does not account for the great plasticity that wolves can display in their life history patterns [8]: wolf pack members can change packs over the years [28,33,62,65], pack territories can be usurped by other packs [33], packs can split [33,66–68], and individual wolves can take different mates over time [69]. Hence, our results should be understood as insights into the demography of a standard wolf population and are not suited to illustrate particular cases.
Our model has not considered the possibility that wolves avoid zones where they are systematically killed. This behaviour has never been described, and, in particular, it is not known if young individuals can avoid sink areas. However, even if this previous assumption was true, it is unlikely that zones where wolves are eliminated could be changed over years, since they are mainly defined by human activities, in particular farms where there is a high record of depredation rates.
Our study is aimed at identifying management strategies to help maintaining a viable population while allowing for population control to reduce depredations on livestock. One important conclusion is that viability thresholds under a zoning strategy are extremely sensitive to the number of packs and to slight changes in demographic parameters. In particular, population viability critically relies on securing a sufficient number of packs in the wolf zone while keeping their mortality rates as low as possible. As a consequence, for a population under or at its zoned viability threshold, the removal of wolves should be firmly discouraged. Although zoning strategies are likely to be implemented in the future for wolves in western Europe, such strategies should be considered carefully and implemented only when enough demographic data are available, so that reliable estimates of population size and parameters are available. Another conclusion of our analysis is that an adaptive strategy that would remove a moderate percentage of the population when its instantaneous growth rate is moderate (around 5% per year) would maximize the effect of depredation control while minimizing the risk of extinction. Such a strategy would be less sensitive to uncertainty in yearly population size and demographic parameter estimates. Notice, however, that adaptive management strategies are assessed in our model with constant decision rules over 50 years, and it is unlikely this will happen in the real world as political and social priorities evolve.
The question of wolf management has become a public and political matter in countries (including France, Norway, Sweden, Switzerland, and USA), where previously extirpated wolf populations are now roaring back, inflicting damages to cattle farming activities that have lost the tradition to cope with large carnivores. Wolves naturally returned to France from Italy in 1992, and in 2000, 30 individuals were believed to be present in the French Alps, 50 for the whole mountain range [10]. From 1993 to 2000, 1184 attacks accounting for 5355 dead sheep have been compensated for a global cost of 0.95 million € [10]. The French government proposed in 2000 two management plans: a ‘sheep farming support and wolf management plan’ [13] that sets a framework for designing non-wolf and wolf zones through local consultation, and a ‘protocol to reduce canid attacks on domestic livestock’ [14] that allows for up to six removals per year if attacks occur repeatedly on a farm. These management plans must comply with wolf protection under the Bern Convention and the Habitat Directive 92/43/EEC, which forbid wolf killing to prevent serious damage to livestock, but allow for some derogations provided that there is no other satisfactory solution and that the exception will not be detrimental to the survival of the population concerned. The ‘concerned population’ has been defined as the western Alps population, including French, Italian and Swiss wolves. We do not consider immigration in our model, although it is possible that a few wolves join this population, this remains undocumented and we conservatively consider the population viability in isolation. There is no definition for viability or ‘favourable conservation status’, as this may relate to a minimum viable population (MVP) or to an ecologically functional one [70]. As a pack is the functional unit of a wolf population, it should also have a clear definition such as the one required by the US Endangered Species Act for delisting: a pack is a dominant pair that has been reproducing on the same territory for three years and where at least two pups survived each year until 31 December [61]. For the Alpine wolf population, accurate population size and demographic parameter estimates are still lacking, but available data for France seem to exclude our most optimistic scenario [10]. Although cooperation between countries in wolf management has been advocated [71], each country appears to have its own policy. According to our simulations, repeated removals as allowed under the fully implemented protocol and management plan as described above may drive the population to extinction in a near future.
Focusing on an absolute number of packs that would secure the viability of the Alpine wolf population remains hazardous given the current uncertainty on population size and parameters. We would only suggest that no zoning should occur before the population reaches more than 12 packs (Fig. 5). Our simulations suggest that it should nonetheless be possible to implement a moderate number of wolf removals following years of moderate or large population growth. We emphasize that these results should be regarded qualitatively rather than quantitatively and should be used primarily to compare management options [20]. In addition, these results should ensure that alternative strategies such as livestock protection or increase of wild prey stocks are also still considered by decision makers.
Our study has broader implications for the management of social carnivores. An important conclusion of our model is that the difference between a viable and unviable population takes place over a short parameter space (Figs. 4 and 5). This result is analogous to that found by Vucetich and Creel [72], who modelled viability of pack-living African wild dogs (Lycaon pictus). In general zoning strategies should be designed carefully, since one would not want to aim too close to the smallest number of packs, and this raises serious concern for many social large carnivore species confined to isolated reserves within human-dominated landscapes and that are managed by a de facto zoning. If the reserve size is just sufficient to host a viable population, it is critical that no human-induced mortality occurs inside reserves. Reserves have recently been shown to potentially act as an attractor for poachers [73]. Our study reveals that, in the case of a social canid, conservation actions would be more efficient by focusing on the reduction of mortality inside reserves rather than on increasing reserve size. This backs up the conclusion based on field studies that population size [2] is by itself a poor predictor of population persistence. One more general conclusion of our modelling exercise is that the control of population or the design of reserves, particularly for social species where the parameter space between viability and decline is reduced, requires the development of species-specific demographic models. Indeed, the social structure of the species needs to be fully explicit in the life cycle graph. This can be achieved by incorporating classes of social status rather than age classes, with probabilistic transitions between them.
Acknowledgements
This study was funded in part by the French ‘Ministère de l’Éducation nationale, de la Recherche et des Technologies', ‘Action concertée incitative Jeunes chercheurs 2001’ awarded to Regis Ferrière, and by the European Research Training Network ModLife (Modern Life-History Theory and its Application to the Management of Natural Resources), funded through the Human Potential Programme of the European Commission (Contract HPRN-CT-2000-00051). We thank C. Bessa-Gomes (University Paris-6), L. Boitani (University of Rome), U. Breitenmoser (KORA), B. Lequette (P.N. Mercantour), P. Migot (ONCFS), F. Moutou (AFSSA Alfort), O. Robinet (DNP–MATE), V. Vignon (OGE) and J.-M. Weber (KORA) for advice during this research. We also thank two anonymous referees for constructive comments.


