1 Introduction
Butterfly colour patterns have evolved as mechanisms for visual communication such as camouflage, sexual signalling, warning colouration (aposematism), and mimicry. Biologists have been interested in the developmental origin and evolutionary diversification of these patterns for more than a century. Early work focussed on the comparative morphology of patterns and explored various ways in which the pattern responded to experimental perturbation during development. Comparative morphological studies revealed that a great unity underlies the diverse patterns of moths and butterflies. Most butterflies and many moths have patterns composed of discrete elements whose homology can be traced across genera and families as easily as the homologies among the bones of the vertebrate skeleton. The system of homologies among pattern elements is now called the nymphalid groundplan [1–3]. Experimental work on pattern perturbation revealed that some of the elements of the nymphalid ground plan, such as the bands of the central symmetry system, the eyespot-like border ocelli, and the marginal pattern elements develop around discrete organizing centres. These organizing centres are specialized groups of cells that occur at various locations on the wing surface and on the wing margin and send out signals that affect the spatial pattern of pigment synthesis in their vicinity [3]. More recent investigations on the nature of these organizing centres have focussed on the developmental genetics of eyespot patterns. This work has revealed several genes that are involved in the development of the organizing centres and various aspects of the morphology of the eyespots [4,5]. In parallel to the experimental work, several investigators have attempted a variety of approaches to the mathematical modeling of butterfly colour patterns [6–8]. Below we present a brief review of the current status of this modeling effort.
1.1 General features of butterfly patterns
Butterfly colour patterns are essentially two-dimensional patterns of pigment synthesis. A fraction of the epidermal cells on each wing surface differentiate into scale cells (see, e.g., [9,10]), which send out a large flat appendage, the scale, into which pigments are secreted. With few exceptions, each scale cell synthesises a single type of pigment [11,12]. The overall colour pattern is thus constructed as a fine-tiled mosaic of coloured scales. One of the problems of pattern formation is how a particular scale cell is induced to synthesise the right pigment for its particular location on the wing.
Butterfly wing patterns are highly organised. Each pattern is built up from a standard array of pattern elements. This general organising principle of colour patterning was first discovered in the family Nymphalidae [1,2], and hence has become known as the nymphalid groundplan [3]. Species-specific colour patterns develop because of the selective expression or suppression of individual pattern elements and due to the developmental regulation of the exact shape and pigmentation of each element. Butterflies outside the family Nymphalidae appear to use subsets of the pattern elements of the nymphalid groundplan [3,11].
The position and shape of each element of the colour pattern are controlled by signalling sources at various locations on the wing surface. The wing veins and the wing margin appear to be the primary inductive sources for pattern formation [3,11]. Pattern determination in butterflies has been shown to occur in two stages. The first stage consists of the specification of organising or signalling centres on the undifferentiated wing surface. In species where this has been studied, this process occurs during the early to mid portions of the last larval stage in the still growing wing imaginal disk [3,13]. The second stage consists of the definition of the boundaries of the future patterned synthesis of each of the pigments that will make up the pattern, which are established by signals generated by the organising centres. This process occurs late in larval life and continues into the early pupal stage [3]. This second stage results in an invisible spatial prepattern of cell commitment to a particular pigment synthetic pathway. Actual pigment synthesis does not begin until the end of the pupal stage, a few days before emergence of the adult butterfly.
1.2 What problems can be addressed through the interaction of experiment and modeling?
One of the attractive features of butterfly wing patterns from an analytical and theoretical viewpoint is its two-dimensional nature. Each wing surface is a flat and essentially static monolayer of cells. Hence pattern formation is not due to the migration of determined cells into particular patterns, as occurs in colour pattern formation in vertebrates, but due to the local differentiation of cells in response to processes of cell-to-cell communication. This static two-dimensional nature of the colour pattern makes it a particularly attractive target for simulation modelling of pattern formation, because the full system can be represented on a two-dimensional display, without the need to collapse dimensions. Moreover, the fact that cells do not migrate relative to each other greatly facilitates modelling because the wing can be represented as a static grid.
Mathematical modelling of pattern formation, or of any other system for that matter, can have two primary purposes, depending on the amount of information that is available about the actual mechanisms of pattern formation that operate in a given situation. If a lot is known about the mechanisms that generate pattern in a particular system, then mathematical models can be developed by writing the relevant equations for the known processes and determining whether these are sufficient to generate the desired pattern, given realistic initial and boundary conditions. The results of such simulations will reveal whether all necessary components have been identified. If a system can be fully simulated, then the mathematical model can be used to investigate how the system would behave under a broad variety of experimental conditions. The value of such an approach is that it enables an investigator to do virtual experiments of a kind that might not be feasible in the real system.
If relatively little information is available about the underlying mechanisms that give rise to the patterns under consideration, then mathematical modelling can sometimes be used to discover the minimally sufficient conditions that can generate the desired pattern. There is no guarantee, however, that such minimally sufficient conditions will also prove to be necessary conditions, because in many situations, a number of different equally parsimonious models could produce the desired result. In order for this style of modelling to converge to the real mechanism it is necessary to impose constraining conditions by which alternative models can be eliminated. In biological patterning systems such constraints are provided by pattern diversity and by the response of the pattern to experimental and genetic perturbation.
The enormous diversity of patterns poses a particularly powerful constraint. In many cases, closely related species have different patterns, yet because of their genetic similarity such discrepancies can be assumed to be due to quantitative differences in the underlying generating mechanisms, rather than to qualitative differences [3]. Hence, if a particular model mechanism cannot produce the pattern diversity seen in closely related species by simple variation in parameter values, then the model is unlikely to represent an accurate summary of the underlying patterning mechanism. Similarly, if the model under consideration cannot accurately reproduce the response of the pattern to mechanical injury, or to various mutations, it is unlikely to accurately represent the actual mechanism of pattern formation. In butterfly wing pattern formation the above approach has been used to eliminate a broad diversity of candidate model mechanisms, because these cannot produce the requisite diversity of patterns [14]. Only one particular form of a reaction diffusion mechanism proposed by Meinhardt [15] proved to be capable of producing the correct morphology and diversity of locations of the signalling centres that control eyespot development [14]. In Section 3, we deal with globalpatterning, which cover whole wing surfaces, and we will take as an illustrative example of the general patterning principle of local-activation-lateral inhibition (LALI) this version of the Gierer–Meinhardt model [16]. It is important to note that in this latter case this is not the only specific model that will produce appropriate results on global patterning. This means that we cannot use computational results in Section 3 to distinguish between models. On the other hand, it does mean that the behaviour we are observing is generic to the LALI class of models.
2 Eyespot patterns
The development of eyespot patterns in the Nymphalidae is, at present, the best understood mechanism of pattern formation (see Fig. 1). Eyespots develop around small groups of cells that act as signalling or inducing sources. If these cells are killed early in development, the eyespot fails to develop [17,18], and if these cells are transplanted to a different location on the wing they induce an ectopic eyespot in their new surroundings [17,18]. Species of butterflies differ in the number of eyespots on their wing, in the exact location of these eyespots, and in the size and pigmentation of these eyespots. Hence, in order to understand eyespot formation it is necessary to understand how the organising centres come to be where they are and the mechanism by which they induce specific pattern of pigment synthesis in their surrounding. The interaction of mathematical modelling and experimental perturbation has played a key role in developing our current understanding of these processes.
Eyespot patterns in a butterfly wing.
Nijhout [14] showed that point-like patterns can be produced in the exact locations of the organising centres by an activator/inhibitor reaction–diffusion mechanism that assumes that the wing veins act as fixed boundary conditions for the activator and as reflecting boundaries for the inhibitor. In biological terms this implies that the veins, or cells associated with the wing veins, are sources of one of the diffusing reactants. Variation in parameter values can displace the positions of these point-like patterns, and mimic the effect of certain mutations on the positions of the centres of eyespots (e.g., [19]). These reaction–diffusion models can be quite sensitive to small variation in parameter values and initial conditions. However, it has been shown that pattern selection can be robustly controlled under certain types of boundary conditions and also with domain growth [20,21].
The mathematical model predicted a rather complex time evolution of the spatial pattern of activator concentration, before it settles to point-like pattern at the stable steady-state [14]. Several years later, Carroll et al. [13] demonstrated that the gene Distal-less is expressed uniquely in the cells of the organising centres of eyespots. Moreover, the spatial pattern of expression of Distal-less undergoes exactly the same complex changes as those predicted by the mathematical model [13,22]. It appears therefore that Distal-less is somehow associated with a portion of the patterning mechanism that behaves as the activator in a reaction–diffusion system.
Once the point-like patterns are established, these in turn begin to act as organising centres for the induction of pigment synthesis in their vicinity. Mathematical simulation results of timed cautery experiments on the size of the subsequent eyespot diameter suggest that a signal spreads out from these centres with dynamics that resembles diffusion [3,23]. It appears therefore that the cells that express Distal-less begin to produce a signal that propagates by diffusion into the adjoining cells and somehow induces these cells to synthesise the pigments appropriate for an eyespot. Carroll and his co-workers have demonstrated that the expression of several genes spreads out in a circular pattern from the site of Distal-less expression. Among these genes are spalt, cubitus interruptus, engrailed, and, interestingly, Distal-less itself [4,24]. Genes such as Bigeye, Cyclops and Comet affect the diameter and shape of the eyespot [19,25–27] and must thus somehow be involved in controlling the spread of expression of these early genes.
The pigments of eyespots consist of melanin in the central disk and outer dark ring, and ommochromes in the outer pale-coloured ring [11]. How these genes control specific pigment synthesis in eyespots has not yet been investigated, but the control of pigment synthesis in other portions of the pattern in swallowtail butterflies (Papilionidae) has been investigated by Koch et al. [28]. These authors have shown that the switch between yellow and black pigmentation in the wing of Papilio glaucus involves regulation of the expression of the enzyme dopa decarboxylase (DDL) which is required for the synthesis of both black melanins and yellow papiliopochromes, and the enzyme N-b-alanyl dopamine-synthase (BAS) which is required for the synthesis of yellow papiliochromes. Yellow pigment synthesis occurs first in development and is caused by the spatially patterned high activity of BAS and a low activity of DDL in presumptive yellow regions of the wing. This is followed by a patterned high activity of only DDL in the areas of the wing that will become black. Mutations that turn yellow areas of the wing black appear to act by decreasing the initial low level of activity of DDL in presumptive yellow areas, followed by a rise in DDL activity at the time it occurs in the normally black areas of the wing. It appears therefore that a relatively simple switch, involving the patterned activation and inhibition of two enzymes, can regulate the pattern of synthesis of the principal pigments on butterfly wings. An interaction among genes like spalt, Distal-less and engrailed must be involved in controlling the expression of these pigment-synthetic enzymes, but exactly how this regulation works remains to be elucidated.
3 Global patterning
Global pigmentation patterns on lepidopteran wings, which cover whole dorsal or ventral wing monolayers, can be very complicated in structure and they are sometimes used for identification of species. Owing to the pioneering work of Schwanwitsch [1] and Süffert [2] on the nymphalid ground plan, the complicated patterns on the wings can be understood as a composite of a relatively small number of pattern elements. For example, (1) the symmetry system consists of colour bands that run anterior to posterior across the wing; (2) the border ocelli system consists of a series of eyespots in the distal half of the wing; (3) the marginal bands are a pair of narrow bands near the wing margin; (4) the dependent patterns are venous stripes, that is, a colour pattern of the outline of the wing veins; (5) the ripple patterns run proximal to distal in the wing in a manner similar to the ripples in wind-blown sand [3].
In spite of these simplifications, the problem of global colour pattern formation in wings is still not fully resolved and there exist very few mathematical models to account for the diversity of colour pattern in wings. We briefly review them in the next section.
3.1 Models for global pattern formation
3.1.1 Diffusing-morphogen-gene-activation model [6]
A simple model for the development of the commonly observed crossbands of pigmentation shortly after pupation was proposed by Murray [6]. This model is based on a diffusing-morphogen-gene-activation system and extends the idea of a determination stream proposed by Kühn and von Engelhardt [29], namely, that the anterior and posterior margins of the wing are sources from which emanates a wave of morphogen concentration. Murray's model hypothesises that the morphogen activates a gene product which, in turn, determines colour pattern. The model equations are solved either on a sector of a circle, representing a wing, or a rectangle, representing a wing cell with appropriate boundary conditions [6,23]. Murray showed that this simple model could exhibit a wide variety of observed patterns. For example, it exhibits patterns consistent with those observed after microcautery surgery. The theoretical results are consistent with the observations of Schwantwitsch [1]. Varying the scale and geometry of the model wing leads to more complicated patterns that are consistent with those observed on certain butterfly and moth wings, while considering the model on a wing cell and varying the source strengths also leads to commonly observed patterns.
3.1.2 Simple diffusion model [7]
A simple diffusion mechanism of a single morphogen was proposed for the formation of the wing pigmentation patterns of three species of butterflies by Bard and French [7]. Their model is based on three main assumptions. First, there may be morphogen sources in the foci of eyespots and morphogen sinks at some parts of the wing margin. Second, the morphogen has a finite half life and diffuses simply and freely away from the sources throughout a wing of hexagonally packed cells. Third, the overt pattern derives from cells interpreting the local morphogen concentration with respect to thresholds which determine scale colours. The final pattern follows lines of constant morphogen concentration and may, depending on the distribution of sources, comprise rings, curves, or bands. With a biologically realistic diffusion constant and a morphogen half life less than 6 h, the model can generate many features of butterfly wing patterns as stable patterns of morphogen concentration, the compound spots of Tenaris domitilla, the large rings of Diaethria marchalii and the pattern of eyespots, rings and asymmetric bands of Ragadia minoa [7].
3.1.3 Reaction–diffusion model [8]
A reaction–diffusion model on a geometrically accurate wing domain was presented for the formation of global pigmentation patterns in the butterfly wing of Papilio dardanus by Sekimura et al. [8]. The model is based on the idea that a system of reacting and diffusing chemicals could evolve from an initially uniform spatial distribution to concentration profiles that vary spatially – the so-called diffusion driven instability [30]. By mathematical analysis and computer simulations of the model equations, Sekimura et al. suggested that the global wing colouration is essentially due to underlying stripe-like patterns of some pigment inducing morphogen. This model does not need to assume supplementary morphogen sources and sinks in some parts of the wing to get patterns. They also highlighted the importance of key factors such as parameter values for mode selection, threshold values which determine colour, wing shape and boundary conditions.
In the next section, we review the reaction–diffusion model in some detail with brief description of the butterfly, Papilio dardanus, and present some new computational results.
3.2 A reaction–diffusion model for global pattern formation in the butterfly wing of Papilio dardanus
3.2.1 Wing colour patterns of the butterfly Papilio dardanus
The species of butterfly Papilio dardanus is widely distributed across sub-Saharan Africa and well known for the spectacular phenotypic polymorphism in females. The females have evolved more than a dozen different wing colour patterns, many of which mimic different species of unpalatable butterflies and moths.
The female wing patterns are quite complicated and diverse, and at first glance it seems difficult to find an underlying logical relationship between them, although they are clearly due to simple genetic variation in a single species. Nijhout [3] recognized that the black portions of the colour pattern constitute the principal pattern elements. These elements differ in size and shape in different mimetic forms, and this variation can have dramatic effects on the overall appearance of the pattern. Our goal, therefore, is to present a mechanism that need account for only the black pattern elements.
In contrast to the spectacular phenotypic polymorphism in females, the males are monomorphic and strikingly different from the females, exhibiting a characteristic yellow and black colour pattern and tailed hind wings. Some populations of Papilio dardanus have females with male-like colour patterns. These male-like females can be distinguished from normal males by a slightly broader area of black along the basal anterior margin of the forewing, and a lobe-like extension of this dark pattern from the anterior wing margin (Fig. 2). Genetic heterozgotes of such male-like patterns with the hippocoon pattern result in a range of intermediate phenotypes between male-like and hippocoon-like pattern (Fig. 3).
(a) Male (top) and (b) male-like female (bottom) forms of Papilio dardanus. The male-like female forms can be strictly distinguished from normal males by a lobe-like extension of black pattern from the anterior wing margin.
Intermediate colour patterns of the male-like female (a)–(c) and a mimetic form hippocoon (d) of Papilio dardanus.
3.2.2 Model equations
We solve the non-dimensionalised reaction-diffusion system with Gierer–Meinhardt reaction kinetics
| (1) |
| (2) |
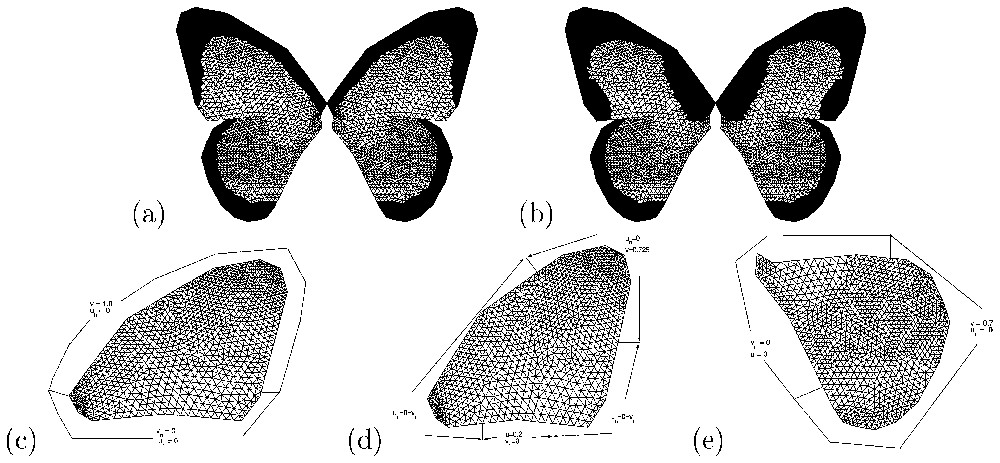
Results of numerical simulations (v component) of the Gierer–Meinhardt model Eqs. (1) and (2)). The forewing: (a) male pattern with parameter values chosen to isolate the (1,0) mode (d=520.157, γ=67, c0=0.85). (b) Male-like female pattern with parameter values corresponding to the (3,0) mode and c0=0.68. For the hindwing, parameter values as in (a) and (b) but with c0=0.69 in (a) and c0=0.91 in (b). Boundary conditions: (c) corresponds to forewing in (a), (d) to forewing in (b) and (e) to the hindwings. These also illustrate the nature of the triangular mesh used in the numerical simulations [34].
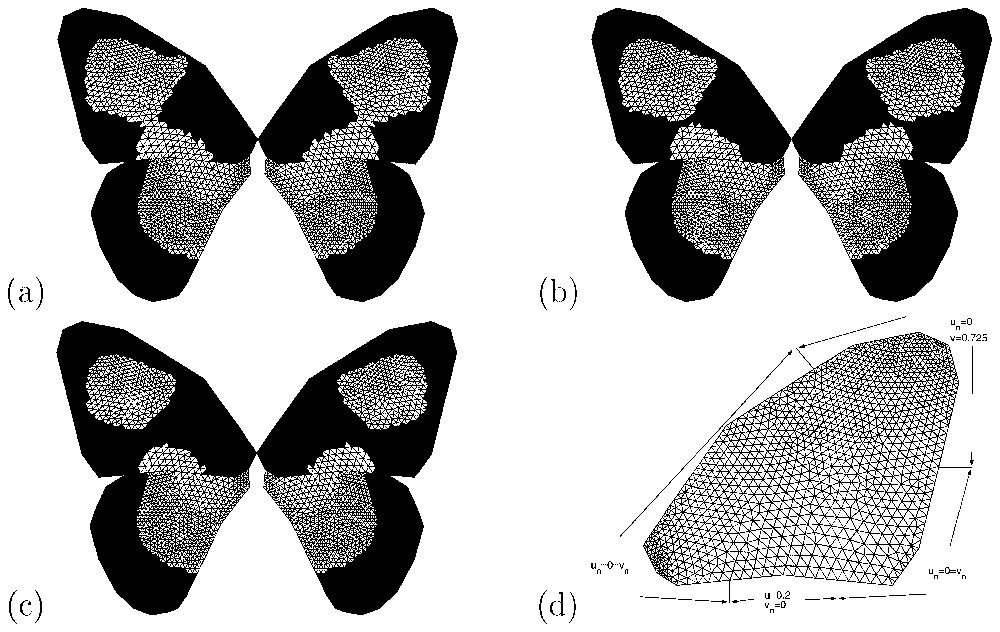
Results of numerical simulations (v component) of the Gierer–Meinhardt model (Eqs. (1) and (2)) for some intermediate male-like female patterns of Papilio dardanus. For the forewing domain, the values of c0 are (a) 0.655, (b) 0.661 and (c) 0.6625, while for the hindwing it is unchanged from that used in Fig. 4a. The boundary conditions for the forewing are illustrated in (d).
Initial conditions are prescribed as small perturbations about the homogeneous steady state if it exists.
3.2.3 Numerical results
3.2.3.1 Mimetic and non-mimetic patterns in females.
In a previous paper [8], we demonstrated that our model can account for many aspects of the pigmentation patterning in the wing of Papilio dardanus. One of the main results was that wing colouration would be reproduced by assuming there was a simple underlying stripe-like pattern of some pigment-inducing morphogen. We also emphasised that the diversity of female colour patterns can be obtained by variation of only a few key factors such as parameter values for mode selection, threshold values that determine colour, wing shape and boundary conditions. These results could be important from a genetic point of view because they may give us insight into the mechanisms by which a single genetic locus [31–33] could control the entire diversity of patterns observed.
3.2.3.2 Male and male-like female patterns.
From the mathematical point of view, the male patterns are essentially different from the male-like female patterns. We assume that the male patterns are related to parameter values (d and γ in Eqs. (1) and (2)) selected to isolate the (1,0) mode on a unit square domain. On the other hand, the structured male-like female patterns are assumed to be related to the parameters isolating the (3,0) mode on a unit square, which could generate other female patterns such as hippocoon. The length scales of the wing domains are approximately equal to those of the unit square.
In all our numerical simulations for male-like female patterns we fix parameter values as follows: a=0.1, b=1.0, k=0.5, γ=619.45 and d=70.8473. The numerical simulations show the plots of v only. The profiles of u can easily be deduced from these plots as they are in phase with those of v. We further assume that cells within the wing are not necessarily homogeneous in their response to one of the chemical concentrations, in this case v. We therefore specify a threshold function of the form of a plane where α or β or both are non-zero and c0 is a non-negative constant. Here colouration or shading is determined as follows: if cells experience chemical concentration v⩾αy+βx+c0 they are black, otherwise they become coloured. Note that if both α and β are zero, then the threshold gradient is reduced to a constant threshold, while if one of α or β is zero, then cells are homogeneous in one direction but have a response gradient in the other direction. There is no biological evidence to justify the existence of a gradient threshold. However, there is experimental evidence [9,10] that cells do have other properties such as adhesivity, that depend on distance from the body. The shading parameters for the hindwing are fixed as α=0.0111, β=−0.025. The fixed parameter values for the forewing are α=−0.0111, β=−0.025 and c0 is varied to obtain different patterns. The gradient threshold values are determined by trial and error. The forewing and hindwing domains are considered independent, hence numerical simulations are independently carried out on each domain.
In Fig. 4, we show results of numerical simulations of the Gierer–Meinhardt model (Eqs. (1) and (2)) corresponding to male and male-like female patterns of Papilio dardanus in Fig. 2. The boundary conditions applied here and the parameter values are such that only one minimum in morphogen concentration is obtained.
3.2.3.3 Intermediate male-like female patterns.
In Fig. 5, we also present numerical simulations of the model for intermediate male-like female patterns shown in Fig. 3. As noted above, we assume that male-like female patterns result from parameters that isolate the (3,0) mode on a unit square. By choosing different boundary conditions, a transition from one minimum to two minima of the morphogen concentration v of (Eqs. (1) and (2)) in the two-dimensional patterning domain can be observed. Fig. 5 shows the results of numerical simulations illustrating some intermediate patterns. Here, the boundary conditions differ from those used to simulate the male-like female pattern in Fig. 2. By changing the value of c0 of the threshold function (c0=0.6625, 0.661 and 0.655), we generate some intermediate patterns ranging from more or less a typical male-like female pattern (Fig. 5a) to an extreme pattern with two separate white parts in the wing (Fig. 5c) similar to hippocoon.
3.2.4 Predictions from the model
To illustrate how our model could be used as a predictive tool, we consider the following two cases (for more details, see [35]): (i) cutting part of the forewing by simply removing part of patterning domain, and (ii) making a hole in the forewing. Our simulations results (not shown here) on the effects of cuts in the wing blade predict that large cuts will cause significant alterations of the pattern, whereas small cuts results in minor or no changes in the pattern. Holes in the wing do not appear to have major effect on pattern formation. This latter result differs from the finding of Kühn and von Engelhardt [29], who showed that holes in the wing could severely alter the banding pattern on the wings of Ephestia kuhniella. The colour patterns of Papilio dardanus are, however, not homologous to the banding pattern of Ephestia [3], and arise by a mechanism that is quite different form that envisioned by Kühn and von Engelhardt. Our findings have significant implicatons for understanding how the evolution of colour pattern is influenced and perhaps constrained by evolutionary changes in wing shape.
4 Conclusions
To understand pigmentation pattern formation in butterfly wings, it is important to determine the mechanism by which signalling molecules activate pigment synthesis and are spatially distributed in the wing. The best understood mechanism of pattern formation is that of eyespot pattern formation, in which the spatial pattern of expressions of the gene Distal-less and several genes have been examined.
In contrast to the case of eyespot patterns, where the results of experiments on surgery, and genetic studies, exist, little is known for global patterns, as yet, for Papilio dardanus, although the mechanism of the so-called H locus, which has been assumed to control the mimicry of a species of butterfly Papilio dardanus, has been well studied. The extension of the study of male to intermediate male-like female colour patterns has once again reinforced the conclusion that such varied patterns can be exhibited by small changes in the parameter values of the underlying mathematical model. According to our results, the key factors are parameter values related to mode isolation, that is, parameter values within the model that excite a particular pattern while damping down the other patterns, wing shape, boundary conditions and variation of threshold values, which seem to be in good accordance with experimental evidence. Indeed, it is known that the effects of boundary conditions such as morphogen signalling sources, boundary shape and threshold function that determine the colour, are important to understand pigmentation pattern in the butterfly wing.
The generality of our numerical finite element method has allowed us to investigate other biologically observed patterns related to the butterfly wing of Papilio dardanus. Such effects can easily be investigated mathematically/computationally in the model equations without any change in the numerical finite element technique developed by our group. In particular, we were able to use our model equations to hypothetically predict the effects of shape change to global and local pattern formation [35]. Furthermore, this advantage makes the numerical technique a powerful tool in investigating other biologically related problems (see for example [36]).
It is known that the pigmentation process occurs as the butterfly wing imaginal disc grows from the late larval stage to the adult. Future research will focus on investigation of pattern forming processes during development of the wing disc. Modelling will also aim to investigate growth on a realistic domain geometry for the butterfly wing to determine under what conditions the observed adult wing pattern is formed.
Acknowledgements
TS was supported by a Grant from the Human Frontier Science Program (GR0323/1999-M) and also by a Grant-in-Aid for Scientific Research from the Ministry of Education, Science, Sports and Culture of Japan (No. 14034258). PKM was supported in part by a Royal Society Leverhulme Trust Fellowship. AM acknowledges support from EPSRC Grant GR/R03914 awarded to AJW and PKM.