1 Relationship between transcript frequency and abundance
In the genetics–linguistics analogy, a transcriptome is a text in which a life plan is ‘expressed’ with a genomic vocabulary. By analyzing SAGE tag [1] and 3′ EST [2] data, we found that the human transcriptome follows the statistical constraint, characteristic for natural language, known as Zipf's law [3]. In a corpus of texts, Zipf's law dictates that the frequency of each word, f, and its abundance rank, r (r=1 for the most frequent word, r=2 for the second most frequent word, and so on) are related according to the power-law , with for all languages [4]. In a double logarithmic axis plot, such a relation is represented by a linear dependence of f as a function of r with a slope of −1. In muscle and liver, the organs composed primarily of a homogeneous population of differentiated cells, the frequency, f, of each transcript and its abundance rank, r, distributed very close to the line f=0.1/r (Fig. 1a). In other sources, such as cell lines and epithelial tissue, only high-rankers (r<100), which comprise less than 1% of the transcript variety, deviated from this trend (Fig. 1b). Reduction of tissue-specific transcripts in cell lines and their dilution in complex cell populations explains such deviation, at least in part. Compiling data for different transcriptomes affected the plot similarly (Fig. 1c). Interestingly, the plot appeared universal to the compiled transcriptomes at enough multiplicities, regardless of the data sources. In normalized libraries [5], the Zipf-like structure was lost completely (Fig. 1d).
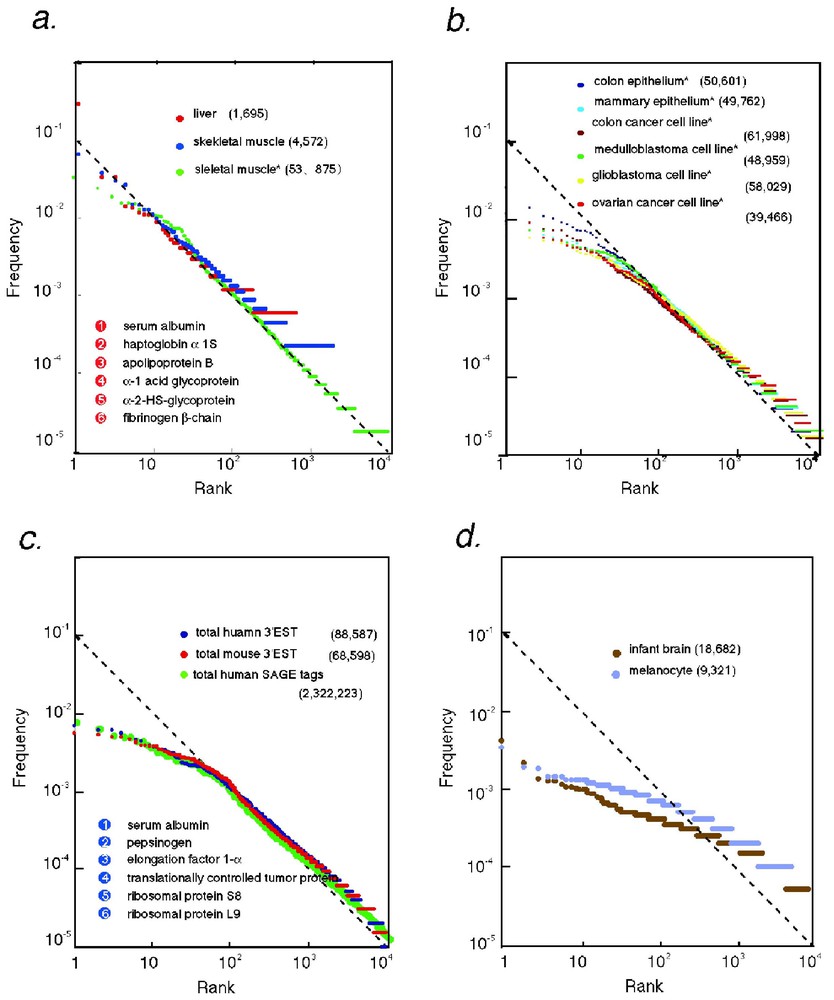
Log frequency log rank plot (Zipf's plot) of transcriptome data. The frequency of occurrence (f) of each transcript in 3′ EST and SAGE tag () collections representing various transcriptomes were plotted against the abundance rank (r). The broken line represents f=0.1/r. (a) Organs with homogeneous populations of differentiated cells. For example, the most abundant transcript (r=1) in liver, albumin, occurred about 12% in EST data for liver. Gene names for r=1–6 in liver are given. (b) Cell lines and complex tissues. (c) Compiled data from 51 human EST sets, 31 mouse EST sets, and 64 SAGE tag sets. Gene names for r=1–6 in compiled human transcriptome (3′ EST) are given. (d) Occurrence of 3′ EST in normalized libraries. The total tag occurrence for each data set is given in parentheses. The frequency data were obtained from http://bodymap.ims.u-tokyo.ac.jp/datasets/index.html (3′ EST) and ftp://ncbi.nlm.nih.gov/pub/sage/ (SAGE). The data for liver are combined data for two human liver libraries. The frequencies of total SAGE tags are obtained from re-analysis of all available human SAGE tags. Clustering 3′ ESTs for two representative normalized libraries in dbEST, 1N1B and 2NbHM, generated the data for normalized libraries.
2 An evolutionary model of expression level variation
In transcript abundance, the slope (|k|) is very close to 1, similarly to the classical example in natural language, which suggests the underlying stochastic process that robustly dictates the value of the slope as well as the linearity in log–log plot. We know that the abundance of each transcript is dictated by the DNA sequence on the genome known as cis-elements and the mutations in these elements cause alteration in its abundance. Accordingly it is natural to assume that the abundance distribution results from an evolutionary process. We propose here an evolutional model that explains linearity in log–log plot and the slope (=1) with only simple assumptions as follows: (1) the mutations in cis-elements cause a stochastic change in the expression level that is proportional to the original level of expression; (2) at the initial state, the genome contains from a small number of genes with an arbitrary distribution of gene expression. The gene number gradually increases over generations by gaining new genes by gene duplication [6].
The first assumption can be written as the relation fi(t+1)=λi(t)fi(t), where fi(t) is the expression level of gene i at generation t, and λi(t) is a random variable extracted from a time-independent distribution π(λ).
After T generations, we obtain:
| (1) |
As generations pass, the deviation of the distribution becomes large, and expression level of some genes becomes very small. If they become lower than the minimal level, then the genes are regarded as disappeared.
Because we cannot determine the initial distribution fi(0) of formula (1), a priori, the model (1) should be extended slightly. At the initial state, the genome contains a small number of genes with an arbitrary distribution of gene expression. The genome grows over generations by gaining new genes by gene duplication. While the number of gene (N) increases, the total number of mRNA molecules in a cell (W) also increases, according to the following formula:
By simulation of this process, we show that transcriptome distribution converges to Zipf's law (Fig. 2). The evolutionary model is essentially the analogy of the city size growth model, proposed by Blank and Solomon (2000) [7]. In their city size model, the population growth (ΔW) is the cause of the increase in the number of cities (ΔN). In our evolutionary model, increase in total mRNA (ΔW) is driven by the growth of gene number (ΔN).

Simulated emergrence of Zipf-like distribution in transcriptome with evolutionary model. (a) Distribution after 50 generations, (b) after 100 generations, (c) after 200 generations. The continuous line is the Zipf's law function (f=a/r). The distribution converged to Zipf's law within a few hundred generations. The number of genes at initial state was 50, and the number was increased exponentially (2% par generation). But the initial state and the exponent parameter values have no substantial influence on the result of the distribution. Other parameters were set as K=0.001, π(λ) was set as the normal distribution N(μ,σ2) with μ=1.0, σ2=0.05. Again, the resultant distribution was not sensitive to the exact value of the parameters.
3 Interpretation of transcriptome data
Zipf's law predicts various important numerical features of the transcriptome. According to this law, 50% of transcripts in a differentiated cell represent only 83 mRNA species. Because the accumulated sum of f for all transcripts is 1, the predicted number of different transcripts in a cell is restricted to 12 367. These values are in accordance with the classical view of an average transcriptome where less than 100 genes are responsible for 50% of the cellular mRNA content and about 10 000 mRNA species comprise the rest [8]. Assuming that the plot for a compiled transcriptome (Fig. 1c) remains unchanged after further compilation of different transcriptomes ( for SAGE tags), the predicted total number of transcripts in a whole body is approximately 210 000. The further benefit of the discovery of such a constraint is that it may eventually assist researchers in designing experiments with tissue mRNA and interpreting results from them. In transcript profiling by DNA microarray, for example, the relation of f and r can be considered as the relation between sensitivity of transcript detection and the number of hybridizing signals.
Applicability of Zipf's law has been reported not only for natural languages but also in several social, economical and behavioral phenomena, such as city size and income [3], and clicks in World Wide Web surfing [9]. Although there have been many controversies, in essence, three kinds of mathematical models have survived to explain such phenomena: The random network model [10] for WWW, Mandelbrot's optimization model [11] for linguistical Zipf's law and a multiplicative model applied to city size [7]. Recently, power-law distributions were also found in wide variety of genomic properties, such as populations of protein families [6,12–14], protein folds [6,14], pseudogenes [14] and protein domains [15,16], although the slope is not always close to 1 in these cases.
After this work was submitted, two papers were published reporting that Zipf's law holds in a wide variety of eukaryotes, supporting our evolutionary model [17,18]. In one of these papers, Furusawa and Kaneko [18] applied a random network model in mRNA production to explain Zipf's distribution, in which they assumed that transcriptional regulation can be modeled as an analogy of a catalytic reaction.


