1 Introduction
Due to its propensity to develop into an epidemic, human trypanosomiasis is one of the most serious public health problems affecting Africa. Though in recrudescence, the disease threatens close to 60 million people in sub-Saharan countries. The different processes involved in the transmission of the disease are very complex and stochastic events play an important role. The importance of spatial location in the transmission of sleeping sickness has been underlined by some authors [1–3]. Indeed, in a heterogeneous environment, contacts between vectors – tsetse flies (Glossina spp.) – and humans vary significantly over space. Existing mathematical models fail to take into account the spatial distribution of humans and flies, their random movements and human–fly contact. In conventional compartmental models, transmission is described using a system of differential equations [4–8]. Over the past four years, the model of Artzrouni and Gouteux [7] was improved to cover two patches displaying distinct epidemiological characteristics [9]. This improved approach, however, has two drawbacks: the first is the unavoidable oversimplification of heterogeneous areas, and the second lies in the a priori unsolvable mathematical difficulties that arise from the increased number of distinct transmission areas.
In this context, an alternative is to use an individual-based model (IBM) or an agent-based model (ABM) in a multi-agent system of synchronisation and observation [10]. IBM or ABM are models in which each computer-generated basic entity has its own life cycle, its own and rational defined behaviour. In an IBM, these entities, called ‘individual’ or ‘object’, correspond to real biological actors with attributes restricted to those relevant to their evolution and interactions in the model. In an ABM, these entities, called ‘agents’, reify the biological entities and their interactions [11,12]. They represent the behaviour of one or several characters of the phenomena. The spatial location, the scalability, the links, the aggregation are represented as well. In IBM, only the basic entities are represented and the behaviours are roughly approximated. In some case, an IBM may be restricted to the matrix and its individuals' indexed components. In an ABM, each agent is reactive (when it reacts to a stimulus), pro-active (capable of independent actions), social (through its interactions with others) and autonomous with regards to others (since its behaviour is not driven by another agent). Moreover, its movements are not limited to a grid [13–15]. Since an agent is an autonomous and proactive entity, it is not totally event driven either. This kind of model can involve relatively little mathematics, but it can prove to be very complex due to the amount of data processing.
The aim of this new approach is first to identify the agents (individual or spatial), their relationships and their evolution over time, and then to observe results from the model at the population level. It would then be possible to deduce if some of the hypotheses made for the disease were true given the assumptions about the agents. A multi-agent model integrates some relevant processes at work, which are not integrated in deterministic models, such as the dynamic occupation of space [10].
More recently, Artzrouni and Gouteux [16] submitted a preliminary stochastic model of a microsimulation that was the first IBM addressing transmission of the Gambian form of the disease. This model is interesting in that it opens up the possibility of introducing a spatial dimension in the epidemic process. However, only by assuming a constant influx of infected tsetse flies from outside the study area, it can account for low and stable transmission [16]. The low-level transmission able to maintain itself for several years remains a central epidemiological enigma [17,18]. Models based on differential equations can explain this phenomenon on a very large scale but at a small scale – that is, at the scale at which the transmission usually takes place – such models become unrealistic, since they use fractions of vectors or infected people. Indeed, the differential equations paradigm assumes that populations are large and can be considered as continuous quantities. It was therefore interesting to explore an innovative approach, intrinsically discrete, spatial and agent based. This model considers tsetse flies and humans as agents and thus simulates their dynamic use of space. This paper describes the model, presents test results obtained from its application to data from the Bipindi sleeping sickness focus in Cameroon, and discusses new prospects arising from the model. This focus is the most active in the country and was intensively and comprehensively studied using molecular biology techniques – fine-tuning the usual entomological surveys – as well as epidemiological surveys conducted among the local population [19–22].
2 Material and methods
2.1 Overview of the parasitological cycle
The values assigned to epidemiological parameters are those used in other existing models (Table 1) and their justifications are provided in Artzrouni and Gouteux [7] and Gouteux and Artzrouni [23].
Characteristics of the biological agents. The distribution between two extreme values is linear
| Glossina agents | |
| Lifespan | 1 to 3 months |
| Incubation phase | 15 days to 1 month |
| Infective phase | Until death |
| Blood meals frequency | Every 3 days |
| Susceptibility rate | According to age |
| Movements | Random |
| Initial infection rate | 2.4% |
| Humans agents | |
| First phase | 4 months to 8 years |
| Second phase | 5 months to 7 months |
| Time spent in plantation | 2 days |
| Time spent in village | 1 day |
| Time spent in forest | 8 days |
| Mortality rate | 5% |
| Susceptibility rate | 62% |
| Movements | Random (10% of sedentary people) |
| Initial infection rate | 0.0% |
2.1.1 The human hosts
The parasite – Trypanosoma brucei gambiense – is injected into the bloodstream of a human when an infective tsetse fly bites him or her. In most cases, the parasite subsequently multiplies in the lymph nodes and blood, transferring a healthy susceptible human into the group of first phase patients. We also assume, as in Rodgers [4,5], a susceptibility rate of 0.62 (the probability that a susceptible human eventually becomes infected after an infected vector bites him). This value is just an order of magnitude for a parameter that is difficult to estimate. With this parameter, it would become possible to introduce subtle individual distinctions, such as variable responses of the human host in terms of age, sex, ethnic group, etc. The human lifespan attains 50 years locally, but this value is ignored, since simulations span six or 13 years only. As regards the duration of the different phases of the disease, we arbitrarily set the lower and upper limits of the first phase to four months and eight years, respectively, and for the second phase to 5 and 7 months, respectively. The duration of these phases was selected at random from a set range of lower to upper limits. These values are realistic values consistent with the observed virulence of the epidemic in the forest focus of Central Africa before medical screening [24–27]. Only first-stage carriers can transmit the parasite easily through fly bites. When these carriers enter the second stage or go to hospital for treatment, they are considered ‘removed’. Their risks of being bitten and of transmitting the parasite become in those cases negligible.
2.1.2 The vector
The cycle of Trypanosoma brucei spp. in the alimentary tract of the tsetse fly is the most complex found among salivary trypanosomes [28]. After ingestion of the parasite, a long incubation phase of about 24 days begins. During it, the tsetse fly does not transmit the parasite. The duration of this phase was selected at random from an arbitrarily set range of 15 days to one month. The trypanosome multiplies by longitudinal division and eventually changes into an infective metacyclic trypanosome, i.e., into the form that can be transmitted back to a host. The tsetse then enters in the phase termed ‘active transmission period’, which persists until its death. The mean life span of a tsetse fly is from one to three months. This value is chosen at random in the model. The tsetse fly takes a blood meal from an animal or human host every three days on average. It may ingest the parasite if it bites a person in the first phase of the disease, but very seldom from a patient in second phase. The fly is most likely to be infected in its first blood meal [29,30]. The newborn fly is termed ‘teneral’. The probability that a tsetse develops an infection from an infective bite decreases with its age (Fig. 1). Since the population is considered stable, a newborn uninfected tsetse fly is introduced in the model each time a fly dies.

Probability of infection according the age of fly. Day-by-day estimation of infection risk (%) following a blood meal on an infected host.
2.1.3 Non human hosts
In the Gambian form of sleeping sickness, the parasite is specifically adapted to human hosts but is found to be of low virulence to experimental animals (cf. [31], as recently reviewed by Gibson [32]). Infected pigs or wild animals show no pathological symptoms and do recover spontaneously after a short time. However, they may infect tsetse flies. Thus, it is possible that animals play a part in the transmission of Trypanosoma brucei gambiense [33]. In Bipindi and others foci in Cameroon, infections with this parasite have been detected in domestic and wild animals [18]. The present model therefore includes animals as an additional reservoir for parasites. The susceptibility to infection of animals by human parasites through the bite of an infected tsetse fly was initially set at 0.62.
2.2 Epidemiological data
Located in southern Cameroon, the Bipindi sleeping sickness focus includes a dozen of villages. Data used in the simulation runs emanate from the village of Lambi (500 inhabitants), epicentre of this focus, surrounded by an open population of 5000 tsetse flies. We defined a circular zone with a radius of 3 km and centred on the village. Inside this zone, the landscape surrounding the village is a mosaic of vegetation types that includes plantations, subsistence crop fields, abandoned fields, thalwegs and forests. Table 2 summarises the major characteristics of this focus as deduced from maps and field observations. Medical surveys in 1998 report a 1.2% prevalence of the disease in the population. The proportion of sedentary people (i.e., that never leave the village) is estimated at around 10%.
The Lambi village area. Characteristics of the location agents. The main animal hosts in Village are pigs. Elsewhere, there are wild animals. The total is the estimated populations in the area. From an arbitrary distribution, the equilibrium densities of tsetse flies are obtained very quickly after some steps of time
| Location agents | Surface (%) | Densities of Glossina | Distribution of |
| (tsetse km−2) | animals (%) | ||
| Forest | 45.0 | 49.6 | 16.6 |
| Thalwegs | 5.5 | 236.7 | 16.6 |
| Forest footpaths | 4.5 | 289.4 | 16.6 |
| Cocoa plantations | 22.5 | 57.0 | 16.6 |
| Crop fields | 10.5 | 124.0 | 8.4 |
| Abandoned fields | 5.5 | 236.7 | 8.4 |
| Water-holes | 0.5 | 2604.2 | 8.4 |
| Village | 6.0 | 217.0 | 8.4 |
| Total | 28 km2 | 5000 tsetse | 300 animals |
3 Results
3.1 Description of the model
This ABM structured around agent, group and role interactions was developed using the Aalaadin meta-model developed by Ferber and Gutnecht [34]. Agents belong to well-defined groups (or levels) where they have well-defined roles in their interaction with one another. The model itself is described using the Cassiopea procedure [35], where the class structures of agents are described first, followed by the interactions that take place among them. If relationships change over time, a third step is devoted to defining this evolution. Each human or tsetse fly appears in the model under its own traits: longevity, current phase of the disease, time since entering that phase, etc. The interactions among agents are based on its groups and roles: each agent belongs to one or more groups and plays one or more roles in each group. A detailed presentation of the model is in Muller [36]. The program, with installation and user guides, is available at http://www.emse.fr/~gmuller.
For programming, we used the MadKit platform [37] from the Aalaadin meta-model [34]. Due to the large number of agents in Lambi simulation (eight locations, 500 humans, 5000 Glossina), a single simulation using a powerful computer (Pentium IV®, 128 Mo RAM, 1.4 GHz) ran for over 48 h. Through experiments, we reduced the number of agents by a factor of 10 with no adverse effect on the system. The initial proportions of the types of agents had to be retained (50 humans, 500 Glossina). Thus the time for five concurrent simulations is no more than 10 h.
3.1.1 Spatialisation
There are different ways of representing space. One solution is to define space as a grid. We opt for yet another approach: we ‘agentify’ it [38,39]. That is, space is structured by agents interrelated through their affiliations to different groups and roles, in a way somewhat similar to a network. This solution is advantageous, for two reasons. First, the mesh size is directly related to the number of agents used, with a possibility to link up with a geographic information system (GIS) [40–42]. Since a GIS represents locations as polygons with attributes (e.g., area, number of humans in each phase of the disease, etc.) attached to each location, it seems easy to associate these attributes with location agents of the model. Second, links between different areas are captured in the group and/or role relationships of agents. Although the number of agents needed increases with a more precise representation, this drawback is offset by the advantages of this approach.
3.1.2 Application to the epidemiological context
The model considers locations, vectors and humans as agents in an epidemiological complex. The spatial dimension is introduced through the ‘agentification’ of the main sites occupied by the human and tsetse agents: village, lands surrounding the village (including water supply outlets, plantations and abandoned fields) and forests (including footpaths and river banks). The group–role interactions that take place between location agents define the spatialisation links. Animals are not represented as agents, but their number within each location is taken into account. System agents (schedulers and watchers) are present as well and their function is to synchronise the agents and extract some variables – such as the prevalence of the disease, etc. – that make it possible to monitor the evolution and even to visualise this evolution by means of a graphic display module. Moreover, interactions are static, which implies that the behaviour of an agent does not change in the course of a simulation. The time step is common to all agents and corresponds approximately to 12 h. This makes it possible to handle the daily switch of human behaviour between night and day, tsetse flies displaying an essentially diurnal activity. The total length of time spanned by one simulation corresponds to six years, i.e. approximately 4000 iterations. In some cases, the simulation duration is extended to 13 years. As for the tsetse population, the number of humans is considered constant. When an agent playing the role of human in the second phase should die, it comes back in the system in the healthy state.
3.1.3 Characteristics of the human agents
The simulated agents move according to the qualitative traits of the real-life agents: the young and the aged remain in villages and lead sedentary lives, and the others are hunter-farmers, who travel to cocoa plantations (the main cash crop), forests and water supply outlets. The travel mode used by each individual is determined by the role he or she plays, the choice of destination area from a given set, and the length of time spent in each area, based on the type of area selected (Table 1).
3.1.4 Characteristics of the location agents
A location agent is characterised by: (1) the surface area (as a proportion to the total surface area) and the position of its bounding box; (2) the number of flies and humans present in an area, (3) the number of animals that reside in the area, regardless of species. The location agents are the supervisor of the other agents' movements (tsetse and human agents) and permit the visualisation of system activities. They are the only ones who know the current numbers of tsetse flies and animals in the area they cover. Thus, one of their jobs is to send bite messages to human agents. Indeed, they can deduce tsetse fly densities and the number of bites inflicted on humans. The number of animals determines the dilution level of the tsetse bites. The more the animals in a unit surface area, the less likely the bites will involve humans.
3.1.5 Example of an interaction between agents
Fig. 2 describes a scenario with regards to the order of appearance of the three types of agents: human 1, tsetse 3 and tsetse 8 in location 5 (both tsetse agents being in the infective phase), and the emission of a bite message. It also highlights a useful trait of the system: when an infective tsetse agent emits a bite message, whether the bite will effectively be infective or not, is determined by the human agent. Fig. 2 shows that after an initial bite message emanating from tsetse agent 8 (enrolled in the same location as human agent 1), the possibility of infective interaction was rejected, in accordance with the result of a 62% probability calculation based on simple algorithm (carried out by human agent 1).
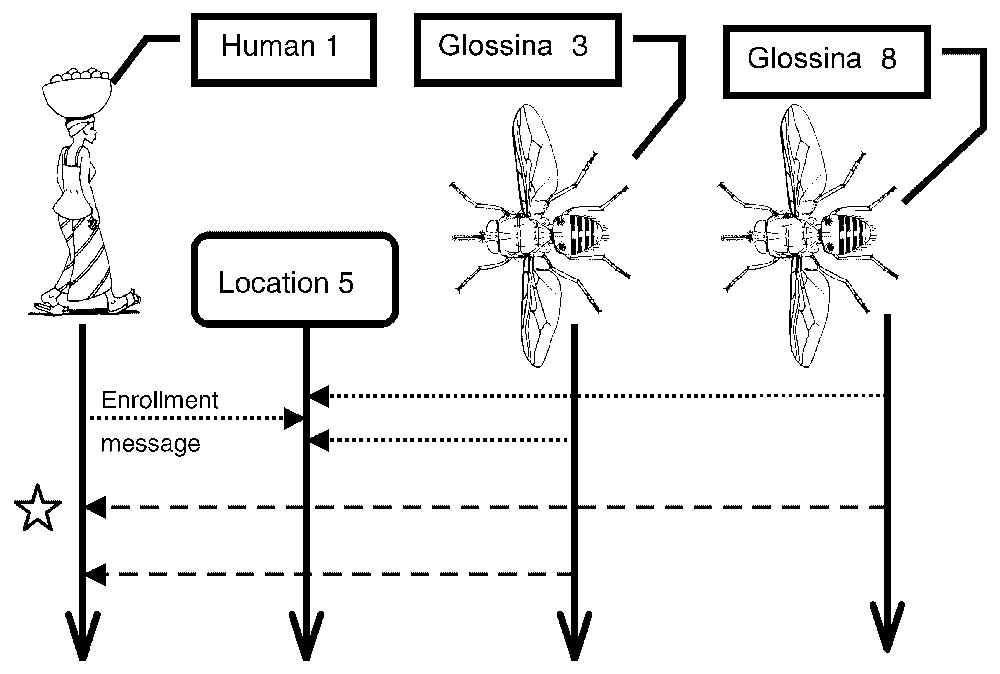
Example of scenario (scenario 1). This scenario involves four agents. Human 1 and Glossina 3 and 8 are enrolled in Location 5. Both Glossina are infecting and bite on the human. After each bite message, a probability calculation determines whether or not Human 1 will develop the disease. Here, only one bite contaminates the human (star).
Fig. 3 depicts an imaginary example of agent groupings in relation to their group and role interactions. Cocoa plantations and forests are clustered around one village. The three ellipses surround groups from three distinct settlements. Plantations and forests may belong to different villages, and, as a result, infected people from one village may transmit the disease to non-infected people from another village via the tsetse flies present in intersecting areas. A human agent belonging to the group from village 1 can only appear in forest zones 1, 2, 3 and 8, plantations 4, 6 and 7, and the village itself. Human agents from villages 1 and 2 can meet in plantation 4. Lastly, a tsetse agent present in plantation 4 can only bite human agents in this plantation but not elsewhere.
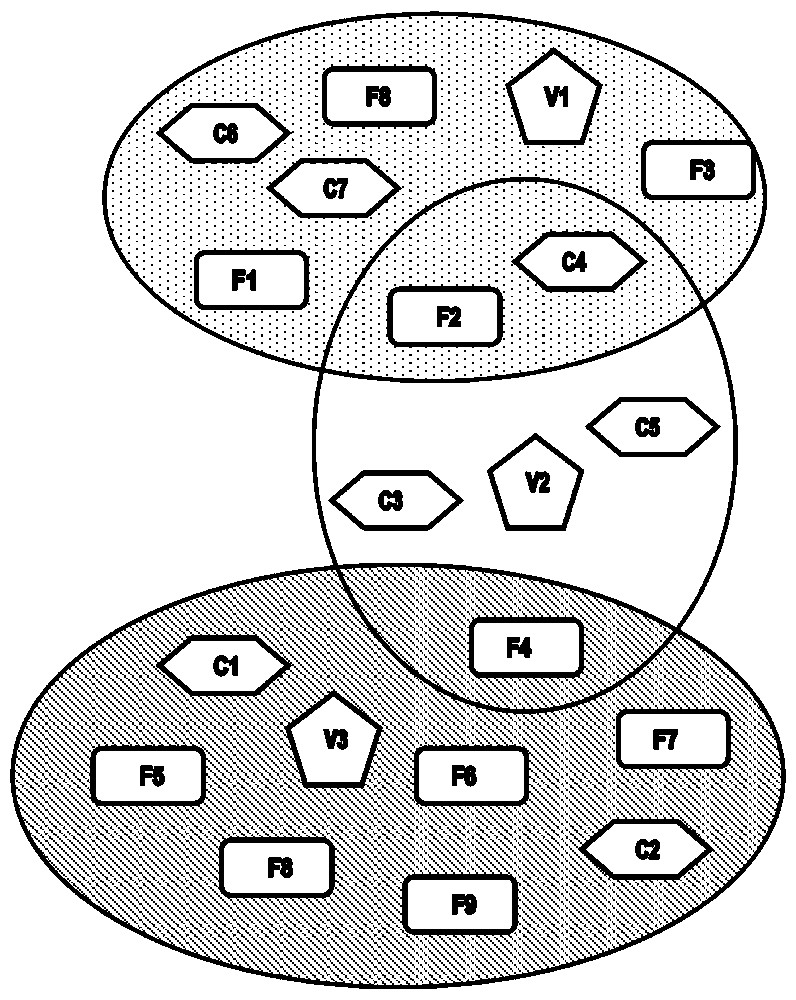
Example of scenario (scenario 2). This example shows the clustering in three groups of location agents (C: cocoa plantations, F: forests) around villages (V). Ellipses represent groups.
The tree diagram visible in Fig. 4 displays the architecture of the groups, roles and agents system and the ways in which the agents perceive one another. When human agent 1 wants to be in a particular location, it considers the areas linked to its village (village 1): it has access to cocoa plantation 1, forest 2 and village 1. It selects plantation 1 at random and sends a message to its location agent so that it updates its counters (for the number of humans in each phase of the disease). Once human 1 and tsetse 1 are in the same location (plantation 1) and the tsetse needs a blood meal, it selects one of the temporary agents in the group ‘village 1’ with the role ‘in-Plantation 1’. Should it select human agent 1 at random, then it can send a bite message to it. Similarly, there is a special signal on leaving a location so that the relevant location agent may adjust its counters.

Architecture of the groups–roles–agents system. An agent ‘sees’ only other agents of his group, here ‘village 1’. This example of scenario shows an option available for the agents human 1 and tsetse 1. The tsetse 1 goes in cocoa plantation C1 following a random choice. Idem for Human 1, but his displacement is also determined by his property (sedentary or not). Later, the possible encounter of these two agents in C1 (in-P1 role) is as well at random.
3.2 The Bipindi focus simulation
Three types of location are taken into account: lands surrounding village, village and forest. Each location displays particular characteristics as regards the number of individuals present and the surface area it covers, making it possible to differentiate forests, forest footpaths, water-holes (cassava retting sites, bathing or washing areas), cocoa plantations, subsistence crop fields, abandoned fields, thalwegs (river banks or swampy areas) and villages, given on the whole eight location agents (Table 2). From the initial distribution, the random displacement of the flies produces quickly a state of steady balance (Table 2). Fig. 5 presents the results obtained after 10 simulations of 13 years using data from the Lambi village. There are 50 Humans in the village. The number of infected human agents remains approximately between 5 and 8 during the simulation runs, giving a prevalence of 10 to 16%. If we artificially increase the number of infected flies, the prevalence level reaches 10% in the second year, and 40% after 6 years (Fig. 5).

The human trypanosomiasis focus of Lambi. Simulations with the Lambi's field parameters (solid line). The percentage of infected flies, whose depend on the location considered, is on average 2.4%. Simulation with an artificially increased number of infected flies (dotted line). The percentage of infected flies is fixed to 10% for all locations. Prevalence: number of cases divided by the total human population (average for ten simulations). The simulation duration is extended to 13 years.
3.3 Sensitivity to spatialisation
The effect of the size and number of transmission areas are of special interest. Fig. 7 shows simulation results after a change to the organisation of space. Each line uses the average values from ten simulation runs. This example shows how the model reacts to spatialisation: the less the locations (cf. example V in Fig. 6), the more the infected humans throughout the simulation runs. The second simulation trial for spatialisation (Fig. 7) suggested different kinds of areas. The results show that staying in a territory-type area is more risky. The influence due to different types of areas is not obvious, since those selected here differ mostly in their surface area. These observations contribute to the idea that the spatial organisation plays an important part in the transmission of this disease. In particular, it would seem that more the system is heterogeneous and spatially complex, more the spread appears stable.

Sensitivity of transmission for spatialisation (2). Simulations with two different kinds of locations. Territory: location where the humans live (plantations, abandoned fields, crop-fields, thalwegs: globally more flies, less space); Forest: location where the Humans can go but are not going frequently (water holes, forest footpaths, deep forest: lot of space, less flies). There are 50 humans in the village. Results are given for ten simulations.
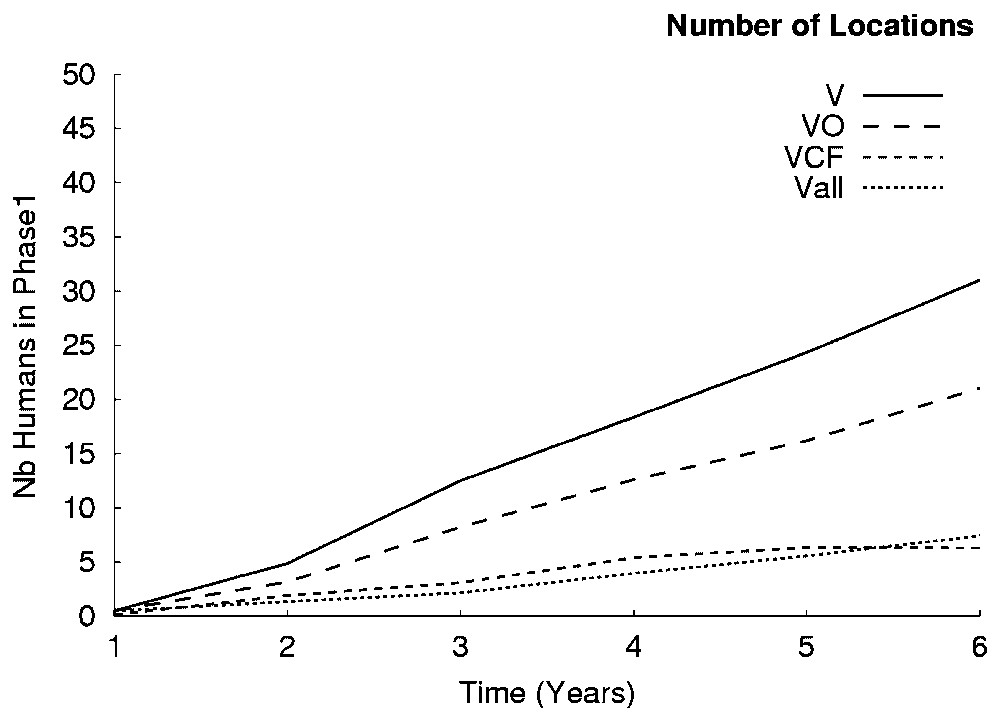
Sensitivity of transmission for spatialisation (1). Variation in number of location agents. Vall: Lambi example, eight location agents (Table 2). VCF: the locations of Lambi example are merged into two types, territory and forest, resulting in three location agents: one Village, one Territory, one Forest. VO: idem, territory and forest are merged into a new Location agent (without realistic meaning). V: idem, only one location, the Village where all flies, humans and pigs are concentrate. During all these merges, we aggregated fly, human, pig and the surfaces attributes of location agents. There are 50 humans in the village. Results are given for ten simulations.
3.4 Sensitivity for duration of first phase
The prevalence is very sensitive to duration of the first phase, as Fig. 8 shows. With the first phase chosen between 4 months and 12 years, the prevalence reach up to 18%. With a short Phase 1 corresponding to a duration spanning from 4 months to one year, the prevalence was down to 4–5%. Trials of simulations with shorter duration of the first phase showed lower prevalence. What is remarkable is that in these cases the prevalence is relatively stable over a long period (13 years).
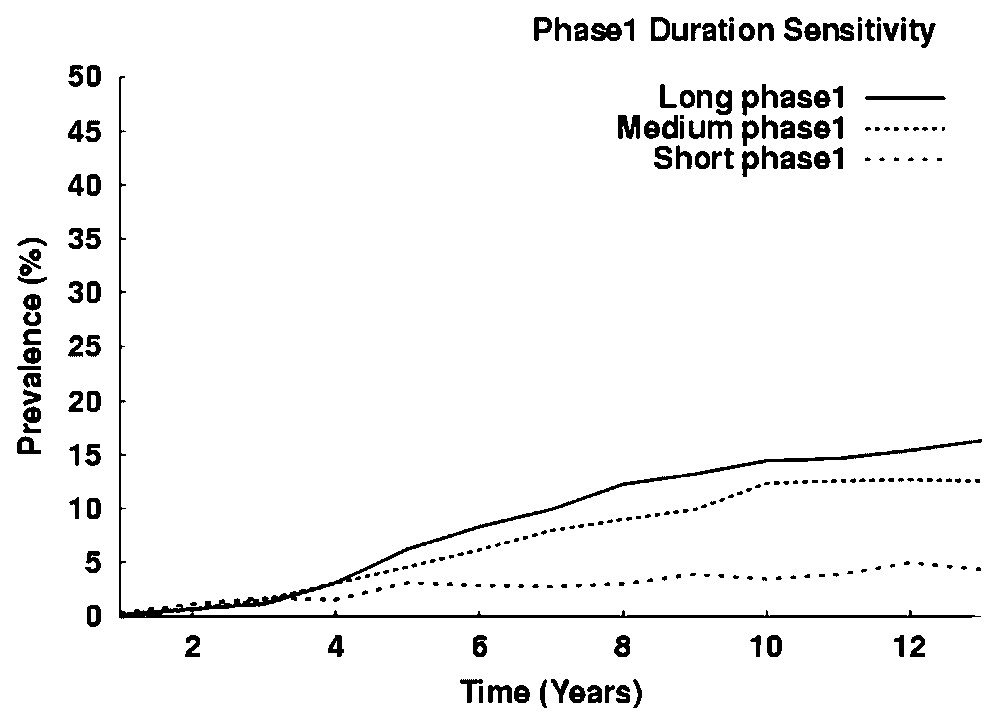
Sensitivity of transmission for duration of phase 1. Simulations with different durations of phase 1. Long phase 1 corresponds to a duration between 4 months and 12 years, Medium phase 1, 4 months to 8 years and Short phase 1, 4 months to one year. There are 50 humans in the village. Results are given for ten simulations. Prevalence in percentage of the total human population.
4 Discussion
ABMs are little explored as yet, but may offer great potential [43]. This method is quite new in epidemiology and do seem to hold promise [44]. For modelling sleeping sickness, the ABM appears appropriate, for two principal reasons. In this disease, (1) the transmission depends greatly on stochastic events and, (2) geographical locations are deciding factors. The aim is to develop an ABM that would evaluate trypanosomiasis risks in areas following their ecological and human specificities and which serves as a tool for the search for strategies of optimum control.
4.1 Upgrading possibilities
To reduce the number of co-evolving tsetse agents, it was envisaged to restrict the representation of the tsetse to teneral (newborn) and infective flies alone, as suggested by Artzrouni and Gouteux [14]. In the present model, the movements of the flies are random, which is not what happens in reality [2]. An upgraded version, presently in preparation, incorporates a set of ground rules concerning these movements as a way to better reflect the real-life behavioural complexity of the tsetse flies. Water holes and areas of high pig density will act as ‘attractors’ that would slow down the progress of the flies. In a similar way, forest borders will be considered as pathways for flies when the concentration effect of the flies in these ecotones are mapped and agentified as proper locations. The linkage with a Geographical Information System (GIS) may be envisaged. Other improvements include the incorporation of a matrix model simulating the evolution of tsetse populations to modulate the number of flies according to variations of the seasonal survival rates [45]. The model will also be improved in its handling of the different population dynamics of humans and pigs. The main characteristic of the ABM is to enlarge their complexity easily to represent reality; this improvement of the model remains limited only by the computer capacities. On the other hand, taking into account new processes in mathematical models necessitates new models that are not always feasible or efficient.
4.2 Phases duration problems and questions
The epidemiological profile of various foci of sleeping sickness is mainly determined by the duration of the first phase, as it is shown in Fig. 8 and proved by mathematical models [7,23]. However, these parameters are always very roughly estimated in the field. The question is the following: may this model be used to test the true duration of the two phases of the disease? Here we use four years on average for the duration of the first phase in a hypothetically uncontrolled case. Fig. 8 shows that this focus may reach a relatively low and durable prevalence of 4–6% with shortening the phase I. In reality, the Bipindi focus was medically controlled with active and passive screening, and this control certainly reduces the first phase more strongly. The low prevalence (under rate of 2%) may be mainly dependent on the first-phase duration. We can answer this question only if we test the combination of the two medical strategies used, each of them modifying the parameters in different ways. Active screening by an operational team lowers drastically and suddenly the durations of both first and second phases. Passive screening in the primary health care operates on the second phase only and with a long-term action. Nevertheless, this ABM requires further explorative simulations and, in particular, a general sensitivity study.
4.3 Epidemiological importance of animals
The rate of blood feeding on humans is an essential parameter for the transmission [17,18]. On the other hand, do the infections of the animals contribute to the stability of the system and the maintenance of few annual cases of the disease over many years [17,33]? However, the scope of the model has not yet been explored, but some simulations may prove that the presence of an animal reservoir is responsible for the stability observed in combination with other parameters, such as the spatial complexity and the duration of the first phase (Figs. 6–8). Of interest, it should also be possible to simulate the periodic epidemics of pig fever. Although pigs may live up to 15 years, they usually die earlier from periodic epidemics, or sometimes from mass slaughter during village festivities. Such a brutal reduction of the pig population forces the flies to feed on humans instead. Thus, the size variations of the pig population may be very important parameters to monitor sleeping sickness propagation. These simulations, which are currently in hand, as well as the sensibility studies, are needed to explore the various aspects of the transmission.
Acknowledgements
We would like to thank the two anonymous referees for their critical reading and constructive comments of the first version of the manuscript. We are also grateful to Prof. W. Shu of University of Buea, Cameroon, for his helpful suggestions.


