Sur un modèle densité-dépendant de compétition pour une ressource

Claude Lobry; Alain Rapaport; Frédéric Mazenc

doi:10.1016/j.crvi.2005.11.004

Biomodélisation / Biological modelling

Sur un modèle densité-dépendant de compétition pour une ressource

Présenté par : Pierre Auger

Claude Lobry ¹ ; Alain Rapaport ¹ ; Frédéric Mazenc ¹

¹ Projet MERE, INRA–INRIA, LASB ENSAM, 2, place Viala, 34060 Montpellier, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 2, pp. 63-70.

Résumés

Français
Anglais

Nous utilisons le concept de caractéristique à l'équilibre d'une population, consommant une unique ressource limitante, pour discuter de façon simple de l'issue de la compétition de plusieurs espèces pour cette seule ressource. La caractéristique à l'équilibre est une courbe qui est associée à chaque espèce et qui est susceptible d'être déterminée empiriquement. Les données de la caractéristique à l'équilibre et de la dynamique de renouvellement de la ressource permettent, sous certaines hypothèses, de donner des conditions de coexistence ou d'exclusion des espèces.

We use the concept of steady-state characteristic of a population using a single limiting resource, in order to discuss the issue of the competition of many species for the same resource. The steady-state characteristic is a curve that is associated to each species, likely to be determined empirically. Once one knows the steady-state characteristics and the dynamic of the renewal of the resource, it is possible to predict to some extent the issue of the competition and to give sufficient conditions for coexistence.

Métadonnées

Reçu le : 2005-06-10
Accepté le : 2005-11-15
Publié le : 2005-12-20

PMID

DOI : 10.1016/j.crvi.2005.11.004

Mot clés : Ressource, Compétition, Densité-dépendance, Ratio-dépendance
Keywords: Resource, Competition, Density-dependence, Ratio-dependence

Affiliations des auteurs :

Claude Lobry ¹ ; Alain Rapaport ¹ ; Frédéric Mazenc ¹

¹ Projet MERE, INRA–INRIA, LASB ENSAM, 2, place Viala, 34060 Montpellier, France

@article{CRBIOL_2006__329_2_63_0,
     author = {Claude Lobry and Alain Rapaport and Fr\'ed\'eric Mazenc},
     title = {Sur un mod\`ele densit\'e-d\'ependant de comp\'etition pour une ressource},
     journal = {Comptes Rendus. Biologies},
     pages = {63--70},
     publisher = {Elsevier},
     volume = {329},
     number = {2},
     year = {2006},
     doi = {10.1016/j.crvi.2005.11.004},
     language = {fr},
}

TY  - JOUR
AU  - Claude Lobry
AU  - Alain Rapaport
AU  - Frédéric Mazenc
TI  - Sur un modèle densité-dépendant de compétition pour une ressource
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 63
EP  - 70
VL  - 329
IS  - 2
PB  - Elsevier
DO  - 10.1016/j.crvi.2005.11.004
LA  - fr
ID  - CRBIOL_2006__329_2_63_0
ER  -

%0 Journal Article
%A Claude Lobry
%A Alain Rapaport
%A Frédéric Mazenc
%T Sur un modèle densité-dépendant de compétition pour une ressource
%J Comptes Rendus. Biologies
%D 2006
%P 63-70
%V 329
%N 2
%I Elsevier
%R 10.1016/j.crvi.2005.11.004
%G fr
%F CRBIOL_2006__329_2_63_0

Claude Lobry; Alain Rapaport; Frédéric Mazenc. Sur un modèle densité-dépendant de compétition pour une ressource. Comptes Rendus. Biologies, Volume 329 (2006) no. 2, pp. 63-70. doi : 10.1016/j.crvi.2005.11.004. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2005.11.004/

Version originale du texte intégral

Abridged English version

Today, the theory of the chemostat has been widely studied in the literature (see, for instance, the textbook [14]). The classical model describing the competition of several species $x_{i}$ on a single resource s is the following one:

{\begin{matrix} \dot{s} = f (s) - \sum_{i} μ_{i} (s) x_{i} \\ {\dot{x}}_{i} = (μ_{i} (s) - d_{i}) x_{i} \end{matrix}

(1)

One of the main results of this theory is known as the Competition Exclusion Principle [8], which states that several species

x_{i}

cannot coexist at equilibrium. Nevertheless, for certain ecosystems, the prediction given by this principle is not observed in concrete experiments [8].

In this work, we propose to replace in (1) the classical functional responses $μ_{i} (\cdot)$ , that are only resource dependent, by growth functions $h_{i} (\cdot)$ that depend on both the available resource s and the quantity of consumers $x_{i}$ . Then, the ith equation of the model (1) becomes:

{\dot{x}}_{i} = (h_{i} (s, x_{i}) - d_{i}) x_{i}

(2)

Here, the function

h_{i} (\cdot)

is assumed to be increasing with respect to s and decreasing with respect to

x_{i}

.

We introduce the concept of steady-state characteristic $ψ_{i} (\cdot)$ for each species i, which maps for each fixed s the steady state $ψ_{i} (s)$ of the single equation (2) for initial condition $x_{i} (0) > 0$ . Then, we show that all the essential information for determining the asymptotic behavior of the species $x_{i}$ in competition with other species on the resource s relies on the knowledge of the characteristics $ψ_{i} (\cdot)$ .

Our main result is the following: assume that the function $f (\cdot)$ is bounded and negative for s larger than a certain number $K > 0$ . Let $s_{e}$ be a solution of the equation

f (s) = \sum_{i} d_{i} ψ_{i} (s)

such that

f (s_{e}) > 0

and

f^{'} (s_{e}) < 0

. Then,

(s_{e}, \dots, ψ_{i} (s_{e}), \dots)

is a locally exponentially stable equilibrium of the system:

{\begin{matrix} \dot{s} = f (s) - \sum_{i} h_{i} (s, x_{i}) x_{i} \\ {\dot{x}}_{i} = (h_{i} (s, x_{i}) - d_{i}) x_{i} \end{matrix}

This persistence result generalizes previous results where the $h_{i} (\cdot)$ 's are of ‘Contois’ type [6], or where $f (\cdot)$ is linear [9]. Finally, considering functional responses that depend on both the resource and the consumer is also a way of generalizing ratio-dependent models, such as those introduced by Arditi and Ginsburg in prey–predator interaction models [2].

1 Introduction

Le chémostat a été introduit il y a plus d'un demi-siècle dans l'étude de la croissance des micro-organismes, et le modèle mathématique ci-dessous :

{\begin{matrix} \frac{d s (t)}{d t} = d (S_{in} - s (t)) - μ (s (t)) x (t) \\ \frac{d x (t)}{d t} = (c μ (s (t)) - d) x (t) \end{matrix}

(3)

a été proposé pour la croissance d'une espèce. La théorie mathématique, fort simple, de ce modèle remonte à Spicer, et date de la même époque (cf. [8] et sa bibliographie). Par changement d'unité, on peut se ramener au cas où

c = 1

, ce que nous faisons pour la suite. Nous appelons, selon la terminologie de l'écologie, réponse fonctionnelle la fonction

μ (\cdot)

en facteur de x dans la première équation de (3). C'est cette même fonction que l'on retrouve également en facteur de x dans la seconde équation (dans le cas

c = 1

), et qui s'interprète donc aussi comme le taux de croissance (hors disparition) de la population.

Un modèle analogue de compétition entre plusieurs organismes dans le même dispositif a été ensuite étudié, soit :

{\begin{matrix} \frac{d s (t)}{d t} = d (S_{in} - s (t)) - \sum_{j = 1}^{n} μ_{j} (s (t)) x_{j} (t) \\ \frac{d x_{i} (t)}{d t} = (μ_{i} (s (t)) - d_{i}) x_{i} (t) (i = 1, \dots, n) \end{matrix}

(4)

pour lequel il a été montré que la coexistence n'était pas possible, une des espèces éliminant toutes les autres [8]. Cette prédiction théorique a été corroborée par certaines expériences de laboratoire, mais est également infirmée par de nombreux écosystèmes naturels ou artificiels [8].

D'autres travaux ont considéré le modèle plus général :

{\begin{matrix} \frac{d s (t)}{d t} = f (s (t)) - \sum_{j = 1}^{n} μ_{j} (s (t)) x_{j} (t) \\ \frac{d x_{i} (t)}{d t} = (μ_{i} (s (t)) - d_{i}) x_{i} (t) (i = 1, \dots, n) \end{matrix}

(5)

où la fonction

f (\cdot)

n'est plus contrainte à être linéaire comme dans le chémostat, ce qui permet de représenter le cas d'une compétition pour une ressource biotique (dans ce cas, on prendra une fonction f de type logistique). Pour ce modèle, il a été aussi constaté qu'il ne peut pas y avoir de coexistence « à l'équilibre ». Dans les deux cas, la raison mathématique en est très simple. À l'équilibre, que ce soit dans les systèmes (4) ou (5), il faut que les n équations :

0 = (μ_{i} (s_{e}) - d_{i}) x_{i e} (i = 1, \dots, n)

(6)

soient satisfaites. Dans le cas d'un équilibre où toutes les espèces sont présentes, cela implique que tous les

x_{i}

sont non nuls et donc que les n équations :

0 = (μ_{i} (s_{e}) - d_{i}) (i = 1, \dots, n)

(7)

soient satisfaites, ce qui n'est pas possible en général, puisqu'il n'y a qu'une seule inconnue

s_{e}

.

En 1976, Armstrong et McGehee [3,12] ont fait remarquer que la coexistence ne se fait pas nécessairement à l'équilibre et que des oscillations forcées (modèle du chémostat (4) où $S_{in}$ ou $d_{i}$ peuvent être des fonctions périodiques du temps) ou endogènes (cas du système (5)) peuvent expliquer la coexistence. Ces travaux sont à l'origine de nombreux résultats sur les modèles (4) et (5), dont certains, mathématiquement sophistiqués, ont contribué à élucider une partie des mécanismes qui assurent la coexistence des espèces (toujours dans le contexte des modèles de compétition pour une ressource).

En 1989, Arditi et Ginzburg [2], dans le contexte de l'étude de la relation « proie–prédateur » ont proposé de remplacer la réponse fonctionnelle $s \to μ (s)$ par une fonction « densité-dépendante », c'est-à-dire de la forme $s \to μ (\frac{s}{x})$ . Cette approche a été très fructueuse pour l'amélioration de la compréhension de la relation proie–prédateur et des chaînes trophiques, mais ne semble pas avoir été explorée dans le cadre de l'étude de la compétition. C'est dans cet esprit que nous proposons de modifier le modèle de croissance d'une population de façon très simple, en introduisant une dépendance par rapport à la densité de la population dans la réponse fonctionnelle des modèles (4) et (5). Nous démontrons ainsi un résultat simple assurant, sous des hypothèses assez larges, l'existence d'un équilibre localement stable pour lequel il y a coexistence des espèces.

2 Le modèle « un consommateur – une ressource »

La quantité de ressource disponible à l'instant t est désignée par $s (t)$ et la quantité de consommateur par $x (t)$ . Le taux de croissance de la population est une fonction continue et différentiable de s et de x, que nous désignons par $h (s, x)$ . Nous supposons également que le taux de disparition (la disparition pouvant être la conséquence de la mortalité, de migrations, de prélèvements, etc.) du consommateur est constant et égal à d. Ainsi le modèle de croissance de la population du consommateur est donné par :

\frac{d x (t)}{d t} = (h (s (t), x (t)) - d) x (t)

(8)

Nous supposons que le taux de croissance de la population satisfait les hypothèses suivantes :

Hypothèses H1

1. La fonction $(s, x) \to h (s, x)$ est définie pour tout $s ⩾ 0$ et tout $x ⩾ 0$ , continue et dérivable.
2. $h (s, x) ⩾ 0$ et $h (0, x) = 0$ .
3. La fonction $s \to h (s, x)$ est strictement croissante.
4. Pour tout $s > 0$ fixé, la fonction $x \to h (s, x)$ est strictement décroissante et tend vers 0 quand x tend vers l'infini.

Proposition 1

Sous l' Hypothèse H1 , les propriétés suivantes sont vérifiées.

(i) Pour tout $s ⩾ 0$ constant, et pour toute condition initiale $x_{0} ⩾ 0$ , la solution correspondante de l'équation différentielle (8) tend vers un unique état d'équilibre, noté $ψ (s)$ , lorsque t tend vers l'infini.
(ii) La fonction $s \to ψ (s)$ est nulle sur un certain intervalle $[0, s^{*}]$ , puis croissante à partir de $s^{*}$ .

Preuve

Soit $s > 0$ fixé. D'après nos hypothèses, la fonction $x \to h (s, x) - d$ est strictement décroissante, et strictement négative pour x suffisamment grand. Ainsi, soit $x \to h (s, x) - d$ s'annule pour une valeur positive ou nulle, que l'on note $ψ (s)$ , soit $h (s, 0) - d < 0$ et l'on pose $ψ (s) = 0$ . Le point (i) de la Proposition 1 est alors une application immédiate de la théorie élémentaire des équations différentielles ordinaires [4].

Soit $s^{*} > 0$ défini par $h (s^{*}, 0) = d$ (et par +∞ si d est plus grand que $h (s, 0)$ pour tout s). D'après nos hypothèses de croissance sur $h (\cdot)$ , la fonction $ψ (\cdot)$ est identiquement nulle pour s plus petit que $s^{*}$ , et devient strictement positive et croissante après. Le point (ii) de la proposition est ainsi démontré. □

Définition 1

Nous appelons caractéristique à l'équilibre la fonction $s \to ψ (s)$ , définie par la Proposition 1 ci-dessus (cf. Fig. 1).

Fig. 1
Exemple de caractéristique à l'équilibre.

Remarque 1

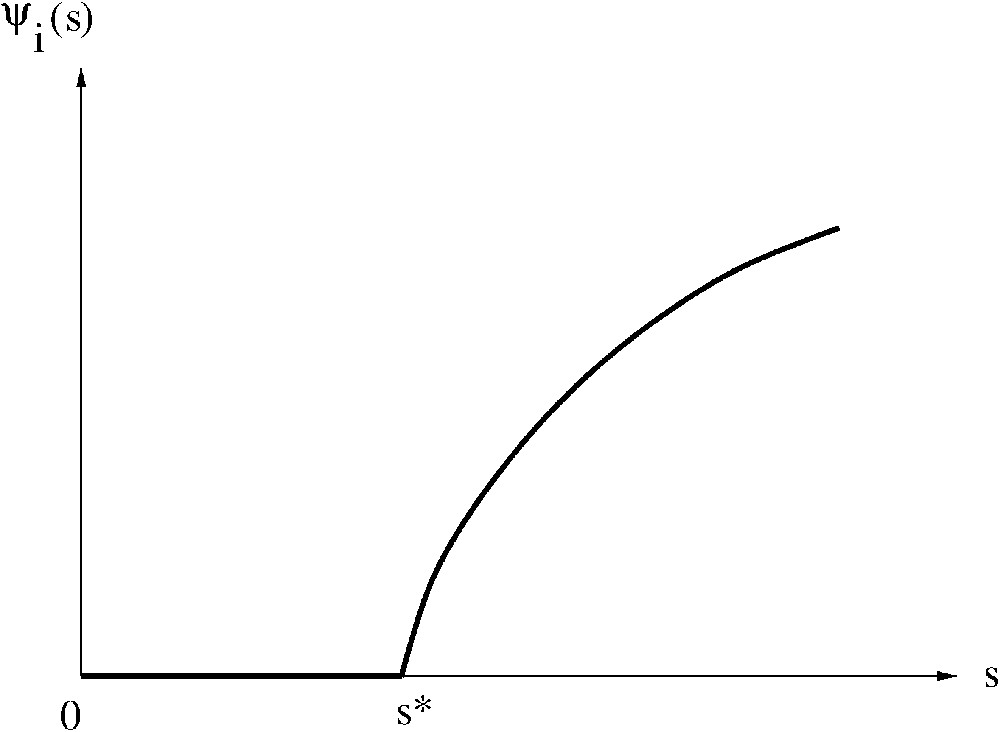
La caractéristique à l'équilibre que nous venons de définir est une partie de ce qu'on appelle usuellement l' « isocline du prédateur » dans la relation « proie–prédateur » du modèle (9) ci-dessous

{\begin{matrix} \frac{d s}{d t} = f (s) - h (s, x) x \\ \frac{d x}{d t} = (h (s, x) - d) x \end{matrix}

(9)

Nous avons préféré lui donner ici un autre nom car, d'une part il ne s'agit pas d'une isocline au sens strict du terme et, d'autre part, nous allons en faire un usage différent de celui classiquement fait dans l'étude des systèmes dynamiques en dimension deux.

Remarque 2

En théorie mathématique des systèmes, la quantité s s'appellerait « entrée » du système décrit par l'Éq. (8). Dans un article récent [1], l'importance des systèmes pour lesquels à chaque entrée on peut associer un unique équilibre a été démontrée. Cette correspondance a été appelée input-to-state characteristic. Bien que notre fonction $ψ (\cdot)$ ne soit qu'un cas particulier de cette notion, nous n'avons pas conservé cette appellation qui nous paraît obscure dans le contexte de la dynamique des populations. De même, nous aurions pu nous référer à certaines des méthodes générales mises au point par ces auteurs, mais nous avons préféré garder une approche mathématique élémentaire. Cela dit, nous devons reconnaître ici que la théorie mathématique des systèmes développée pour les besoins de l'automatique est notre principale source d'inspiration [11], et que les méthodes proposées dans [1] ont également des applications en écologie [7].

Exemple 1

{\begin{matrix} h (s, x) = μ (s) r (x) \\ μ (s) = \frac{μ_{\max} s}{e + s} \\ r (x) = \frac{1}{1 + α x^{\frac{1}{3}}} (α > 0) \end{matrix}

(10)

On reconnaît dans la fonction

μ (\cdot)

le modèle classique de croissance de Monod. Cette fonction de croissance est multipliée par une fonction

r (\cdot)

qui réduit la croissance d'autant plus que la taille de la population est grande. Un calcul élémentaire montre que la fonction caractéristique de croissance est, dans ce cas :

ψ (s) = | \begin{matrix} 0, & s \in [0, s^{*}] \\ α^{−3} {(\frac{μ_{\max} s}{d (e + s)} - 1)}^{3}, & s ⩾ s^{*} \end{matrix}

(11)

où

s^{*} = d e / (μ_{\max} - d)

si

d < μ_{\max}

, et

s^{*} = + \infty

sinon.

Exemple 2

{\begin{matrix} h (s, x) = μ (\frac{s}{α + x}) (α > 0) \\ μ (s) = \frac{μ_{\max} s}{e + s} \end{matrix}

(12)

Dans ce cas, la fonction

ψ (\cdot)

est identiquement nulle lorsque

μ_{\max} ⩽ d

. Sinon,

ψ (s) = | \begin{matrix} 0, & s \in [0, s^{*}] \\ \frac{μ_{\max} - d}{d e} s - α, & s ⩾ s^{*} \end{matrix}

(13)

où

s^{*} = α d e / (μ_{\max} - d)

. Le modèle « ratio dépendant » est le cas limite obtenu pour

α = 0

.

Exemple 3

{\begin{matrix} h (s, x) = μ (s) \\ μ (s) = \frac{μ_{\max} s}{e + s} \end{matrix}

(14)

Dans ce cas, les Hypothèses H1 ne sont pas satisfaites (puisque la fonction

h (\cdot)

est constante par rapport à la variable x et la fonction

ψ (\cdot)

n'est pas définie). Revenons à l'Éq. (8) et constatons que trois cas sont possibles, lorsque

d < μ_{\max}

.

– Si $s < s^{*}$ , toutes les solutions de (8) tendent vers 0.
– Si $s = s^{*}$ , toutes les solutions de (8) sont constantes.
– Si $s > s^{*}$ , toutes les solutions non identiquement nulles de (8) tendent vers +∞

avec

s^{*}

défini, comme dans l'Exemple 1, par l'équation

μ (s^{*}) = d

. Ce cas peut être vu comme le cas limite de l'Exemple 1 lorsque la fonction

r (\cdot)

possède une décroissance vers 0 de moins en moins forte, c'est-à-dire lorsque α tend vers 0.

Théorème 1

Considérons le système(9), dont nous supposons que la réponse fonctionnelle $h (\cdot)$ satisfait lesHypothèses H1 (donc dont la caractéristique à l'équilibre $ψ (\cdot)$ est bien définie), et supposons de plus que la fonction f est bornée, strictement positive pour $0 < s < K$ et strictement négative pour $s > K$ . Si $s_{e}$ est une solution de l'équation

f (s) = d ψ (s)

(15)

telle que

f (s_{e}) > 0

et

f^{'} (s_{e}) < 0

, alors

(s_{e}, x_{e})

avec

x_{e} = ψ (s_{e}) = f (s_{e}) / d

est un équilibre localement (exponentiellement) stable du système (9).

Preuve

Elle est extrêmement simple. Nous devons d'abord montrer que $(s_{e}, x_{e})$ est une solution du système de deux équations :

0 = f (s) - h (s, x) x

(16)

0 = (h (s, x) - d) x

(17)

L'Éq. (17) est satisfaite par définition de la fonction

ψ (\cdot)

. Si nous remplaçons dans (16)

h (s, x)

par d et

x_{e}

par

ψ (s_{e})

, nous obtenons

0 = f (s_{e}) - d ψ (s_{e})

, ce qui est précisemment l'hypothèse faite dans le théorème. La stabilité se démontre en calculant la matrice jacobienne du système (9) au point

(s_{e}, x_{e})

(voir Annexe A) et en vérifiant que l'équation caractéristique de cette dernière possède bien deux racines à parties réelles strictement négatives, ce qui, dans le cas d'une matrice

2 \times 2

, est immédiat. Nous ne poursuivons pas, car le Théorème 1 est un cas particulier du Théorème 2 énoncé ci-dessous. □

Le Théorème 1 ne présente aucune originalité et n'est là que pour rappeler ce que nous généralisons. Il est d'autre part connu que, sans hypothèse supplémentaire, cet équilibre n'a aucune raison d'être globalement stable.

3 Le modèle de compétition « n consommateurs – une ressource »

Nous considérons dans ce paragraphe le modèle :

{\begin{matrix} \frac{d s (t)}{d t} = f (s (t)) - \sum_{i = 1}^{n} h_{i} (s (t), x_{i} (t)) x_{i} (t) \\ \frac{d x_{i} (t)}{d t} = (h_{i} (s (t), x_{i} (t)) - d_{i}) x_{i} (t) \\ (i = 1, \dots, n) \end{matrix}

(18)

qui est le modèle usuel (5) de compétition pour une ressource dans lequel nous avons remplacé les réponses fonctionnelles

μ_{i} (\cdot)

« ressource dépendantes » par des réponses fonctionnelles

h_{i} (\cdot)

dépendant des densités des consommateurs. Nous pouvons alors énoncer le résultat suivant.

Théorème 2

Considérons le système(18)dont nous supposons que tous les $h_{i} (\cdot)$ satisfont lesHypothèses H1 (donc dont les caractéristiques à l'équilibre $ψ_{i} (\cdot)$ sont bien définies). Supposons de plus que la fonction $f (\cdot)$ est bornée, strictement positive pour $0 < s < K$ et strictement négative pour $s > K$ . Si $s_{e}$ est une solution de l'équation

f (s) = \sum_{i = 1}^{n} d_{i} ψ_{i} (s)

(19)

telle que

f (s_{e}) > 0

et

f^{'} (s_{e}) < 0

alors

(s_{e}, ψ_{1} (s_{e}), ψ_{2} (s_{e}), \dots ψ_{i} (s_{e}), \dots ψ_{n} (s_{e}))

est un équilibre localement (exponentiellement) stable du système (18).

Preuve

Nous devons montrer que

(s_{e}, ψ_{1} (s_{e}), ψ_{2} (s_{e}), \dots ψ_{i} (s_{e}), \dots ψ_{n} (s_{e}))

est une solution du système de

n + 1

équations

0 = f (s) - \sum_{i = 1}^{n} h_{i} (s, x_{i}) x_{i}

(20)

0 = (h_{i} (s, x_{i}) - d_{i}) x_{i} (i = 1, \dots, n)

(21)

Par définition des

ψ_{i} (\cdot)

, les n Éqs. (21) sont toutes satisfaites quand on remplace

x_{i}

par

ψ_{i} (s)

. Remplaçons alors dans (20) les

x_{i}

par

ψ_{i} (s)

. Il vient :

0 = f (s) - \sum_{i = 1}^{n} d_{i} ψ_{i} (s)

(22)

qui est précisément l'équation dont l'hypothèse du théorème suppose qu'elle possède une solution

s_{e}

. Il reste à montrer que cet équilibre est stable. Pour cela, il suffit de calculer la matrice jacobienne et de montrer que ses valeurs propres sont à parties réelles négatives. Ceci exige quelques calculs élémentaires sur les nombres complexes, que nous repoussons en Annexe A. □

Le Théorème 1 est clairement le cas particulier du Théorème 2 dans le cas où $n = 1$ .

Il est clair que pour tous les i tels que $s_{i} < s_{e}$ , les $x_{i e}$ à l'équilibre correspondant sont strictement positifs, alors que pour tous les autres indices i, les $x_{i}$ correspondant sont nuls et les espèces correspondantes sont éliminées. On en déduit que, les caractéristiques des consommateurs étant données par les $h_{i} (\cdot)$ et les $d_{i}$ , on pourra toujours trouver un $f (\cdot)$ assez grand pour que toutes les espèces soient présentes à l'équilibre. Cette proposition peut s'interpréter inversement : pour un $f (\cdot)$ donné et un entier n arbitraire, on peut définir des $h_{i} (\cdot)$ et des $d_{i}$ tels que toutes les espèces soient présentes à l'équilibre.

4 Discussion

4.1 Réalisme biologique des Hypothèses H1

Pour de nombreuses d'espèces, il est réaliste d'imaginer que le taux de croissance d'une population, toutes choses égales par ailleurs, diminue quand la taille de la population augmente. C'est un phénomène de compétition « intraspécifique » pour l'accès à la ressource. Toutefois, il peut exister, pour certaines espèces, une forme de mutualisme qui contredirait cette hypothèse. Il existe un cas, celui de la croissance d'une espèce dans un milieu liquide, où la diffusion du substrat peut devenir un facteur limitant si les organismes ont tendance à constituer des colonies plus ou moins sphériques. Dans ce cas, seule la zone en périphérie a accès à la ressource et alors la considération du rapport volume/surface conduit à introduire une réduction du taux de croissance tel que dans l'Exemple 2. Le cas classique de la « loi d'action de masse » pure où la fonction $h (\cdot)$ ne dépend pas de x (Exemple 3) apparaît comme un cas limite dégénéré de notre modèle. C'est une dégénérescence forte, car la caractéristique à l'équilibre cesse d'exister en tant que fonction. C'est pourquoi les conclusions de notre Théorème 2 ne sont plus vraies dans le modèle classique « proie dépendant ».

Le cas de la « ratio dépendance », dès lors qu'on introduit un petit paramètre α comme dans l'Exemple 3, apparaît comme un cas particulier de notre modèle. L'introduction de ce petit paramètre ne change rien d'essentiel à la philosophie développée par les partisans de la ratio-dépendance. Une partie des arguments en faveur de la ratio dépendance peut donc être reprise en faveur de notre modèle.

Nous avons supposé un taux de disparition d constant. Poursuivant la même logique il serait judicieux de le rendre lui aussi dépendant de la densité et d'écrire

\frac{d x (t)}{d t} = (h (s (t), x (t)) - d (x (t))) x (t)

(23)

Il est possible de le faire sans changer les conclusions de cette note, mais la présentation aurait été un petit peu plus compliquée. Toujours par souci de simplicité, nous avons supposé que la réponse fonctionnelle est égale au taux de croissance. On sait que, si ces derniers sont proportionnels, on peut, par simple changement d'unités, éliminer la constante de proportionnalité. Mais, même dans le cas où il n'y a pas proportionnalité, on peut sans peine étendre les résultats de la note.

Dans la Réf. [10] sont développés, dans le contexte de l'écologie microbienne, des arguments en faveur de réponses fonctionnelles du type de notre Exemple 3.

4.2 Critique du modèle de compétition proposé

Le modèle défini par les Éqs. (18) n'est pas la conséquence logique du modèle défini par les Éqs. (9), comme les Éqs. (4) le sont de (3). En effet, dans ce dernier cas, il était supposé que tous les individus d'une espèce ont à tout moment le même accès à la ressource, et il y a une certaine logique à supposer qu'il en est de même pour un mélange d'individus d'espèces différentes. Dans notre cas, dans la mesure où nous supposons une certaine forme de compétition entre les individus d'une même espèce pour accéder à la ressource, il serait peu logique de ne pas supposer qu'elle existe aussi entre les individus des espèces différentes. Cela se traduirait mathématiquement par l'introduction de fonctions $h (\cdot)$ dépendant de toutes les variables $x_{i}$ :

(s, x_{1}, \dots, x_{n}) \to h (s, x) = h (s, x_{1}, \dots, x_{n})

(24)

croissantes par rapport à s et décroissantes par rapport à toutes les autres variables. Malheureusement nous ne disposons pas à ce jour d'une théorie achevée pour ce cas plus complexe.

Toutefois, nous pouvons justifier notre modèle avec l'argument suivant. Dans tous les cas où les individus de la même espèce ont tendance à rester ensemble (que ce soit la conséquence d'un comportement grégaire ou la conséquence de la division cellulaire dans le cas de micro-organismes), les effets de la compétition intraspécifique seront plus importants que ceux de la compétition interspécifique. Mathématiquement, grâce aux théorèmes généraux de stabilité structurelle [5], nous pouvons affirmer que, si les dérivées partielles de $h_{i} (\cdot)$ par rapport aux variables $x_{j}$ (j différent de i) sont assez petites en valeur absolue devant la valeur absolue de la dérivée partielle par rapport à $x_{i}$ , les conclusions du Théorème 2 restent identiques. En d'autres termes, si la compétition interspécifique est faible devant la compétition intraspécifique, la coexistence des espèces est possible. On retrouve le fait élémentaire bien connu dans le cas des équations de Lotka Volterra. Cependant, il reste souhaitable que des résultats mathématiques plus poussés viennent quantifier ce résultat.

4.3 Critique de l'étude à l'équilibre

Les remarques de Armstrong et McGhee restent valables, mais il faudrait continuer à examiner le modèle (18), non plus du seul point de vue des équilibres, mais aussi de celui de la persistance « tout court ». Dans la note [9], il est montré que, dans le cas du chémostat ( $f (\cdot)$ linéaire et $d_{i}$ égaux), seule la persistance à l'équilibre est possible. Mais les travaux récents de [7] montrent le même phénomène dans un cas ou la mortalité des espèces dépend de la densité de la population des espèces.

Dans [6], une condition suffisante de persistance est démontrée pour le modèle particulier où la fonction $f (\cdot)$ est une logistique et où les $h_{i} (\cdot)$ sont des fonctions de type « Contois ». Dans la note [13], un résultat du même type est proposé dans le cadre plus général que nous proposons ici.

Annexe A

Soit un système de n équations différentielles

{\dot{y}}_{i} = F_{i} (y_{1}, \dots, y_{i}, \dots, y_{n}) (i = 1, \dots, n)

(A.1)

et

(y_{1 e}, \dots, y_{i e}, \dots, y_{n e})

un équilibre de ce système, c'est-à-dire une solution du système de n équations :

0 = F_{i} (y_{1}, \dots, y_{i}, \dots, y_{n}) (i = 1, \dots, n)

(A.2)

La condition suivante est une condition suffisante classique de stabilité de cet équilibre.

Définition 2

La matrice jacobienne du système (A.1) à l'équilibre est la matrice $n \times n$ définie par :

J = {[\frac{\partial F_{i}}{\partial y_{j}} (y_{1 e}, \dots, y_{j e}, \dots, y_{n e})]}_{i, j = 0 \dots n}

(A.3)

Soit λ une valeur propre de la matrice J, c'est-à-dire un nombre réel ou complexe tel qu'il existe un vecteur V non nul vérifiant $J V = λ V$ . Rappelons que si pour toute valeur propre λ de J, la partie réelle de λ est strictement négative, alors l'équilibre est exponentiellement stable (cf. [4]). Dans notre problème la matrice jacobienne (de taille $n + 1$ ) prend la forme suivante :

J = [\begin{matrix} f^{'} (s_{e}) - \sum_{i = 1}^{n} a_{i} & \dots & b_{i} - d_{i} & \dots & b_{n} - d_{n} \\ a_{1} & - b_{1} & 0 & \dots & 0 \\ ⋮ & ⋱ \\ a_{i} & 0 & - b_{i} & 0 & 0 \\ ⋮ & ⋱ \\ a_{n} & 0 & \dots & 0 & - b_{n} \end{matrix}]

(A.4)

avec

a_{i} = \frac{\partial h_{i}}{\partial s} (s_{e}, x_{i e}) x_{i e} et b_{i} = - \frac{\partial h_{i}}{\partial x_{i}} (s_{e}, x_{i e}) x_{i e}

(A.5)

On notera, d'après les Hypothèses H1, que les constantes

a_{i}

et

b_{i}

sont positives, et strictement positives lorsque

x_{i e}

et

s_{e}

sont non nuls. Soit

V = {(v_{0}, v_{1}, \dots, v_{n})}^{t}

tel que

J V = λ V

. De la ligne 0 de (A.4), nous déduisons :

(f^{'} (s_{e}) - \sum_{i = 1}^{n} a_{i}) v_{0} + \sum_{i = 1}^{n} (b_{i} - d_{i}) v_{i} = λ v_{0}

(A.6)

et de la i-ème ligne de (A.4)

a_{i} v_{0} - b_{i} v_{i} = λ v_{i}

(A.7)

De (A.7), nous déduisons la propriété suivante :

– soit $v_{0} = 0$ , et comme un au moins des $v_{i}$ doit être non nul, on doit avoir $λ = - b_{i}$ pour cet indice i. La valeur propre correspondante à un tel vecteur propre est donc réelle négative ;
– soit $v_{0} \neq 0$ , et alors nous pouvons calculer $v_{i}$ en fonction de $v_{0}$ et reporter dans (A.6), ce qui donne, après avoir fait passer une partie du premier membre dans le second :
$(f^{'} (s_{e}) - \sum_{i = 1}^{n} a_{i}) v_{0} = λ v_{0} - \sum_{i = 1}^{n} (b_{i} - d_{i}) \frac{a_{i}}{λ + b_{i}} v_{0}$ (A.8)

Nous pouvons simplifier par

v_{0}

, qui est en facteur et qui est non nul. Procédons maintenant par contradiction. Supposons alors que l'Éq. (A.9) ci-dessous en λ :

(f^{'} (s_{e}) - \sum_{i = 1}^{n} a_{i}) = λ - \sum_{i = 1}^{n} (b_{i} - d_{i}) \frac{a_{i}}{λ + b_{i}}

(A.9)

possède une solution réelle ou complexe

λ = α + i β

, avec

α ⩾ 0

. Notons

Re [z]

la partie réelle d'un nombre complexe z. Nous avons (puisque α a été supposé positif ou nul) :

Re [(b_{i} - d_{i}) \frac{a_{i}}{α + i β + b_{i}}] = \frac{(b_{i} - d_{i}) a_{i} (α + b_{i})}{{(α + b_{i})}^{2} + β^{2}} ⩽ a_{i}

(A.10)

Donc, nous pouvons conclure que :

Re [λ - \sum_{i = 1}^{n} (b_{i} - d_{i}) \frac{a_{i}}{λ + b_{i}}] ⩾ α - \sum_{i = 1}^{n} a_{i} ⩾ - \sum_{i = 1}^{n} a_{i}

(A.11)

D'autre part, puisque

f^{'} (s_{e})

est par hypothèse strictement négatif, nous avons également :

Re [f^{'} (s_{e}) - \sum_{i = 1}^{n} a_{i}] < - \sum_{i = 1}^{n} a_{i}

(A.12)

Or, les inégalités (A.11) et (A.12) sont incompatibles avec l'égalité (A.9). Donc, le nombre α est strictement négatif, ce qui achève la preuve.

Bibliographie

[1] D. Angeli; E. Sontag Monotone control systems, IEEE Trans. Autom. Control, Volume 48 (2003) no. 10, pp. 1684-1698

[2] R. Arditi; L.R. Ginzburg Coupling in predator-prey dynamics: the ratio dependence, J. Theor. Biol., Volume 139 (1989), pp. 311-326

[3] R.A. Armstrong; R. McGehee Coexistence of species competing for shared resources, Theor. Popul. Biol., Volume 9 (1989), pp. 317-328

[4] V. Arnold Equations Différentielles Ordinaires, Éditions MIR, Moscou, 1988

[5] V. Arnold Chapitres supplémentaires de la Théorie des Équations différentielles ordinaires, Éditions MIR, Moscou, 1980

[6] R.S. Cantrell; C. Cosner; S. Ruan Intraspecific interference and consumer-resource dynamics, Discrete Cont. Dyn. Syst., Ser. B, Volume 4 (2004), pp. 527-548

[7] P. De Leenheer; D. Angeli; E. Sontag A feedback perspective for chemostat models with crowding effects, Lecture Notes in Control and Inform. Sci., Volume 294 (2003), pp. 167-174

[8] J.P. Grover Resource Competition, Chapman and Hall, 1997

[9] C. Lobry; F. Mazenc; A. Rapaport Persistence in ecological models of competition for a single resource, C. R. Acad. Sci. Paris, Ser. I, Volume 340 (2005), pp. 199-204

[10] C. Lobry, J. Harmand, A study about the coexistence of N species in the presence of a single resource, C. R. Acad. Sci. Paris, Ser. I, in press

[11] C. Lobry; T. Sari; S. Touhami Slow and fast feed back in control systems, J. Biol. Syst., Volume 7 (1999) no. 3

[12] R. McGehee; R.A. Armstrong Some mathematical problems concerning the ecological principle of competitive exclusion, J. Diff. Equat., Volume 23 (1977), pp. 30-52

[13] F. Mazenc, C. Lobry, A. Rapaport, Persistence in ratio-dependent models of consumer-resource dynamics, in: The Sixth Mississippi State Conference on Differential Equations and Computation Simulations, 13–14 May 2005

[14] H.L. Smith; P. Waltmann The Theory of the Chemostat, Cambridge University Press, 1995

Commentaires - Politique