A thermodynamic view of networks

Derek J. Raine; Yohann Grondin

doi:10.1016/j.crvi.2006.01.009

Biological medelling / Biomodélisation

A thermodynamic view of networks
[Une vue thermodynamique des réseaux]

Présenté par : Michel Thellier

Derek J. Raine ¹ ; Yohann Grondin ¹

¹ Department of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK

Comptes Rendus. Biologies, Volume 329 (2006) no. 3, pp. 156-167.

Résumés

Anglais
Français

Networks can be described by the frequency distribution of the number of links associated with each node (the degree of the node). Of particular interest are the power law distributions, which give rise to the so-called scale-free networks, and the distributions of the form of the simplified canonical law (SCL) introduced by Mandelbrot, which give what we shall call the Mandelbrot networks. Many dynamical methods have been obtained for the construction of scale-free networks, but no dynamical construction of Mandelbrot networks has been demonstrated. Here we develop a systematic technique to obtain networks with any given distribution of the degrees of the nodes. This is done using a thermodynamic approach in which we maximise the entropy associated with degree distribution of the nodes of the network subject to certain constraints. These constraints can be chosen systematically to produce the desired network architecture. For large networks we therefore replace a dynamical approach to the stationary state by a thermodynamical viewpoint. We use the method to generate scale-free and Mandelbrot networks with arbitrarily chosen parameters. We emphasise that this approach opens the possibility of insights into a thermodynamics of networks by suggesting thermodynamic relations between macroscopic variables for networks.

Les réseaux peuvent être décrits par la distribution de la fréquence du nombre de liens associés à chacun des nœuds. La distribution en loi de puissance, qui donne lieu aux réseaux libres d'échelle, et la loi canonique simplifiée, introduite par Mandelbrot, qui donne lieu à ce que nous appellerons les réseaux de Mandelbrot, présentent un intérêt particulier. S'il existe de nombreuses méthodes dynamiques pour la construction des réseaux libres d'échelle, il n'en existe pas pour les réseaux de Mandelbrot. Nous développons ici une technique permettant d'obtenir des réseaux avec n'importe quelle distribution des degrés des nœuds. Pour ce faire, nous utilisons une approche thermodynamique, dans laquelle l'entropie associée à la distribution des degrés des nœuds du réseau est soumise à certaines contraintes. Ces contraintes peuvent être choisies systématiquement afin de produire l'architecture désirée. Pour de grands réseaux, nous remplaçons donc une approche dynamique de l'état stationnaire par un point de vue thermodynamique. Nous utilisons cette méthode pour générer des réseaux libres d'échelle et de Mandelbrot avec des paramètres choisis arbitrairement. Nous soulignons que cette approche ouvre la possibilité d'entrevoir une thermodynamique des réseaux en suggérant des relations thermodynamiques entre variables macroscopiques associées aux réseaux.

Métadonnées

Reçu le : 2005-05-12
Accepté le : 2006-01-17
Publié le : 2006-02-28

PMID

DOI : 10.1016/j.crvi.2006.01.009

Keywords: Intensive and extensive variables, Scale-free networks, Connectivity, Thermodynamics, Life, Cell
Mot clés : Variables intensives et extensives, Réseau libre d'échelle, Connectivité, Thermodynamique, Vie, Cellule

Affiliations des auteurs :

Derek J. Raine ¹ ; Yohann Grondin ¹

¹ Department of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK

@article{CRBIOL_2006__329_3_156_0,
     author = {Derek J. Raine and Yohann Grondin},
     title = {A thermodynamic view of networks},
     journal = {Comptes Rendus. Biologies},
     pages = {156--167},
     publisher = {Elsevier},
     volume = {329},
     number = {3},
     year = {2006},
     doi = {10.1016/j.crvi.2006.01.009},
     language = {en},
}

TY  - JOUR
AU  - Derek J. Raine
AU  - Yohann Grondin
TI  - A thermodynamic view of networks
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 156
EP  - 167
VL  - 329
IS  - 3
PB  - Elsevier
DO  - 10.1016/j.crvi.2006.01.009
LA  - en
ID  - CRBIOL_2006__329_3_156_0
ER  -

%0 Journal Article
%A Derek J. Raine
%A Yohann Grondin
%T A thermodynamic view of networks
%J Comptes Rendus. Biologies
%D 2006
%P 156-167
%V 329
%N 3
%I Elsevier
%R 10.1016/j.crvi.2006.01.009
%G en
%F CRBIOL_2006__329_3_156_0

Derek J. Raine; Yohann Grondin. A thermodynamic view of networks. Comptes Rendus. Biologies, Volume 329 (2006) no. 3, pp. 156-167. doi : 10.1016/j.crvi.2006.01.009. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2006.01.009/

Version originale du texte intégral

Version française abrégée

Les réseaux, vus comme une collection d'entités physiques (les nœuds), et leurs interactions (les liens) fournissent un modèle possible pour les systèmes complexes.

Nous nous intéressons ici à la distribution des degrés des nœuds en tant que caractéristiques structurales importantes décrivant les réseaux réels. Une caractéristique de nombreux réseaux réels est qu'ils sont libres d'échelle, c'est-à-dire qu'ils ont une distribution des nœuds qui suit une loi de puissance. La construction de réseaux ayant une distribution donnée des nœuds fait appel à des méthodes intuitives, bien que des méthodes plus systématiques aient récemment été développées. Elles invoquent l'évolution de réseaux dans lesquels une loi de croissance spécifique détermine la distribution des nœuds à l'état final.

Nous proposons ici une approche des réseaux adoptant un point de vue thermodynamique. Cela se justifie, car, dans de nombreux cas, la structure des réseaux est déterminée par l'environnement au travers de sélections. Nous montrons ici que cette approche aboutit directement à des réseaux ayant n'importe quelle distribution des nœuds. Nous illustrons cette méthode en construisant des réseaux libres d'échelle et une classe connexe de réseaux qui suit ce que Mandelbrot a nommé la distribution « canonique simplifiée ». Cela nous permet de décrire les réseaux en termes de thermodynamique et donc en terme d'information fournie par la fonction entropie. En particulier, nous discutons comment cette approche peut être présentée en terme de variables intensives et extensives associées aux réseaux. Nous suggérons qu'une bonne description puisse impliquer une mesure intensive de la complexité du réseau au travers de ce que nous appelons le paramètre de « complexité-β ». Nous montrons cependant que ceci n'est pas contenu dans la fonction entropie associée à la distribution des nœuds.

La construction des réseaux s'exprime en termes thermodynamiques par le fait que le réseau final a son entropie maximisée lorsqu'il est soumis à certaines contraintes. Pour ce faire, nous introduisons d'abord l'entropie, Ω, associée à la distribution des nœuds et définie, à une constante près, par :

Ω = - \sum_{r} p_{r} \log p_{r}

où

p_{r}

est la probabilité d'avoir un nœud de degré de connectivité r.

Supposons que le réseau soit soumis à une contrainte $C (p_{r}) = constante = E$ . En faisant l'analogie avec un gaz parfait, par exemple, il est possible d'imposer la contrainte $\sum_{r} ɛ (r) p_{r} = E$ , où l'énergie totale est liée à la probabilité $p_{r}$ d'occuper les niveaux d'énergie $ɛ (r)$ . Nous devons donc maximiser Ω sous cette contrainte pour obtenir la distribution de Boltzmann $p_{r} = q_{r} = q \exp [- β ɛ (r)]$ , où β est une constante déterminée par la contrainte et q une constante telle que la somme des probabilités $q_{r}$ soit égale à 1. Appliqué aux réseaux avec $ɛ (r) = r$ , cela produit des réseaux exponentiels.

Nous avons ici le problème inverse : nous cherchons une fonction $C (p_{r})$ telle que la maximisation de Ω sous contraintes donne la distribution de probabilité souhaitée, $p_{r} = q_{r}$ , des degrés de connectivité des nœuds. La fonction :

C (p_{r}) = - β^{−1} \sum_{r} p_{r} \log q_{r}

où β est un paramètre (multiplicateur de Lagrange), donne le résultat escompté. Notez que pour

q_{r} = q \exp [- β ɛ (r)]

la fonction précédente se réduit à

\sum_{r} ɛ (r) p_{r}

, comme dans l'exemple du dessus. Établir un résultat général nécessite de considérer la maximisation d'une fonction Ω, soumise à une contrainte

C = constante

(ainsi que

\sum_{r} p_{r} = constante = 1

). C'est un problème qui est habituellement soluble par la méthode des multiplicateurs de Lagrange. Pour éviter cela, nous montrons que

W = Ω - β C = - \sum_{r} p_{r} \log (p_{r} / q_{r})

satisfait la condition pour un point stationnaire à

p_{r} = q_{r}

, comme suit. Faisons varier

p_{r}

aux alentours de

q_{r}

, c'est-à-dire

p_{r} = q_{r} - δ p_{r}

où les éléments

δ p_{r}

sont de petites quantités qui sont choisies telles que

\sum_{r} δ p_{r} = 0

, de manière à garder

\sum_{r} p_{r} = 1

, puisqu'il s'agit de probabilités. Donc :

δ W = \sum_{r} ({\frac{\partial W}{\partial p_{r}} |}_{p_{r} = q_{r}} δ p_{r}) = \sum_{r} {(- 1 - \log p_{r} + \log q_{r})}_{p_{r} = q_{r}} δ p_{r} = - \sum_{r} δ p_{r} = 0

Il est aisé de voir qu'il s'agit d'un maximum, car

δ^{2} W = - \sum_{r} (δ p_{r}^{2} / 2 q_{r}) < 0

, étant donné que chacun des termes de la somme est positif. Ainsi, connaissant la distribution de probabilité, il est possible de déduire directement la contrainte appropriée.

Pour construire un réseau, nous partons d'un réseau arbitraire et nous modifions l'état de connexion des nœuds en modifiant leurs degrés de connectivité. Le point clé est de montrer que cela peut se faire par une méthode qui préserve une contrainte arbitraire, ce qui justifiera notre interprétation thermodynamique.

Pour un réseau exponentiel, la procédure est relativement directe et consiste en un simple mécanisme de rebranchement. Un nœud est choisi aléatoirement et l'extrémité d'un de ses liens, choisie aléatoirement, est détachée, puis à nouveau attachée à un autre nœud. Le nouveau réseau ainsi obtenu est conservé si l'entropie a augmenté et rejeté autrement.

Pour d'autres cas, la procédure est quelque peu plus compliquée et la contrainte ne peut pas être maintenue constante en début de processus. En revanche, celle-ci doit converger vers une valeur constante, appropriée à la valeur de β choisie. En pratique, la contrainte n'est pas exactement constante, mais elle l'est en moyenne sur un certain nombre de pas de temps. Reconnecter les liens n'est cependant pas suffisant et il est nécessaire d'ajouter et de retirer des liens, comme suit.

Une paire de nœud est sélectionnée aléatoirement et son état de connectivité est modifié avec une probabilité $P_{r s}$ si les nœuds sont liés ou une probabilité ( $1 - P_{r s}$ ) sinon, avec r et s les degrés des nœuds. Ces probabilités, à déterminer, sont introduites pour exercer un contrôle sur la variation de la contrainte. Ainsi, la probabilité $P_{r s}$ est recalculée à chaque pas de temps pour assurer la convergence de la contrainte, d'après la condition suivante :

Q (1 - P_{r s}) (Δ_{-, r} + Δ_{-, s}) + (1 - Q) P_{r s} (Δ_{+, r} + Δ_{+, s}) = 0

où

Δ_{-, r}

et

Δ_{+, r}

sont les variations de la contrainte lorsque l'extrémité d'un lien connecté à un nœud de degré r est retiré ou ajouté, où

Δ_{-, s}

et

Δ_{+, s}

sont les variations de la contrainte lorsque l'extrémité d'un lien connecté à un nœud de degré s est retirée ou ajoutée, et où Q est la probabilité qu'une paire de nœuds, choisie aléatoirement, soit connectée.

Une modification sera acceptée si l'entropie résultante a augmenté, ou acceptée avec une probabilité $\propto \exp (- K Δ Ω)$ autrement, où K est une constante.

Pour un réseau libre d'échelle, dont la distribution des degrés de connectivité suit une loi de puissance telle que :

q_{r} \propto r^{- β}

la contrainte doit être :

C (p_{r}) = \sum_{r} p_{r} \log (r)

Par conséquent, l'expression de l'entropie à maximiser sera :

Ω - β C = - \sum_{r} p_{r} \log p_{r} - β \sum_{r} p_{r} \log (r)

où β est un paramètre du programme devant correspondre à la pente de la distribution des degrés des nœuds, une fois l'entropie maximisée. Ceci est montré par simulations.

Un réseau de Mandelbrot est une version généralisée des réseaux libres d'échelle dont la distribution des degrés de connectivité suit la loi de Mandelbrot :

q_{r} \propto \frac{1}{{(r + ρ)}^{β}}

où ρ est un paramètre du modèle.

La contrainte correspondante est une version généralisée de la contrainte précédente, telle que :

C (p_{r}) = \sum_{r} p_{r} \log (r + ρ)

Nos simulations montrent, de nouveau, que la pente des distributions des réseaux obtenus est très proche de β.

Le voisinage local moyen d'un nœud est décrit par sa clique, C. Elle décrit la fraction des nœuds liés à un nœud donné et qui sont eux-mêmes liés entre eux, moyennée sur l'ensemble des nœuds du réseau. Nous pouvons aussi considérer comment les voisins des voisins sont liés. En continuant d'un nombre de pas égal au diamètre L du réseau, c'est-à-dire le plus long des plus courts chemins, nous arrivons au point où tous les voisins sont liés entre eux.

Pour étudier ceci, nous considérons un réseau représenté par sa matrice adjacente ( $a_{i j}$ ) où les éléments $a_{i j} = 1$ si les nœuds i et j sont connectés, et $a_{i j} = 0$ sinon. Le carré de cette matrice donne le nombre de différents chemins entre les nœuds i et j. La matrice qui en résulte, où les valeurs non nulles sont remplacées par la valeur 1 et les éléments de la diagonale par 0, correspond à la matrice adjacente des seconds voisins.

Les termes de la diagonale contiennent des informations sur le degré de clique. Par exemple, la trace de la matrice au cube est liée au coefficient C, et la trace des produits successifs de degrés n donne une hiérarchie de coefficients de clique $C_{n}$ . Le degré de clique en relation avec le diamètre, $C / L$ , est petit pour les réseaux aléatoires et ordonnés et est grand autrement. Il présente donc la propriété d'un paramètre de complexité que nous appelons « complexité-β ».

Nous présentons la « complexité-β » en fonction de la pente β de la distribution des degrés de connectivité pour des réseaux de Mandelbrot. Il est à noter que, plus la pente est importante, plus la valeur $C / L$ est petite, ce qui est cohérent avec l'interprétation de β comme mesure de complexité.

La distribution des degrés ne fixe cependant pas la « complexité-β » du réseau. En effet, expérimentalement, la construction de réseaux par croissance et attachement préférentiel produit des réseaux libres d'échelle qui ne sont pas de petit monde, alors que des réseaux de petit monde et libres d‘échelle sont connus. Il est aussi apparent, comme nous allons le montrer, que la distribution des nœuds ne détermine pas complètement les corrélations entre connexions.

La variation du paramètre C peut s'effectuer par un mécanisme simple de reconnexion croisée entre deux paires de nœuds, sans modification du degré de connectivité des nœuds.

Les liens d'un réseau de Mandelbrot sont reconnectés de manière croisée, aléatoirement. Durant ce processus, les extrema de C sont notés, et le ratio $R = C_{\max} / C_{\min}$ , calculé. Sur plusieurs répétitions, nous obtenons $〈 R 〉 = 1, 65 \pm 0, 16$ .

Nous construisons maintenant la séquence de matrices adjacentes pour plusieurs classes de réseaux. Pour chacune des classes, les fonctions de distribution des degrés sont approximativement de la même forme. Cela dénote, d'un point de vue statistique, une certaine invariance de la structure. La « complexité-β » doit changer le long de cette séquence, mais la difficulté de voir ce changement est clairement liée à la difficulté de construire des réseaux de complexités différentes. Il est donc intéressant de rechercher l'amplitude des corrélations et de les localiser.

Nous avons supposé jusqu’à présent que l'entropie des réseaux était contenue dans la distribution des degrés des nœuds, considérant ainsi que les nœuds étaient connectés de manière aléatoire. Ce n'est pas vrai pour les réseaux libres d'échelle et de Mandelbrot, où il existe des corrélations entre nœuds. Nous avons besoin de montrer qu'elles sont négligeables en première approximation. Par analogie, dans un gaz parfait, les molécules sont indépendantes et l'énergie est proportionnelle à la densité du nombre de particules. Dans un gaz non parfait, les particules sont corrélées et l'énergie est aussi associée aux interactions, comme dans un réseau avec une distribution non aléatoire des liens. Les corrélations contribuent à l'ordre et doivent être incluses dans l'entropie.

Soit $Q_{r s}$ la probabilité qu'une paire de nœuds r et s soit connectée, telle que :

Q_{r s} = \frac{2 n_{r s}}{N (N - 1)}

avec

n_{r s}

le nombre de liens entre nœuds de degré r et s.

Si les liens entre nœuds ne sont pas corrélés :

Q_{r s} = \frac{2 r n_{r} s n_{s}}{N^{2} (N - 1) \bar{k}} = Q_{random}

Nous mesurons l‘entropie par lien, relative à un réseau aléatoire, donnée en moyenne par :

H_{L} = - \frac{1}{N} \sum_{pair} [Q_{r s} \log Q_{r s} + (1 - Q_{r s}) \log (1 - Q_{r s})]

D'où le rapport :

\frac{- \sum_{pair} [Q_{random} \log Q_{random} + (1 - Q_{random}) \log (1 - Q_{random})]}{- \sum_{pair} [Q_{r s} \log Q_{r s} + (1 - Q_{r s}) \log (1 - Q_{r s})]} ⩽ 1,

sera égal à 1 si les liens sont indépendants et inférieur autrement.

Nous montrons pour des réseaux de Mandelbrot que l'entropie réside en partie dans les connexions.

Ainsi, en première approximation, les propriétés macroscopiques de ces réseaux peuvent être obtenues à partir de la fonction d'entropie liée aux nœuds. Le fait que l'entropie ne soit pas entièrement contenue dans la distribution des degrés des nœuds signifie qu'il y aura plus d'un maximum local de l'expression complète de l'entropie pour une distribution donnée, correspondant à différentes corrélations.

La pente β n'est donc pas uniquement un analogue de la « température » mais joue aussi le rôle d'un paramètre de Lagrange, multiplicateur de la contrainte « d’énergie ». Il reste à déterminer les autres fonctions thermodynamiques de l'état du réseau à partir de l'entropie. Un résultat général est que toute contrainte de la forme $\sum p_{r} ɛ (r) = constante$ mène a la loi des gaz parfaits, indépendamment de la forme de $ɛ (r)$ . Nous le montrons ci-dessous.

L'énergie libre des nœuds d'un réseau de N nœuds est donnée par :

F / N = - \sum p_{r} \log p_{r} - β \sum p_{r} ɛ (r) - α \sum p_{r}

avec

ɛ (r)

« l'énergie » d'un nœud.

En maximisant, nous obtenons :

n_{r} = \frac{N}{Z} \exp (- β ɛ (r)),

où la fonction de partition Z est définie par

Z = \sum e^{- β ɛ (r)}

. Pour un gaz parfait dans un volume

V, Z

est de la forme zV. Nous établissons maintenant l'équation d'état. Pour cela, définissons l'énergie interne comme :

U = \sum ɛ (r) n_{r}

L'entropie devient alors :

S = - \frac{\partial}{\partial β} (N β \log Z)

Ainsi :

U = \frac{N}{Z} \sum ɛ (r) e^{- β ɛ (r)} = - \frac{S}{β} + \frac{N}{β} \log Z

d'où, avec

Z = z V

:

P = {(\frac{\partial U}{\partial V})}_{S} = \frac{N}{β} \frac{1}{V}

Ainsi, pour un réseau, le point crucial est de définir le volume tel que

Z = z V

. Pour ce faire, posons M le nombre total de liens. Donc :

M = \sum r n_{r} = \frac{N}{Z} \sum r e^{- β ɛ (r)}

d'où :

Z = \frac{N}{M} \sum r e^{- β ɛ (r)} = V z

en prenant

V = N / M = k^{−1}

. Le résultat est indépendant de la forme de

ɛ (r)

.

Il est évident que cela nous donne l'approximation des gaz parfaits de l'équation d'état du réseau car, en utilisant l'entropie des nœuds, nous ne prenons pas en compte les interactions entre nœuds. Afin d'obtenir une relation plus poussée, nous devons utiliser une expression de l'entropie incluant les corrélations entre nœuds.

Dans cet article, nous avons montré que nous pouvons construire des réseaux à partir de prescriptions thermodynamiques. Cela devrait permettre de développer une caractérisation macroscopique basée sur la fonction entropie. Dans des réseaux où l'essentiel de l'entropie est contenu dans la distribution des degrés des nœuds, nous espérons qu'une description macroscopique approchée impliquera un petit nombre de variables globales. Nous émettons l'hypothèse que les variables macroscopiques incluraient un paramètre décrivant, d'une certaine manière, la complexité des réseaux.

1 Introduction

Complex systems are a major area of study and are of interest as they feature properties that emerge only when a certain level of complexity has been reached. This corresponds in some sense to the stage when individual agents become strongly interdependent and the system itself can be interpreted as another agent at a higher scale. Networks, regarded as collections of physical entities (the nodes), and their interactions (the links) provide a possible model for complex systems. Thus, in fields as varied as social sciences, communications and biology, empirical as well as theoretical studies have brought to the fore properties of such complex systems (reviewed in e.g. [1]). Characteristics, as, for example, that of a ‘small world’ [2], arise from this network approach to systems. Here we are interested in the degree distribution of the nodes as an important structural characteristic that describes real networks, and the extent to which this can give rise to higher-level descriptions. A characteristic of many real networks is that they are ‘scale-free’ with a nodal distribution that is a power law. The construction of such networks, as well as many others, of given nodal distributions has been to some extent a mixture of intuition and guesswork [1], although systematic methods have been developed more recently [3]. The methods largely involve the evolution of networks in which a specific growth law determines the nodal distribution of the final state.

We propose here to approach networks from a thermodynamical point of view. This is justified because in many cases a network structure is determined by the environment through selection (see e.g. [4]). Here we shall show how a thermodynamic approach can yield a network of any nodal distribution directly. We will then illustrate this method by building scale free networks and a related class of networks following what Mandelbrot has called the ‘simplified canonical’ distribution [5,6]. Our approach allows us to think of the networks in term of thermodynamics and hence in terms of the information provided by the entropy function. In particular we discuss how this approach might be presented in terms of intensive and extensive variables of networks. We suggest that a useful description might involve an intensive measure of ‘complexity’ of a network through what we call the β-complexity parameter. However, we show that this is not contained in the entropy function associated with the nodal distribution.

2 Thermodynamic method

For our purpose undirected networks are distinguished by the degree distribution of their nodes, where the degree of a node is the number of edges connected to it. If our aim were simply to obtain a network of N nodes exhibiting a specified number of nodes $N q_{r}$ of each degree r we could proceed as follows. Let $p_{r}$ be the probability for a node to have connectivity degree r. Take any network as starting point (say a random one) with a distribution $p_{r} = p_{r}^{0}$ of node degrees. Furthermore, take any utility function of a form that approaches a maximum as $p_{r} \to q_{r}$ , for example $- \sum_{r} {(p_{r} - q_{r})}^{2}$ . Then rewire the network, changing $p_{r}$ , in such a way that the utility function is maximised. This is the most efficient approach if we are seeking only a specific nodal distribution, but this not the most relevant for our purpose. Our aim is to express the network construction in thermodynamic terms such that the final network has its entropy maximised subject to certain constraints. So we choose as our ‘utility function’ an expression for the network entropy.

We first introduce the point entropy of the network, Ω, which is associated with the nodal distribution, and is defined, up to a constant, by:

Ω = - \sum_{r} p_{r} \log p_{r}

(1)

Suppose that the network is subject to a constraint

C (p_{r}) = constant = E

(say). For example, by analogy with a perfect gas, we might impose the constraint

\sum_{r} ɛ (r) p_{r} = E

, the total energy arising from the occupation of energy levels

ɛ (r)

with probability

p_{r}

. We should then maximise Ω subject to this constraint to obtain the Boltzmann distribution

p_{r} = q_{r} = q \exp [- β ɛ (r)]

, where β is a constant determined by the constraint and q a constant such that the probabilities

q_{r}

sum to 1. Applied to networks with the choice

ɛ (r) = r

, this yields the exponential networks [7,8].

Here we have the inverse problem: we seek a function $C (p_{r})$ such that maximising Ω subject to $C (p_{r}) = constant$ leads to the desired probability distribution $p_{r} = q_{r}$ for the degrees of the nodes. The function:

C (p_{r}) = - β^{−1} \sum_{r} p_{r} \log q_{r}

(2)

achieves the desired result, where β is a parameter (Lagrange multiplier). Note that for

q_{r} = q \exp [- β ɛ (r)]

it reduces to

\sum_{r} ɛ (r) p_{r}

as in our example above. To derive the result in general requires us to deal with the maximisation of a function, Ω, subject to a constraint C= constant, (and also

\sum_{r} p_{r} = constant = 1

), a problem usually approached by the method of Lagrange multipliers. To avoid this we show that

W = Ω - β C = - \sum_{r} p_{r} \log (p_{r} / q_{r})

satisfies the condition for a stationary point at

p_{r} = q_{r}

as follows. Let us vary the

p_{r}

about

q_{r}

, that is we set

p_{r} = q_{r} - δ p_{r}

where the

δ p_{r}

are small quantities chosen such that

\sum_{r} δ p_{r} = 0

in order to keep

\sum_{r} p_{r} = 1

, since the

p_{r}

are probabilities. Then:

δ W = \sum_{r} ({\frac{\partial W}{\partial p_{r}} |}_{p_{r} = q_{r}} δ p_{r}) = \sum_{r} {(- 1 - \log p_{r} + \log q_{r})}_{p_{r} = q_{r}} δ p_{r} = - \sum_{r} δ p_{r} = 0

It is easy to see that this is a maximum since

δ^{2} W = - \sum_{r} (δ p_{r}^{2} / 2 q_{r}) < 0

, since each term in the sum is positive.

Thus, from expression (2), and knowing the probability distribution, we can directly deduce the appropriate constraint. In other language, the utility function is $Ω - β C$ . (To avoid confusion note that the point we are making here is not the form of the result (2), which is in any case essentially just the relative entropy again, but that this form allows us to use the standard thermodynamical methods.)

In order to build a network with specified nodal distribution we start from an arbitrary network and change the state of connection of the nodes by modifying their degree of connectivity. To achieve this we have the options of rewiring, adding or removing links. To implement the method we have to specify how the modifications will be carried out to increase the entropy while maintaining the constraint. The crux of the article is to show that this can be done, that is that one can find a rewiring method that will preserve any given constraint. This will justify our thermodynamic interpretation of network properties.

For the exponential network with $C (p_{r}) = \sum_{r} r p_{r}$ , the procedure is relatively straightforward using just a rewiring process (i.e. with no addition or removal of links). Let the network have N nodes. Consider a node chosen at random and randomly take one of its links. Suppose this attaches to a node of degree r; we re-attach it to a node, chosen randomly again, of rank s. To see the effect on the constraint consider the quantity $N C = \sum_{r} r (N p_{r})$ where $N p_{r}$ is the number of nodes of degree r. On deleting a connection to the node of degree r (and hence creating one of degree $r - 1$ ) the constraint NC changes by:

Δ_{-, r} = N Δ C = r \times Δ (N p_{r}) + (r - 1) \times Δ (N p_{r - 1})

where

Δ (N p_{r})

is the change in the number of nodes of degree r. Then, since we have destroyed one node of degree r we have

Δ (N p_{r}) = - 1

and since we have created one of degree

r - 1

, we have

Δ (N p_{r - 1}) = + 1

. Thus

Δ_{-, r} = - 1

. On reinstating the link to the new node C changes by:

Δ_{+, s} = N Δ C = s \times Δ (N p_{s}) + (s + 1) \times Δ (N p_{s + 1}) = + 1

since we destroy one node of class s and create one of class

s + 1

. Thus, the overall change in NC is zero, and this rewiring therefore keeps C constant. If the rewiring also increases the entropy we replace the initial network by the new one and repeat the process. Otherwise we keep the original network and continue.

For other constraint functions the procedure is somewhat more complicated. The value of the constraint is linked to the value of the Lagrange multiplier β in the final network. Therefore, when addressing the evolution of a network numerically, we cannot require that the constraint be constant in the early stages of the iteration, but only that it converge to a constant value appropriate to the value of β that we have chosen. In practice, even at later stages, we do not attempt to keep the constraint exactly constant at each evolutionary step, but only on average over a number of steps. Even so, pure rewiring turns out to be insufficient. The evolution requires the addition and removal of links as follow.

A pair of nodes is selected randomly. Let the probability that they are linked be Q. Suppose that the two nodes have degrees r and s. The state of the connection is then modified with either a probability $P_{r s}$ if the nodes are to be linked, or a probability ( $1 - P_{r s}$ ) if a link is to be removed. These probabilities, to be determined, are introduced to exert control on the variation of the constraint.

The probable variation in the constraint by removal of a link is given by $Q (1 - P_{r s}) (Δ_{-, r} + Δ_{-, s})$ where, as above, $(Δ_{-, r} + Δ_{-, s})$ corresponds to the variation of the constraint when a link is removed from nodes r and s. We have:

N Δ C = Δ_{-, r} + Δ_{-, s} = [Δ (N p_{r}) \log q_{r} + Δ (N p_{s}) \log q_{s} + Δ (N p_{r - 1}) \log q_{r - 1} + Δ (N p_{s - 1}) \log q_{s - 1}] = \log (\frac{q_{r - 1} q_{s - 1}}{q_{r} q_{s}})

Similarly, the probable variation in the constraint by addition of a link to nodes r and s is given by

(1 - Q) P_{r s} (Δ_{+, r} + Δ_{+, s})

, with:

N Δ C = Δ_{+, r} + Δ_{+, s} = \log (\frac{q_{r + 1} q_{s + 1}}{q_{r} q_{s}})

In order to ensure that the constraint evolves toward a constant value we require the following condition:

Q (1 - P_{r s}) (Δ_{-, r} + Δ_{-, s}) + (1 - Q) P_{r s} (Δ_{+, r} + Δ_{+, s}) = 0

(3)

with Δ's as above. The probability

P_{r s}

is calculated at each stage in order to satisfy condition (3) so that the constraint evolves toward a stable value. Finally, completely disconnected nodes are not accepted: all the nodes have to be connected to the single network.

Once processed, a modification will be accepted if the entropy subject to constraint has increased as a result of the rewiring. Otherwise, the new configuration will be accepted with a probability $\exp (- K Δ Ω)$ , where K is some appropriate constant (determined by trial and error).

The following distributions are the results from simulations starting, for the purpose of consistency, from the same initial networks. These are random networks (although any other class could be envisaged) with $N = 2000$ nodes and a mean degree connectivity of $k = \sum_{r} r p_{r}^{0} = 8$ . These parameters are chosen to give networks large enough to represent an infinite network over a wide enough range of node classes, yet to still give a reasonable computing time.

3 Scale-free networks

By definition the degree distribution of a scale free network follows a power law

q_{r} \propto r^{- β}

According to expression (2) this implies that the constraint be set as

C (p_{r}) = \sum_{r} p_{r} \log (r)

(4)

The entropy expression to be maximised will consequently be

Ω - β C = - \sum_{r} p_{r} \log p_{r} - β \sum_{r} p_{r} \log (r)

where β is a parameter, set for the system at the beginning of the iteration, that we expect to be the slope of the degree distribution once the entropy is maximised.

Simulations are made using the above previously described model for several values of β. We give in Fig. 1, as an illustration of the method, the degree distribution of the system once the entropy has reached a maximum steady state value with β set to 2.5. The constraint at this stage varies about a constant value close to unity with an amplitude of $\pm 1.5 \times 10^{−2}$ . As shown on the graph, the degree distribution follows a power law with a slope of −2.5. There is a cut-off at nodes of high connectivity (low probability), which is a reflection of the finite size of the network.

Fig. 1
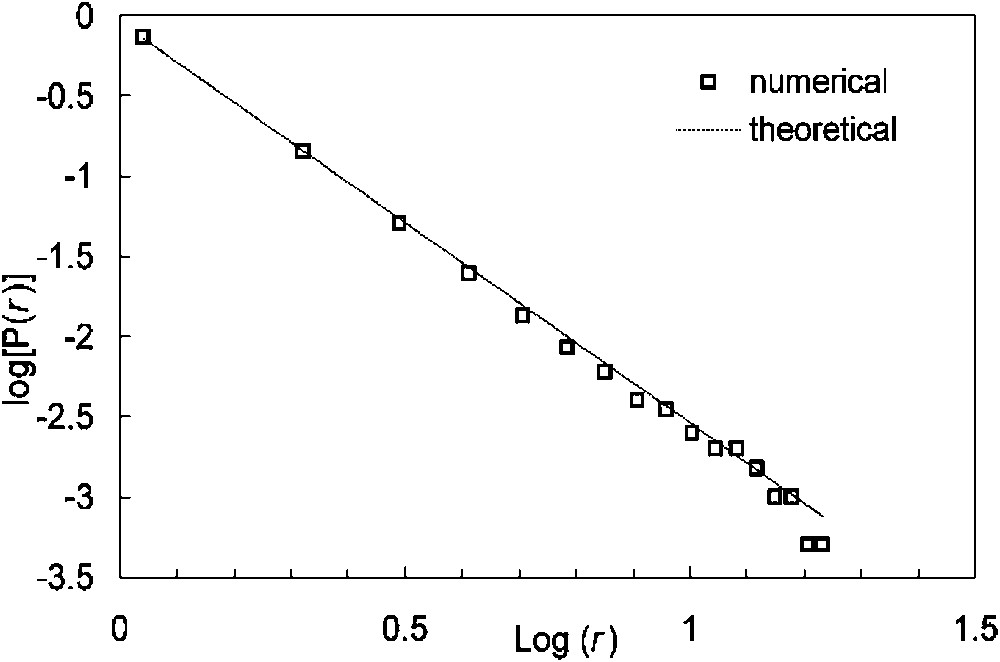
Degree distribution of the nodes obtained numerically compared to the expected theoretical one for a scale-free network. The theoretical distribution is set to have $\sum_{r} p_{r} = 1$ with β=2.5.

For the various values of parameter β, the slope of the degree distribution obtained numerically is close to β. Note that until the finite size effects set in at high connectivity the method gives results that are highly reproducible with little scatter about the power law distribution.

4 Mandelbrot networks

The Mandelbrot network is a generalised version of the scale-free network. The distribution of the degrees of the nodes follows the Mandelbrot law (or simplified canonical law):

q_{r} \propto \frac{1}{{(r + ρ)}^{β}}

where ρ is parameter of the model. The corresponding constraint

C (p_{r})

is a generalisation of expression (4) (and so consequently is the corresponding expression for entropy) and is given by:

C (p_{r}) = \sum_{r} p_{r} \log (r + ρ)

Simulations are made as before, but with the new constraint.

We give in Fig. 2 an example of the degree distribution of the system with the parameters $β = 3$ and $ρ = 10$ once the entropy has reached a maximum steady state. The constraint at this stage varies around a constant value of the order of unity with an amplitude of $\pm 2.5 \times 10^{−4}$ and therefore can be considered as constant. The distribution fits the simplified canonical law very well except for nodes of high degree, where again the effects of finite network size come into play.

Fig. 2
Degree distribution of the nodes computed numerically for a Mandelbrot network compared to the expected theoretical one. The theoretical distribution is set to have $\sum_{r} p_{r} = 1$ , with β=3 and ρ=10.

Furthermore, the slope of the degree distribution for various values of β is again in very good agreement with what we expect.

Fig. 3 shows an example of a power law network and a Mandelbrot network obtained by our method and displayed using the Pajek software [9].

Fig. 3
Illustration of a scale-free network (left) and a Mandelbrot network (right). The difference arises from the fact that the Mandelbrot distribution contains a lower proportion of very low connectivity nodes. This difference will be reflected in parameters such as the cluster coefficient and the average path length.

5 β-complexity

The average local neighbourhood of a node is described by the ‘clique-ishness’ parameter C [2] (not to be confused with our constraint function $C (p_{r}))$ . This describes the fraction of nodes linked to a given node that are themselves linked, averaged over the nodes of the network. We can similarly consider how the neighbours of neighbours are themselves linked. Continuing, after a number of steps equal to the diameter L of the network, that is the longest of the shortest paths, we come to the point where all neighbours of this order are themselves linked [10]. In some sense therefore this process illustrates the extent to which the local properties of a network are reflected in its global properties.

To investigate this we consider networks from an algebraic point of view. A network can be written in term of its adjacency matrix $(a_{i j})$ in which the element $a_{i j} = 1$ if the ith and jth node are linked and $a_{i j} = 0$ otherwise. The square of such a matrix will give the number of different path between nodes of index i and j (Fig. 4). The resulting matrix, rewritten by replacing all non-zero values with 1, and diagonal values with zero, gives the adjacency matrix of the second neighbours.

Fig. 4
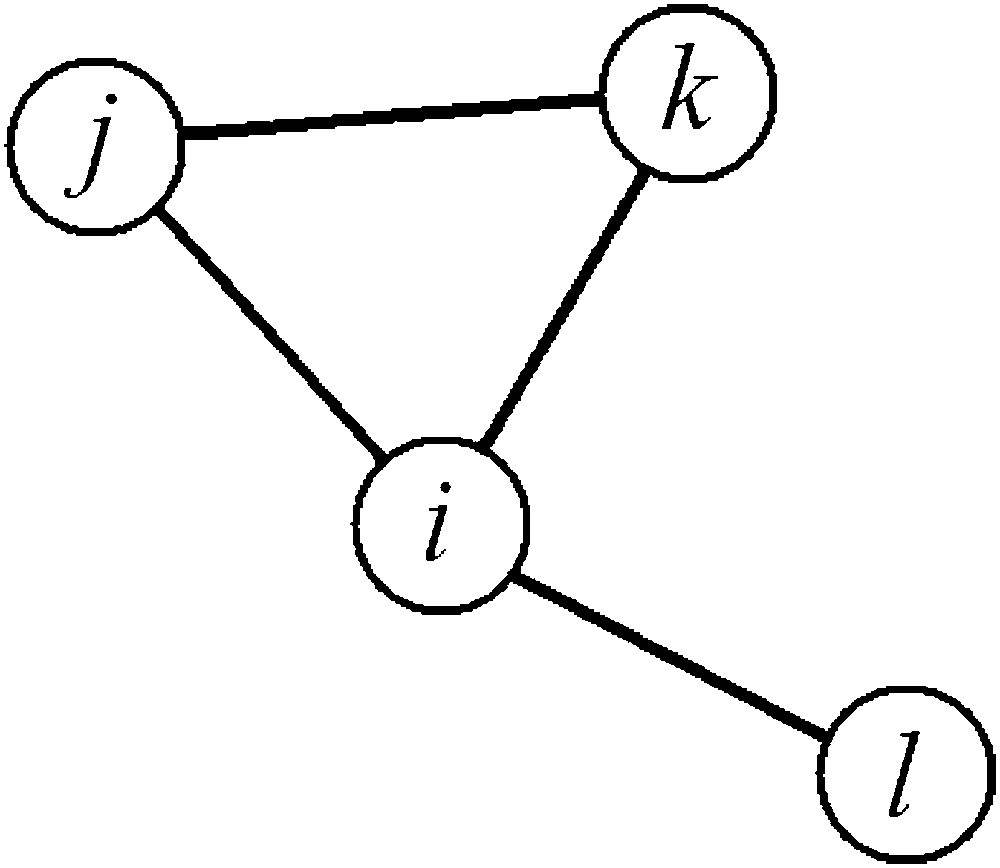
The element ij of the adjacency matrix $A^{n}$ , $a_{i j}^{[n]}$ , gives the number of path of length n going from node i to node j. Here for example, for n=2, there is only one possible path using 2 edges to go from node i to node j, that is the one passing through node k. For n=3, there will 2 possible paths going from node i to i, which forms a triangle. In this case $a_{i i}^{[3]} = 2$ with the first path passing, in order, through nodes j and k and the second one through nodes k and j.

The diagonal terms of the product matrices contain information on the degree of clustering. For example, the trace of the cubed adjacency matrix is related to the coefficient C. The trace of the successive products of degree n gives a hierarchy of clustering coefficients $C_{n}$ . The number of these coefficients that provide new information on the network structure is of order of the network diameter L (after which every node is connected to almost every other node). For ‘small-world’ networks [2] the degree of clustering in relation to the network diameter, $C / L$ , can be shown to be small for both random and ordered networks [1,8] and larger otherwise and hence has the property of a complexity parameter. Extending this to general networks, we have called $C / L$ the β-complexity of a network [8].

The averaged cluster coefficient C of the system is calculated as:

C = N^{−1} \sum_{N} \frac{a_{i i}^{[3]}}{r (r - 1)}

where

a_{i i}^{[3]}

is the coefficient of the cubic adjacency matrix (Fig. 4), corresponding to the number of triangles formed by the node i of degree r and the denominator is the number of possible triangles. The diameter L is the characteristic path length calculated as the average of the shortest distance between pairs of randomly selected nodes.

We show in Fig. 5 the run of β-complexity over the slope β of the degree distribution for the Mandelbrot networks constructed by our thermodynamic method in Section 4. Note that steeper slopes correspond to fewer highly connected nodes and a lower value of $C / L$ ; this is consistent with the interpretation of β as a measure of complexity [8].

Fig. 5
The value C/L plotted against the slope of the distribution for the Mandelbrot networks constructed as described to Section 4.

The degree distribution however, does not fix the β-complexity of a network. This follows experimentally from the fact that the Barabási construction yields a scale-free network that is not a small world, while small world scale-free networks, such as yeast coexpression networks and hierarchical networks are known and can be modelled (see [11,12] and references therein). The nodal distribution does not fully determine the correlations between connections. We shall illustrate this with an explicit example. In the remainder of this paper we shall show how this fact has important consequences for the thermodynamics of networks.

6 Where are the correlations?

Variation of the C parameter can be carried out by a simple mechanism of cross-rewiring two pairs of nodes. That is, choose node i connected to node j and node k connected to node l with the condition there is no link between pair $i, l$ or pair $k, j$ . Then rewire node i to node l and node k to node j. This process ensures an alteration of the clustering coefficient without modifying the degree distribution of the network.

Random cross-rewiring is carried out over a number of steps $> N k$ on Mandelbrot networks that are generated according the method introduced above. During the process the maximum and the minimum C are recorded and the ratio $R = C_{\max} / C_{\min}$ taken. Over several occurrences of that process of generation and cross-rewiring we obtain a ratio $〈 R 〉 = 1.65 \pm 0.16$ .

To investigate this further we have looked at the nodal distribution for the iterated adjacency matrix. We have constructed the sequence of adjacency matrices for several classes of networks. We give in Fig. 6 the degree distribution function corresponding to these. For networks of a few thousand nodes the successive distributions soon become noisy, so we have taken a moving average over adjacent degrees on each side of a given one.

Fig. 6
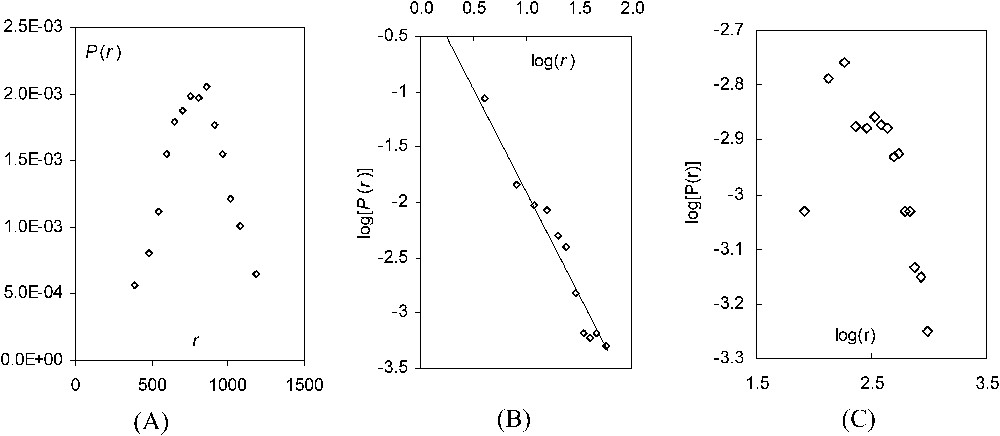
Degree distribution of nodes for several network classes each from the cubic adjacency matrix. (A) Random network, (B) scale-free network, (C) Mandelbrot network. The noise has been reduced by binning the data.

For each class, the degree distribution functions are of approximately the same shape as the original, aside from the fact that the transformations affect the mean degree of connectivity. This denotes, from a statistical point of view, an approximate invariance of the structure of the network connectivity. Eventually this sequence must come to an end because after sufficient iterations (approximately the diameter of the network) every node is connected to every other. The β-complexity must therefore change along this sequence. The difficulty of seeing this change above the noise in the initial iterations is clearly related to the difficulty of constructing networks with different complexity. It is of interest therefore to see the magnitude of the correlation entropy and where it resides.

7 Node entropy and link entropy

We have so far considered the entropy (disorder) of the networks contained in the distribution of the connectivity of the nodes (the ‘point’ entropy). This would be the complete entropy only if the nodes are randomly connected in the sense that the probability of a link between nodes of degrees r and s is independent of r and s. This is not the case: in both scale-free and (hence) Mandelbrot networks correlations exist between nodes [1]. We need to show that this can be neglected in a first approximation. An analogy with a gas might be illuminating. In a perfect gas the molecules are independent so the energy (and entropy) is proportional to the number density of particles. This is analogous to a network with independent links. In an imperfect gas the particles are correlated and the energy is associated not just with the particles, but also with their interactions. This is like a network with any non-random distribution of links. The correlations contribute to the order and hence should be included in the entropy.

To investigate this we consider the probability of finding a link connected, at least, to a node of degree r:

P_{r} = \frac{n_{r} r}{N k}

in a network with N nodes,

n_{r} = N p_{r}

, the number of nodes of degree r and of mean connectivity

k = \sum_{r} r p_{r}

. Let there be

n_{r s}

links between nodes of degree r and s. The total number of links in the network is

N k / 2

, so the probability that a link joins nodes of degree r and s is given by:

P_{r s} = \frac{2 n_{r s}}{N k}

If there are no correlations between the degrees, then:

P_{r s} = P_{r} P_{s}

(5)

Let

Q_{r s}

denote the probability that a pair of nodes of degree r and s are linked, so:

Q_{r s} = \frac{2 n_{r s}}{N (N - 1)}

where

N (N - 1) / 2

is the number of pairs of nodes, linked or not, hence the number of possible links.

If the links between nodes are uncorrelated:

Q_{r s} = \frac{2 r n_{r} s n_{s}}{N^{2} (N - 1) \bar{k}} = Q_{random}

We now look at the correlation in a network by computing the entropy per link relative to a random network. In any network a pair of nodes can either be linked, with probability

Q_{r s}

, or not linked with probability

1 - Q_{r s}

. The mean entropy per link is therefore:

H_{L} = - \frac{1}{N} \sum_{pair} [Q_{r s} \log Q_{r s} + (1 - Q_{r s}) \log (1 - Q_{r s})]

Thus the ratio:

\frac{- \sum_{pair} [Q_{r s} \log Q_{r s} + (1 - Q_{r s}) \log (1 - Q_{r s})]}{- \sum_{pair} [Q_{random} \log Q_{random} + (1 - Q_{random}) \log (1 - Q_{random})]} ⩽ 1

will be unity for independent linkage and less than unity for dependent links.

For a random network the numerically computed quantity $H_{L}$ is close to that expected (so the ratio is close to unity) thus verifying our procedures. Fig. 7 shows the calculation of the ratio for the Mandelbrot network that we have constructed above. It is clear that the ratio now differs significantly from unity so part of the entropy resides in the non-randomness of the links.

Fig. 7
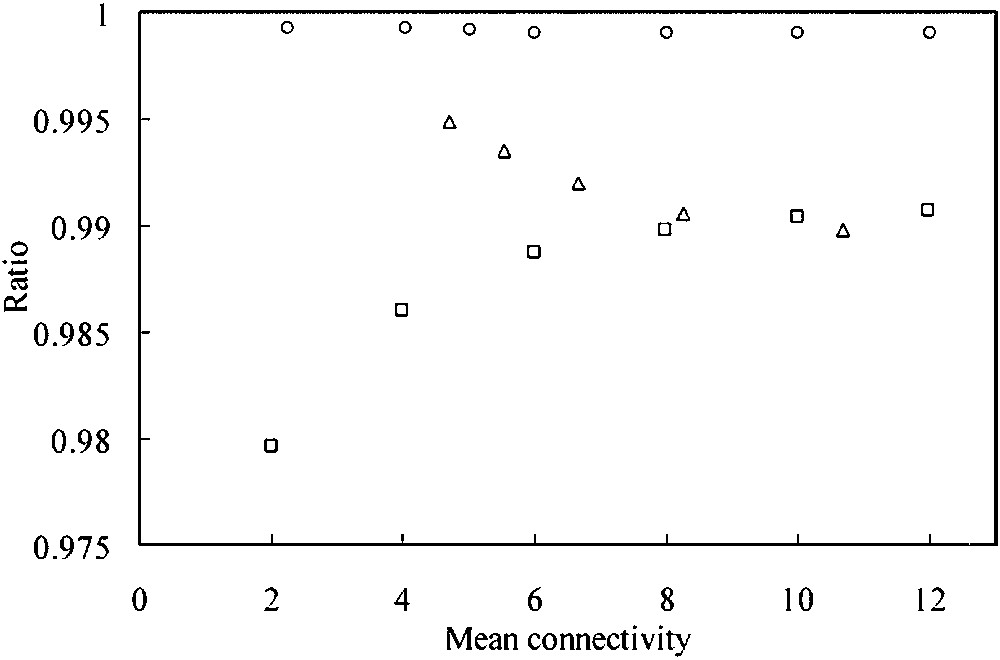
Ratio of the entropy for links independent of the nodal degrees to that of the dependent ones. The circles are for random networks, the triangles are for scale free networks obtained using the Barabási–Albert approach [1] and the triangles for the Mandelbrot networks. Each value is the average of 10 simulations using the same parameters.

Our conclusion is that to a first approximation the macroscopic properties of these networks can be obtained from an entropy function related to the node distribution. The fact that the entropy is not entirely contained in the node distribution means that there will be more than one local maximum of the full entropy function for a given node distribution, corresponding to different correlations [13].

Note that our model is the opposite of Ising-like models of interacting nodes where the energy (and entropy) is associated entirely with the interactions of nodes. Our model leads to the desired connectivity distributions (compare [14]).

In the next section we discuss the macroscopic properties from this approach that allows us to understand the above results.

8 Network complexity and the equation of state

In the context of the thermodynamic approach to the construction of networks we see how the slope β is not only analogous to a ‘temperature’ but plays exactly the role of a Lagrange parameter multiplying the ‘energy’ constraint. It is then a matter of computation to determine the other thermodynamic functions of the state of the network from the entropy. It is in fact a general result that any constraint of the form $\sum p_{r} ɛ (r) = constant$ leads to the perfect gas law whatever the form of $ɛ (r)$ [15]. We can show this as follows.

Let $p_{r}$ be the probability that a node has r links and let the ‘energy’ at a node be $ɛ (r)$ . Then the nodal (point) free energy of a network of N nodes is given by:

F / N = - \sum p_{r} \log p_{r} - β \sum p_{r} ɛ (r) - α \sum p_{r}

Maximising the free energy as usual leads to:

n_{r} = \frac{N}{Z} \exp (- β ɛ (r))

(6)

where the partition function Z is defined by

Z = \sum e^{- β ɛ (r)}

. For a perfect gas in a volume V, this has the form zV. We now derive the equation of state. Define the internal energy as:

U = \sum ɛ (r) n_{r}

Using (6) and the definition of Z, the entropy

S = - N \sum p_{r} \log p_{r}

becomes:

S = - \frac{\partial}{\partial β} (N β \log Z)

Thus

U = \frac{N}{Z} \sum ɛ (r) e^{- β ɛ (r)} = - \frac{S}{β} + \frac{N}{β} \log Z

From this, using

Z = z V

, we can find:

P = {(\frac{\partial U}{\partial V})}_{S} = \frac{N}{β} \frac{1}{V}

Thus, for the network, the crucial point is to define the volume in such a way that

Z = z V

. To do this, let M be the total number of links. Then:

M = \sum r n_{r} = \frac{N}{Z} \sum r e^{- β ɛ (r)}

and hence:

Z = \frac{N}{M} \sum r e^{- β ɛ (r)} = V z

if we take

V = N / M = k^{−1}

. We can think of this, in the gas analogy, as relating the specific volume to the inverse of the density. The result is independent of the form of

ɛ (r)

.

It is clear that this gives us the ‘perfect gas’ approximation to the equation of state of the network because, by using the node entropy, we are failing to take into account the interaction between the nodes. To obtain a deeper relationship between network entropy and thermodynamics we must use an entropy that includes the correlations between nodes, for example leading to a class of networks of a fixed complexity.

9 Discussion

In the development of the thermodynamics of material systems in thermal equilibrium the experimental facts were discovered first and the underlying microscopic description only later. In the theory of networks we start from the microscopic viewpoint and face the challenge of trying to derive macroscopic variables to characterise network properties in a useful way. In this article we have shown that we can construct networks according to a thermodynamics prescription. The fact that we now have a thermodynamic view of networks should enable us to develop such a macroscopic characterisation based on the entropy function. In networks where most of the entropy is contained in the distribution of the degrees of the nodes we expect that an approximate macroscopic description will involve a small number of global variables. We have speculated that in general the macroscopic variables will include a parameter describing in some way the complexity of the networks.

Acknowledgements

We thank Michel Thellier, Camille Ripoll, Francois Kepes and Patrick Amar for discussions.

Bibliographie

[1] R. Albert; A.-L. Barabási Statistical mechanics of complex networks, Rev. Mod. Phys., Volume 74 (2002), pp. 47-97

[2] D.J. Watts Small Worlds: The Dynamics of Networks between Order and Randomness, Princeton University Press, 1999

[3] S.N. Dorogovtsev; J.F.F. Mendes Evolution of Networks, Oxford University Press, 2003

[4] C. Adami Introduction to Artificial Life, Springer, NY, 1998

[5] B. Mandelbrot Structure formelle des textes et communication, Word, Volume 10 (1954), p. 1

[6] J. Vohradsky; J.J. Ramsden FASEB J. (2001) | DOI

[7] D.J. Raine, V. Norris, Network complexity, in: P. Amar, F. Kepes, V. Norris, P. Tracqui (Eds.), Modeling and Simulation of Biological Processes in the Context of the Genome. Conference Proceedings, Autrans, 2002, pp. 67–75

[8] D.J. Raine; Y. Grondin; M. Thellier; V. Norris Networks as constrained thermodynamic systems, C. R. Biologies, Volume 326 (2003), pp. 65-74

[9] http://vlado.fmf.uni-lj.si/pub/networks/pajek/default.htm

[10] D.J. Raine; V. Norris Network structure of metabolic pathways, J. Biol. Phys. Chem., Volume 1 (2001), pp. 89-94

[11] V. Van Noort; B. Snel; M.A. Huynen The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model, EMBO Rep., Volume 5 (2004), pp. 280-284

[12] E. Ravasz; A.-L. Barabási Hierarchical organization in complex networks, Phys. Rev. E Stat. Nonlin. Soft. Matter Phys., Volume 67 (2003), p. 026112

[13] P.L. Krapivsky; S. Redner Organization of growing random networks, Phys. Rev. E, Volume 63 (2001), p. 066123

[14] J. Berg; M. Lässig Correlated random networks, Phys. Rev. Lett., Volume 89 (2002) (228701-1)

[15] P.M. Morse Thermal Physics, Benjamin, 1968

Commentaires - Politique