Linéarisation autour d'un témoin pour prédire la réponse de cultures

Ibnou Dieng; Éric Gozé; Robert Sabatier

doi:10.1016/j.crvi.2006.01.005

Résumés

Français
Anglais

Une nouvelle méthode pour modéliser les interactions génotype × environnement : APLAT. Le rendement de génotypes prédit par un modèle de simulation de cultures est développé en série de Taylor à l'ordre 1 au voisinage du vecteur de paramètres d'un génotype de référence. À l'aide de cette linéarisation locale, l'estimation des paramètres de ces génotypes se fait par régression linéaire des rendements observés sur la sensibilité des sorties du modèle de simulation de cultures par rapport aux paramètres.

A new method for modelling genotype × environment interaction: APLAT. The yield predicted by a crop-simulation model is developed as a Taylor series in the neighbourhood of a parameter vector of a control genotype. With this local linearisation, these genotype parameters can be estimated by a linear regression of the observed yield on the derivatives of the crop-simulation model predictions with respect to its parameters.

Abridged English version

In Sahel, genotype × environment interactions are often large: this is the justification behind multilocation and pluriannual trials. Because of these sizeable environment effects and interactions, the prediction of an expected yield with a linear mixed model is generally imprecise.

Improving this prediction can be achieved by modelling the environment effect. It is then partly shifted from the random part to the fixed part of a mixed model, by the use of a crop-simulation model like DHC, IRSIS, SarraH... This could not be possible with the empirical genotype × environment interactions analysis methods like AMMI and joint regression, which do not make use of environmental variables. The factorial regression method does make use of environmental variables; however, it requires their effect on the production to be linear, which might not be the case.

Unfortunately, most crop-simulation models bear a number of parameters, the estimation of which requires a specific and costly experiment. As a consequence, these parameters are usually known, but for a small set of reference genotypes. It would not be sensible to invest in a parameter estimation experiment for every new genotype that is proposed for selection.

To overcome this problem, one can notice that multisite experiments usually share a control variety for which parameters have already been estimated. In this paper, we propose to develop as a Taylor series the modelled response about the parameters of this control genotype. The other genotypes' parameters can then be estimated by a linear regression of the observed yields on the sensitivity to parameters, i.e., on the derivatives of the response with respect to the parameters. With this estimation, one can predict the new genotype responses in environments where they have not been tested. In a given location, this estimation can benefit from the available historic climatic records to estimate a distribution of probable yields.

Let $f (Z_{j}, θ_{i})$ denote the yield of a genotype i predicted by a crop simulation in an environment j and $Y_{i j}$ the observed yield. We can write:

Y_{i j} = f (Z_{j}, θ_{i}) + ξ_{j} + u_{i j}

where

Z_{j}

is the vector of the jth environment regressors and

θ_{i}

the P-vector of the ith genotype parameters. The bias

ξ_{j}

is that of the crop-simulation model. We suppose that it depends only on environment and is the same for all genotypes in a same environment. The error term

u_{i j}

is supposed random with expectation 0 and variance

σ_{u}^{2}

Let us consider a control genotype, i.e., whose parameters are known or at least already estimated. Let $θ_{0}$ be the vector of parameters of this control genotype and let us suppose that f is a $C^{1}$ class function in a neighbourhood of $θ_{0}$ and $f^{'}$ derivable in this neighbourhood. Moreover, let us suppose $θ_{i}$ in the neighbourhood of $θ_{0}$ . Then, a Taylor series expansion yields:

f (Z_{j}, θ_{i}) = f (Z_{j}, θ_{0}) + \sum_{p = 1}^{P} [{\frac{\partial f}{\partial θ^{(p)}} |}_{θ = θ_{0}, Z = Z_{j}}] (θ_{i}^{(p)} - θ_{0}^{(p)}) + ○ [{(θ_{i} - θ_{0})}^{'} (θ_{i} - θ_{0})]

with

θ_{i}^{(p)}

the pth component of the parameters vector of the ith genotype,

θ_{0}^{(p)}

that of the control genotype.

Let $X_{j}^{(p)} = [\frac{\partial f}{\partial θ^{(p)}} |_{θ = θ_{0}, Z = Z_{j}}]$ and $β_{i}^{(p)} = θ_{i}^{(p)} - θ_{0}^{(p)}$ for $p = 1, \dots, P$ . As f is not known in closed form, one has to estimate its derivatives by numerical approximation. The function $X_{j}^{(p)}$ is a function of environment j, while $β_{i}^{(p)}$ is a function of genotype i. Then, the local linearization yields:

Y_{i j} - Y_{0 j} = \sum_{p = 1}^{P} X_{j}^{(p)} \cdot β_{i}^{(p)} + ε_{i j}

where

Y_{0 j}

is the control response in the environment j and

ε_{i j} = u_{i j} - u_{0 j}

. So,

E (ε_{i j}) = 0

V (ε_{i j}) = 2 σ_{u}^{2}

C ov (ε_{i j}, ε_{i^{'} j^{'}}) = 0

, but

C ov (ε_{i j}, ε_{i^{'} j}) = σ_{u}^{2}

This equation can be put in the form of a linear model with correlated errors:

Y - (Y_{0} \otimes 1_{I}) = X \cdot β + ε

In this equation, Y is the vector of responses of the I genotypes in the J environments,

Y_{0}^{'} = (Y_{01} \dots Y_{0 J})

1_{I}

is unit vector of size

I \times 1

. The symbol ⊗ indicates the Kronecker product and ε is a random error vector. Its covariance matrix is

σ_{u}^{2} Ω

where:

Ω = (\begin{matrix} ω_{1} \\ ⋱ & 0 \\ ω_{j} \\ 0 & ⋱ \\ ω_{J} \end{matrix}) and ω_{j} = (\begin{matrix} 2 & 1 \\ ⋱ \\ 1 & 2 \end{matrix})

The number of columns of the square matrices Ω and

ω_{j}

are respectively the number of observations for all the environments and the number of observations for environment j.

Also, $X = [\begin{matrix} X^{(1)} \otimes I_{I} \dots X^{(P)} \otimes I_{I} \end{matrix}]$ where $X^{(p)'} = [\begin{matrix} X_{1}^{(p)} \dots X_{J}^{(p)} \end{matrix}]$ is a $J \times 1$ vector and $I_{I}$ is the $I \times I$ unit matrix. The dimension of X is then $I J \times P I$ .

Finally, $β^{'} = [\begin{matrix} β^{(1)'} \dots β^{(P)'} \end{matrix}]$ where $β^{(p)'} = [\begin{matrix} β_{1}^{(p)} \dots β_{I}^{(p)} \end{matrix}]$ .

We call this method APLAT for Approximation Par Linéarisation Autour d'un Témoin.

Because of the large number of columns of X, some dimension reduction method like Partial Least Squares regression is necessary. The dimension of the space spanned by the regressors is then reduced from rank of X to k. The PLS regression is usually carried out with the NIPALS (Nonlinear estimation by Iterative Partial Least Squares) algorithm, where the calculation of the components is performed simultaneously with a set of regressions by ordinary least squares. Here, the error covariance matrix is $σ_{u}^{2} Ω$ , not $σ_{u}^{2} I_{I J}$ , generalized least squares should be used instead. As Ω is symmetric and positive semi-definite, a work around consists in factorizing its inverse, finding a matrix η such that $η^{'} η = Ω^{−1}$ .

Then, estimating β by PLS with regressions by generalized least squares is equivalent to consider the model:

η Y - η (Y_{0} \otimes 1_{I}) = η X \cdot β + η ε

where

{\tilde{β}}_{PLS}

is the estimation with regressions made by ordinary least squares.

The number of components is chosen to minimize the PRESS (Prediction Error Sum of Squares) criterion.

To calculate the confidence interval of the coefficients, we used a bootstrap technique. Let $z_{i, PLS}^{(p) ⋆ b}$ be the random variable defined by:

z_{i, PLS}^{(p) ⋆ b} = \frac{{\tilde{β}}_{i, PLS}^{(p) ⋆ b} - {\tilde{β}}_{i, PLS}^{(p)}}{{\tilde{s}}^{⋆} ({\tilde{β}}_{i, PLS}^{(p) ⋆ b})}

where

{\tilde{β}}_{i, PLS}^{(p)}

is the

(p \cdot i)

th element of

{\tilde{β}}_{PLS}

{\tilde{β}}_{i, PLS}^{(p) ⋆ b}

is obtained at the bth draw with

b = 1, \dots, B

and

{\tilde{s}}^{⋆} ({\hat{β}}_{i, PLS}^{(p) ⋆ b})

is the standard error of

{\tilde{β}}_{PLS}^{⋆ b}

. Let

{\hat{F}}_{B}

be the empirical distribution function of

z_{i, PLS}^{(p) ⋆ b}

. The fractile

{\hat{F}}_{B}^{−1} (α)

is estimated by

\hat{t} (α)

such that

# {z_{i, PLS}^{(p) ⋆ b} ⩽ \hat{t} (α)} = α B

A percentile-t confidence interval for the $(p \cdot i)$ th element of β is in the following form:

[{\tilde{β}}_{i, PLS}^{(p)} - \tilde{s} ({\tilde{β}}_{i, PLS}^{(p)}) \cdot \hat{t} (1 - α), {\tilde{β}}_{i, PLS}^{(p)} - \tilde{s} ({\tilde{β}}_{i, PLS}^{(p)}) \cdot \hat{t} (α)]

To evaluate the quality of the new model, we compared its MSEP (Mean Squared Error of Prediction) with that of the average model defined for our data as follows:

Y_{i j} = m + g_{i} + E_{j} + δ_{i j}

where m is the population mean and

g_{i}

the genotype effect. The term

E_{j}

is the year effect and it is assumed random with expectation 0 and variance

σ_{E}^{2}

. Errors

δ_{i j}

are distributed independently with expectation 0 and variance

σ_{δ}^{2}

. The terms

E_{j}

and

δ_{i j}

are assumed to be mutually independent.

The data set consists of plant yields of 26 groundnut genotypes. The experiments have been carried out at Bambey (14°42N and 16°28W) in Senegal, over a period of five years from 1994 to 1998. The data of each year were kept in turn as a test sample. Yields are expressed in kilograms of pods per hectare.

We used SarraH, a crop simulation model developed by CIRAD in collaboration with CERAAS, to calculate X. Taking into account the available number of data, we estimated two of its varietal parameters.

The PRESS is minimal with six components for models adjusted without the data of 1994, 1995 and 1997. For each of the others, the PRESS is minimal with nine components. However, we decided to keep only five components, as the PRESS was not very different from its minimum value.

The APLAT MSEPs are lower than the average model MSEP, except for prediction of 1998 data. Then the prediction of yield for these models by APLAT was better than that made with the average model four times out of five.

With the APLAT method, the prediction of a genotype in a new environment comes at a relatively low price, using mostly available data, except for the environmental data, which has to be recorded for every site of the experiment, according to the crop-simulation model needs. This method seems promising, but requires additional studies with more numerous data.

1 Introduction

Au Sahel, les interactions genotype × environnement constatées lors des essais multilocaux et pluriannuels sont généralement importantes. Sur les réponses moyennes par variété et par environnement, le modèle linéaire généralement adopté s'écrit :

Y_{i j} = m + g_{i} + E_{j} + {(g E)}_{i j} + e_{i j}

(1)

où

Y_{i j}

est la réponse du génotype i de l'environnement j, m la moyenne générale et

g_{i}

l'effet fixe du génotype i. L'effet

E_{j}

de l'environnement j et l'interaction

{(g E)}_{i j}

peuvent être fixes ou aléatoires. Pour l'objectif de prédiction des réponses de génotypes dans l'ensemble des environnements potentiels auxquels ils sont destinés, l'optique aléatoire est plus pertinente. Ainsi, supposons ces deux effets et le terme d'erreur

e_{i j}

aléatoires, iid et indépendants les uns des autres avec

E (E_{j}) = E [{(g E)}_{i j}] = E (e_{i j}) = 0

V (E_{j}) = σ_{E}^{2}

V [{(g E)}_{i j}] = σ_{g E}^{2}

V (e_{i j}) = σ_{e}^{2}

où

E (\cdot)

V (\cdot)

désignent l'espérance et la variance.

Choisir un génotype i dans un environnement j suppose d'estimer l'espérance de sa performance dans j. La précision de cette estimation est fonction de $σ_{E}^{2}$ , $σ_{g E}^{2}$ et de $σ_{e}^{2}$ . Dans cette zone du Sahel, l'environnement est variable, c'est-à-dire que $σ_{E}^{2}$ et $σ_{g E}^{2}$ sont grands, ce qui dégrade cette précision. Pour l'améliorer, une solution est de modéliser les variations de $Y_{i j}$ en fonction de l'environnement par l'utilisation de modèles de simulation de cultures tels que DHC [1], IRSIS [2], SarraH [3], etc. De ce fait, une partie de l'effet aléatoire de l'environnement est reportée dans la partie fixe du modèle. Cette approche n'est pas possible avec les modèles classiques de l'interaction génotype × environnement. En effet, la méthode AMMI, Additive Main effects and Multiplicative Interactions [4] ainsi que la régression conjointe [5,6] ne tiennent pas compte des nouveaux environnements pour y prédire les réponses des génotypes. La régression factorielle [4,5] en tient compte, mais suppose que l'action des variables des environnements sur la production est linéaire, ce qui n'est pas certain.

Cependant, les paramètres des modèles de simulation de cultures ne sont pour la plupart connus que pour un petit nombre de génotypes, car leur évaluation demande une expérimentation spécifique et des mesures coûteuses.

L'objectif de cette étude se pose alors en ces termes : comment prédire le comportement de génotypes dans de nouveaux environnements en tenant compte de ces derniers, sans coût excessif ?

2 Le modèle proposé

Si nous partons du modèle de simulation de cultures, chacune des sorties de ce modèle, le rendement potentiel par exemple, peut s'interpréter comme la réponse d'un génotype i dans un environnement j :

Y_{i j} = f (Z_{j}, θ_{i}) + ξ_{j} + u_{i j}

(2)

où

Z_{j}

est le vecteur des variables telles que la pluie, la température, etc., mesurées sur l'environnement j et

θ_{i}

le vecteur de longueur P des paramètres du génotype i. L'erreur

ξ_{j}

est le biais du modèle de simulation de cultures ; nous supposons qu'elle ne dépend que de l'environnement j : elle est donc la même pour tous les génotypes d'un même environnement. Le terme

u_{i j}

est pris aléatoire, avec

E (u_{i j}) = 0

V (u_{i j}) = σ_{u}^{2}

Comme on l'a dit précédemment, les paramètres des modèles de simulation de cultures ne sont généralement connus que pour un petit nombre de génotypes. Considérons un modèle de simulation de cultures et un génotype de référence dont les paramètres sont connus et appelons $θ_{0}$ le vecteur de ses paramètres. Alors, supposons f de classe $C^{1}$ dans un voisinage de $θ_{0}$ et $f^{'}$ dérivable sur ce voisinage. De plus supposons $θ_{i}$ au voisinage de $θ_{0}$ . En pratique, les génotypes dont nous chercherons à estimer leurs paramètres seront choisis de telle sorte qu'ils ne soient pas trop éloignés du génotype de référence. Alors, un développement en série de Taylor à l'ordre 1 nous donne :

f (Z_{j}, θ_{i}) = f (Z_{j}, θ_{0}) + \sum_{p = 1}^{P} {[\frac{\partial f}{\partial θ^{(p)}}]}_{θ = θ_{0}, Z = Z_{j}} (θ_{i}^{(p)} - θ_{0}^{(p)}) + ○ [{(θ_{i} - θ_{0})}^{'} (θ_{i} - θ_{0})]

(3)

avec

θ_{i}^{(p)}

θ_{0}^{(p)}

p^{e}

composante du vecteur de paramètres respectivement du génotype i et du génotype de référence.

Posons $X_{j}^{(p)} = {[\frac{\partial f}{\partial θ^{(p)}}]}_{θ = θ_{0}, Z = Z_{j}}$ : c'est une fonction de l'environnement j et $β_{i}^{(p)} = θ_{i}^{(p)} - θ_{0}^{(p)}$ une fonction du génotype i. La fonction $X_{j}^{(p)}$ est la dérivée partielle de la sortie du modèle de simulation de cultures pour l'environnement j par rapport à la $p^{e}$ composante du vecteur de paramètres de la variété de référence. Comme la fonction f n'est pas généralement connue analytiquement, ces sensibilités peuvent être obtenues par une méthode de dérivation numérique. Nous avons retenu tout simplement :

X_{j}^{(p)} = {[\frac{\partial f}{\partial θ^{(p)}}]}_{θ = θ_{0}, Z = Z_{j}} ≃ {[\frac{f (θ_{0}^{(p)} + h_{θ_{0}^{(p)}}) - f (θ_{0}^{(p)} - h_{θ_{0}^{(p)}})}{2 h_{θ_{0}^{(p)}}}]}_{Z = Z_{j}}

avec

h_{θ_{0}^{(p)}}

très petit, de l'ordre de

θ_{0}^{(p)} \times 10^{−4}

en pratique. D'autres méthodes existent, celle-ci étant la plus simple et économe en calculs.

Avec ces notations et d'après l'Éq. (2), qui permet d'écrire $f (Z_{j}, θ_{0}) = Y_{0 j} - ξ_{j} - u_{0 j}$ , nous pouvons écrire, en négligeant $○ [{(θ_{i} - θ_{0})}^{'} (θ_{i} - θ_{0})]$ :

Y_{i j} - Y_{0 j} = \sum_{p = 1}^{P} X_{j}^{(p)} \cdot β_{i}^{(p)} + ε_{i j}

(4)

où

ε_{i j} = u_{i j} - u_{0 j}

. Ainsi,

E (ε_{i j}) = 0

V (ε_{i j}) = 2 σ_{u}^{2}

C ov (ε_{i j}, ε_{i^{'} j^{'}}) = 0

, mais

C ov (ε_{i j}, ε_{i^{'} j}) = σ_{u}^{2}

Si nous disposons de I génotypes et de J environnements, nous pouvons poser le modèle suivant :

Y - (Y_{0} \otimes 1_{I}) = X \cdot β + ε

(5)

Le vecteur Y représente le rendement de tous les génotypes dans tous les environnements ; il est de longueur IJ, $Y_{0}^{'} = (Y_{01} \dots Y_{0 J})$ et $1_{I}$ est un vecteur formé de 1, de longueur I. Le symbole ⊗ désigne le produit de Kronecker. Le vecteur ε est un vecteur d'erreur aléatoire. Sa matrice de covariance est de la forme $σ_{u}^{2} Ω$ , avec :

Ω = (\begin{matrix} ω_{1} \\ ⋱ & 0 \\ ω_{j} \\ 0 & ⋱ \\ ω_{J} \end{matrix}) où ω_{j} = (\begin{matrix} 2 & 1 \\ ⋱ \\ 1 & 2 \end{matrix})

Les matrices Ω et

ω_{j}

sont carrées de nombre de lignes, respectivement le nombre d'observations de tous les environnements et le nombre d'observations de l'environnement j.

Ensuite, $X = [\begin{matrix} X^{(1)} \otimes I_{I} \dots X^{(P)} \otimes I_{I} \end{matrix}]$ où $X^{(p)'} = [\begin{matrix} X_{1}^{(p)} \dots X_{J}^{(p)} \end{matrix}]$ est de longueur J et $I_{I}$ est la matrice identité d'ordre I. La matrice X est donc de dimension $I J \times P I$ .

Enfin, $β^{'} = [\begin{matrix} β^{(1)'} \dots β^{(P)'} \end{matrix}]$ avec $β^{(p)'} = [\begin{matrix} β_{1}^{(p)} \dots β_{I}^{(p)} \end{matrix}]$ .

Nous proposons d'appeler cette méthode par l'acronyme APLAT : Approximation Par Linéarisation Autour d'un Témoin. Elle consiste à approcher, localement, le rendement prédit par un modèle de simulation de cultures, par série de Taylor à l'ordre 1 au voisinage du vecteur de paramètres d'un génotype de référence. Cette linéarisation permet, par régression linéaire, l'estimation des paramètres de ces génotypes. Par la suite, la prédiction de l'écart entre le rendement de ces génotypes et celui du génotype de référence dans des environnements nouveaux, c'est-à-dire où ils ne sont pas encore testés, pourra se faire si le climat de ces derniers est connu.

3 Estimation des paramètres et validation du modèle

Il y a en général beaucoup de paramètres dans un modèle de simulation de cultures et peu d'environnements dans un essai multienvironnement, ce qui rend souvent PI grand par rapport à IJ. Pour notre exemple, nous avons utilisé SarraH comme modèle de simulation de cultures. Ce modèle dispose de 61 paramètres, qui sont fonction du génotype. Avec un tel nombre de prédicteurs, l'estimation de β s'est faite par régression PLS, Partial Least Squares [7]. Il s'agit donc pour nous d'écrire un modèle linéaire de prédiction des rendements des génotypes pour de nouveaux environnements par les sensibilités par rapport aux paramètres des génotypes des sorties d'un modèle de simulation de cultures, fondé sur la construction de composantes orthogonales dans l'image de X. Ceci permet de réduire l'espace des régresseurs de rang de X à k dimensions. La régression PLS s'effectue selon le principe de l'algorithme NIPALS, Nonlinear estimation by Iterative Partial Least Squares [7], où un ensemble de régressions partielles par moindres carrés ordinaires est effectué, en même temps que le calcul des composantes. Ici, la matrice de covariance de ε est égale à $σ_{u}^{2} Ω$ et non à $σ_{u}^{2} I_{I J}$ . La solution serait d'effectuer toutes les régressions partielles par moindres carrés généralisés. Mais cette matrice de covariance est inconnue. Elle s'écrit tout de même, à une constante multiplicative près, en fonction de Ω, qui elle est connue. La matrice Ω étant symétrique et semi-définie positive, par décomposition de Cholesky, il existe une matrice η tel que $η^{'} η = Ω^{−1}$ .

Ainsi, estimer β par PLS avec les régressions partielles par moindres carrés généralisés consiste à poser le modèle suivant :

η Y - η (Y_{0} \otimes 1_{I}) = η X \cdot β + η ε

(6)

où

{\tilde{β}}_{PLS}

est l'estimation avec les régressions partielles effectuées par moindres carrés ordinaires.

Dans ce cas, la variance de l'erreur ηε s'écrit :

E ({η ε ε}^{'} η^{'}) = η E ({ε ε}^{'}) η^{'} = σ_{u}^{2} {η Ω η}^{'} = σ_{u}^{2} η {(η^{'} η)}^{−1} η^{'} = σ_{u}^{2} {η η}^{−1} {(η^{'})}^{−1} η^{'} = σ_{u}^{2} I_{I J}

Le nombre de composantes à retenir est déterminé par le PRESS, Prediction Error Sum of Squares [7].

Nous avons calculé les intervalles de confiance des coefficients estimés par la méthode bootstrap [8]. Cette technique permet d'estimer la loi inconnue d'un estimateur par une loi empirique obtenue à partir d'une procédure de rééchantillonnage fondée sur des tirages aléatoires avec remise des données. Les intervalles de confiance construits sont de type percentile-t [9]. Soit $z_{i, PLS}^{(p) ⋆ b}$ la variable aléatoire définie par :

z_{i, PLS}^{(p) ⋆ b} = \frac{{\tilde{β}}_{i, PLS}^{(p) ⋆ b} - {\tilde{β}}_{i, PLS}^{(p)}}{{\tilde{s}}^{⋆} ({\tilde{β}}_{i, PLS}^{(p) ⋆ b})}

(7)

où

{\tilde{β}}_{i, PLS}^{(p)}

est le

{(p \cdot i)}^{e}

élément de

{\tilde{β}}_{PLS}

{\tilde{β}}_{i, PLS}^{(p) ⋆ b}

obtenu au

b^{e}

tirage avec

b = 1, \dots, B

{\tilde{s}}^{⋆} ({\tilde{β}}_{i, PLS}^{(p) ⋆ b})

l'écart-type estimé de

{\tilde{β}}_{PLS}^{⋆ b}

. Soit

{\hat{F}}_{B}

la fonction de répartition empirique des

z_{i, PLS}^{(p) ⋆ b}

. Le fractile d'ordre α,

{\hat{F}}_{B}^{−1} (α)

est estimé par la valeur

\hat{t} (α)

telle que :

\frac{1}{B} \sum_{b = 1}^{B} 1_{{z_{i, PLS}^{(p) ⋆ b} ⩽ \hat{t} (α)}} = α

Donc un intervalle de confiance percentile-t pour le ${(p . i)}^{e}$ élément de β peut s'écrire :

[{\tilde{β}}_{i, PLS}^{(p)} - \tilde{s} ({\tilde{β}}_{i, PLS}^{(p)}) \cdot \hat{t} (1 - α), {\tilde{β}}_{i, PLS}^{(p)} - \tilde{s} ({\tilde{β}}_{i, PLS}^{(p)}) \cdot \hat{t} (α)]

(8)

L'évaluation de la qualité du modèle proposé est faite avec l'erreur quadratique moyenne de prédiction MSEP, Mean Squared Error of Prediction [10]. La MSEP est utilisée comme critère pour comparer différents modèles dont le modèle moyen [11], défini pour nos donnés par :

Y_{i j} = m + g_{i} + E_{j} + δ_{i j}

(9)

où m est la moyenne de la population et

g_{i}

l'effet génotype. L'effet

E_{j}

de l'environnement j est supposé aléatoire, d'espérance nulle et de variance

σ_{E}^{2}

. Les erreurs

δ_{i j}

sont indépendantes, d'espérance nulle et de variance

σ_{δ}^{2}

. De plus,

E_{j}

δ_{i j}

sont supposés indépendants.

Le logiciel R [12] a été utilisé la fonction qui a servi pour les régression est de J.-F. Durand [13].

4 Les données utilisées

Nous avons des résultats d'essais agronomiques d'arachide menés de 1994 à 1998 sur la station expérimentale du Ceraas, située à Bambey (14°42N et 16°28O), au Sénégal. Ces essais pluriannuels ont concerné au total 26 génotypes à cycle de développement de 90 jours et répondaient à l'objectif de recherche de génotypes physiologiquement adaptés à la sécheresse.

La variété de référence choisie est la 55-437, c'est une variété hâtive de 90 jours ; elle a donc une longueur de cycle proche de celle des autres variétés utilisées. Elle a été choisie parce que ses données étaient disponibles.

Dans ce milieu à forte variabilité des pluies dans l'espace et même dans le temps pour un même lieu, nous avons considéré chacune des cinq années d'expérimentation comme un environnement (Fig. 1).

Fig. 1
Répartition des pluies sur la station de Bambey, au Sénégal, de 1994 à 1998.

Pour valider notre modèle, nous avons réservé successivement chacune des années et estimé les paramètres des génotypes sur les années restantes. Pour chaque année, les rendements observés ont été comparés à ceux prédits par la méthode APLAT. Les rendements sont exprimés en kilogrammes de gousses par hectare.

SarraH a été utilisé pour calculer X. Compte tenu du nombre de données disponibles, seuls deux paramètres ( $P = 2$ ) ont été considérés parmi les 61 de SarraH. Le premier paramètre est en fait un coefficient multiplicateur qui agit sur cinq paramètres de SarraH : coefficient moyen d'angle des feuilles, coefficient de conversion en assimilat, coefficient d'efficience d'assimilation des feuilles à la phase végétative juvénile, coefficient d'efficience d'assimilation des feuilles à la première phase de maturation, phase sensible de remplissage des grains et coefficient d'efficience d'assimilation des feuilles à la deuxième phase de maturation, phase non sensible. Le deuxième paramètre est le poids moyen des gousses.

5 Résultats

Au Sahel, l'interaction G×E est largement due aux aléas climatiques, dont la probabilité peut être estimée à l'aide de longues chroniques de relevés météo au sol. Cependant, relier l'interaction G×E et la pluviométrie à l'aide d'un modèle de simulation de cultures n'est habituellement possible que pour des variétés dont on a estimé les paramètres, au prix d'une expérimentation spécifique. Le modèle APLAT permet de prédire cette interaction avec les seules données d'une expérimentation multilocale classique, sans autre instrumentation que des stations météo simples.

Pour les modèles sans les données respectivement de 1994, 1995 et 1997, le PRESS minimal est atteint avec six composantes. Pour les deux autres modèles, le PRESS est minimal avec neuf composantes, mais nous avons réduit leur espace à cinq dimensions, car le PRESS n'y est pas trop différent de ses valeurs minimales (Fig. 2).

Fig. 2
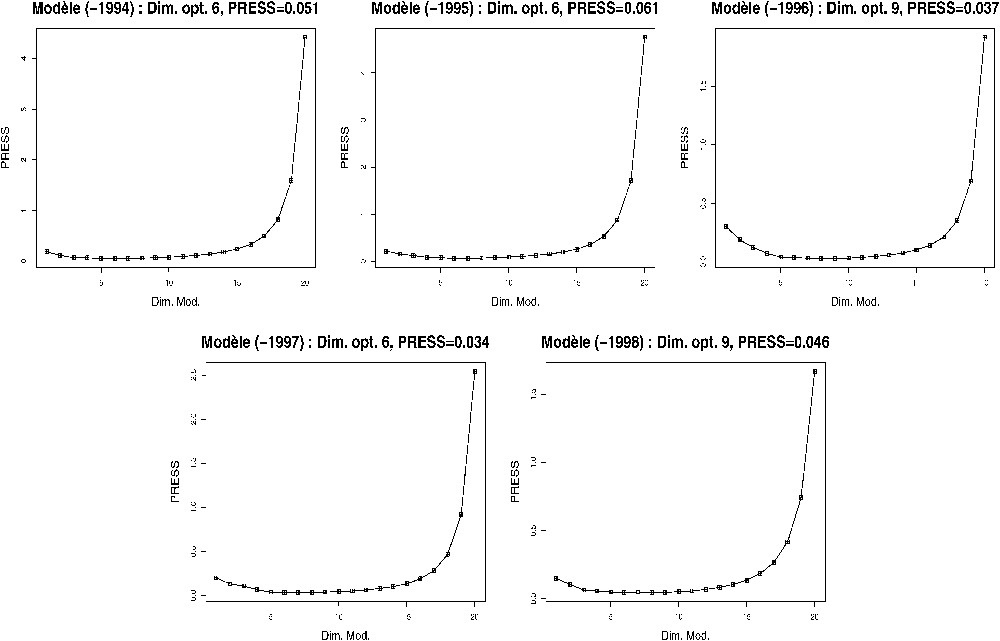
Evolution du PRESS en fonction du nombre de composantes. Le modèle (-1994) utilise les données, sauf celles de l'année 1994, et ainsi de suite.

Les coefficients des régressions PLS et les intervalles de confiance qui leur sont associés sont représentés sur la Fig. 3.

Fig. 3
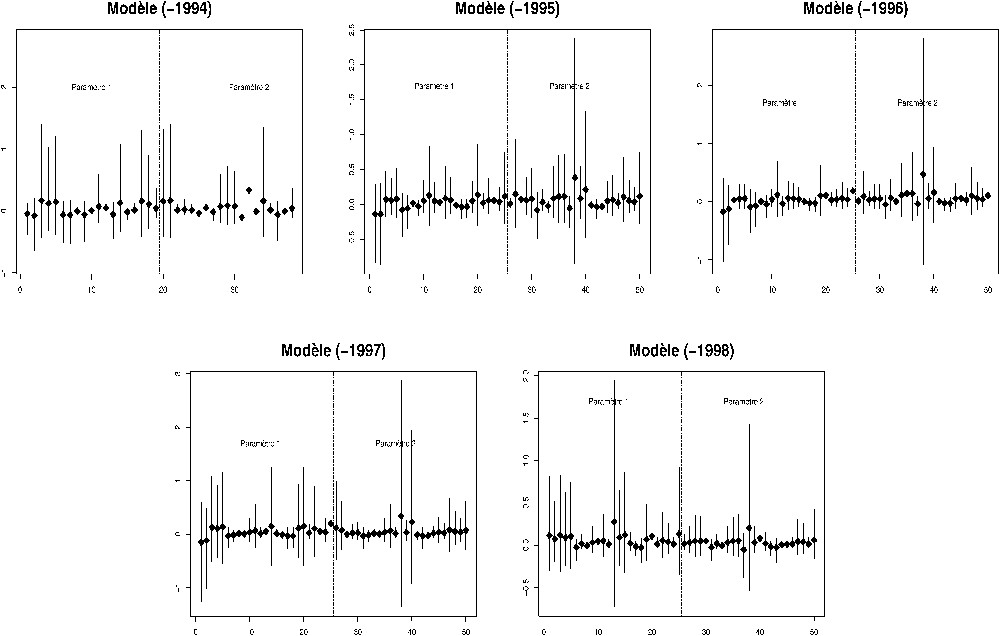
Intervalle de confiance percentile-t à 95% des coefficients estimés. Le modèle (-1994) utilise les données, sauf celles de l'année 1994, et ainsi de suite. Sur l'axe des abscisses figurent les génotypes par ordre alphabétique pour chacun des deux paramètres. Le symbole ⧫ représente l'estimation des coefficients.

Les MSEP estimées pour les modèles APLAT, sauf celle sans les données de l'année 1998, sont inférieures aux MSEP des modèles moyens correspondants (Tableau 1). Ce qui signifie que, pour ces modèles, prédire le rendement par la méthode APLAT est meilleur que par la moyenne des rendements du passé. Ainsi, quatre fois sur cinq, la méthode APLAT s'est révélée meilleure que le modèle moyen. Toutefois, cette étude souffre de la faible taille de notre échantillon.

	APLAT	Modèle moyen
Modèle (-1994)	24 687,3	64 651,6
Modèle (-1995)	5915,0	7160,6
Modèle (-1996)	35 446,1	37 814,8
Modèle (-1997)	10 038,3	18 201,1
Modèle (-1998)	118 304,9	84 963,6

6 Conclusion

La méthode APLAT peut être vue comme un outil d'aide à la décision pour la sélection au Sahel. Dans l'exemple où un sélectionneur doit tester plusieurs génotypes dans un nouvel environnement, cette méthode lui permettra d'écarter d'emblée certains génotypes qui donneront une production faible, en lieu et place d'essais multilocaux ou pluriannuels dans ces environnements contrastés ou d'une tentative de paramétrisation d'un modèle de simulation de cultures qui implique un coût élevé. Son attention sera portée par la suite sur l'ensemble restreint des génotypes retenus avec APLAT, où il pourra appliquer les schémas classiques de sélection.

Cette nouvelle approche semble prometteuse, mais il faut des études supplémentaires. Notamment disposer de données agronomiques plus conséquentes pour l'éprouver.

Remerciements

Nous remercions Danièle Clavel pour les données de l'étude et Jean-Claude Combres pour toutes les discussions autour du modèle SarraH.