Adaptive dynamics: modelling Darwin's divergence principle

Stéphane Génieys; Vitaly Volpert; Pierre Auger

doi:10.1016/j.crvi.2006.08.006

Résumés

Anglais
Français

A model illustrating Darwin's divergence principle is presented. It shows how competition for resources can explain evolutionary branching. It is based on an assumption of degenerate competition. Mathematically, it is a partial differential equation with an integral term, and it describes a new mechanism of self-organization.

Nous présentons un modèle illustrant le principe de divergence de Darwin. Il montre comment la compétition pour les ressources peut expliquer les branchements évolutifs. Il est basé sur une hypothèse de compétition dégénérée. Mathématiquement, il s'agit d'une équation aux dérivées partielles comprenant un terme intégral, et il décrit un nouveau mécanisme d'émergence de structure.

Version française abrégée

Nous considérons le modèle suivant :

\frac{\partial f}{\partial t} (t, x) - d Δ f (t, x) = a f (t, x) (K - C (f) (t, x))

(1)

où t désigne le temps,

x \in Ω

un trait morphologique (Ω étant l'espace morphologique), et

f (t, x)

est la densité de population ayant le trait x à l'instant t.

Le terme de diffusion $d Δ f (t, x)$ décrit l'étalement de la population dans l'espace morphologique dû aux mutations.

Le terme $a f (t, x) (K - C (f) (t, x))$ est inspiré de l'équation logistique, où a est le cœfficient de prolifération et K la capacité limite de l'environnement. Le terme $C (f) (t, x)$ incorpore l'hypothèse de compétition dégénérée :

C (f) (t, x) = \int_{Ω} φ (x - x^{'}) f (t, x^{'}) d x^{'}

(2)

signifiant que la morphologie x est en compétition avec les autres morphologies

x^{'}

, et

φ (x - x^{'})

décrivant l'intensité de cette compétition. On suppose ici que l'espace morphologique est un intervalle de

R

Ω = [0, L]

et que le noyau de compétition φ est donné par :

φ (y) = \frac{1}{2 b} 1_{[- b, b]} (y)

(3)

où

1_{[- b, b]}

est la fonction indicatrice de

[- b, b]

Dans cette étude, on considère des conditions aux limites périodiques, bien qu'elles aient peu de sens biologique, ce qui permet de faire une étude de bifurcation simple. D'après les simulations numériques, les résultats sont essentiellement identiques avec des conditions aux limites de Neumann homogènes. D'autre part, le cas où l'espace morphologique est de dimension 2, plus riche, fera l'objet d'une étude ultérieure.

Pour le cas monodimensionnel avec conditions périodiques, on met en évidence un paramètre de bifurcation :

p = \frac{d}{a K b^{2}}

Si ce paramètre est inférieur à sa valeur critique, l'équilibre homogène $f \equiv K$ des équations (1)–(3) est instable, et une structure apparaît (voir Fig. 1).

Fig. 1
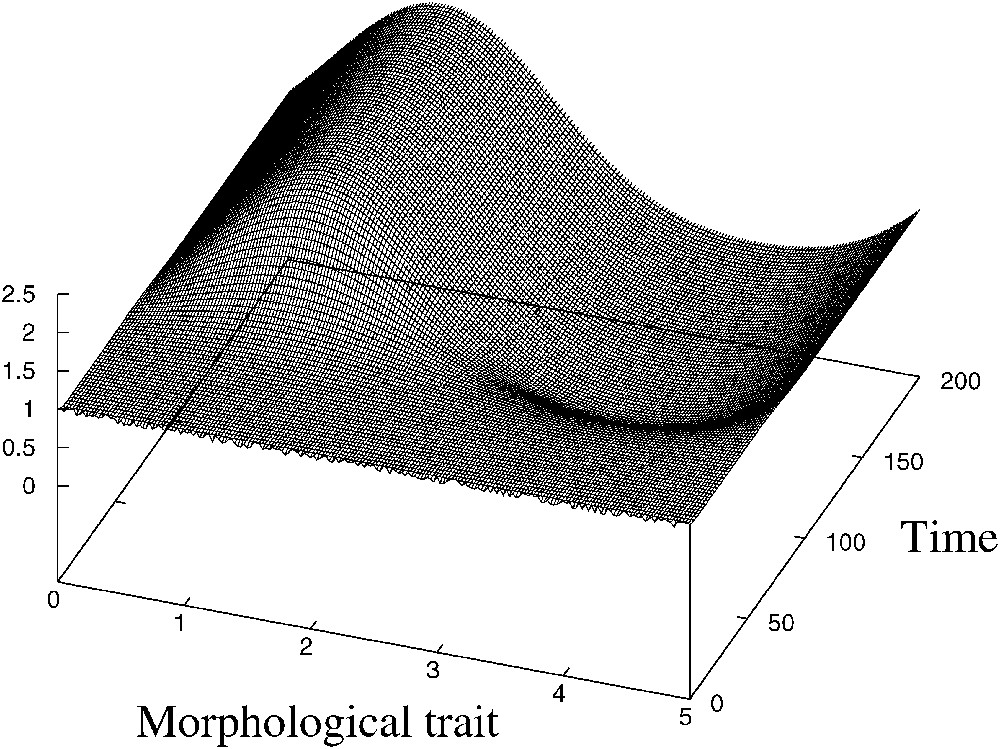
Emergence of structure. Parameters are a=1, K=1, b=3 d=0.05, L=5.

Sous ces conditions entraînant la structuration, une population initialement monomorphique subira plusieurs branchements successifs pour devenir polymorphique. D'après les simulations numériques, cette population polymorphique est un état d'équilibre stable.

Ce résultat nous paraît illustrer ce que Darwin appelle le « principe de divergence des caractères », qui est un mécanisme fondamental d'apparition de nouveaux lignages.

On étudie aussi un cas où le noyau de compétition φ est asymétrique :

φ (y) = \frac{1}{2 b} 1_{[- b + δ, b + δ]} (y)

L'étude est similaire au cas symétrique, le paramètre de bifurcation est le même (mais sa valeur critique est différente) et, sous les hypothèses entraînant la structuration, une population monomorphique subit des branchements successifs pour se séparer en plusieurs sous-populations. Ensuite, les simulations numériques suggèrent que toutes les sous-populations se déplacent dans l'espace morphologique, dans la direction de plus faible compétition (voir Fig. 3).

Fig. 3
Asymmetric evolution. Parameters are a=1, K=1, b=3, δ=0.3, d=0.01, L=40.

1 Introduction

The concept of degeneracy was introduced by Edelman (see, e.g., [1]) and designates the ability of elements that are structurally different to perform the same function. Atamas used this concept in [2] to obtain cellular automata simulations illustrating evolutionary branchings. He modelled a population of elements recognizing different resources according to their morphology. A certain amount of degeneracy was included, causing similar morphologies to recognize the same resources. This introduced a competition between the recognizers, which caused an originally monomorphic population to split into two sub-populations in order to lower this competition.

The aim of the present work is to set this phenomenon into a mathematical framework and we use for that a partial differential equation with an integral term. Other mathematical formalisms have been used to approach this problem, including probabilistic models [3] and Hamilton–Jacobi equations [4].

2 Setting of the model

We consider the following equation:

\frac{\partial f}{\partial t} (t, x) - d Δ f (t, x) = a f (t, x) (K - C (f) (t, x))

(4)

where t denotes the time,

x \in Ω

a morphological trait (Ω is the morphological space) and

f (t, x)

is a population distribution on Ω.

The diffusion term $d Δ f (t, x)$ describes the spreading of the population in the morphological space due to mutations.

The term $a f (t, x) (K - C (f) (t, x))$ comes from the logistic equation, where a is a proliferation coefficient and K the limiting capacity of the environment. The operator $C (f) (t, x)$ describes a degenerate competition:

C (f) (t, x) = \int_{Ω} φ (x - x^{'}) f (t, x^{'}) d x^{'} = (φ * f) (t, x) .

(5)

It means that a morphology x competes with all the other morphologies $x^{'}$ , the function $φ (x - x^{'})$ describing the intensity of this competition. Since we assume that this intensity only depends on the difference $x - x^{'}$ , $C (f)$ is simply a convolution product. We restrict here to the one-dimensional case, and assume that $Ω = [0, L] \subset R$ . In this study we consider periodic boundary conditions, although they have few biological meaning, which allows a simple bifurcation analysis. Numerical simulations suggest that the results are essentially similar with homogeneous Neumann boundary conditions (not shown: a simulation with the same parameters as in Fig. 2 but with homogeneous Neumann boundary conditions gives a result almost identical to Fig. 2). The case of a bidimensional morphological space, more complex, will be studied in a future work.

Fig. 2
Evolutionary branching. Periodic boundary conditions. Parameters are a=1, K=1, b=3, d=0.05, L=40.

Here the competition kernel φ is defined by:

φ (y) = \frac{1}{2 b} 1_{[- b, b]} (y) = {\begin{matrix} \frac{1}{2 b} & if y \in [- b, b] \\ 0 & if y \notin [- b, b] \end{matrix}

(6)

Let us emphasize that the coefficients a, K and b describe ecological phenomena (proliferation and competition), whereas d quantifies an evolutionary phenomenon (spreading in morphological space due to mutations), which is likely to be much slower.

3 Stability analysis

Eqs. (4)–(6) have two homogeneous equilibria, $f \equiv 0$ and $f \equiv K$ . Linearizing this equation around $f \equiv K$ gives:

\frac{\partial f}{\partial t} (t, x) - d Δ f = - a K φ * f (t, x)

and applying the Fourier transform with respect to x:

\frac{\partial \hat{f}}{\partial t} (t, ξ) = - d ξ^{2} \hat{f} (t, ξ) - a K \hat{φ} (ξ) \hat{f} (t, ξ) = - (a K \hat{φ} (ξ) + d ξ^{2}) \hat{f} (t, ξ)

where ξ is the dual variable of x in the frequency space.

The stability of $f \equiv K$ with respect to a perturbation with frequency ξ is given by $(a K \hat{φ} (ξ) + d ξ^{2})$ : it is stable if $Re (a K \hat{φ} (ξ) + d ξ^{2}) 0$ and unstable otherwise.

For φ defined by Eq. (6):

\hat{φ} (ξ) = \frac{\sin (b ξ)}{b ξ}

Hence, denoting:

p_{c} = \max_{ξ \in [0, + \infty [} (- \frac{\sin (b ξ)}{{(b ξ)}^{3}})

we can state the following preparation.

Proposition

The homogeneous equilibrium $f \equiv K$ of Eqs.(4)–(6)is linearly stable if the bifurcation parameter:

p = \frac{d}{a K b^{2}}

is larger than the critical value

p_{c}

, and unstable otherwise.

The critical value $p_{c}$ is approximately 0.01. The stability result means that if the evolutionary parameter d is small enough compared to the ecological parameters a, K and b (which means that evolutionary changes are slow compared to ecological ones), an inhomogeneous structure will emerge and the population will self-organize.

This case is presented in Fig. 1. The initial condition is the equilibrium $f \equiv K$ slightly perturbed and an inhomogeneous structure of given frequency emerges.

It is a new mechanism of self-organization, different from Turing structures (see [5]). Indeed, for Turing structures to appear, two populations are needed (an activator competing with an inhibitor), whereas in the present mechanism, the structure emerges due to the competition inside a single population. Moreover, this mechanism is not a diffusion-driven instability as Turing's, and it is actually possible in the absence of diffusion.

4 Darwin's divergence principle

Under the conditions of self-organization presented in Section 3, an initially monomorphic population will undergo several successive branchings to become polymorphic. According to the numerical simulations, this polymorphic population is a stable asymptotic equilibrium: see Fig. 2, where the parameters are the same as in Fig. 1, except that the morphospace is larger $(L = 40)$ , and that the initial condition is different (the population is initially monomorphic). This monomorphic population first proliferates, but then it experiences an intense competition, which is favorable to its most different descendants:

“the more diversified these descendants become, the better will be their chance of succeeding in the battle of life. Thus the small differences distinguishing varieties of the same species will steadily tend to increase till they come to equal the greater differences between species of the same genus, or even of distinct genera.” (Darwin [6])

Darwin designates this principle by the terms “divergence of characters” and considers it as a fundamental mechanism explaining the production of new lineages.

5 Asymmetric competition

Assume now that φ is given by:

φ (y) = \frac{1}{2 b} 1_{[- b + δ, b + δ]} (y)

In this case

Re (\hat{φ} (ξ)) = \cos (δ ξ) \frac{\sin (b ξ)}{b ξ}

and the critical value of the bifurcation parameter p is now:

p_{c} = \max_{ξ \in [0, + \infty [} (- \cos (δ ξ) \frac{\sin (b ξ)}{{(b ξ)}^{3}})

As in the symmetric case, for $p p_{c}$ , a monomorphic population undergoes several successive branchings and splits into several subpopulations. Then, numerical simulations suggest that these subpopulations all move in the direction of smallest competition (see Fig. 3).

Finally, numerical simulations suggest that when the bifurcation parameter p tends to zero, the solution converges to a sum of Dirac distributions moving in the morphological space in the direction of smallest competition. The analytical determination of the velocity of this movement will be the subject of a future work [7]. Note that the usual travelling wave theory for the Fisher–KPP equation [8,9] cannot be used directly here due to the destabilizing effect of the competition term (5) with the kernel (6), and the lack of $L^{\infty}$ bound of the solution.